The Important Role of Cosmic-Ray Re-Acceleration
Abstract
1. Introduction
2. The Re-Acceleration Contribution
2.1. The LIS Spectrum from Voyager 1
2.2. Stochastic Re-Acceleration
2.3. Diffusive Shock Re-Acceleration at the Source
3. A DSRA Model
3.1. Re-Acceleration and Acceleration
- enhancement of particle momentum up to a maximum value dependent on time scales of the system (SNR age, acceleration time, energy losses);
- hardening of parent spectra steeper than
3.2. Crushed Cloud Presence
- Galactic Cosmic Rays are re-accelerated by first order Fermi energization mechanism in the interaction region between shock and its environment. Their spectrum, if steeper than the slope due to shock compression ratio, will become hard as . Initial density of the upstream medium, , is compressed of a factor ;
- in the right conditions, freshly accelerated particles can be injected at the shock through the first order Fermi mechanism;
- with sufficiently high density, a thin adiabatic shell forms behind the shock. There, energized particles undergo to a further compression before escape, with a consequent enhancement of their energy. The density is enhanced by a further factor s.
3.3. Energy Losses
3.4. -Ray Emission
4. Two Important Cases: A Supernova Remnants and an OB Star Wind
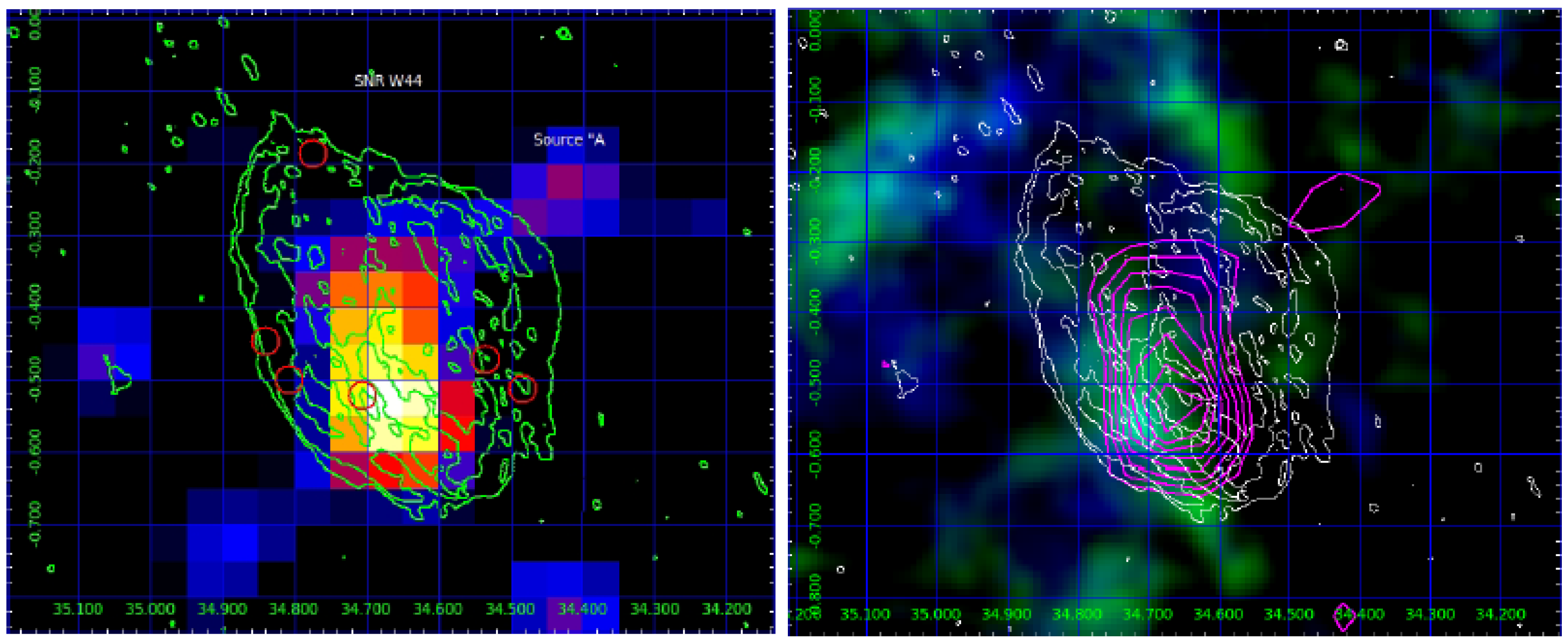
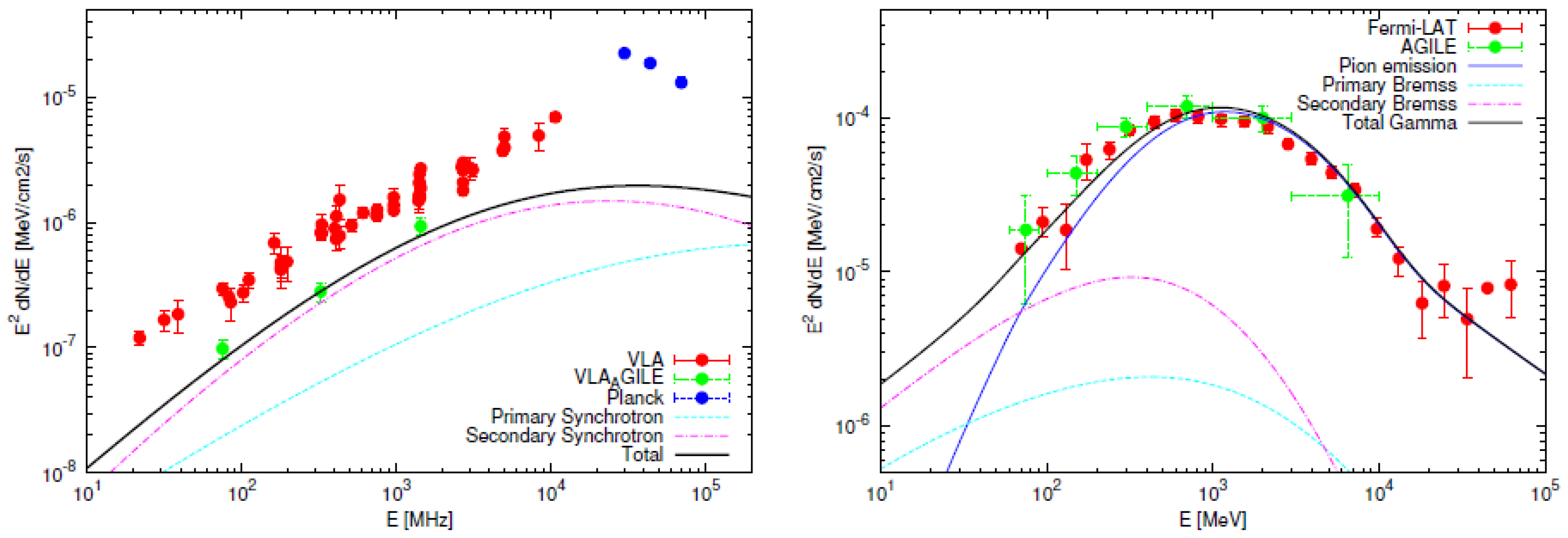
4.1. The Supernova Remnant W44
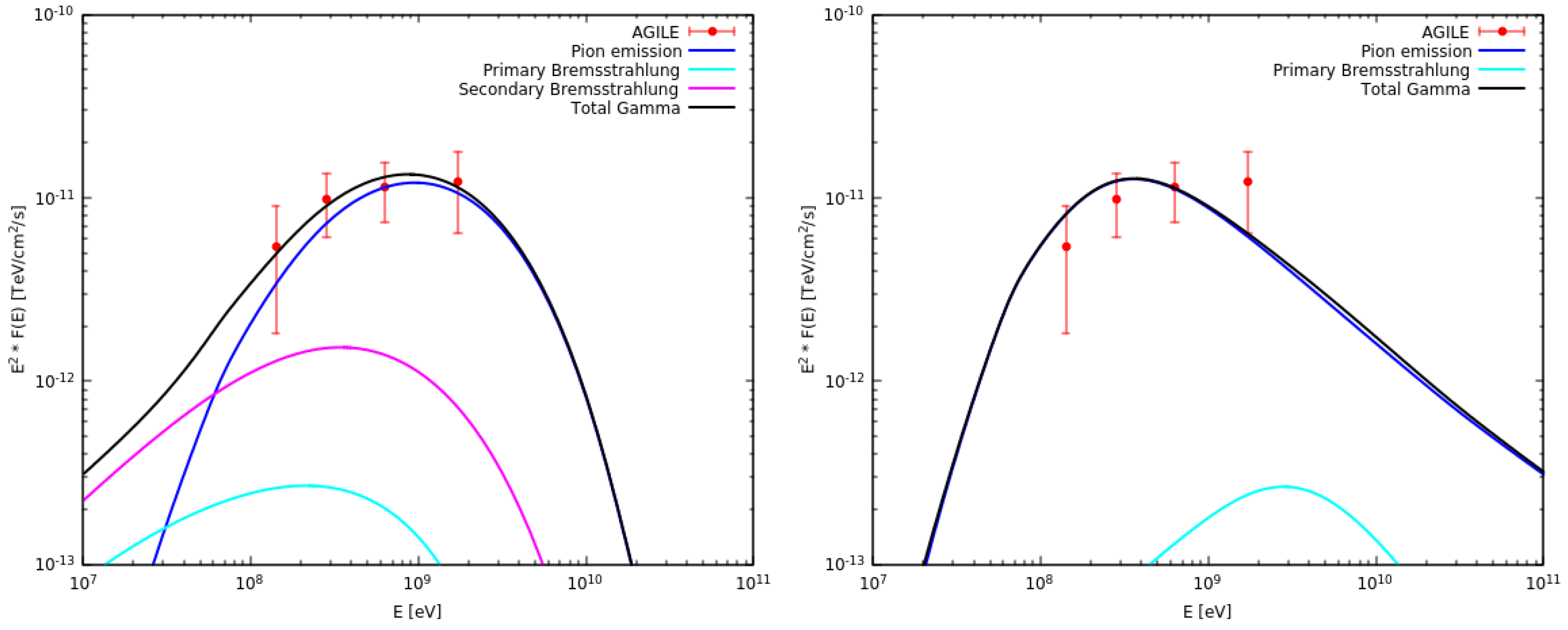
4.2. The -Ori Wind
5. Conclusions
Funding
Conflicts of Interest
References
- Amato, E. The origin of galactic cosmic rays. Int. J. Mod. Phys. D 2014, 23. [Google Scholar] [CrossRef]
- Blasi, P. The origin of galactic cosmic rays. Astron. Astrophys. 2013, 21, 70. [Google Scholar] [CrossRef]
- De Mitri, I. Measurement of the Cosmic Ray Energy Spectrum with ARGO-YBJ. In Proceedings of the Frontier Research in Astrophysics, Mondello, Palermo, Italy, 26–31 May 2014. [Google Scholar]
- Huang, J. Primary proton and helium spectra at energy range from 50 TeV to 1015 eV observed with (YAC-I + Tibet-III) hybrid experiment. In Proceedings of the 33th ICRC, Rio De Janeiro, Brazil, 2–9 July 2013; p. 1047. [Google Scholar]
- Apel, W.; Arteaga-Velzquez, J.C.; Bekk, K.; Bertaina, M.; Blumer, J.; Bozdog, H.; Brancus, I.M.; Cantoni, E.; Chiavassa, A.; Cossavella, F.; et al. Ankle-like feature in the energy spectrum of light elements of cosmic rays observed with KASCADE-Grande. Phys. Rev. 2013, 87, 1101. [Google Scholar] [CrossRef]
- Cardillo, M.; Amato, E.; Blasi, P. On the Cosmic Ray spectrum from type II supernovae expanding in their red giant presupernova wind. Astrop. Phys. 2015, 69, 1–10. [Google Scholar] [CrossRef]
- Adriani, O.; Barbarino, G.C.; Bazilevskaya, G.A.; Bellotti, R.; Boezio, M.; Bogomolov, E.A.; Bonechi, L.; Bongi, M.; Bonvicini, V.; Bottai, S.; et al. An anomalous positron abundance in cosmic rays with energies 1.5–100 gev. Nature 2009, 458, 607–609. [Google Scholar] [CrossRef] [PubMed]
- Adriani, O.; Barbarino, G.C.; Bazilevskaya, G.A.; Bellotti, R.; Boezio, M.; Bogomolov, E.A.; Bonechi, L.; Bongi, M.; Bonvicini, V.; Borisov, S.; et al. PAMELA Measurements of Cosmic-Ray Proton and Helium Spectra. Science 2011, 332, 69. [Google Scholar] [CrossRef] [PubMed]
- Aguilar, M.; Alberti, G.; Alpat, B.; Alvino, A.; Ambrosi, G.; Andeen, K.; Anderhub, H.; Arruda, L.; Azzarello, P.; Bachlechner, A.; et al. First Result from the Alpha Magnetic Spectrometer on the International Space Station: Precision Measurement of the Positron Fraction in Primary Cosmic Rays of 0.5–350 GeV. Phys. Rev. Lett. 2013, 110. [Google Scholar] [CrossRef]
- Aguilar, M.; Aisa, D.; Alvino, A.; Ambrosi, G.; Andeen, K.; Arruda, L.; Attig, N.; Azzarello, P.; Bachlechner, A.; Barao, F.; et al. Electron and Positron Fluxes in Primary Cosmic Rays Measured with the Alpha Magnetic Spectrometer on the International Space Station. Phys. Rev. Lett. 2014, 113, 121102. [Google Scholar] [CrossRef]
- Aguilar, M.; Aisa, D.; Alpat, B.; Alvino, A.; Ambrosi, G.; Andeen, K.; Arruda, L.; Attig, N.; Azzarello, P.; Bachlechner, A.; et al. Precision Measurement of the Proton Flux in Primary Cosmic Rays from Rigidity 1 GV to 1.8 TV with the Alpha Magnetic Spectrometer on the International Space Station. Phys. Rev. Lett. 2015, 114, 171103. [Google Scholar] [CrossRef]
- Aguilar, M.; Aisa, D.; Alpat, B.; Alvino, A.; Ambrosi, G.; Andeen, K.; Arruda, L.; Attig, N.; Azzarello, P.; Bachlechner, A.; et al. Precision Measurement of the Helium Flux in Primary Cosmic Rays of Rigidities 1.9 GV to 3 TV with the Alpha Magnetic Spectrometer on the International Space Station. Phys. Rev. Lett. 2015, 115, 211101. [Google Scholar] [CrossRef] [PubMed]
- Aloisio, R.; Blasi, P. Propagation of galactic cosmic rays in the presence of self-generated turbulence. J. Cosmol. Astropart. Phys. 2013, 7, 001. [Google Scholar] [CrossRef]
- Blasi, P.; Amato, E.; Serpico, P.D. Spectral breaks as a signature of cosmic-ray induced turbulence in the galaxy. Phys. Rev. Lett. 2012, 109, 061101. [Google Scholar] [CrossRef]
- Kachelriess, M.; Ostapchenko, S. Deriving the cosmic ray spectrum from gamma-ray observations. Phys. Rev. D 2012, 86, 4. [Google Scholar] [CrossRef]
- Neronov, A.; Semikoz, D.V.; Taylor, A.M. Low-Energy Break in the Spectrum of Galactic Cosmic Rays. Phys. Rev. Lett. 2012, 108, 051105. [Google Scholar] [CrossRef]
- Tomassetti, N. Origin of the Cosmic-Ray Spectral Hardening. Astrophys. J. Lett. 2012, 752, L13. [Google Scholar] [CrossRef]
- Thoudam, S.; Hörandel, J.R. Nearby supernova remnants and the cosmic-ray spectral hardening at high energies. Mon. Not. R. Astron. Soc. 2012, 421, 1209–1214. [Google Scholar] [CrossRef]
- Thoudam, S.; Hörandel, J.R. Revisiting the hardening of the cosmic-ray energy spectrum at TeV energies. Mon. Not. R. Astron. Soc. 2013, 435, 2532–2542. [Google Scholar] [CrossRef]
- Fan, Y.Z.; Zhang, B.; Chang, J. Electron/positron Excesses in the Cosmic Ray Spectrum and Possible Interpretations. Int. J. Mod. Phys. D 2010, 19, 2011–2058. [Google Scholar] [CrossRef]
- Bucciantini, N.; Arons, J.; Amato, E. Modelling spectral evolution of pulsar wind nebulae inside supernova remnants. Mon. Not. R. Astron. Soc. 2011, 410, 381–398. [Google Scholar] [CrossRef]
- Tavani, M.; Barbiellini, G.; Argan, A.; Boffelli, F.; Bulgarelli, A.; Caraveo, P.; Cattaneo, P.W.; Chen, A.W.; Cocco, V.; Costa, E.; et al. The AGILE Mission. Astron. Astrophys. 2009, 502, 995–1013. [Google Scholar] [CrossRef]
- Atwood, W.B.; Abdo, A.A.; Ackermann, M.; Althouse, W.; Anderson, B.; Axelsson, M.; Baldini, L.; Ballet, J.; Band, D.L.; Barbiellini, G.; et al. The Large Area Telescope on the Fermi Gamma-Ray Space Telescope Mission. Astrophys. J. 2009, 697, 1071–1102. [Google Scholar] [CrossRef]
- Hinton, J.A. The status of the H.E.S.S. project. New Astron. Rev. 2004, 48, 331–337. [Google Scholar] [CrossRef]
- Ferenc, D. The MAGIC gamma-ray observatory. Nuc. Instr. Meth. Phys. Res. 2005, 553, 274–281. [Google Scholar] [CrossRef]
- Krennrich, F.; Bond, I.H.; Boyle, P.J.; Bradbury, S.M.; Buckley, J.H.; Carter-Lewis, D.; Celik, O.; Cui, W.; Daniel, M.; D’Vali, M.; et al. VERITAS: The Very Energetic Radiation Imaging Telescope Array System. New Astr. Rev. 2004, 48, 345–349. [Google Scholar] [CrossRef]
- Ackermann, M.; Ajello, M.; Allafort, A.; Baldini, L.; Ballet, J.; Barbiellini, G.; Baring, M.G.; Bastieri, D.; Bechtol, K.; Bellazzini, R.; et al. Detection of the Characteristic Pion-Decay Signature in Supernova Remnants. Science 2013, 339, 807–811. [Google Scholar] [CrossRef]
- Cardillo, M.; Tavani, M.; Giuliani, A.; Yoshiike, S.; Sano, H.; Fukuda, T.; Fukui, Y.; Castelletti, G.; Dubner, G. The supernova remnant W44: Confirmations and challenges for cosmic-ray acceleration. Astron. Astrophys. 2014, 565, A74. [Google Scholar] [CrossRef]
- Giuliani, A.; Cardillo, M.; Tavani, M.; Fukui, Y.; Yoshiike, S.; Torii, K.; Dubner, G.; Castelletti, G.; Barbiellini, G.; Bulgarelli, A.; et al. Neutral Pion Emission from Accelerated Protons in the Supernova Remnant W44. Astrophys. J. 2011, 742, 30–34. [Google Scholar] [CrossRef]
- Morlino, G.; Caprioli, D. Strong evidences of hadron acceleration in Tycho’s Supernova Remnant. Astron. Astrophys. 2012, 538, A81–95. [Google Scholar] [CrossRef]
- Malkov, M.A.; Diamond, P.H.; Sagdeev, R.Z. Mechanism for spectral break in cosmic ray proton spectrum of supernova remnant W44. NatCo 2011, 2, 194–198. [Google Scholar] [CrossRef][Green Version]
- Osborne, J.L.; Ptuskin, V.S. Cosmic-ray reacceleration in the interstellar medium. Sov. Astron. Lett. 1988, 14, 132. [Google Scholar]
- Drury, L.O.C.; Strong, A.W. Cosmic-ray reacceleration: A critical look. In Proceedings of the 34th International Cosmic Ray Conference (ICRC2015), The Hague, The Netherlands, 30 July–6 August 2015. [Google Scholar]
- Drury, L.O.C.; Strong, A.W. Power requirements for cosmic ray propagation models involving diffusive reacceleration; estimated and implications fot the damping of interstellar turbulence. Astron. Astrophys. 2017, 597, 117. [Google Scholar] [CrossRef]
- Cheng, K.S.; Chernyshov, D.O.; Dogiel, V.A.; Ko, C.M. Multi-wavelength emission from the Fermi bubble. III. Stochastic (Fermi) re-acceleration of relativistic electrons emitted by SNRs. Astrophys. J. 2015, 804, 135. [Google Scholar] [CrossRef]
- Blasi, P. On the spectrum of stable secondary nuclei in cosmic rays. Mon. Not. R. Astron. Soc. 2017, 471, 1662–1670. [Google Scholar] [CrossRef]
- Cardillo, M.; Amato, E.; Blasi, P. Supernova Remnant W44: A case of cosmic-ray reacceleration. Astron. Astrophys. 2016, 595, A58. [Google Scholar] [CrossRef]
- Lee, S.H.; Patnaude, D.J.; Raymond, J.C.; Nagataki, S.; Slane, P.O.; Ellison, D.C. Modeling bright γ-ray and radio emission at faust cloud shock. Astrophys. J. 2015, 206, 71. [Google Scholar] [CrossRef]
- Tang, X.; Chevalier, R.A. Time-dependent Diffusive Shock Acceleration in Slow Supernova Remnant Shocks. Astrophys. J. 2015, 800, 103. [Google Scholar] [CrossRef]
- Uchiyama, Y.; Funk, S.; Katagiri, H.; Katsuta, J.; Lemoine-Goumard, M.; Tajima, H.; Tanaka, T.; Torres, D.F. Fermi Large Area Telescope Discovery of GeV Gamma-Ray Emission from the Vicinity of SNR W44. Astrophys. J. 2012, 749, L35–L39. [Google Scholar] [CrossRef]
- Caprioli, D.; Zhang, H.; Spitkovsky, A. Diffusive shock re-acceleration. J. Plasma Phys. 2018, 84, 3. [Google Scholar] [CrossRef]
- Cardillo, M.; Marchili, N.; Piano, G.; Giuliani, A.; Tavani, M.; Molinari, S. The Orion Region: Evidence of enhanced cosmic-ray density in a stellar wind forward shock interaction with a high density shell. Astron. Astrophys. 2019, 622, A57. [Google Scholar] [CrossRef]
- Fermi, E. On the origin of the Cosmic Radiation. Phys. Rev. 1949, 75, 1169–1174. [Google Scholar] [CrossRef]
- Potgieter, M.S.; Vos, E.E.; Nndanganeni, R.R.; Boezio, M.; Munini, R. A Very Local Interstellar Spectrum for Galactic Electrons. arXiv 2013, arXiv:1308.1666P. [Google Scholar]
- Webber, W.R.; McDonald, F.B. Recent Voyager 1 data indicate that on 25 August 2012 at a distance of 121.7 AU from the Sun, sudden and unprecedented intensity changes were observed in anomalous and galactic cosmic rays. Geophys. Res. Lett. 2013, 40, 1665–1668. [Google Scholar] [CrossRef]
- Bisschoff, D.; Potgieter, M.S. New local interstellar spectra for protons, helium and carbon derived from PAMELA and Voyager 1 observations. Astrophys. Space Sci. 2016, 361, 48. [Google Scholar] [CrossRef]
- Potgieter, M.S. Very Local Interstellar Spectra for Galactic Electrons, Protons and Helium. Braz. J. Phys. 2014, 44, 581–588. [Google Scholar] [CrossRef]
- Thornbury, A.; Drury, L.O. Power requirements for cosmic ray propagation models involving re-acceleration and a comment on second-order Fermi acceleration theory. Mon. Not. R. Astron. Soc. 2014, 442, 3010–3012. [Google Scholar] [CrossRef]
- Heinbach, U.; Simon, M. Propagation of Galactic Cosmic Rays under diffusive reacceleration. Astrophys. J. 1995, 441, 209–221. [Google Scholar] [CrossRef]
- Strong, A.W.; Moskalenko, I.V. Propagation of Cosmic-Ray Nucleons in the Galaxy. Astrophys. J. 1998, 509, 212–228. [Google Scholar] [CrossRef]
- Aguilar, M.; Ali Cavasonza, L.; Ambrosi, G.; Arruda, L.; Attig, N.; Aupetit, S.; Azzarello, P.; Bachlechner, A.; Barao, F.; Barrau, A.; et al. Precision Measurement of the Boron to Carbon Flux Ratio in Cosmic Rays from 1.9 GV to 2.6 TV with the Alpha Magnetic Spectrometer on the International Space Station. Phys. Rev. Lett. 2016, 117, 231102. [Google Scholar] [CrossRef]
- Dobler, G.; Finkbeiner, D.P.; Cholis, I.; Slatyer, T.; Weiner, N. The Fermi Haze: A Gamma-ray Counterpart to the Microwave Haze. Astrophys. J. 2010, 717, 825–842. [Google Scholar] [CrossRef]
- Su, M.; Slatyer, T.R.; Finkbeiner, D.P. Giant Gamma-ray Bubbles from Fermi-LAT: Active Galactic Nucleus Activity or Bipolar Galactic Wind? Astrophys. J. 2010, 724, 1044–1082. [Google Scholar] [CrossRef]
- Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Atrio-Barandela, F.; Aumont, J.; Baccigalupi, C.; Balbi, A.; Banday, A.J.; Barreiro, R.B.; et al. Planck intermediate results. IX. Detection of the Galactic haze with Planck. Astron. Astrophys. 2013, 554, 139. [Google Scholar] [CrossRef]
- Bloemen, J.B.G.M.; Dogiel, V.A.; Dorman, V.L.; Ptuskin, V.S. Galactic diffusion and wind models of cosmic-ray transport. I—Insight from CR composition studies and gamma-ray observations. Astron. Astrophys. 1993, 267, 372–387. [Google Scholar]
- Breitschwerdt, D.; Dogiel, V.A.; Völk, H.J. The gradient of diffuse gamma-ray emission in the Galaxy. Astron. Astrophys. 2002, 385, 216–238. [Google Scholar] [CrossRef]
- Breitschwerdt, D.; McKenzie, J.F.; Völk, H.J. Galactic winds. I—Cosmic ray and wave-driven winds from the Galaxy. Astron. Astrophys. 1991, 245, 79–98. [Google Scholar]
- Mertsch, P.; Petrosian, V. The Fermi bubbles from stochastic acceleration of electrons in a Galactic outflow. Astron. Astrophys. 2018, 622, A203. [Google Scholar] [CrossRef]
- Jogler, T.; Funk, S. Revealing W51C as a cosmic ray source using Fermi-LAT data. Astrophys. J. 2016, 816, 100. [Google Scholar] [CrossRef]
- Uchiyama, Y.; Blandford, R.D.; Funk, S.; Tajima, H.; Tanaka, T. Gamma-ray Emission from Crushed Clouds in Supernova Remnants. Astrophys. J. 2010, 723L, L122–126. [Google Scholar] [CrossRef]
- Abdo, A.A.; Ackermann, M.; Ajello, M.; Baldini, L.; Ballet, J.; Barbiellini, G.; Baring, M.G.; Bastieri, D.; Baughman, B.M.; Bechtol, K.; et al. Gamma-Ray Emission from the Shell of Supernova Remnant W44 Revealed by the Fermi LAT. Science 2010, 327, 1103. [Google Scholar] [CrossRef]
- Blandford, R.D.; Cowie, L.L. Radio emission from supernova remnants in a cloudy interstellar medium. Astrophys. J. 1982, 260, 625–634. [Google Scholar] [CrossRef]
- Ackermann, M.; Ajello, M.; Allafort, A.; Antolini, E.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; Bechtol, K.; Bellazzini, R.; et al. Gamma-Ray observations of the Orion Molecular Clouds with the Fermi-Large Area Telescope. Astrophys. J. 2012, 756, 4. [Google Scholar] [CrossRef]
- Marchili, N.; Piano, G.; Cardillo, M.; Giuliani, A.; Molinari, S.; Tavani, M. A new gamma-ray source unveiled by AGILE in the region of Orion. Astron. Astrophys. 2018, 615, A82. [Google Scholar] [CrossRef]
- Yan, Q. CR nuclei measurements with AMS-02: Latest results and perspectives. In Proceedings of the XSCRC2017: Cross sections for Cosmic Rays, CERN, Geneva, Switzerland, 29–31 March 2017. [Google Scholar]
- Aloisio, R.; Blasi, P.; Serpico, P. Nonlinear cosmic ray Galactic transport in the light of AMS-02 and Voyager data. Astron. Astrophys. 2015, 583, A95. [Google Scholar] [CrossRef]
- Lagage, P.O.; Cesarsky, C.J. The maximum energy of cosmic rays accelerated by supernova shocks. Astron. Astrophys. 1983, 125, 249–257. [Google Scholar]
- Bell, A.R. Turbulent amplification of magnetic field and diffusive shock acceleration of cosmic rays. Mon. Not. R. Astron. Soc. 2004, 353, 550–558. [Google Scholar] [CrossRef]
- Caprioli, D.; Pop, A.; Spitkovsky, A. Simulations and theory of ion injection at nonrelativistic collisionless shocks. Astrophys. J. Lett. 2015, 798, L28. [Google Scholar] [CrossRef]
- Caprioli, D.; Spitkovsky, A. Simulations of Ion Acceleration at Non-relativistic Shocks. I. Acceleration Efficiency. Astrophys. J. 2014, 783, 91. [Google Scholar] [CrossRef]
- Blasi, P. Nonlinear shock acceleration in the presence of seed particles. Astrop. Phys. 2004, 21, 45–57. [Google Scholar] [CrossRef][Green Version]
- Crutcher, R.M. Magnetic Fields in Molecular Clouds: Observations Confront Theory. Astrophys. J. 1999, 520, 706–713. [Google Scholar] [CrossRef]
- Hollenbach, D.; McKee, C.F. Molecule Formation and Infrared Emission in Fast Interstellar Shocks. III. Results for J Shocks in Molecular Clouds. Astrophys. J. 1989, 342, 306–336. [Google Scholar] [CrossRef]
- Draine, B.T. Physics of the Interstellar and Intergalactic Medium; Princeton University Press: Princeton, NJ, USA, 2011; ISBN 978-0-691-12214-4. [Google Scholar]
- Kelner, S.R.; Aharonian, F.A.; Bugayov, V.V. Energy spectra of gamma rays, electrons, and neutrinos produced at proton-proton interactions in the very high energy regime. Phys. Rev. D 2006, 74, 3. [Google Scholar] [CrossRef]
- Ginburg, V.L. Elementary Processes for Cosmic Ray Astrophysics; Gordon and Breach Science Publishers: New York, NY, USA, 1969. [Google Scholar]
- Ptuskin, V.S.; Zirakashvili, V.N. Limits on diffusive shock acceleration in supernova remnants in the presence of cosmic-ray streaming instability and wave dissipation. Astron. Astrophys. 2003, 403, 1–10. [Google Scholar] [CrossRef]
- Grenier, I.A.; Casandjian, J.-M.; Terrier, R. Unveiling Extensive Clouds of Dark Gas in the Solar Neighborhood. Science 2005, 307, 1292–1295. [Google Scholar] [CrossRef] [PubMed]
- Castelletti, G.; Dubner, G.; Brogan, C.; Kassim, N.E. The low-frequency radio emission and spectrum of the extended SNR W44: New VLA observations at 74 and 324 MHz. Astron. Astrophys. 2007, 471, 537–549. [Google Scholar] [CrossRef]
- Claussen, M.J.; Frail, D.A.; Goss, W.M.; Gaume, R.A. Polarization observations of 1720 MHz OH masers toward the three supernova remnants W28, W44, and IC 443. Astrophys. J. 1997, 489, 143–159. [Google Scholar] [CrossRef]
- Drury, L.O.C.; Duffy, P.; McKee, J.G. Limits on diffusive shock acceleration in dense and incompletely ionised media. Astron. Astrophys. 1996, 309, 1002–1010. [Google Scholar]
- Bally, J. Overview of the Orion Complex. Handbook of Star Forming Regions, Volume I: The Northern Sky ASP Monograph Publications. 2008. Available online: http://adsabs.harvard.edu/abs/2008hsf1.book..459B (accessed on 23 April 2019).
- Pillitteri, I.; Wolk, S.J.; Megeath, S.T. A Star-forming ring around κ-Ori 250 pc from the sun. Astrophys. J. Lett. 2016, 820, L28. [Google Scholar] [CrossRef]
- Caraveo, P.A.; Bennett, K.; Bignami, G.F.; Hermsen, W.; Kanbach, G.; Lebrun, F.; Masnou, J.L.; Mayer-Hasselwander, H.A.; Paul, J.A.; Sacco, B.; et al. COS-B observation of high-energy gamma-ray emission from the Orion cloud complex. Astron. Astrophys. 1980, 91, L3–L5. [Google Scholar]
- Digel, S.W.; Hunter, S.D.; Mukherjee, R. EGRET observations of gamma-ray emission from the interstellar gas in Orion. Astrophys. J. 1995, 441, 270–280. [Google Scholar] [CrossRef]
- Dame, T.M.; Hartmann, D.; Thaddeus, P. The Milky Way in Molecular Clouds: A New Complete CO Survey. Astrophys. J. 2001, 547, 792–813. [Google Scholar] [CrossRef]
- Casse, M.; Paul, J.A. Local Gamma Rays and Cosmic-Ray acceleration by supersonic stellar winds. Astrophys. J. 1980, 237, 236–243. [Google Scholar] [CrossRef]
- Cesarsky, C.J.; Montmerle, T. Gamma-Rays from Active regions in the Galaxy: The possible contribution of stellar winds. Space Sci. Rev. 1983, 36, 173–193. [Google Scholar] [CrossRef]
- Ip, W.-H. Cosmic ray acceleration by protostellar winds in the Orion molecular complex. Astron. Astrophys. 1995, 300, 283. [Google Scholar]
- Voelk, H.J.; Forman, M. Cosmic Rays and Gamma-rays from OB stars. Astrophys. J. 1982, 253, 188–198. [Google Scholar] [CrossRef]

© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cardillo, M. The Important Role of Cosmic-Ray Re-Acceleration. Galaxies 2019, 7, 49. https://doi.org/10.3390/galaxies7020049
Cardillo M. The Important Role of Cosmic-Ray Re-Acceleration. Galaxies. 2019; 7(2):49. https://doi.org/10.3390/galaxies7020049
Chicago/Turabian StyleCardillo, Martina. 2019. "The Important Role of Cosmic-Ray Re-Acceleration" Galaxies 7, no. 2: 49. https://doi.org/10.3390/galaxies7020049
APA StyleCardillo, M. (2019). The Important Role of Cosmic-Ray Re-Acceleration. Galaxies, 7(2), 49. https://doi.org/10.3390/galaxies7020049




