2D MHD Simulations of the State Transitions of X-Ray Binaries Taking into Account Thermal Conduction
Abstract
1. Introduction
2. Numerical Methods
2.1. Basic Equations
2.2. Initial Conditions
2.3. Grids and Boundary Conditions
3. Results
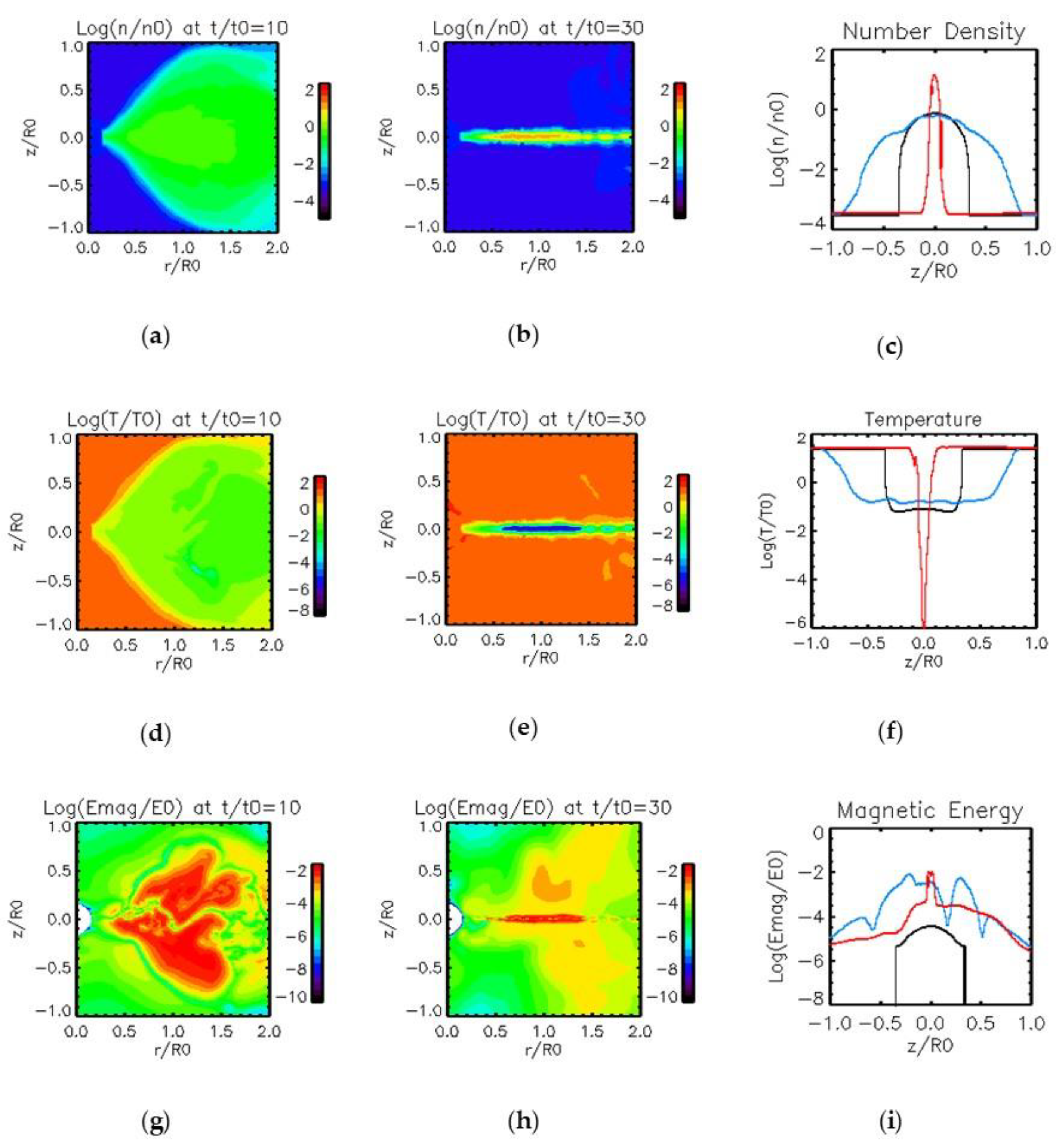
3.1. Results of Model 1
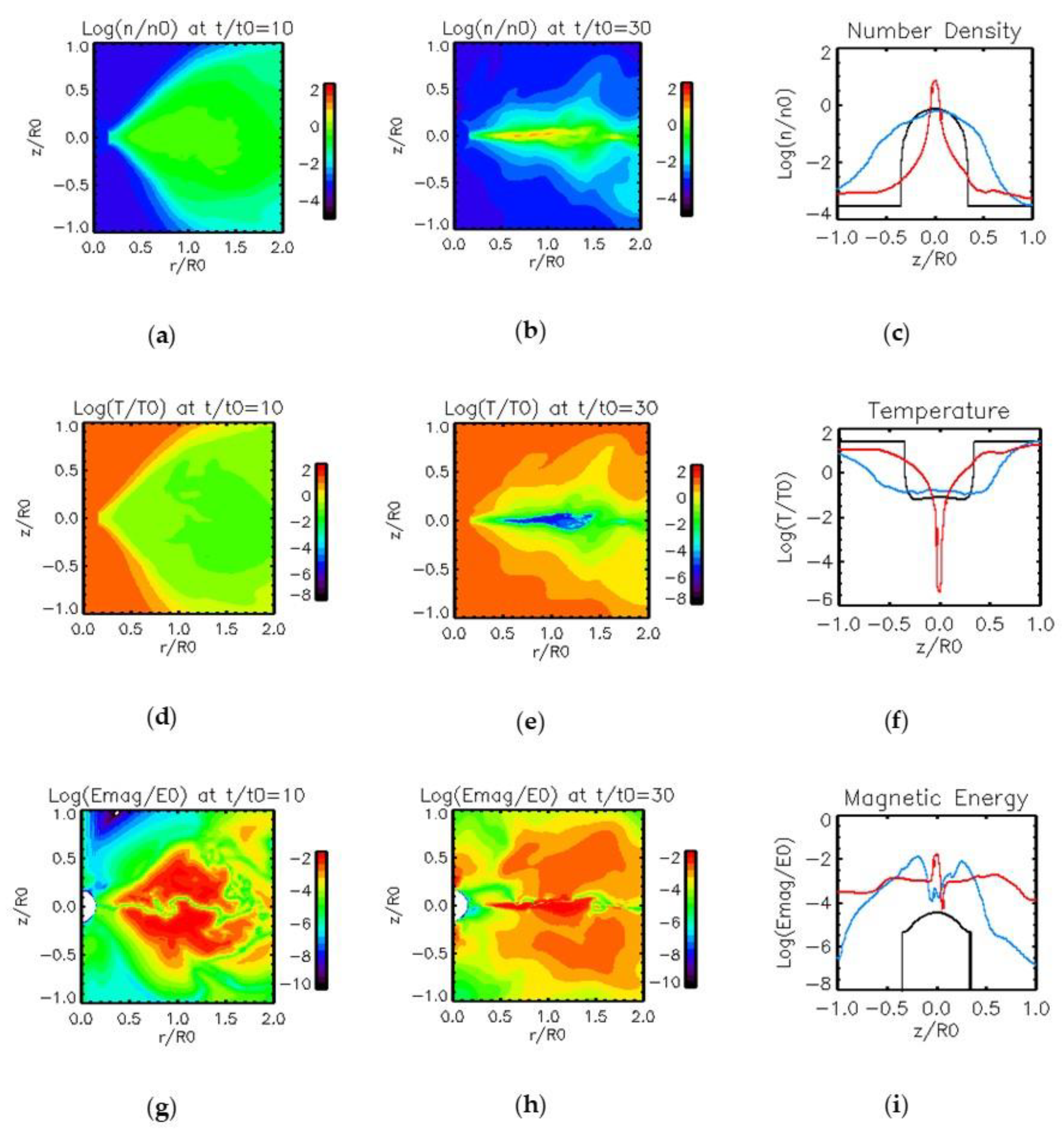
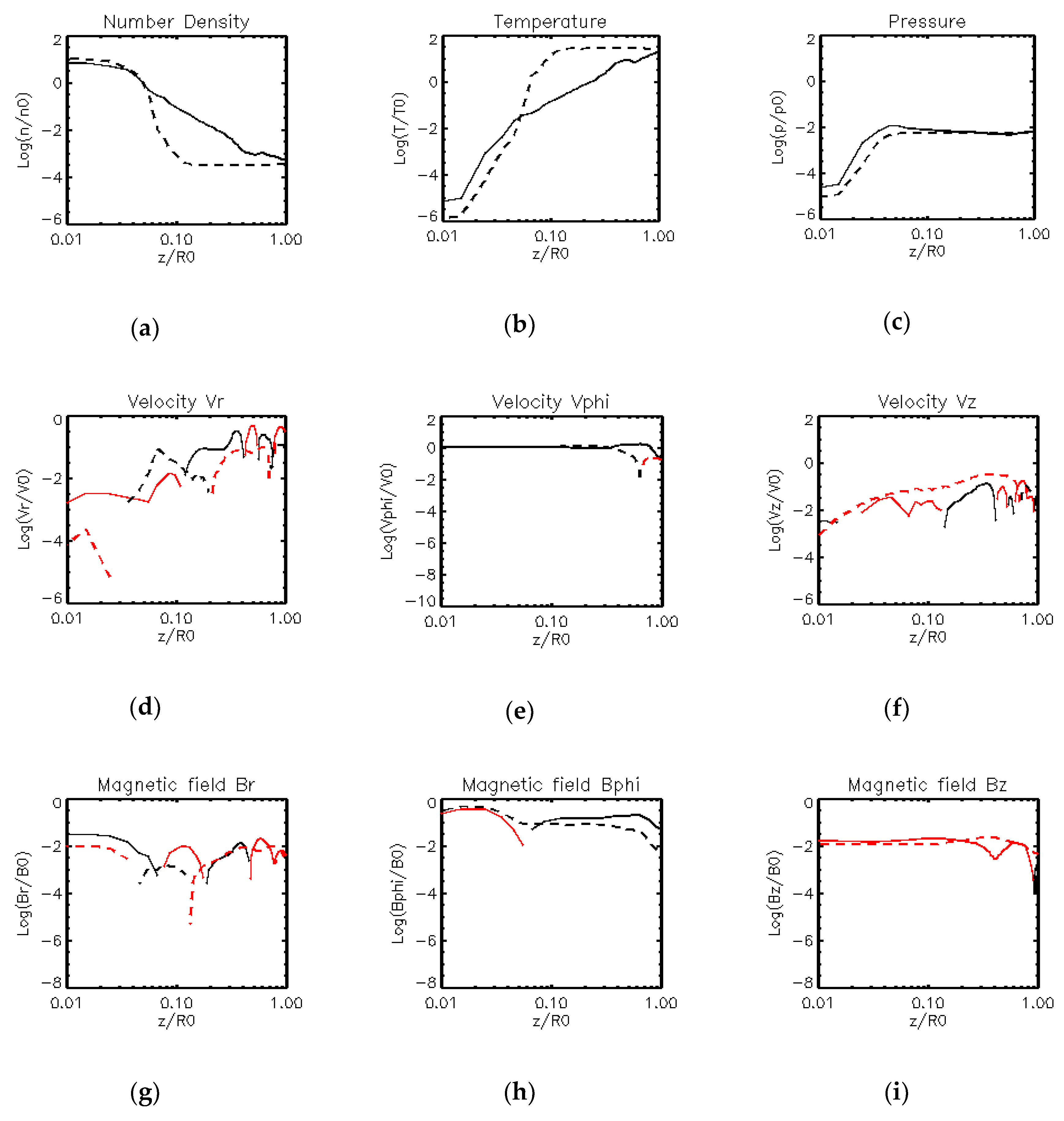
3.2. Results of Model 2
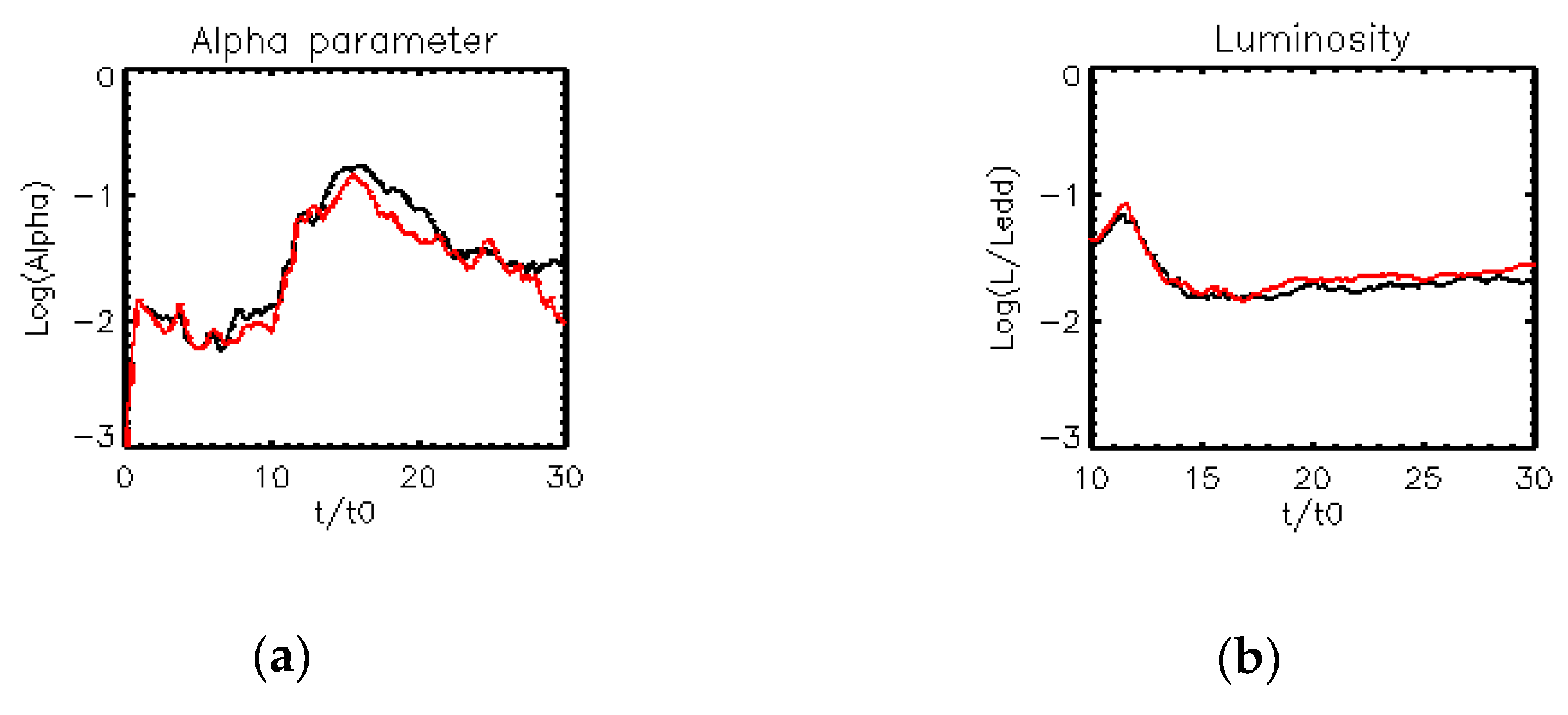
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Remillard, R.A.; McClintock, J.E. X-ray properties of black-hole binaries. Ann. Rev. Astron. Astrophys. 2006, 44, 49–92. [Google Scholar] [CrossRef]
- Narayan, R.; Yi, I. Advection-dominated accretion: Underfed black holes and neutron stars. Astrophys. J. 1995, 452, 710–735. [Google Scholar] [CrossRef]
- Abramowicz, M.A.; Chen, X.; Kato, S.; Lasota, J.P.; Regev, O. Thermal equilibria of accretion disks. Astrophys. J. 1995, 438, L37–L39. [Google Scholar] [CrossRef]
- Shakura, N.I.; Sunyaev, R.A. Black holes in binary systems. Observational Appearance. Astron. Astrophys. 1973, 24, 337–355. [Google Scholar]
- Machida, M.; Nakamura, K.E.; Matsumoto, R. Formation of magnetically supported disks during hard-to-soft transitions in black hole accretion flows. Publ. Astron. Soc. Jpn. 2006, 58, 193–202. [Google Scholar] [CrossRef]
- Das, U.; Sharma, P. Radiatively inefficient accretion flow simulations with cooling: Implications for black hole transitions. Mon. Not. R. Astron. Soc. 2013, 435, 2431–2444. [Google Scholar] [CrossRef]
- Wu, M.C.; Xie, F.G.; Yuan, Y.F.; Gan, Z. Hot Accretion flow with radiative cooling: State transitions in black hole X-ray binaries. Mon. Not. R. Astron. Soc. 2016, 459, 1543–1553. [Google Scholar] [CrossRef]
- Balbus, S.A.; Hawley, J.F. A powerful local shear instability in weakly magnetized disks I. Linear analysis. Astrophys. J. 1991, 376, 214–222. [Google Scholar] [CrossRef]
- Hawley, J.F.; Balbus, S.A. A powerful local shear instability in weakly magnetized disks II. Nonlinear evolution. Astrophys. J. 1991, 376, 223–233. [Google Scholar] [CrossRef]
- Yokoyama, T.; Shibata, K. Magnetic reconnection coupled with heat conduction. Astrophys. J. 1997, 474, L61–L64. [Google Scholar] [CrossRef]
- Yokoyama, T.; Shibata, K. A two-dimensional magnetohydrodynamic simulation of chromosphereic evaporation in a solar flare based on a magnetic reconnection model. Astrophys. J. 1998, 494, L113–L116. [Google Scholar] [CrossRef]
- Yokoyama, T.; Shibata, K. Magnetohydrodynamic simulation of a solar flare with chromosphereic evaporation effect based on the magnetic reconnection model. Astrophys. J. 2001, 549, 1160–1174. [Google Scholar] [CrossRef]
- Isobe, H.; Shibata, K.; Yokoyama, T.; Imanishi, K. Hydrodynamic Modeling of a Flare Loop Connecting the Accretion Disk and Central Core of Young Stellar Objects. Publ. Astron. Soc. Jpn 2003, 55, 967–980. [Google Scholar] [CrossRef]
- Meyer, F.; Meyer-Hofmeister, E. Accretion disk evaporation by a coronal siphon flow. Astron. Astrophys. 1994, 288, 175–182. [Google Scholar]
- Meyer-Hofmeister, E.; Meyer, F. The effect of heat conduction on the interaction of disk and corona around black holes. Astron. Astrophys. 2006, 449, 443–447. [Google Scholar]
- CANS (Coordinated Astronomical Numerical Software). Available online: http://www-space.eps.s.u-tokyo.ac.jp/~yokoyama/etc/cans/index-e.html (accessed on 31 October 2018).
- Van der Vorst, H.A. Bi-CGSTAB: A fast and smoothly converging variant of Bi-CG for the solution of Nonsysmmetric Linear Systems. SIAM J. Sci. Stat. Comput. 1992, 13, 631–644. [Google Scholar] [CrossRef]
- Templates. Available online: http://www.netlib.org/templates/double/ (accessed on 23 December 2018).
- Pacyńsky, B.; Wiita, P.J. Thick accretion disks and supercritical luminosities. Astron. Astrophys. 1980, 88, 23–31. [Google Scholar]
- Priest, E.R. Solar Magnetohydrodynamics; D. Reidel Publishing Company: Dordrecht, The Netherlands, 1982; pp. 84–91. ISBN 9027718834. [Google Scholar]
- Shukurov, A. Introduction to galactic dynamos. In Mathematical Aspects of Natural Dynamos; Dormy, E., Soward, A.M., Eds.; Taylor and Francis: New York, NY, USA, 2007; pp. 319–366. ISBN 9781420055269. [Google Scholar]
- Oliver, G.; Elstner, D.; Ziegler, U. Towards a hybrid dynamo model for the Milky Way. Astron. Astrophys. 2013, 560, A93. [Google Scholar]
- Papaloizou, J.C.B.; Pringle, J.E. The dynamical stability of differentially rotating discs with constant specific angular momentum. Mon. Not. R. Astron. Soc. 1984, 208, 721–750. [Google Scholar] [CrossRef]
- Field, G.B. Thermal instability. Astrophys. J. 1965, 142, 531–567. [Google Scholar] [CrossRef]
- Begelman, M.C.; McKee, C.F. Global effects of thermal conduction on two-phase media. Astrophys. J. 1990, 358, 375–391. [Google Scholar] [CrossRef]
| Variable | Quantity | Unit | Value |
|---|---|---|---|
| , | Length | ||
| , , | Velocity | ||
| Time | |||
| Density | |||
| Number Density | |||
| Temperature | |||
| Pressure | |||
| , , | Magnetic field |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nakamura, K.E.; Machida, M.; Matsumoto, R. 2D MHD Simulations of the State Transitions of X-Ray Binaries Taking into Account Thermal Conduction. Galaxies 2019, 7, 22. https://doi.org/10.3390/galaxies7010022
Nakamura KE, Machida M, Matsumoto R. 2D MHD Simulations of the State Transitions of X-Ray Binaries Taking into Account Thermal Conduction. Galaxies. 2019; 7(1):22. https://doi.org/10.3390/galaxies7010022
Chicago/Turabian StyleNakamura, Kenji E., Mami Machida, and Ryoji Matsumoto. 2019. "2D MHD Simulations of the State Transitions of X-Ray Binaries Taking into Account Thermal Conduction" Galaxies 7, no. 1: 22. https://doi.org/10.3390/galaxies7010022
APA StyleNakamura, K. E., Machida, M., & Matsumoto, R. (2019). 2D MHD Simulations of the State Transitions of X-Ray Binaries Taking into Account Thermal Conduction. Galaxies, 7(1), 22. https://doi.org/10.3390/galaxies7010022





