Two-Temperature Magnetohydrodynamics Simulations of Propagation of Semi-Relativistic Jets
Abstract
1. Introduction
2. Numerical Method
2.1. Basic Equations
2.2. Numerical Model
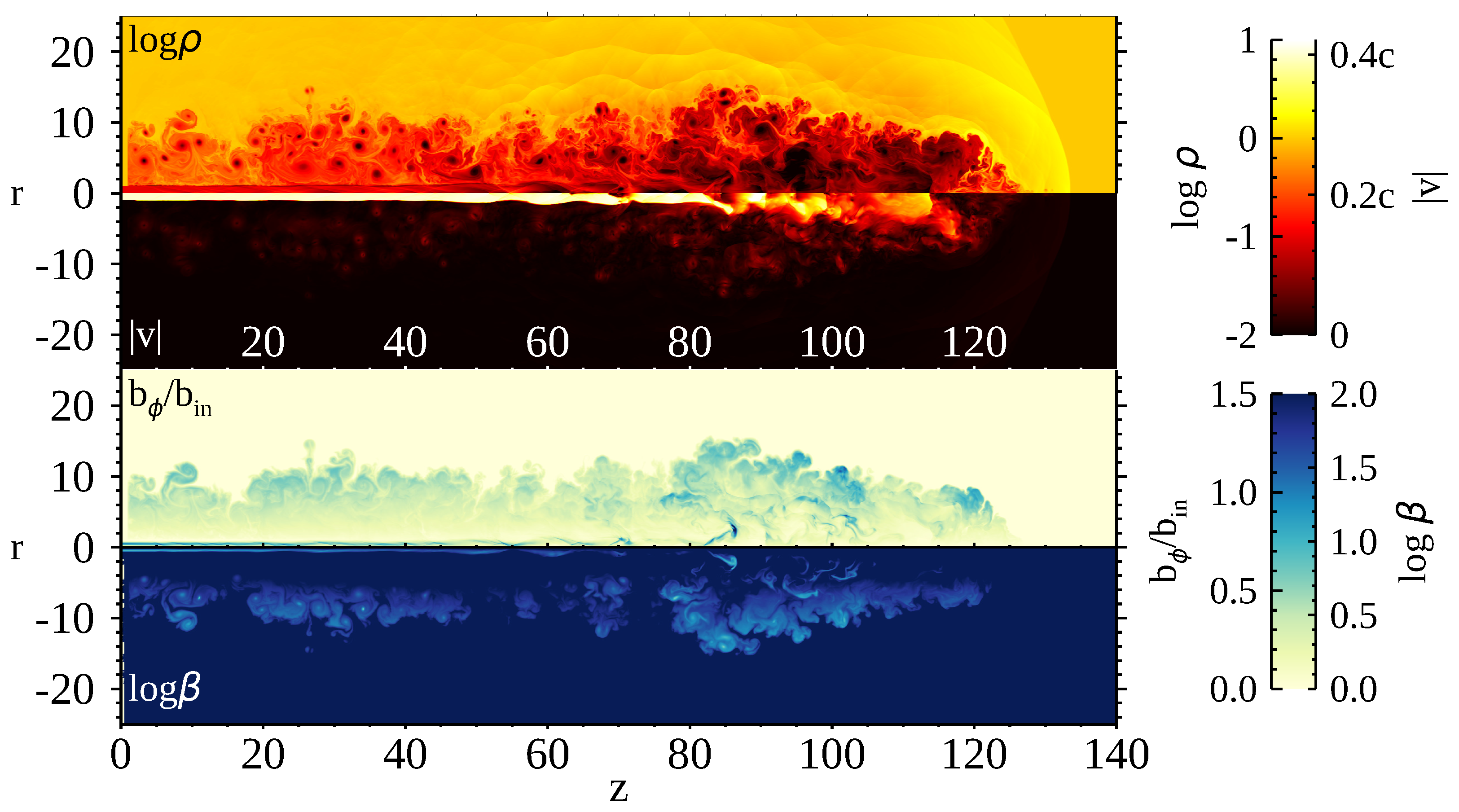
3. Numerical Results
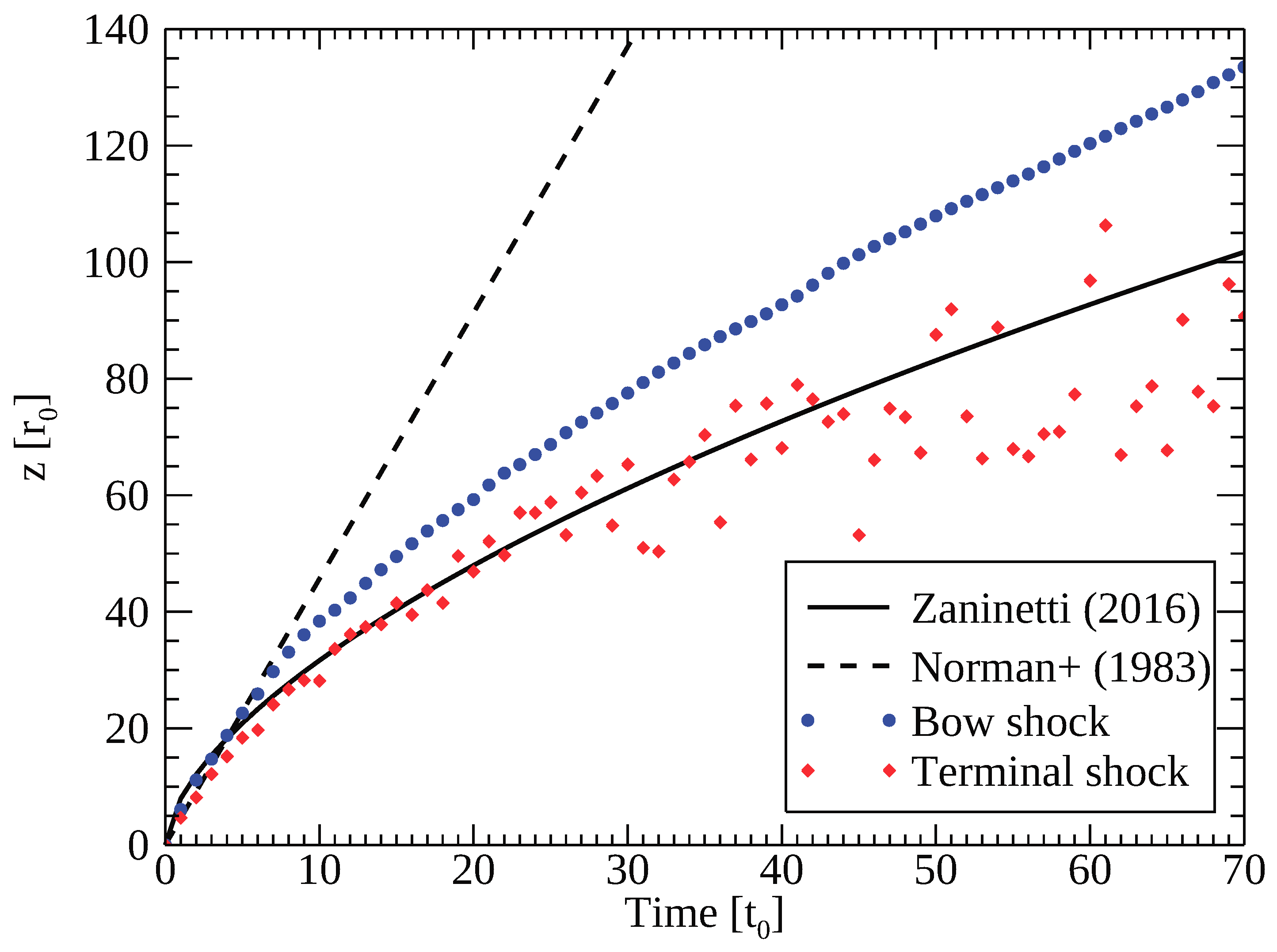
3.1. Jet Dynamics
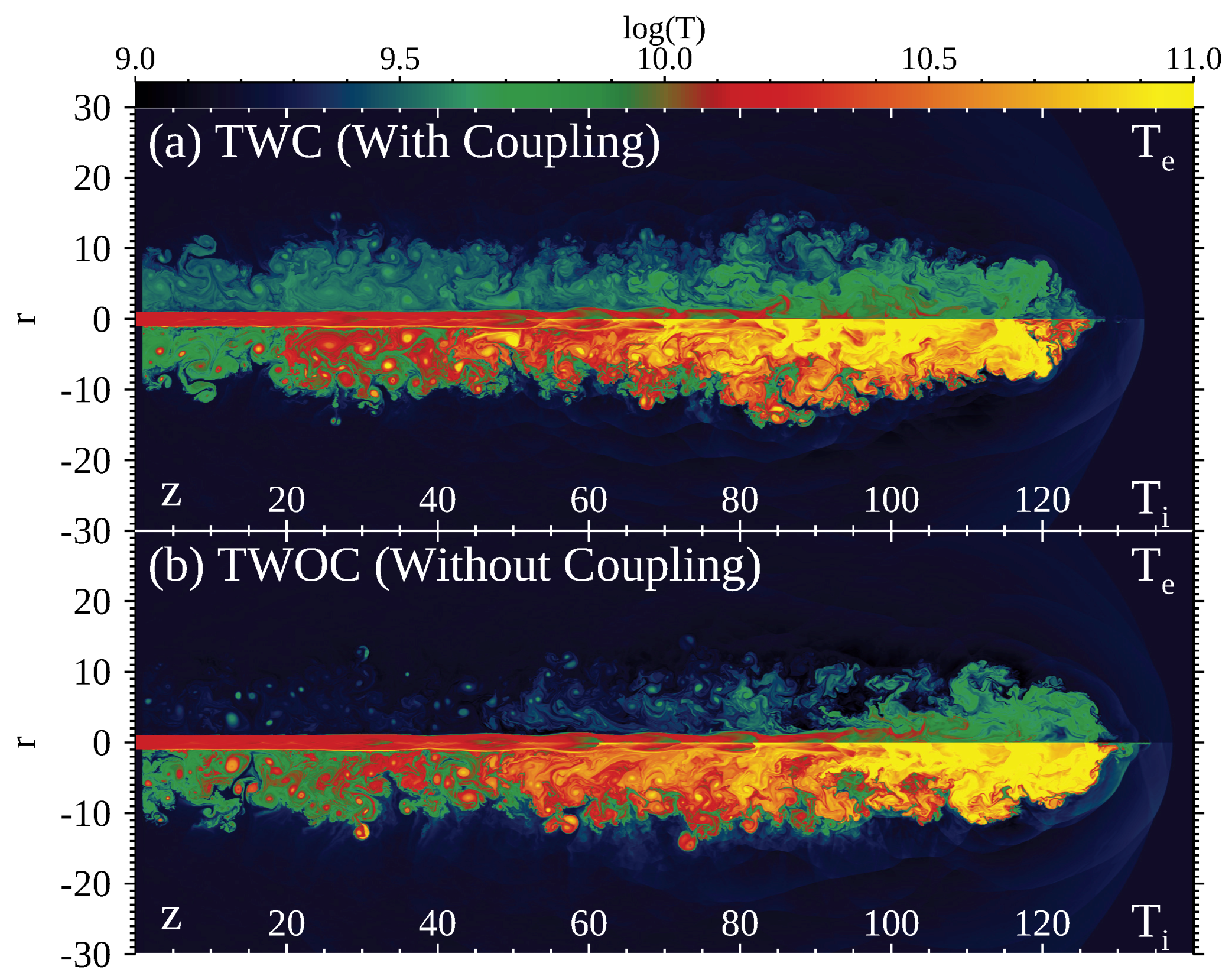
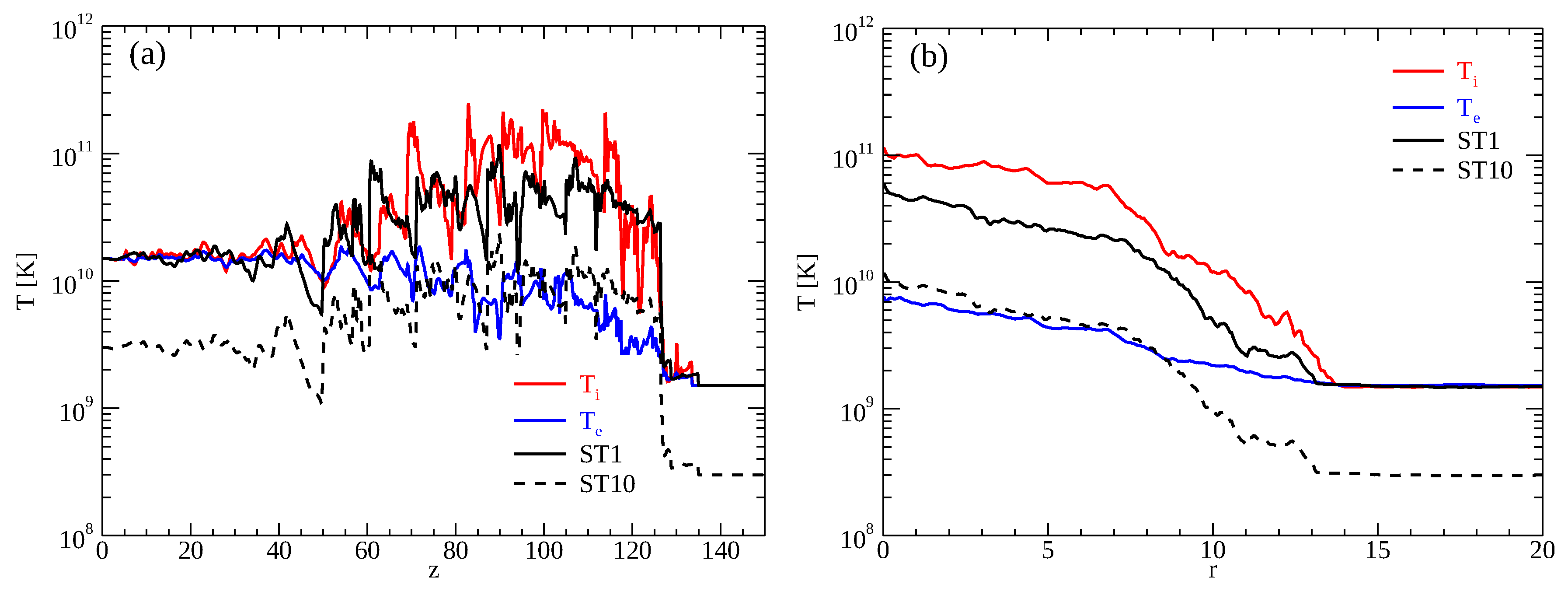
3.2. Electron and Ion Temperature Distributions
4. Discussion
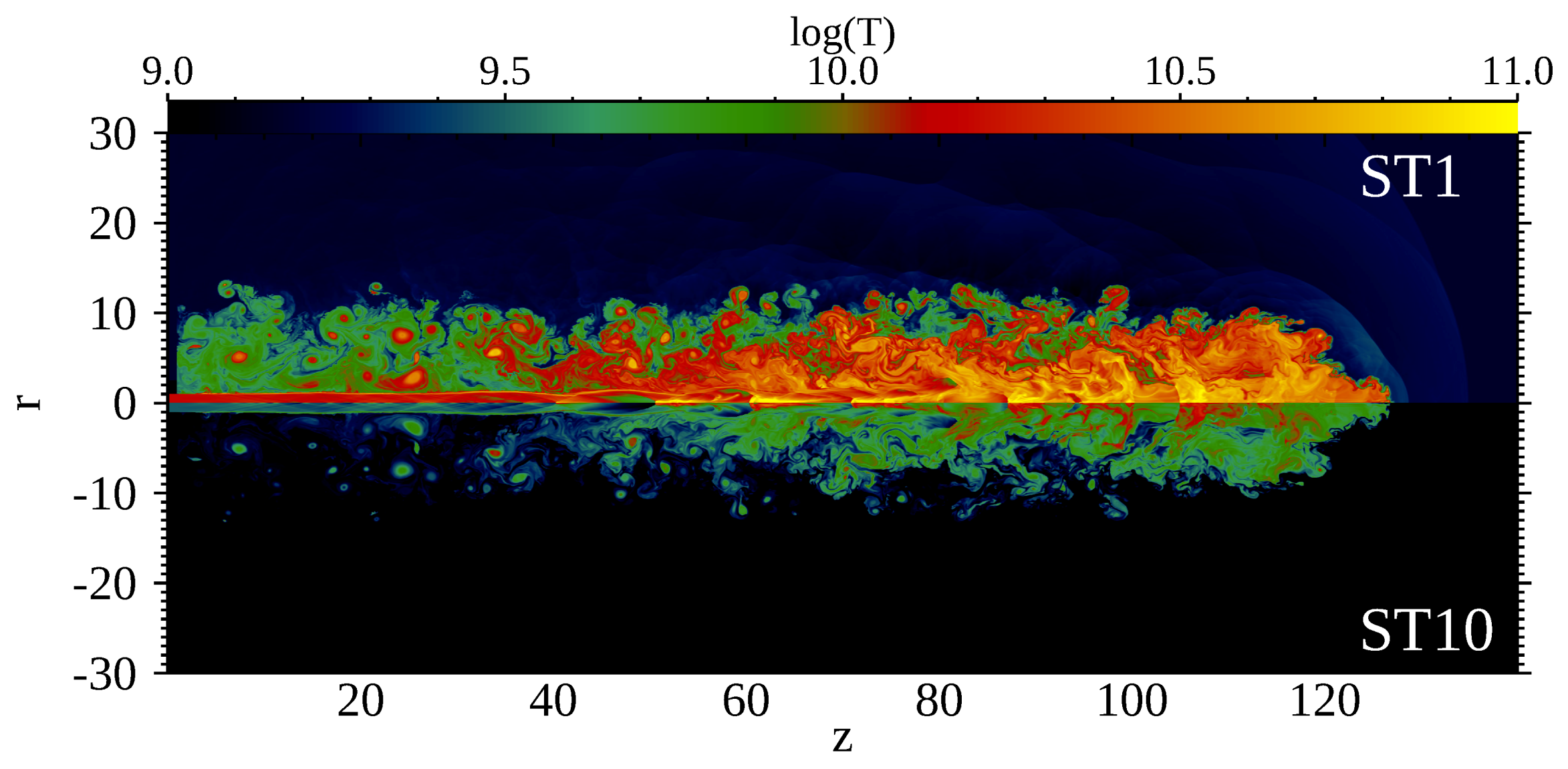
4.1. Comparison with Model ST
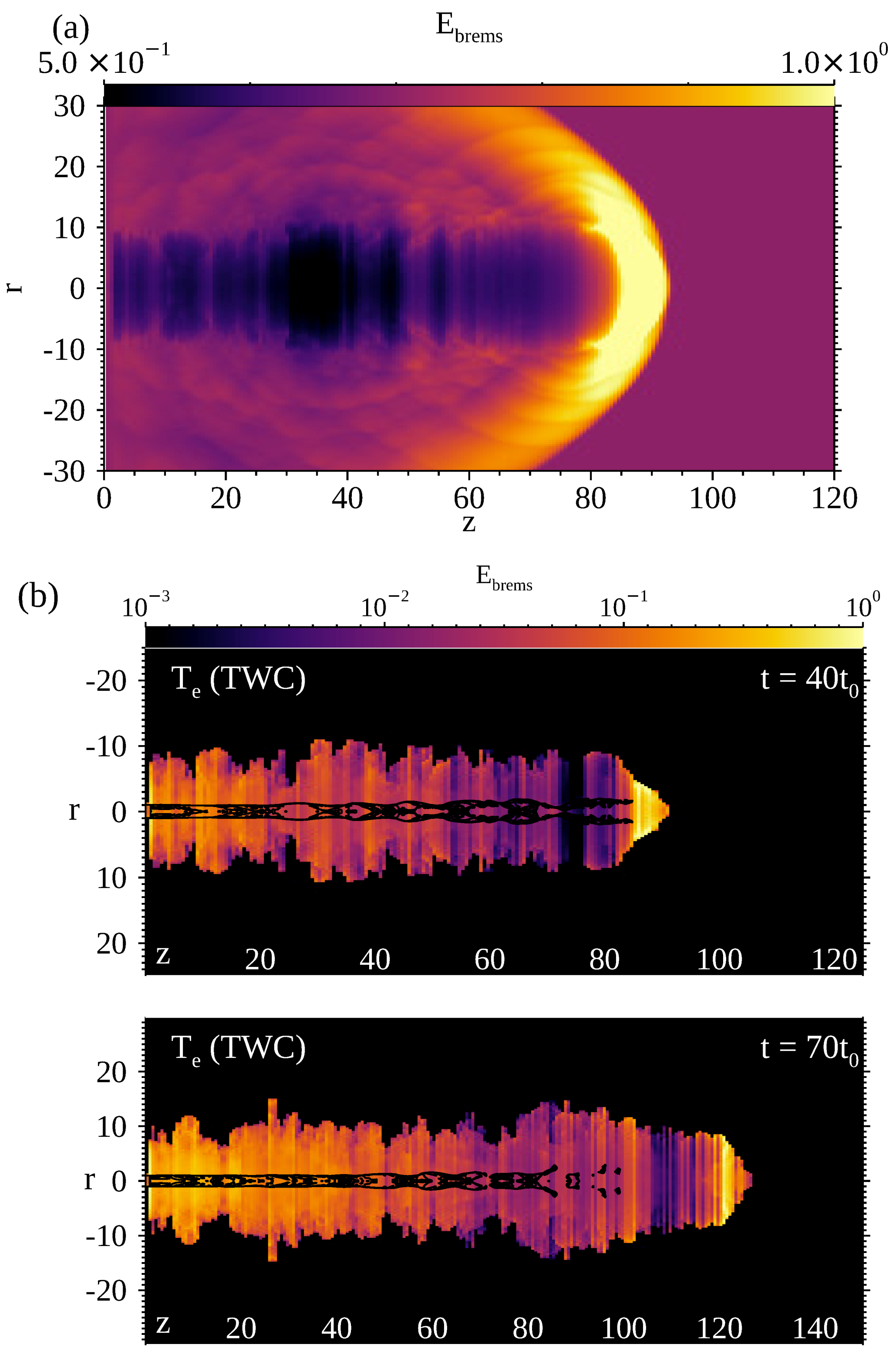
4.2. Bremstrahlung Images of Jets
4.3. Electron Heating through the Various Physical Mechanisms
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Conservation Form
References
- Marchenko, V.; Harris, D.E.; Ostrowski, M.; Stawarz, Ł.; Bohdan, A.; Jamrozy, M.; Hnatyk, B. Novel Analysis of the Multiwavelength Structure of the Relativistic Jet in Quasar 3C 273. Astrophys. J. 2017, 844, 11. [Google Scholar] [CrossRef]
- de Vries, M.N.; Wise, M.W.; Huppenkothen, D.; Nulsen, P.E.J.; Snios, B.; Hardcastle, M.J.; Birkinshaw, M.; Worrall, D.M.; Duffy, R.T.; McNamara, B.R. Detection of non-thermal X-ray emission in the lobes and jets of Cygnus A. High Energy Astrophys. Phenom. 2018, 478, 4010–4029. [Google Scholar] [CrossRef]
- Kino, M.; Kawakatu, N.; Ito, H.; Nagai, H. High energy emission from AGN cocoons in clusters of galaxies. Astron. Nachr. 2009, 330, 257. [Google Scholar] [CrossRef]
- Smith, D.A.; Wilson, A.S.; Arnaud, K.A.; Terashima, Y.; Young, A.J. A Chandra X-Ray Study of Cygnus A. III. The Cluster of Galaxies. Astrophys. J. 2002, 565, 195–207. [Google Scholar] [CrossRef]
- Norman, M.L.; Winkler, K.H.A.; Smarr, L.; Smith, M.D. Structure and dynamics of supersonic jets. Astron. Astrophys. 1982, 113, 285–302. [Google Scholar]
- Guo, F. On the Importance of Very Light Internally Subsonic AGN Jets in Radio-mode AGN Feedback. Astrophys. J. 2016, 826, 17. [Google Scholar] [CrossRef]
- Guo, F.; Duan, X.; Yuan, Y.F. Reversing cooling flows with AGN jets: Shock waves, rarefaction waves and trailing outflows. Mon. Not. R. Astron. Soc. 2018, 473, 1332–1345. [Google Scholar] [CrossRef]
- Zaninetti, L. Classical and relativistic conservation of momentum flux in radio-galaxies. Appl. Phys. Res. 2015, 7, 43–62. [Google Scholar] [CrossRef]
- Zaninetti, L. Classical and Relativistic Flux of Energy Conservation in Astrophysical Jets. J. High Energy Phys. Gravit. Cosmol. 2016, 1, 41–56. [Google Scholar] [CrossRef]
- Mizuta, A.; Yamada, S.; Takabe, H. Propagation and Dynamics of Relativistic Jets. Astrophys. J. 2004, 606, 804–818. [Google Scholar] [CrossRef]
- Sakemi, H.; Machida, M.; Akahori, T.; Nakanishi, H.; Akamatsu, H.; Kurahara, K.; Farnes, J. Magnetic field analysis of the bow and terminal shock of the SS 433 jet. Publ. Astron. Soc. Jpn. 2018, 70, 27. [Google Scholar] [CrossRef]
- Asada, K.; Inoue, M.; Uchida, Y.; Kameno, S.; Fujisawa, K.; Iguchi, S.; Mutoh, M. A Helical Magnetic Field in the Jet of 3C 273. Publ. Astron. Soc. Jpn. 2002, 54, L39–L43. [Google Scholar] [CrossRef]
- Komissarov, S.S. Numerical simulations of relativistic magnetized jets. Mon. Not. R. Astron. Soc. 1999, 308, 1069–1076. [Google Scholar] [CrossRef]
- Koessl, D.; Mueller, E.; Hillebrandt, W. Numerical simulations of axially symmetric magnetized jets. I–The influence of equipartition magnetic fields. II–Apparent field structure and theoretical radio maps. III–Collimation of underexpanded jets by magnetic fields. Astron. Astrophys. 1990, 229, 378–415. [Google Scholar]
- Lind, K.R.; Payne, D.G.; Meier, D.L.; Blandford, R.D. Numerical Simulations of Jets and Other Astrophysical Flows. Bull. Am. Astron. Soc. 1989, 21, 1158. [Google Scholar]
- Moll, R.; Spruit, H.C.; Obergaulinger, M. Kink instabilities in jets from rotating magnetic fields. Astron. Astrophys. 2008, 492, 621–630. [Google Scholar] [CrossRef]
- Mizuno, Y.; Lyubarsky, Y.; Nishikawa, K.I.; Hardee, P.E. Three-dimensional Relativistic Magnetohydrodynamic Simulations of Current-driven Instability. III. Rotating Relativistic Jets. Astrophys. J. 2012, 757, 16. [Google Scholar] [CrossRef]
- Jones, T.W.; Ryu, D.; Engel, A. Simulating Electron Transport and Synchrotron Emission in Radio Galaxies: Shock Acceleration and Synchrotron Aging in Axisymmetric Flows. Astrophys. J. 1999, 512, 105–124. [Google Scholar] [CrossRef]
- Aloy, M.A.; Müller, E.; Ibáñez, J.M.; Martí, J.M.; MacFadyen, A. Relativistic Jets from Collapsars. Astrophys. J. 2000, 531, L119–L122. [Google Scholar] [CrossRef]
- Nakamura, M.; Tregillis, I.L.; Li, H.; Li, S. A Numerical Model of Hercules A by Magnetic Tower: Jet/Lobe Transition, Wiggling, and the Magnetic Field Distribution. Astrophys. J. 2008, 686, 843–850. [Google Scholar] [CrossRef]
- Takizawa, M. A Two-Temperature Model of the Intracluster Medium. Astrophys. J. 1998, 509, 579–586. [Google Scholar] [CrossRef]
- Mahadevan, R.; Quataert, E. Are Particles in Advection-dominated Accretion Flows Thermal? Astrophys. J. 1997, 490, 605–618. [Google Scholar] [CrossRef]
- Eardley, D.M.; Lightman, A.P.; Shapiro, S.L. Cygnus X-1 - A two-temperature accretion disk model which explains the observed hard X-ray spectrum. Astrophys. J. 1975, 199, L153–L155. [Google Scholar] [CrossRef]
- Ressler, S.M.; Tchekhovskoy, A.; Quataert, E.; Chandra, M.; Gammie, C.F. Electron thermodynamics in GRMHD simulations of low-luminosity black hole accretion. Mon. Not. R. Astron. Soc. 2015, 454, 1848–1870. [Google Scholar] [CrossRef]
- Sa̧dowski, A.; Wielgus, M.; Narayan, R.; Abarca, D.; McKinney, J.C.; Chael, A. Radiative, two-temperature simulations of low-luminosity black hole accretion flows in general relativity. Mon. Not. R. Astron. Soc. 2017, 466, 705–725. [Google Scholar] [CrossRef]
- Chael, A.; Rowan, M.; Narayan, R.; Johnson, M.; Sironi, L. The role of electron heating physics in images and variability of the Galactic Centre black hole Sagittarius A*. Mon. Not. R. Astron. Soc. 2018, 478, 5209–5229. [Google Scholar] [CrossRef]
- Ryan, B.R.; Ressler, S.M.; Dolence, J.C.; Gammie, C.; Quataert, E. Two-temperature GRRMHD Simulations of M87. Astrophys. J. 2018, 864, 126. [Google Scholar] [CrossRef]
- Oda, H.; Machida, M.; Nakamura, K.E.; Matsumoto, R. Thermal Equilibria of Optically Thin, Magnetically Supported, Two-temperature, Black Hole Accretion Disks. Astrophys. J. 2010, 712, 639–652. [Google Scholar] [CrossRef]
- Stepney, S.; Guilbert, P.W. Numerical FITS to important rates in high temperature astrophysical plasmas. Mon. Not. R. Astron. Soc. 1983, 204, 1269–1277. [Google Scholar] [CrossRef]
- Dermer, C.D.; Liang, E.P.; Canfield, E. Luminosity enhancement factor for thermal Comptonization and the electron energy balance. Astrophys. J. 1991, 369, 410–421. [Google Scholar] [CrossRef]
- Matsumoto, Y.; Asahina, Y.; Kudoh, Y.; Kawashima, T.; Matsumoto, J.; Takahashi, H.R.; Minoshima, T.; Zenitani, S.; Miyoshi, T.; Matsumoto, R. Magnetohydrodynamic Simulation Code CANS+: Assessments and Applications. arXiv, 2016; arXiv:1611.01775. [Google Scholar]
- Miyoshi, T.; Kusano, K. An MHD Simulation of the Magnetosphere Based on the HLLD Approximate Riemann Solver; AGU Fall Meeting Abstracts; American Geophysical Union: Washington, DC, USA, 2005. [Google Scholar]
- Suresh, A.; Huynh, H.T. Accurate Monotonicity-Preserving Schemes with Runge Kutta Time Stepping. J. Comput. Phys. 1997, 136, 83–99. [Google Scholar] [CrossRef]
- Dedner, A.; Kemm, F.; Kröner, D.; Munz, C.D.; Schnitzer, T.; Wesenberg, M. Hyperbolic Divergence Cleaning for the MHD Equations. J. Comput. Phys. 2002, 175, 645–673. [Google Scholar] [CrossRef]
- Kudoh, Y.; Hanawa, T. Approximate Riemann solvers for the cosmic ray magnetohydrodynamical equations. Mon. Not. R. Astron. Soc. 2016, 462, 4517–4531. [Google Scholar] [CrossRef]
- Matsumoto, Y.; Amano, T.; Kato, T.N.; Hoshino, M. Stochastic electron acceleration during spontaneous turbulent reconnection in a strong shock wave. Science 2015, 347, 974–978. [Google Scholar] [CrossRef] [PubMed]
- Asahina, Y.; Ogawa, T.; Kawashima, T.; Furukawa, N.; Enokiya, R.; Yamamoto, H.; Fukui, Y.; Matsumoto, R. Magnetohydrodynamic Simulations of a Jet Drilling an H I Cloud: Shock Induced Formation of Molecular Clouds and Jet Breakup. Astrophys. J. 2014, 789, 79. [Google Scholar] [CrossRef]
- Norman, M.L.; Winkler, K.H.A.; Smarr, L. Propagation and morphology of pressure-confined supersonic jets. In Astrophysical Jets; Ferrari, A., Pacholczyk, A.G., Eds.; Astrophysics and Space Science Library: Berlin, Germany, 1983; Volume 103, pp. 227–250. [Google Scholar]
- Scheck, L.; Aloy, M.A.; Martí, J.M.; Gómez, J.L.; Müller, E. Does the plasma composition affect the long-term evolution of relativistic jets? Mon. Not. R. Astron. Soc. 2002, 331, 615–634. [Google Scholar] [CrossRef]
- Gallo, E.; Fender, R.; Kaiser, C.; Russell, D.; Morganti, R.; Oosterloo, T.; Heinz, S. A dark jet dominates the power output of the stellar black hole Cygnus X-1. Nature 2005, 436, 819–821. [Google Scholar] [CrossRef]
- Chael, A.; Narayan, R.; Johnson, M.D. Two-temperature, Magnetically Arrested Disc simulations of the jet from the supermassive black hole in M87. arXiv, 2018; arXiv:1810.01983. [Google Scholar]
- Howes, G.G. A prescription for the turbulent heating of astrophysical plasmas. Mon. Not. R. Astron. Soc. 2010, 409, L104–L108. [Google Scholar] [CrossRef]
- Rowan, M.E.; Sironi, L.; Narayan, R. Electron and Proton Heating in Transrelativistic Magnetic Reconnection. Astrophys. J. 2017, 850, 29. [Google Scholar] [CrossRef]
- Kawazura, Y.; Barnes, M.; Schekochihin, A.A. Thermal disequilibration of ions and electrons by collisionless plasma turbulence. arXiv, 2018; arXiv:1807.07702. [Google Scholar]
- Guo, X.; Sironi, L.; Narayan, R. Electron Heating in Low-Mach-number Perpendicular Shocks. I. Heating Mechanism. Astrophys. J. 2017, 851, 134. [Google Scholar] [CrossRef]
- Guo, X.; Sironi, L.; Narayan, R. Electron Heating in Low Mach Number Perpendicular Shocks. II. Dependence on the Pre-shock Conditions. Astrophys. J. 2018, 858, 95. [Google Scholar] [CrossRef]
| Parameter | Value |
|---|---|
| (= | 0.1 |
| 0.38 c | |
| 6 | |
| K | |
| K | |
| (= | 10 |
| Model Name | Approximation | Coulomb Coupling | Eqs. | |||
|---|---|---|---|---|---|---|
| TWC | Two-temperature | Yes | 5/3 | 4/3 | Self consistent | (1)–(5) |
| TWOC | Two-temperature | No | 5/3 | 4/3 | Self consistent | (1)–(5) |
| ST1 | Single-temperature | - | 5/3 | - | 1 | (1)–(4) |
| ST10 | Single-temperature | - | 5/3 | - | 10 * | (1)–(4) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ohmura, T.; Machida, M.; Nakamura, K.; Kudoh, Y.; Asahina, Y.; Matsumoto, R. Two-Temperature Magnetohydrodynamics Simulations of Propagation of Semi-Relativistic Jets. Galaxies 2019, 7, 14. https://doi.org/10.3390/galaxies7010014
Ohmura T, Machida M, Nakamura K, Kudoh Y, Asahina Y, Matsumoto R. Two-Temperature Magnetohydrodynamics Simulations of Propagation of Semi-Relativistic Jets. Galaxies. 2019; 7(1):14. https://doi.org/10.3390/galaxies7010014
Chicago/Turabian StyleOhmura, Takumi, Mami Machida, Kenji Nakamura, Yuki Kudoh, Yuta Asahina, and Ryoji Matsumoto. 2019. "Two-Temperature Magnetohydrodynamics Simulations of Propagation of Semi-Relativistic Jets" Galaxies 7, no. 1: 14. https://doi.org/10.3390/galaxies7010014
APA StyleOhmura, T., Machida, M., Nakamura, K., Kudoh, Y., Asahina, Y., & Matsumoto, R. (2019). Two-Temperature Magnetohydrodynamics Simulations of Propagation of Semi-Relativistic Jets. Galaxies, 7(1), 14. https://doi.org/10.3390/galaxies7010014





