Abstract
The search for periodic signals from blazars has become a widely discussed topic in recent years. In the scenario that such periodic changes originate from the innermost regions of blazars, the signals bear imprints of the processes occurring near the central engine, which are mostly inaccessible to our direct view. Such signals provide insights into various aspect of blazar studies, including disk-jet connection, magnetic-field configuration and, more importantly, strong gravity near the supermassive black holes and release of gravitational waves from binary supermassive-black-hole systems. In this work, we report the detection of a periodic signal in the radio light curve of blazar J1043+2408 spanning ∼10.5 years. We performed multiple methods of time-series analysis, namely, epoch folding, Lomb–Scargle periodogram, and discrete autocorrelation function. All three methods consistently revealed a repeating signal with a periodicity of ∼560 days. To robustly account for the red-noise processes usually dominant in the blazar variability and other possible artefacts, a large number of Monte Carlo simulations were performed. This allowed us to estimate high significance (99.9% local and 99.4% global) against possible spurious detection. As possible explanations, we discuss a number of scenarios, including binary supermassive-black-hole systems, Lense–Thirring precession, and jet precession.
1. Introduction
Blazars, a class of radio-loud active galactic nuclei (AGN), are the most energetic sources in the universe. The sources have relativistic jets beamed upon us that shine brightly in nonthermal emission, covering a wide electromagnetic spectrum—from radio to most energetic -rays. As jets accelerate matter with high speeds down the jet orientated close to the observer’s line of sight, relativistic effects become dominant, resulting in the Doppler-boosted emission that is highly variable over the entire electromagnetic spectrum [1]. The broadband spectral energy distribution (SED) of blazars can often be identified with a double-peaked feature in the frequency-flux plane. The lower peak, usually found between radio and X-ray, arises as a result of the synchrotron emission by energetic particles accelerating in the jet magnetic field, whereas the origin of the high-frequency component, extending from X-rays to TeV energies, is still a debated topic. In leptonic models, e.g., References [2,3], it results due to inverse-Compton scattering of the soft-seed photons by the energetic particles. In the synchrotron self-Compton scenario (SSC), the same population of high-energy electrons responsible for the synchrotron emission upscatter the photons to higher energy. However, in the external Compton scenario (EC), seed photons might originate at the various components of an AGN, e.g., accretion disk [4], broad-line region [5], and dusty torus [6]. Hadronic models, on the other hand, ascribe the high energy emission from blazars to the interaction of relativistic protons in the presence of radiation fields (e.g., References [7,8,9]).
Blazars consist of two types of sources: flat-spectrum radio quasars (FSRQ) and BL Lacertae (BL Lac) objects. FSQRs are the more powerful sources that show emission lines in the optical continuum and have the synchrotron peak in the lower part of the spectrum, whereas BL Lac objects are less powerful ones that show weak or no emission lines and have a synchrotron peak in the higher part of the spectrum. BL Lacs represent an extreme class of sources with maximum synchrotron-emission output reaching up to soft X-rays (10 Hz), and inverse-Compton emission output ranging from hard X-rays to TeV emission. The sources do not possess strong circumnuclear photon fields and are believed to accrete at relatively low rates (see Reference [10] and references therein).
Blazars display variability in a wide range of temporal frequencies and, equivalently, on diverse timescales, ranging from a few minutes to decades. The statistical nature of such variability can be fairly represented by a featureless power-law power spectral density (PSD) (see in this context References [11,12] and references therein). However, signatures of quasiperiodic oscillations (QPO) in the multifrequency blazar light curves, including radio, optical, X-ray and -ray, have been found. The timescales of reported periodicity range from a few hours to a few years (see References [13,14,15,16], for QPOs in blazars).
In particular, at radio frequencies, QPO on diverse timescales have been recorded in a number of blazars: In BL Lac source PKS 0219-164, a strong signal of QPO with a 270 d period, along with possible low-frequency harmonics, was detected [14]. Similarly, in BL Lac source AO 0235+164, QPOs with periods ranging from about one year up to several years have been reported ([17,18]. FSRQ J1359+4011 was also reported to exhibit persistent ∼150 day periodic modulation in the 15 GHz observations [19]. In addition, several other blazar sources were found to show QPOs in the radio frequencies, e.g., FSRQ PKS 1510-089 [20], blazar NRAO 530 [21], and FSRQ PKS 1156+295 [22,23,24].
BL Lac J1043+2408 (RA = 10, Dec = +24, and z = 0.563446 [25]) has been detected by most of the currently available instruments operating within a wide range of electromagnetic frequencies. The source is cataloged by Fermi/LAT as 3FGL J1043.1+2407 [26], and in the soft X-ray (0.1–2.4 keV) it was frequently observed by ROSAT [27]. During The Micro-Arcsecond Scintillation-Induced Variability Survey III, its optical (R-band) brightness was recorded to be 16.84 magnitudes [28]. The blazar is regularly monitored in the 15 GHz radio band by the 40 m telescope of the Owens Valley Radio Observatory (OVRO) since 2008.
In this paper, we analyze the long-term (∼10.5 years) radio observations of blazar J1043+2408 and report detection of 563 d periodicity in the light curve. In Section 2 we discuss data acquisition. We present time-series analysis of the light curve using the epoch-folding, Lomb–Scargle periodogram (LSP), and discrete autocorrelation function methods; we also elaborate on the Monte Carlo simulation technique that is used to compute the statistical significance of the detected periodicity. In Section 4, we discuss various possible scenarios that can lead to the observed periodic signal; finally, we summarize our conclusion in Section 5.
2. Data Acquisition
The 15 GHz radio observations of source J1043+2408 were obtained from Owens Valley Radio Observatory (OVRO; [29]). We analyzed the observations, with an average sampling of a week, from epoch 8 January 2008 to 8 July 2018 (equivalently, from MJD 54473 to 58307), spanning 3820 days (∼10.5 years).
3. Analysis and Results
The 15 GHz band light curve of blazar J1043+2408 from the last decade is presented in Figure 1. In the figure, it can be clearly seen that, not only does the source display long-term variability, but it also shows periodic flux modulation, such that, in each cycle, the flux nearly doubles between minimum and maximum. To quantify the observed long-term variability, we estimated a fractional variability [30,31] of % , indicating moderate variability over the period.

Figure 1.
∼10.5-year-long 15 GHz observations of blazar J1043+2408 from OVRO.
3.1. Periodicity Search
We carried out periodicity search analysis using three well-known methods of time-series analysis: epoch folding, Lomb–Scargle periodogram, and discrete autocorrelation function. The methods, analyses, and results are discussed in detail below.
3.1.1. Epoch Folding
Epoch-folding, a widely discussed method of time-series analysis, was first worked out by Leahy et al. (1983) [32] and later improved by a number of authors (e.g., References [33,34]). Unlike traditional discrete Fourier periodogram, which expects periodic components to be of the sinusoidal shape, the method is less sensitive to the modulating shape of the periodic components. This method is also largely unaffected by the irregularity in the sampling of the observations, and, therefore, well suited for the periodic search in the data with gaps. In this method, a time series with N data points and varying about a mean value of is folded on several trial periods and phase bins. Then, quantity is expressed as:
is estimated, where and represent the mean and standard deviation, respectively, of each of M-phase bins. For observations distributed as Gaussian noise, we generally find . However in case of observations containing periodic signals, takes a value that is significantly different (or the maximum) from the average value (for details, refer to Reference [35]). The method has been frequently tested in the context of the periodicity analysis of blazar light curves, e.g., Reference [36].
We computed values of the source light curve for the trial periods ranging between 200 and 1000 days using a time step of 14 days. The pulse profiles corresponding to these trial periods were generated and, subsequently, tested for constancy using Equation (1). The left panel of Figure 2 presents the distribution of the values over the trial periods considered. The maximum deviation seen at days, represents the most probable period. The uncertainties here represent the half-width at maximum (HWHM) of the Gaussian fit of the peak centered around a 563 day trial period. The right panel of Figure 2 shows the pulse profile corresponding to the period. The observed period was further tested by using the following methods.
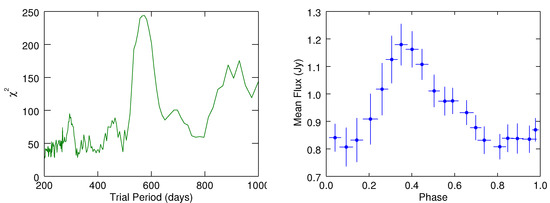
Figure 2.
Epoch-folding of the radio light curve of blazar J1043+2408. Left panel: values for the trial periods between 200 and 1000 days. Right panel: pulse profile of the periodic component at the timescale of 563 days representing maximum value.
3.1.2. Lomb–Scargle Periodogram
The Lomb–Scargle Periodogram (LSP) [37,38] is one of the most popular methods of time-series analysis (see References [12,14,15]). The method, as a form of least-square fitting of the sinusoidal waves to the data, is less sensitive to gaps in the data when compared to the traditional discrete Fourier transform (DFT). The fitting process enhances the periodogram features (or peaks) that can possibly represent periodic signals in light curves. The LSP of the source light curve was computed for the minimum and maximum frequencies of d, and = 1/14 d, respectively. It should be pointed out that the choice of the total number of periodogram frequencies, , plays an important role in the evaluation of the periodogram; we would like to select its value keeping in mind that a small value lacks precision on the location of the most prominent period, whereas a large value could be computationally inconvenient. In this work, the total number of periodogram frequencies were evaluated using
where , and days represents the total length of the observations (see Reference [39]). The LSP of the ∼10.5-year-long OVRO light curve of blazar J1043+2408 is presented in Figure 3. It can be seen that in the periodogram a distinct peak stands out around the timescale of days; this suggests the presence of a strong periodic signal at the timescale. The uncertainties in the period were estimated by taking the HWHM of the most prominent peak (see References [14,15]). Moreover, to assess the effect of , we also computed LSP using . This made the dominant period shift to 567 days with larger uncertainties of 47 days. We see that the results are consistent with the previous finding by the epoch-folding method.
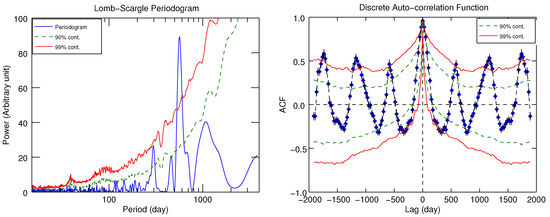
Figure 3.
Lomb–Scargle periodogram (left panel) and discrete autocorrelation function (right panel) of the ∼10.5-year-long 15 GHz observations of blazar J1043+2408. The dashed green and red curves represent the 90% and 99% significance levels, respectively, from MC simulations.
3.1.3. Discrete Auto-Cross-Correlation Function
To further confirm the presence of the above periodic timescale using a different method, we performed discrete correlation function analysis as described in Reference [40]. The method has been mostly applied to investigate cross-correlation between two time series with uneven spacing (see References [10,11,12,31]). With only one light curve, the method becomes a discrete autocorrelation function (ACF), which can be exploited to reveal the periodic signals in a light curve. The ACF, although related to PSD in frequency space, is computed in the time domain and therefore it is free of the sampling effects such as windowing and aliasing. The method has been frequently employed in periodicity search in blazar light curves (e.g., [10,41]). The discrete ACF of the radio light curve of the blazar is presented in the right panel of Figure 3, which clearly reveals the presence of the periodic behavior represented by the ACF peaks recurring after an interval of days. Once again, HWHM for the first peak is used as a measure of uncertainty. It should be noted that all three estimates of uncertainty measures, as provided by the HWHM of the Gaussian fit of the most prominent features, are consistent within 2% of the significant period.
3.1.4. Significance Estimation and Monte Carlo Simulation
After we employed three different methods to detect periodicity in the light curve, it should be pointed out that, in general, the statistical properties of blazar light curves can be characterized as red-noise processes that can potentially mimic a transient periodic behavior, especially in the low-frequency domain (see References [11,14,42] for the discussion). In addition, spurious peaks might arise owing to other sampling effects, including discrete sampling, finite observation period, and uneven sampling of the light curve. Therefore, it is important to consider these effects in significance estimation against spurious detection. To address the issue, we followed the power-response method (PSRESP) [43], a method extensively used in the characterization of the AGN power-spectrum density (see References [10,12,14,15], and references therein). First, the source periodogram was modeled with a power-law PSD of the form ; where , , and C represent temporal frequency, spectral slope, and Poisson noise level, respectively. To maximize the probability that the PSD model best represents the observed periodogram, and were used. A large number (typically 10,000) of light curves were then simulated following the Monte Carlo (MC) method described in Reference [44]. The method fully randomizes both amplitude and phase. However, the method could have possible caveats due to the fact that it produces Gaussian-distributed light curves, which may not represent the probability density function of the observations (see Reference [45]). Nevertheless, as the periodic features in all methods clearly stand out, we expect that any significant deviations in significance estimation would fall within the range of uncertainties.
The simulated light curves were resampled to match the sampling of the source light curve. To estimate the significance of the periodic feature seen in the LSP, the LSP distribution of the simulated light curves was utilized to estimate a local and global significance of the periodic feature against spurious detections (for further details see References [10,12,14,15]). Local significance tells us how likely it is for the observed feature at a particular frequency to be significant, whereas global significance, which considers LSP distribution at all the considered frequencies, accounts for the fact that we do not have a priori knowledge of the location of the frequency at which the most significant feature might occur (see Reference [14]). The local significance of the observed periodic feature at the ∼563 day period turned out to be ∼99.4%, and similarly the global significance of the LSP peak at the period ∼563 day was evaluated to be 99.6%. The local 90% and 99% LSP significance contours are represented by the dashed green and the red curves, respectively, in the left panel Figure 3. It can be seen that the red noise has a predominance of spectral powers in the low-frequency regime or, equivalently, longer timescales.
In a similar way, we used the distribution of the simulated ACFs to estimate the local 90% and 99% significance contours shown by the dashed green and the red curves, respectively, in the autocorrelation function shown in the right panel of Figure 3. The observed high significances imply a low probability of spurious detections and therefore suggest that the signal, intrinsic to the source light curve, should have a physical origin.
4. Discussion
Study of periodic oscillations in blazars could be a novel method to investigate the processes occurring at the innermost regions of the active central engines. The studies could provide important insights into a number of blazar aspects including strong gravity environment around fast spinning supermassive black holes (SMBH), magnetic field configuration near the accretion disk, disk-jet connection and release of gravitational waves (GW) from the binary supermassive-black-hole systems. There could be a number of processes that can explain the observed periodic flux modulations. Below, we discuss some of them.
First, for the observed period () of 563 days, the corresponding period in the source rest frame (P) at is 360 days, as estimated using . If we take the value as the Keplerian period around the central black hole, , we can estimate the corresponding radius of the orbit as given by
where a is the length of the semimajor axis of the elliptic orbits. For a black hole of mass of the radius of the Keplerian orbit is estimated as ∼100 or, equivalently, ∼0.005 parsecs. This result can be interpreted in terms of a binary supermassive-black-hole system (e.g., Reference [46]), which potentially can explain presence of yearlike periodic timescales in AGN (see Reference [47] for a review). For the binary mass ratios in the range of 0.01–0.1 (see, e.g., References [48,49]), the orbital decay timescale in the GW-driven regime can be computed as
(see Reference [50]); the timescale turns out to be less than a thousand years. Indeed, existence of binary SMBH is consistent with the prediction by the hierarchical galaxy-formation models. As a matter of fact, the closest binary SMBH so far detected lies within a subparsec separation (∼0.35 pc) [51] in Mrk 533, a Seyfert type 2 AGN. Therefore, if the above periodicity results from such a system, we should expect that the system undergoes gravitational coalescence within a few centuries, accompanied with the emission of gravitational waves of frequency ∼ Hz. However, the probability of observing such a close (milliparsec) system of binary SMBH might be too small (see Reference [52]). However, on the other hand, in the case of strong disk-jet connection (e.g., in Reference [53]; see also Reference [11]), the periodic modulations induced due to binary SMBH system could propagate down the jet affecting the Doppler-boosted emission. In such a case, true periodic timescales at the BH could be longer than the observed one due to relativistic effects, i.e., , where Doppler factor, , and , and are the bulk Lorentz factor, relativistic speed, and angle to the line of sight, respectively. Consequently, the corresponding Keplerian orbit of the secondary black hole could be larger and therefore lie farther away from the primary BH. For instance, if a jet component carrying the periodic signal travels along the jet viewed at ∼1 with a bulk Lorentz factor of ∼15, the orbit estimated using a dilated timescale gives a distance of a ∼0.1 parsecs. Such a subparsec separation incidentally represents a relatively stable configuration in the evolution of binary SMBH systems (see Reference [54]). The left panel of Figure 4 shows the radii of the Keplerian circular orbits of the possible secondary black hole corresponding to periodic modulations propagating with three different bulk Lorentz factors, , and 20, along the blazar jet that is viewed within .
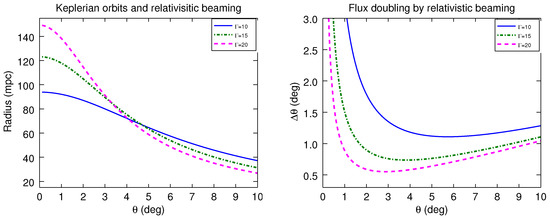
Figure 4.
Left panel: Change in the radii (in milli-parsecs; mpc) of the Keplerian circular orbits around the black hole of mass of corresponding to the 563 d periodic signal carried by the emission regions traveling with the bulk Lorentz factors, , and 20, along the blazar jet viewed close to the line of sight. Right panel: The change in the viewing angle as a function of viewing angle for , and 20 required to double the apparent flux, keeping intrinsic flux constant, via relativistic beaming. A radio spectral index = 0.6, typical of blazars, is used here.
Similarly, the periodic changes can also be associated with the relativistic motion of emission regions along the helical path of the magnetized jets (e.g., References [55,56]). In particular, when the emission regions move along the helical path of a jet with a high bulk Lorentz factor, due to the relativistic effects, the periodic changes in the viewing angle cause the Doppler boosted emission to be periodically modulated. The rest frame flux () and observed flux () are related through the equations
(Similar to Equation B4 in Reference [57]). For blazars having typical radio spectral index (), the change in the angle of line of sight required to double the observed flux, while keeping the flux in the source rest frame constant, for various jet angles and three bulk Lorentz factors , is displayed in the right panel of Figure 4. As the figure shows, for typical blazar viewing angles in the 1–5 range, a slight change in the viewing angle, e.g., ∼1.5, is sufficient to double the observed brightness.
In another likely scenario, the detected QPO with a periodicity of ∼563 days could be explained in the context of instabilities intrinsic to a blazar accretion disk. For example, bright hotspots on the disk that revolve around the BH could result in the year timescale periodicity. Assuming they follow circular Keplerian orbits, they could be located at ∼ from the BH. In the General Relativistic treatment of rotating massive objects, the nearby inertial frames are distorted by frame-dragging resulting in the nodal precession of the tilted orbits, known as the Lense–Thirring precession. Periodic behaviors in astronomical systems can also be linked to the Lense–Thirring precession of accretion disks (e.g., References [58,59]). The timescale of such precession is proportional to the distance (from the BH) cubed and also to the mass of the central black hole so that the timescale, , can be expressed as
where , M and r represent a dimensionless spin parameter, mass of the BH, and the radial distance of the emission region from the BH, respectively. For a maximally spinning () central black hole with a mass of , a timescale of 360 days places the emission region around ∼12. The periodic oscillations could be the result of the jet precession due to such warped accretion disks. However, such a periodic timescale would be thousands of years, and hence may not be relevant here [60,61]. In radio-loud AGNs, magnetic flux accumulation in the accretion disk can result in the formation of so-called magnetically choked accretion flow. In that case, owing to sudden changes in density and magnetic flux, disk instabilities, e.g., the Rayleigh–Taylor and Kelvin–Helmholtz instabilities, are set up; this, in turn, can induce QPOs at the disk–magnetosphere interface [62,63]. Similar QPOs have been observed in the recent magneto-hydrodynamical simulations of large-scale jets [64]. The periodic timescale of these QPOs could range from a few days to a few years depending upon the black-hole mass and the spin parameter.
5. Conclusions
The long-term (∼10.5 years) radio (15 GHz) observations of the blazar J1043+2408 were analyzed for possible periodicities using three methods widely used in astronomical time-series analysis: epoch-folding, Lomb–Scargle periodogram, and autocorrelation function. The study revealed a strong periodic signal with a ∼560 day periodicity. A large number of Monte Carlo simulations of the light curves were used to establish a high significance (>99%) of the signal against possible spurious detection. We conclude that, while other above-discussed scenarios cannot be completely ruled out, periodic modulations induced by gravitational perturbation in a binary SMBH system seem a more plausible mechanism at the root of the observed periodic radio signal.
Acknowledgments
I acknowledge the financial support by the Polish National Science Center through grant UMO-2017/26/D/ST9/01178. This research has made use of data from the OVRO 40-m monitoring program (Richards, J. L. et al. 2011, ApJS, 194, 29), which is supported in part by NASA grants NNX08AW31G, NNX11A043G, and NNX14AQ89G, and NSF grants AST-0808050 and AST-1109911. I thank James Webb for carefully reading the manuscript. I would like to thank the anonymous referees for their constructive comments and suggestions that greatly improved the manuscript.
Conflicts of Interest
The author declares no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AGN | Active Galactic Nuclei |
| ACF | Autocorrelation function |
| BL Lac | BL Lacertae object |
| BH | Black hole |
| FSRQ | Flat Spectrum Radio Quasar |
| LSP | Lomb–Scargle Periodogram |
| MC | Monte Carlo |
| OVRO | Owens Valley Radio Observatory |
| PSD | Power spectral density |
| QPO | Quasiperiodic oscillation |
| SMBH | Supermassive black hole |
References
- Meier, D.L. Black Hole Astrophysics: The Engine Paradigm; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Maraschi, L.; Ghisellini, G.; Celotti, A. A jet model for the gamma-ray emitting blazar 3C 279. Astrophys. J. 1992, 397, L5–L9. [Google Scholar] [CrossRef]
- Bloom, S.D.; Marscher, A.P. An Analysis of the Synchrotron Self-Compton Model for the Multi-Wave Band Spectra of Blazars. Astrophys. J. 1996, 461, 657. [Google Scholar] [CrossRef]
- Dermer, C.D.; Schlickeiser, R. Thermal Comptonization Model for the High Energy Emission of Seyfert Active Galactic Nuclei. Astrophys. J. 1993, 416, 458. [Google Scholar] [CrossRef]
- Sikora, M. High-energy radiation from active galactic nuclei. Astrophys. J. Suppl. Ser. 1994, 90, 923. [Google Scholar] [CrossRef]
- Błażejowski, M.; Sikora, M.; Moderski, R.; Madejski, G.M. Comptonization of Infrared Radiation from Hot Dust by Relativistic Jets in Quasars. Astrophys. J. 2000, 545, 107. [Google Scholar] [CrossRef]
- Mannheim, K.; Biermann, P.L. Gamma-ray flaring of 3C 279—A proton-initiated cascade in the jet? Astron. Astrophys. 1992, 253, L21. [Google Scholar]
- Aharonian, F.A. TeV gamma rays from BL Lac objects due to synchrotron radiation of extremely high energy protons. New Astron. 2000, 5, 377. [Google Scholar] [CrossRef]
- Mücke, A.; Protheroe, R.J.; Engel, R.; Rachen, J.P.; Stanev, T. BL Lac objects in the synchrotron proton blazar model. Astropart. Phys. 2003, 18, 593. [Google Scholar] [CrossRef]
- Bhatta, G.; Mohorian, M.; Bilinsky, I. Hard X-ray Properties of NuSTAR Blazars. Astron. Astrophys. 2018, 619, A93. [Google Scholar] [CrossRef]
- Bhatta, G.; Stawarz, L.; Markowitz, A.; Balasubramaniam, K.; Zola, S.; Zdziarski, A.A.; Jamrozy, M.; Ostrowski, M.; Kuzmicz, A.; Ogloza, W.; et al. Signatures of the disk-jet coupling in the Broad-line Radio Quasar 4C+74.26. Astrophys. J. 2018, 866, 132. [Google Scholar] [CrossRef]
- Bhatta, G.; Ostrowski, M.; Markowitz, A.; Akitaya, H.; Arkharov, A.A.; Bachev, R.; Benítez, E.; Borman, G.A.; Carosati, D.; Cason, A.D.; et al. Multifrequency Photo-polarimetric WEBT Observation Campaign on the Blazar S5 0716+714: Source Microvariability and Search for Characteristic Timescales. Astrophys. J. 2016, 831, 92B. [Google Scholar] [CrossRef]
- Gupta, A. Multi-Wavelength Intra-Day Variability and Quasi-Periodic Oscillation in Blazars. Galaxies 2018, 6, 1. [Google Scholar] [CrossRef]
- Bhatta, G. Radio and γ-Ray Variability in the BL Lac PKS 0219-164: Detection of Quasi-periodic Oscillations in the Radio Light Curve. Astrophys. J. 2017, 487, 7B. [Google Scholar] [CrossRef]
- Bhatta, G.; Zola, S.; Ostrowski, M.; Winiarski, M.; Ogłoza, W.; Dróżdż, M.; Siwak, M.; Liakos, A.; Kozieł-Wierzbowska, D.; Gazeas, K.; et al. Detection of Possible Quasi-periodic Oscillations in the Long-term Optical Light Curve of the BL Lac Object OJ 287. Astrophys. J. 2016, 832, 47. [Google Scholar] [CrossRef]
- Zola, S.; Valtonen, M.; Bhatta, G.; Goyal, A.; Debski, B.; Baran, A.; Krzesinski, J.; Siwak, M.; Ciprini, S.; Gopakumar, A.; et al. A Search for QPOs in the Blazar OJ287: Preliminary Results from the 2015/2016 Observing Campaign. Galaxies 2016, 4, 41. [Google Scholar] [CrossRef]
- Liu, F.K.; Zhao, G.; Wu, X.-B. Harmonic QPOs and Thick Accretion Disk Oscillations in the BL Lacertae Object AO 0235+164. Astrophys. J. 2006, 650, 749. [Google Scholar] [CrossRef]
- Raiteri, C.M.; Villata, M.; Aller, H.D.; Aller, M.F.; Heidt, J.; Kurtanidze, O.M.; Lanteri, L.; Maesano, M.; Massaro, E.; Montagni, F.; et al. Optical and radio variability of the BL Lacertae object AO 0235+16: A possible 5-6 year periodicity. Astron. Astrophys. 2001, 377, 396. [Google Scholar] [CrossRef]
- King, O.G.; Hovatta, T.; Max-Moerbeck, W.; Meier, D.L.; Pearson, T.J.; Readhead, A.C.; Reeves, R.; Richards, J.L.; Shepherd, M.C. A quasi-periodic oscillation in the blazar J1359+4011. Mon. Not. R. Astron. Soc. 2013, 436, L114. [Google Scholar] [CrossRef]
- Xie, G.Z.; Yi, T.F.; Li, H.Z.; Zhou, S.B.; Chen, L.E. Periodicity analysis of the radio curve of PKS 1510-089 and implications for its central structure. Astrophys. J. 2008, 135, 2212. [Google Scholar] [CrossRef]
- An, T.; Baan, W.A.; Wang, J.-Y.; Wang, Y.; Hong, X.-Y. Periodic radio variabilities in NRAO 530: A jet–disc connection? Mon. Not. R. Astron. Soc. 2013, 434, 3487. [Google Scholar] [CrossRef]
- Wang, J.-Y.; An, T.; Baan, W.A.; Lu, X.-L. Periodic radio variabilities of the blazar 1156+295: Harmonic oscillations. Mon. Not. R. Astron. Soc. 2014, 443, 58. [Google Scholar] [CrossRef]
- Hovatta, T.; Tornikoski, M.; Lainela, M.; Lehto, H.J.; Valtaoja, E.; Torniainen, I.; Aller, M.F.; Aller, H.D. Statistical analyses of long-term variability of AGN at high radio frequencies. Astron. Astrophys. 2007, 469, 899. [Google Scholar] [CrossRef]
- Hovatta, T.; Lehto, H.J.; Tornikoski, M. Wavelet analysis of a large sample of AGN at high radio frequencies. Astron. Astrophys. 2008, 488, 897. [Google Scholar] [CrossRef]
- Hewett, P.C.; Wild, V. Improved redshifts for SDSS quasar spectra. Mon. Not. R. Astron. Soc. 2010, 405, 2302. [Google Scholar] [CrossRef]
- Acero, F.; Ackermann, M.; Ajello, M.; Albert, A.; Atwood, W.B.; Axelsson, M.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; et al. Fermi Large Area Telescope Third Source Catalog. Astrophys. J. Suppl. Ser. 2015, 218, 23. [Google Scholar] [CrossRef]
- Massaro, E.; Giommi, P.; Leto, C.; Marchegiani, P.; Maselli, A.; Perri, M.; Piranomonte, S.; Sclavi, S. Roma-BZCAT: A multifrequency catalogue of blazars. Astron. Astrophys. 2009, 495, 691. [Google Scholar] [CrossRef]
- Pursimo, T.; Ojha, R.; Jauncey, D.L.; Rickett, B.J.; Dutka, M.S.; Koay, J.Y.; Lovell, J.E.; Bignall, H.E.; Kedziora-Chudczer, L.; Macquart, J.P. The Micro-Arcsecond Scintillation-Induced Variability (MASIV) Survey. III. Optical Identifications and New Redshifts. Astrophys. J. 2013, 767, 14. [Google Scholar] [CrossRef]
- Richards, J.L.; Max-Moerbeck, W.; Pavlidou, V.; King, O.G.; Pearson, T.J.; Readhead, A.C.; Reeves, R.; Shepherd, M.C.; Stevenson, M.A.; Weintraub, L.C.; et al. Blazars in the Fermi Era: The OVRO 40 m Telescope Monitoring Program. Astrophys. J. Suppl. Ser. 2011, 194, 29. [Google Scholar] [CrossRef]
- Vaughan, S.; Edelson, R.; Warwick, R.S.; Uttley, P. On characterizing the variability properties of X-ray light curves from active galaxies. Mon. Not. R. Astron. Soc. 2003, 345, 1271. [Google Scholar] [CrossRef]
- Bhatta, G.; Webb, J. Microvariability in BL Lacertae: “Zooming” into the Innermost Blazar Regions. Galaxies 2018, 6, 2. [Google Scholar] [CrossRef]
- Leahy, D.A.; Elsner, R.F.; Weisskopf, M.C. On searches for periodic pulsed emission—The Rayleigh test compared to epoch folding. Astrophys. J. 1983, 272, 256. [Google Scholar] [CrossRef]
- Davies, S.R. An improved test for periodicity. Mon. Not. R. Astron. Soc. 1990, 244, 93–95. [Google Scholar]
- Davies, S.R. Davies Periodicity Test Revisited. Mon. Not. R. Astron. Soc. 1991, 251, 64P. [Google Scholar] [CrossRef]
- Larsson, S. Parameter estimation in epoch folding analysis. Astron. Astrophys. Suppl. Ser. 1996, 117, 197. [Google Scholar] [CrossRef]
- Zhang, B.-K.; Zhao, X.-Y.; Wang, C.-X.; Dai, B.-Z. Optical quasi-periodic oscillation and color behavior of blazar PKS 2155-304. Res. Astron. Astrophys. 2014, 14, 933–941. [Google Scholar] [CrossRef]
- Lomb, N.R. Least-squares frequency analysis of unequally spaced data. Astrophys. Space Sci. 1976, 39, 447. [Google Scholar] [CrossRef]
- Scargle, J.D. Studies in astronomical time series analysis. II—Statistical aspects of spectral analysis of unevenly spaced data. Astrophys. J. 1982, 263, 835. [Google Scholar] [CrossRef]
- VanderPlas, J.T. Understanding the Lomb–Scargle Periodogram. Astrophys. J. Suppl. Ser. 2018, 236, 16. [Google Scholar] [CrossRef]
- Edelson, R.A.; Krolik, J.H. The discrete correlation function—A new method for analyzing unevenly sampled variability data. Astrophys. J. 1988, 333, 646. [Google Scholar] [CrossRef]
- Villata, M.; Raiteri, C.M.; Aller, H.D.; Aller, M.F.; Teräsranta, H.; Koivula, P.; Wiren, S.; Kurtanidze, O.M.; Nikolashvili, M.G.; Ibrahimov, M.A.; et al. The WEBT campaigns on BL Lacertae. Time and cross-correlation analysis of optical and radio light curves 1968–2003. Astron. Astrophys. 2004, 424, 497. [Google Scholar] [CrossRef]
- Press, W.H. Flicker noises in astronomy and elsewhere. Comments Astrophys. 1978, 7, 103. [Google Scholar]
- Uttley, P.; McHardy, I.M.; Papadakis, I.E. Measuring the broad-band power spectra of active galactic nuclei with RXTE. Mon. Not. R. Astron. Soc. 2002, 332, 231. [Google Scholar] [CrossRef]
- Timmer, J.; Koenig, M. On generating power law noise. Astron. Astrophys. 1995, 300, 707. [Google Scholar]
- Emmanoulopoulos, D.; McHardy, I.M.; Papadakis, I.E. Generating artificial light curves: Revisited and updated. Mon. Not. R. Astron. Soc. 2013, 433, 907. [Google Scholar] [CrossRef]
- Valtonen, M.J.; Lehto, H.J.; Takalo, L.O.; Sillanpaa, A. Testing the 1995 binary black hole model of OJ287. Astrophys. J. 2011, 729, 33–38. [Google Scholar] [CrossRef]
- Komossa, S. Observational evidence for binary black holes and active double nuclei. Mem. Soc. Astron. Ital. 2006, 77, 733. [Google Scholar]
- Begelman, M.C.; Blandford, R.D.; Rees, M.J. Massive black hole binaries in active galactic nuclei. Nature 1980, 287, 307. [Google Scholar] [CrossRef]
- Sillanpaa, A.; Haarala, S.; Valtonen, M.J.; Sundelius, B.; Byrd, G.G. OJ 287—Binary pair of supermassive black holes. Astrophys. J. 1988, 325, 628. [Google Scholar] [CrossRef]
- Peters, P.C. Gravitational Radiation and the Motion of Two Point Masses. Phys. Rev. 1964, 136, 1224. [Google Scholar] [CrossRef]
- Kharb, P.; Lal, D.V.; Merritt, D. A candidate sub-parsec binary black hole in the Seyfert galaxy NGC 7674. Nat. Astron. 2017, 1, 727. [Google Scholar] [CrossRef]
- Ackermann, M.; Ajello, M.; Albert, A.; Atwood, W.B.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; Gonzalez, J.B.; Bellazzini, R.; et al. Multiwavelength Evidence for Quasi-periodic Modulation in the Gamma-Ray Blazar PG 1553+113. Astrophys. J. Lett. 2015, 813, L41. [Google Scholar] [CrossRef]
- Blandford, R.D.; Payne, D.G. Hydromagnetic flows from accretion discs and the production of radio jets. Mon. Not. R. Astron. Soc. 1982, 199, 883. [Google Scholar] [CrossRef]
- Rieger, F.M. Supermassive binary black holes among cosmic gamma-ray sources. Astrophys. Space Sci. 2007, 309, 271. [Google Scholar] [CrossRef]
- Camenzind, M.; Krockenberger, M. The lighthouse effect of relativistic jets in blazars—A geometric origin of intraday variability. Astron. Astrophys. 1992, 255, 59. [Google Scholar]
- Mohan, P.; Mangalam, A. Kinematics of and Emission from Helically Orbiting Blobs in a Relativistic Magnetized Jet. Astrophys. J. 2015, 805, 91. [Google Scholar] [CrossRef]
- Urry, C.M.; Padovani, P. Unified Schemes for Radio-Loud Active Galactic Nuclei. Publ. Astron. Soc. Pac. 1995, 107, 803. [Google Scholar] [CrossRef]
- Stella, L.; Vietri, M. Lense-Thirring Precession and Quasi-periodic Oscillations in Low-Mass X-Ray Binaries. Astrophys. J. Lett. 1998, 492, L59. [Google Scholar] [CrossRef]
- Motta, S.; Muñoz-Darias, T.; Casella, P.; Belloni, T.; Homan, J. Low-frequency oscillations in black holes: A spectral-timing approach to the case of GX 339-4. Mon. Not. R. Astron. Soc. 2011, 418, 2292. [Google Scholar] [CrossRef]
- Liska, M.; Hesp, C.; Tchekhovskoy, A.; Ingram, A.; van der Klis, M.; Markoff, S. Formation of precessing jets by tilted black hole discs in 3D general relativistic MHD simulations. Mon. Not. R. Astron. Soc. 2018, 474, L81. [Google Scholar] [CrossRef]
- Graham, M.J.; Djorgovski, S.G.; Stern, D.; Drake, A.J.; Mahabal, A.A.; Donalek, C.; Glikman, E.; Larson, S.; Christensen, E. A systematic search for close supermassive black hole binaries in the Catalina Real-time Transient Survey. Mon. Not. R. Astron. Soc. 2015, 453, 1562. [Google Scholar] [CrossRef]
- Li, L.-X.; Narayan, R. Quasi-periodic Oscillations from Rayleigh-Taylor and Kelvin-Helmholtz Instability at a Disk-Magnetosphere Interface. Astrophys. J. 2004, 601, 414. [Google Scholar] [CrossRef]
- Fu, W.; Lai, D. Dynamics of the innermost accretion flows around compact objects: Magnetosphere-disc interface, global oscillations and instabilities. Mon. Not. R. Astron. Soc. 2012, 423, 831. [Google Scholar] [CrossRef]
- McKinney, J.C.; Tchekhovskoy, A.; Blandford, R.D. General relativistic magnetohydrodynamic simulations of magnetically choked accretion flows around black holes. Mon. Not. R. Astron. Soc. 2012, 423, 3083. [Google Scholar] [CrossRef]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).