Classical and Relativistic Evolution of an Extra-Galactic Jet with Back-Reaction
Abstract
1. Introduction
- The velocity of the jet is constant over many kpc and takes the value v. Due to the fact that it is thought that this velocity is nearly relativistic, it is parametrized as , where c is the velocity of light. As an example, [6] analyzed some wide-angle tail radio galaxies and found a terminal velocity of .
2. Conservation of the Flux of Energy
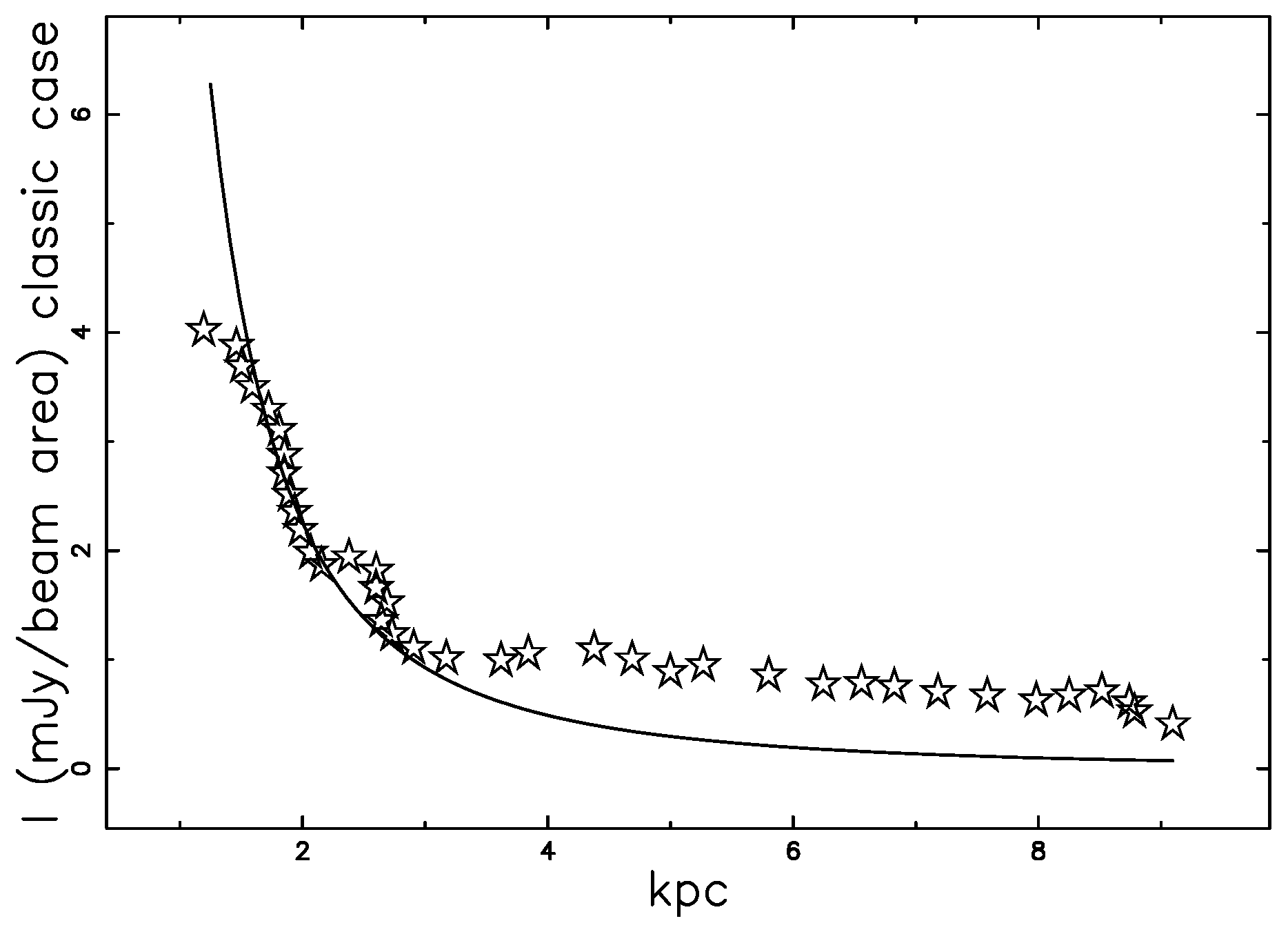
2.1. The Turbulent Jet
- The rate of momentum flow, J, represented by:is constant; here, x is the distance from the initial circular hole, is the jet’s diameter at distance x, is the maximum velocity along the the centerline, is:where:and is the density of the surrounding medium; see Equation (5.6-3) in [13].
- The jet’s density is constant over the expansion and equal to that of the surrounding medium. The pressure is absent in this theory.
2.2. The Lane–Emden Profile
2.3. Preliminaries
2.4. Classical Solution to First Order
2.5. Solution to Second Order
3. Conservation of the Relativistic Flux of Energy
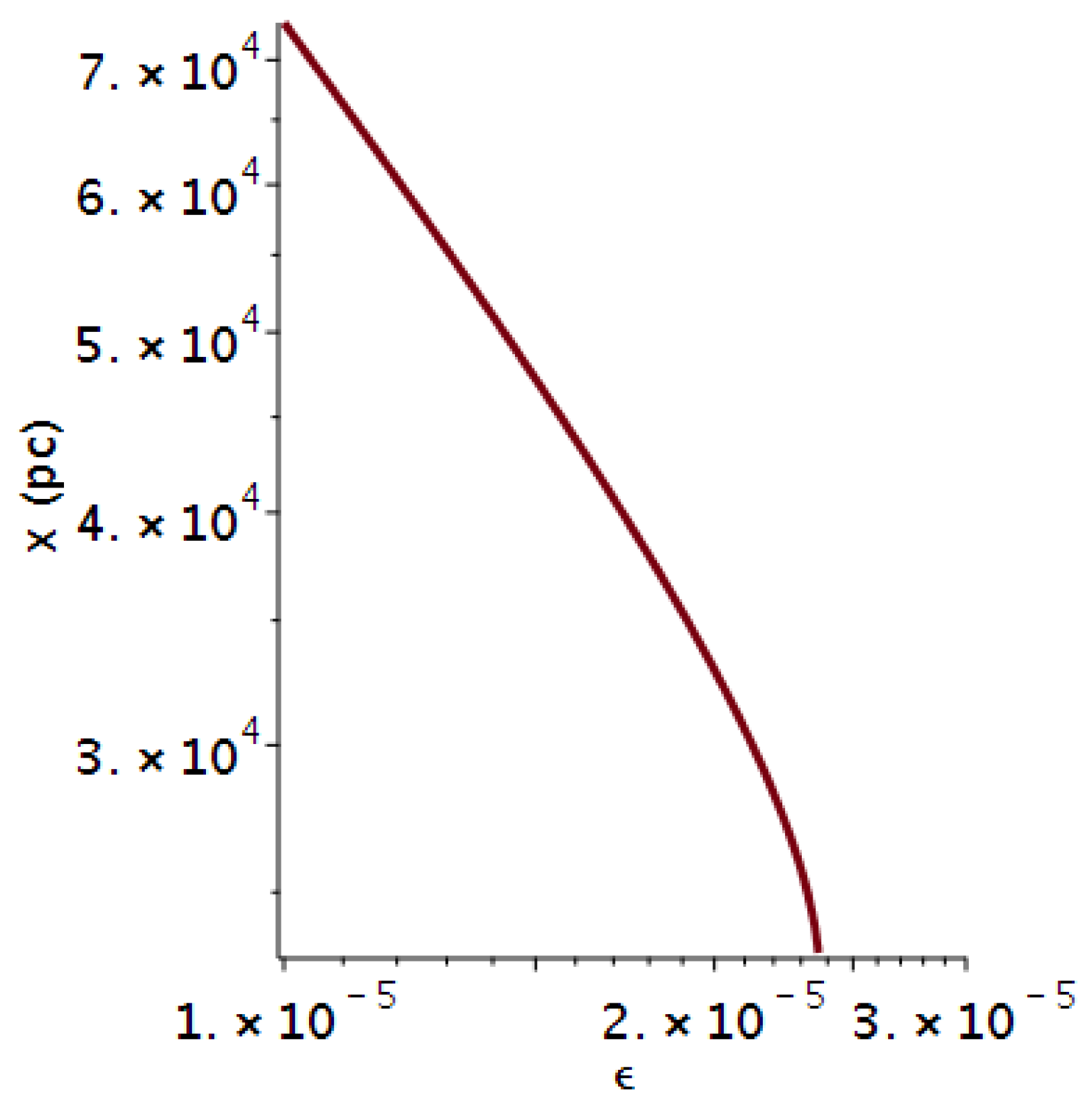
Relativistic Solution to Second Order
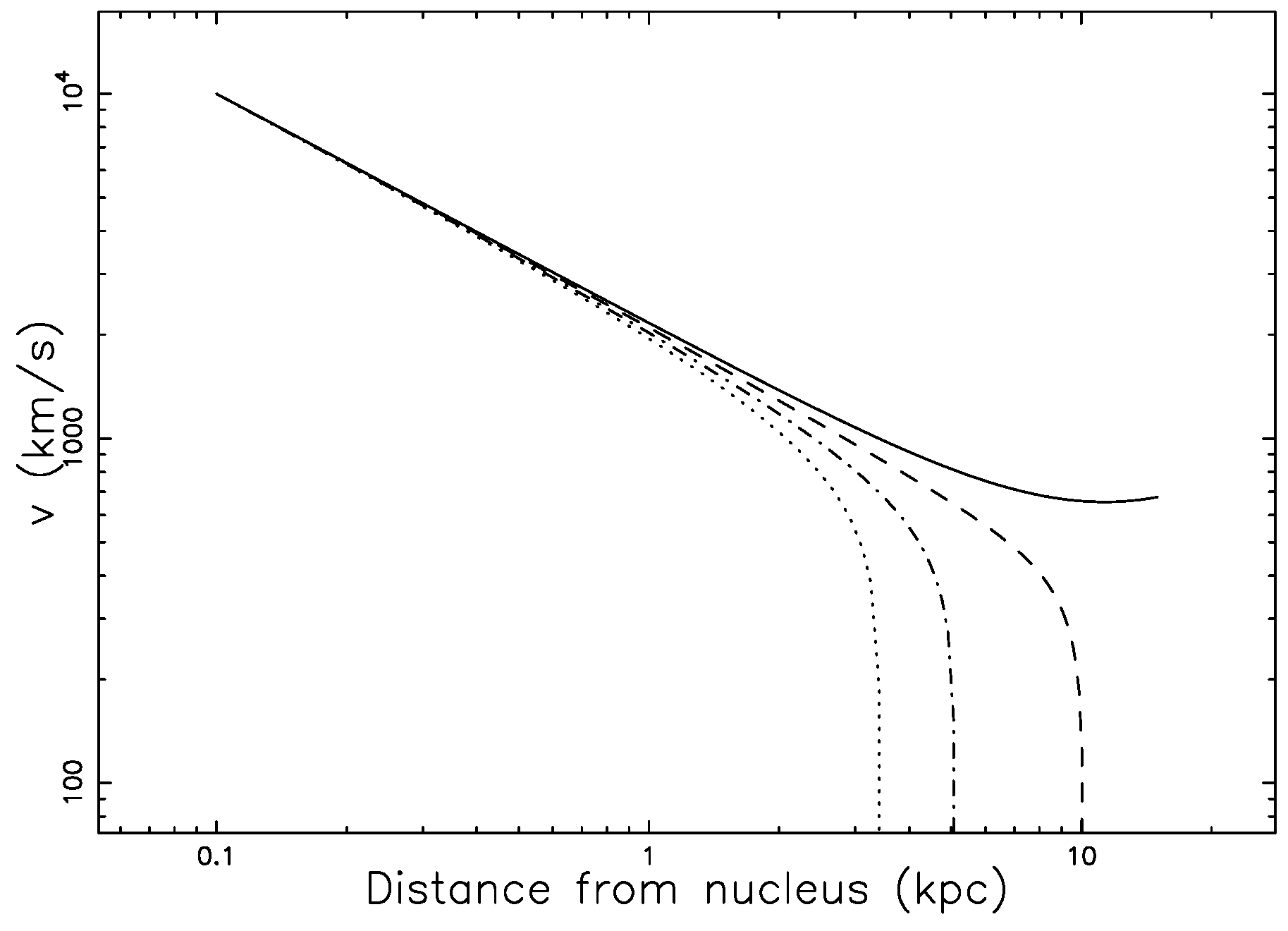
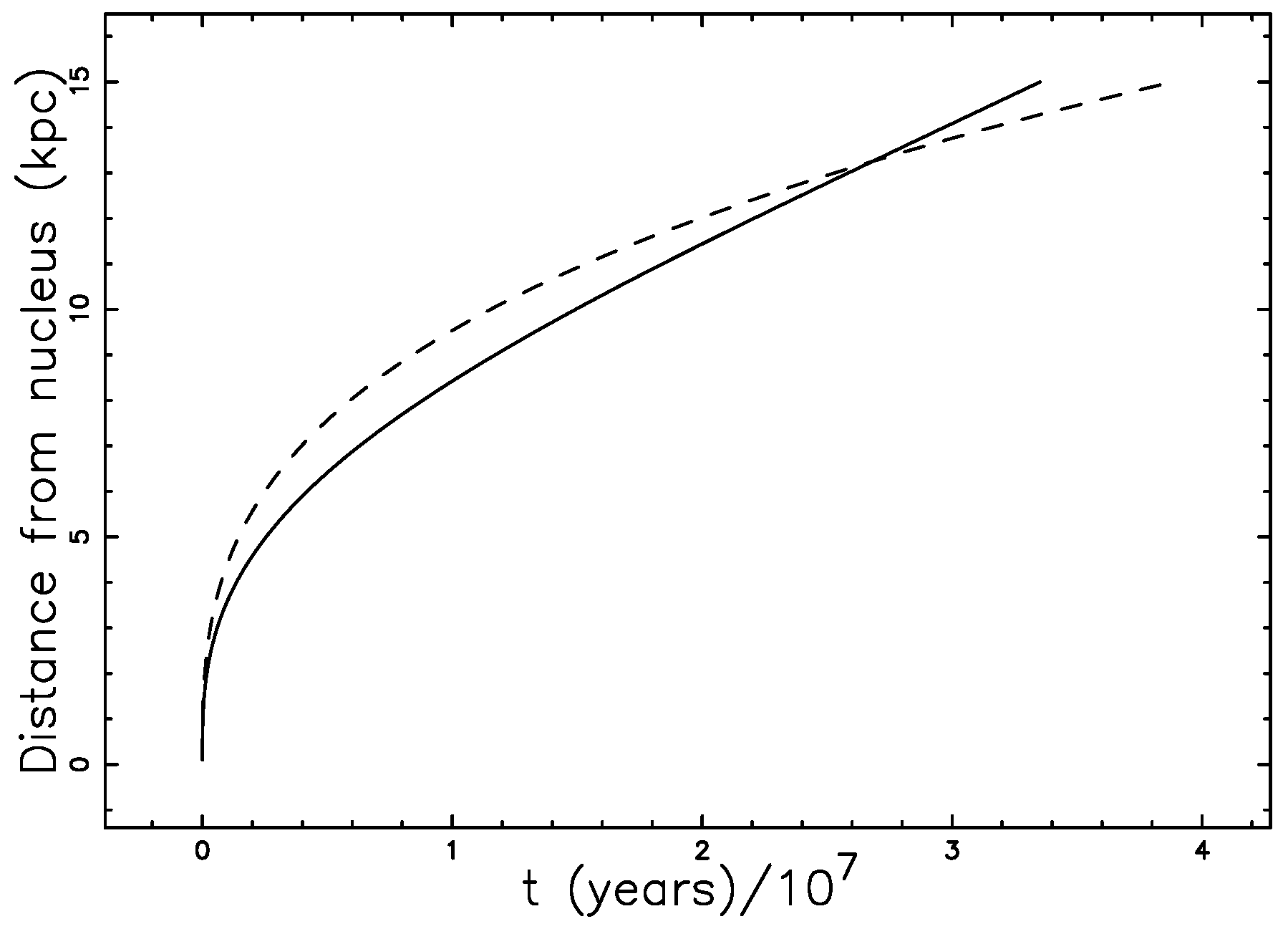
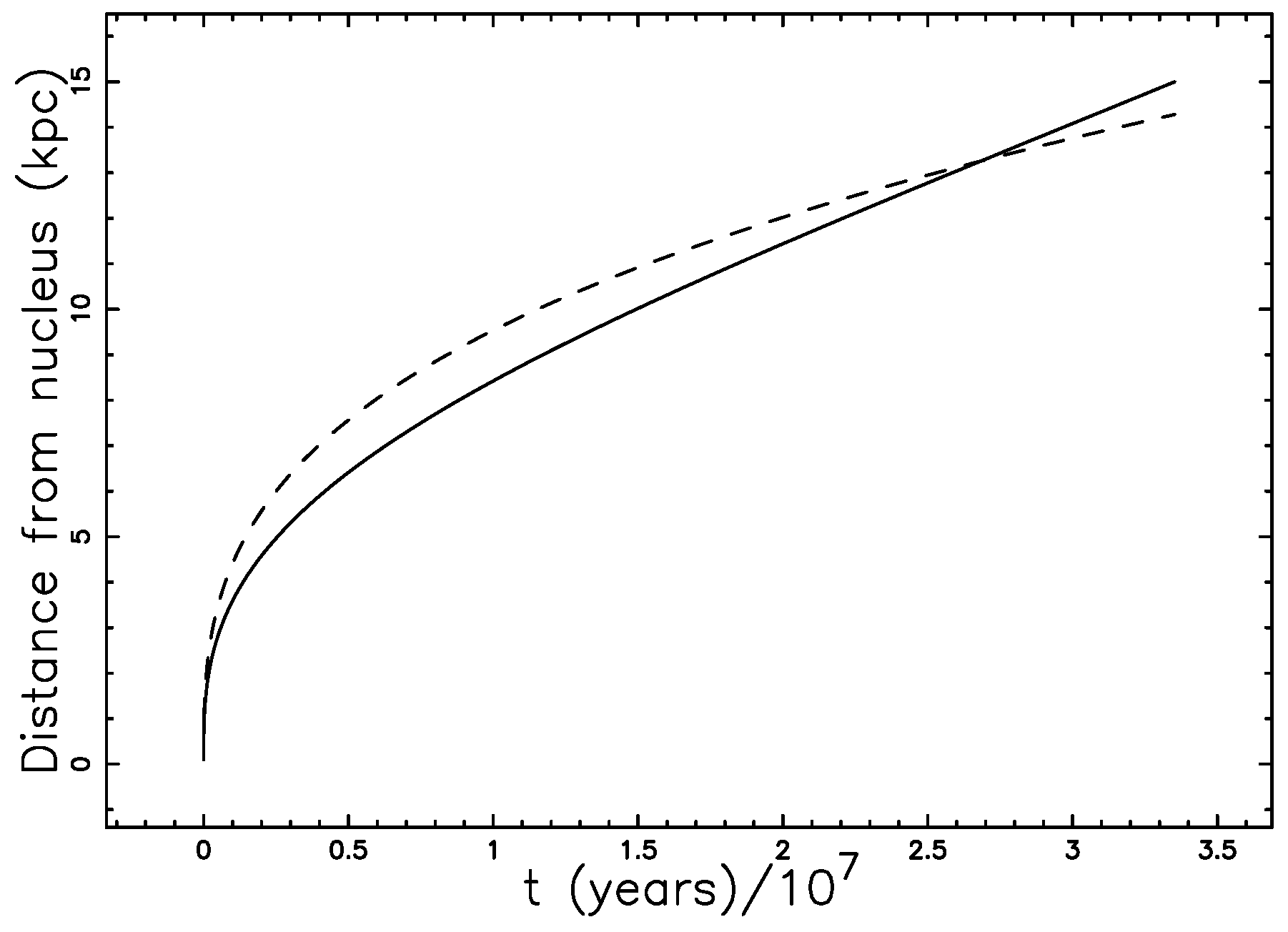
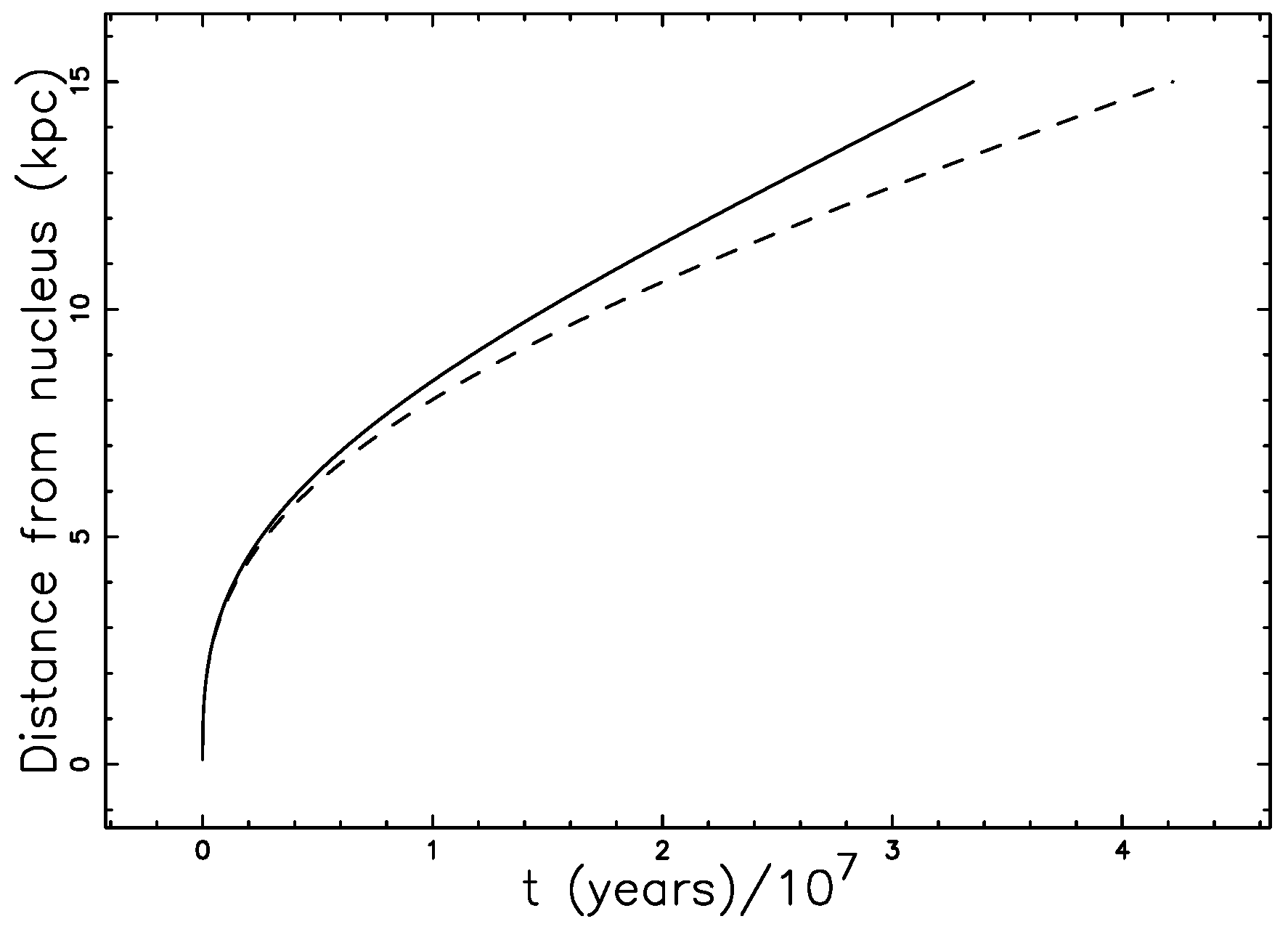
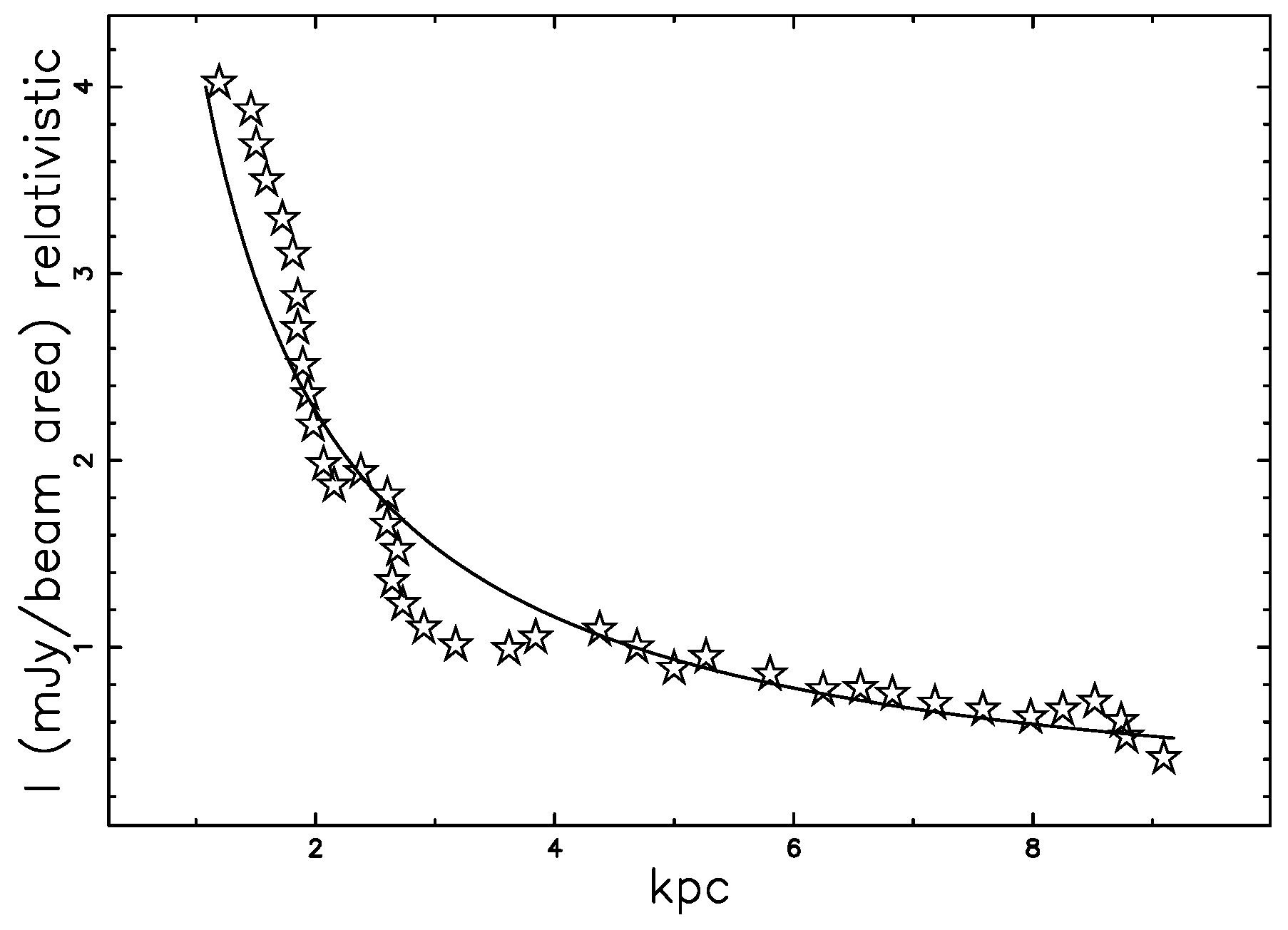
4. Astrophysical Applications
4.1. Direct Conversion
4.2. The Magnetic Field of Equipartition
5. Conclusions
Funding
Conflicts of Interest
References
- Curtis, H.D. Descriptions of 762 Nebulae and Clusters Photographed with the Crossley Reflector. Publ. Lick Obs. 1918, 13, 9–42. [Google Scholar]
- Fanaroff, B.L.; Riley, J.M. The morphology of extragalactic radio sources of high and low luminosity. Mon. Not. R. Astron. Soc. 1974, 167, 31P–36P. [Google Scholar] [CrossRef]
- Kembhavi, A.K.; Narlikar, J.V. Quasars and Active Galactic Nuclei: An Introduction; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Bridle, A.H.; Perley, R.A. Extragalactic Radio Jets. Annu. Rev. Astron. Astrophys. 1984, 22, 319–358. [Google Scholar] [CrossRef]
- Liu, F.K.; Zhang, Y.H. A new list of extra-galactic radio jets. Astron. Astrophys. 2002, 381, 757–760. [Google Scholar] [CrossRef]
- Hardcastle, M.J.; Sakelliou, I. Jet termination in wide-angle tail radio sources. Mon. Not. R. Astron. Soc. 2004, 349, 560–575. [Google Scholar] [CrossRef]
- Laing, R.A.; Bridle, A.H. Relativistic models and the jet velocity field in the radio galaxy 3C 31. Mon. Not. R. Astron. Soc. 2002, 336, 328–352. [Google Scholar] [CrossRef]
- Nawaz, M.A.; Wagner, A.Y.; Bicknell, G.V.; Sutherland, R.S.; McNamara, B.R. Jet-intracluster medium interaction in Hydra A—I. Estimates of jet velocity from inner knots. Mon. Not. R. Astron. Soc. 2014, 444, 1600–1614. [Google Scholar] [CrossRef]
- Nawaz, M.A.; Bicknell, G.V.; Wagner, A.Y.; Sutherland, R.S.; McNamara, B.R. Jet-intracluster medium interaction in Hydra A—II. The effect of jet precession. Mon. Not. R. Astron. Soc. 2016, 458, 802–815. [Google Scholar] [CrossRef]
- Zaninetti, L. Classical and relativistic conservation of momentum flux in radio-galaxies. Appl. Phys. Res. 2015, 7, 43–62. [Google Scholar] [CrossRef]
- Zaninetti, L. Classical and Relativistic Flux of Energy Conservation in Astrophysical Jets. J. High Energy Phys. Gravit. Cosmol. 2016, 1, 41–56. [Google Scholar] [CrossRef]
- Kellermann, K.I.; Richards, E.A. Radio Observations of the Hubble Deep Field. In The Hubble Deep Field; Livio, M., Fall, S.M., Madau, P., Eds.; Cambridge University Press: Cambridge, UK, 1998; p. 60. [Google Scholar]
- Bird, R.; Stewart, W.; Lightfoot, E. Transport Phenomena, 2nd ed.; John Wiley and Sons: New York, NY, USA, 2002. [Google Scholar]
- Landau, L. Fluid Mechanics, 2nd ed.; Pergamon Press: London, UK, 1987. [Google Scholar]
- Goldstein, S. Modern Developments in Fluid Dynamics; Dover: New York, NY, USA, 1965. [Google Scholar]
- Reichardt, V. Gesetzmabigkeiten der freien Turbulenz. VDI-Forschungsheft 1942, 414, 141. [Google Scholar]
- Reichardt, V. Vollstandige Darstellung der turbulenten Geschwindigkeitsverteilung in glatten Leitungen. Z. Angew. Math. Mech. 1951, 31, 208–219. [Google Scholar] [CrossRef]
- Schlichting, H. Boundary Layer Theory; McGraw-Hill: New York, NY, USA, 1979. [Google Scholar]
- De Young, D.S. The Physics of Extragalactic Radio Sources; University of Chicago Press: Chicago, IL, USA, 2002. [Google Scholar]
- Laing, R.A.; Bridle, A.H. Adiabatic relativistic models for the jets in the radio galaxy 3C 31. Mon. Not. R. Astron. Soc. 2004, 348, 1459–1472. [Google Scholar] [CrossRef]
- Lane, H.J. On the Theoretical Temperature of the Sun, under the Hypothesis of a gaseous Mass maintaining its Volume by its internal Heat, and depending on the laws of gases as known to terrestrial Experiment. Am. J. Sci. 1870, 148, 57–74. [Google Scholar] [CrossRef]
- Emden, R. Gaskugeln: Anwendungen der Mechanischen Warmetheorie auf Kosmologische und Meteorologische Probleme; B.G. Teubner: Berlin, Germany, 1907. [Google Scholar]
- Chandrasekhar, S. An Introduction to the Study of Stellar Structure; Dover: New York, NY, USA, 1967. [Google Scholar]
- Binney, J.; Tremaine, S. Galactic Dynamics, 2nd ed.; Princeton University Press: Princeton, NJ, USA, 2011. [Google Scholar]
- Zwillinger, D. Handbook of Differential Equations; Academic Press: New York, NY, USA, 1989. [Google Scholar]
- Hansen, C.J.; Kawaler, S.D. Stellar Interiors. Physical Principles, Structure, and Evolution; Springer: Berlin, Germany, 1994. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables; Dover: New York, NY, USA, 1965. [Google Scholar]
- Von Seggern, D. CRC Standard Curves and Surfaces; CRC: New York, NY, USA, 1992. [Google Scholar]
- Thompson, W.J. Atlas for Computing Mathematical Functions; Wiley-Interscience: New York, NY, USA, 1997. [Google Scholar]
- Olver, F.W.J.; Lozier, D.W.; Boisvert, R.F.; Clark, C.W. NIST Handbook of Mathematical Functions; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Ashby, N. Relativity in the Global Positioning System. Living Rev. Relativ. 2003, 6, 1. [Google Scholar] [CrossRef] [PubMed]
- Ashby, N.; Nelson, R.A. GPS, Relativity, and Extraterrestrial Navigation. In Proceedings of the IAU Symposium #261, Relativity in Fundamental Astronomy: Dynamics, Reference Frames, and Data Analysis, Virginia Beach, VA, USA, 27 April–1 May 2009; American Astronomical Society: Washington, DC, USA, 2009; Volume 261, p. 889. [Google Scholar]
- Adachi, M.; Kasai, M. An Analytical Approximation of the Luminosity Distance in Flat Cosmologies with a Cosmological Constant. Prog. Theor. Phys. 2012, 127, 145–152. [Google Scholar] [CrossRef]
- Aviles, A.; Bravetti, A.; Capozziello, S.; Luongo, O. Precision cosmology with Padé rational approximations: Theoretical predictions versus observational limits. Phys. Rev. D 2014, 90, 043531. [Google Scholar] [CrossRef]
- Wei, H.; Yan, X.P.; Zhou, Y.N. Cosmological applications of Pade approximant. J. Cosmol. Astropart. Phys. 2014, 1, 45. [Google Scholar] [CrossRef]
- Lang, K.R. Astrophysical Formulae, 2nd ed.; Springer: New York, NY, USA, 1980. [Google Scholar]


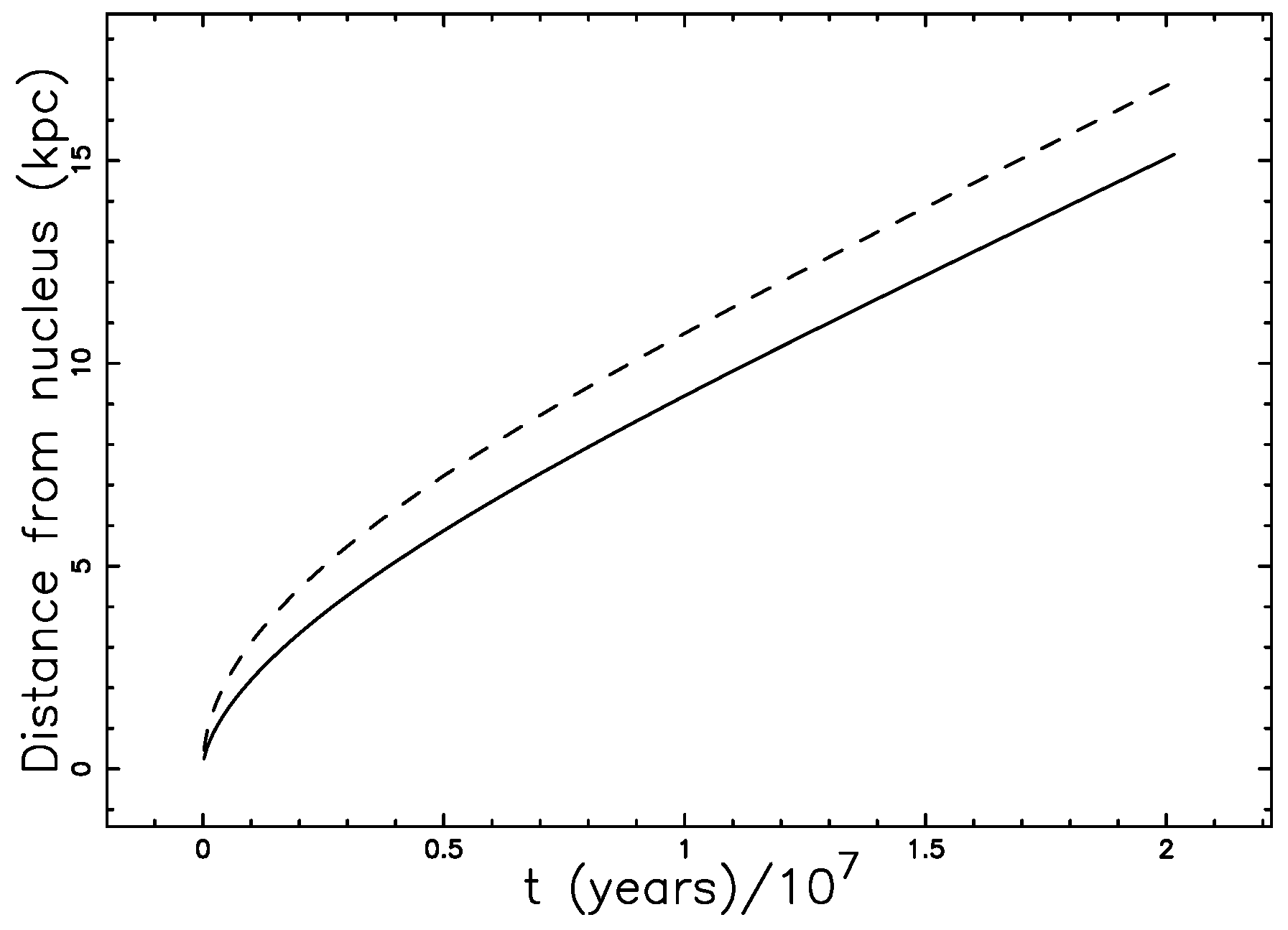
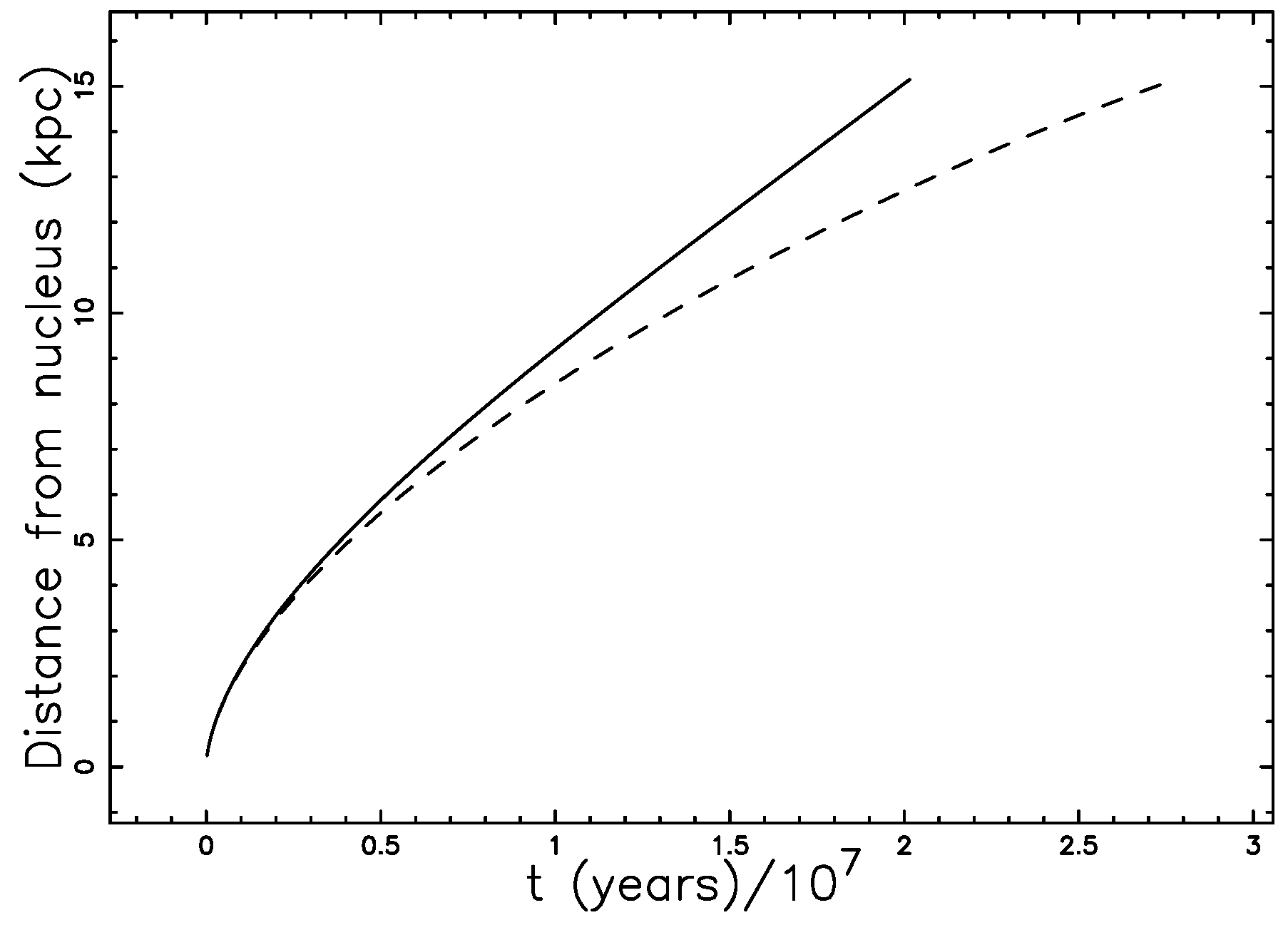
| Parameter | Value |
|---|---|
| (pc) | 100 |
| () | 10,000 |
| b (pc) | 10,000 |
| Parameter | Value |
|---|---|
| (pc) | 100 |
| 0.9 | |
| b (pc) | 10,000 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zaninetti, L. Classical and Relativistic Evolution of an Extra-Galactic Jet with Back-Reaction. Galaxies 2018, 6, 134. https://doi.org/10.3390/galaxies6040134
Zaninetti L. Classical and Relativistic Evolution of an Extra-Galactic Jet with Back-Reaction. Galaxies. 2018; 6(4):134. https://doi.org/10.3390/galaxies6040134
Chicago/Turabian StyleZaninetti, Lorenzo. 2018. "Classical and Relativistic Evolution of an Extra-Galactic Jet with Back-Reaction" Galaxies 6, no. 4: 134. https://doi.org/10.3390/galaxies6040134
APA StyleZaninetti, L. (2018). Classical and Relativistic Evolution of an Extra-Galactic Jet with Back-Reaction. Galaxies, 6(4), 134. https://doi.org/10.3390/galaxies6040134





