The Laboratory Astrophysics Spectroscopy Programme at Imperial College London
Abstract
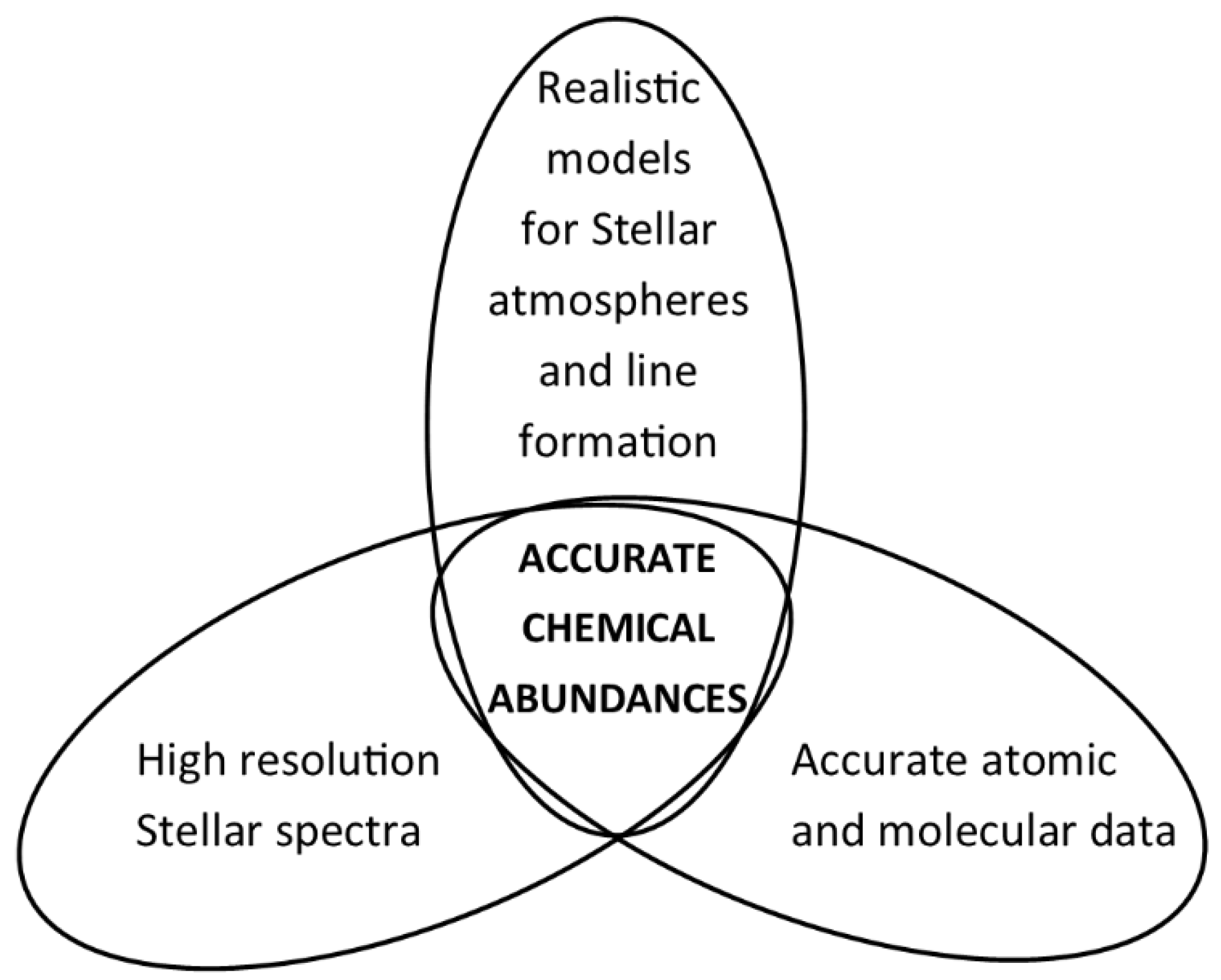
1. Introduction
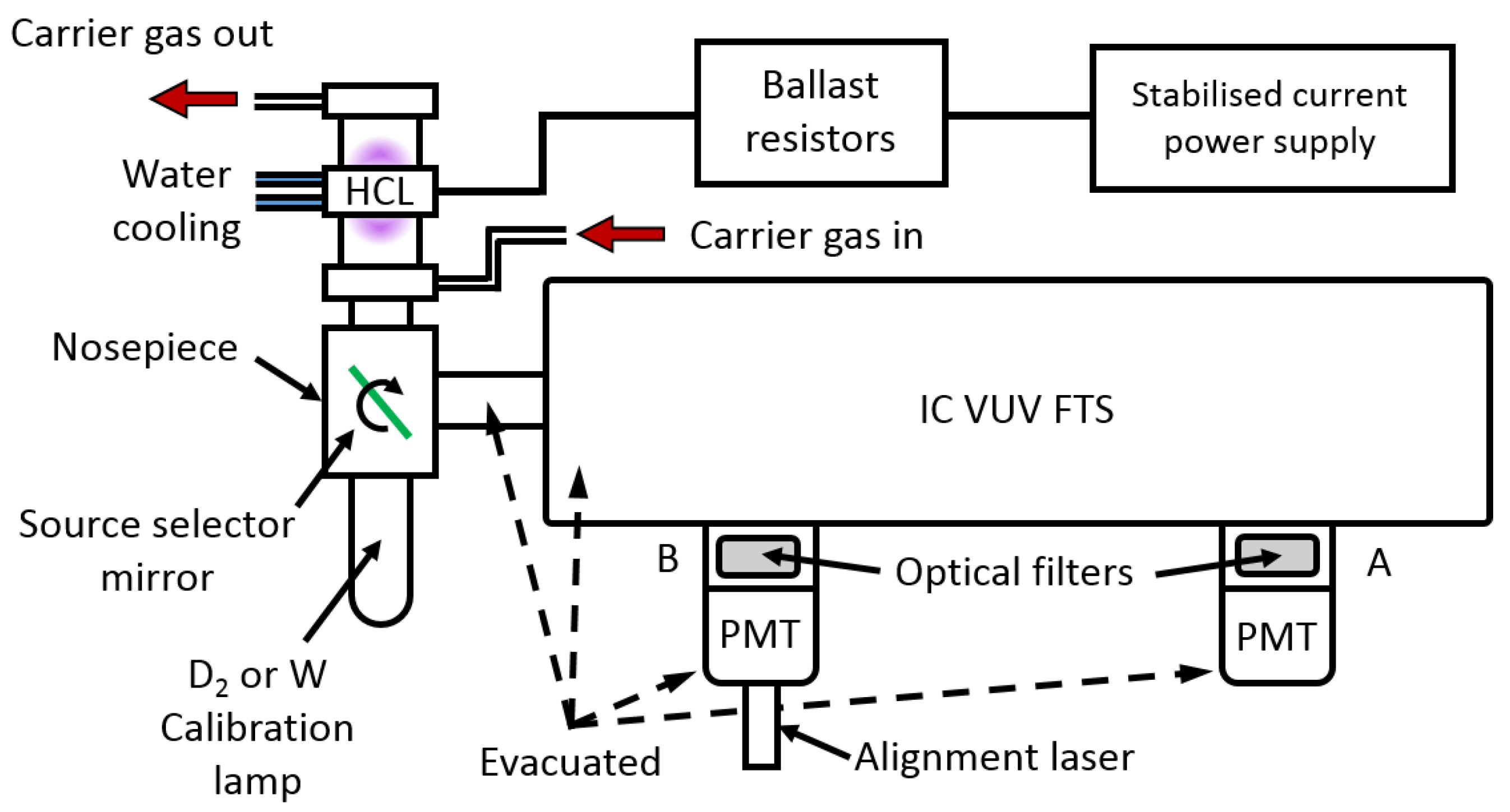
2. Our Experimental Set-Up
- Combination of high resolution and wide wavelength range
- Linear wavenumber scale
- Slowly varying intensity response function
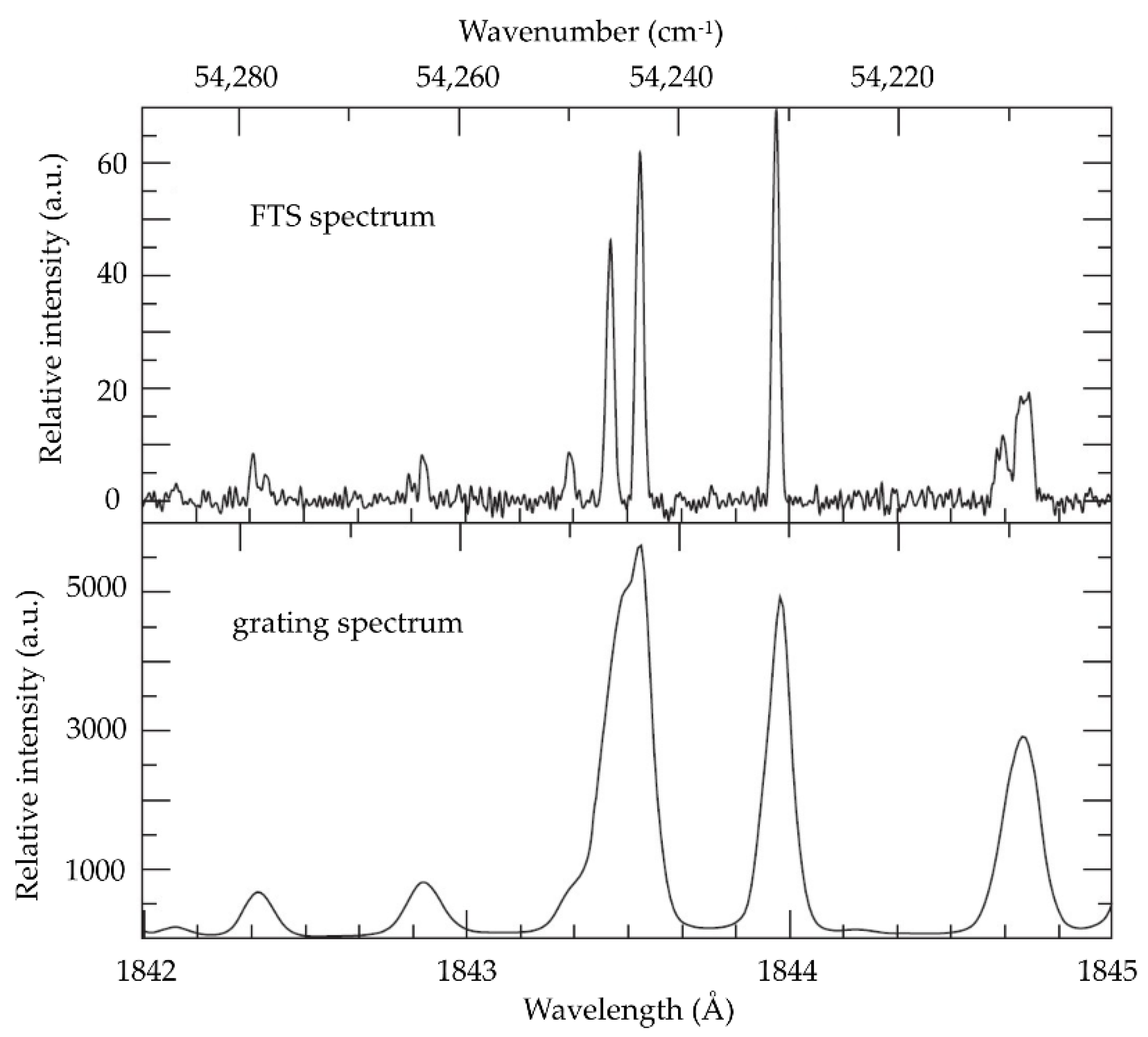
3. Our Laboratory Measurements
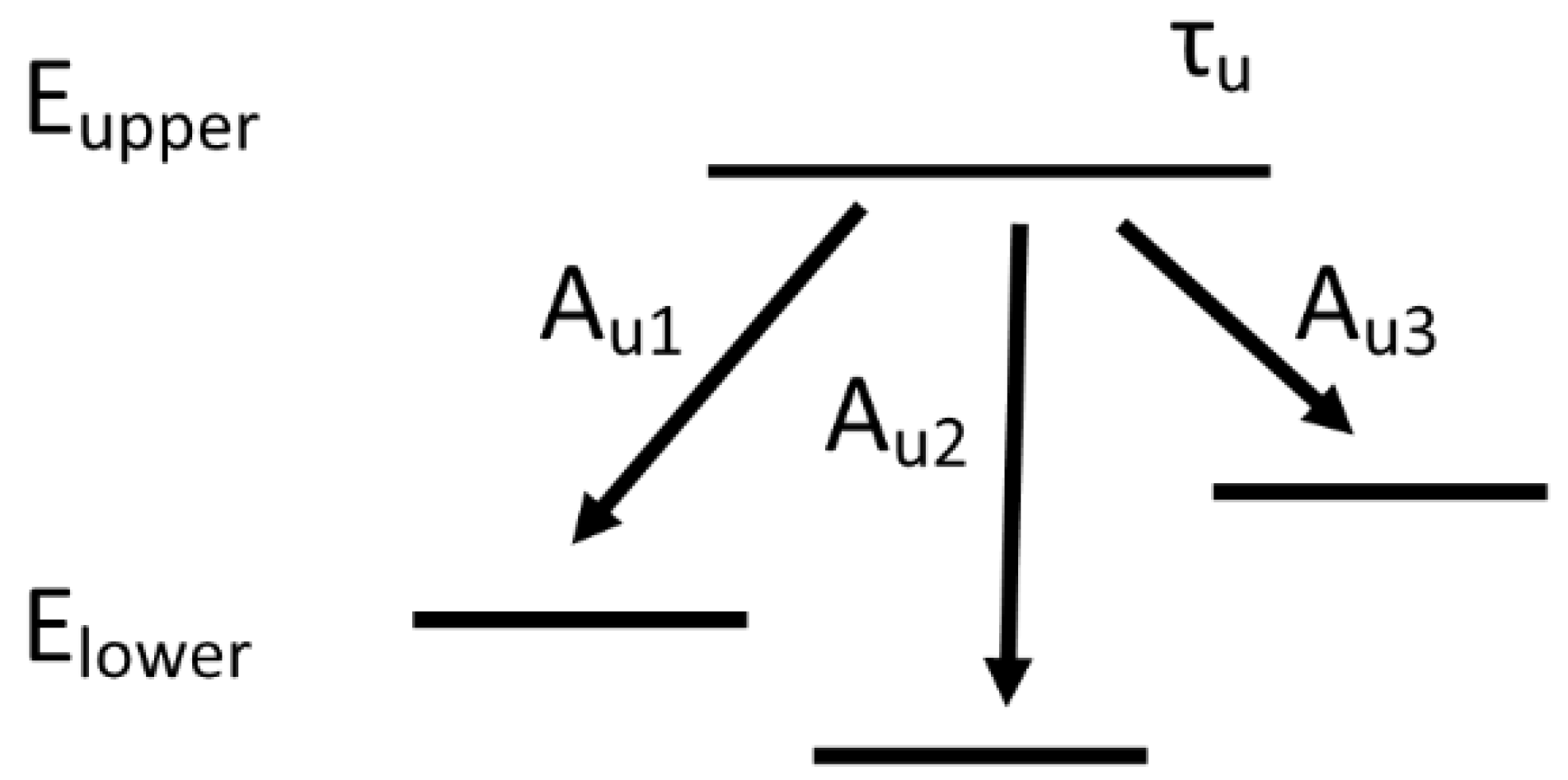
3.1. Transition Probabilities
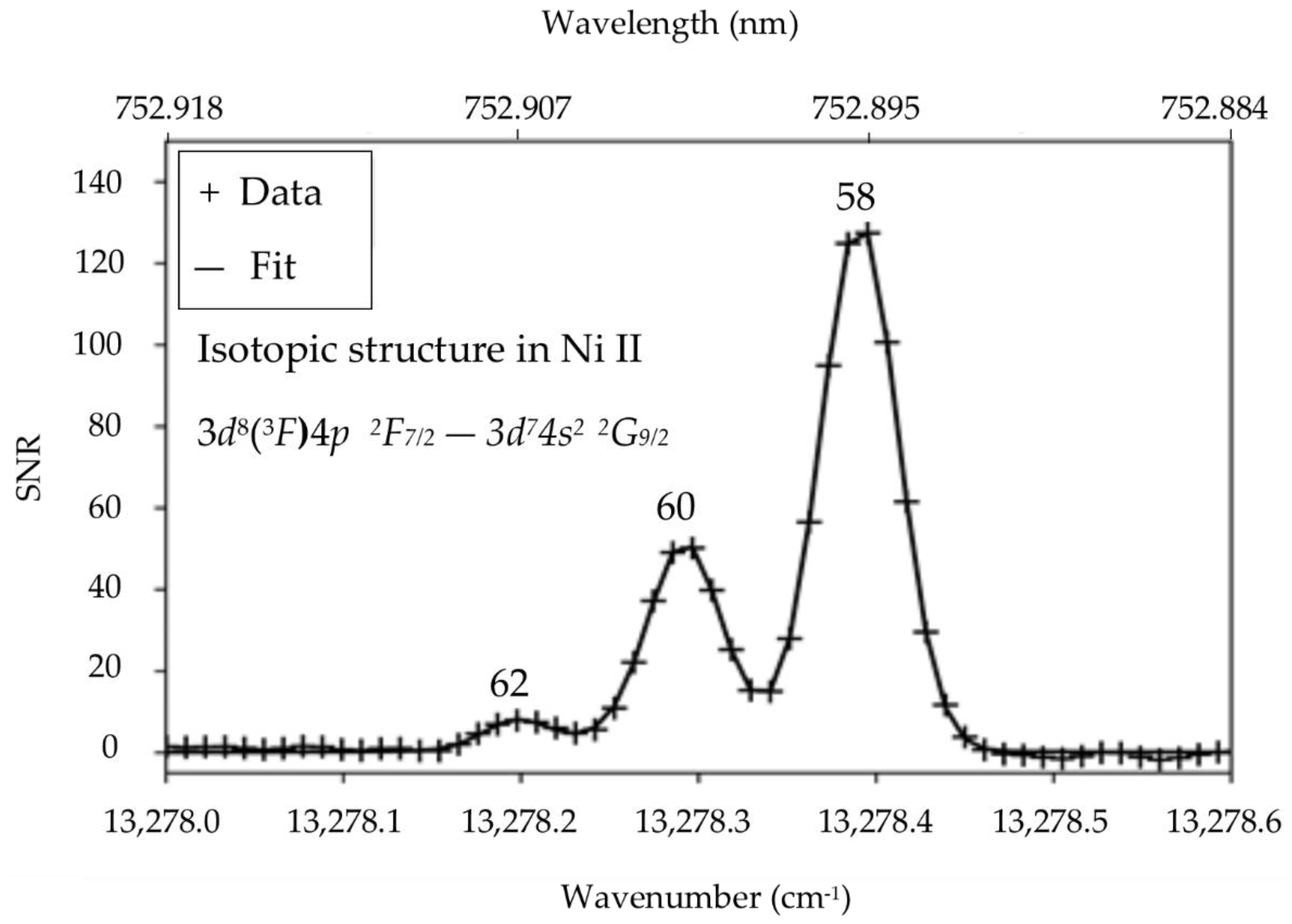
3.2. Wavelengths, Energy Levels, Hyperfine and Isotopic Structure
4. Future Work and Collaborations
- Light proton-capture elements: Li, C, O
- α-elements: Mg, Si, Ca, Ti
- Light elements with odd atomic number: Na, Al, K
- Iron-peak elements: Sc, V, Cr, Mn, Fe, Co, Ni, Cu, Zn
- Neutron-capture elements: Rb, Sr,Y, Zr, Ba, La, Ru, Ce, Nd, Eu
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Pickering, J.C. Laboratory Astrophysics: Improving the Atomic Data by Fourier Transform Spectrometry. Phys. Scr. 1999, T83, 27–34. [Google Scholar] [CrossRef]
- Pickering, J.C. High resolution Fourier transform spectroscopy with the Imperial College (IC) UV-FT spectrometer, and its applications to astrophysics and atmospheric physics: A review. Vib. Spectrosc. 2002, 29, 27–43. [Google Scholar] [CrossRef]
- Pickering, J.C.; Blackwell-Whitehead, R.; Thorne, A.P.; Ruffoni, M.P.; Holmes, C.E. Laboratory measurements of oscillator strengths and their astrophysical applications. Can. J. Phys. 2011, 89, 387–393. [Google Scholar] [CrossRef]
- Wahlgren, G.M. Atomic data for stellar astrophysics: From the UV to the IR. Can. J. Phys. 2011, 89, 345–356. [Google Scholar] [CrossRef]
- Nave, G.; Sansonetti, C.J.; Townley-smith, K.; Pickering, J.C.; Thorne, A.P.; Liggins, F.; Clear, C. Comprehensive atomic wavelengths, energy levels, and hyperfine structure for singly ionized iron-group elements. Can. J. Phys. 2017, 816, 811–816. [Google Scholar] [CrossRef]
- Lawler, J.E.; Sneden, C.; Cowan, J.J.; Den Hartog, E.A.; Wood, M.P. Laboratory transition probabilities for studies of nucleosynthesis of Fe-group elements. Can. J. Phys. 2017, 10, 783–789. [Google Scholar] [CrossRef]
- Allende Prieto, C. Solar and stellar photospheric abundances. Living Rev. Sol. Phys. 2016, 13, 1–40. [Google Scholar] [CrossRef]
- Barklem, P.S. Accurate abundance analysis of late-type stars: advances in atomic physics. Astron. Astrophys. Rev. 2016, 24, 1–54. [Google Scholar] [CrossRef]
- Clear, C.P. The Spectrum and Term Analysis of Singly Ionised Nickel. Ph.D. Thesis, Imperial College London, London, UK, 2018. [Google Scholar]
- Davis, S.P.; Abrams, M.C.; Brault, J.W. Fourier Transform Spectrometry; Academic Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Nave, G.; Griesmann, U.; Brault, J.W.; Abrams, M.C. XGREMLIN: Interferograms and spectra from Fourier transform spectrometers analysis, Astrophysics Source Code Library, record ascl:1511.004, 2015. Available online: https://github.com/gnave/Xgremlin (accessed on 12 October 2018).
- Smillie, D.G.; Pickering, J.C.; Nave, G.; Smith, P.L. The spectrum and term analysis of Co III measured using Fourier Transform and grating spectroscopy. Astrophys. J. Suppl. Ser. 2016, 223, 12. [Google Scholar] [CrossRef]
- Learner, R.C.M.; Thorne, A.P. Wavelength calibration of Fourier-transform emission spectra with applications to Fe I. J. Opt. Soc. Am. B 1988, 5, 2045–2059. [Google Scholar] [CrossRef]
- Whaling, W.; Anderson, W.H.C.; Carle, M.T.; Brault, J.W.; Zarem, H.A. Argon ion linelist and level energies in the hollow-cathode discharge. J. Quant. Spectrosc. Radiat. Transf. 1995, 53, 1–22. [Google Scholar] [CrossRef]
- Amarsi, A.M.; Lind, K.; Asplund, M.; Barklem, P.S.; Collet, R. Non-LTE line formation of Fe in late-type stars - III. 3D non-LTE analysis of metal-poor stars. Mon. Not. R. Astron. Soc. 2016, 463, 1518–1533. [Google Scholar] [CrossRef]
- Lind, K.; Amarsi, A.M.; Asplund, M.; Barklem, P.S.; Bautista, M.; Bergemann, M.; Collet, R.; Kiselman, D.; Leenaarts, J.; Pereira, T.M.D. Non-LTE line formation of Fe in late-type stars- IV. Modelling of the solar centre-to-limb variation in 3D. Mon. Not. R. Astron. Soc. 2017, 4322, 4311–4322. [Google Scholar] [CrossRef]
- Bergemann, M.; Collet, R.; Schoenrich, R.; Andrae, R.; Kovalev, M.; Ruchti, G.; Hansen, C.J.; Magic, Z. Non-local thermodynamic equilibrium stellar spectroscopy with 1D and 3D models - II. Chemical properties of the Galactic metal-poor disk and the halo. Astrophys. J. 2016, 847, 16. [Google Scholar] [CrossRef]
- Bergemann, M.; Collet, R.; Amarsi, A.M.; Kovalev, M.; Ruchti, G.; Magic, Z. Non-local thermodynamic equilibrium stellar spectroscopy with 1D and 3D models—I. Methods and application to magnesium abundances in standard stars. Astrophys. J. 2017, 847, 15. [Google Scholar] [CrossRef]
- Borrero, J.M.; Rubio, L.R.B.; Barklem, P.S.; Iniesta, J.C.T. Accurate atomic parameters for near-infrared spectral lines. Astron. Astrophys. 2003, 404, 749–762. [Google Scholar] [CrossRef]
- Wiese, W.L. Spectroscopic diagnostics of low temperature plasmas: techniques and required data. Spectrochim. Acta Part B At. Spectrosc. 1991, 46, 831–841. [Google Scholar] [CrossRef]
- Wiese, W.L. Atomic Oscillator Strengths for Light Elements–Progress and Problems. J. Korean Phys. Soc. 1998, 33, 207–213. [Google Scholar]
- Musielok, J.; Wiese, W.L.; Veres, G. Atomic transition probabilities and tests of the spectroscopic coupling scheme for N I. Phys. Rev. A 1995, 51, 3588–3597. [Google Scholar] [CrossRef] [PubMed]
- Nitz, D.E.; Curry, J.J.; Buuck, M.; Demann, A.; Mitchell, N.; Shull, W. Transition probabilities of Ce I obtained from Boltzmann analysis of visible and near-infrared emission spectra. J. Phys. B At. Mol. Opt. Phys. 2018, 51, 045007. [Google Scholar] [CrossRef]
- Huber, M.C.E.; Sandeman, R.J. The measurement of oscillator strengths. Reports Prog. Phys. 1986, 49, 397–490. [Google Scholar] [CrossRef]
- Thorne, A.P.; Litzén, U.; Johansson, S. Spectrophysics; Springer: Berlin, Germany, 1999; ISBN 3-540-65117-9. [Google Scholar]
- Kurucz, R.L. Kurucz Database. Available online: http://kurucz.harvard.edu/atoms.html (accessed on 12 October 2018).
- Pickering, J.C.; Thorne, A.P.; Perez, R. Oscillator strengths of transitions in Ti II in the visible and ultraviolet regions. Astrophys. J. Suppl. Ser. 2001, 132, 403–409. [Google Scholar] [CrossRef]
- Lawler, J.E.; Bergeson, S.D.; Wamsley, R.C. Advanced experimental techniques for measuring oscillator strengths of vacuum ultraviolet lines. Phys. Scr. 1993, 1993, 29–35. [Google Scholar] [CrossRef]
- Pehlivan Rhodin, A.; Belmonte, M.T.; Engström, L.; Lundberg, H.; Nilsson, H.; Hartman, H.; Pickering, J.C.; Clear, C.; Quinet, P.; Fivet, V.; et al. Lifetime measurements and oscillator strengths in singly ionized scandium and the solar abundance of scandium. Mon. Not. R. Astron. Soc. 2017, 472, 3337–3353. [Google Scholar] [CrossRef]
- Ruffoni, M.P.; Allende Prieto, C.; Nave, G.; Pickering, J.C. Infrared laboratory oscillator strengths of Fe I in the H-band. Astrophys. J. 2013, 779, 17. [Google Scholar] [CrossRef]
- Ruffoni, M.P.; Den Hartog, E.A.; Lawler, J.E.; Brewer, N.R.; Lind, K.; Nave, G.; Pickering, J.C. Fe I oscillator strengths for the Gaia-ESO survey. Mon. Not. R. Astron. Soc. 2014, 441, 3127–3136. [Google Scholar] [CrossRef]
- Den Hartog, E.A.; Ruffoni, M.P.; Lawler, J.E.; Pickering, J.C.; Lind, K.; Brewer, N.R. Fe I oscillator strengths for transitions from high-lying even-parity levels. Astrophys. J. Suppl. Ser. 2014, 215, 23. [Google Scholar] [CrossRef]
- Belmonte, M.T.; Pickering, J.C.; Ruffoni, M.P.; Den Hartog, E.A.; Lawler, J.E.; Guzman, A.; Heiter, U. Fe I Oscillator Strengths for Transitions from High-lying Odd-parity Levels. Astrophys. J. 2017, 848, 125. [Google Scholar] [CrossRef]
- Majewski, S.R.; Schiavon, R.P.; Frinchaboy, P.M.; et al. The Apache Point Observatory Galactic Evolution Experiment (APOGEE). Astron. J. 2017, 154, 94. [Google Scholar] [CrossRef]
- Gilmore, G.; Randich, S.; Asplund, M.; Binney, J.; Bonifacio, P.; Drew, J.; Feltzing, S.; Ferguson, A.; Jeffries, R.; Micela, G.; et al. The Gaia-ESO Public Spectroscopic Survey. Messenger 2012, 147, 25–31. [Google Scholar]
- Holmes, C.E.; Pickering, J.C.; Ruffoni, M.P.; Blackwell-Whitehead, R.; Nilsson, H.; Engström, L.; Hartman, H.; Lundberg, H.; Belmonte, M.T. Experimentally Measured Radiative Lifetimes and Oscillator Strengths in Neutral Vanadium. Astrophys. J. Suppl. Ser. 2016, 224, 35. [Google Scholar] [CrossRef]
- Lyubchik, Y.; Jones, H.R.A.; Pavlenko, Y.V.; Viti, S.; Pickering, J.C.; Blackwell-Whitehead, R.J. Atomic lines in infrared spectra for ultracool dwarfs. Astron. Astrophys. 2004, 416, 655–659. [Google Scholar] [CrossRef]
- Blackwell-Whitehead, R.J.; Lundberg, H.; Nave, G.; Pickering, J.C.; Jones, H.R.A.; Lyubchik, Y.; Pavlenko, Y.V.; Viti, S. Experimental Ti i oscillator strengths and their application to cool star analysis. Mon. Not. R. Astron. Soc. 2006, 373, 1603–1609. [Google Scholar] [CrossRef]
- Blackwell-Whitehead, R.J.; Xu, H.L.; Pickering, J.C.; Nave, G.; Lundberg, H. Experimental oscillator strengths for the spectrum of neutral manganese. Mon. Not. R. Astron. Soc. 2005, 361, 1281–1286. [Google Scholar] [CrossRef]
- Ryabchikova, T.; Piskunov, N.; Kurucz, R.L.; Stempels, H.C.; Heiter, U.; Pakhomov, Y.; Barklem, P.S. A major upgrade of the VALD database. Phys. Scr. 2015, 90, 054005. [Google Scholar] [CrossRef]
- Dubernet, M.L.; Antony, B.K.; Ba, Y.A.; Babikov, Y.L.; Bartschat, K.; Boudon, V.; Braams, B.J.; Chung, H.-K.; Daniel, F.; Delahaye, F.; et al. The virtual atomic and molecular data centre (VAMDC) consortium. J. Phys. B At. Mol. Opt. Phys. 2016, 49, 074003. [Google Scholar] [CrossRef]
- Laverick, M.; Lobel, A.; Merle, T.; Royer, P.; Martayan, C.; David, M.; Hensberge, H.; Thienpont, E. The Belgian repository of fundamental atomic data and stellar spectra (BRASS). I. Cross-matching atomic databases of astrophysical interest. Astron. Astrophys. 2018, 612, A60. [Google Scholar] [CrossRef]
- Heiter, U.; Lind, K.; Asplund, M.; Barklem, P.S.; Bergemann, M.; Magrini, L.; Masseron, T.; Mikolaitis; Pickering, J.C.; Ruffoni, M.P. Atomic and molecular data for optical stellar spectroscopy. Phys. Scr. 2015, 90, 054010. [Google Scholar] [CrossRef]
- Shetrone, M.; Bizyaev, D.; Lawler, J.E.; Prieto, C.A.; Johnson, J.A.; Smith, V.V.; Cunha, K.; Holtzman, J.; García Pérez, A.E.; Mészáros, S.Z.; et al. The SDSS-III apogee spectral line list for H-Band spectroscopy. Astrophys. J. Suppl. Ser. 2015, 221, 24. [Google Scholar] [CrossRef]
- Vujnović, V.; Wiese, W.L. A Critical Compilation of Atomic Transition Probabilities for Singly Ionized Argon. J. Phys. Chem. Ref. Data 1992, 21, 919–939. [Google Scholar] [CrossRef]
- Wiese, W.L. The Critical Assessment of Atomic Oscillator Strengths. Phys. Scr. 1996, T65, 188–191. [Google Scholar] [CrossRef]
- Taylor, B.N.; Kuyatt, C.E. Guidelines for Evaluating and Expressing the Uncertainty of NIST Measurement Results. NIST Tech. Note 1994, 1297. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.437.5767&rep=rep1&type=pdf (accessed on 20 December 2018).
- Pehlivan Rhodin, A. Experimental and Computational Atomic Spectroscopy for Astrophysics: Oscillator Strengths and Lifetimes for Mg I, Si I, Si II, Sc I and Sc II. Ph.D. Thesis, Lund University, Lund, Sweden, March 2018. [Google Scholar]
- Sikstrom, C.M.; Nilsson, H.; Litzen, U.; Blom, A.; Lundberg, H. Uncertainty of oscillator strengths derived from lifetimes and branching fractions. J. Quant. Spectrosc. Radiat. Transf. 2002, 74, 355–368. [Google Scholar] [CrossRef]
- Pickering, J.C.; Johansson, S.; Smith, P.L. The FERRUM project: Branching ratios and atomic transition probabilities of Fe II transitions from the 3d6(a3F)4p subconfiguration in the visible to VUV spectral region. Astron. Astrophys. 2001, 337, 361–367. [Google Scholar] [CrossRef]
- Belmonte, M.T.; Djurovic, S.; Pelaez, R.J.; Aparicio, J.A.; Mar, S. Improved and expanded measurements of transition probabilities in UV Ar II spectral lines. Mon. Not. R. Astron. Soc. 2014, 445, 3345–3351. [Google Scholar] [CrossRef]
- Hibbert, A. Successes and Difficulties in Calculating Atomic Oscillator Strengths and Transition Rates. Galaxies 2018, 6, 77. [Google Scholar] [CrossRef]
- Kramida, A. Assessing Uncertainties of Theoretical Atomic Transition Probabilities with Monte Carlo Random Trials. Atoms 2014, 2, 86–122. [Google Scholar] [CrossRef] [PubMed]
- Bergemann, M.; Pickering, J.C.; Gehren, T. NLTE analysis of Co I/Co II lines in spectra of cool stars with new laboratory hyperfine splitting constants. Mon. Not. R. Astron. Soc. 2010, 401, 1334–1346. [Google Scholar] [CrossRef]
- Dalton, G.; Trager, S.; Abrams, D.C.; Bonifacio, P.; Aguerri, J.A.L.; Middleton, K.; Benn, C.; Dee, K.; Sayède, F.; Lewis, I.; et al. Final design and progress of WEAVE: the next generation wide-field spectroscopy facility for the William Herschel Telescope. Proc. SPIE Ground-Based Airborne Instrum. Astron. VI 2016, 9908, 99081G. [Google Scholar] [CrossRef]
- Martell, S.L.; Sharma, S.; Buder, S.; Duong, L.; Schlesinger, K.J.; Simpson, J.; Lind, K.; Ness, M.; Marshall, J.P.; Asplund, M.; et al. The GALAH survey: Observational overview and Gaia DR1 companion. Mon. Not. R. Astron. Soc. 2017, 465, 3203–3219. [Google Scholar] [CrossRef]
- Jong, R.S. de; 4MOST Consortium. Complementing asteroseismology with 4MOST spectroscopy. Astron. Nachr. 2016, 337, 964–969. [Google Scholar] [CrossRef]
- Cashman, F.H.; Kulkarni, V.P.; Kisielius, R.; Ferland, G.J.; Bogdanovich, P. Atomic Data Revisions for Transitions Relevant to Observations of Interstellar, Circumgalactic, and Intergalactic Matter. Astrophys. J. Suppl. Ser. 2017, 230, 8. [Google Scholar] [CrossRef]
- Zwölf, C.M.; Moreau, N.; Dubernet, M.L. New model for datasets citation and extraction reproducibility in VAMDC. J. Mol. Spectrosc. 2016, 327, 122–137. [Google Scholar] [CrossRef]

| Spectral range | 140–800 nm |
| Max. path difference | 20 cm |
| Resolving power | 2,000,000 at 200 nm |
| Min resolution limit | 0.025 cm−1 at 50,000 cm−1 |
| Max free spectral range | 64,000 cm−1 |
| Beamsplitter | Magnesium fluoride |
| Detector | Photomultiplier tube (PMT) |
| Dimensions | 1.5 × 0.25 × 0.25 m |
| Element | Spectral Range | Total Log(gf) (New) | Uncert (Dex) | Reference |
|---|---|---|---|---|
| Fe I | 213–1033 nm | 120 (22) | 0.02–0.1 | Belmonte et al., (2017) [33] |
| Sc II | 158–425 nm | 57 (57) | 0.03–0.11 | Pehlivan et al., (2017) [29] |
| V I | 304–2000 nm | 208 (13) | 0.02–0.1 | Holmes et al., (2016) [36] |
| Fe I | 320–1102 nm | 203 (81) | 0.02–0.11 | Den Hartog et al., (2014) [32] |
| Fe I | 352–1087 nm | 142 (64) | 0.02–0.14 | Ruffoni et al., (2014) [31] |
| Fe I | 1.5–1.7 µm | 28 (28) | 0.05–0.11 | Ruffoni et al., (2013) [30] |
| Mn I | 321–1400 nm | 20 (15) | 0.02–0.05 | Blackwell-Whitehead et al., (2011) [37] |
| Ti I | 465–3892 nm | 88 (67) | 0.04–0.08 | Blackwell-Whitehead et al., (2006) [38] |
| Mn I | 209–2780 nm | 44 (24) | 0.03–0.1 | Blackwell-Whitehead et al., (2005) [39] |
| Survey [ref.] | Instrument | Spectral Region | Resolving Power | Number Elements (Uncert Dex) | Date |
|---|---|---|---|---|---|
| APOGEE [34] | APOGEE | 1.51–1.7 µm | ~22,500 | 15 (0.1) | Ongoing |
| Gaia-ESO [35] | FLAMES-GIRAFFE | 400–480 nm | 16,200– | >~20 | Ongoing |
| 510–560 nm | 25,900 | ||||
| 630–680 nm | |||||
| 850–900 nm | |||||
| FLAMES-UVES | 410–680 nm | 47,000 | |||
| GALAH [56] | HERMES | 471.8–490.3 nm 564.9–587.3 nm 648.1–673.9 nm 759.0–789.0 nm | 28,000 (50,000) | 30 (0.05) | Ongoing |
| WEAVE [55] | WEAVE | 366–959 nm | 5000 20,000 | 2019 | |
| 4MOST [57] | HRS | 392.6–436.5 nm 516–573.8 nm 612–681 nm | >18,000 | 15 | 2021 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Belmonte, M.T.; Pickering, J.C.; Clear, C.P.; Concepción Mairey, F.; Liggins, F. The Laboratory Astrophysics Spectroscopy Programme at Imperial College London. Galaxies 2018, 6, 109. https://doi.org/10.3390/galaxies6040109
Belmonte MT, Pickering JC, Clear CP, Concepción Mairey F, Liggins F. The Laboratory Astrophysics Spectroscopy Programme at Imperial College London. Galaxies. 2018; 6(4):109. https://doi.org/10.3390/galaxies6040109
Chicago/Turabian StyleBelmonte, María Teresa, Juliet C. Pickering, Christian P. Clear, Florence Concepción Mairey, and Florence Liggins. 2018. "The Laboratory Astrophysics Spectroscopy Programme at Imperial College London" Galaxies 6, no. 4: 109. https://doi.org/10.3390/galaxies6040109
APA StyleBelmonte, M. T., Pickering, J. C., Clear, C. P., Concepción Mairey, F., & Liggins, F. (2018). The Laboratory Astrophysics Spectroscopy Programme at Imperial College London. Galaxies, 6(4), 109. https://doi.org/10.3390/galaxies6040109




