Simulations and Modeling of Intermediate Luminosity Optical Transients and Supernova Impostors
Abstract
1. Introduction
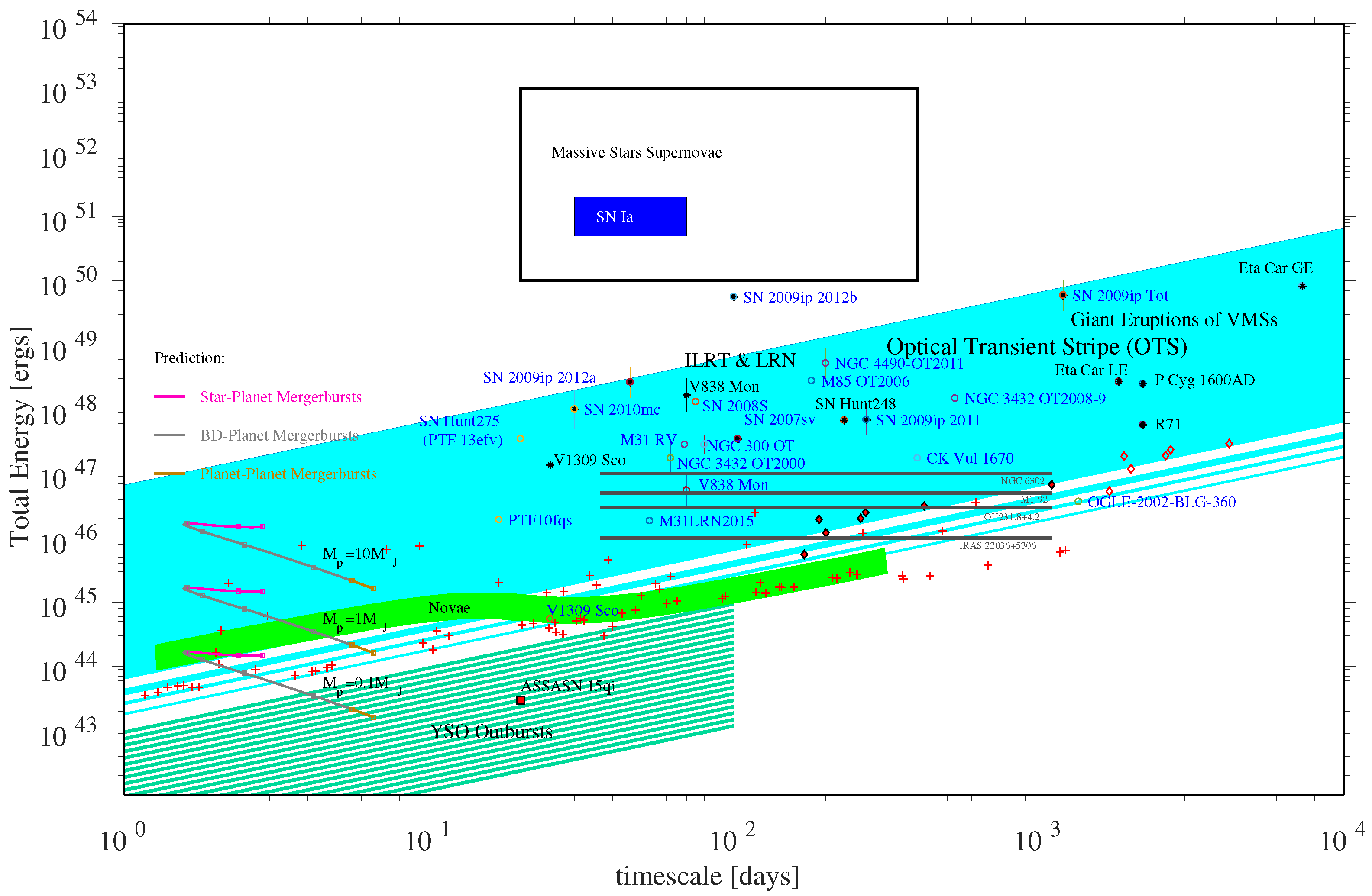
2. Common Properties of ILOTs
3. Types of ILOTs
- ILRT: Intermediate Luminosity Red Transients. Events involving evolved stars, such as Asymptotic Giant Branch (AGB) stars and similar objects, such as stars on the Red Giant Branch (RGB). The scenario which leads to these events is most probably a companion which accretes mass and the gravitational energy of the accreted mass supplies the energy of the eruption. Examples include NGC 300 OT, SN 2008S, and M31LRN 2015 (note the self-contradiction in the names of the last two transients).
- GEs: Giant Eruptions. Eruptive events of Luminous Blue Variables (LBVs) or other kinds of very massive stars (VMS), also known as SN impostors. We note that the weaker eruptions of LBVs, known as S Dor eruptions, are not included. From all ILOTs, these GEs are the ones with the highest energy. The energy released in one or in a sequence of these GEs can reach a few erg. Examples include the seventeenth century GE of P Cyg, the nineteenth century GEs of Car, and the pre-explosion eruptions of SN 2009ip. ILRTs are the low mass relatives of LBV GEs.
- LRN (or RT): Luminous Red Novae or Red Transients or Merger-Bursts. Refers to a quite diverse group. These transients are powered by a complete merger of two stars. The eruption can be preceded by a characteristic merger light-curve, as was observed for V1309 Sco. During the eruption, the observer sees a process of destruction of the less compressed star onto the denser star which is accompanied by the release of gravitational energy that powers the transient. Examples for LRN include V838 Mon and V1309 Sco and possibly, the more massive eruption NGC 4490-OT.
- Weaker Mergerburst between a planet and a brown dwarf (BD). It was suggested that in such a scenario the planet is shredded into a disk around the BD, and the energy from accretion lead to an outburst [5]. The destruction of the planet before it plunges into the BD may occur since its average density is smaller than the average density of the BD it encounters. The planet must enter the tidal radius of the BD for the scenario to be applicable. That may occur if the planet is in a highly eccentric orbit and gets perturbed. Once the planet is destructed as a result of the sequence of events, the remnant of the merger will resamble other LRNs, but on a shorter time scale and smaller energy. Nevertheless, this process is super Eddington. Mergerbursts between a planet and a BD occupy the lower part of the OTS on the ETD.
- Weak Outburst of a Young Stellar Object (YSO). In reference [6], it was suggested that the unusual outburst of the YSO ASASSN-15qi [19] is an ILOT event, similar in many respects to LRN events, such as V838 Mon, but much fainter and of lower total energy. The erupting system was young, but unlike the LRN, the secondary object that was tidally destroyed onto the primary main sequence (MS) star that was suggested to be a Saturn-like planet instead of a low mass MS companion. Such ILOTs are unusual in the sense that they have low power and reside below the OTS. These outbursts are related to FUor outbursts (e.g., reference [20]), which are pre-MS that experience an extreme change in magnitude with slow (years) decline and spectral type. They can be regarded as the more energetic counterparts of the EXor class of outburst, of which EX Lupis is a prototype [21]. These are pre-MS variables that show flares of a few months to a few years and of several magnitudes of amplitude as a result of episodic mass accretion. Another transient, ASASSN-13db [22], may also be a related object.
- ILOT which created a Planetary Nebulae (PN). In reference [4] we identified some intriguing similarities between PNe and ILOTs: (a) a linear velocity–distance relation; (b) a bipolar structure; (c) a total kinetic energy of ≈– erg. We therefore suggest that some PNe may have formed in an ILOT event lasting a few months (a short “lobe-forming” event). The power source is similar, namely, mass accretion onto a MS companion from the AGB (or ExAGB). The velocity of the fastest gas parcels in such an outburst will be in the order of the escape speed of the MS star, namely a few , though most of the gas is expected to interact with the AGB wind and slow down to a few . Examples include the PN NGC 6302, the pre-PNe OH231.8+4.2, M1-92, and the IRAS 22036+5306. This process was demonstrated in simulations [23], in which a very short impulsive mass ejection event from a binary system, namely an ILOT, developed a PN with clumpy lobes, quite similar to NGC 6302.
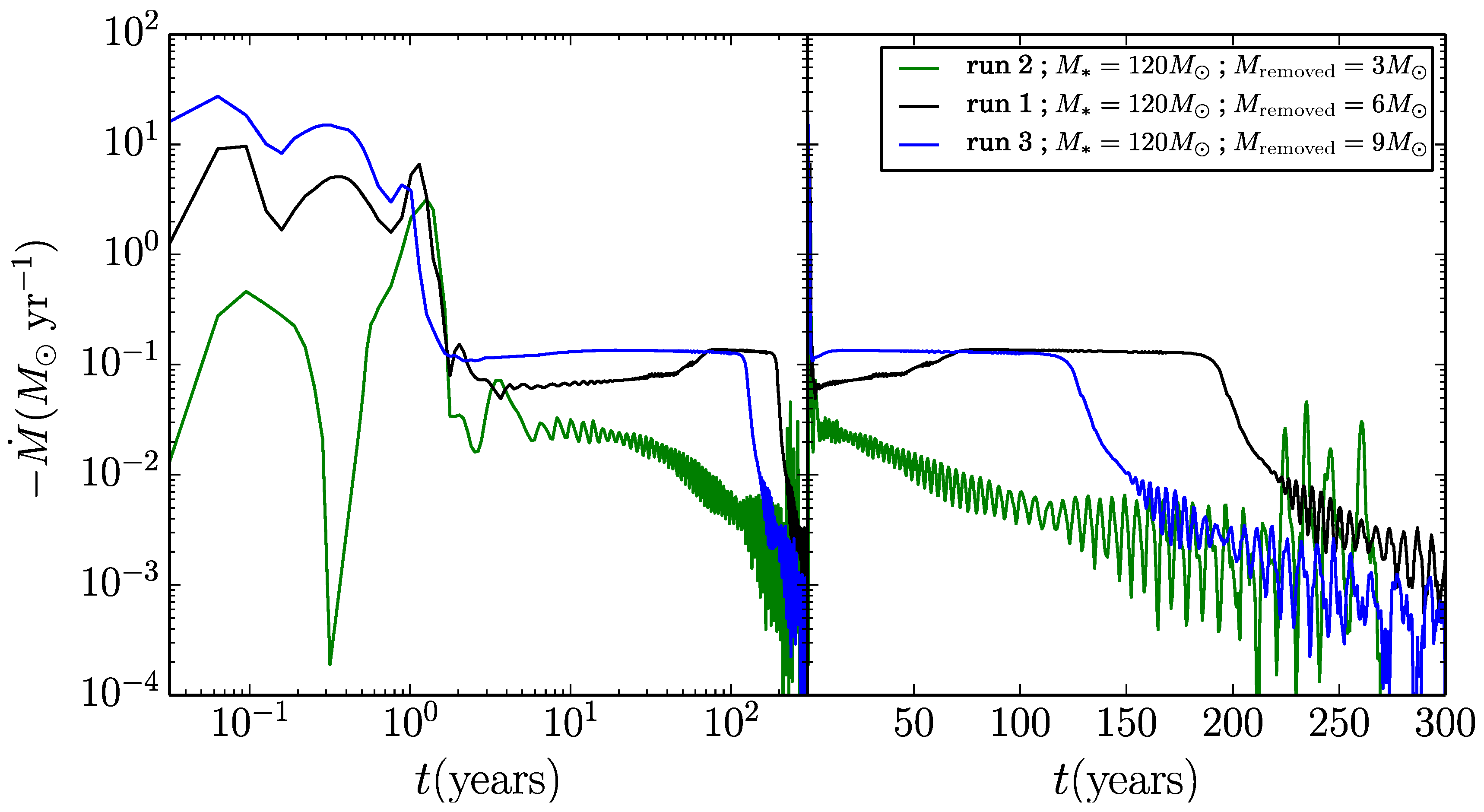
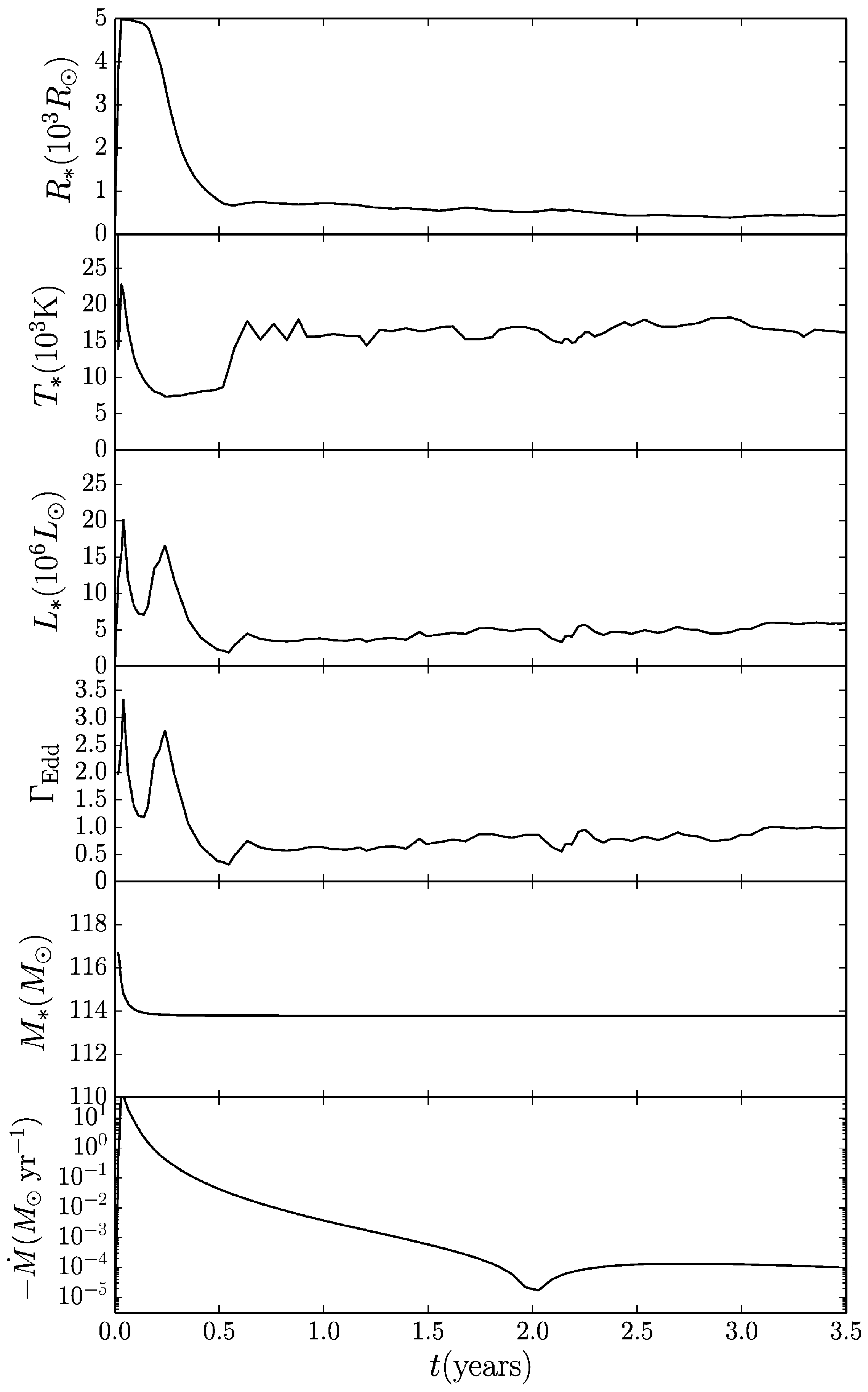
4. GEs in Very Massive Stars
5. Summary and Discussion
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AGB | Asymptotic Giant Branch |
| ASASSN | All-Sky Automated Survey for Supernovae |
| BD | Brown Dwarf |
| CSPN | Central Star of Planetary Nebula |
| ETD | Energy-Time Diagram |
| GE | Giant Eruption |
| HAPI | High Accretion Powered ILOT |
| ILOT | Intermediate Luminosity Optical Transient |
| ILRT | Intermediate Luminosity Red Transient |
| LBV | Luminous Blue Variable |
| LRN | Luminous Red Nova |
| MESA | Modules for Experiments in Stellar Astrophysics |
| MS | Main Sequence |
| OTS | Optical Transient Stripe |
| PN | Planetary Nebulae |
| SN | Supernova |
| VMS | Very Massive Star |
| YSO | Young Stellar Object |
References
- Della Valle, M.; Livio, M. The Calibration of Novae as Distance Indicators. Astrophys. J. 1995, 452, 704–709. [Google Scholar] [CrossRef]
- Yaron, O.; Prialnik, D.; Shara, M.M.; Kovetz, A. An Extended Grid of Nova Models. II. The Parameter Space of Nova Outbursts. Astrophys. J. 2005, 623, 398. [Google Scholar] [CrossRef]
- Shara, M.M.; Yaron, O.; Prialnik, D.; Kovetz, A.; Zurek, D. An Extended Grid of Nova Models. III. Very Luminous, Red Novae. Astrophys. J. 2010, 725, 831. [Google Scholar] [CrossRef]
- Soker, N.; Kashi, A. Formation of Bipolar Planetary Nebulae by Intermediate-luminosity Optical Transients. Astrophys. J. 2012, 746, 100. [Google Scholar] [CrossRef]
- Bear, E.; Kashi, A.; Soker, N. Mergerburst transients of brown dwarfs with exoplanets. Mon. Not. R. Astron. Soc. 2011, 416, 1965–1970. [Google Scholar] [CrossRef]
- Kashi, A.; Soker, N. An intermediate luminosity optical transient (ILOTs) model for the young stellar object ASASSN-15qi. Mon. Not. R. Astron. Soc. 2017, 468, 4938–4943. [Google Scholar] [CrossRef]
- Kashi, A.; Frankowski, A.; Soker, N. NGC 300 OT2008-1 as a Scaled-down Version of the Eta Carinae Great Eruption. Astrophys. J. Lett. 2010, 709, L11. [Google Scholar] [CrossRef]
- Tylenda, R.; Soker, N.; Szczerba, R. On the progenitor of V838 Monocerotis. Astron. Astrophys. 2005, 441, 1099–1109. [Google Scholar] [CrossRef][Green Version]
- Soker, N.; Tylenda, R. Violent stellar merger model for transient events. Mon. Not. R. Astron. Soc. 2006, 373, 733–738. [Google Scholar] [CrossRef]
- Tylenda, R.; Soker, N. Eruptions of the V838 Mon type: Stellar merger versus nuclear outburst models. Astron. Astrophys. 2006, 451, 223–236. [Google Scholar] [CrossRef]
- Kashi, A.; Soker, N. Operation of the jet feedback mechanism (JFM) in intermediate luminosity optical transients (ILOTs). Res. Astron. Astrophys. 2016, 16, 99. [Google Scholar] [CrossRef]
- Kashi, A.; Soker, N. Type II intermediate-luminosity optical transients (ILOTs). Mon. Not. R. Astron. Soc. 2017, 467, 3299. [Google Scholar] [CrossRef][Green Version]
- Balick, B. The evolution of planetary nebulae. I—Structures, ionizations, and morphological sequences. Astron. J. 1987, 94, 671–678. [Google Scholar] [CrossRef]
- Corradi, R.L.; Schwarz, H.E. Morphological populations of planetary nebulae: Which progenitors? I. Comparative properties of bipolar nebulae. Astron. Astrophys. 1995, 293, 871–888. [Google Scholar]
- Manchado, A.; Guerrero, M.A.; Stanghellini, L.; Serra-Ricart, M. The IAC Morphological Catalog of Northern Galactic Planetary Nebulae; Instituto de Astrofisica de Canarias: La Laguna, Spain, 1996. [Google Scholar]
- Parker, Q.A.; Bojičić, I.S.; Frew, D.J. HASH: The Hong Kong/AAO/Strasbourg Hα planetary nebula database. J. Phys. Conf. Ser. 2016, 728, 032008. [Google Scholar] [CrossRef]
- Sahai, R.; Morris, M.R.; Villar, G.G. Young Planetary Nebulae: Hubble Space Telescope Imaging and a New Morphological Classification System. Astron. J. 2011, 141, 134. [Google Scholar] [CrossRef]
- Adams, S.M.; Kochanek, C.S.; Gerke, J.R.; Stanek, K.Z.; Dai, X. The search for failed supernovae with the Large Binocular Telescope: Confirmation of a disappearing star. Mon. Not. R. Astron. Soc. 2017, 468, 4968–4981. [Google Scholar] [CrossRef]
- Herczeg, G.J.; Dong, S.; Shappee, B.J.; Chen, P.; Hillenbrand, L.A.; Jose, J.; Kochanek, C.S.; Prieto, J.L.; Stanek, K.Z.; Kaplan, K.; et al. The Eruption of the Candidate Young Star ASASSN-15QI. Astron. J. 2016, 831, 133. [Google Scholar] [CrossRef]
- Audard, M.; Abrahám, P.; Dunham, M.M.; Green, J.D.; Grosso, N.; Hamaguchi, K.; Kastner, J.H.; Kóspál, A.; Lodato, G.; Romanova, M.M.; et al. Episodic Accretion in Young Stars. In Protostars Planets VI; University of Arizona Press: Tucson, AZ, USA, 2014; pp. 387–410. [Google Scholar]
- Herbig, G.H. EX Lupi: History and Spectroscopy. Astron. J. 2007, 133, 2679. [Google Scholar] [CrossRef]
- Sicilia-Aguilar, A.; Oprandi, A.; Froebrich, D.; Fang, M.; Prieto, J.L.; Stanek, K.; Scholz, A.; Kochanek, C.S.; Henning, T.; Gredel, R.; et al. The 2014–2017 outburst of the young star ASASSN-13db. A time-resolved picture of a very-low-mass star between EXors and FUors. Astron. Astrophys. 2017, 607, A127. [Google Scholar] [CrossRef]
- Akashi, M.; Soker, N. Impulsive ejection of gas in bipolar planetary nebulae. Mon. Not. R. Astron. Soc. 2013, 436, 1961–1967. [Google Scholar] [CrossRef]
- Kashi, A.; Soker, N. Periastron Passage Triggering of the 19th Century Eruptions of Eta Carinae. Astrophys. J. 2010, 723, 602. [Google Scholar] [CrossRef]
- Livio, M.; Pringle, J.E. Wobbling Accretion Disks, Jets, and Point-symmetric Nebulae. Astrophys. J. 1997, 486, 835. [Google Scholar] [CrossRef]
- Soker, N. Collimated Fast Winds in Wide Binary Progenitors of Planetary Nebulae. Astrophys. J. 2001, 558, 157. [Google Scholar] [CrossRef][Green Version]
- Soker, N.; Livio, M. Disks and jets in planetary nebulae. Astrophys. J. 1994, 421, 219–224. [Google Scholar] [CrossRef]
- Kwok, S.; Hrivnak, B.J.; Su, K.Y. Discovery of a Disk-collimated Bipolar Outflow in the Proto-Planetary Nebula IRAS 17106-3046. Astrophys. J. Lett. 2000, 544, L149. [Google Scholar] [CrossRef]
- Sahai, R.; Nyman, L.-Å. Discovery of a Symmetrical Highly Collimated Bipolar Jet in Hen 2-90. Astrophys. J. Lett. 2000, 538, L145. [Google Scholar] [CrossRef]
- Sahai, R.; Vlemmings, W.H.; Gledhill, T.; Contreras, C.S.; Lagadec, E.; Nyman, L.Å.; Quintana-Lacaci, G. ALMA Observations of the Water Fountain Pre-planetary Nebula IRAS 16342-3814: High-velocity Bipolar Jets and an Expanding Torus. Astrophys. J. Lett. 2017, 835, L13. [Google Scholar] [CrossRef] [PubMed]
- Kwok, S. On the Origin of Morphological Structures of Planetary Nebulae. Galaxies 2018, 6, 66. [Google Scholar] [CrossRef]
- García-Arredondo, F.; Frank, A. Collimated Outflow Formation via Binary Stars: Three-Dimensional Simulations of Asymptotic Giant Branch Wind and Disk Wind Interactions. Astrophys. J. 2004, 600, 992. [Google Scholar] [CrossRef]
- Blackman, E.G.; Frank, A.; Welch, C. Magnetohydrodynamic Stellar and Disk Winds: Application to Planetary Nebulae. Astrophys. J. 2001, 546, 288. [Google Scholar] [CrossRef]
- Akashi, M.; Soker, N. Bipolar rings from jet-inflated bubbles around evolved binary stars. Mon. Not. R. Astron. Soc. 2016, 462, 206–216. [Google Scholar] [CrossRef][Green Version]
- Akashi, M.; Soker, N. Shaping planetary nebulae with jets in inclined triple stellar systems. Mon. Not. R. Astron. Soc. 2017, 469, 3296–3306. [Google Scholar] [CrossRef][Green Version]
- Kashi, A.; Davidson, K.; Humphreys, R.M. Recovery from Giant Eruptions in Very Massive Stars. Astrophys. J. 2016, 817, 66. [Google Scholar] [CrossRef]
- Fryxell, B.; Olson, K.; Ricker, P.; Timmes, F.X.; Zingale, M.; Lamb, D.Q.; MacNeice, P.; Rosner, R.; Truran, J.W.; Tufo, H. FLASH: An Adaptive Mesh Hydrodynamics Code for Modeling Astrophysical Thermonuclear Flashes. Astrophys. J. Suppl. Ser. 2000, 131, 273. [Google Scholar] [CrossRef]
- Paxton, B.; Bildsten, L.; Dotter, A.; Herwig, F.; Lesaffre, P.; Timmes, F. Modules for Experiments in Stellar Astrophysics (MESA). Astrophys. J. Suppl. Ser. 2011, 192, 3. [Google Scholar] [CrossRef]
- Paxton, B.; Cantiello, M.; Arras, P.; Bildsten, L.; Brown, E.F.; Dotter, A.; Mankovich, C.; Montgomery, M.H.; Stello, D.; Timmes, F.X.; et al. Modules for Experiments in Stellar Astrophysics (MESA): Planets, Oscillations, Rotation, and Massive Stars. Astrophys. J. Suppl. Ser. 2013, 208, 4. [Google Scholar] [CrossRef]
- Paxton, B.; Marchant, P.; Schwab, J.; Bauer, E.B.; Bildsten, L.; Cantiello, M.; Dessart, L.; Farmer, R.; Hu, H.; Langer, N.; et al. Modules for Experiments in Stellar Astrophysics (MESA): Binaries, Pulsations, and Explosions. Astrophys. J. Suppl. Ser. 2015, 220, 15. [Google Scholar] [CrossRef]
- Paxton, B.; Schwab, J.; Bauer, E.B.; Bildsten, L.; Blinnikov, S.; Duffell, P.; Farmer, R.; Goldberg, J.A.; Marchant, P.; Sorokina, E.; et al. Modules for Experiments in Stellar Astrophysics (MESA): Convective Boundaries, Element Diffusion, and Massive Star Explosions. Astrophys. J. Suppl. Ser. 2018, 234, 34. [Google Scholar] [CrossRef]
- Davidson, K.; Ishibashi, K.; Martin, J.C.; Humphreys, R.M. Eta Carinae’s Declining Outflow Seen in the UV, 2002–2015. Astrophys. J. 2018, 858, 109. [Google Scholar] [CrossRef]
- Davidson, K.; Martin, J.; Humphreys, R.M.; Ishibashi, K.; Gull, T.R.; Stahl, O.; Weis, K.; Hillier, D.J.; Damineli, A.; Corcoran, M.; et al. A Change in the Physical State of η Carinae? Astron. J. 2005, 129, 900. [Google Scholar] [CrossRef]
- Mehner, A.; Davidson, K.; Humphreys, R.M.; Walter, F.M.; Baade, D.; De Wit, W.J.; Martin, J.; Ishibashi, K.; Rivinius, T.; Martayan, C.; et al. Eta Carinae’s 2014.6 spectroscopic event: Clues to the long-term recovery from its Great Eruption. Astron. Astrophys. 2015, 578, A122. [Google Scholar] [CrossRef]
- Kashi, A. An indication for the binarity of P Cygni from its 17th century eruption. Mon. Not. R. Astron. Soc. 2010, 405, 1924–1929. [Google Scholar] [CrossRef][Green Version]
- Michaelis, A.M.; Kashi, A.; Kochiashvili, N. Periodicity in the light curve of P Cygni-Indication for a binary companion? New Astron. 2018, 65, 29. [Google Scholar] [CrossRef]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kashi, A. Simulations and Modeling of Intermediate Luminosity Optical Transients and Supernova Impostors. Galaxies 2018, 6, 82. https://doi.org/10.3390/galaxies6030082
Kashi A. Simulations and Modeling of Intermediate Luminosity Optical Transients and Supernova Impostors. Galaxies. 2018; 6(3):82. https://doi.org/10.3390/galaxies6030082
Chicago/Turabian StyleKashi, Amit. 2018. "Simulations and Modeling of Intermediate Luminosity Optical Transients and Supernova Impostors" Galaxies 6, no. 3: 82. https://doi.org/10.3390/galaxies6030082
APA StyleKashi, A. (2018). Simulations and Modeling of Intermediate Luminosity Optical Transients and Supernova Impostors. Galaxies, 6(3), 82. https://doi.org/10.3390/galaxies6030082




