1. Introduction
Astrophysical jets are produced by a variety of sources, but the biggest and most luminous examples originate from active galactic nuclei (AGNs). These jets have relativistic bulk motion (with Lorentz factors
), and are likely composed of an electron–positron dominant plasma [
1].
It has long been recognised that jets must interact with their surroundings in order to remain tightly collimated over distances that span up to the megaparsec scale [
2]. As a jet propagates away from the AGN, it must displace the denser intergalactic medium (IGM) surrounding the galaxy. The initially over-pressured astrophysical jets will expand laterally as they propagate away from the AGN; because the flows are supersonic, the jet will over-expand and become under-pressured in comparison with the IGM, and thus be driven radially inwards. A series of recollimation shocks will be set up within the jet as it oscillates about an equilibrium pressure.
Radio emission from these jets results almost exclusively from synchrotron radiation, the polarization of which allows us to infer some characteristics of the magnetic field across the jet.
It is often assumed that magnetic flux-freezing tethers the jet plasma and magnetic field together; hence, a transverse shock would suppress the longitudinal field component and order the magnetic field perpendicularly to the flow velocity. Conversely, a shearing flow would enhance the longitudinal magnetic field component, giving rise to a field ordered parallel to the jet; this is generally correct [
3], and Kahn [
4] produced a fairly successful model with flux-freezing and shearing. It has been shown that moderate compression of a randomly tangled magnetic field can drastically increase the degree of order of the field, as seen from angles close to the plane of compression e.g., [
5,
6,
7]. This compression also increases the plasma emissivity [
8] (
Section 3), meaning that the observed synchrotron radiation has a higher intensity and degree of polarization e.g., [
9,
10].
Although other phenomena may have greater influence on the overall jet structure e.g., [
11], recollimation shocks should obviously leave polarization signatures in the emission of jets [
12], so it may be possible to use recollimation shocks as a diagnostic in determining the some properties of their host AGN [
13,
14].
2. Fluid Dynamics and Simulations
Euler’s equations ensure conservation of mass, momentum and energy for inviscid fluids [
15], and are written as
where the number density
N, momentum density
, and energy density
E are the conservation properties in the observer’s frame of reference, pressure
P is Lorentz invariant, and the velocity
is relative to the grid. The conserved variables relate to the rest frame values of number density
n and energy density
e by the following Lorentz transforms:
for Lorentz factor
. The Euler equations are presented here in conservation form:
, where the solution vector
contains the conservation quantities,
is the flux vector and
is the source term. This is vital for codes utilising shock-capturing methods (including the code used for this work); non-conservative equations may result in misplaced shocks and unstable solutions, depending on the simulation type [
16] (Chapter 2.10).
2.1. Semi-Dynamical Simulations
Semi-dynamical models represent the action of a shock through jump conditions in the parameters, which gives a sharp edge to the shock. The shocked plasma is also assumed to cool rapidly and only emit near the shock, thus ignoring emission contributions from upstream and inter-shock regions.
Early examples of this approach modelled jet knots with planar propagating shock waves, to some degree of success [
6,
17]. Fixed, conical recollimation shocks with a randomly tangled magnetic field upstream were simulated [
12], and Cawthorne [
18] built upon by this model by adding a parallel upstream magnetic field component, and convolving the results with a circular beam, for comparison with observations. These models strongly suggest that knots in radio jets may result from conical shocks; later simulations of stationary shocks in jets 3C 120 [
19] and 1803+784 [
20] replicated characteristics observed in these sources.
Instead of treating the magnetic field disorder as unresolved on the scale of the simulation e.g., [
6], Marscher [
21] used a conical recollimation shock and a grid of cells, each with a randomly-oriented uniform magnetic field. The observations were well replicated, except that the model underestimated the
-ray to X-ray luminosity ratio.
2.2. Numerical Simulations
Shocks may be more accurately represented by numerical simulations because their shapes, positions and strengths are calculated, instead of assumed. However, the use of ordered magnetic fields in many numerical simulations means that plasma compression due to a relatively weak shock, such as a recollimation shock, will have little effect on the field polarization.
An early, non-relativistic numerical simulation of the jet in M87 predicted the spacing of the knots in the jet fairly accurately. Later, a more sophisticated numerical simulation was able to passively advect a randomly tangled magnetic field with the flow of the jet, and determine the spectral ageing of the plasma’s relativistic electron population [
22]. In the model, the jet propagates into an ambient gas of equal pressure, with marker particles advected from the injection region. Each marker particle has an associated parallelepiped vector triad that is initially an orthogonal set of unit vectors. The distortion of the magnetic field at the particle’s position is monitored through parallelepiped deformation. The dynamics of the flow were simulated first, and then the synchrotron emission was determined using the parallelepipeds. This approach gave results that quantitatively agreed with the observed polarization and brightness distributions, but strongly over-predicted fractional polarization.
Many more numerical recollimation shock and/or jet simulations have been produced, with notable contributions from the group including J. L. Gómez and J. M. Martí e.g., [
23,
24,
25]. Magnetohydrodynamical (MHD) simulations have also been used to produce jet simulations; these treat the magnetic field as dynamically important, e.g., [
26,
27,
28]. However, the MHD approach requires extremely high resolutions to represent the disordered field that observations lead us to expect [
29], resulting in a prohibitively large simulational run-time if MHD code were to be used in this work.
3. Methodology
A three-dimensional, numerical, parallelized Godunov code for relativistic hydrodynamics [
30,
31] is being used to produce simulations of astrophysical jets. The code uses RHLLE (an approximate Riemann solver [
32,
33]) to implement the Godunov approach in the simulations, by evolving the initial discontinuities at cell-boundaries with time.
It was determined that the code could be modified in such a way that the parallelepiped vector triads advect through the simulation in a manner to the conserved variables. By doing this, it can be seen whether randomly tangled magnetic fields advected through recollimation shocks can produce the features observed in knots and radio-cores. The parallelepipeds are initially an orthogonal set of unit vectors; as the fluid experiences shear, compression or expansion, the parallelepiped representing the enclosed volume should be appropriately deformed in shape, orientation and/or size. Parallelepiped deformation may then be used to determine the magnetic field configuration throughout the flow.
This adaptation of the method used by Matthews and Scheuer [
22] (discussed in
Section 2.2) has the advantage of using a fixed grid of markers that remain evenly distributed throughout the simulation, regardless of fluid flow. The other major endeavour is to evaluate the radiative transfer in a separate code. This will involve implementing the findings of Cawthorne and Hughes [
7] in order to calculate the observed emission.
Due to complications detailed in
Section 4, the method of determining parallelepiped deformation is currently under scrutiny. When the necessary modifications have been implemented, the simulations will be compared to observations, which are expected to show corresponding features in polarization and emission characteristics.
4. Results
In order to verify that the parallelepipeds accurately monitor their volume elements, a simulation was produced in which a relativistic, planar shock impinges on ambient medium of equal density. As the density of the jet and ambient medium are initially equal, it may be assumed that the mass density at any point in the simulation is the inverse of the parallelepiped volume
, where
,
and
are the vectors that monitor the parallelepiped’s shape. It was found that the parallelepipeds do monitor the compression of the plasma quite well, as can be seen in
Figure 1.
Clearly, as the inverse of both the parallelepiped volume and the shock-normal vector magnitude give reasonable estimates of the density, we are dealing with a special case. When dealing with recollimation shocks, we must expect shocks that are not normal to the local velocity field. Currently, work is being done to confirm that the parallelepipeds are correctly advecting in three-dimensional simulations, and radiative transfer code is in the process of being written.
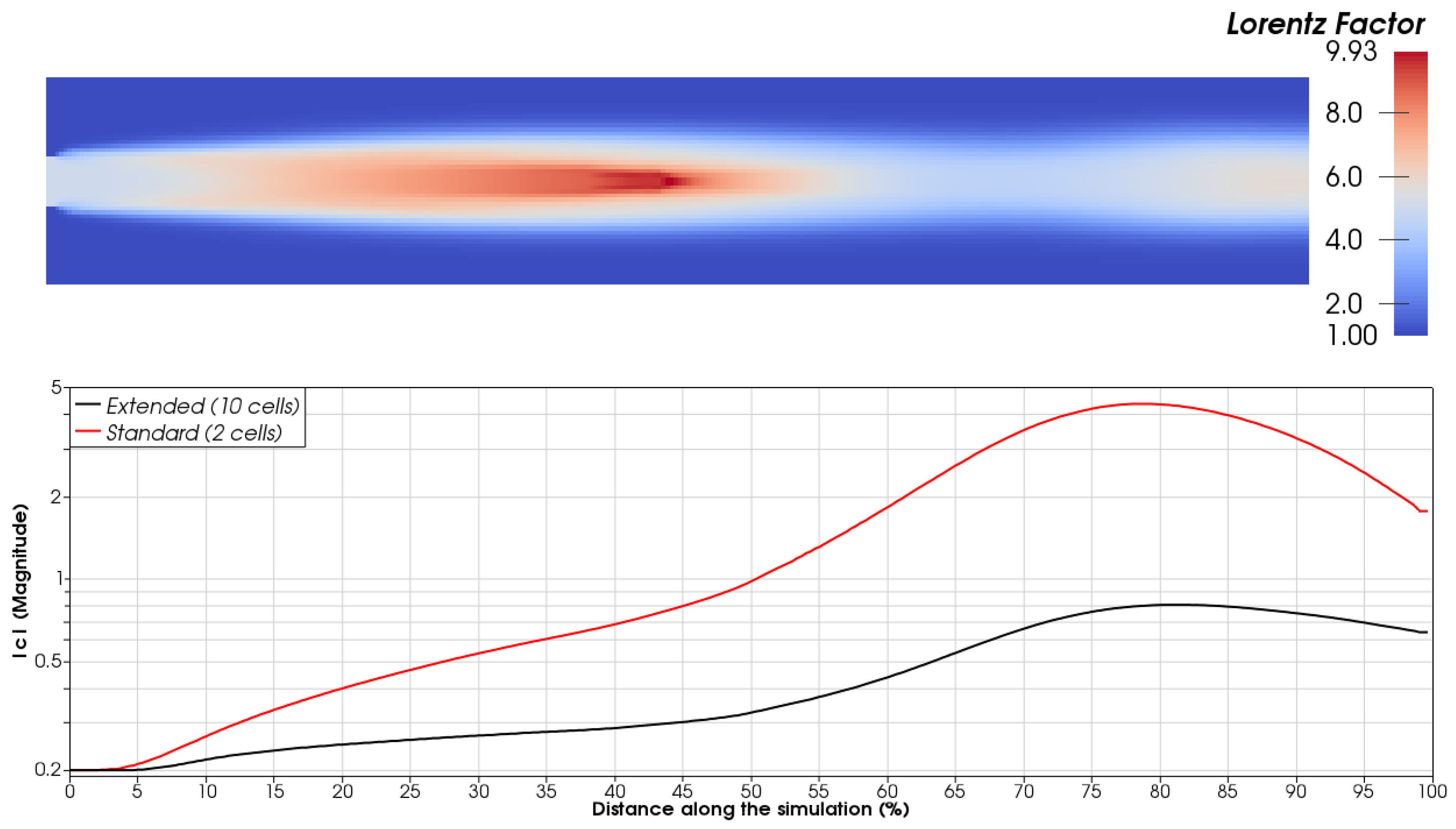
For a more complex, three-dimensional case, a jet was initialized as a cylinder of uniform radius and velocity
, embedded within the stationary ambient medium, which is overdense by a factor of 10, and underpressured by a factor of 0.33, with respect to the initialized jet. These values are fixed for the inlet plane (
), while the rest of the simulation (
) is able to evolve with time. It was found that if the parallelepipeds were prevented from evolving for an extended region of
(effectively having separate boundary conditions for the hydrodynamic variables and the parallelepipeds), the amount of shear they demonstrated was greatly reduced (see
Figure 2). This stopped the large inlet plane discontinuity between the jet and ambient medium affecting the parallelepipeds, and the effect was exacerbated by the shear layer. However, it is also clear from
Figure 2 that a steady growth of the parallelepiped component parallel to the jet is still present, to a degree greater than expected from the modest variations in the component of velocity parallel to the jet axis.
As an alternative approach, code is currently being written which determines the streamline between each grid-point and the jet inlet; advecting slightly displaced particles from each streamline origin should enable the calculation of parallelepiped deformation for each grid-point.
Author Contributions
This manuscript was primarily written by C.D.K., and revised by both T.V.C. and P.A.H.; likewise, the analysis was mostly performed by C.D.K., with suggestions for methodology, discussion and interpretation provided by the other two authors.
Acknowledgments
C.D.K. receives a Science and Technology Facilities Council studentship.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kino, M.; Takahara, F. Constraints on the energetics and plasma composition of relativistic jets in FR II sources. Mon. Not. R. Astron. Soc. 2004, 349, 336–346. [Google Scholar] [CrossRef][Green Version]
- Scheuer, P.A.G. Models of extragalactic radio sources with a continuous energy supply from a central object. Mon. Not. R. Astron. Soc. 1974, 166, 513–528. [Google Scholar] [CrossRef]
- Bridle, A.H. Systematics of large-scale radio jets. In Extragalactic Radio Sources, Proceedings of the International Astronomical Union Symposium, Albuquerque, NM, USA, 3–7 August 1981; Heeschen, D.S., Wade, C.M., Eds.; Springer: Dordrecht, The Netherlands, 1982; Volume 97, pp. 121–128. [Google Scholar]
- Kahn, F.D. A turbulent radio jet. Mon. Not. R. Astron. Soc. 1983, 202, 553–560. [Google Scholar] [CrossRef][Green Version]
- Laing, R.A. Magnetic fields in extragalactic radio sources. Astrophys. J. 1981, 248, 87–104. [Google Scholar] [CrossRef]
- Aller, H.D.; Aller, M.F.; Hughes, P.A. Polarized radio outbursts in BL Lacertae. I—Polarized emission from a compact jet. II—The flux and polarization of a piston-driven shock. Astrophys. J. 1985, 298, 296–315. [Google Scholar] [CrossRef]
- Cawthorne, T.V.; Hughes, P.A. The radiative transfer of synchrotron radiation through a compressed random magnetic field. Astrophys. J. 2013, 771, 60. [Google Scholar] [CrossRef]
- Pacholczyk, A.G. Radio Astrophysics: Nonthermal Processes in Galactic and Extragalactic Sources; W. H. Freeman and Company: San Francisco, CA, USA, 1970. [Google Scholar]
- Cohen, M.H.; Meier, D.L.; Arshakian, T.G.; Homan, D.C.; Hovatta, T.; Kovalev, Y.Y.; Lister, M.L.; Pushkarev, A.B.; Richards, J.L.; Savolainen, T. Studies of the Jet in Bl Lacertae. I. Recollimation Shock and Moving Emission Features. Astrophys. J. 2014, 787, 151. [Google Scholar] [CrossRef]
- Gómez, J.L.; Lobanov, A.P.; Bruni, G.; Kovalev, Y.Y.; Marscher, A.P.; Jorstad, S.G.; Mizuno, Y.; Bach, U.; Sokolovsky, K.V.; Anderson, J.M.; et al. Probing the innermost regions of AGN jets and their magnetic fields with RadioAstron. I. Imaging BL Lacertae at 21 microarcsecond resolution. Astrophys. J. 2016, 817, 96. [Google Scholar] [CrossRef]
- Gourgouliatos, K.N.; Komissarov, S.S. Reconfinement and loss of stability in jets from active galactic nuclei. Nat. Astron. 2018, 2, 167–171. [Google Scholar] [CrossRef]
- Cawthorne, T.V.; Cobb, W.K. Linear polarization of radiation from oblique and conical shocks. Astrophys. J. 1990, 350, 536–544. [Google Scholar] [CrossRef]
- Hervet, O.; Boisson, C.; Sol, H. An innovative blazar classification based on radio jet kinematics. Astron. Astrophys. 2016, 592, A22. [Google Scholar] [CrossRef]
- Hervet, O.; Meliani, Z.; Zech, A.; Boisson, C.; Cayatte, V.; Sauty, C.; Sol, H. Shocks in relativistic transverse stratified jets. A new paradigm for radio-loud AGN. Astron. Astrophys. 2017, 606, A103. [Google Scholar] [CrossRef]
- Zanotti, O.; Manca, G.M. Lecture notes for the COMPSTAR school on computational astrophysics. In A Very Short Introduction to Godunov Methods; Albert Einstein Institute: Potsdam, Germany, 2010. [Google Scholar]
- Anderson, J.D. Computational Fluid Dynamics: The Basics with Applications; McGraw Hill Education: New Delhi, India, 1995. [Google Scholar]
- Cawthorne, T.V.; Wardle, J.F.C. Kinematic constraints on models of the BL Lacertea object OJ 287 from VLBI polarization observations. Astrophys. J. 1988, 332, 696–701. [Google Scholar] [CrossRef]
- Cawthorne, T.V. Polarization of synchrotron radiation from conical shock waves. Mon. Not. R. Astron. Soc. 2006, 367, 851–859. [Google Scholar] [CrossRef]
- Agudo, I.; Gómez, J.L.; Casadio, C.; Cawthorne, T.V.; Roca-Sogorb, M. A recollimation shock 80 mas from the core in the jet of the radio galaxy 3C 120: Observational evidence and modeling. Astrophys. J. 2012, 752, 92. [Google Scholar] [CrossRef]
- Cawthorne, T.V.; Jorstad, S.G.; Marscher, A.P. Polarization structure in the core of 1803+784: A signature of recollimation shocks? Astrophys. J. 2013, 772, 14. [Google Scholar] [CrossRef]
- Marscher, A.P. Turbulent, extreme multi-zone model for simulating flux and polarization variability in blazars. Astrophys. J. 2014, 780, 87. [Google Scholar] [CrossRef]
- Matthews, A.P.; Scheuer, P.A.G. Models of radio galaxies with tangled magnetic fields. I—Calculation of magnetic field transport, Stokes parameters and synchrotron losses. II—Numerical simulations and their interpretation. Mon. Not. R. Astron. Soc. 1990, 242, 616–635. [Google Scholar] [CrossRef]
- Agudo, I.; Gómez, J.L.; Martí, J.M.; Ibáñez, J.M.; Marscher, A.P.; Alberdi, A.; Aloy, M.A.; Hardee, P.E. Jet stability and the generation of superluminal and stationary components. Astrophys. J. 2001, 549, L183–L186. [Google Scholar] [CrossRef]
- Roca-Sogorb, M.; Perucho, M.; Gómez, J.L.; Martí, J.M.; Antón, L.; Aloy, M.A.; Agudo, I. The influence of helical magnetic fields in the dynamics and emission of relativistic jets. In Approaching Micro-Arcsecond Resolution with VSOP-2: Astrophysics and Technologies, Proceedings of the Astronomical Society of the Pacific Conference Series, Sagamihara, Japan, 3–7 December 2007; Hagiwara, Y., Fomalont, E., Tsuboi, M., Yasuhiro, M., Eds.; Astronomical Society of the Pacific: San Francisco, CA, USA, 2009; Volume 402, p. 353. [Google Scholar]
- Fromm, C.M.; Perucho, M.; Porth, O.; Younsi, Z.; Ros, E.; Mizuno, Y.; Zensus, J.A.; Rezzolla, L. Jet-torus connection in radio galaxies. Relativistic hydrodynamics and synthetic emission. Astron. Astrophys. 2018, 609, A80. [Google Scholar] [CrossRef]
- Mizuno, Y.; Gómez, J.L.; Nishikawa, K.I.; Meli, A.; Hardee, P.E.; Rezzolla, L. Recollimation shocks in magnetized relativistic jets. Astrophys. J. 2015, 809, 38. [Google Scholar] [CrossRef]
- Porth, O.; Komissarov, S.S. Causality and stability of cosmic jets. Mon. Not. R. Astron. Soc. 2015, 452, 1089–1104. [Google Scholar] [CrossRef]
- Martí, J.M.; Perucho, M.; Gómez, J.L. The internal structure of overpressured, magnetized, relativistic jets. Astrophys. J. 2016, 831, 163. [Google Scholar] [CrossRef]
- Murphy, E.; Cawthorne, T.V.; Gabuzda, D.C. Analysing the transverse structure of the relativistic jets of active galactic nuclei. Mon. Not. R. Astron. Soc. 2013, 430, 1504–1515. [Google Scholar] [CrossRef]
- Duncan, G.C.; Hughes, P.A. Simulations of relativistic extragalactic jets. Astrophys. J. 1994, 436, L119–L122. [Google Scholar] [CrossRef]
- Hughes, P.A.; Miller, M.A.; Duncan, G.C. Three-dimensional hydrodynamic simulations of relativistic extragalactic jets. Astrophys. J. 2002, 572, 713–728. [Google Scholar] [CrossRef]
- Harten, A.; Lax, P.D.; van Leer, B. On upstream differencing and Godunov-type schemes for hyperbolic conservation laws. SIAM Rev. 1983, 25, 35–61. [Google Scholar] [CrossRef]
- Einfeldt, B. On Godunov type methods for the Euler equations with a general equation of state. In Shock Tubes and Waves, Proceedings of the Sixteenth International Symposium, Aachen, Germany, 26–31 July 1987; Groenig, H., Ed.; VCH Verlagsgesellschaft mbH: Weinheim, Germany, 1988; pp. 671–676. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).