Effelsberg Monitoring of a Sample of RadioAstron Blazars: Analysis of Intra-Day Variability
Abstract
1. Introduction
2. Sample Selection, Observations and Data Reduction
3. Variability Parameters
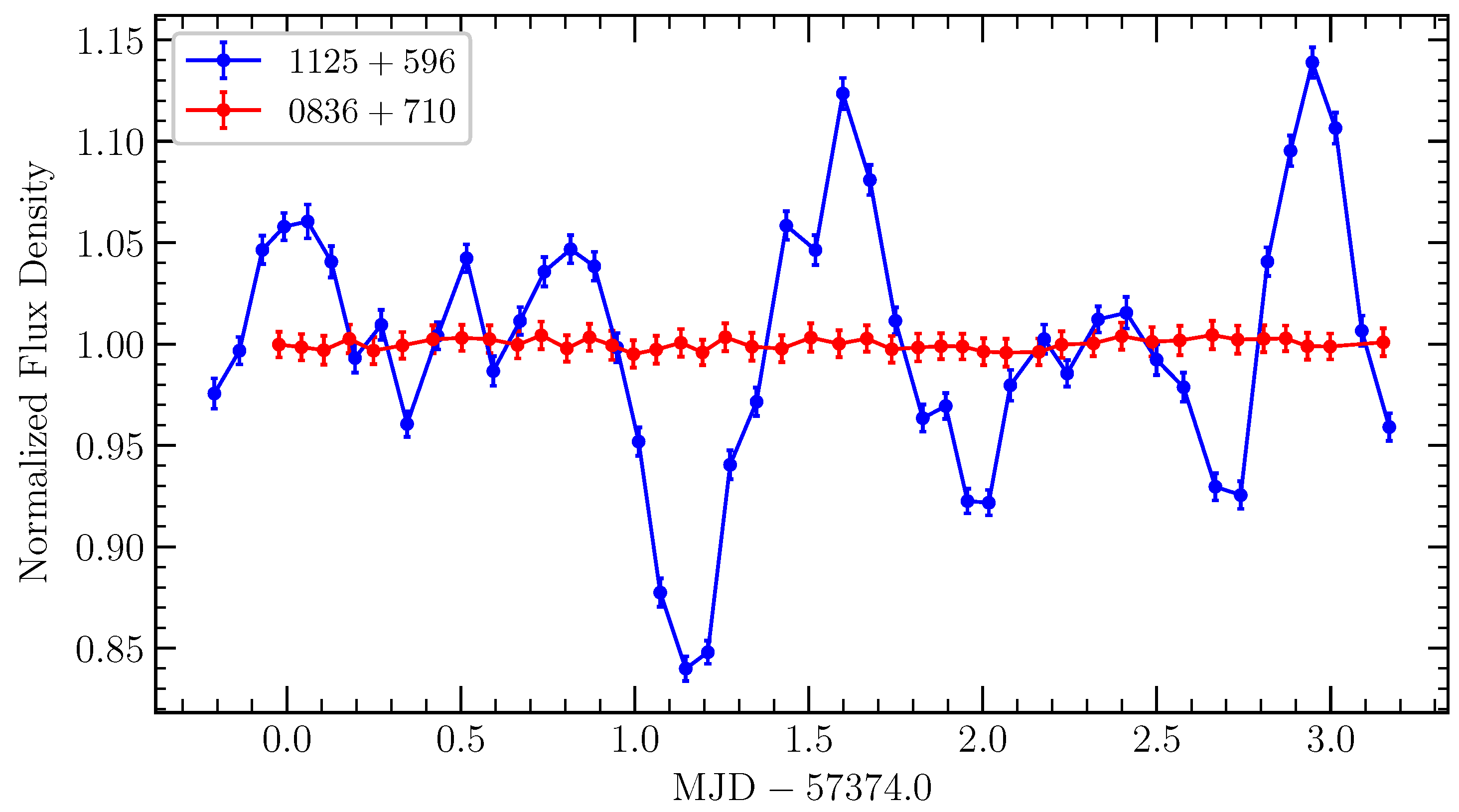
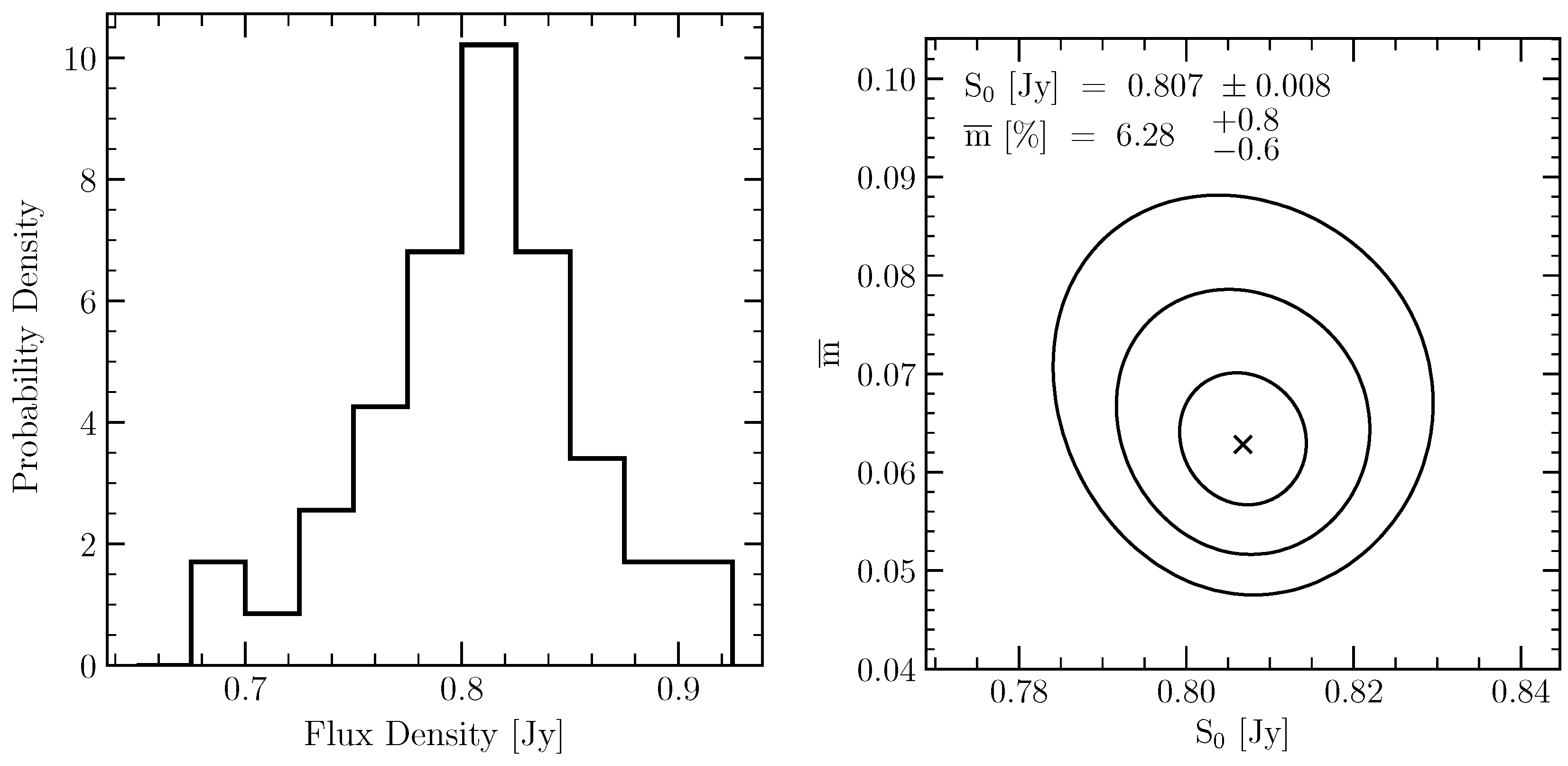
3.1. Raw Modulation Index
3.2. Intrinsic Modulation Index
3.3. and Reduced
4. Statistical Results
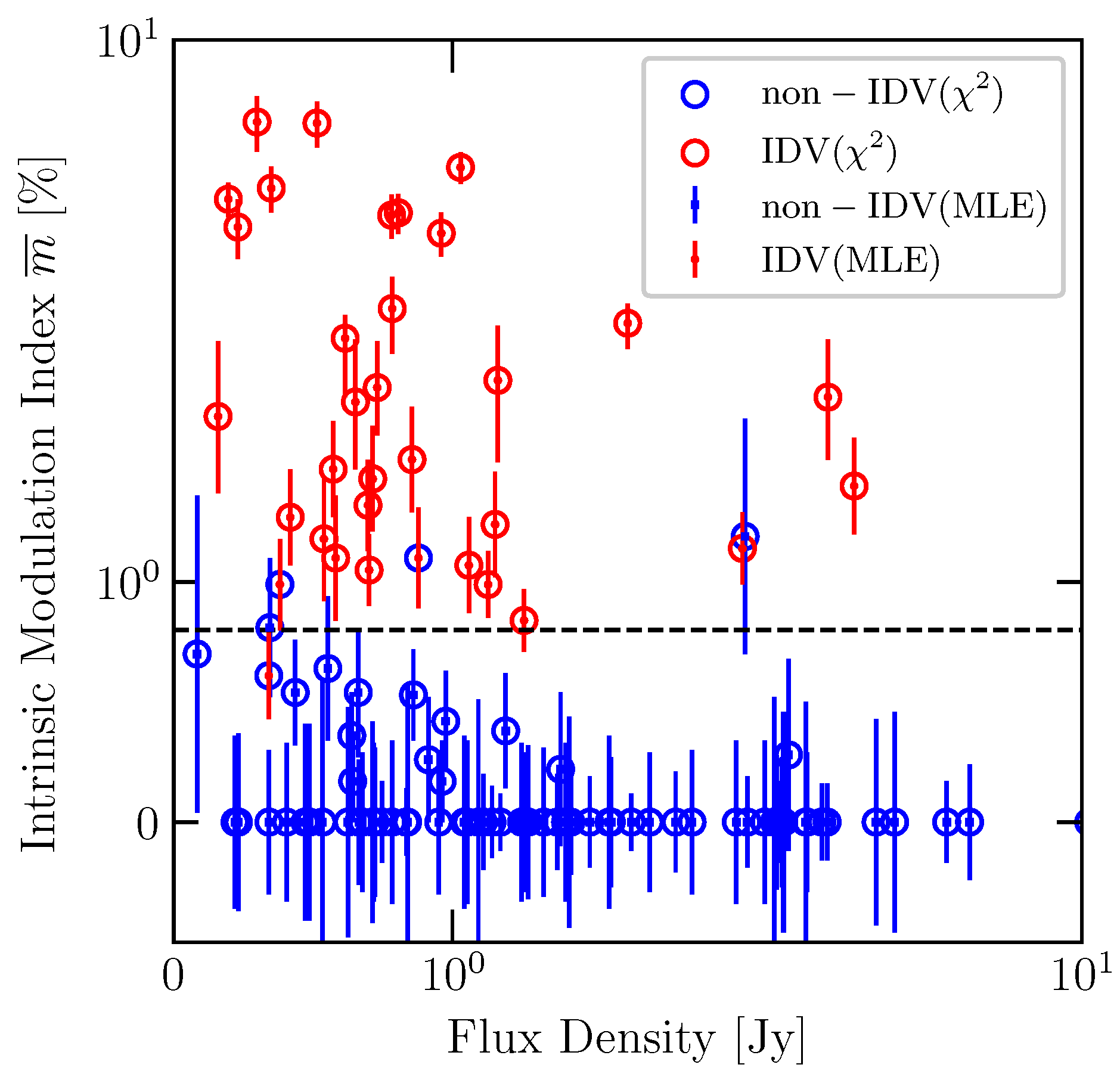
4.1. Variability Classification
4.2. Sample Properties
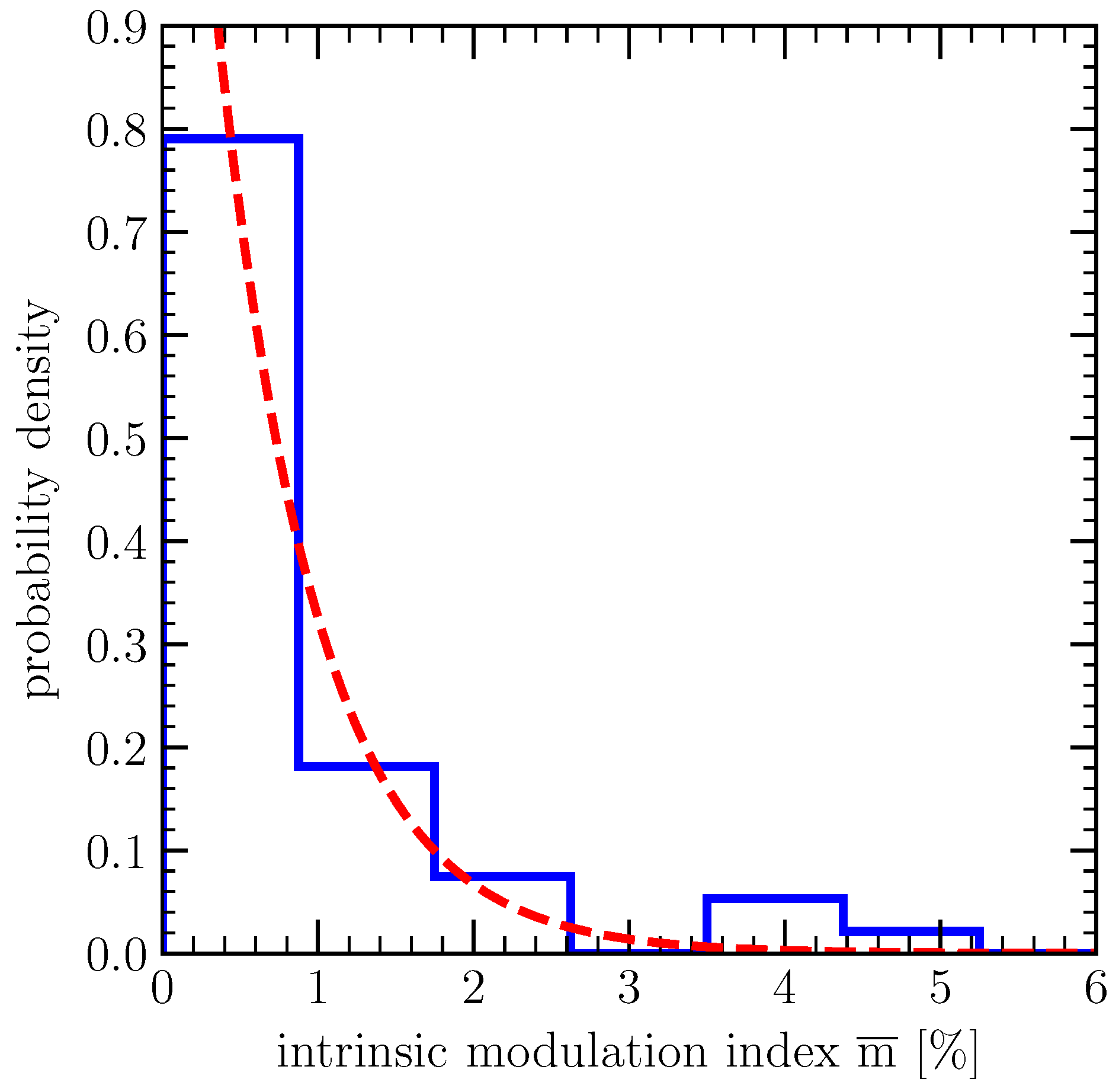
4.3. Intrinsic Modulation Index
5. Population Comparisons
5.1. Likelihood Analysis
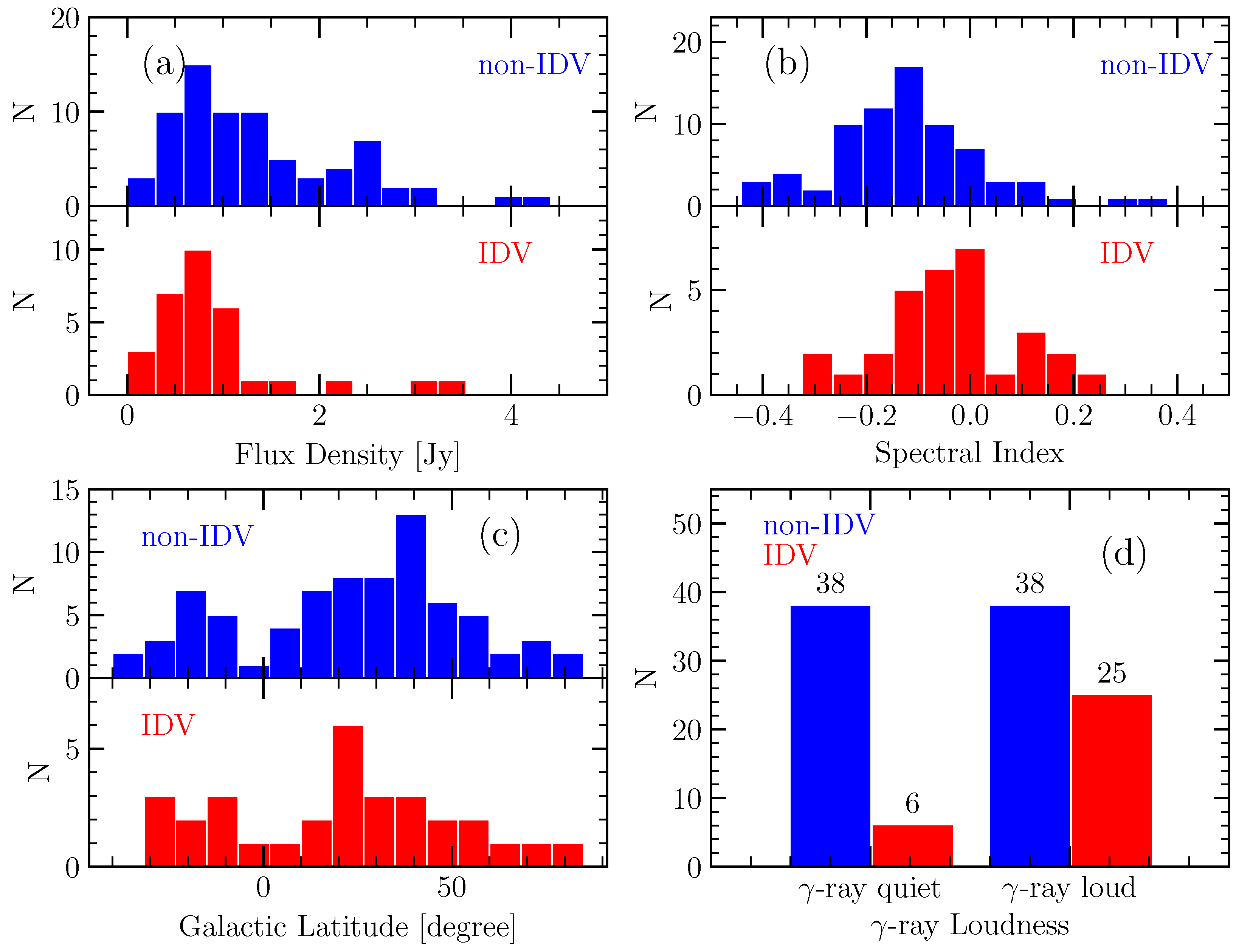
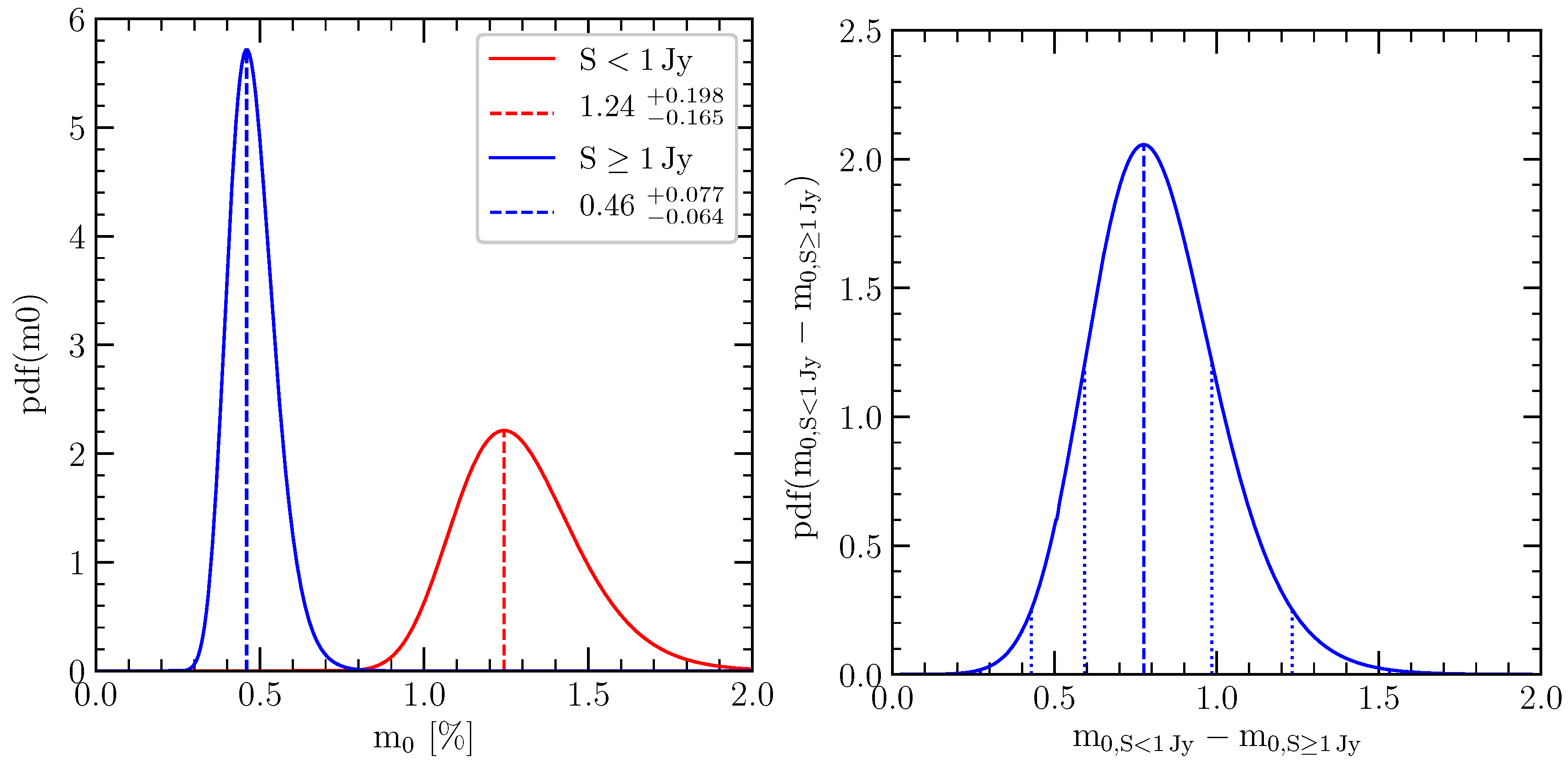
5.2. Flux Density and Redshift
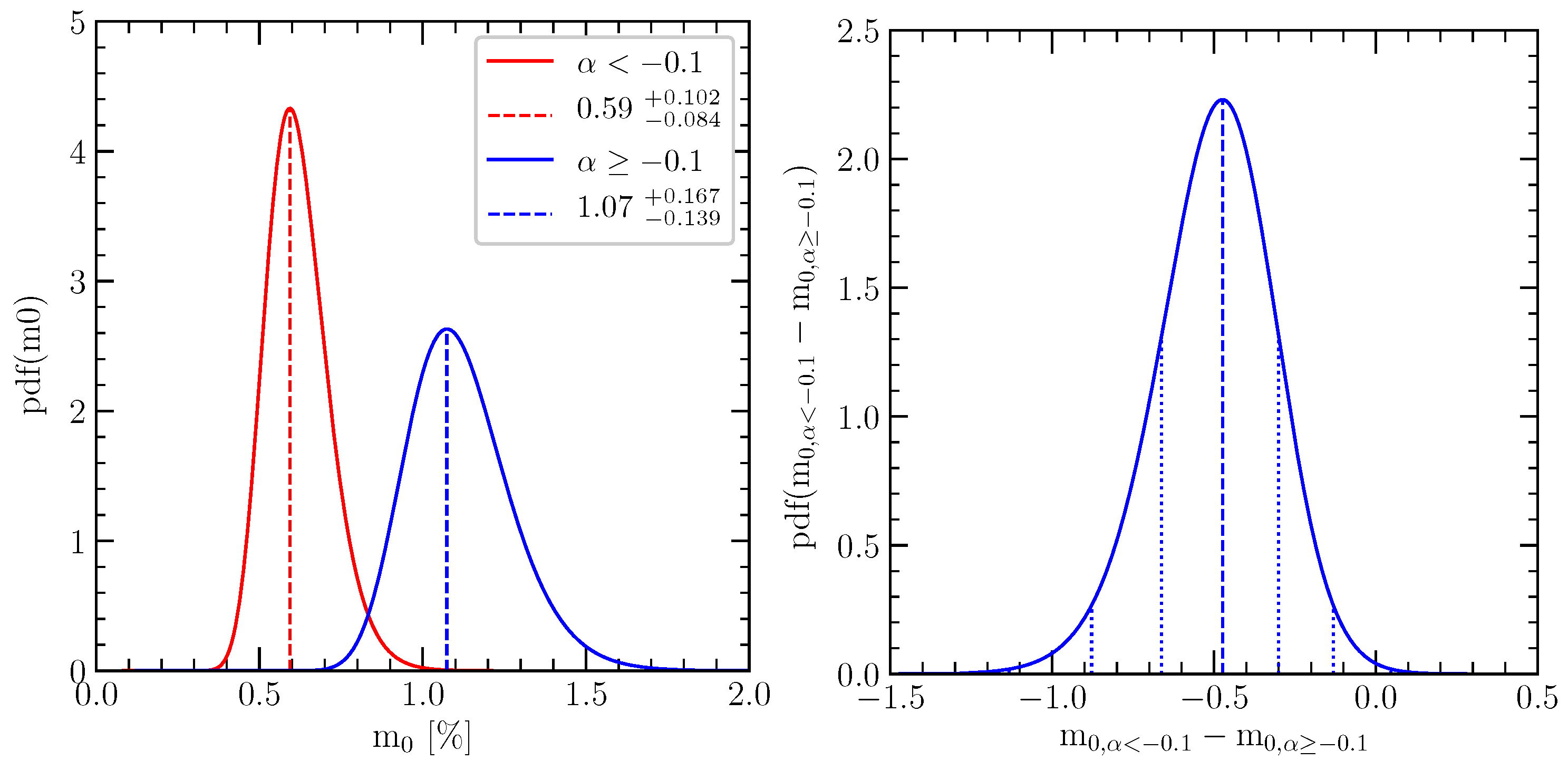
5.3. Spectral Index
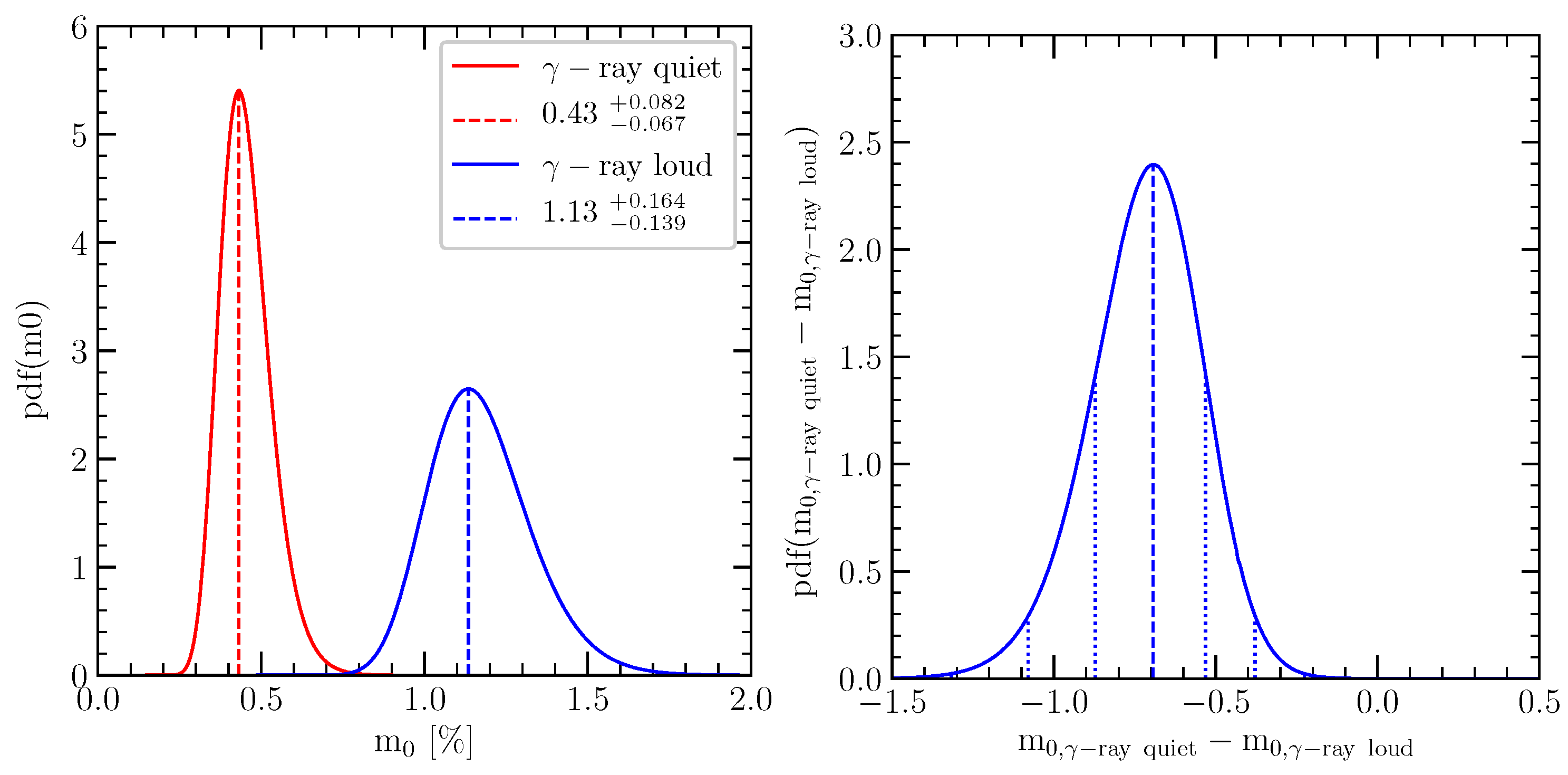
5.4. -Ray Loudness
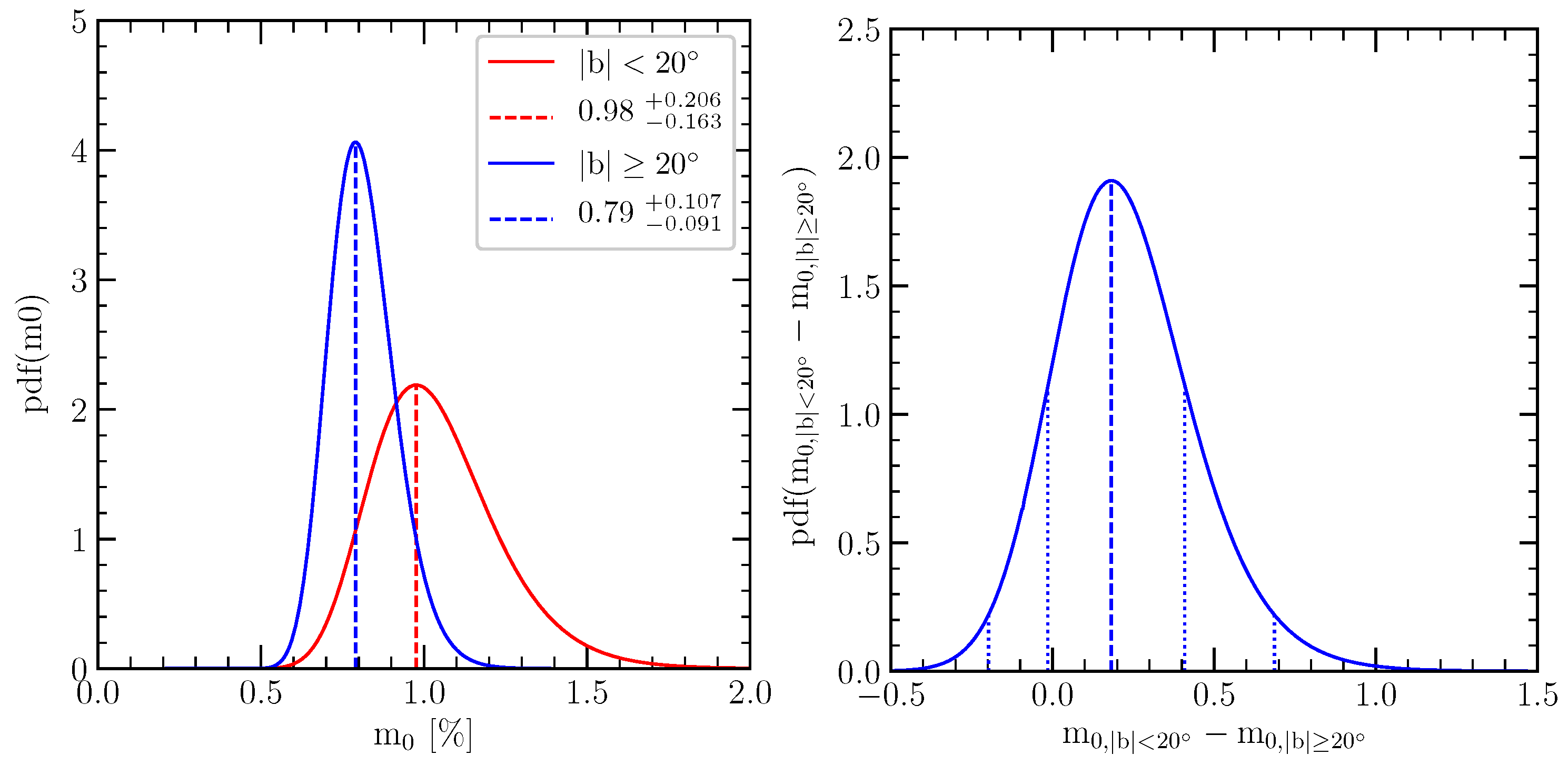
5.5. Galactic Latitude
6. Discussion
6.1. Robustness of the Statistics
6.2. Variability Dependencies
6.3. Influence on SVLBI Measurements
7. Summary and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Results of IDV Monitoring with the Effelsberg 100 m Telescope
| Name | Epoch | Flux Density | IDV | b | z | -ray | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| [Jy] | [%] | [] | [mas] | ||||||||
| 0010 + 405 | B | 1.586 | −21.44 | −0.24 | 0.255 | 0.70 | 0.78 | ||||
| 0014 + 813 | B | 0.133 | 18.80 | −0.01 | 3.366 | 0.63 | 0.75 | ||||
| 0016 + 731 | B | 4.485 | + | 10.73 | −0.13 | 1.781 | 0.57 | 0.79 | |||
| 0059 + 581 | A | 2.607 | + | −4.44 | −0.06 | 0.644 | 0.61 | 0.66 | + | ||
| 0110 + 318 | C | 1.047 | −30.51 | −0.30 | 0.603 | + | |||||
| D | 4.053 | + | |||||||||
| E | 0.214 | ||||||||||
| 0125 + 487 | B | 1.935 | −13.41 | +0.27 | 0.067 | ||||||
| 0219 + 428 | D | 1.175 | −16.77 | −0.22 | 0.444 | 1.83 | 0.42 | + | |||
| 0234 + 285 | E | 0.459 | −28.53 | −0.17 | 1.213 | 0.44 | + | ||||
| 0235 + 164 | E | 1.720 | −39.11 | +0.01 | 0.940 | 0.65 | 0.88 | + | |||
| 0248 + 430 | D | 1.411 | −14.40 | −0.18 | 1.310 | 0.73 | 0.33 | ||||
| 0307 + 380 | B | 132.310 | + | −16.94 | +0.01 | 0.816 | + | ||||
| C | 33.472 | + | |||||||||
| D | 222.547 | + | |||||||||
| E | 6.742 | + | |||||||||
| 0322 + 222 | D | 5.238 | + | −28.02 | −0.09 | 2.060 | 0.61 | + | |||
| 0323 + 342 | C | 2.188 | −18.76 | −0.22 | 0.061 | + | |||||
| D | 1.452 | ||||||||||
| 0333 + 321 | C | 0.361 | −18.77 | −0.10 | 1.258 | 0.88 | 0.36 | + | |||
| D | 1.178 | ||||||||||
| E | 0.906 | ||||||||||
| 0340 + 362 | D | 66.610 | + | −14.69 | −0.14 | 1.484 | + | ||||
| 0428 + 205 | B | 0.110 | −18.56 | −0.39 | 0.219 | 3.22 | 0.06 | ||||
| 0430 + 289 | E | 7.324 | + | −12.60 | −0.24 | 0.970 | + | ||||
| 0507 + 179 | B | 1.090 | −12.79 | +0.06 | 0.416 | 0.66 | 0.54 | + | |||
| 0529 + 483 | B | 0.826 | 8.23 | −0.03 | 1.162 | 0.47 | 0.67 | + | |||
| E | 2.855 | + | |||||||||
| 0602 + 405 | B | 1.210 | 9.35 | −0.17 | |||||||
| 0633 + 734 | B | 0.367 | 25.06 | −0.08 | 1.850 | + | |||||
| 0642 + 449 | B | 0.159 | 17.95 | −0.21 | 3.396 | 0.67 | 0.64 | ||||
| 0716 + 714 | A | 4.345 | + | 28.02 | +0.22 | 0.300 | 0.55 | 0.69 | + | ||
| B | 14.321 | + | |||||||||
| C | 9.358 | + | |||||||||
| D | 17.003 | + | |||||||||
| E | 2.805 | + | |||||||||
| 0730 + 504 | D | 1.382 | 27.11 | −0.09 | 0.720 | 0.38 | 0.45 | + | |||
| 0742 + 103 | E | 0.341 | 16.59 | −0.38 | 2.624 | 0.99 | 0.35 | ||||
| 0749 + 540 | B | 6.029 | + | 30.51 | −0.06 | 0.200 | 1.03 | 0.47 | + | ||
| C | 5.651 | + | |||||||||
| D | 4.565 | + | |||||||||
| 0804 + 499 | A | 0.397 | 32.56 | +0.05 | 1.435 | 0.34 | 0.78 | + | |||
| B | 0.641 | ||||||||||
| 0812 + 367 | C | 1.167 | 31.86 | −0.17 | 1.027 | 0.76 | 0.67 | ||||
| 0814 + 425 | A | 0.932 | 33.40 | −0.27 | 0.530 | 0.94 | 0.48 | + | |||
| B | 1.531 | ||||||||||
| E | 15.203 | + | |||||||||
| 0827 + 243 | E | 0.524 | 31.88 | +0.19 | 0.941 | + | |||||
| 0831 + 557 | A | 0.408 | 36.56 | −0.66 | 0.241 | 3.10 | 0.04 | ||||
| B | 0.181 | ||||||||||
| C | 0.097 | ||||||||||
| D | 0.151 | ||||||||||
| 0846 + 513 | C | 0.658 | 39.14 | +0.12 | 0.585 | 0.46 | 0.76 | + | |||
| 0851 + 202 | D | 6.754 | + | 35.82 | +0.13 | 0.306 | 0.50 | 0.46 | + | ||
| E | 0.456 | ||||||||||
| 0859 + 470 | A | 0.065 | 41.56 | −0.36 | 1.465 | 0.64 | + | ||||
| B | 0.300 | ||||||||||
| 0917 + 449 | A | 0.233 | 44.82 | −0.13 | 2.186 | 0.54 | 0.72 | + | |||
| 0917 + 624 | A | 0.256 | 40.99 | −0.20 | 1.446 | 0.50 | 0.70 | + | |||
| 0923 + 392 | A | 0.176 | 46.16 | −0.20 | 0.695 | 0.70 | 0.62 | ||||
| 0925 + 504 | A | 9.431 | + | 45.42 | −0.01 | 0.370 | 0.57 | 0.70 | + | ||
| B | 18.678 | + | |||||||||
| C | 56.887 | + | |||||||||
| D | 60.041 | + | |||||||||
| E | 9.787 | + | |||||||||
| 0942 + 468 | C | 0.247 | 48.83 | −0.13 | 0.639 | 1.28 | 0.35 | ||||
| 0945 + 408 | A | 0.161 | 50.28 | −0.11 | 1.250 | 0.49 | 0.66 | + | |||
| 0951 + 693 | C | 0.880 | 40.90 | −0.11 | |||||||
| 0954 + 658 | A | 0.543 | 43.13 | −0.04 | 0.368 | 0.89 | + | ||||
| E | 0.510 | ||||||||||
| 0955 + 326 | A | 0.095 | 52.32 | −0.33 | 0.531 | 0.64 | 0.37 | ||||
| 0955 + 476 | A | 0.777 | 50.73 | −0.06 | 1.882 | 0.31 | 0.87 | + | |||
| 1015 + 359 | A | 0.679 | 56.43 | +0.09 | 1.230 | 0.35 | 0.64 | + | |||
| 1040 + 244 | E | 3.876 | + | 61.01 | +0.02 | 0.563 | 0.39 | 0.69 | + | ||
| 1044 + 476 | C | 0.275 | 58.44 | −0.43 | 0.799 | 1.77 | 0.47 | ||||
| 1044 + 719 | A | 0.505 | 42.29 | −0.16 | 1.150 | 0.37 | 0.70 | + | |||
| E | 0.574 | ||||||||||
| 1053 + 815 | A | 1.122 | 34.75 | −0.01 | 0.706 | + | |||||
| 1101 + 384 | A | 0.634 | 65.03 | −0.10 | 0.030 | 0.85 | + | ||||
| E | 0.569 | ||||||||||
| 1123 + 264 | A | 0.212 | 70.89 | −0.03 | 2.352 | 0.34 | 0.71 | ||||
| B | 0.829 | ||||||||||
| C | 0.390 | ||||||||||
| D | 1.491 | ||||||||||
| E | 0.185 | ||||||||||
| 1125 + 596 | A | 9.795 | + | 54.67 | −0.02 | 1.795 | 0.24 | 0.78 | + | ||
| C | 20.143 | + | |||||||||
| D | 76.008 | + | |||||||||
| E | 8.054 | + | |||||||||
| 1144 + 402 | A | 0.489 | 71.47 | −0.00 | 1.090 | 0.23 | 0.73 | + | |||
| D | 0.703 | ||||||||||
| 1150 + 497 | D | 0.462 | 64.98 | −0.10 | 0.334 | 0.73 | 0.50 | + | |||
| 1150 + 812 | B | 0.178 | 35.84 | −0.05 | 1.250 | 0.51 | |||||
| 1156 + 295 | A | 0.140 | 78.37 | −0.17 | 0.725 | 0.61 | 0.77 | + | |||
| B | 5.142 | + | |||||||||
| C | 1.548 | ||||||||||
| D | 1.906 | ||||||||||
| E | 0.967 | ||||||||||
| 1214 + 588 | B | 0.348 | 57.97 | −0.13 | 2.551 | 0.89 | 0.36 | ||||
| C | 0.289 | ||||||||||
| 1219 + 285 | D | 0.695 | 83.29 | −0.09 | 0.102 | 0.58 | 0.36 | + | |||
| 1222 + 216 | E | 0.056 | 81.66 | −0.27 | 0.432 | 0.78 | + | ||||
| 1333 + 589 | B | 3.800 | + | 57.48 | +0.16 | 0.570 | 1.44 | 0.20 | |||
| C | 1.528 | ||||||||||
| 1357 + 769 | A | 1.741 | 39.77 | −0.10 | 1.585 | 0.42 | 0.82 | + | |||
| E | 8.218 | + | |||||||||
| 1404 + 286 | D | 0.200 | 73.25 | +0.00 | 0.94 | 0.40 | |||||
| 1417 + 385 | C | 2.528 | + | 68.38 | +0.02 | 1.830 | 0.48 | 0.86 | + | ||
| D | 2.597 | + | |||||||||
| 1435 + 638 | A | 0.106 | 49.73 | −0.36 | 2.068 | 1.11 | 0.33 | ||||
| 1520 + 319 | B | 1.121 | 57.02 | −0.01 | 1.487 | 0.32 | 0.84 | + | |||
| 1547 + 507 | C | 15.284 | + | 49.06 | −0.02 | 2.171 | 1.03 | 0.56 | |||
| D | 18.832 | + | |||||||||
| E | 7.844 | + | |||||||||
| 1617 + 229 | D | 6.534 | + | 43.03 | −0.05 | 1.987 | 0.29 | 0.84 | |||
| 1633 + 382 | A | 0.280 | 42.34 | −0.14 | 1.813 | 1.14 | 0.18 | + | |||
| B | 0.268 | ||||||||||
| C | 0.696 | ||||||||||
| E | 0.148 | ||||||||||
| 1638 + 398 | C | 0.270 | 41.42 | −0.08 | 1.660 | 0.28 | 0.82 | + | |||
| 1641 + 399 | A | 0.157 | 40.95 | −0.20 | 0.593 | 1.28 | 0.24 | + | |||
| 1642 + 264 | D | 1.286 | 38.40 | −0.21 | |||||||
| 1642 + 690 | E | 0.171 | 36.62 | −0.12 | 0.751 | 0.75 | 0.50 | ||||
| 1714 + 219 | E | 0.139 | 30.22 | −0.17 | 0.358 | ||||||
| 1726 + 455 | C | 1.275 | 33.28 | +0.00 | 0.717 | 0.34 | 0.87 | + | |||
| D | 0.646 | ||||||||||
| 1751 + 288 | B | 0.123 | 24.46 | +0.08 | 1.115 | 0.82 | 0.86 | ||||
| C | 0.627 | ||||||||||
| 1758 + 388 | B | 0.817 | 26.03 | −0.16 | 2.092 | 0.30 | 0.87 | ||||
| C | 0.550 | ||||||||||
| 1807 + 279 | B | 0.198 | 20.97 | −0.39 | 1.760 | ||||||
| D | 1.843 | ||||||||||
| 1807 + 698 | A | 0.425 | 29.17 | −0.08 | 0.051 | 0.83 | 0.64 | + | |||
| B | 0.493 | ||||||||||
| 1817 + 387 | C | 3.412 | + | 22.46 | +0.56 | 0.540 | |||||
| E | 0.530 | ||||||||||
| 1823 + 568 | B | 3.527 | + | 26.08 | −0.03 | 0.664 | 0.43 | 0.82 | + | ||
| 1842 + 681 | C | 1.322 | 25.85 | −0.09 | 0.472 | 0.77 | + | ||||
| 1843 + 356 | C | 0.348 | 16.53 | −0.22 | 0.764 | ||||||
| 1846 + 322 | C | 2.781 | + | 14.71 | −0.12 | 0.798 | 4.49 | + | |||
| D | 2.796 | + | |||||||||
| 1849 + 670 | A | 1.209 | 25.04 | +0.19 | 0.657 | 0.54 | 0.86 | + | |||
| B | 2.991 | + | |||||||||
| 1850 + 402 | E | 0.113 | 16.97 | −0.07 | 2.120 | ||||||
| 1923 + 210 | C | 0.256 | 2.26 | −0.12 | 1.29 | 0.21 | |||||
| 1926 + 611 | A | 11.904 | + | 19.45 | −0.04 | 0.71 | 0.64 | + | |||
| E | 0.722 | ||||||||||
| 1928 + 738 | B | 0.567 | 23.54 | −0.24 | 0.302 | 1.01 | 0.50 | ||||
| 1954 + 513 | C | 0.771 | 11.76 | −0.22 | 1.220 | 0.66 | 0.67 | ||||
| E | 0.771 | ||||||||||
| 2005 + 403 | C | 0.389 | 4.30 | −0.12 | 1.736 | ||||||
| 2005 + 642 | A | 0.553 | 16.73 | +0.38 | 1.574 | ||||||
| 2007 + 777 | B | 5.390 | + | 22.73 | −0.19 | 0.342 | 0.72 | 0.64 | + | ||
| D | 10.748 | + | |||||||||
| 2010 + 723 | A | 1.923 | 20.18 | −0.27 | |||||||
| 2013 + 370 | E | 0.158 | 1.22 | −0.03 | + | ||||||
| 2021 + 614 | D | 0.559 | 13.78 | −0.19 | 0.227 | 0.79 | 0.36 | ||||
| 2022 + 542 | C | 0.570 | 9.66 | −0.90 | 0.30 | ||||||
| 2023 + 760 | A | 2.677 | + | 21.13 | +0.07 | 0.594 | + | ||||
| 2107 + 353 | C | 0.852 | −8.35 | +0.13 | 0.202 | 1.48 | 0.18 | + | |||
| 2136 + 141 | E | 0.293 | −27.54 | −0.14 | 2.427 | 0.60 | 0.66 | ||||
| 2155 + 312 | B | 4.932 | + | −18.24 | +0.02 | 1.486 | + | ||||
| E | 2.416 | ||||||||||
| 2200 + 420 | D | 1.473 | −10.44 | −0.08 | 0.069 | 0.37 | 0.45 | + | |||
| E | 0.793 | ||||||||||
| 2201 + 315 | C | 0.148 | −18.78 | −0.09 | 0.295 | 0.94 | 0.45 | + | |||
| 2209 + 236 | C | 1.310 | −26.09 | +0.13 | 1.125 | 0.85 | + | ||||
| D | 3.085 | + | |||||||||
| 2223 + 210 | C | 0.444 | −30.09 | −0.24 | 1.959 | 1.26 | 0.17 | ||||
| D | 0.143 | ||||||||||
| 2230 + 114 | E | 0.117 | −38.58 | −0.20 | 1.037 | 1.04 | 0.40 | + | |||
| 2309 + 454 | B | 7.917 | + | −13.70 | +0.13 | 1.447 | |||||
| D | 10.230 | + | |||||||||
| E | 1.766 | ||||||||||
| 2351 + 456 | B | 0.152 | −15.85 | −0.26 | 1.992 | 0.50 | + |
References
- Kovalev, Y.; Kardashev, N.S.; RadioAstron Collaboration. Space VLBI mission RadioAstron: Current status and early science program. In Proceedings of the Meeting “Resolving The Sky—Radio Interferometry: Past, Present and Future”, Manchester, UK, 17–20 April 2012; p. 40. [Google Scholar]
- Sokolovsky, K.V. RadioAstron Early Science Program Space-VLBI AGN survey: Strategy and first results. arXiv, 2013; arXiv:1303.5451. [Google Scholar]
- Kovalev, Y.Y.; Kardashev, N.S.; Kellermann, K.I.; Edwards, P.G. The RadioAstron space VLBI project. In Proceedings of the 2014 XXXIth URSI General Assembly and Scientific Symposium (URSI GASS), Beijing, China, 16–23 August 2014. [Google Scholar]
- Witzel, A.; Heeschen, D.S.; Schalinski, C.; Krichbaum, T. Kurzzeit-Variabilität extragalaktischer Radioquellen. Mitteilungen der Astronomischen Gesellschaft Hamburg 1986, 65, 239. [Google Scholar]
- Heeschen, D.S.; Krichbaum, T.; Schalinski, C.J.; Witzel, A. Rapid variability of extragalactic radio sources. Astron. J. 1987, 94, 1493–1507. [Google Scholar] [CrossRef]
- Quirrenbach, A. Variability and VLBI Observations of Extragalactic Radio Surces. In Reviews in Modern Astronomy; Klare, G., Ed.; Springer: Berlin/Heidelberg, Germany, 1992; Volume 5, pp. 214–228. [Google Scholar]
- Lovell, J.E.J.; Rickett, B.J.; Macquart, J.P.; Jauncey, D.L.; Bignall, H.E.; Kedziora-Chudczer, L.; Ojha, R.; Pursimo, T.; Dutka, M.; Senkbeil, C.; et al. The Micro-Arcsecond Scintillation-Induced Variability (MASIV) Survey. II. The First Four Epochs. Astrophys. J. 2008, 689, 108–126. [Google Scholar] [CrossRef]
- Kedziora-Chudczer, L.; Jauncey, D.L.; Wieringa, M.H.; Walker, M.A.; Nicolson, G.D.; Reynolds, J.E.; Tzioumis, A.K. PKS 0405-385: The Smallest Radio Quasar? Astrophys. J. Lett. 1997, 490, L9–L12. [Google Scholar] [CrossRef]
- Jauncey, D.L.; Macquart, J.P. Intra-day variability and the interstellar medium towards 0917 + 624. Astron. Astrophys. 2001, 370, L9–L12. [Google Scholar] [CrossRef]
- Dennett-Thorpe, J.; de Bruyn, A.G. Interstellar scintillation as the origin of the rapid radio variability of the quasar J1819 + 3845. Nature 2002, 415, 57–60. [Google Scholar] [CrossRef] [PubMed]
- Bignall, H.E.; Jauncey, D.L.; Lovell, J.E.J.; Tzioumis, A.K.; Kedziora-Chudczer, L.; Macquart, J.P.; Tingay, S.J.; Rayner, D.P.; Clay, R.W. Rapid Variability and Annual Cycles in the Characteristic Timescale of the Scintillating Source PKS 1257-326. Astrophys. J. 2003, 585, 653–664. [Google Scholar] [CrossRef]
- Bignall, H.E.; Macquart, J.P.; Jauncey, D.L.; Lovell, J.E.J.; Tzioumis, A.K.; Kedziora-Chudczer, L. Rapid Interstellar Scintillation of PKS 1257-326: Two-Station Pattern Time Delays and Constraints on Scattering and Microarcsecond Source Structure. Astrophys. J. 2006, 652, 1050–1058. [Google Scholar] [CrossRef]
- Liu, B.R.; Liu, X.; Marchili, N.; Liu, J.; Mi, L.G.; Krichbaum, T.P.; Fuhrmann, L.; Zensus, J.A. Two-year monitoring of intra-day variability of quasar 1156 + 295 at 4.8 GHz. Astron. Astrophys. 2013, 555, A134. [Google Scholar] [CrossRef][Green Version]
- Qian, S.J.; Zhang, X.Z. An Intrinsic Model for the Polarization Position Angle Swing Observed in QSO 1150 + 812. J. Astron. Astrophys. 2004, 4, 37–50. [Google Scholar] [CrossRef]
- Krichbaum, T.P.; Witzel, A.; Zensus, J.A. The Role of Millimeter VLBI Observations in AGN Research. arXiv, 2002; arXiv:astro-ph/0204062. [Google Scholar]
- Wagner, S.J.; Witzel, A.; Heidt, J.; Krichbaum, T.P.; Qian, S.J.; Quirrenbach, A.; Wegner, R.; Aller, H.; Aller, M.; Anton, K.; et al. Rapid Variability in S5 0716 + 714 Across the Electromagnetic Spectrum. Astron. J. 1996, 111, 2187. [Google Scholar] [CrossRef]
- Liu, X.; Mi, L.G.; Liu, J.; Cui, L.; Song, H.G.; Krichbaum, T.P.; Kraus, A.; Fuhrmann, L.; Marchili, N.; Zensus, J.A. Intra-day variability observations and the VLBI structure analysis of quasar S4 0917 + 624. Astron. Astrophys. 2015, 578, A34. [Google Scholar] [CrossRef]
- Kellermann, K.I.; Pauliny-Toth, I.I.K. The Spectra of Opaque Radio Sources. Astrophys. J. Lett. 1969, 155, L71. [Google Scholar] [CrossRef]
- Kovalev, Y.Y.; Kardashev, N.S.; Kellermann, K.I.; Lobanov, A.P.; Johnson, M.D.; Gurvits, L.I.; Voitsik, P.A.; Zensus, J.A.; Anderson, J.M.; Bach, U.; et al. RadioAstron Observations of the Quasar 3C273: A Challenge to the Brightness Temperature Limit. Astrophys. J. Lett. 2016, 820, L9. [Google Scholar] [CrossRef]
- Johnson, M.D.; Kovalev, Y.Y.; Gwinn, C.R.; Gurvits, L.I.; Narayan, R.; Macquart, J.P.; Jauncey, D.L.; Voitsik, P.A.; Anderson, J.M.; Sokolovsky, K.V.; et al. Extreme Brightness Temperatures and Refractive Substructure in 3C273 with RadioAstron. Astrophys. J. Lett. 2016, 820, L10. [Google Scholar] [CrossRef]
- Liu, J.; Liu, X.; Cui, L.; Ding, Z.; Krichbaum, T.P.; Kraus, A.; Marchili, N.; Zensus, J.A. UNSS: The Urumqi Northern Sky Survey for Rapid Variability in Compact Radio Sources. in press.
- Lovell, J.E.J.; Jauncey, D.L.; Bignall, H.E.; Kedziora-Chudczer, L.; Macquart, J.P.; Rickett, B.J.; Tzioumis, A.K. First Results from MASIV: The Microarcsecond Scintillation-induced Variability Survey. Astron. J. 2003, 126, 1699–1706. [Google Scholar] [CrossRef]
- Kraus, A.; Krichbaum, T.P.; Wegner, R.; Witzel, A.; Cimò, G.; Quirrenbach, A.; Britzen, S.; Fuhrmann, L.; Lobanov, A.P.; Naundorf, C.E.; et al. Intraday variability in compact extragalactic radio sources. II. Observations with the Effelsberg 100 m radio telescope. Astron. Astrophys. 2003, 401, 161–172. [Google Scholar]
- Baars, J.W.M.; Genzel, R.; Pauliny-Toth, I.I.K.; Witzel, A. The absolute spectrum of CAS A—An accurate flux density scale and a set of secondary calibrators. Astron. Astrophys. 1977, 61, 99–106. [Google Scholar]
- Ott, M.; Witzel, A.; Quirrenbach, A.; Krichbaum, T.P.; Standke, K.J.; Schalinski, C.J.; Hummel, C.A. An updated list of radio flux density calibrators. Astron. Astrophys. 1994, 284, 331–339. [Google Scholar]
- Fuhrmann, L.; Krichbaum, T.P.; Witzel, A.; Kraus, A.; Britzen, S.; Bernhart, S.; Impellizzeri, C.M.V.; Agudo, I.; Klare, J.; Sohn, B.W.; et al. Testing the inverse-Compton catastrophe scenario in the intra-day variable blazar S5 0716 + 71. III. Rapid and correlated flux density variability from radio to sub-mm bands. Astron. Astrophys. 2008, 490, 1019–1037. [Google Scholar] [CrossRef]
- Richards, J.L.; Max-Moerbeck, W.; Pavlidou, V.; King, O.G.; Pearson, T.J.; Readhead, A.C.S.; Reeves, R.; Shepherd, M.C.; Stevenson, M.A.; Weintraub, L.C.; et al. Blazars in the Fermi Era: The OVRO 40 m Telescope Monitoring Program. Astrophys. J. Suppl. Ser. 2011, 194, 29. [Google Scholar] [CrossRef]
- Acero, F.; Ackermann, M.; Ajello, M.; Albert, A.; Atwood, W.B.; Axelsson, M.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; et al. Fermi Large Area Telescope Third Source Catalog. Astrophys. J. Suppl. Ser. 2015, 218, 23. [Google Scholar] [CrossRef]
- Pushkarev, A.B.; Kovalev, Y.Y. Milky Way scattering properties and intrinsic sizes of active galactic nuclei cores probed by very long baseline interferometry surveys of compact extragalactic radio sources. Mon. Not. R. Astron. Soc. 2015, 452, 4274–4282. [Google Scholar] [CrossRef]
- Richards, J.L.; Hovatta, T.; Max-Moerbeck, W.; Pavlidou, V.; Pearson, T.J.; Readhead, A.C.S. Connecting radio variability to the characteristics of gamma-ray blazars. Mon. Not. R. Astron. Soc. 2014, 438, 3058–3069. [Google Scholar] [CrossRef]
- Scholz, F.W.; Stephens, M.A. K-sample Anderson–Darling Tests. J. Am. Stat. Assoc. 1974, 82, 918–924. [Google Scholar]
- Bignall, H.E.; Jauncey, D.L.; Lovell, J.E.J.; Kedziora-Chudczer, L.; Macquart, J.P.; Tzioumis, A.K.; Rickett, B.J.; Ojha, R.; Carter, S.; Cimó, G.; et al. Interstellar scintillation as a probe of microarcsecond scale structure in quasars. In Proceedings of the European VLBI Network on New Developments in VLBI Science and Technology, Toledo, Spain, 12–15 October 2004; pp. 19–22. [Google Scholar]
- Dennett-Thorpe, J.; de Bruyn, A.G. The Discovery of a Microarcsecond Quasar: J1819 + 3845. Astrophys. J. Lett. 2000, 529, L65–L68. [Google Scholar] [CrossRef]
- Readhead, A.C.S. Equipartition brightness temperature and the inverse Compton catastrophe. Astrophys. J. 1994, 426, 51–59. [Google Scholar] [CrossRef]
- Heeschen, D.S. Flickering of extragalactic radio sources. Astron. J. 1984, 89, 1111–1123. [Google Scholar] [CrossRef]
- Kovalev, Y.Y.; Aller, H.D.; Aller, M.F.; Homan, D.C.; Kadler, M.; Kellermann, K.I.; Kovalev, Y.A.; Lister, M.L.; McCormick, M.J.; Pushkarev, A.B.; et al. The Relation Between AGN Gamma-Ray Emission and Parsec-Scale Radio Jets. Astrophys. J. Lett. 2009, 696, L17–L21. [Google Scholar] [CrossRef]
- Pushkarev, A.B.; Kovalev, Y.Y.; Lister, M.L. Radio/Gamma-ray Time Delay in the Parsec-scale Cores of Active Galactic Nuclei. Astrophys. J. Lett. 2010, 722, L7–L11. [Google Scholar] [CrossRef]
- Lister, M.L.; Homan, D.C.; Kadler, M.; Kellermann, K.I.; Kovalev, Y.Y.; Ros, E.; Savolainen, T.; Zensus, J.A. A Connection Between Apparent VLBA Jet Speeds and Initial Active Galactic Nucleus Detections Made by the Fermi Gamma-Ray Observatory. Astrophys. J. Lett. 2009, 696, L22–L26. [Google Scholar] [CrossRef]
- Ramakrishnan, V.; León-Tavares, J.; Rastorgueva-Foi, E.A.; Wiik, K.; Jorstad, S.G.; Marscher, A.P.; Tornikoski, M.; Agudo, I.; Lähteenmäki, A.; Valtaoja, E.; et al. The connection between the parsec-scale radio jet and γ-ray flares in the blazar 1156 + 295. Mon. Not. R. Astron. Soc. 2014, 445, 1636–1646. [Google Scholar] [CrossRef][Green Version]
- Casadio, C.; Gómez, J.L.; Grandi, P.; Jorstad, S.G.; Marscher, A.P.; Lister, M.L.; Kovalev, Y.Y.; Savolainen, T.; Pushkarev, A.B. The Connection between the Radio Jet and the Gamma-ray Emission in the Radio Galaxy 3C 120. Astrophys. J. 2015, 808, 162. [Google Scholar] [CrossRef]
- Hada, K.; Kino, M.; Doi, A.; Nagai, H.; Honma, M.; Akiyama, K.; Tazaki, F.; Lico, R.; Giroletti, M.; Giovannini, G.; et al. High-sensitivity 86 GHz (3.5 mm) VLBI Observations of M87: Deep Imaging of the Jet Base at a Resolution of 10 Schwarzschild Radii. Astrophys. J. 2016, 817, 131. [Google Scholar] [CrossRef]
- Haffner, L.M.; Reynolds, R.J.; Tufte, S.L.; Madsen, G.J.; Jaehnig, K.P.; Percival, J.W. The Wisconsin Hα Mapper Northern Sky Survey. Astrophys. J. Suppl. Ser. 2003, 149, 405–422. [Google Scholar] [CrossRef]
- Rickett, B.J.; Lazio, T.J.W.; Ghigo, F.D. Interstellar Scintillation Observations of 146 Extragalactic Radio Sources. Astrophys. J. Suppl. Ser. 2006, 165, 439–460. [Google Scholar] [CrossRef]
- Lazio, J.; Ojha, R.; Fey, A.L.; Kedziora-Chudczer, L.; Cordes, J.M.; Jauncey, D.L.; Lovell, J.E. Milliarcsecond Observations of Microarcsecond AGN. In Proceedings of the Conference “Frontiers of Astrophysics: A Celebration of NRAO’s 50th Anniversary”, Charlottesville, VA, USA, 18–21 June 2007; p. 372. [Google Scholar]
- Ojha, R.; Fey, A.L.; Jauncey, D.L.; Lovell, J.E.J.; Johnston, K.J. Milliarcsecond Structure of Microarcsecond Sources: Comparison of Scintillating and Nonscintillating Extragalactic Radio Sources. Astrophys. J. 2004, 614, 607–614. [Google Scholar] [CrossRef]
- Hovatta, T.; Valtaoja, E.; Tornikoski, M.; Lähteenmäki, A. Doppler factors, Lorentz factors and viewing angles for quasars, BL Lacertae objects and radio galaxies. Astron. Astrophys. 2009, 494, 527–537. [Google Scholar] [CrossRef]
- Savolainen, T.; Homan, D.C.; Hovatta, T.; Kadler, M.; Kovalev, Y.Y.; Lister, M.L.; Ros, E.; Zensus, J.A. Relativistic beaming and gamma-ray brightness of blazars. Astron. Astrophys. 2010, 512, A24. [Google Scholar] [CrossRef]
- Maraschi, L.; Ghisellini, G.; Celotti, A. A jet model for the gamma-ray emitting blazar 3C 279. Astrophys. J. Lett. 1992, 397, L5–L9. [Google Scholar] [CrossRef]
- Dermer, C.D.; Schlickeiser, R.; Mastichiadis, A. High-energy gamma radiation from extragalactic radio sources. Astron. Astrophys. 1992, 256, L27–L30. [Google Scholar]
- Sikora, M.; Begelman, M.C.; Rees, M.J. Comptonization of diffuse ambient radiation by a relativistic jet: The source of gamma rays from blazars? Astrophys. J. 1994, 421, 153–162. [Google Scholar] [CrossRef]
- Mannheim, K. The proton blazar. Astron. Astrophys. 1993, 269, 67–76. [Google Scholar]
- Marscher, A.P. Accurate formula for the self-Compton X-ray flux density from a uniform, spherical, compact radio source. Astrophys. J. 1983, 264, 296. [Google Scholar] [CrossRef]
- Lee, S.S.; Lobanov, A.P.; Krichbaum, T.P.; Zensus, J.A. Acceleration of Compact Radio Jets on Sub-parsec Scales. Astrophys. J. 2016, 826, 135. [Google Scholar] [CrossRef]
- Hollenbach, D.J.; Tielens, A.G.G.M. Dense Photodissociation Regions (PDRs). Annu. Rev. Astron. Astrophys. 1997, 35, 179–216. [Google Scholar] [CrossRef]
- Magnani, L.; Hartmann, D.; Speck, B.G. A Catalog of Molecular Gas at High Galactic Latitudes. Astrophys. J. Suppl. Ser. 1996, 106, 447. [Google Scholar] [CrossRef]
- Redfield, S.; Linsky, J.L. The Structure of the Local Interstellar Medium. IV. Dynamics, Morphology, Physical Properties, and Implications of Cloud-Cloud Interactions. Astrophys. J. 2008, 673, 283–314. [Google Scholar] [CrossRef]
- Walker, M.A.; Tuntsov, A.V.; Bignall, H.; Reynolds, C.; Bannister, K.W.; Johnston, S.; Stevens, J.; Ravi, V. Extreme Radio-wave Scattering Associated with Hot Stars. Astrophys. J. 2017, 843, 15. [Google Scholar] [CrossRef]
- Pearson, T.J. Non-Imaging Data Analysis. In Synthesis Imaging in Radio Astronomy II; Taylor, G.B., Carilli, C.L., Perley, R.A., Eds.; Astronomical Society of the Pacific: San Francisco, CA, USA, 1999; Volume 180, p. 335. [Google Scholar]
| 1 | |
| 2 | |
| 3 |
| Epoch | Date (dd.mm–dd.mm.yyyy) | Duration [h] | Number of Observed Sources | Average Sampling [] | Duty Cycle [] | [%] |
|---|---|---|---|---|---|---|
| A | 18.07–20.07.2014 | 62.0 | 37 | 14.8 | 0.40 | 0.50 |
| B | 12.09–15.09.2014 | 66.6 | 45 | 15.9 | 0.35 | 0.40 |
| C | 31.07–06.08.2015 | 73.6 | 42 | 14.3 | 0.34 | 0.40 |
| D | 17.12–21.12.2015 | 82.4 | 39 | 14.5 | 0.37 | 0.35 |
| E | 20.12–24.12.2016 | 84.4 | 41 | 14.0 | 0.34 | 0.60 |
| Likelihood Analysis | Anderson–Darling Test | |||||
|---|---|---|---|---|---|---|
| Subsample | Source Num. | [%] | [%] | Significance | Significance | |
| 1 Jy | 53 | |||||
| 1 Jy | 54 | |||||
| −0.1 | 51 | |||||
| −0.1 | 56 | |||||
| -ray quiet | 44 | |||||
| -ray loud | 63 | |||||
| 34 | <1 | <1 | ||||
| 73 | ||||||
| TMIN | TMAX | |||||
|---|---|---|---|---|---|---|
| Subsample | [%] | [%] | Significance | [%] | [%] | Significance |
| 1 Jy | ||||||
| 1 Jy | ||||||
| −0.1 | ||||||
| −0.1 | ||||||
| -ray quiet | ||||||
| -ray loud | ||||||
| <1 | ||||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Bignall, H.; Krichbaum, T.P.; Liu, X.; Kraus, A.; Kovalev, Y.Y.; Sokolovsky, K.V.; Angelakis, E.; Zensus, J.A. Effelsberg Monitoring of a Sample of RadioAstron Blazars: Analysis of Intra-Day Variability. Galaxies 2018, 6, 49. https://doi.org/10.3390/galaxies6020049
Liu J, Bignall H, Krichbaum TP, Liu X, Kraus A, Kovalev YY, Sokolovsky KV, Angelakis E, Zensus JA. Effelsberg Monitoring of a Sample of RadioAstron Blazars: Analysis of Intra-Day Variability. Galaxies. 2018; 6(2):49. https://doi.org/10.3390/galaxies6020049
Chicago/Turabian StyleLiu, Jun, Hayley Bignall, Thomas P. Krichbaum, Xiang Liu, Alex Kraus, Yuri Y. Kovalev, Kirill V. Sokolovsky, Emmanouil Angelakis, and J. Anton Zensus. 2018. "Effelsberg Monitoring of a Sample of RadioAstron Blazars: Analysis of Intra-Day Variability" Galaxies 6, no. 2: 49. https://doi.org/10.3390/galaxies6020049
APA StyleLiu, J., Bignall, H., Krichbaum, T. P., Liu, X., Kraus, A., Kovalev, Y. Y., Sokolovsky, K. V., Angelakis, E., & Zensus, J. A. (2018). Effelsberg Monitoring of a Sample of RadioAstron Blazars: Analysis of Intra-Day Variability. Galaxies, 6(2), 49. https://doi.org/10.3390/galaxies6020049






