On Nearly Newtonian Potentials and Their Implications to Astrophysics
Abstract
1. Introduction
2. The Problem of Motion in GRT
2.1. Linearized Gravity and PPN Approximation
- (A)
- Near and inside the pulsar (and its companion, if it is also a neutron star), the gravitational field is strong and the weak-field assumption no longer holds. In such cases, the internal gravity is regarded as somewhat frozen.
- (B)
- When it comes to generation of gravitational waves (of wavelength and their back-reaction on the orbit (of size r and period ), the post-Newtonian approximation is only valid in the near zone (), and breaks down in the radiation zone where gravitational waves propagate and boundary conditions are defined, like the “no incoming radiation” condition [12].
2.2. The Nearly Newtonian Approach
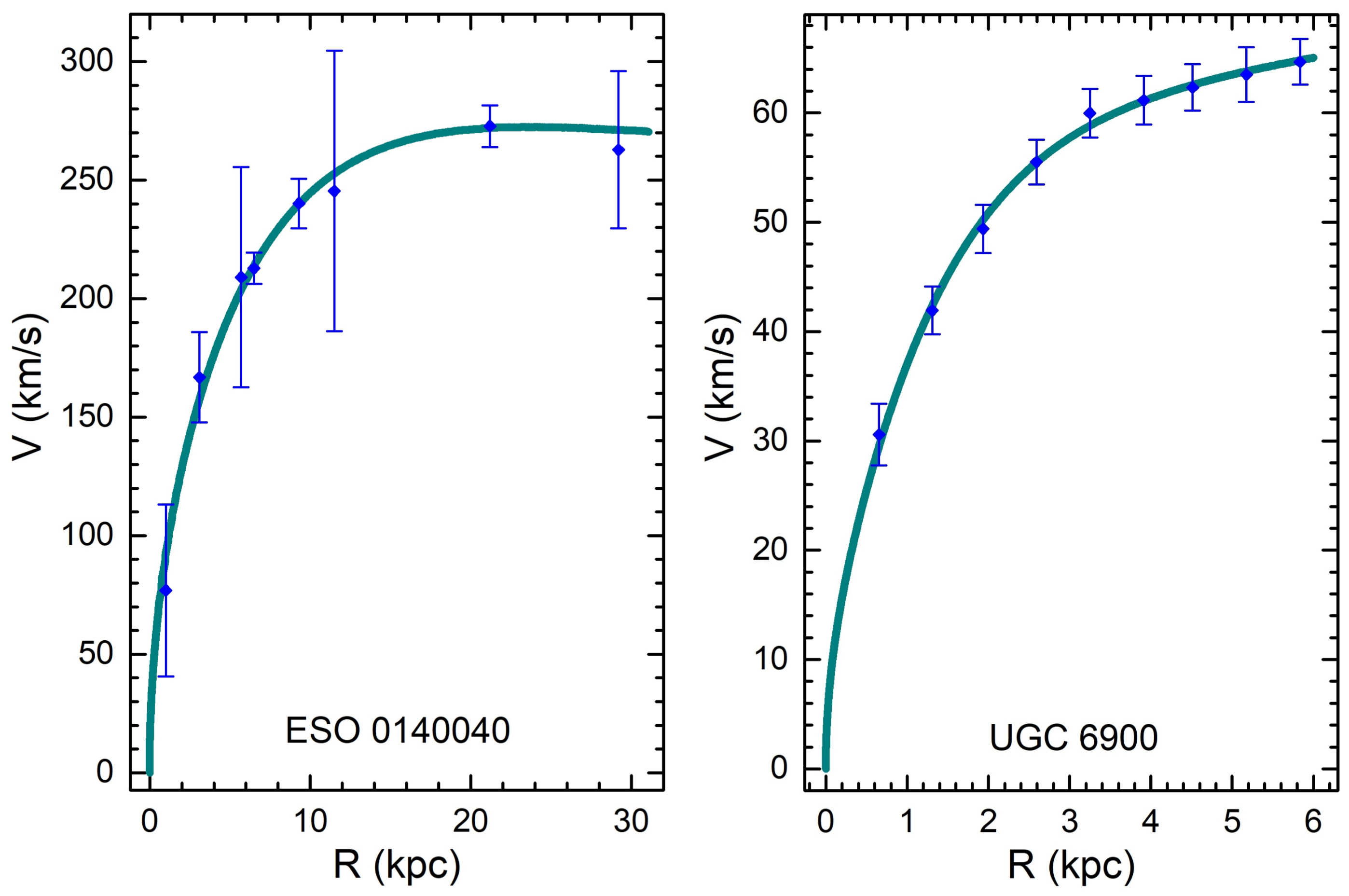
3. Astrophysical Applications
4. Conclusions
Acknowledgments
Conflicts of Interest
Abbreviations
| GRT | General Relativity theory |
| PPN | Post-Newtonian approximation |
| LSB | Low Surface brightness (galaxies) |
References
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Properties of the binary black hole merger GW150914. Phys. Rev. Lett. 2016, 116, 241102. [Google Scholar] [CrossRef] [PubMed]
- Einstein, A.; Infeld, L.; Horffmann, B. The gravitational equations and the problem of Motion. Ann. Math. 1938, 39, 65–100. [Google Scholar] [CrossRef]
- Fock, V. The law of gravitation and the laws of motion. In The Theory of Space, Time and Gravitation; Pergamon Press Ltd.: New York, NY, USA, 1964; pp. 238–317. ISBN 9781483184906. [Google Scholar]
- Infeld, L.; Plebanski, J. Motion and Relativity; Pergamon Press Ltd.: New York, NY, USA, 1960; ISBN 9781483280387. [Google Scholar]
- Einstein, A.; Grommer, J. Allgemein Relativitätstheorie und Bewegungsgesetz. Sitzber. Preuss. Akad. Wiss. Phys. Math. 1927, 2, 1–11. [Google Scholar]
- Gupta, S.N. Eletromagnetism and gravitation. Phys. Rev. 1954, 96, 1683. [Google Scholar] [CrossRef]
- Will, C.M. Theory and Experiment in Gravitational Physics; Cambrigde University Press: Cambrigde, UK, 1993; p. 396. ISBN 0521439736. [Google Scholar]
- Will, C.M. The Confrontation between General Relativity and Experiment. Living Rev. Relativ. 2006, 9, 3–13. [Google Scholar] [CrossRef] [PubMed]
- Smalley, L.L. Post-Newtonian approximation of the Poincaré gauge theory of gravitation. Phys. Rev. D 1980, 21, 328. [Google Scholar] [CrossRef]
- Hohmann, M. Parameterized post-Newtonian limit of Horndeski’s gravity theory. Phys. Rev. D 2015, 96, 064019. [Google Scholar] [CrossRef]
- Burke, W.L. The Coupling of Gravitational Radiation to Nonrelativistic Sources. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 1969. [Google Scholar]
- Wex, N. Testing the Motion of Strongly Self-Gravitating Bodies with Radio Pulsars. In Fundamental Theories of Physics; Puetzfeld, D., Lämmerzahl, C., Schutz, B., Eds.; Springer International Publishing: New York, NY, USA, 2015; p. 653. [Google Scholar]
- The Pierre Auger Collaboration. Correlation of the highest-energy cosmic rays with nearby extragalactic objects. Science 2007, 318, 938–943. [Google Scholar] [CrossRef]
- The Pierre Auger Collaboration; Aab, A.; Abreu, P.; Aglietta, M.; Al Samarai, I.; Albuquerque, I.F.M.; Allekotte, I.; Almela, A.; Alvarez Castillo, J.; Alvarez-Muñiz, G.A.; et al. Observation of a large-scale anisotropy in the arrival directions of cosmic rays above 8 × 1018 eV. Science 2017, 357, 1266–1270. [Google Scholar] [CrossRef]
- Richstone, D.; Ajhar, E.A.; Bender, R.; Bower, G.; Dressler, A.; Faber, S.M.; Filippenko, A.V.; Gebhardt, K.; Green, R.; Ho, L.C.; et al. Supermassive Black Holes and the Evolution of Galaxies. Nature 1998, 395, A14–A19. [Google Scholar]
- Ferrarese, L.; Merrit, D. Supermassive black-holes. Phys. World 2002, 15, 41. [Google Scholar] [CrossRef][Green Version]
- Ferrarese, L.; Ford, H. Supermassive Black Holes in Galactic Nuclei: Past, Present and Future Research. Space Sci. Rev 2005, 116, 523–627. [Google Scholar] [CrossRef]
- Misner, C.; Thorne, K.S.; Wheeler, J.A. The Newtonian limit. In Gravitation; W. H. Freeman and Company: New York, NY, USA, 1973; pp. 412–416. ISBN 0-7167-0344-0. [Google Scholar]
- Einstein, A. The Meaning of Relativity; Princeton University Press: Princeton, NJ, USA, 1953; ISBN 9780691164083. [Google Scholar]
- Moffat, J.W. New theory of gravitaion. Phys. Rev. D 1979, 19, 3554–3558. [Google Scholar] [CrossRef]
- Moffat, J.W. Non symmetrical gravitational theory. Phys. Lett. B 1995, 355, 447–452. [Google Scholar] [CrossRef]
- Van Meter, J.R. Dark-matter-like solutions to Einstein’s unified field equations. Phys. Rev. D 2018, 97, 044018. [Google Scholar] [CrossRef]
- Dalmazi, D.; Fortes, H.G.M. Nonsymmetric tensor description of massive spin-2 particles in a curved background. Phys. Rev. D 2017, 95, 065028. [Google Scholar] [CrossRef]
- Svítek, O.; Tahamtan, T. Nonsymmetric dynamical thin-shell wormhole in Robinson—Trautman class. Eur. Phys. J. C 2018, 78, 167. [Google Scholar] [CrossRef]
- Ivanov, S.; Zlatanović, M. Connections on non-symmetric (generalized) Riemannian manifold and gravity. Class. Quantum Gravity 2015, 33, 075016. [Google Scholar] [CrossRef]
- Kalinowski, M.W. Pioneer 10 and 11 Spacecraft Anomalous Acceleration in the light of the Nonsymmetric Kaluza-Klein (Jordan-Thiry) Theory. Fortschr. Phys. 2015, 63, 11–12. [Google Scholar] [CrossRef]
- Capistrano, A.J.S.; Roque, W.L.; Valada, R.S. Weyl conformastatic perihelion advance. Mon. Not. R. Astron. Soc. 2014, 444, 1639–1646. [Google Scholar] [CrossRef][Green Version]
- Capistrano, A.J.S.; Penãgos, J.A.M.; Alárcon, M.S. Anomalous precession of planets for a Weyl conformastatic solution. Mon. Not. R. Astron. Soc. 2016, 463, 1587–1591. [Google Scholar] [CrossRef]
- Weyl, H. Zur Gravitationstheorie. Ann. Phys. 1917, 54, 117–145. [Google Scholar] [CrossRef]
- Rosen, N. A Particle at Rest in a Static Gravitational Field. Rev. Mod. Phys. 1949, 21, 503. [Google Scholar] [CrossRef]
- Zipoy, M.D. Topology of some spheroidal metrics. J. Math. Phys. 1966, 7, 1137–1143. [Google Scholar] [CrossRef]
- Gautreau, R.; Hoffman, R.B.; Armenti, A. Static multiparticle systems in general relativity. Il Nuovo Cimento B 1972, 7, 71. [Google Scholar] [CrossRef]
- Hoenselaers, C.; Kramer, D.; Stephani, H.; MacCallum, M. Exact Solutions of Einstein’s Field Equations; Cambridge University Press: Cambridge, UK, 2003; ISBN-13 978-0521467025. [Google Scholar]
- Vieira, R.S.S.; Ramos-Caro, J.; Saa, A. Vertical stability of circular orbits in relativistic razor-thin disks. Phys. Rev. D 2016, 94, 104016. [Google Scholar] [CrossRef]
- González, G.A.; Gutiérrez-Piñeres, A.C.; Ospina, P.A. Conformastatic disk-haloes in Einstein-Maxwell gravity. Phys. Rev. D 2008, 78, 064058. [Google Scholar] [CrossRef]
- Gutiérrez-Piñeres, A.C.; González, G.A.; Quevedo, H. Finite axisymmetric charged dust disks in conformastatic spacetimes. PRD 2008, 87, 044010. [Google Scholar] [CrossRef]
- Ujevic, M.; Letelier, P.S. Stability of general relativistic geometric thin disks. Phys. Rev. D 2004, 70, 084015. [Google Scholar] [CrossRef]
- Ujevic, M.; Letelier, P.S. Stability of general relativistic static thick disks: the isotropic Schwarzschild thick disk. Gen. Relativ. Grav. 2001, 39, 1345–1365. [Google Scholar] [CrossRef][Green Version]
- Vogt, D.; Letelier, P.S. Exact general relativistic discs and the advance of perihelion. Mon. Not. R. Astron. Soc. 2008, 384, 834–842. [Google Scholar] [CrossRef]
- Pitjeva, E.V. Ephemerides EPM2008: The Updated Models, Constants, Data. In Proceedings of the Journées “Systémes de Référence Spatio-Temporels” and X Lohrmann-Kolloquium, Dresden, Germany, 22–24 September 2008; Available online: http://syrte.obspm.fr/jsr/journees2008/pdf/ (accessed on 20 May 2016).
- Iorio, L. The recently determined anomalous perihelion precession of Saturn. Astron. J. 2009, 137, 3615. [Google Scholar] [CrossRef]
- Pitjeva, E.V.; Pitjev, N.P. Relativistic effects and dark matter in the Solar system from observations of planets and spacecraft. Mon. Not. R. Astron. Soc. 2013, 432, 3431–3437. [Google Scholar] [CrossRef]
- Pitjev, N.P.; Pitjeva, E.V. Constraints on dark matter in the solar system. Astron. Lett. 2013, 39, 141–149. [Google Scholar] [CrossRef]
- Fienga, A.; Laskar, J.; Kuchynka, P.; Manche, H.; Desvignes, G.; Gastineau, M.; Cognard, I.; Theureau, G. The INPOP10a planetary ephemeris and its applications in fundamental physics. Celest. Mech. Dyn. Astron. 2011, 111, 363–385. [Google Scholar] [CrossRef]
- Wilhelm, K.; Dwivedi, B.N. Secular perihelion advances of the inner planets and asteroid Icarus. New Astron. 2014, 31, 51–55. [Google Scholar] [CrossRef]
- Nambuya, G.G. Azimuthally symmetric theory of gravitation—I. On the perihelion precession of planetary orbits. Mon. Not. R. Astron. Soc. 2010, 403, 1381–1391. [Google Scholar] [CrossRef]
- Busemann, H.; Nguyen, A.N.; Cody, G.D.; Hoppe, P.; David, A.L.D.; Rhond, K.; Stroud, M.R.; Zega, T.J.; Nittler, L.R. Ultra-primitive interplanetary dust particles from the comet 26P/Grigg–Skjellerup dust stream collection. Earth Planet. Sci. Lett. 2009, 288, 44–57. [Google Scholar] [CrossRef]
- Levison, H.F.; Terrell, D.; Wiegert, P.A.; Dones, L.; Duncan, M.J. On the origin of the unusual orbit of Comet 2P/Encke. Icarus 2006, 182, 161–168. [Google Scholar] [CrossRef]
- Moreno, F.; Pozuelos, F.; Aceituno, F.; Casanova, V.; Sota, A.; Castellano, J.; Reina, E. Comet 22P/Kopff: Dust environment and grain ejection anisotropy from visible and infrared observations. Astrophys. J. 2011, 752, 136. [Google Scholar] [CrossRef]
- Capistrano, A.J.S.; Barrocas, G.R.G. Rotation curves of LSBGs and dwarf galaxies in a nearly-Newtonian solution. Mon. Not. R. Astron. Soc. 2018, 475, 2204–2214. [Google Scholar] [CrossRef]
- Rubin, V.C.; Kent Ford, W., Jr. Rotation of the Andromeda Nebula from a Spectroscopic Survey of Emission Regions. Astrophys. J. 1970, 159, 379–403. [Google Scholar] [CrossRef]
- Sanders, R.H. The Dark Matter Problem—A Historical Perspective; Cambridge University Press: New York, NY, USA, 2010; ISBN 9780521113014. [Google Scholar]
- Bertone, B.; Hooper, D. A History of dark matter. arXiv, 2016; arXiv:1605.04909. [Google Scholar]
- Lelli, F.; McGaugh, S.S.; Schombert, J.M.; Pawlowski, M.S. One Law to Rule Them All: The Radial Acceleration Relation of Galaxies. Astrophys. J. 2017, 836, 152. [Google Scholar] [CrossRef]
- Blumenthal, G.R.; Faber, S.M.; Flores, V.; Primack, J.R. Contraction of dark matter galactic halos due to baryonic infall. Astrophys. J. 1984, 301, 27–34. [Google Scholar] [CrossRef]
- de Blok, W.J.G.; McGaugh, S.S.; Rubin, V.C. High-Resolution Rotation Curves of Low Surface Brightness Galaxies. I. Data. Astrophys. J. 2001, 122, 5. [Google Scholar] [CrossRef]
- Karukes, E.V.; Salucci, P. The universal rotation curve of dwarf disc galaxies. Mon. Not. R. Astron. Soc. 2017, 465, 4703–4722. [Google Scholar] [CrossRef]
- Hartle, J.B. Gravity: An Introduction To Einstein’s General Relativity; Addison-Wesley Professional: San Francisco, CA, USA, 2003; pp. 126–130. ISBN 080-538-662-9. [Google Scholar]
- Griffiths, J.B.; Podolsky, J. Exact Space-Times in Einstein’s General Relativity; Cambridge University Press: Cambridge, UK, 2009; Chapter 10; ISBN 110-740-618-8. [Google Scholar]
- Cooperstock, F.I.; Tieu, S. General Relativity resolves galactic rotation without exotic Dark Matter. arXiv, 2005; arXiv:astro-ph/0507619. [Google Scholar]
| Object | ||||||
|---|---|---|---|---|---|---|
| Mercury | 43.098 ± 0.503 | 42.97817 | 43.1047 | 42.8569 | ||
| 26P/Grigg-Skjellerup | 0.54 | 0.4106 | 0.430490 | 0.391913 | ||
| 22p/Kopff | 0.288 | 0.2474 | 0.255405 | 0.240378 | ||
| Object | EPM2008 | EPM2011 | INPOP10a | |||
|---|---|---|---|---|---|---|
| Mercury | −3.7945 | −2.0237 | 0.4047 | |||
| Earth | −0.1869 | 1.8694 | −0.1669 | |||
| Saturn | −5.7876 | −0.2829 | 0.1910 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Capistrano, A.J.S. On Nearly Newtonian Potentials and Their Implications to Astrophysics. Galaxies 2018, 6, 48. https://doi.org/10.3390/galaxies6020048
Capistrano AJS. On Nearly Newtonian Potentials and Their Implications to Astrophysics. Galaxies. 2018; 6(2):48. https://doi.org/10.3390/galaxies6020048
Chicago/Turabian StyleCapistrano, Abraao J. S. 2018. "On Nearly Newtonian Potentials and Their Implications to Astrophysics" Galaxies 6, no. 2: 48. https://doi.org/10.3390/galaxies6020048
APA StyleCapistrano, A. J. S. (2018). On Nearly Newtonian Potentials and Their Implications to Astrophysics. Galaxies, 6(2), 48. https://doi.org/10.3390/galaxies6020048





