Practical Aspects of X-ray Imaging Polarimetry of Supernova Remnants and Other Extended Sources
Abstract
1. Introduction
2. Measuring X-ray Polarisation with Gas-Pixel-Detectors on a Photon by Photon Statistics Base
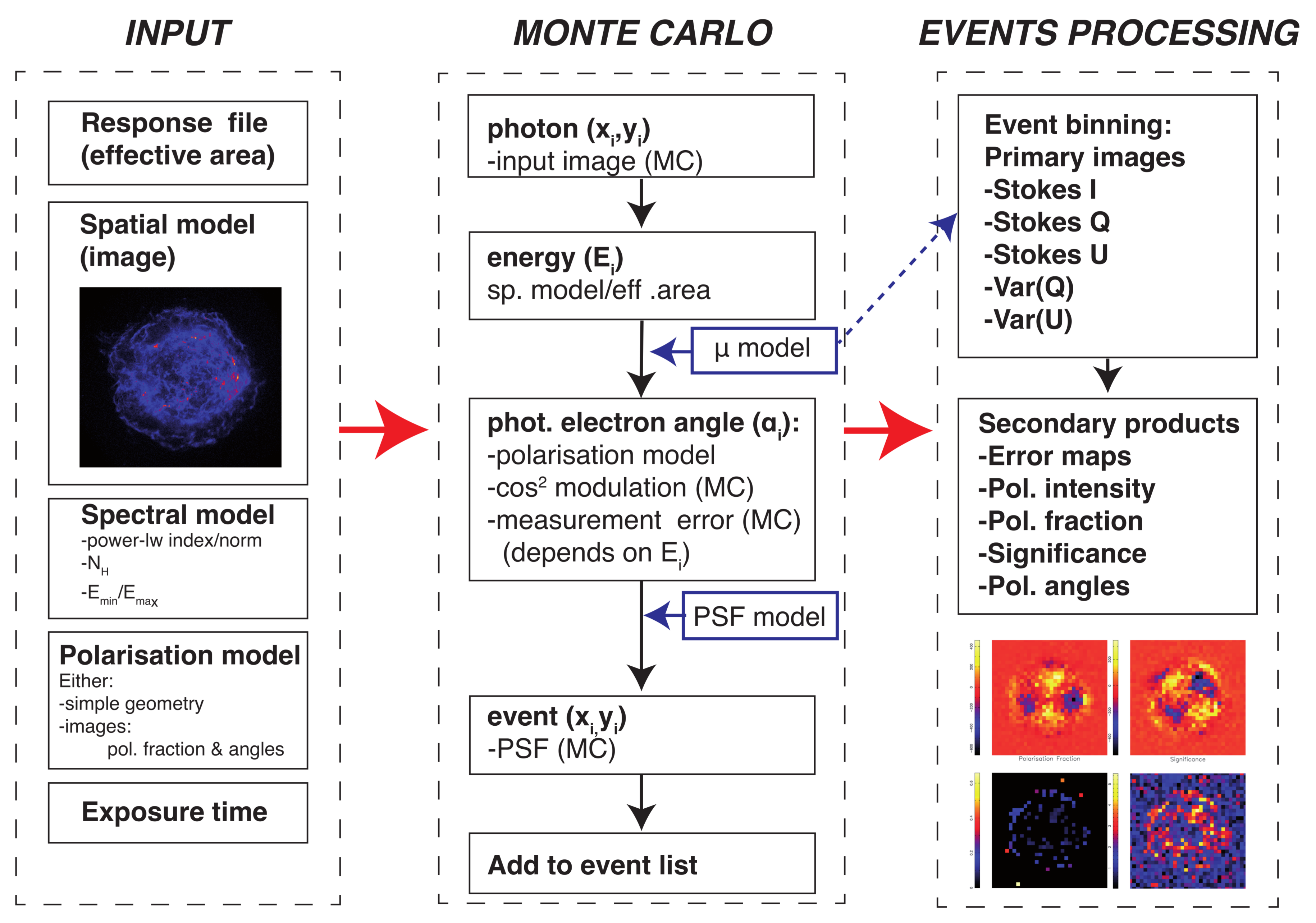
3. A Monte Carlo Code for X-ray Gas Pixel Detectors
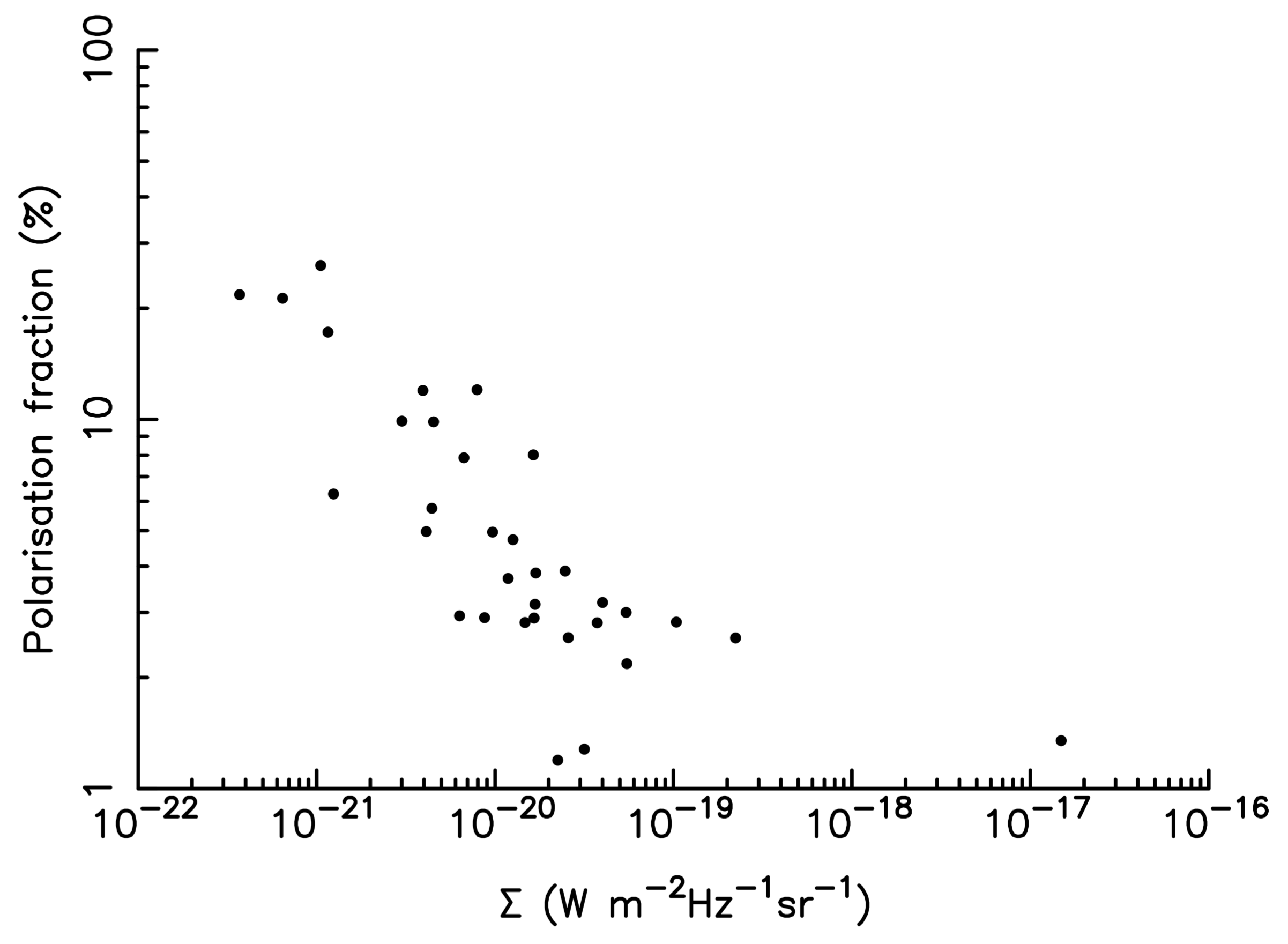
4. The Expected X-ray Polarisation Signals from Shell-Type Supernova Remnants
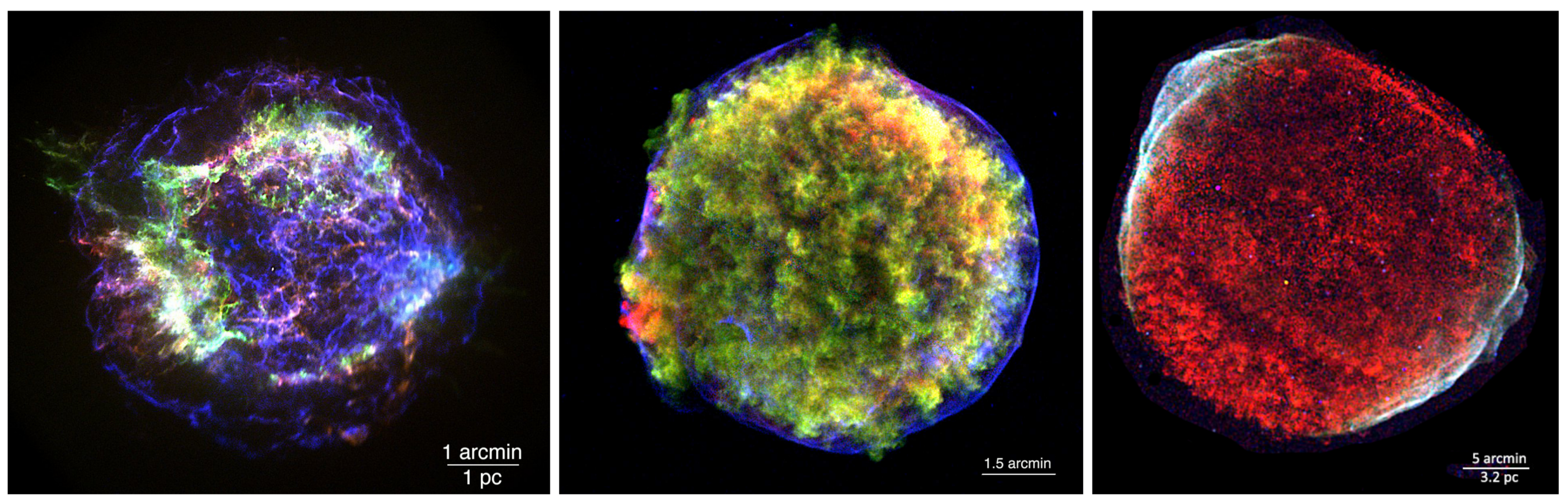
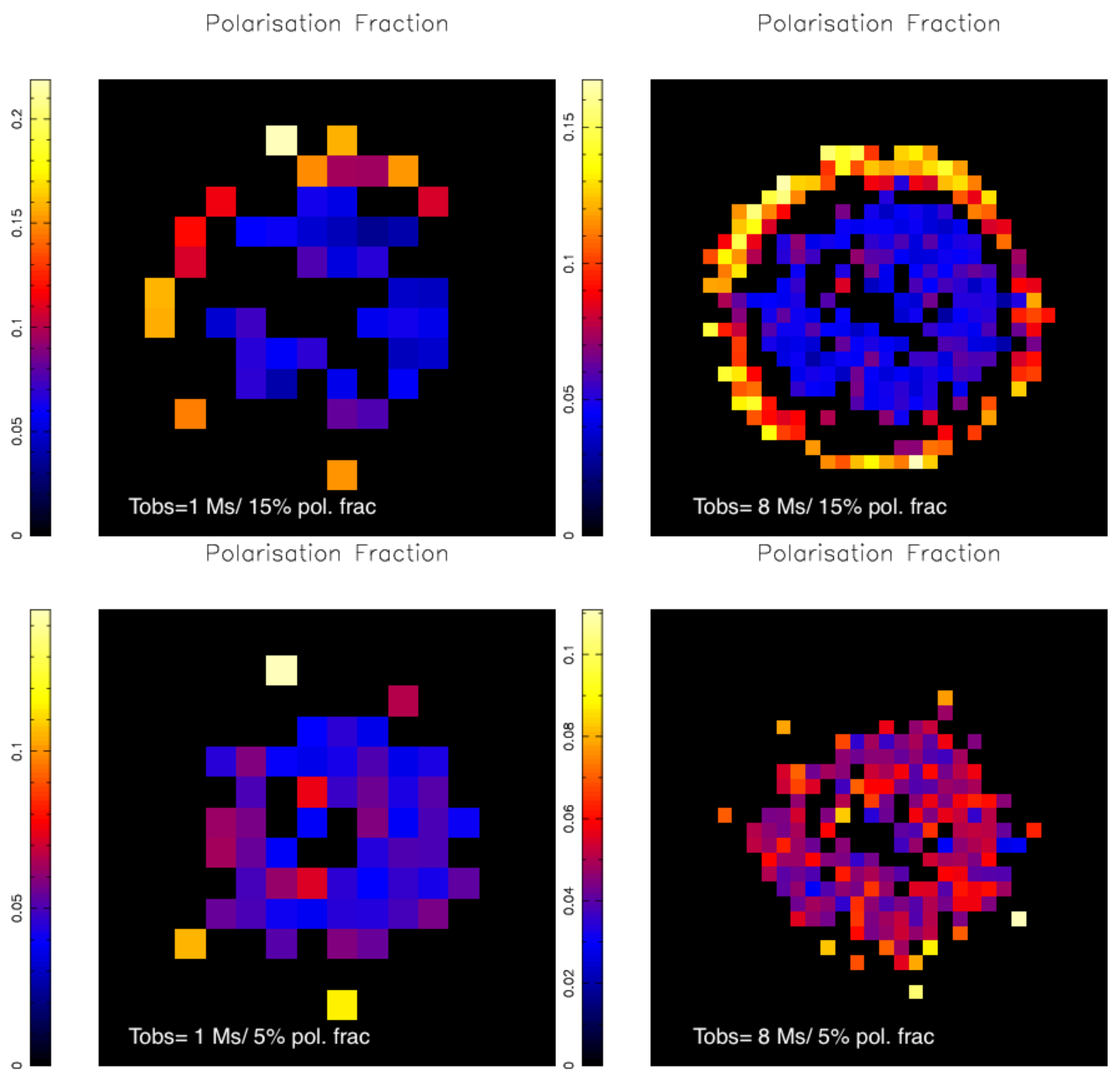
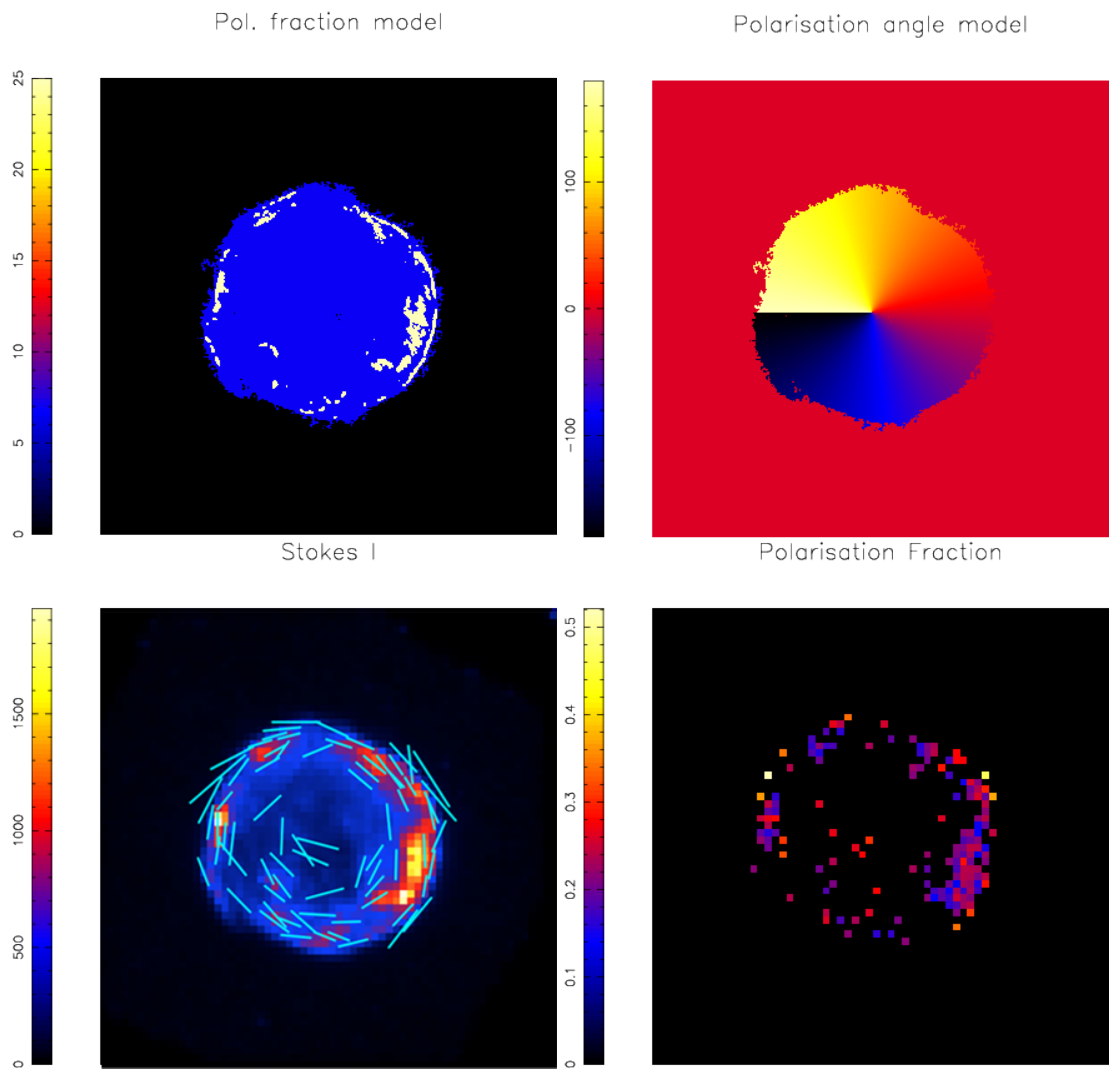
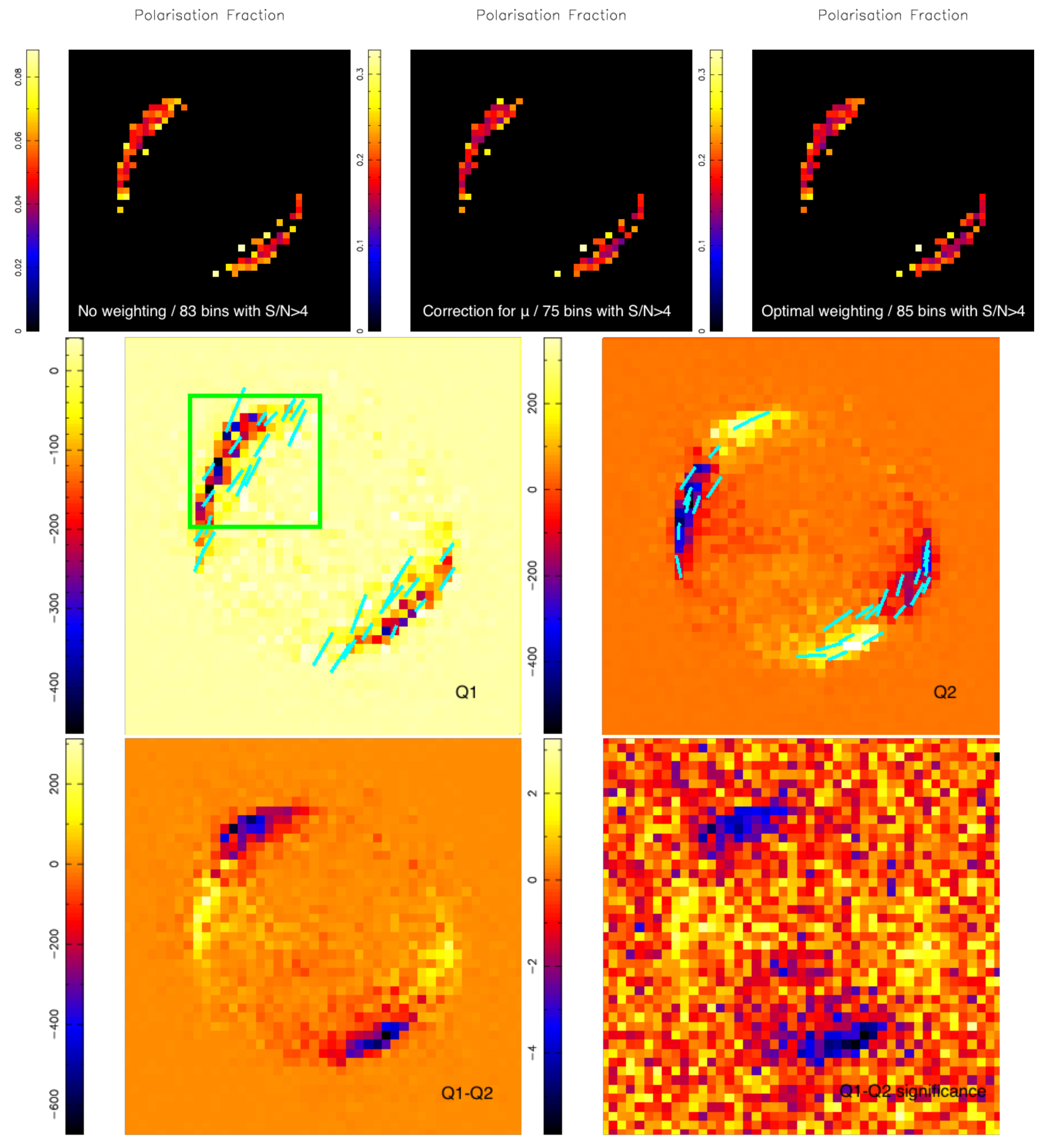
5. Simulations of Supernova Remnants
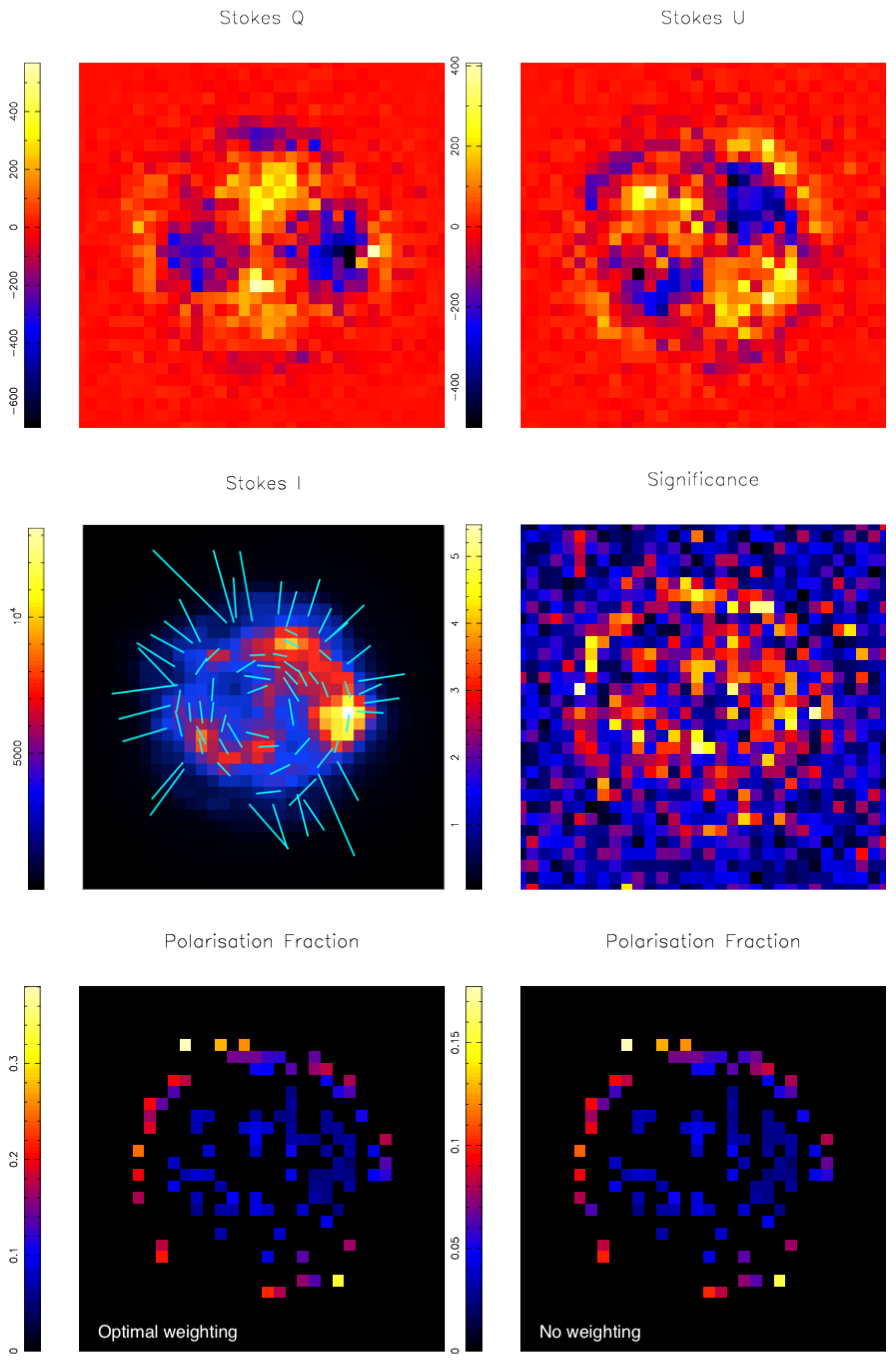
5.1. Cas A
5.2. Tycho’s SNR (SN 1572)
5.3. SN 1006
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| SNR(s) | supernova remnant(s) |
| PWN(e) | pulsar wind nebula(e) |
| GPD | gas pixel detector |
| MDPI | Multidisciplinary Digital Publishing Institute |
| DOAJ | Directory of open access journals |
| TLA | Three letter acronym |
| LD | linear dichroism |
References
- Vink, J. Supernova remnants: The X-ray perspective. Astron. Astrophys. Rev. 2012, 20, 49. [Google Scholar] [CrossRef]
- Novick, R.; Weisskopf, M.C.; Berthelsdorf, R.; Linke, R.; Wolff, R.S. Detection of X-Ray Polarization of the Crab Nebula. Astrophys. J. Lett. 1972, 174, L1–L8. [Google Scholar] [CrossRef]
- Weisskopf, M.C.; Cohen, G.G.; Kestenbaum, H.L.; Long, K.S.; Novick, R.; Wolff, R.S. Measurement of the X-ray polarization of the Crab Nebula. Astrophys. J. Lett. 1976, 208, L125–L128. [Google Scholar] [CrossRef]
- Weisskopf, M.C.; Silver, E.H.; Kestenbaum, H.L.; Long, K.S.; Novick, R. A precision measurement of the X-ray polarization of the Crab Nebula without pulsar contamination. Astrophys. J. Lett. 1978, 220, L117–L121. [Google Scholar] [CrossRef]
- Oort, J.H.; Walraven, T. Polarization and composition of the Crab nebula. Bull. Astron. Neth. 1956, 12, 285. [Google Scholar]
- Mayer, C.H.; Hollinger, J.P. Polarized Brightness Distribution Over Cassiopeia a, the Crab Nebula, and Cygnus a at 1.55 cm Wavelength. Astrophys. J. 1968, 151, 53. [Google Scholar] [CrossRef]
- Bietenholz, M.F.; Kronberg, P.P. The magnetic field of the Crab Nebula and the nature of its ‘jet’. Astrophys. J. Lett. 1990, 357, L13–L16. [Google Scholar] [CrossRef]
- Moran, P.; Kyne, G.; Gouiffès, C.; Laurent, P.; Hallinan, G.; Redfern, R.M.; Shearer, A. A recent change in the optical and γ-ray polarization of the Crab nebula and pulsar. Mon. Not. R. Astron. Soc. 2016, 456, 2974–2981. [Google Scholar] [CrossRef]
- Costa, E.; Soffitta, P.; Bellazzini, R.; Brez, A.; Lumb, N.; Spandre, G. An efficient photoelectric X-ray polarimeter for the study of black holes and neutron stars. Nature 2001, 411, 662–665. [Google Scholar] [CrossRef] [PubMed]
- Bellazzini, R.; Spandre, G.; Minuti, M.; Baldini, L.; Brez, A.; Latronico, L.; Omodei, N.; Razzano, M.; Massai, M.M.; Pesce-Rollins, M.; et al. A sealed Gas Pixel Detector for X-ray astronomy. Nucl. Instrum. Methods Phys. Res. A 2007, 579, 853–858. [Google Scholar] [CrossRef]
- Soffitta, P.; Barcons, X.; Bellazzini, R.; Braga, J.; Costa, E.; Fraser, G.W.; Gburek, S.; Huovelin, J.; Matt, G.; Pearce, M.; et al. XIPE: The X-ray imaging polarimetry explorer. Exp. Astron. 2013, 36, 523–567. [Google Scholar] [CrossRef]
- Weisskopf, M.C.; Ramsey, B.; O’Dell, S.; Tennant, A.; Elsner, R.; Soffitta, P.; Bellazzini, R.; Costa, E.; Kolodziejczak, J.; Kaspi, V.; et al. The Imaging X-ray Polarimetry Explorer (IXPE). In Space Telescopes and Instrumentation 2016: Ultraviolet to Gamma Ray; SPIE: Bellingham, WA, USA, 2016; Volume 9905, p. 990517. [Google Scholar]
- Zhang, S.N.; Feroci, M.; Santangelo, A.; Dong, Y.W.; Feng, H.; Lu, F.J.; Nandra, K.; Wang, Z.S.; Zhang, S.; Bozzo, E.; et al. eXTP: Enhanced X-ray Timing and Polarization mission. In Space Telescopes and Instrumentation 2016: Ultraviolet to Gamma Ray; SPIE: Bellingham, WA, USA, 2016; Volume 9905, p. 99051Q. [Google Scholar]
- Kislat, F.; Clark, B.; Beilicke, M.; Krawczynski, H. Analyzing the data from X-ray polarimeters with Stokes parameters. Astropart. Phys. 2015, 68, 45–51. [Google Scholar] [CrossRef]
- Muleri, F.; Soffitta, P.; Baldini, L.; Bellazzini, R.; Brez, A.; Costa, E.; Fabiani, S.; Krummenacher, F.; Latronico, L.; Lazzarotto, F.; et al. Spectral and polarimetric characterization of the Gas Pixel Detector filled with dimethyl ether. Nucl. Instrum. Methods Phys. Res. A 2010, 620, 285–293. [Google Scholar] [CrossRef]
- De Ona Wilhelmi, E.; Vink, J.; Bykov, A.; Zanin, R.; Bucciantini, N.; Amato, E.; Bandiera, R.; Olmi, B.; Uvarov, Y.; XIPE Science Working Group. Unveiling the magnetic structure of VHE SNRs/PWNe with XIPE, the X-ray imaging-polarimetry explorer. In Proceedings of the 6th International Symposium on High Energy Gamma-Ray Astronomy, Heidelberg, Germany, 11–15 July 2017; Volume 1792, p. 070023. [Google Scholar]
- Meier, P. Variance of a weighted mean. Biometrics 1953, 9, 59–73. [Google Scholar] [CrossRef]
- Shahar, D. Minimizing the Variance of a Weighted Average. Open J. Stat. 2017, 7, 216–224. [Google Scholar] [CrossRef]
- Fabiani, S.; Costa, E.; Del Monte, E.; Muleri, F.; Soffitta, P.; Rubini, A.; Bellazzini, R.; Brez, A.; de Ruvo, L.; Minuti, M.; et al. The Imaging Properties of the Gas Pixel Detector as a Focal Plane Polarimeter. Astrophys. J. Suppl. Ser. 2014, 212, 25. [Google Scholar] [CrossRef]
- Morrison, R.; McCammon, D. Interstellar photoelectric absorption cross sections, 0.03–10 keV. Astrophys. J. 1983, 270, 119–122. [Google Scholar] [CrossRef]
- Shklovsky, J.S. Supernovae as a Source of Cosmic Rays. In Proceedings of the Liege International Astrophysical Colloquia, Liege, Belgium, 10–12 September 1953; Volume 5, p. 515. [Google Scholar]
- Malkov, M.A.; Drury, L. Nonlinear theory of diffusive acceleration of particles by shock waves. Rep. Prog. Phys. 2001, 64, 429–481. [Google Scholar] [CrossRef]
- Bell, A.R. Turbulent amplification of magnetic field and diffusive shock acceleration of cosmic rays. Mon. Not. R. Astron. Soc. 2004, 353, 550–558. [Google Scholar] [CrossRef]
- Marcowith, A.; Bret, A.; Bykov, A.; Dieckman, M.E.; O’C Drury, L.; Lembège, B.; Lemoine, M.; Morlino, G.; Murphy, G.; Pelletier, G.; et al. The microphysics of collisionless shock waves. Rep. Prog. Phys. 2016, 79, 046901. [Google Scholar] [CrossRef] [PubMed]
- Koyama, K.; Petre, R.; Gotthelf, E.V.; Hwang, U.; Matsuura, M.; Ozaki, M.; Holt, S.S. Evidence for Shock Acceleration of High-Energy Electrons in the Supernova Remnant SN 1006. Nature 1995, 378, 255–258. [Google Scholar] [CrossRef]
- Aharonian, F.A.; Atoyan, A.M. On the origin of TeV radiation of SN 1006. Astron. Astrophys. 1999, 351, 330–340. [Google Scholar]
- Vink, J.; Laming, J.M. On the magnetic fields and particle acceleration in Cassiopeia A. Astrophys. J. 2003, 584, 758–769. [Google Scholar] [CrossRef]
- Helder, E.A.; Vink, J.; Bykov, A.M.; Ohira, Y.; Raymond, J.C.; Terrier, R. Observational Signatures of Particle Acceleration in Supernova Remnants. Space Sci. Rev. 2012, 173, 369–431. [Google Scholar] [CrossRef]
- Dickel, J.R.; Jones, E.M. Magnetic Fields in Young Supernova Remnants. In Galactic and Intergalactic Magnetic Fields; Beck, R., Wielebinski, R., Kronberg, P.P., Eds.; IAU Symposium: Paris, France, 1990; Volume 140, p. 81. [Google Scholar]
- Dickel, J.R.; Milne, D.K. Magnetic fields in supernova remnants. Aust. J. Phys. 1976, 29, 435–460. [Google Scholar] [CrossRef]
- Zirakashvili, V.N.; Ptuskin, V.S. Diffusive Shock Acceleration with Magnetic Amplification by Nonresonant Streaming Instability in Supernova Remnants. Astrophys. J. 2008, 678, 939–949. [Google Scholar] [CrossRef]
- West, J.L.; Jaffe, T.; Ferrand, G.; Safi-Harb, S.; Gaensler, B.M. When Disorder Looks Like Order: A New Model to Explain Radial Magnetic Fields in Young Supernova Remnants. Astrophys. J. Lett. 2017, 849, L22. [Google Scholar] [CrossRef]
- Milne, D.K.; Dickel, J.R. 5 GHz polarization observations of 33 galactic radio sources. Aust. J. Phys. 1975, 28, 209–230. [Google Scholar] [CrossRef]
- Ginzburg, V.L.; Syrovatskii, S.I. Cosmic Magnetobremsstrahlung (synchrotron Radiation). Annu. Rev. Astron. Astrophys. 1965, 3, 297–350. [Google Scholar] [CrossRef]
- Bykov, A.; Uvarov, Y. Polarized synchrotron X-ray emission from supernova shells: XIPE/IXPE perspective. In Journal of Physics Conference Series; IOP Publishing: Bristol, UK, 2017; Volume 932, p. 012051. [Google Scholar]
- Dickel, J.R.; Strom, R.G.; Milne, D.K. The Radio Structure of the Supernova Remnant G315.4-2.3 (MSH 14-63). Astrophys. J. 2001, 546, 447–454. [Google Scholar] [CrossRef][Green Version]
- Reynoso, E.M.; Hughes, J.P.; Moffett, D.A. On the Radio Polarization Signature of Efficient and Inefficient Particle Acceleration in Supernova Remnant SN 1006. Astron. J. 2013, 145, 104. [Google Scholar] [CrossRef]
- Dickel, J.R.; van Breugel, W.J.M.; Strom, R.G. Radio structure of the remnant of Tycho’s supernova (SN 1572). Astron. J. 1991, 101, 2151–2159. [Google Scholar] [CrossRef]
- DeLaney, T.; Koralesky, B.; Rudnick, L.; Dickel, J.R. Radio Spectral Index Variations and Physical Conditions in Kepler’s Supernova Remnant. Astrophys. J. 2002, 580, 914–927. [Google Scholar] [CrossRef]
- Braun, R.; Gull, S.F.; Perley, R.A. Physical process which shapes Cassiopeia A. Nature 1987, 327, 395–398. [Google Scholar] [CrossRef]
- Anderson, M.C.; Keohane, J.W.; Rudnick, L. The polarization and depolarization of radio emission from supernova remnant Cassiopeia A. Astrophys. J. 1995, 441, 300–306. [Google Scholar] [CrossRef]
- De Horta, A.Y.; Filipovic, M.D.; Crawford, E.J.; Stootman, F.H.; Pannuti, T.G.; Bozzetto, L.M.; Collier, J.D.; Sommer, E.R.; Kosakowski, A.R. Radio-Continuum Emission from the Young Galactic Supernova Remnant G1.9 + 0.3. Serbian Astron. J. 2014, 189, 41–51. [Google Scholar]
- Bamba, A.; Fukazawa, Y.; Hiraga, J.S.; Hughes, J.P.; Katagiri, H.; Kokubun, M. Suzaku Wide-Band Observations of SN1006. Publ. Astron. Soc. Jpn. 2008, 60, 153–161. [Google Scholar] [CrossRef]
- Helder, E.A.; Vink, J. Characterizing the Nonthermal Emission of Cassiopeia A. Astrophys. J. 2008, 686, 1094–1102. [Google Scholar] [CrossRef]
- Uchiyama, Y.; Aharonian, F.A. Fast Variability of Nonthermal X-Ray Emission in Cassiopeia A: Probing Electron Acceleration in Reverse-Shocked Ejecta. Astrophys. J. Lett. 2008, 677, L105–L108. [Google Scholar] [CrossRef]
- Gotthelf, E.V.; Koralesky, B.; Rudnick, L.; Jones, T.W.; Hwang, U.; Petre, R. Chandra detection of the forward and reverse shocks in Cassiopeia A. Astrophys. J. Lett. 2001, 552, L39–L43. [Google Scholar] [CrossRef]
- Hwang, U.; Laming, J.M.; Badenes, C.; Berendse, F.; Blondin, J.; Cioffi, D. A million second Chandra view of Cassiopeia A. The Astrophysical Journal Letters, 615(2), L117. A Million Second Chandra View of Cassiopeia A. Astrophys. J. Lett. 2004, 615, L117–L120. [Google Scholar] [CrossRef]
- Eriksen, K.A.; Hughes, J.P.; Badenes, C.; Fesen, R.; Ghavamian, P.; Moffett, D.; Plucinksy, P.P.; Rakowski, C.E.; Reynoso, E.M.; Slane, P. Evidence for Particle Acceleration to the Knee of the Cosmic Ray Spectrum in Tycho’s Supernova Remnant. Astrophys. J. Lett. 2011, 728, L28. [Google Scholar] [CrossRef]
- Rothenflug, R.; Ballet, J.; Dubner, G.; Giacani, E.; Decourchelle, A.; Ferrando, P. Geometry of the non-thermal emission in SN 1006. Astron. Astrophys. 2004, 425, 121–131. [Google Scholar] [CrossRef]
- Bellazzini, R.; Angelini, F.; Baldini, L.; Bitti, F.; Brez, A.; Cavalca, F.; Del Prete, M.; Kuss, M.; Latronico, L.; Omodei, N.; et al. Gas pixel detectors for X-ray polarimetry applications. Nucl. Instrum. Methods Phys. Res. A 2006, 560, 425–434. [Google Scholar] [CrossRef]
| 1. | |
| 2. | |
| 3. | Currently xpolim is not publicly available, but an executable for MacOS will be made available on request by the J. Vink. Depending on the demand and availability of funding for further development of xpolim, we will work toward a documented and portable version of the source code. |
| 4. |

| Object | Typical | Peak | Orientation B | Remarks | Ref. | |
|---|---|---|---|---|---|---|
| RCW 86 | 8% | 15% | radial | 22 cm | some regions % | [36] |
| SN 1006 | 17% | 60% | mostly radial | 20 cm | peak not in X-ray rims | [37] |
| SN 1572 | 7% | 25% | radial/fine struct. (4) | 6 cm | peak at limbs | [38] |
| SN 1604 | 6% | 12% (?) | radial/fine struct. (20) | 6 cm | [39] | |
| Cas A | 5% | ~20% | radial | 6 cm | outer plateau % | [40,41] |
| G1.9 + 0.3 | 6% | % | radial | 6 cm | Faraday rotation? | [42] |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vink, J.; Zhou, P. Practical Aspects of X-ray Imaging Polarimetry of Supernova Remnants and Other Extended Sources. Galaxies 2018, 6, 46. https://doi.org/10.3390/galaxies6020046
Vink J, Zhou P. Practical Aspects of X-ray Imaging Polarimetry of Supernova Remnants and Other Extended Sources. Galaxies. 2018; 6(2):46. https://doi.org/10.3390/galaxies6020046
Chicago/Turabian StyleVink, Jacco, and Ping Zhou. 2018. "Practical Aspects of X-ray Imaging Polarimetry of Supernova Remnants and Other Extended Sources" Galaxies 6, no. 2: 46. https://doi.org/10.3390/galaxies6020046
APA StyleVink, J., & Zhou, P. (2018). Practical Aspects of X-ray Imaging Polarimetry of Supernova Remnants and Other Extended Sources. Galaxies, 6(2), 46. https://doi.org/10.3390/galaxies6020046





