1. Introduction
Ever since Einstein’s 1915 prediction of the angle by which a ray of light is bent by the eclipsed Sun, and its spectacular (albeit now seen as somewhat controversial) confirmation by observations led by Arthur Eddington during the 1919 solar eclipse [
1], the effects of gravity on light have been viewed as a mechanism by which the predictions of a gravity theory like general relativity can be tested directly.
This remains the case today. Indeed, gravitational lensing is viewed as a possible means to distinguish between competing theories of gravitation and cosmology: in particular, between theories of modified gravity versus the collisionless cold dark matter (CDM) that forms the basis of the CDM “standard model” of cosmology.
The discovery of the colliding clusters 1E0657-558, also known colloquially as the Bullet Cluster, was initially viewed by many as a decisive case in favor of a CDM model [
2], as the lensing associated with cluster components depleted in gas (normally, the dominant baryonic component) seemed inconsistent with theories of modified gravity. More recently, however, the colliding clusters Abell 520 [
3,
4] appeared as a counterexample. The lensing associated with gas-rich core regions of this object that contain no visible galaxies can only be understood if the presence of some dark matter is assumed, which is not consistent with the collisionless nature of CDM in the standard model.
The gravitational lensing maps obtained from the observation of colliding clusters are examples of weak lensing. There are also cases of strong lensing observed in the deep sky. These come in the form of Einstein rings, a visually stunning phenomena where the image of a background object is heavily distorted, forming a partial or full ring around a foreground object as a result of the latter’s gravity. Measuring the angular size of the ring can be compared to the observed distances (obtained from redshifts) to the foreground and background objects, from which one can make deductions about the size of the lensing mass.
Our Modified Gravity (MOG) theory, also known as Scalar-Tensor-Vector Gravity (STVG) [
5,
6], is a classical theory of gravity based on a Lagrangian principle. Phenomenologically, the theory comprises metric gravity with a variable gravitational constant greater than Newton’s, and a repulsive vector field of finite range that partially cancels out the attractive force. The gravitational constant and the mass of the vector field are themselves promoted to scalar fields. This theory is known to yield results that are consistent with precision solar system experiments. It was applied successfully to a sample of over 100 spiral galaxies, correctly modeling their detailed rotation curves without dark matter [
7,
8]. Furthermore, the theory was also used for cosmological investigations, successfully modeling the acoustic power spectrum of the cosmic microwave background and the galaxy-galaxy power spectrum [
6].
The MOG theory was also used to model the weak gravitational lensing of the Bullet Cluster [
9,
10]. The predictions of MOG were found to be consistent with observation, demonstrating that it is, in fact, possible for a modified gravity theory to yield agreement with the Bullet Cluster.
In this paper, we first present a condensed review of the MOG theory, focusing on the development of the weak field, low velocity equations motion on the one hand, and the equations governing ultrarelativistic particles on the other. This material is presented in
Section 2. In
Section 3, we apply the theory to a small set of strong lensing objects for which detailed observational data are available. In
Section 4, we investigate the Bullet Cluster and Abell 520. This section contains our main result, demonstrating that the behavior of both clusters is consistent with the MOG theory. Finally, in
Section 5 we present our conclusions and outlook.
In this paper, we use the following conventions: the symbol is used to denote covariant differentiation with respect to the metric , while the symbols R, , and g represent the Ricci scalar, the cosmological constant, and the determinant of the metric tensor, respectively. We define the Ricci tensor as . Unless otherwise noted, we set the speed of light, ; we use the metric signature .
3. Einstein Rings
When light from a distant source is deflected by a massive object, an observer aligned with the distant source and the massive object may see a ring-like image of the distant source. Such images are often referred to as Einstein rings.
If the distances to the remote source and to the massive object are known, the apparent size of the Einstein ring provides a direct means to estimate the effective gravitational mass of the massive object. In the case of the dark matter model, this effective gravitational mass is the sum of the masses of baryonic matter and exotic dark matter. In the case of a modified gravity such as MOG, in the absence of exotic dark matter, the effective gravitational (lensing) mass is the mass of baryonic matter, enhanced by modified gravity effects.
Specifically, the apparent radius
of an Einstein ring is given by, in radians [
16]:
where
,
, and
are the angular diameter distances (related to the comoving distance
by
in the case of a flat,
cosmology) to the lensing object, the source, and between the lensing object and the source, respectively. For the dark matter theory, the lensing mass is the sum of baryonic and dark matter masses:
. For MOG, the lensing mass is given by Equation (
32), with
. Given
,
,
, and
, Equations (
33) and (
34) allow us to solve for
.
Together, Equations (
28) and (
33) provide a testable relationship between the velocity dispersion
and the lensing mass
. The lensing mass can be estimated using Equation (
34) from Einstein ring observations, whereas the velocity dispersion of the lensing object can be observed directly.
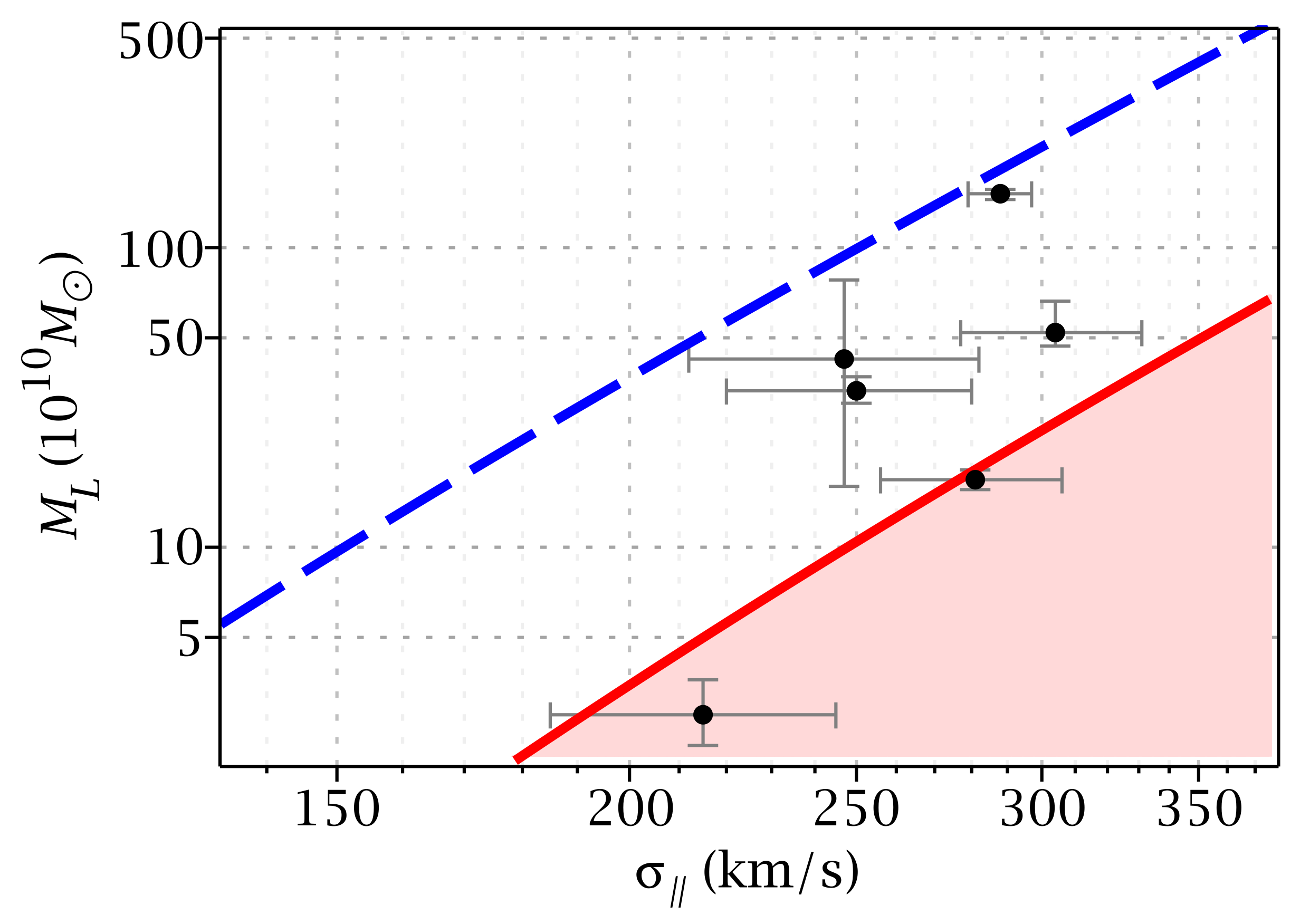
3.1. Some Strong Lensing Candidates
For a small set of lensing galaxies, observational data for both
and
are available. Ref. [
17] studied 21 strong lensing candidates, for which they estimated
from the size of the lensed images. The velocity dispersion of six of these galaxies has been measured [
18,
19,
20,
21,
22,
23]. The lensing masses and velocity dispersions for these six objects are included in
Table 1, and plotted in
Figure 1.
It appears that these six lensing objects do not follow any clearly discernible trend. This is perhaps to be expected, given the difficulty of measuring the velocity dispersions of such very distant objects. On the other hand, none of the six lenses have velocity dispersions that would place them more than
in the “forbidden region” (shaded area in
Figure 1), where the velocity dispersion would be excessive compared to the lensing mass.
3.2. Predicting Mass-to-Light Ratios
The luminosity of a distant galaxy can be obtained by optical observation. On the other hand, the mass of a distant galaxy usually cannot be measured: it must be inferred from the galaxy’s observable properties using an applicable model of galaxy evolution. The predicted amount of baryonic matter in a galaxy, therefore, depends strongly on the choice of model and may vary significantly between models.
On the other hand, when a galaxy is a strong lensing object, its effective mass can be calculated as per our preceding discussion, by observing the size of the Einstein ring and using the redshifts of the lensing and lens objects as proxies for distance.
Under the MOG theory, the effective lensing mass is due entirely to the baryonic content of the galaxy and the variable gravitational constant that is associated with it; as such, the baryonic mass
can be estimated using Equation (
33). Given the known luminosities
L of the lensing objects, the ratio of
can be then calculated. We present the predicted baryonic mass-to-light ratios for all 21 lensing objects listed in
Table 1. The average for the 21 listed galaxies if
. In comparison, the baryonic mass-to-light ratio in the disk of the Milky Way is
[
24]. Our results from MOG imply that at higher redshifts galaxies may have lower mass-to-light ratios. This is in agreement with the evolution of the mass-to-light ratio in galaxies. At higher redshifts the mass function is dominated by massive stars and the result is a lower
; this is confirmed by observation [
25].
4. Abell 520 and the Bullet Cluster
Large clusters of galaxies and, in particular, collisions of such clusters have been observed in recent years and formed the subject of much discussion concerning the validity of the standard CDM model of cosmology.
In the CDM scenario, when two large clusters collide, much of the gas present in the galaxies slows down and heats up. This was indeed observed using X-ray telescopy, which detected X-ray radiation from large quantities of hot (∼ K) gas at the locus of the collision. Stars and CDM halos of galaxies, on the other hand, pass through each other in a collisionless manner and continue along the original trajectories of the colliding clusters, their path modified only by gravitational interactions.
When background objects are viewed through colliding clusters, significant weak lensing should be observable. The lensing is proportional to the gas mass at the locus of the collision. Lensing proportional to the combined stellar and CDM mass (a sum that is dominated by the CDM mass) will be seen at the locus of the visible galaxies.
In particular, the case of the Bullet Cluster 1E0657-558 has been viewed by many as a strong indication in favor of the CDM scenario, since the visual brightness of the post-collision galaxies, combined with any sensible mass-to-light ratios, do not even come close to yielding the mass that would be necessary to produce the observed lensing. In contrast, the colliding clusters Abell 520 indicate weak lensing that, under the standard CDM scenario, can only be explained if significant quantities of CDM were present in the object’s core. This is at odds with the standard assumption that the CDM medium is truly collisionless, interacting only gravitationally. Cold dark matter, like stars, would have continued without collisions and would be located where galaxies are currently visible. In actuality, no visible galaxies are observed near the core of Abell 520 [
3].
4.1. Applying MOG to Colliding Clusters
As we have seen in the previous sections, much of the phenomenology of the MOG theory is captured by the concept of an effective lensing mass, as given by Equation (
32). The lensing mass
determines both the bending of light and low-velocity, weak field dynamics far from a source (nearer the source, the repulsive vector force of the theory must also be taken into account). The value of
, given by Equation (
18), ranges from near zero for small objects (e.g., a single star) all the way up to ∼19 for very large, compact gravitational sources.
This phenomenology has been developed for single, isolated, point-like sources of gravity, and cannot be applied trivially to extended distributions of matter, as the MOG theory is inherently nonlinear. Nonetheless, we expect this phenomenology to remain valid, at least approximately and as an upper limit for , for extended objects such as large clusters of galaxies.
Assuming the validity of the MOG theory, the value of
can be estimated from observation. Consider an object with known dynamical (lensing) mass
and luminosity
L. Assuming a stellar mass-to-light ratio
(which may be determined using standard galaxy evolution models) yields an estimated stellar mass
. The amount of gas present is characterized by the gas fraction,
, which relates the lensing mass to the mass of gas
deduced from direct observation, and is defined as
Together, the gas and stellar mass yield the baryonic (non-exotic) mass:
In the MOG theory, the effective mass is
times the baryonic mass (stars and gas) with no exotic dark matter present. This allows us to determine
as
This determination of
can be contrasted with the values of
that we can calculate directly from either the lensing mass
or the baryonic mass
using Equations (
32) and (
33).
The Bullet Cluster 1E0657-558 has been studied in detail from the MOG perspective: it has been shown [
9] that the weak lensing map associated with this cluster is consistent with the MOG prediction in the absence of exotic dark matter. In the following, we review the case of the Bullet Cluster and also apply our reasoning to the case of Abell 520.
4.2. The Bullet Cluster 1E0657-558
The Bullet Cluster has been studied extensively by [
26] and others. In particular, they determined the dynamical mass of the two visible cluster components (“main cluster” and “subcluster”) from weak lensing and compared these to the visual magnitudes of these components.
In the
B-band, the mass-to-light ratio for the main cluster was found to be in the range 275–314 for the main cluster and 271–297 for the subcluster, depending on the choice of observational methodology [
2]. In combination with the lensing masses and gas fractions estimated by [
26], these values allow us to estimate the MOG
parameter, as shown in
Table 2. For the purposes of this estimate, we used a stellar mass-to-light ratio of
; however, the final value is not particularly sensitive to
due to the relative smallness of the stellar component in the overall mass.
We can compare these estimates of
with the values of
obtained from the lensing masses. For the main cluster, subcluster, and main gas peak, we obtain the values of
that are given in
Table 2.
These idealized values for characterize point sources. As expected, the values of obtained by comparing observational estimates of the lensing mass versus baryonic mass are smaller. We attribute this to the fact that the components of the Bullet Cluster are themselves extended objects spread over several hundred kpc. By comparing the ideal values of to the values obtained from observation, we find that they come closest for the subcluster. This is consistent with the visual observation that the subcluster is smaller, more compact than its main counterpart. Similarly, the fact that the value of obtained from observation is smallest for the gas peak is indicative of the fact that the gas peak corresponds to a relatively diffuse cloud of gas, not compact galaxies of stars.
4.3. Applying MOG to Abell 520
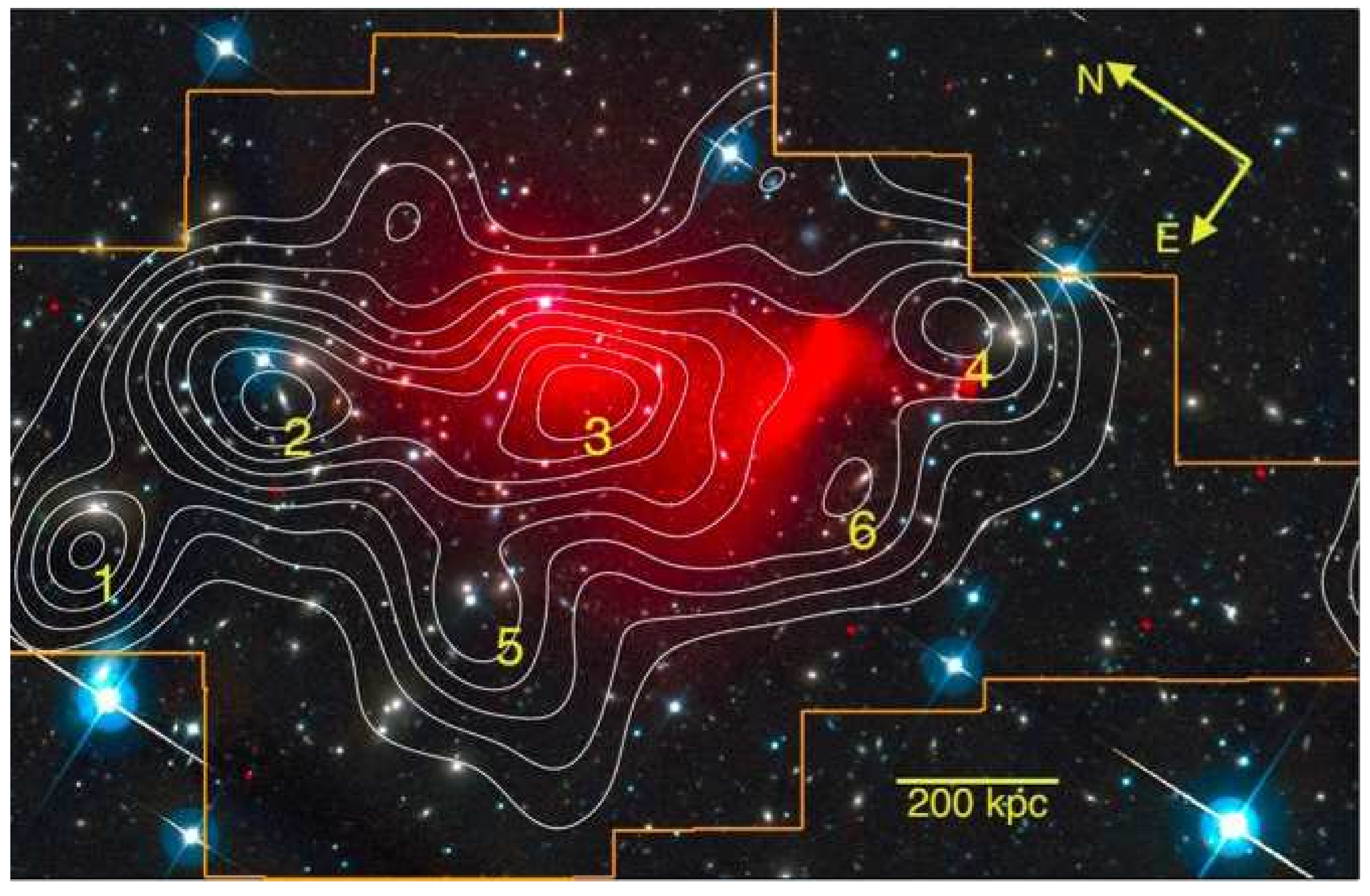
We now turn our attention to the colliding clusters Abell 520. Weak lensing by the Abell 520 cluster was recently explored using data from the Wide Field Planetary Camera of the Hubble Space Telescope [
3]. The authors conclude that this cluster has a dark core that coincides with the peak X-ray luminosity (see
Figure 2) and that there are no visible galaxies in this central core.
This cluster has a main structure labeled P3 and substructures labeled P1, P2, P4, P5 and P6. Visible matter in the central main substructure is mainly gas while the other substructures have a mixture of gas and galaxies.
Using the parameters of the lensing cluster as the projected mass, luminosity of galaxies in B-band, mass to light ratio and the fraction of gas in each subcluster, we can find the MOG
parameter for each of the substructures (see
Table 3).
As in the case of the Bullet Cluster, we find that the values of estimated this way are below the values estimated from the lensing mass alone, treating the substructures as point sources. This is just as expected: for extended objects like these substructures, the point source estimate should serve as an upper limit.
Furthermore, just as we would expect, the values of computed from observation are lower for substructures that have a higher gas content. This coincides with our interpretation that gas structures are diffuse and extended, whereas galaxies are more compact.
5. Conclusions and Outlook
In this paper, we studied the predictions of the MOG modified theory of gravity as applied to weak and strong gravitational lensing.
For strong lensing objects, MOG can be used to predict a relationship between velocity dispersions and lensing masses. This is indeed the same derivation that allows us to use MOG to derive the Tully-Fisher relationship. We found that given the small number of lensing objects for which reliable velocity dispersion data are available in the literature, all are consistent with the predictions and constraints of the MOG theory.
We also applied MOG to the case of the merging clusters 1E0657-558 (the Bullet Cluster) and Abell 520. For the former, a detailed study was conducted in the past [
9], showing excellent agreement between weak lensing observations and the MOG prediction. Here, we demonstrated why this is so: that the effective lensing masses of specific regions of the Bullet Cluster are consistent with their luminosities and mass-to-light ratios under the MOG theory, in the absence of dark matter. We then applied the same reasoning to the merging clusters Abell 520. Under the standard cold dark matter scenario, weak lensing of this cluster can only be explained by assuming the presence of a dark matter core, which is inconsistent with the collisionless nature of the cold dark matter component and the lack of visible galaxies in this core region. For MOG, no such difficulty exists: as in the case of the Bullet Cluster, the lensing masses and luminosities are consistent with the predictions of the theory.
In these studies, we applied the MOG point source solution to the objects that were examined. This necessarily introduced a degree of uncertainty in the predictions: due to the inherently nonlinear nature of the MOG theory, the point source solution can only be considered as a limiting case when spatially extended, diffuse objects are examined. An alternative is to use a density profile and the generalized MOG Poisson equation, as it was done in [
9,
10]. Apart from a difference in the predicted value of
(the point-source solution in the current paper yielded a larger value, as expected) both approaches yield consistent results.
 M.
M.