On the Spectrum and Polarization of Magnetar Flare Emission
Abstract
1. Introduction
2. The Model
2.1. Radiative Processes in Strong Magnetic Fields
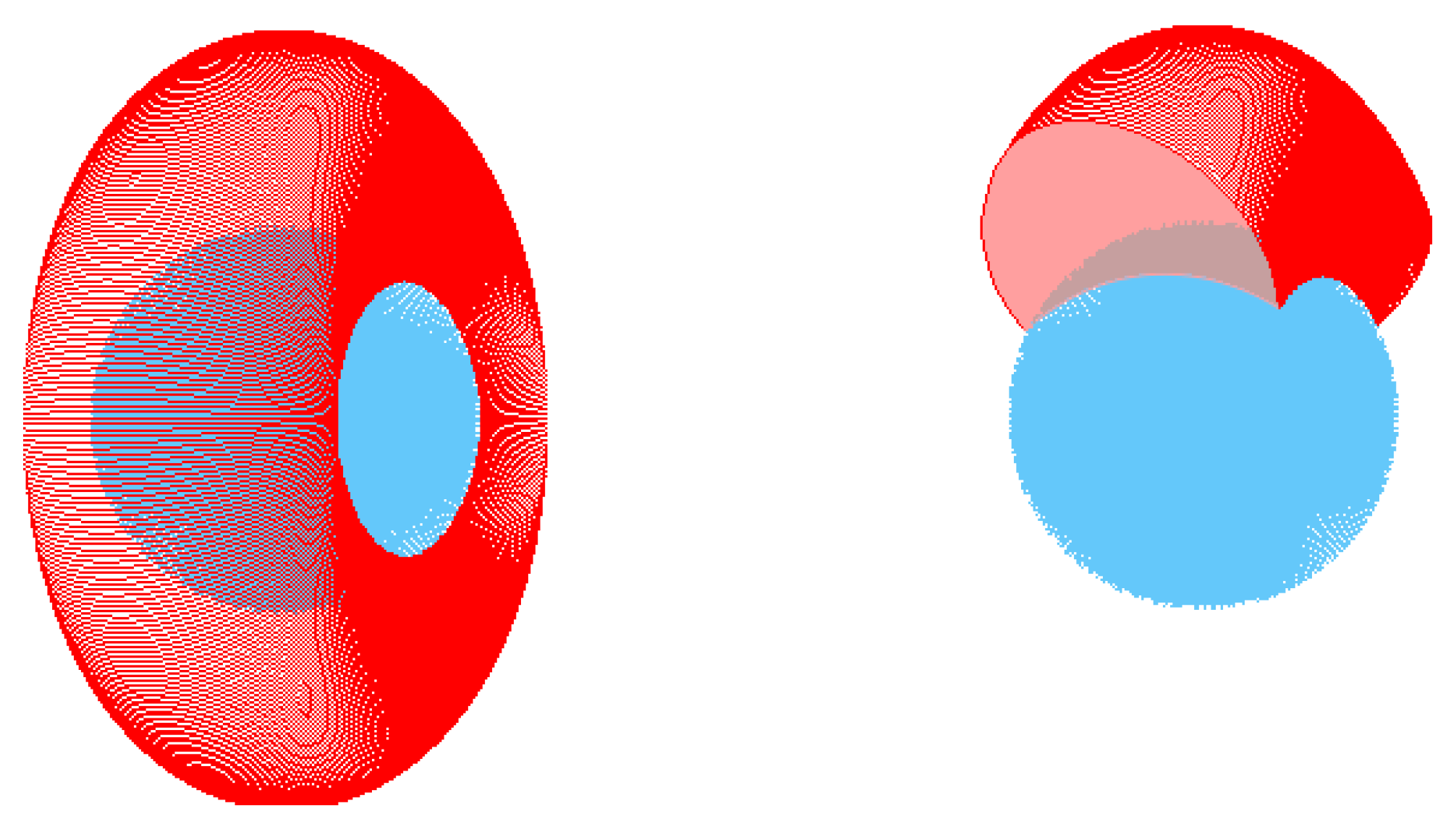
2.2. Radiative Transfer in the Fireball Atmosphere
2.3. Numerical Implementation
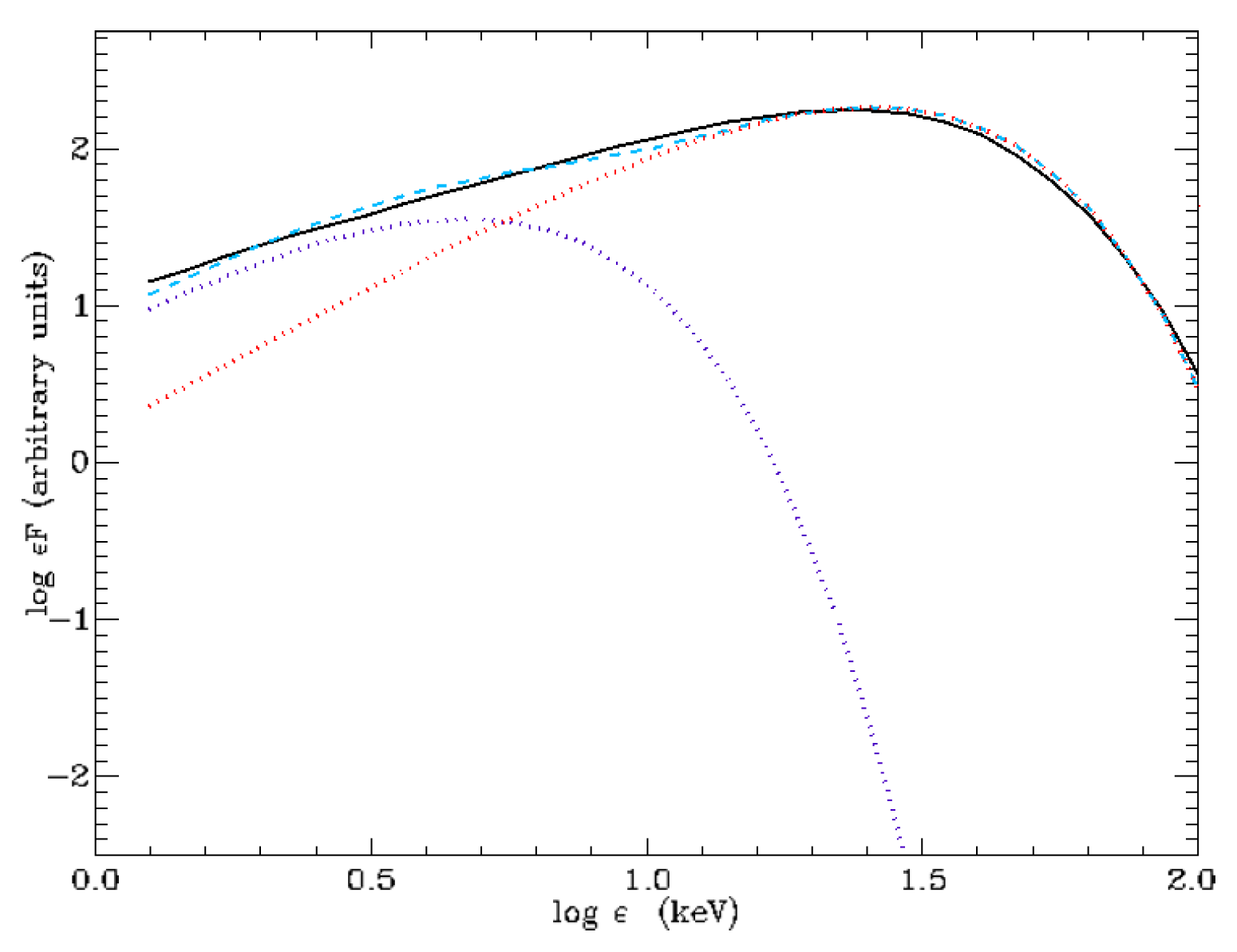
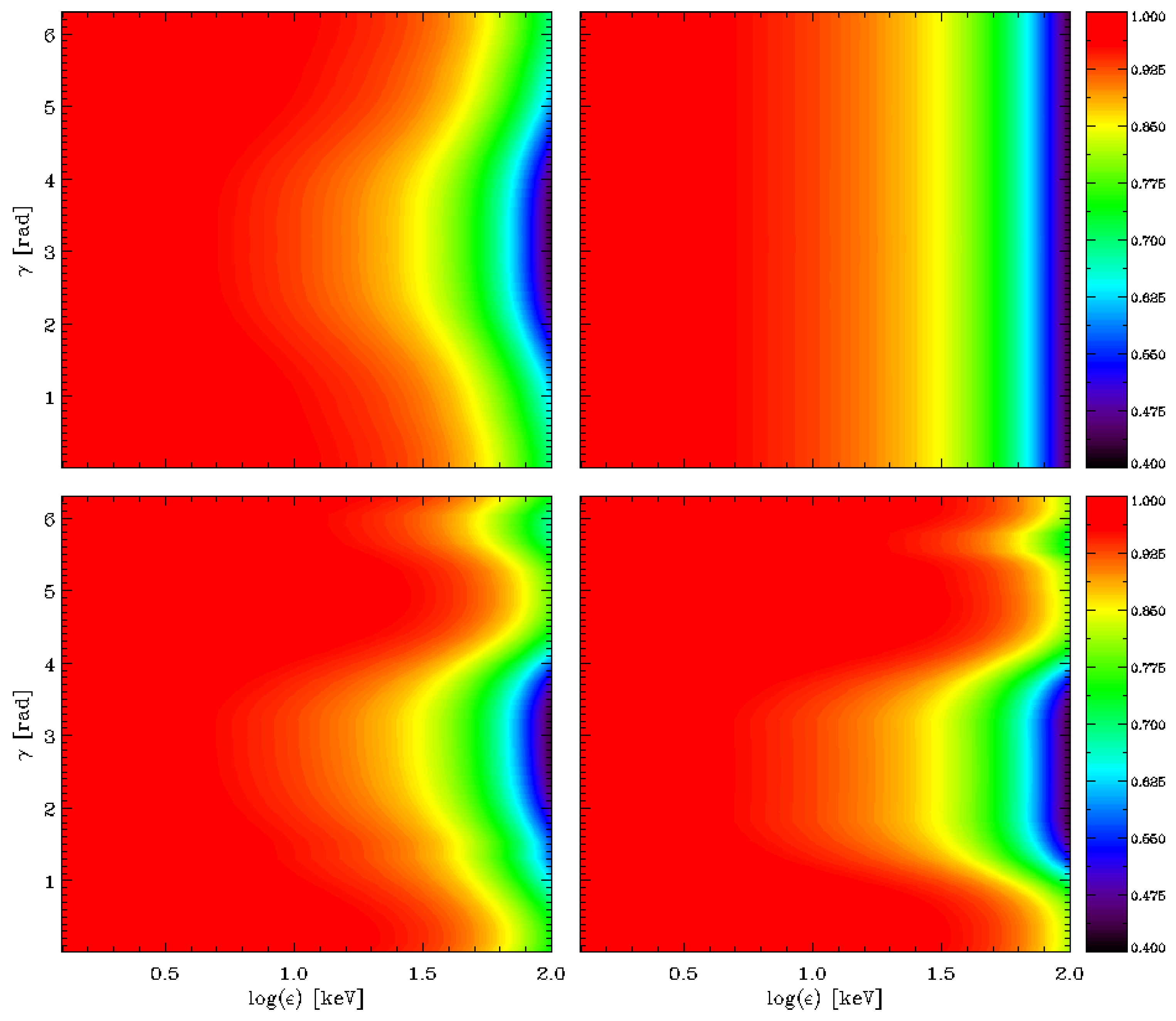
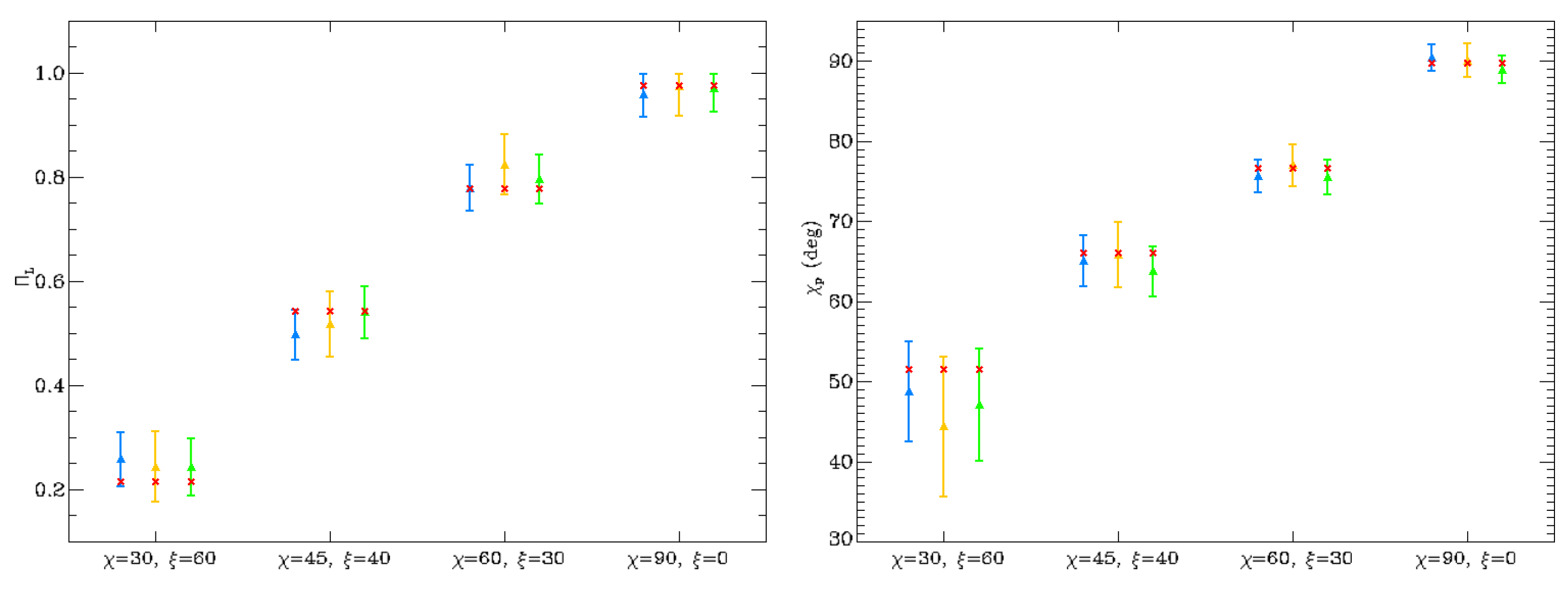
3. Results
4. Conclusions
Author Contributions
Conflicts of Interest
Abbreviations
| IXPE | Imaging X-ray Polarimetry Explorer |
| XIPE | X-ray Imaging Polarimetry Explorer |
| eXTP | Enhanced X-ray Timing and Polarimetry mission |
| NS | Neutron Star |
| SGR | Soft Gamma Repeater |
| AXP | Anomalous X-ray Pulsar |
| O-mode | Ordinary mode |
| X-mode | Extraordinary mode |
| LTE | Local Thermal Equilibrium |
| LOS | Line-Of-Sight |
References
- Mereghetti, S. The strongest cosmic magnets: Soft gamma-ray repeaters and anomalous X-ray pulsars. Astron. Astrophys. Rev. 2008, 15, 225–287. [Google Scholar] [CrossRef]
- Turolla, R.; Zane, S.; Watts, A.L. Magnetars: The physics behind observations. A review. Rep. Prog. Phys. 2015, 78, 116901. [Google Scholar] [CrossRef] [PubMed]
- Duncan, R.C.; Thompson, C. Formation of very strongly magnetized neutron stars-Implications for gamma-ray bursts. Astrophys. J. 1992, 392, L9–L13. [Google Scholar] [CrossRef]
- Thompson, C.; Lyutikov, M.; Kulkarni, S.R. Electrodynamics of magnetars: Implications for the persistent X-ray emission and spin-down of the soft gamma repeaters and anomalous X-ray pulsars. Astrophys. J. 2002, 574, 332. [Google Scholar] [CrossRef]
- Nobili, L.; Turolla, R.; Zane, S. X-ray spectra from magnetar candidates—I. Monte Carlo simulations in the non-relativistic regime. Mon. Not. R. Astron. Soc. 2008, 386, 1527–1542. [Google Scholar] [CrossRef]
- Thompson, C.; Duncan, R.C. Radiative mechanism for outbursts. Mon. Not. R. Astron. Soc. 1995, 275, 255–300. [Google Scholar] [CrossRef]
- Thompson, C.; Duncan, R.C. The giant flare of 1998 August 27 from SGR 1900+14. II. Radiative mechanism and physical constraints on the source. Astrophys. J. 2001, 561, 980. [Google Scholar] [CrossRef]
- Taverna, R.; Turolla, R. On the spectrum and polarization of magnetar flare emission. Mon. Not. R. Astron. Soc. 2017, 469, 3610–3628. [Google Scholar] [CrossRef]
- Israel, G.L.; Romano, P.; Mangano, V.; Dall’Osso, S.; Chincarini, G.; Stella, L.; Campana, S.; Belloni, T.; Tagliaferri, G.; Blustin, A.J.; et al. A swift gaze into the 2006 March 29 burst forest of SGR 1900+14. Astrophys. J. 2008, 685, 1114. [Google Scholar] [CrossRef]
- Olive, J.-F.; Hurley, K.; Sakamoto, T.; Atteia, J.L.; Crew, G.; Ricker, G.; Pizzichini, G.; Barraud, C.; Kawai, N. Time-resolved X-ray spectral modeling of an intermediate burst from SGR 1900+14 observed by HETE-2 FREGATE and WXM. Astrophys. J. 2004, 616, 1148. [Google Scholar] [CrossRef][Green Version]
- Feroci, M.; Caliandro, G.A.; Massaro, E.; Mereghetti, S.; Woods, P.M. Broadband X-ray spectra of short bursts from SGR 1900+14. Astrophys. J. 2004, 612, 408. [Google Scholar] [CrossRef]
- Daugherty, J.K.; Harding, A.K. Compton scattering in strong magnetic fields. Astrophys. J. 1986, 309, 362–371. [Google Scholar] [CrossRef]
- Gonthier, P.L.; Harding, A.K.; Baring, M.G.; Costello, R.M.; Mercer, C.L. Compton scattering in ultrastrong magnetic fields: Numerical and analytical behavior in the relativistic regime. Astrophys. J. 2000, 540, 907. [Google Scholar] [CrossRef]
- Mushtukov, A.A.; Nagirner, D.I.; Poutanen, J. Compton scattering S matrix and cross section in strong magnetic field. Phys. Rev. D 2016, 612, 93–119. [Google Scholar]
- Gnedin, Y.N.; Pavlov, G.G. The transfer equations for normal waves and radiation polarization in an anisotropic medium. J. Exp. Theor. Phys. 1974, 38, 903–908. [Google Scholar]
- Ho, W.C.G.; Lai, D. Atmospheres and spectra of strongly magnetized neutron stars—II. The effect of vacuum polarization. Mon. Not. R. Astron. Soc. 2003, 338, 233–252. [Google Scholar] [CrossRef]
- Lai, D.; Ho, W.C.G.; van Adelsberg, M.; Wang, C.; Heyl, J.S. X-ray Polarimetry: A New Window in Astrophysics; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Herold, H. Compton and Thomson scattering in strong magnetic fields. Phys. Rev. D 1979, 19, 2868. [Google Scholar] [CrossRef]
- Ventura, J. Scattering of light in a strongly magnetized plasma. Phys. Rev. D. 1979, 19, 1684. [Google Scholar] [CrossRef]
- Mészáros, P. High-Energy Radiation from Magnetized Neutron Stars; University Chicago Press: Chicago, IL, USA, 1992. [Google Scholar]
- Harding, A.K.; Lai, D. Physics of strongly magnetized neutron stars. Rep. Prog. Phys. 2006, 69, 2631. [Google Scholar] [CrossRef]
- Haug, E. Bremsstrahlung and pair production in the field of free electrons. Z. Naturforsch. Teil A 1975, 30, 1099–1133. [Google Scholar] [CrossRef]
- Svensson, R. Electron-positron pair equilibria in relativistic plasmas. Astrophys. J. 1982, 258, 335. [Google Scholar] [CrossRef]
- Haug, E. Electron-positron bremsstrahlung in mildly relativistic thermal plasmas. Astron. Astrophys. 1985, 148, 386–390. [Google Scholar]
- Adler, S.L.; Bahcall, J.N.; Callan, C.G.; Rosenbluth, M.N. Photon splitting in a strong magnetic field. Phys. Rev. Lett. 1970, 25, 1061. [Google Scholar] [CrossRef]
- Adler, S.L. Photon splitting and photon dispersion in a strong magnetic field. Ann. Phys. N. Y. 1971, 67, 599–647. [Google Scholar] [CrossRef]
- Stoneham, R.J. Phonon splitting in the magnetised vacuum. J. Phys. A 1979, 12, 2187. [Google Scholar] [CrossRef]
- Bulik, T. Photon splitting in strongly magnetized plasma. Acta Astron. 1998, 48, 695. [Google Scholar]
- Lightman, A. Double Compton emission in radiation dominated thermal plasmas. Astrophys. J. 1981, 244, 392–405. [Google Scholar] [CrossRef]
- Lyubarsky, Y.E. On the X-ray spectra of soft gamma repeaters. Mon. Not. R. Astron. Soc. 2002, 332, 199–204. [Google Scholar] [CrossRef]
- Yang, Y.-P.; Zhang, B. On the polarization properties of magnetar giant flare pulsating tails. Astrophys. J. 2015, 815, 45. [Google Scholar] [CrossRef]
- Taverna, R.; Turolla, R.; González Caniulef, D.; Zane, S.; Muleri, F.; Soffitta, P. Polarization of neutron star surface emission: A systematic analysis. Mon. Not. R. Astron. Soc. 2015, 454, 3254–3266. [Google Scholar] [CrossRef]
- Zane, S.; Turolla, R. Unveiling the thermal and magnetic map of neutron star surfaces though their X-ray emission: Method and light-curve analysis. Mon. Not. R. Astron. Soc. 2006, 366, 727–738. [Google Scholar] [CrossRef]
- Taverna, R.; Muleri, F.; Turolla, R.; Soffitta, P.; Fabiani, S.; Nobili, L. Probing magnetar magnetosphere through X-ray polarization measurements. Mon. Not. R. Astron. Soc. 2014, 438, 1686–1697. [Google Scholar] [CrossRef]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Taverna, R.; Turolla, R. On the Spectrum and Polarization of Magnetar Flare Emission. Galaxies 2018, 6, 35. https://doi.org/10.3390/galaxies6010035
Taverna R, Turolla R. On the Spectrum and Polarization of Magnetar Flare Emission. Galaxies. 2018; 6(1):35. https://doi.org/10.3390/galaxies6010035
Chicago/Turabian StyleTaverna, Roberto, and Roberto Turolla. 2018. "On the Spectrum and Polarization of Magnetar Flare Emission" Galaxies 6, no. 1: 35. https://doi.org/10.3390/galaxies6010035
APA StyleTaverna, R., & Turolla, R. (2018). On the Spectrum and Polarization of Magnetar Flare Emission. Galaxies, 6(1), 35. https://doi.org/10.3390/galaxies6010035




