Studying Microquasars with X-Ray Polarimetry
Abstract
1. Introduction
2. X-Ray Polarization in Microquasars
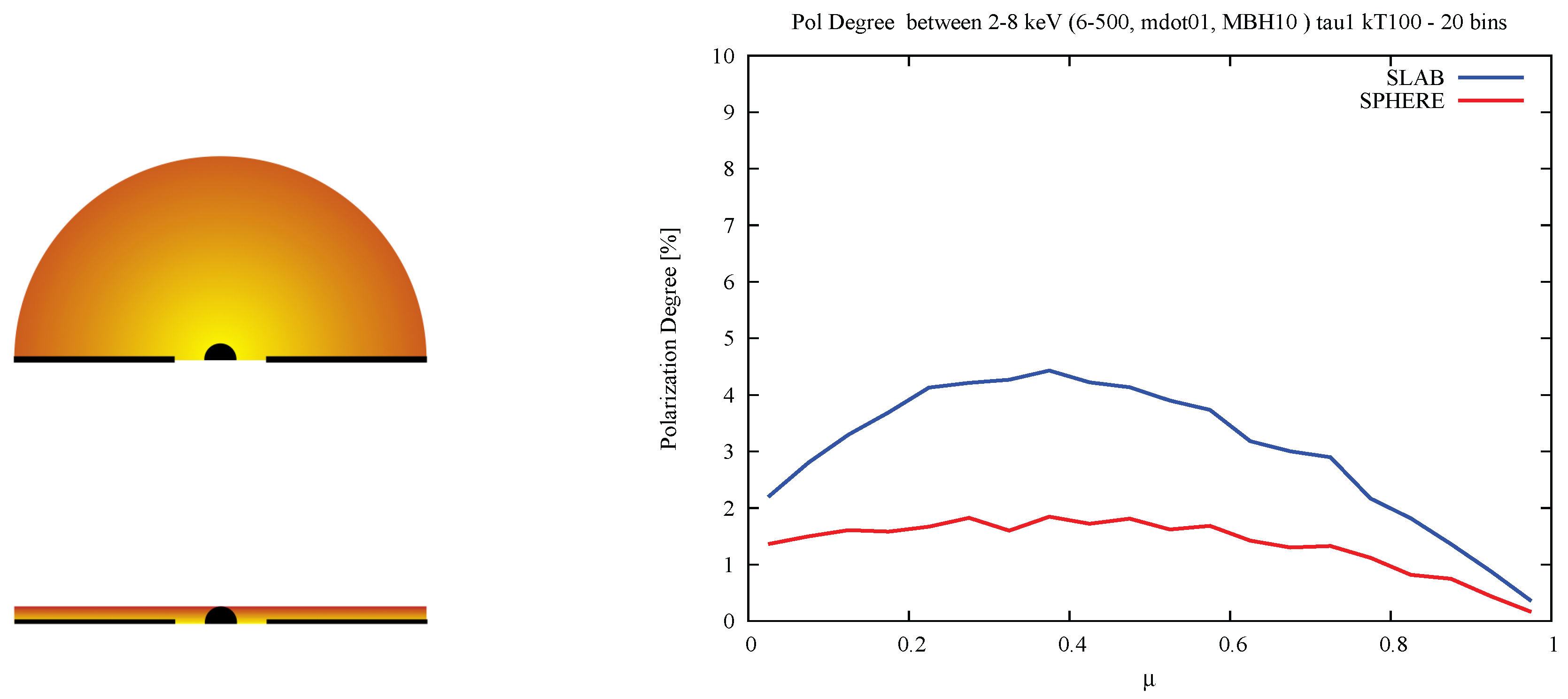
2.1. The Geometry of the Hot Corona
2.2. The Role of the Jet
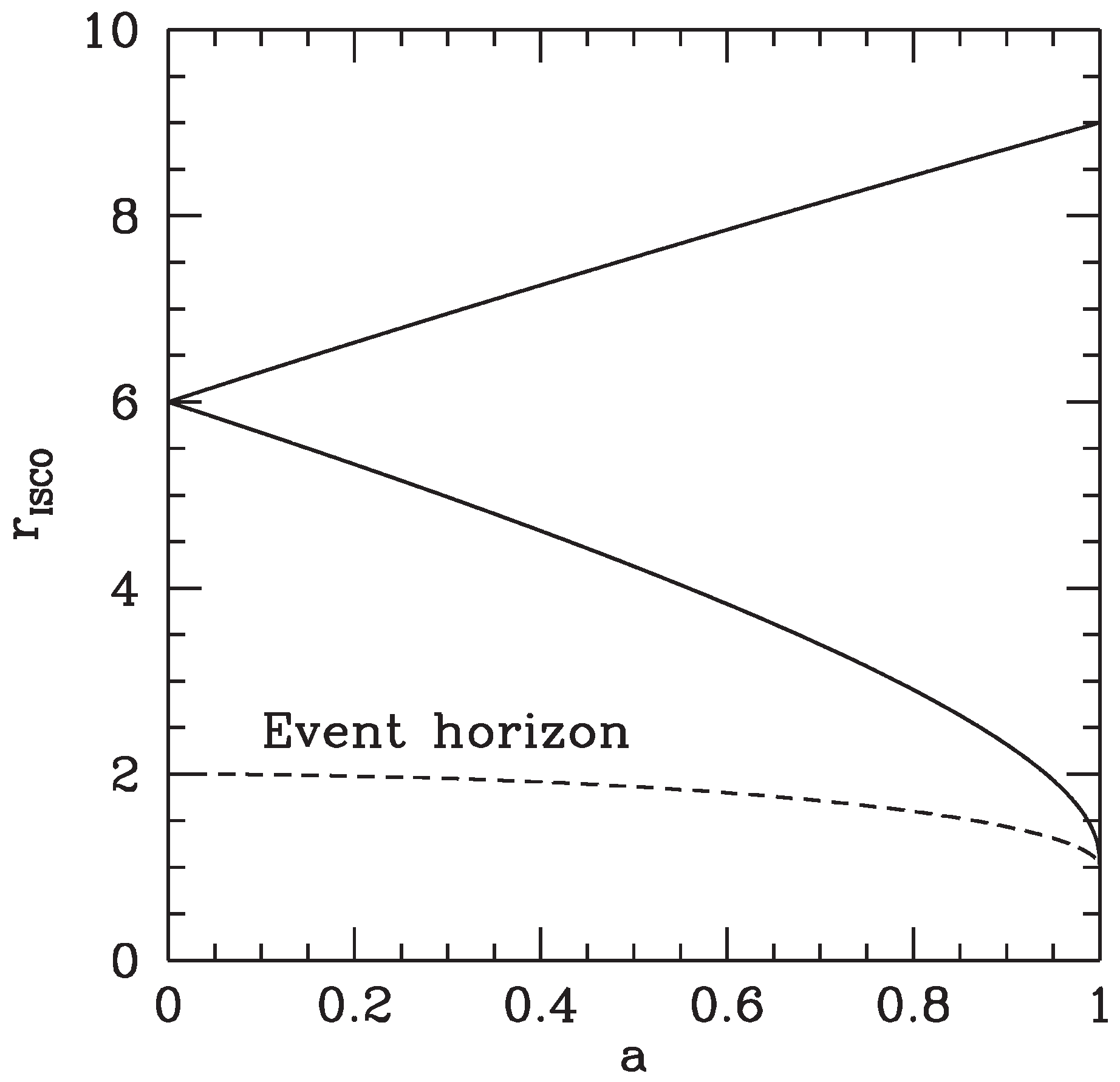
2.3. The Spin of the Black Hole
3. Observational Perspectives
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Done, C.; Gierlinski, M.; Kubota, A. Modelling the behaviour of accretion flows in X-ray binaries. Everything you always wanted to know about accretion but were afraid to ask. Astron. Astrophys. Rev. 2007, 15, 1–66. [Google Scholar] [CrossRef]
- Fender, R.P.; Belloni, T.; Gallo, E. Towards a unified model for black hole X-ray binary jets. Mon. Not. R. Astron. Soc. 2004, 335, 1105–1118. [Google Scholar] [CrossRef]
- Fabian, A.C.; Lohfink, A.; Kara, E.; Parker, M.L.; Vasudevan, R.; Reynolds, C.S. Properties of AGN coronae in the NuSTAR era. Mon. Not. R. Astron. Soc. 2015, 451, 4375–4383. [Google Scholar] [CrossRef]
- Fabian, A.C.; Zoghbi, A.; Ross, R.R.; Uttley, P.; Gallo, L.C.; Brandt, W.N.; Blustin, A.J.; Boller, T.; Caballero-Garcia, M.D.; Larsson, J.; et al. Broad line emission from iron K- and L-shell transitions in the active galaxy 1H0707-495. Nature 2009, 459, 540–542. [Google Scholar] [CrossRef] [PubMed]
- Guerras, E.; Dai, X.; Steele, S.; Liu, A.; Kochanek, C.S.; Chartas, G.; Morgan, C.W.; Chen, B. Extended X-Ray Monitoring of Gravitational Lenses with Chandra and Joint Constraints on X-Ray Emission Regions. Astrophys. J. 2017, 836, 206–223. [Google Scholar] [CrossRef]
- Beheshtipour, B.; Krawczynski, H.; Malzac, J. The X-Ray Polarization of the Accretion Disk Coronae of Active Galactic Nuclei. Astrophys. J. 2017, 850, 14–25. [Google Scholar] [CrossRef]
- Schnittman, J.D.; Krolik, J.H. X-ray Polarization from Accreting Black Holes: Coronal Emission. Astrophys. J. 2010, 712, 908–924. [Google Scholar] [CrossRef]
- Tamborra, F.; Matt, G.; Bianchi, S.; Dovciak, M. MoCA: A Monte Carlo code for Comptonization in Astrophysics. Astron. Astrophys. 2018. submitted. [Google Scholar]
- Zdziarski, A.A. The jet kinetic power, distance and inclination of GRS 1915+105. Mon. Not. R. Astron. Soc. 2014, 444, 1113–1118. [Google Scholar] [CrossRef]
- McNamara, A.L.; Kuncic, Z.; Wu, K. X-ray polarization in relativistic jets. Mon. Not. R. Astron. Soc. 2009, 395, 1507–1514. [Google Scholar] [CrossRef]
- Miller, J.M. Relativistic X-Ray Lines from the Inner Accretion Disks Around Black Holes. Annu. Rev. Astron. Astrophys. 2007, 45, 441–479. [Google Scholar] [CrossRef]
- McClintock, J.E.; Narayan, R.; Davis, S.W.; Gou, L.; Kulkarni, A.; Orosz, J.A.; Penna, R.F.; Remillard, R.A.; Steine, J.F. Measuring the spins of accreting black holes. Class. Quantum Gravity 2011, 28, 114009. [Google Scholar] [CrossRef]
- Stella, L.; Vietri, M. Lense-Thirring Precession and Quasi-periodic Oscillations in Low-Mass X-Ray Binaries. Astrophys. J. 1998, 492, L59–L62. [Google Scholar] [CrossRef]
- Ingram, A.; Maccarone, T.J.; Poutanen, J.; Krawczynski, H. Polarization Modulation from Lense-Thirring Precession in X-Ray Binaries. Astrophys. J. 2015, 807, 53–69. [Google Scholar] [CrossRef]
- Reis, R.C.; Fabian, A.C.; Ross, R.R.; Miller, J.M. Determining the spin of two stellar-mass black holes from disc reflection signatures. Mon. Not. R. Astron. Soc. 2009, 395, 1257–1264. [Google Scholar] [CrossRef][Green Version]
- Shafee, R.; McClintock, J.E.; Narayan, R.; Davis, S.W.; Li, L.; Remillard, R.A. Estimating the Spin of Stellar-Mass Black Holes by Spectral Fitting of the X-Ray Continuum. Astrophys. J. 2010, 712, L113–L116. [Google Scholar] [CrossRef]
- Motta, S.E.; Belloni, T.M.; Stella, L.; Muñoz-Darias, T.; Fender, R. Precise mass and spin measurements for a stellar-mass black hole through X-ray timing: The case of GRO J1655-40. Mon. Not. R. Astron. Soc. 2014, 437, 2554–2565. [Google Scholar] [CrossRef]
- Miller, J.M.; Tomsick, J.A.; Bachetti, M.; Wilkins, D.; Boggs, S.E.; Chistensen, F.E.; Craig, W.W.; Fabian, A.C.; Grefenstette, B.W.; Hailey, C.J.; et al. New Constraints on the Black Hole Low/Hard State Inner Accretion Flow with NuSTAR. Astrophys. J. 2015, 799, L6–L11. [Google Scholar] [CrossRef]
- Connors, P.A.; Stark, R.F.; Piran, T. Polarization features of X-ray radiation emitted near black holes. Astrophys. J. 1980, 235, 224–244. [Google Scholar] [CrossRef]
- Dovciak, M.; Muleri, F.; Goosmann, R.W.; Karas, V.; Matt, G. Thermal disc emission from a rotating black hole: X-ray polarization signatures. Mon. Not. R. Astron. Soc. 2008, 391, 32–38. [Google Scholar] [CrossRef]
- Li, L.-X.; Narayan, R.; McClintock, J.E. Inferring the Inclination of a Black Hole Accretion Disk from Observations of its Polarized Continuum Radiation. Astrophys. J. 2009, 691, 847–865. [Google Scholar] [CrossRef]
- Schnittman, J.D.; Krolik, J.H. X-ray Polarization from Accreting Black Holes: The Thermal State. Astrophys. J. 2009, 701, 1175–1187. [Google Scholar] [CrossRef]
- Chandrasekhar, S. Radiative Transfer; Dover: New York, NY, USA, 1960. [Google Scholar]
- Weisskopf, M.C.; Ramsey, B.; O’Dell, S.; Tennant, A.; Elsner, R.; Soffitta, P.; Bellazzini, R.; Costa, E.; Kolodziejczak, J.; Kaspi, V.; Muleri, F.; et al. The Imaging X-ray Polarimetry Explorer (IXPE). Available online: https://wwwastro.msfc.nasa.gov/for_scientists/papers/2016SPIE9905-17_Weisskopf.pdf (accessed on 1 March 2018).
- Zhang, S.N.; Feroci, M.; Santangelo, A.; Dong, Y.W.; Feng, H.; Lu, F.J.; Nandra, K.; Wang, Z.S.; Zhang, S.; Bozzo, E.; et al. eXTP: Enhanced X-ray Timing and Polarization mission. Available online: http://discovery.ucl.ac.uk/1508070/%20-%20enhanced%20X-ray%20Timing%20and%20Polarimetry%20Mission%20VoR.pdf (accessed on 1 March 2018).
| 1 | It is worth mentioning that a modulation of the polarization signal is expected at the precession frequency itself, i.e., for LF QPOs: [14]. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Matt, G.; Tamborra, F. Studying Microquasars with X-Ray Polarimetry. Galaxies 2018, 6, 32. https://doi.org/10.3390/galaxies6010032
Matt G, Tamborra F. Studying Microquasars with X-Ray Polarimetry. Galaxies. 2018; 6(1):32. https://doi.org/10.3390/galaxies6010032
Chicago/Turabian StyleMatt, Giorgio, and Francesco Tamborra. 2018. "Studying Microquasars with X-Ray Polarimetry" Galaxies 6, no. 1: 32. https://doi.org/10.3390/galaxies6010032
APA StyleMatt, G., & Tamborra, F. (2018). Studying Microquasars with X-Ray Polarimetry. Galaxies, 6(1), 32. https://doi.org/10.3390/galaxies6010032




