Abstract
This work summarizes a program intended to unify three burgeoning branches of the high-energy astrophysics of relativistic jets: general relativistic magnetohydrodynamic (GRMHD) simulations of ever-increasing dynamical range, the microphysical theory of particle acceleration under relativistic conditions, and multiwavelength observations resolving ever-decreasing spatiotemporal scales. The process, which involves converting simulation output into time series of images and polarization maps that can be directly compared to observations, is performed by (1) self-consistently prescribing models for emission, absorption, and particle acceleration and (2) performing time-dependent polarized radiative transfer. M87 serves as an exemplary prototype for this investigation due to its prominent and well-studied jet and the imminent prospect of learning much more from Event Horizon Telescope (EHT) observations this year. Synthetic observations can be directly compared with real observations for observational signatures such as jet instabilities, collimation, relativistic beaming, and polarization. The simplest models described adopt the standard equipartition hypothesis; other models calculate emission by relating it to current density or shear. These models are intended for application to the radio jet instead of the higher frequency emission, the disk and the wind, which will be subjects of future investigations.
1. Introduction
Relativistic jets are powerful, collimated outflows launched from compact objects typically surrounded by accretion disks in black hole X-ray binaries, gamma ray bursts, or active galactic nuclei (AGN) throughout the observable universe. Of particular interest in observational astronomy are relativistic jets from AGN, which are associated with the greatest total energy output among known astrophysical sources. Ever since Heber Curtis observed “a thin line of matter” flowing from the center of M87 in 1918 [1], AGN jet observations have proliferated, as seen in the Gamma-ray Space Telescope catalog and Caltech’s corresponding Owens Valley Radio Observatory (OVRO) 40-mm telescope radio survey of approximately 1200 blazar sources.
Interest in jets has been spurred by recent discoveries relating to their central engines—black holes—including the monumental observational confirmation of Einstein’s prediction of gravitational waves from neutron star and stellar black hole mergers. Pending discoveries relating to the nature of jet emission close to the central engine are rapidly garnering a similar level of interest [2]. Some planned observations spurring theoretical progress are summarized as follows.
The black hole in our Galactic Center, Sgr A*, subtends an angular width at Earth of 5.3 as [3]. A network of intercontinental radio baselines anchored by the Atacama Large mm- and submm-Array (ALMA) is imaging Sgr A* at 230 GHz. The EHT is also expected to provide our first direct observations of the black hole shadow of an extragalactic source such as the misaligned BL Lac blazar M87 [4].
M87 is a giant elliptical galaxy in the Virgo Cluster 54 million lightyears (17 Mpc) away also possessing a large (3.9 as) [3] central black hole. M87 observations by the National Radio Astronomy Organization Very Long Baseline Array (NRAO VLBA) at 15 GHz [5] reveal a substructure indicative of an ordered, helical magnetic field as shown in Figure 1. VLBA observations at 43 GHz have shown limb brightening on smaller scales [6], as seen in Figure 2. If these features persist at EHT scales near M87’s black hole, they will provide sharp criteria for discriminating among phenomenological models input into simulations in this work. Observing the inner regions of M87 near the base of its relativistic jet has the potential for shedding light on long-standing jet mysteries, such as the locus of its most concentrated emission or the composition—leptonic () or hadronic ()—of the jet plasma.

Figure 1.
Very Long Baseline Array (VLBA) 15 GHz (2 cm) image of M87. The swirling jet substructure (twisting about the jet axis) may be indicative of magnetic Kelvin–Helmholtz instabilities. Image adapted with permission from Dan Homan, Yuri Kovalev, Matt Lister, and Ken Kellermann.
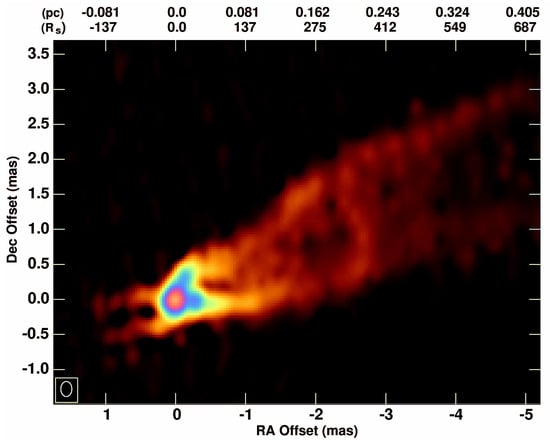
Figure 2.
M87 43 GHz radio image of the inner region, including dominant and counterpropagating jets. Note 1 pc mas. Image courtesy of Craig Walker.
The powerful quasar 3C 279 exemplifies the mystery of rapid variability in jet/accretion disk/black hole (JAB) systems. Quasar 3C 279 has a black hole with a light crossing time of an hour, yet exhibits light curves with doubling times on the scale of minutes [7]. Variability for a wide range of phenomenological models can be assessed by summing over intensity from images at different observer times with routines described in this work. Further targets of observation and modeling include the highly polarized FR I jet of 3C 31 (see Table 1).

Table 1.
Distances to, and central black hole masses of, jet/accretion disk/black hole (JAB) systems.
Substantial progress has also been made on the computational front, as three-dimensional general relativistic magnetohydrodynamic (GRMHD) simulations are now nearly detailed enough to resolve the magnetorotational instability and evolve long enough to exhibit variability on many timescales and the stability of relativistic jets. The high-accuracy relativistic magnetohydrodynamics (HARM) code [13] has set the standard for evolving accretion flow dynamical variables and photon trajectories in the high-spacetime-curvature vicinity of black holes, where general relativity predicts significant distortions to the geodesic path of light. Subsequent simulations are well adapted to the study of powerful, stable relativistic jets, e.g., [14,15] (hereafter MB09 and MTB12). Other GRMHD simulations concentrate gridlines at small angles near the equatorial plane in order to analyze disk emission near the innermost orbits around the central black hole, e.g., [16,17]. Richard Anantua’s 2016 Stanford doctoral dissertation [18] used a general relativistic magnetohydrodynamic (GRMHD) simulation described in MB09 and MTB12 based on the HARM code to match observational features of JAB systems at radio, optical, and gamma ray wavelengths and used the same simulation to determine statistical properties of multiwavelength emission from individual sources and surveys. This paper presents a subset of this work applied to M87 to reverse engineer observational signatures, images, and polarization maps. In our case of single-fluid GRMHD without electron thermodynamics, we neglect the effects of electron conduction on gas dynamics and assume the adiabatic index is a function of total gas (and not electron gas) properties. In what follows, the gravitational radius will be used as a mass, length, and time scale by setting .
2. Materials and Methods
2.1. Simulation
The simulation used here evolves a relativistic jet sourced by a geometrically thick disk accreting onto a rapidly rotating () black hole for a duration of 3300 M. The data are interpolated to 256 × 256 × 256 Cartesian lattice datablocks representing physical domains ranging from 80 M × 80 M × 200 M, to 80 M × 80 M × 1400 M, to 320 M × 320 M × 1400 M. The source code for the particular simulation “observed” can be made available on GitHub with permission of Jonathan McKinney of the University of Maryland, though the routines described are generally applicable to GRMHD jet simulations.
2.2. Observing Simulations
In [18], a robust pipeline was developed to create constant observer time line-of-sight intensity and polarization maps of simulation output from arbitrary observer orientations. The MB09/MTB12 simulation used output solutions for state variables: four velocity , four field , gas energy density , and rest mass density of the GRMHD equations for an astrophysical plasma:
where is the stress tensor,
An equation of state is added:
(where for relativistic electrons) and prescriptions for emission due to a power law distribution of electrons with model-dependent relativistic electron energy density yields self-consistent models.
2.3. Physical Models
2.3.1. Synchrotron Models
For power law synchrotron radiation, the emission scales with electron gas energy density , magnetic field, and frequency as , where the photon spectral index is , and we take . Inspired by equipartition, a simple assumption for the electron gas energy density is that it is a constant fraction of the magnetic field energy density . This relation between electric and magnetic energy densities can be parameterized in a beta model where the constant . A generalization of this, the “bias” model, scales with powers of as .
Synchrotron radiation theory emission and absorption formulae in [18] (cf. Equation (2.24)) conveniently express polarized emissivities and absorption coefficients in terms of the partial pressure due to electrons emitting in the octave around the observed frequency. The partial pressure is then expressed as , where W is a dissipation rate per unit volume and t is the characteristic (radiative or expansion) cooling time. The key advantage of casting the formulae this way is that dissipation from particularly well-motivated physical processes can be explicitly added to the models. The “current density” model scales dissipation as the square of the current density:
which simulations in MB09 and MTB12 have shown to be roughly the z-component of curl(), which is more prominent in the central jet “spine” than the peripheral enclosing “sheath.” The “shear” model relates dissipation to the principle shear component of stress-energy-momentum tensor . The dominant component of the comoving rate of velocity shear of a fluid element is , where s is cylindrical radius. The shear model has
where shear strain and is dynamic viscosity.
2.3.2. Inverse Compton Models
The inverse Compton process is key for modeling gamma ray emission from the AGN selected for this investigation. Simple models in which , where the Doppler factor is the ratio of observed and fluid comoving frequencies , yield gamma ray emission, but a gamma ray synchroton has not yet been excluded [18]. Devising models with variability timescales of 3C 279 inspired by those proposed here may help resolve this degeneracy.
2.4. Polarized Radiative Transfer
The process of converting emission from the aforementioned models into maps of Stokes parameters for the intensity and two independent polarizations is implemented by numerically solving the polarized radiative transfer equations in [18]. Semi-analytic integration of these radiative transfer equations has been applied to stationary, self-similar, and axisymmetric models [2]; however, the 3D, time-dependent calculation by ray tracing over the simulation enables analysis of features such as apparently superluminal knots, non-axisymmetric instabilities, and variability. The ray tracing code adds to the observer plane contributions to each Stokes parameter from planes at various distance/retarded time combinations along the line of sight to construct constant observer time image maps. The observer plane is free to rotate around its center to fix the orientation of the projected jet, and around the simulation to fix observer polar and azimuthal angles. In what follows, we stick to observer times around 2000 M when the simulation appears transient-free and a stable jet appears Poynting-flux-dominated for small radii M and is gradually mass-loaded by entrained particles at larger radii.
3. Results: Comparing Jet Simulations with Observations
3.1. Emulating Spatiotemopral Jet Properties
3.1.1. Collimation
Starting with the simple beta and bias models, we can develop an intuition about the role that the functional dependence of emissivity on magnetic field strength plays in a defining characteristic of jets: collimation. Using the simulation datablock representing the largest physical region and assuming optical thinness, Figure 3 shows that the bias model (where ) has a much broader jet profile than the model (where ). The contours are collimation profiles [19] deduced from VLBA and EHT data. The intensity maps are left in code units, as the equipartition models are not well-suited to represent the detailed emission mechanism over all jet regions displayed, though are still useful tools to illustrate changes in the way a simulation “lights up” in response to changing important dynamical variables.
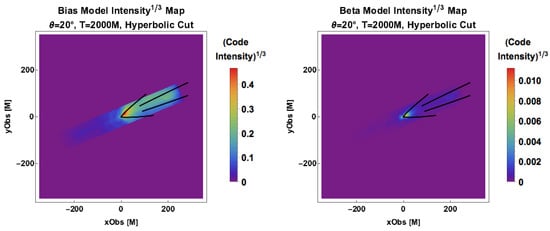
Figure 3.
Intensity maps viewed at observer angle for a simulation where points away from the region have been excised to isolate the jets. The bias model (left) exhibits a broader and more realistic collimation profile than the model (right) compared to the observations (thick black lines). The figures have been transformed by for visual contrast.
3.1.2. Jet Magnetic Field Substructure
Instabilities cause jets to pinch and kink. In the observation in Figure 1, M87 has a distinctive swirling pattern, possibly indicative of magnetic Kelvin–Helmholtz or kink instability. In Figure 4, viewed at 15 using a parabolic geometric jet isolation, we see a similar corkscrew feature for the bias model for the highest-resolution simulation lattice. Again, the normalization of the intensity map is irrelevant, as here we are concerned with intensity contrast, which illustrates the magnetic field substructure in the jet.
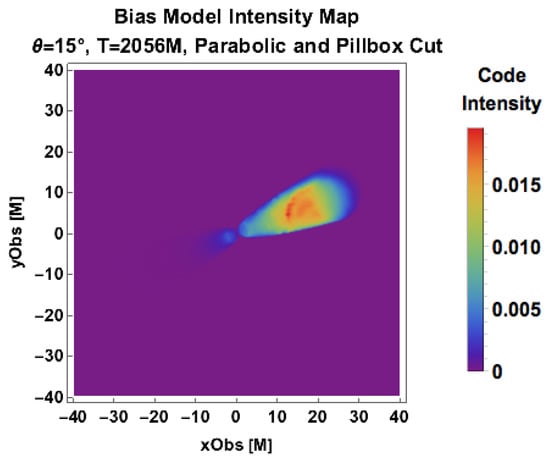
Figure 4.
Jet intensity map at 15 viewing angle from jet axis. Emission is modeled as ( bias model). Using a parabolic region to subtract the disk, all regions away from the locus satisfying are set to zero. A counterpropagating jet is also visible.
3.1.3. Polarization Maps
Due to the polarized nature of synchrotron radiation, it is essential to include polarization in our “observations” of jet emission for synchrotron models. In addition to total intensity, the “Observing” Jet Simulations pipeline can compute maps of other Stokes parameters as in Figure 5, where we have Stokes maps of two linear polarizations Q (left) and U (right) for an optically thin bias model at the highest simulation resolution. The U map is limb brightened and has a region of low polarization near the spine as U changes sign. The Q map is orthogonal to U.

Figure 5.
Linear polarizations Q (left) and U (right) maps at a 20 viewing angle generated from the emissivity function and parabolic geometric jet region isolation.
3.1.4. Instrument-Specific Properties: Cadence and Convolution
The process of observing itself fundamentally affects the astrophysical inferences that can be drawn from the dynamical evolution of a source and its surroundings. The convolution and cadence of images due to an observing instrument set minimum spatial and temporal scales that can be probed. For concreteness, the VLBA 43 GHZ observations [6] occurred with a cadence of an image per 21 days, which for M87 corresponds to 56 M (56 light crossing times of a gravitational radius). In the spatial domain, the point spread function for the EHT is 8.25 as. Here it is noteworthy that there is significant overlap between the spatiotemporal scales of observations and simulations, as illustrated with the bias model “observed” at different times and with/without convolution in Figure 6 (for the highest simulation resolution). The jet substructure clearly varies on the timescale of tens of M and/or with convolution by a Gaussian beam with width of order unity.
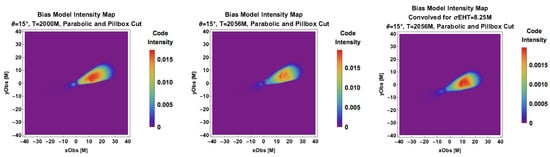
Figure 6.
Jet intensity maps viewed at a observer angle for a simulation where points away from the region have been excised to isolate the jet and counterjet for the bias model. The left map is taken at observed time M, the middle map shows significant variation in the form of an increasingly ordered substructure at M, and the right map displays how the structure is degraded by convolution with a M Gaussian beam.
3.2. Matching Models with Observed Images
Having made some suggestive comparisons of discrete observational signatures with optically thin toy models, we have the necessary background to use the full polarized radiative transfer routines with opacity to replicate observations of a particular source, M87, at a particular frequency, attempting to match all measured properties, including morphology, orientation, and normalized intensity. To this end, we employ the current density and shear models in a comparison with the 43 GHz VLBA observation in Figure 7. One limitation is that the observed image spans a greater spatial extent than the synthetic image, though this can be remedied in the near future when detailed observations are produced on linear scales that are a factor of order unity smaller and/or when detailed simulations extend on scales that are a factor of order unity greater. In the current density model, we see a bright spine at a small cylindrical radius, and we also see current layers in a corona at the jet boundary. The shear model prescription, in which the partial pressure scales as the square of velocity shear, appears relatively more edge brightened, suggesting that shear is prominent at the boundary.
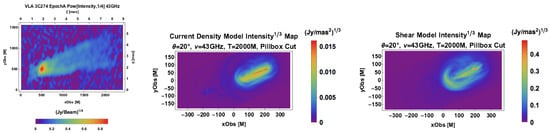
Figure 7.
M87 VLA observation (left) at 43 GHz. The total intensity is monotonically transformed by for visual clarity. The beam dimensions are . Synthetic 43 GHz observations are shown for comparison using the current density (middle) and shear (right) models and transformed by .
4. Discussion
The intensity map in Figure 4 generated from the highly stylized bias model—in which relativistic gas pressure is constant along jets—already shows the helical jet substructure and counterjet visible in the observation in Figure 1 and Figure 2, respectively. The more realistic current density and shear models have greater morphological resemblance to the observations, as seen through the comparison at 43 GHz in Figure 7. Though the models significantly vary from the observations at this stage, we are now better equipped to interpret why different regions of the jet light up in different ways. For example, the current density jet is brightest where, in the simulation, the current density—roughly the z-component of the curl of the magnetic field—is greatest; the shear model can be interpreted as accelerating particles mostly in regions of high velocity shear. The ultimate test of the “Observing” Jet Simulations methodology is whether the right combination of model features can generate synthetic observations nearly indistinguishable from real observations.
Armed with a robust “Observing” Jet Simulations pipeline from GRMHD simulations to synthetic observations [18], the next target is the post-processing of a broad range of astrophysical simulation data matching new observations of JAB systems (with possible extensions to proto-planetary disks, white-dwarf binaries, etc.). One of the nearest jets is in M87, which has been observed in the gamma ray band with the Fermi Large Area Telescope, in the optical band with the Hubble Space Telescope, and in the radio band with the ALMA. M87 is an excellent target of this investigation because of the wealth of existing and planned mm- and sub-mm very long baseline (VLB) EHT observations, as well as the fact that its high central black hole mass makes it the only AGN with jets and a central black hole of comparable angular width from Earth as Sgr A*. Applying this methodology to other sources such as 3C 279 and 3C 31 may elucidate the most likely mechanisms underlying phenomena such as rapid variability and large-scale polarization reversals.
5. Conclusions
The “Observing” Jet Simulations methodology enables us to self-consistently simulate multiwavelength astronomical observations, including a wide range of such effects as Doppler beaming, polarization, and opacity, and to rotate the observer to simulate many sources. The approach used here emphasizes models with clear physical interpretations such as equipartition, current density, and shear. In addition to more physical models, we expect greater dynamical range in simulations and observations to come.
Acknowledgments
Richard Anantua was supported by the California Alliance. Jonathan McKinney provided the simulation used in this work.
Author Contributions
Richard Anantua carried out the calculations presented in this work and wrote this manuscript. Roger Blandford conceived, designed, managed, and coordinated the project. Alexander Tchekhovskoy guided Richard Anantua through the initial stages of radiative transfer code development.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AGN | Active Galactic Nucleus |
| EHT | Event Horizon Telescope |
| GRMHD | General Relativistic Magnetohydrodynamic |
| JAB | Jet/Accretion Disk/Black Hole |
| MDPI | Multidisciplinary Digital Publishing Institute |
| NRAO | National Radio Astronomy Observatory |
| OVRO | Owens Valley Radio Observatory |
| VLBA | Very Long Baseline Array |
| VLBI | Very Long Baseline Interferometry |
References
- Curtis, H.D. Descriptions of 762 Nebulae and Clusters Photographed with the Crossley Reflector. In Publications of the Lick Observatory; Lick Observatory: San Jose, CA, USA, 1918; Volume 13, pp. 9–42. [Google Scholar]
- Blandford, R.D.; Anantua, R.J. The Future of Black Hole Astrophysics in the LIGO-VIRGO-LPF Era. J. Phys. Conf. Ser. 2017, 840, 012023. [Google Scholar] [CrossRef]
- Christian, P.; Loeb, A. Probing the spacetime around supermassive black holes with ejected plasma blobs. Phys. Rev. D 2015, 91, 101301. [Google Scholar] [CrossRef]
- Lu, R.; Broderick, A.E.; Baron, F.; Monnier, J.D.; Fish, V.L.; Doeleman, S.S.; Pankratius, V. Imaging the Supermassive Black Hole Shadow and Jet Base of M87 with the Event Horizon Telescope. Astrophys. J. 2014, 788, 120–129. [Google Scholar] [CrossRef]
- Kovalev, Y.Y.; Lister, M.L.; Homan, D.C.; Kellermann, K.I. The Inner Jet of the Radio Galaxy M87. Astrophys. J. Lett. 2007, 668, 27–30. [Google Scholar] [CrossRef]
- Ly, C.; Walker, R.C.; Junor, W. High-Frequency VLBI Imaging of the Jet Base of M87. Astrophys. J. 2007, 660, 200. [Google Scholar] [CrossRef]
- Ackermann, M.; Anantua, R.; Asano, K.; Baldini, L.; Barbiellini, G.; Bastieri, D.; Gonzalez, J.B.; Bellazzini, R.; Bissaldi, E.; Blandford, R.D.; et al. Minute-Timescale > 100 MeV Gamma-ray Variability During the Giant Outburst of Quasar 3C 279 Observed by FERMI-LAT in 2015 June. Astrophys. J. Lett. 2016, 824, L20. [Google Scholar]
- Blakeslee, J.P.; Jordán, A.; Mei, S.; Côté, P.; Ferrarese, L.; Infante, L.; Peng, E.W.; Tonry, J.L.; West, M.J. The ACS Fornax Cluster Survey. V. Measurement and Recalibration of Surface Brightness Fluctuations and a Precise Value of the Fornax-Virgo Relative Distance. Astrophys. J. 2009, 694, 556–572. [Google Scholar] [CrossRef]
- Gebhardt, K.; Adams, J.; Richstone, D.; Lauer, T.R.; Faber, S.M.; Gültekin, K.; Murphy, J.; Tremaine, S. The Black Hole Mass in M87 from Gemini/NIFS Adaptive Optics Observations. Astrophys. J. 2011, 729, 119. [Google Scholar] [CrossRef]
- Woo, J.; Urry, M. Active Galactic Nucleus Black Hole Masses and Bolometric Luminosities. Astrophys. J. 2002, 579, 530–544. [Google Scholar] [CrossRef]
- Homan, D.C.; Wardle, J.F.C. Direct Distance Measurements to Superluminal Radio Sources. Astrophys. J. 2000, 535, 575–585. [Google Scholar] [CrossRef][Green Version]
- Nilsson, K.; Pursimo, T.; Villforth, C.; Lindfors, E.; Takalo, L.O. The Host Galaxy of 3C 279. Astron. Astrophys. 2009, 505, 601–604. [Google Scholar] [CrossRef]
- Gammie, C.F.; McKinney, J.C.; Toth, G. HARM: A Numerical Scheme for General Relativistic Magnetohydrodynamics. Astrophys. J. Lett. 2003, 589, 444–457. [Google Scholar] [CrossRef]
- McKinney, J.C.; Blandford, R.D. Stability of Relativistic Jets from Rotating, Accreting Black Holes via Fully Three-Dimensional Magnetohydrodynamic Simulations. Mon. Not. R. Astron. Soc. 2009, 394, L126–L130. [Google Scholar] [CrossRef]
- McKinney, J.C.; Tchekhovskoy, A.; Blandford, R.D. General Relativistic Magnetohydrodynamic Simulations of Magnetically Choked Accretion Flows around Black Holes. Mon. Not. R. Astron. Soc. 2012, 423, 1928–1939. [Google Scholar] [CrossRef]
- Ressler, S.M.; Tchekhovskoy, A.; Quataert, E.; Chandra, M.; Gammie, C.F. Electron thermodynamics in GRMHD simulations of low-luminosity black hole accretion. Mon. Not. R. Astron. Soc. 2015, 454, 1848–1870. [Google Scholar] [CrossRef]
- Ressler, S.M.; Tchekhovskoy, A.; Quataert, E.; Gammie, C.F. The Disc-Jet Symbiosis Emerges: Modeling the Emission of Sagittarius A* with Electron Thermodynamics. Mon. Not. R. Astron. Soc. 2017, 467, 3604–3619. [Google Scholar] [CrossRef]
- Anantua, R.J. Towards Multiwavelength Observations of Relativistic Jets from General Relativistic Magnetohydrodynamic Simulations. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2016. Available online: http://richardanantua.com/wp-content/uploads/2015/04/RJA-multiwavelength-observations-relativistic-33.pdf (accessed on 10 October 2017).
- Globus, N.; Levinson, A. The Collimation of Magnetic Jets by Disc Winds. Mon. Not. R. Astron. Soc. 2016, 461, 2605–2615. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).