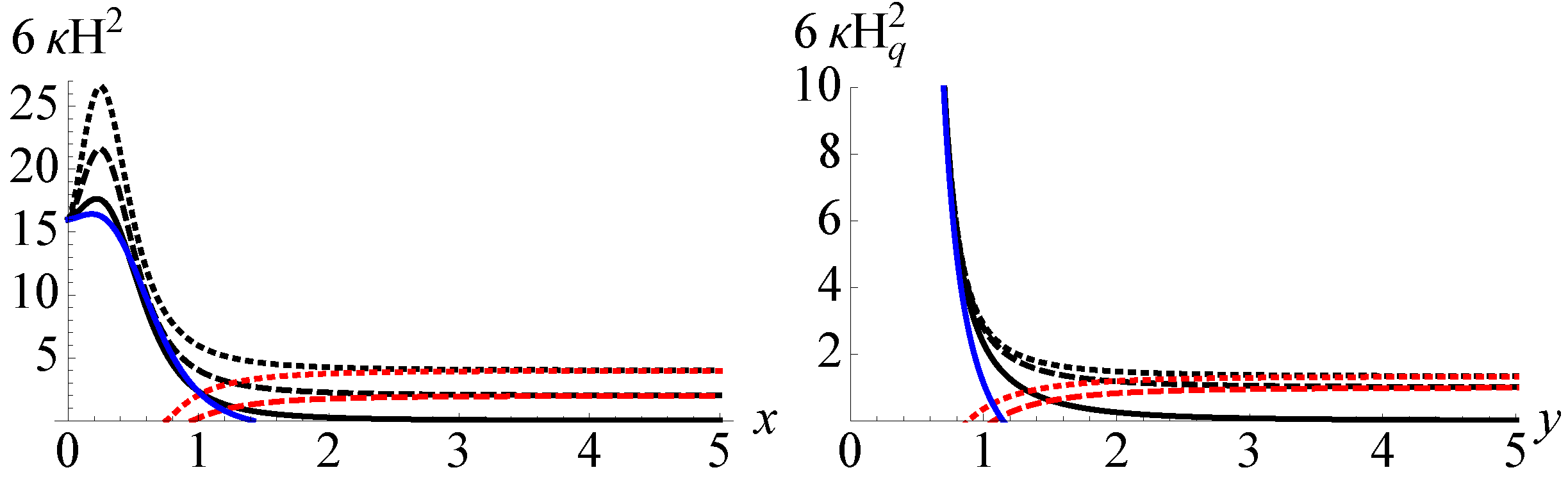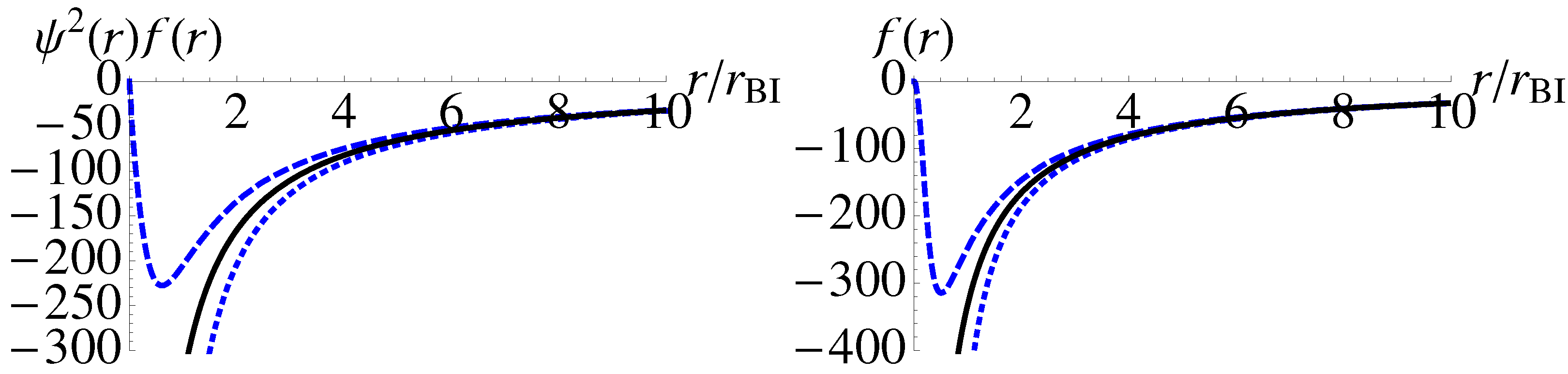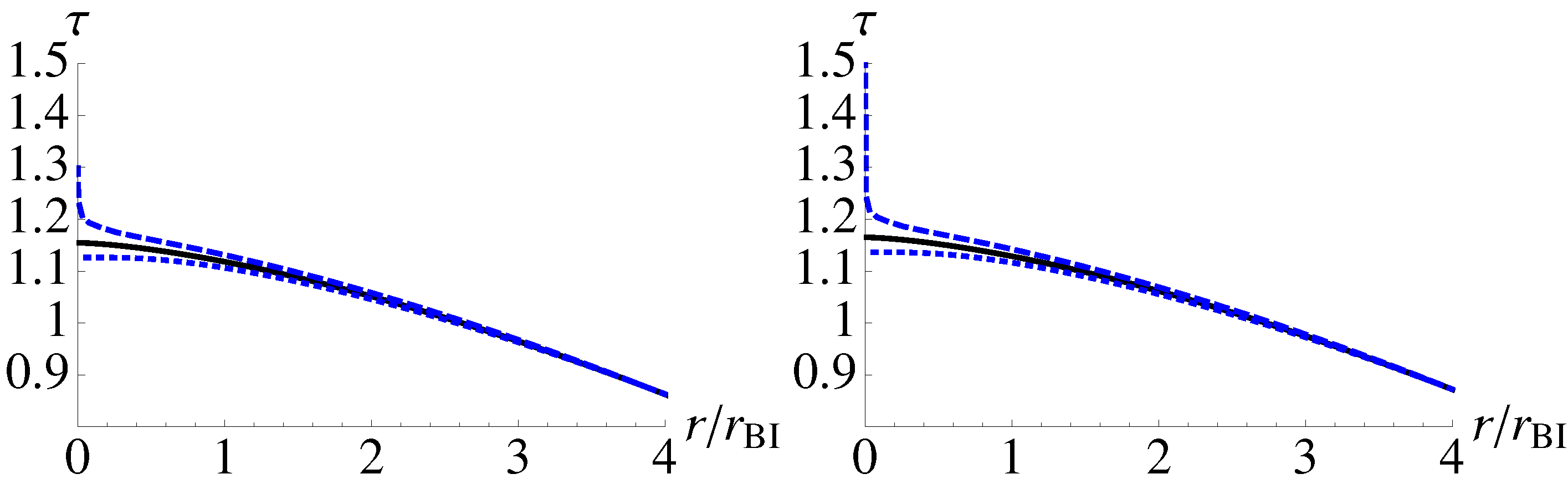1. Introduction
The inevitability of spacetime singularities in the context of General Relativity (GR) has inferred the incompleteness of the theory and has jeopardized the validity of it close to these events [
1]. The most famous examples among the spacetime singularities would be the big bang singularity at the very beginning of the universe as well as the spacelike singularity within a black hole. These singularities are thought to be beyond the validity of GR and it is commonly believed that some sorts of quantum effects or an appropriate construction of a quantum theory of gravity would solve this problem. However, due to several troublesome technical difficulties, these tools have not reached a final answer. In this work we will therefore follow a different but still cogent approach to address this issue based on an extended theory of gravity [
2].
From a phenomenological point of view, an extended theory of gravity should respect the success of GR in the sense that the theory is required to recover GR in the proper limits. Furthermore, the theory should, at least at the classical level, be able to address some of the difficulties that GR cannot explain, such as the aforementioned singularity problems. An attractive candidate is the EiBI theory [
3]. This theory has been widely investigated both from the cosmological and astrophysical points of view [
4,
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18]. The EiBI theory is able to cure the big bang singularity at the cosmological level [
19]. Besides, some black hole singularities, once matter is included, are found to be altered [
20,
21,
22,
23,
24]. However, the theory reduces exactly to GR in vacuum and the singularity predicted in a Schwarzschild black hole is still unavoidable. On the other hand, the recently proposed mimetic formulation is found to be able to generate non-trivial vacuum solutions [
25]. When applied to Einstein-Hilbert action, the theory can explain the mysterious dark matter at the cosmological scale [
25,
26,
27,
28]. The vacuum, static, and spherically symmetric solutions of mimetic GR were also found in references [
29,
30,
31]. The theory would contain more interesting solutions when a certain potential of the mimetic scalar field is considered [
32,
33]. See references [
34,
35] for a review of Born-Infeld theories of gravity and the mimetic gravity, respectively.
In this work, we will combine the EiBI action with the mimetic formulation and call the resulting theory the mimetic Born-Infeld gravity [
36]. The non-trivial vacuum solutions are investigated by considering an expanding universe [
36] and a static, spherically symmetric spacetime [
37]. The former can be interpreted as a primordial stage of our universe before the reheating era. The latter is interesting because the interior structure as well as the spacelike singularity inside a black hole are expected to be amended in the mimetic Born-Infeld gravity.
The paper is organized as follows: In
Section 2, we briefly introduce the mimetic Born-Infeld gravity proposed in reference [
36]. In
Section 3, the vacuum solutions which can describe a primordial stage of our universe are studied. In
Section 4, we study the static and spherically symmetric solutions in a vacuum spacetime, and find that the interior structure as well as the causal structure of the singularity in a black hole are altered [
37]. Finally, we conclude in
Section 5.
2. The Mimetic Born-Infeld Gravity
The mimetic Born-Infeld gravity is based on the use of the mimetic formulation upon the EiBI action (we have assumed
throughout this work)
where
is the matter Lagrangian coupled only to the physical metric
. The mimetic formulation is essentially a redefinition of the physical metric
such that [
25]:
where
and
are the conformal auxiliary metric and the mimetic scalar field, respectively. Besides,
corresponds to the inverse of
. The parametrization (
2) respects the conformal invariance of the theory in the sense that the theory is invariant under a conformal transformation of
. In the action (
1), the tensor
is chosen to be the symmetric part of the Ricci tensor constructed by the affine connection
, and the connection is assumed to be independent of the metric
. According to the mimetic formulation, the physical metric
in the action should be written as
based on the parametrization (
2). The dimensionless constant
quantifies the effective cosmological constant at the low curvature limit.
stands for the absolute value of the determinant of the rank two tensor
. Finally,
characterizes the theory and has inverse dimensions to that of the cosmological constant.
It should be stressed that for the original EiBI gravity as well as the mimetic Born-Infeld gravity, in which only the symmetric part of the Ricci tensor is considered in the action, there is a projective gauge symmetry and the torsion field in the affine connection can be removed by a gauge fixing procedure. A symmetric affine connection can be chosen after the corresponding gauge fixing and an initial torsionless assumption is in general not necessary [
34]. Furthermore, the theory is expected to be free of ghosts since the theory is formulated within the Palatini approach in which the equations of motion contain derivatives (naturally) up to only second order. Even if there is an additional mimetic scalar field in the theory, when we transform the action (
1) into the Einstein frame, it can be shown that the mimetic scalar field does not couple to the metric that defines the scalar curvature. The higher derivative terms as well as the associated ghost problems seem to be avoidable. We would like to refer to reference [
38] in which the authors managed to construct some ghost-free theories of gravity in the mimetic framework under the metric variational principal.
In the mimetic Born-Infeld theory, it is the affine connection
, the auxiliary metric
, and the mimetic scalar field
that should be treated as independent variables. After varying the action with respect to
, the resulting field equation leads to the existence of a second auxiliary metric
such that
is compatible with the affine connection
. Note that a hat symbolizes a matrix quantity. Hereafter, we define a new matrix and its inverse as follows for the sake of convenience [
7]:
such that
. As a result, the field Equation (
3) and the equation of motion of
can be written as
respectively
1. In the above equations,
is defined by
,
represents the energy momentum tensor,
is the four-dimensional identity matrix, and
, where
denotes the trace of a given matrix
. It should be stressed that the mimetic scalar field is confined to fulfill the constraint:
which can also be derived straightforwardly from the parametrization (
2). Finally, the field equation of the mimetic scalar field
is [
36]
In absence of the mimetic field, i.e., , the theory reduces to the original EiBI theory. Once the mimetic field is included, its additional contributions would result in solutions which are absent in the EiBI theory.
3. The Primordial Cosmological Solutions
In this section, we will obtain the cosmological solutions of a vacuum universe (
)
2 in the mimetic Born-Infeld gravity. These solutions can describe an early stage of the universe prior to the reheating epoch. We will investigate how the mimetic field, on top of the Born-Infeld nature of the theory, leads to a different birth of the cosmos.
We start considering a vacuum, homogeneous and isotropic universe which can be described by the Friedmann-Lemaître-Robertson-Walker (FLRW) line element:
where
and
are the lapse function and the scale factor of the physical metric, respectively.
and
are the corresponding quantities of the auxiliary metric
. The symmetries of the spacetime imply that all these quantities only depend on the cosmic time
t. Furthermore, the background solution of the mimetic field
can be obtained via Equations (
7) and (
8):
where
is a positive integration constant corresponding to a characteristic scale factor of the mimetic field. We define as well a dimensionless variable
for the sake of later convenience. In addition, as mentioned above,
indicates that
can be either positive or negative. Note again that the quantity
refers to the homogeneous and isotropic part of
and it should be distinguished from its linearly perturbative counterpart, i.e.,
.
Essentially, the map
, which relates the two metrics
and
, can be obtained by using Equation (6). Using this map and inserting it into Equation (
5), one can obtain the modified Friedmann equations of this model. Due to the presence of the affine structure and the two metrics
g and
q, we will derive the modified Friedmann equations of these metrics by assuming the lapse function
to be unity. The results are
where
and
where
. The dot denotes the cosmic time derivative. Similar to what we did for the physical scale factor, we will define a new dimensionless variable
and we have then
. On the above Friedmann equations, we have defined
Notice that
because the matrix
is a nonnegative matrix. Note that the modified Friedmann equations describing a universe with perfect fluids are explicitly given in reference [
36].
3.1. Cosmological Solutions of a Vacuum Universe
In this subsection, we will show the results of the vacuum cosmological solutions in this model. The solutions are obtained by analyzing the modified Friedmann Equation (
11) for the different configurations of the parameter space
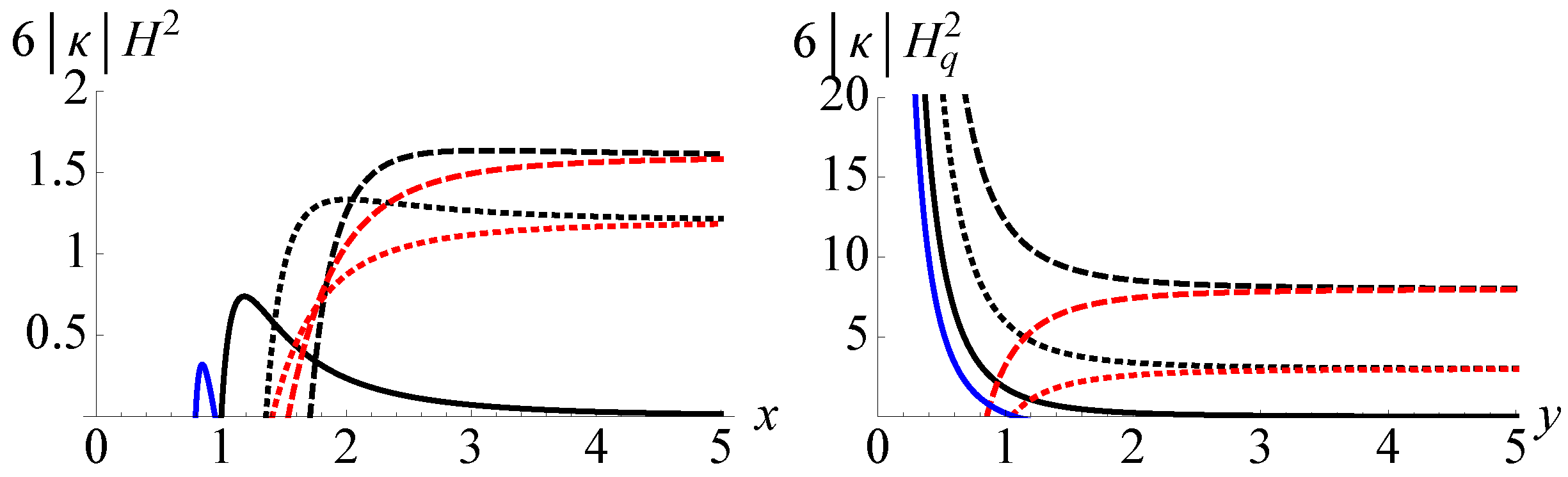
. Given that we live in an expanding universe, we will restrict our analysis to solutions with a positive Hubble rate. As it is well known under a straightforward time reversal, we would recover the contracting solutions easily. The results are presented in
Figure 1 and
Figure 2 and summarized in
Table 1.
Firstly, it can be proven that there is no physical Lorentzian solution for a negative (positive)
if
and
(
and
). We refer to those situations with the label “N” in
Table 1.
Secondly, when
(this implies
as well), the modified Friedmann Equation (
11) become
Therefore, if
, the universe is approximately de Sitter in both metrics. See the dashed and dotted curves in
Figure 1 and
Figure 2. If
, the universe goes from an expanding phase to a contracting phase through a smooth bounce for a finite value of
x and
y. At this bouncing point, the Hubble functions vanish. See the blue curves in
Figure 1 and
Figure 2. Finally, if
, the universe approaches a Minkowskian spacetime when
x and
y are large, i.e.,
. See the black solid curves in
Figure 1 and
Figure 2.
Thirdly, if
and
, the physical metric is approximately de Sitter, while the auxiliary metric has a big bang singularity at
at small scale factors:
See the black and blue curves in
Figure 1. On the other hand, if
and
, the universe has a bounce in both metrics. See the red curves in
Figure 2.
Fourthly, if
and
, the universe has a bounce in both metrics. See the red curves in
Figure 1. On the other hand, if
and
, the physical metric has a bounce when
x goes to its minimum value
, while the auxiliary metric has a big bang singularity at
. See the black and blue curves in
Figure 2.
It should be stressed that the de Sitter (the physical Hubble rate described by Equation (
14)) and the bouncing solutions shown above are non-trivial vacuum solutions in this model. Furthermore, the solutions described by the blue and black curves in
Figure 1 and
Figure 2 are accompanied by a divergence of the auxiliary metric. This kind of pathology is present in the EiBI theory as well. Finally, the solutions described by the red curves in
Figure 1 and
Figure 2 are regular in both metrics and they are exclusive fingerprints of this model. As we will show later, the linear metric perturbations, including scalar, vector, and tensor modes, are stable near the bounce in what respect the physical metric. Note that the regular solutions in the Eddington regimes of the EiBI theory are linearly unstable and these instabilities may result from the corresponding divergence of the auxiliary metric [
8].
3.2. Linear Stabilities Near the Bounce
In the EiBI model, the avoidance of the big bang singularity in the physical metric is accompanied by the divergence of the auxiliary metric. In reference [
8] it was shown that the divergence in the auxiliary metric may lead to instabilities of the cosmological perturbations. Interestingly, in the mimetic Born-Infeld model, we have found some bouncing solutions (the red curves in
Figure 1 and
Figure 2) in which the physical metric and the auxiliary metric are regular. It is then natural to ask whether these bouncing solutions are linearly stable or not.
We consider small perturbations around a vacuum FLRW universe
and perturb the field of the theory linearly:
To proceed, we decompose the perturbed quantities of the physical metric as follows [
39,
40]
such that
. Therefore, in this setup, we have six scalar modes
,
E,
F,
A,
B,
, two transverse vector modes
,
and one transverse-traceless tensor mode
. Physically, we can fix two scalar modes by choosing a gauge because only four of them are independent. For vector modes, we can similarly fix one by choosing a gauge. In reference [
36], we have obtained all the equations governing the evolutions of these perturbations.
To study the linear stabilities close to the bounce in which the two metrics are regular (the red curves in
Figure 1 and
Figure 2), we should obtain the asymptotic behaviors of each mode near the bounce. As in reference [
8], we will choose the Newtonian gauge for scalar modes, that is,
. Then, we will fix
for vector modes. The results for tensor modes and vector modes are the following:
where
and
,
, and
are integration constants. Note that
refers to the rescaled physical scale factor at the bounce,
k stands for Fourier modes, and we assume that the bounce happens at
for simplicity. It can be seen that tensor modes and vector modes are linearly stable near the bounce.
For scalar modes, we choose
, then the equation describing the evolution of the perturbed mimetic scalar field
near the bounce can be written as
, where
The solution then reads
where
and
are integration constants. Therefore,
is stable around the bounce in the sense that the amplitude does not grow. Note that even though the dispersion relation (
21) seems to hint an imaginary frequency mode if some choices of the parameters are assumed, it does not imply a real instability in the sense that this dispersion relation is valid only near the bounce (
). However, a general dispersion relation applicable away from the bounce still remains unknown and whether the unwanted tachyonic instability would appear or not should be investigated further.
The behaviors of the other scalar modes near the bounce can be approximated in terms of
as follows
Given that
can be expressed as in Equation (
22) near the bounce, these scalar modes are all stable when
. Note that we have only focused on the physical perturbations described by
in this work.
4. Spherically Symmetric Solutions in Vacuum
It is a well known fact that the EiBI theory is equivalent to GR in vacuum, hence the theory shares the same vacuum solution of GR. However, as shown in the previous section, the mimetic Born-Infeld theory contains non-trivial vacuum solutions which are absent in GR, i.e., the physical Hubble rate described by Equation (
14) and the bouncing solutions. Therefore, it would be interesting to investigate the vacuum, static, and spherically symmetric solutions in the mimetic Born-Infeld model and to study how the Schwarzschild solution could be altered, especially the spacelike
center of a Schwarzschild black hole. The results shown in this section are based on our recent paper [
37].
We consider again a vacuum spacetime and assume a static and spherically symmetric ansatz:
where
and
x stands for a new radial coordinate which can be written as a function of
r. In this configuration, the mimetic scalar field
and the mimetic field
should depend only on
r.
By calculating the constraint (
7) and considering the field Equation (6), one can obtain the expression of the map
relating the two metrics, hence obtain the following identities
where the function
is defined as
Furthermore, the metric functions of the auxiliary metric
can be obtained by calculating Equations (
5) and (
8). Afterwards, the metric functions of the physical metric
can be derived by inserting the identities (
25). In absence of the mimetic field, we have
and
for all
r. In this case, the Schwarzschild-de Sitter solution is recovered. The non-trivial solutions only appear in the presence of the mimetic field.
Given that the equations describing vacuum, static and spherically symmetric spacetimes in the presence of the mimetic field are complicated, we will resort to numerical methods. We firstly assume
, i.e., a vanishing cosmological constant, for the sake of simplicity. The solutions derived will then be compared with the standard Schwarzschild solution. On a certain radius (
) inside the event horizon, we assume that there is a small amount of the mimetic field, i.e.,
, and the solutions deviate from the Schwarzschild geometry within this radius, that is,
when
. This particular radius
is the point where the initial conditions are imposed. The major goal of this work is to study how a small deviation
in the mimetic field would alleviate the spacelike singularity in the interior of a Schwarzschild black hole. In the rest of this work, we will assume a positive
because of the instability problems ubiquitous to a negative
[
9].
After normalizing the radius by assuming
and
, the numerical results of the metric functions of the physical metric are shown in
Figure 3. The dashed curves are derived by assuming an initial condition
at
, and the dotted curves correspond to an initial condition
at
. Note that the qualitative behaviors of the solutions do not depend on the quantitative values of these conditions once the sign of
is fixed. The solution in absence of the mimetic field, i.e., the Schwarzschild solution, is also shown by the solid curves. In the presence of the mimetic field, the solutions deviate significantly from the Schwarzschild solution when
. If
(dashed), the metric functions and the curvature invariants can be approximated as
,
,
, and
when
. On the other hand, if
(dotted), we have
,
,
, and
when
. Therefore, there is a curvature singularity at
for the two choices of initial conditions.
4.1. The Radially Infalling Proper Time
After exhibiting the difference between the Schwarzschild black hole and the solutions in the presence of the mimetic field, it would be interesting to study the infalling proper time of a timelike observer elapsed to reach the singularity for each solution. For a static and spherically symmetric metric given in Equation (
24), the geodesic equations of a timelike observer are
On the above equations, and L can be regarded as the conserved energy and the angular momentum of the system. Note that we have considered the motion on the plane . For a radial motion, we have .
Then, we consider two different cases to analyze the infalling proper time: (i)
and (ii)
. The first case,
, corresponds to a situation in which an observer is at rest at infinity and falls freely into the black hole. In the second case,
, the observer is initially at rest on the event horizon. The proper time for the second case is called the maximal infalling proper time [
41]. We use the numerical results of the metric functions in the previous subsection and derive the infalling proper time
numerically for these two cases. The results are shown in
Figure 4. We assume that the observer starts to count his/her time when crossing
, that is,
. One can see that for
, the infalling proper time to reach the singularity is finite for both choices of initial conditions. On the other hand, if
, the maximal infalling proper time (
) to reach the singularity is found to be infinite. However, the maximal infalling proper time for the solution described by the dotted curve (
) is even smaller than its GR counterpart.
4.2. The Causal Structure of the Singularity
Another important property of the curvature singularity is its causal structure and we will investigate this issue in this subsection. We firstly focus on the
plane and define a new set of timelike and spacelike coordinate as follows:
and
, where
is a positive constant, and
satisfies
. The line element becomes
and we have
For the solutions with initial conditions
(dashed curves), we find that
when
. This means that the curvature singularity is a lightlike singularity. If we connect the two portions of spacetime: the interior structure described above (
) and the Schwarzschild spacetime (
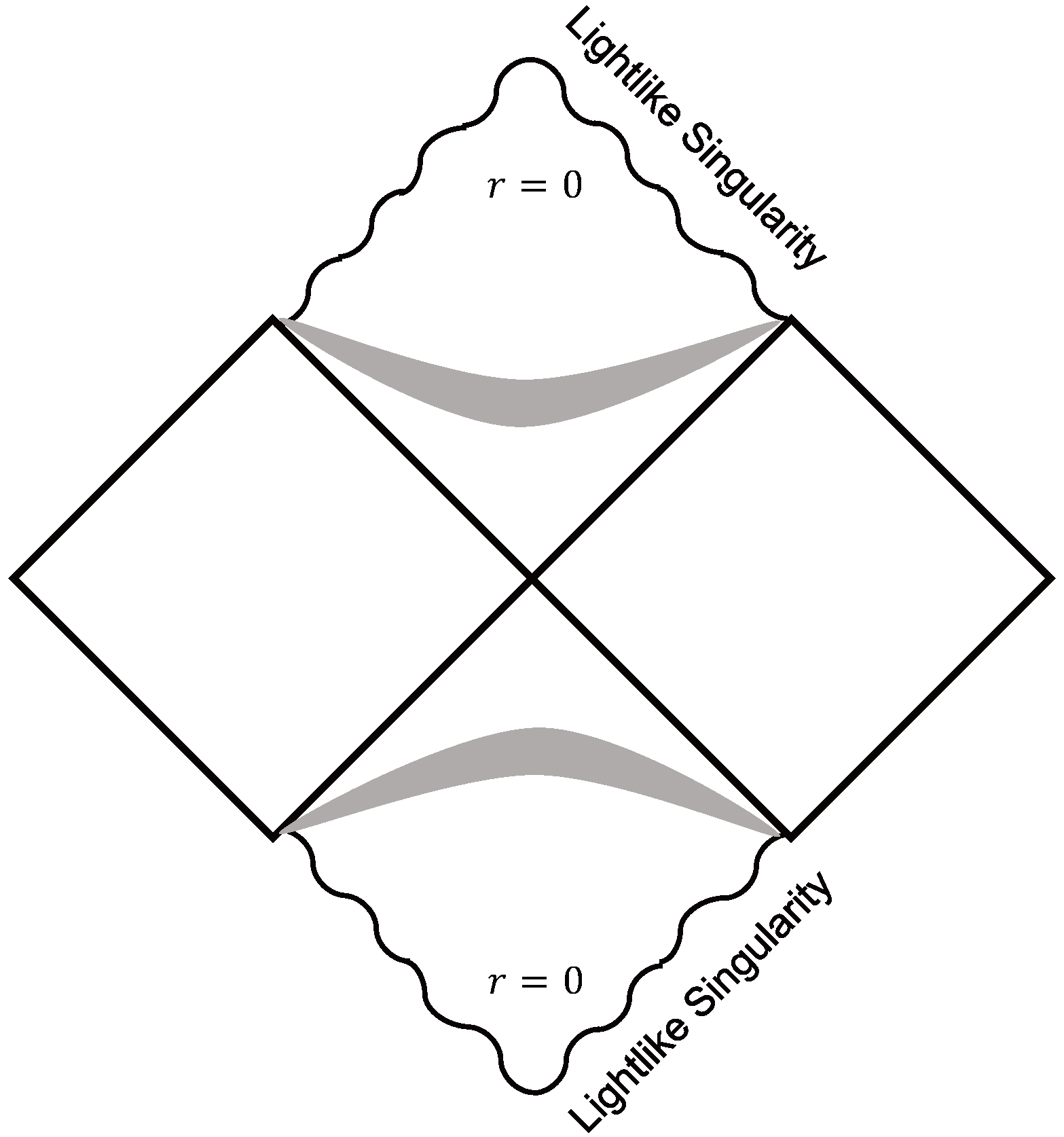
), the causal structure of the lightlike singularity and its corresponding Penrose diagram are depicted in
Figure 5. On the other hand, for the solutions with initial condition
(dotted curves), we have
when
. Therefore, the singularity in this case is a spacelike singularity, similar to the Schwarzschild singularity.
5. Conclusions and Further Discussions
The vacuum cosmological solutions, which describe the primordial universe prior to the reheating epoch, and the vacuum, static, and spherically symmetric solutions of the mimetic Born-Infeld gravity are studied. The theory contains non-trivial vacuum solutions in the presence of the mimetic field, and these solutions could be interesting regarding the singularity issues due to the Born-Infeld nature of the theory.
At the cosmological level, we have found some primordial de Sitter solutions and some bouncing solutions in a vacuum universe. Although some of these solutions are accompanied by some divergences in the auxiliary metric
(see the blue and black curves in
Figure 1 and
Figure 2), there exist some interesting solutions which are bouncing solutions in the two metrics (see the red curves in
Figure 1 and
Figure 2). We have studied the linear perturbations of these particular bouncing solutions and have found that the solutions are linearly stable near the bounce.
For the scrutiny of the vacuum, static, and spherically symmetric solutions, we have found that the curvature singularity within a black hole is unavoidable. However, the behaviors of the metric functions as well as the causal structure near the singularity could be rather different from the Schwarzschild counterpart. For instance, we have found some solutions (
) in which the curvature singularity at the origin is a lightlike singularity. Furthermore, the maximal infalling proper time of a timelike observer to reach the singularity is infinite for this branch of solutions. We would like to stress that the black hole solutions obtained in the mimetic Born-Infeld gravity here are still quite different from those obtained in the original EiBI gravity with matter. For example, in references [
23,
24] it was shown that by considering the standard Maxwell electromagnetic field or a static, spherically symmetric scalar field in the matter Lagrangian, the black hole singularity could be replaced with a wormhole, a nonsingular naked compact object, or a soliton-like solution, depending on the parameters involved.