1. Introduction
Astrophysical jets, originating from sources ranging from young stars (YSO jets) to active galaxies (AGN jets), have been observed in various wavelengths and in some cases a complex structure has been revealed. The evolution, acceleration and collimation of jets is often associated with the presence of a magnetic field and specifically, with the conversion of magnetic to kinetic energy and the effect of the hoop stress.
On many occasions, astrophysical jets display a two-component structure, i.e., a non-uniform profile perpendicular to the jet axis. Evidence for this structure can be found, e.g., in the case of blazars in [
1]. A usual description for these jets includes a fast spine and a slower sheath configuration, which may in turn affect the stability of these outflows. An example is the development of Rayleigh-Taylor type instabilities, induced by differential rotation [
2,
3,
4,
5].
Observations, polarimetric and rotation measure (RM) studies, e.g., from Very Long Baseline Interferometry (VLBI), have been extensively carried out in the last decades and can be used to determine the morphology of these outflows. In particular, spine and sheath structures may also be observed in terms of polarization and RM, which can in turn provide information on the topology of the magnetic field [
6]. Such observations often give evidence for the existence of a large scale, helical magnetic field [
7]. Furthermore, analysis of the distribution of the position angle of the electric field vector (EVPA) concludes that in general, EVPAs are roughly perpendicular or parallel to the direction of the flow, with “jumps” being also observed in some objects [
8].
In this work, we intend to examine any possible effects of this (in)stability on the emission pattern observed from a two-component jet. For this, we will use existing results from relativistic, magnetohydrodynamic (MHD) simulations of two-component jets, presented in [
4]. We will assume an optically thin emission from the inner jet only and, as a first approximation, ignore absorption and Faraday rotation from the outer jet. This is implied by actual observations of specific objects (e.g., [
9]) and from the fact that for small viewing angles, the higher Lorentz factor (and by extension the higher Doppler boost) lead to a stronger emission from the inner jet.
2. Materials and Methods
For the relativistic two-component jet simulations, we used the parallel, grid adaptive MPI-AMRVAC code (MPI-Adaptive Mesh Refinement-Versatile Advection Code) [
10], under the assumption of a translational symmetry along the
z axis. We will adopt the same recipe for the configuration of the jet and the normalization as described in [
3]. Velocity is normalized in units of
c, distance is measured in
and mass is normalized to proton mass
.
First we fix the (outer) radius of the jet at
= 0.1
and the inner radius is arbitrarily chosen to be
. These values are consistent with [
11] and recently [
12], where the half opening angle of the M87 jet was found ~2
at a distance of ~4
and the jet is almost fully collimated at the same scale. The next step is to define the initial conditions for the density, velocity, magnetic field and pressure profiles of the jet (inner and outer regions) and the surrounding, external (static and unmagnetized) medium.
We fix an initial toroidal velocity profile:
where
for the inner jet,
for the outer jet and
(which leads to continuity of
at the interface). Thus
increases with
R until
, then decreases, with a maximum value at
.
For the poloidal velocity, we assume a constant value in each component, so that the corresponding Lorentz factor is
for the inner jet and
for the outer jet, in agreement with [
13]. We note that this is the dominant component of the velocity and the total Lorentz factor can be approximated as
and
respectively.
The magnetic field is described in a similar way: a constant poloidal component in each part of the jet (
) while the toroidal component resembles the form of the toroidal velocity:
The constants are defined by the maximum magnetization of the jet, at . We use values of ranging from to , so the jet is kinetically dominated. Similar to the definition of the toroidal velocity, we select , while the poloidal magnetic field will still be discontinuous at .
Regarding the density, we assume a constant value in each part of the jet and the external medium:
The kinetic luminosity flux and the percentage carried by the inner part are used to calculate the density ratio of the above regions. Assuming a kinetic luminosity flux of ~10
ergs/s, of which 1% is carried by the inner jet, we find that
and
. A visualization of the initial conditions (density, toroidal velocity) can be found in [
4].
The polarized state of the emitted radiation is often described via the Stokes parameters
, with
I corresponding to its intensity. In the most general case of elliptically polarized light,
are non-zero, with the first two quantifying the ellipse and
V quantifies the circular polarization. The linear fractional polarization can be calculated from the Stokes parameters, using the formula:
The EVPA
in the observer’s frame can be calculated from the formulas:
For the ray-casting, we assume an optically thin synchrotron emission regime, where the emitting region is masked via the value of the Lorentz factor and the density, suitably chosen to correspond to the inner jet. The values used for masking the emitting region are obtained from analysis of the final state of the jet, so that the outer jet is ignored at all stages of the ray-casting procedure. The emission is connected to the frequency via a power law ~, where is the emission coefficient.
We will restrict our study to linear polarization only, as circular polarization is in most cases but a small fraction of the observed polarized emission.
Since we now ignore absorption, the unpolarized transfer equation reduces to:
In this case, only the total intensity is treated whereas for the linearly polarized case, Stokes are also taken into account.
The calculations are made in the co-moving frame, where the magnetic field is [
14]:
4. Discussion
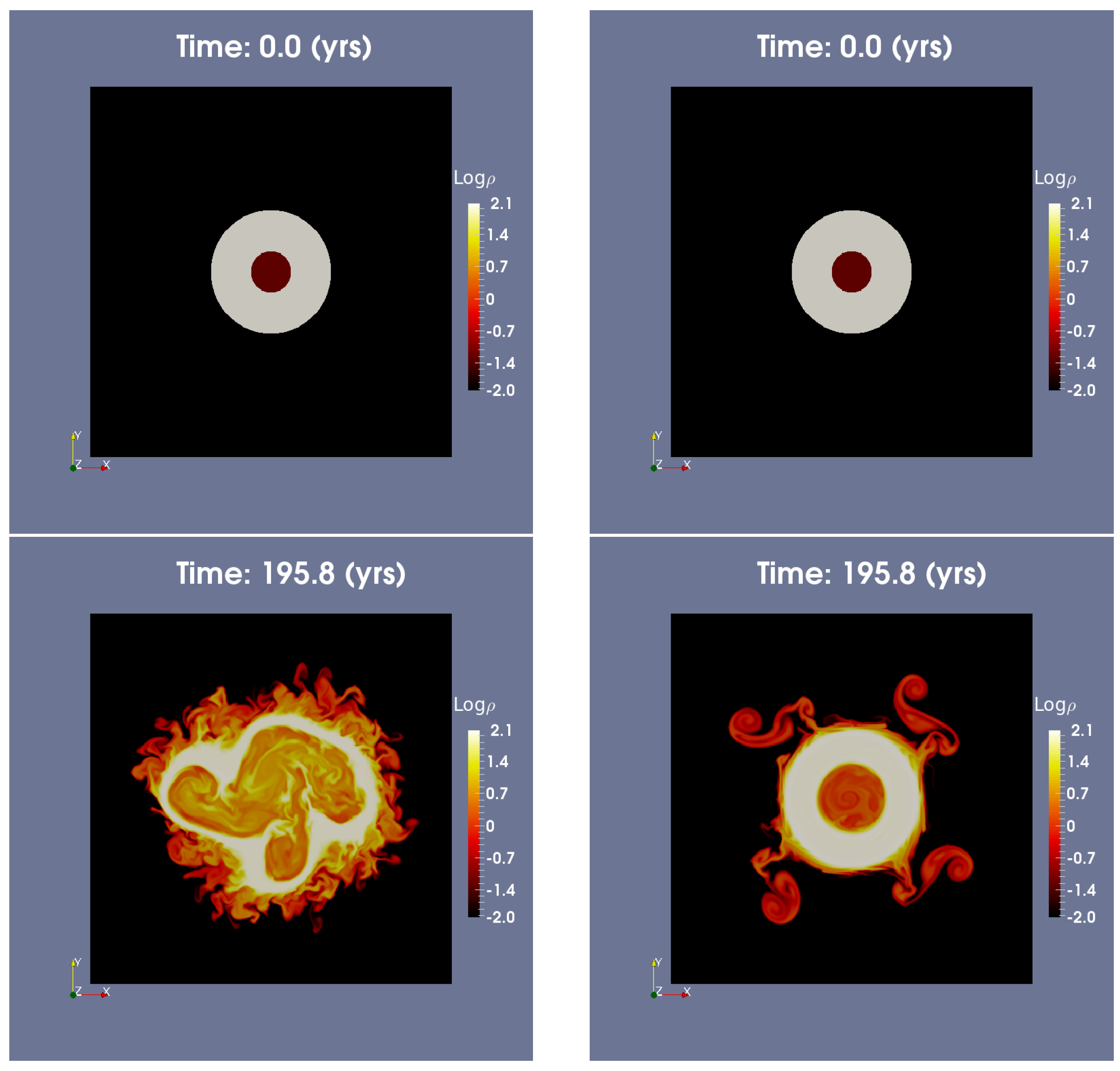
We find that the transverse stability (i.e., normal to the jet axis) of a two-component jet is associated with the magnetization of the outflow and by extension with the magnitude of the toroidal magnetic field component. Outflows with lower values of magnetization result in an unstable configuration, decollimation and finally a decelerating jet, while higher values lead to stability. For a more detailed presentation, see [
4].
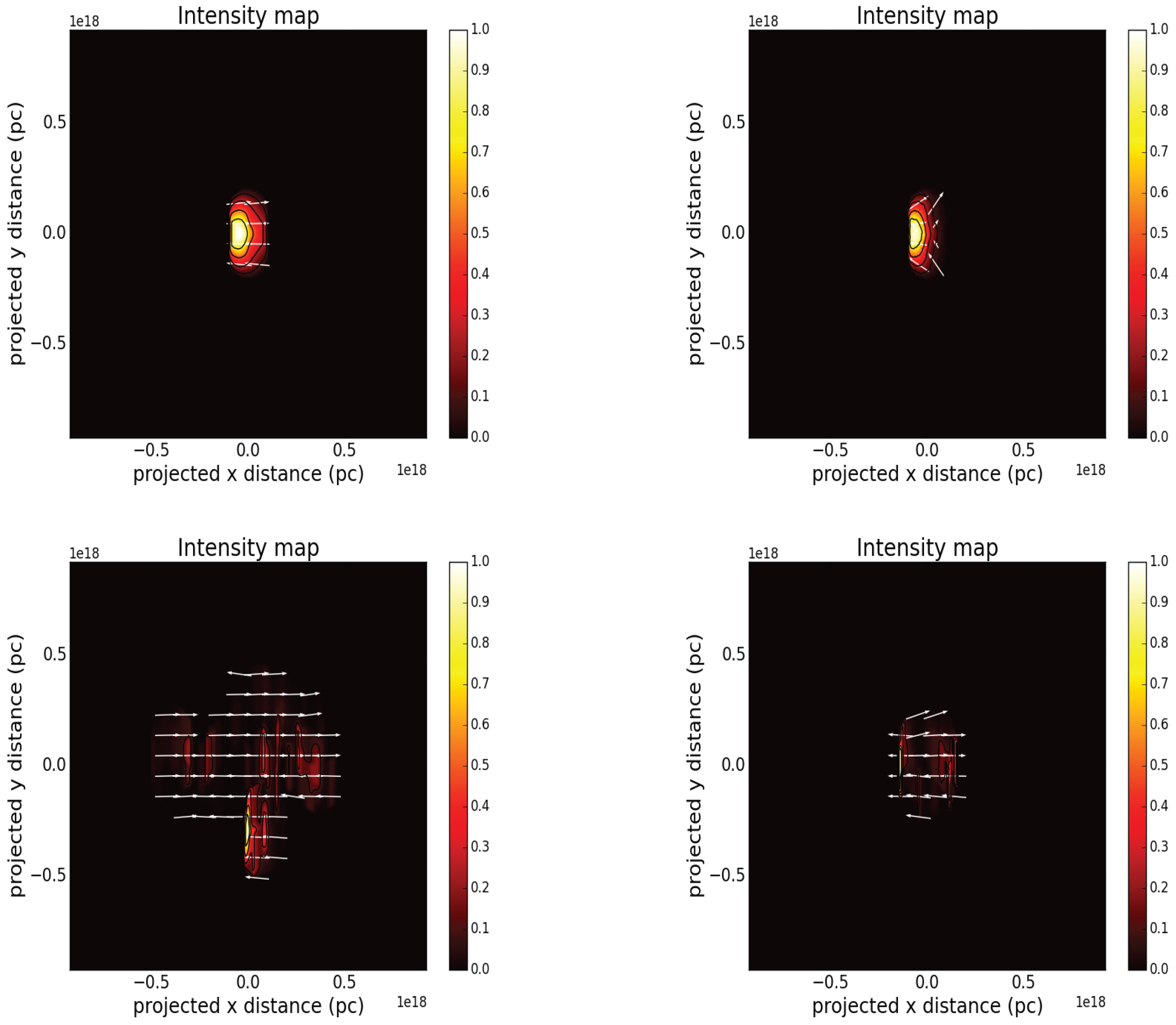
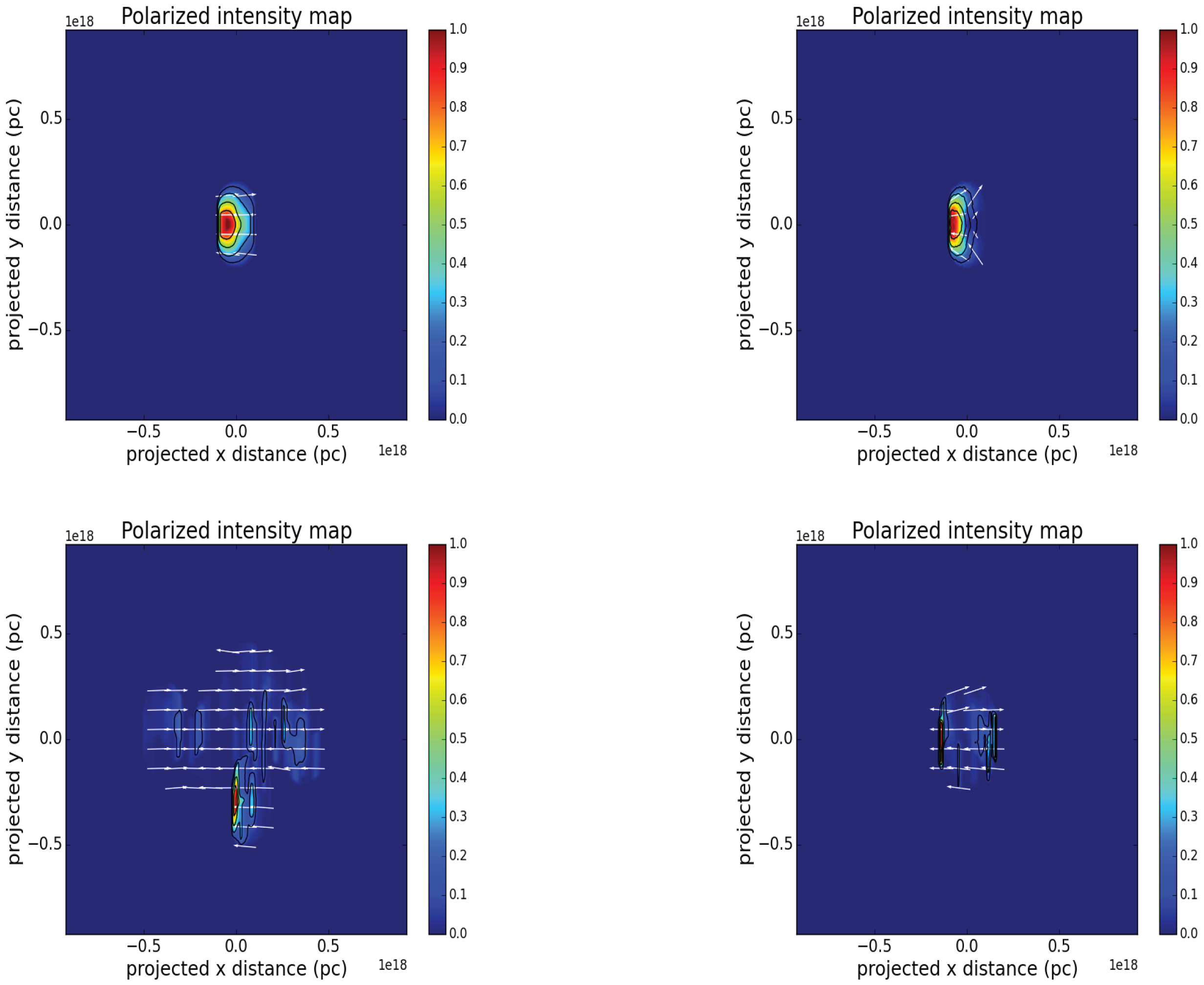
Post-processing the simulation data and using ray-casting reveals that these instabilities, as expected, have an effect on the emission. We examined linear polarization only, as observations show that circular polarization is only but a small fraction.
In the unstable case (with ), the emitting region is extended (as the inner jet also expands), with higher emission being detected in specific parts of the mixed region where the magnetic field is stronger. The stable case (with ) on the other hand, displays a more ordered, smaller emitting region, where again highest emission is located near the interface between the inner and the outer jet, due to the higher magnetic field magnitude.
Overall, we retrieve well known observed trends of AGN jets. This can be seen initially in terms of e.g., the distribution of EVPA. EVPAs, as seen in
Figure 2 and
Figure 3, are in general perpendicular to the jet axis or aligned to the flow (for larger viewing angles not shown here). In the case with
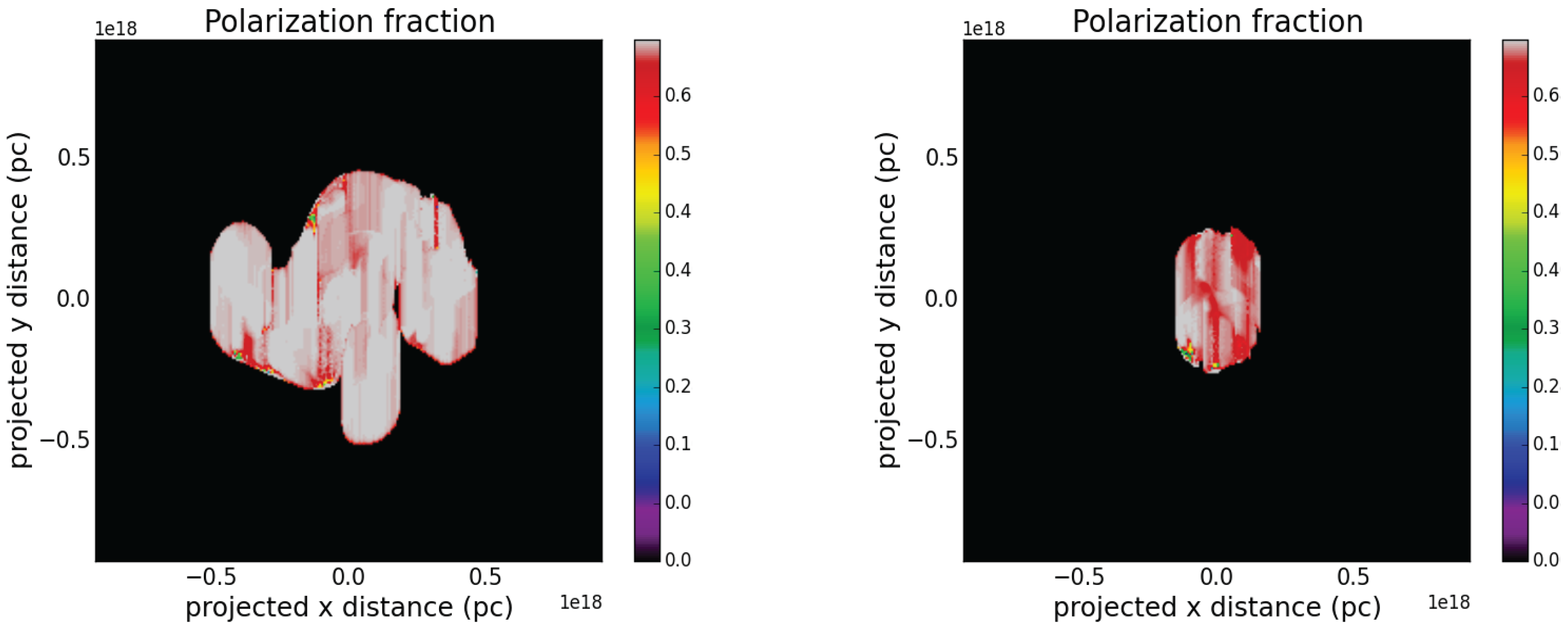
, we also notice a divergence in the direction of EVPAs. Finally, the maximum polarization fraction is ~70% for both cases.
Future work will focus on a more physically realistic approach in our ray-casting procedure, including absorption and Faraday rotation, for different frequencies and viewing angles. We also note that the almost uniform, close to the theoretical maximum value of the polarization fraction, might be due to integrating at a small viewing angle and requires further investigation, including a parametric study of different . The same methods will also be applied to already existing 3D simulation data.