Radiative Signatures of Parsec-Scale Magnetised Jets
Abstract
:1. Introduction
2. Methods
2.1. SRMHD Simulations
2.2. Radiative Transfer Calculations and Synthetic Imaging
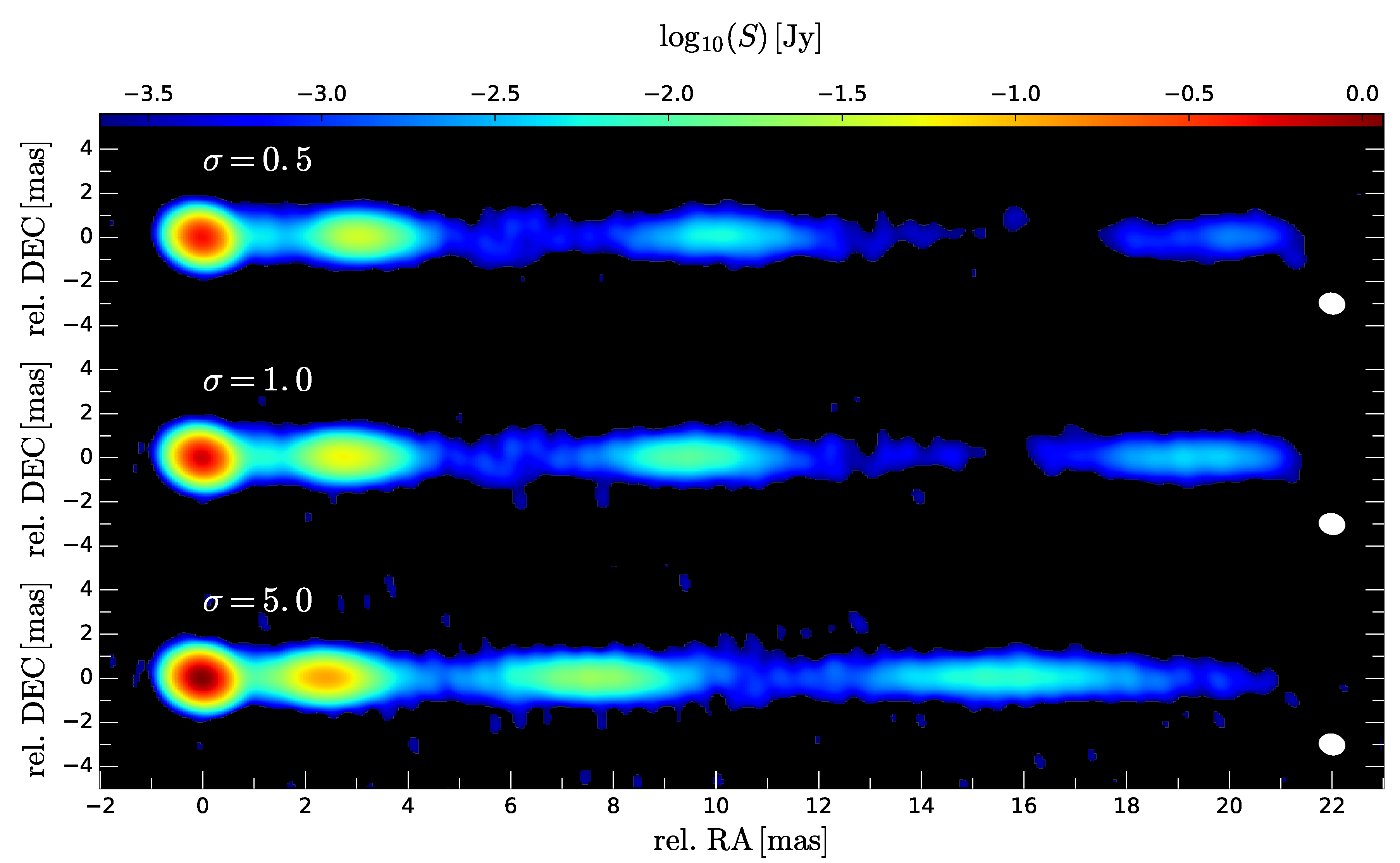
3. Results
4. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Marcaide, J.M.; Shapiro, I.I. High precision astrometry via very-long-baseline radio interferometry: Estimate of the angular separation between the quasars 1038+528A and B. Astroph. J. 1983, 88, 1133–1137. [Google Scholar] [CrossRef]
- Lobanov, A.P. Ultracompact jets in active galactic nuclei. Astron. Astrophys. 1998, 330, 79–89. [Google Scholar]
- Fromm, C.M.; Ros, E.; Perucho, M.; Savolainen, T.; Mimica, P.; Kadler, M.; Lobanov, A.P.; Zensus, J.A. Catching the radio flare in CTA 102. III. Core-shift and spectral analysis. Astron. Astrophys. 2013, 557, A105. [Google Scholar] [CrossRef]
- Gómez, J.L.; Marti, J.M.A.; Marscher, A.P.; Ibanez, J.M.A.; Marcaide, J.M. Parsec-Scale Synchrotron Emission from Hydrodynamic Relativistic Jets in Active Galactic Nuclei. Astrophys. J. Lett. 1995, 449, L19. [Google Scholar] [CrossRef]
- Mimica, P.; Aloy, M.-A.; Agudo, I.; Martí, J.M.; Gómez, J.L.; Miralles, J.A. Spectral Evolution of Superluminal Components in Parsec-Scale Jets. Astrophys. J. 2009, 696, 1142–1163. [Google Scholar] [CrossRef]
- Porth, O.; Fendt, C.; Meliani, Z.; Vaidya, B. Synchrotron Radiation of Self-collimating Relativistic Magnetohydrodynamic Jets. Astrophys. J. 2011, 737, 42. [Google Scholar] [CrossRef]
- Fromm, C.M.; Perucho, M.; Mimica, P.; Ros, E. Spectral evolution of flaring blazars from numerical simulations. Astron. Astrophys. 2016, 588, A101. [Google Scholar] [CrossRef]
- Rezzolla, L.; Zanotti, O. Relativistic Hydrodynamics; Oxford University Press: Oxford, UK, 2013; ISBN-10 0198528906. [Google Scholar]
- Keppens, R.; Meliani, Z.; van Marle, A.J.; Delmont, P.; Vlasis, A.; van der Holst, B. Parallel, grid-adaptive approaches for relativistic hydro and magnetohydrodynamics. J. Comput. Phys. 2011, 231, 718–744. [Google Scholar] [CrossRef]
- Porth, O.; Xia, C.; Hendrix, T.; Moschou, S.P.; Keppens, R. MPI-AMRVAC for Solar and Astrophysics. Astrophys. J. Suppl. Ser. 2014, 214, 4. [Google Scholar] [CrossRef]
- Komissarov, S.S.; Porth, O.; Lyutikov, M. Stationary relativistic jets. Comput. Astrophys. Cosmol. 2015, 1, 9. [Google Scholar] [CrossRef]
- Komissarov, S.S. Numerical simulations of relativistic magnetized jets. Mon. Not. R. Astron. Soc. 1999, 308, 1069–1076. [Google Scholar] [CrossRef]
- Shepherd, M.C. Difmap: An Interactive Program for Synthesis Imaging. Astron. Data Anal. Softw. Syst. VI 1997, 125, 77. [Google Scholar]
- Högbom, J.A. Aperture Synthesis with a Non-Regular Distribution of Interferometer Baselines. Astron. Astrophys. Suppl. 1974, 15, 417. [Google Scholar]
- Falle, S.A.E.G. Self-similar jets. Mon. Not. R. Astron. Soc. 1991, 250, 581–596. [Google Scholar] [CrossRef]
- Mizuno, Y.; Gómez, J.L.; Nishikawa, K.-I.; Meli, A.; Hardee, P.E.; Rezzolla, L. Recollimation Shocks in Magnetized Relativistic Jets. Astrophys. J. 2015, 809, 38. [Google Scholar] [CrossRef]
| 1. | Dashed values indicate the co-moving system. |
| 2. |

| 0.37 | 1.0 | 0.14 | 1.85 | 0.95 | 8.0 | 1.0 | 0.01 | 1.0 | 13/9 | 0.5 |
| 0.37 | 1.0 | 0.19 | 1.00 | 0.95 | 8.0 | 1.0 | 0.01 | 1.0 | 13/9 | 1.0 |
| 0.37 | 1.0 | 0.34 | 0.30 | 0.95 | 8.0 | 1.0 | 0.01 | 1.0 | 13/9 | 5.0 |
| s | z | ||||||
|---|---|---|---|---|---|---|---|
| 5 | 0.3 | 1.0 | 2.2 | 1.0 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fromm, C.M.; Porth, O.; Younsi, Z.; Mizuno, Y.; De Laurentis, M.; Olivares, H.; Rezzolla, L. Radiative Signatures of Parsec-Scale Magnetised Jets. Galaxies 2017, 5, 73. https://doi.org/10.3390/galaxies5040073
Fromm CM, Porth O, Younsi Z, Mizuno Y, De Laurentis M, Olivares H, Rezzolla L. Radiative Signatures of Parsec-Scale Magnetised Jets. Galaxies. 2017; 5(4):73. https://doi.org/10.3390/galaxies5040073
Chicago/Turabian StyleFromm, Christian M., Oliver Porth, Ziri Younsi, Yosuke Mizuno, Mariafelica De Laurentis, Hector Olivares, and Luciano Rezzolla. 2017. "Radiative Signatures of Parsec-Scale Magnetised Jets" Galaxies 5, no. 4: 73. https://doi.org/10.3390/galaxies5040073
APA StyleFromm, C. M., Porth, O., Younsi, Z., Mizuno, Y., De Laurentis, M., Olivares, H., & Rezzolla, L. (2017). Radiative Signatures of Parsec-Scale Magnetised Jets. Galaxies, 5(4), 73. https://doi.org/10.3390/galaxies5040073







