Evidence for Toroidal B-Field Components in AGN Jets on Kiloparsec Scales
Abstract
:1. Introduction
2. Results
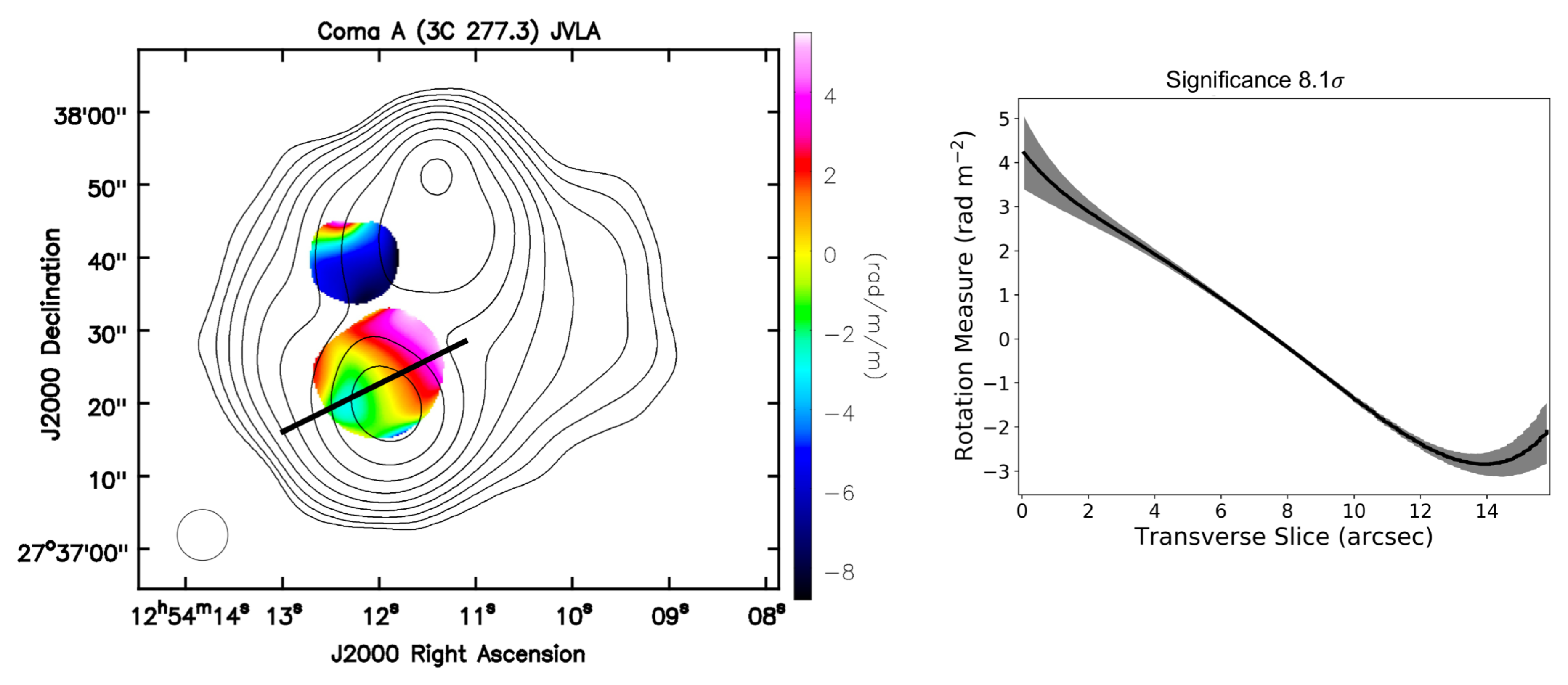
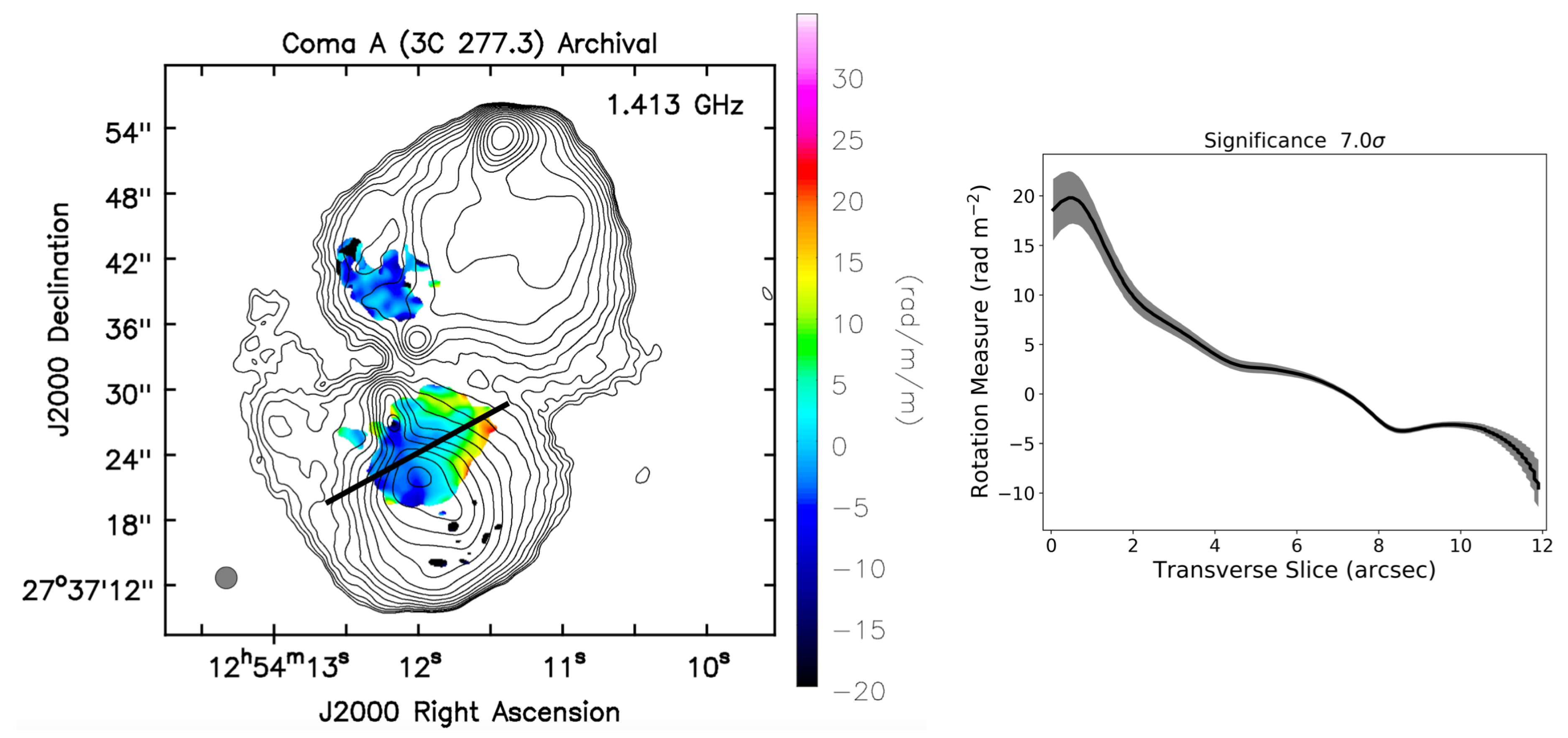
2.1. Coma A
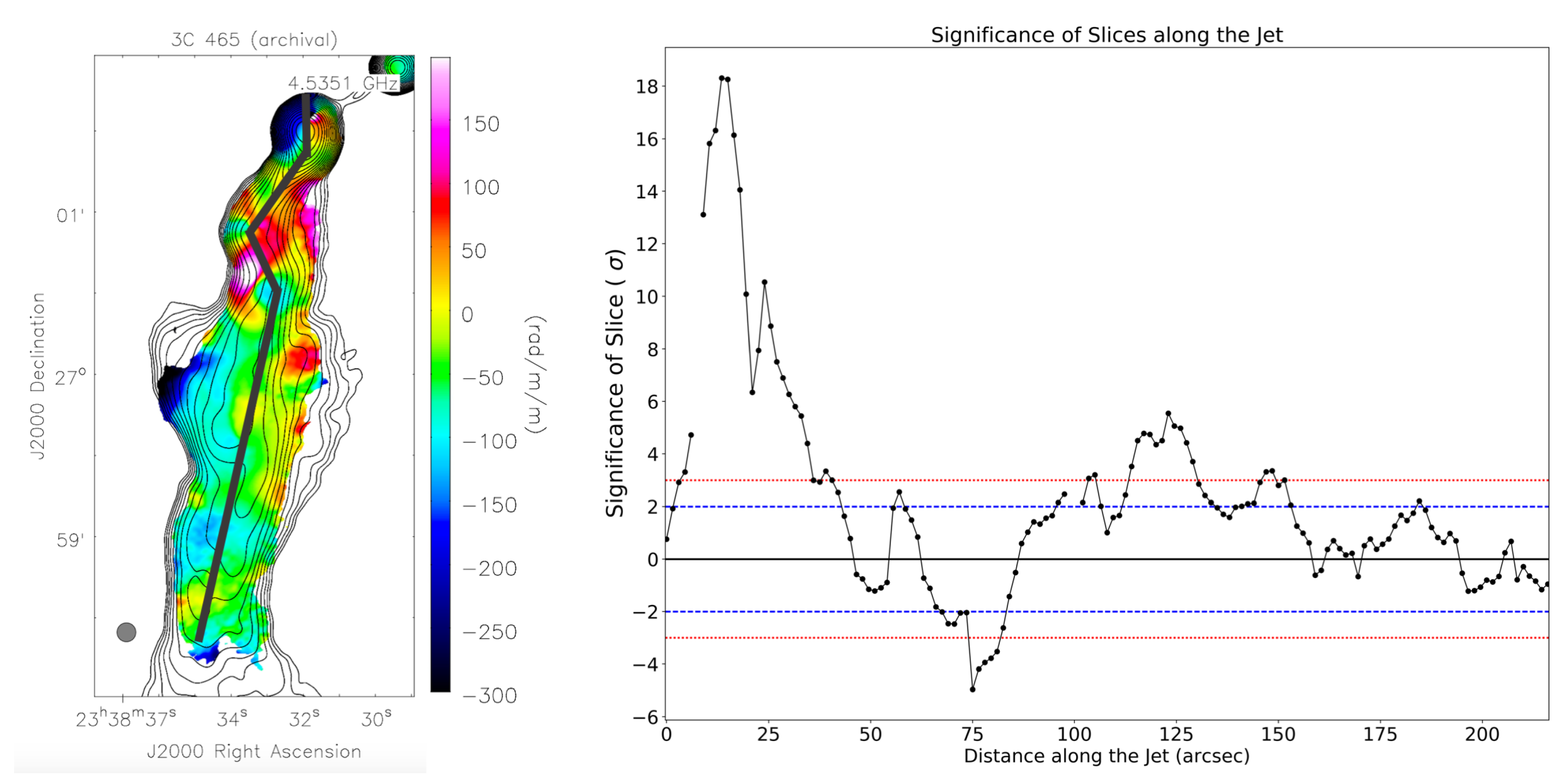
2.2. 3C 465
3. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| RM | Rotation Measure |
| AGN | Active Galactic Nucleus |
| VLBI | Very Long Baseline Interferometry |
| VLBA | Very Long Baseline Array |
| VLA | Very Large Array |
| JVLA | Jansky Very Large Array |
| NRAO | National Radio Astronomy Observatory |
| AIPS | Astronomical Image Processing System |
| CASA | Common Astronomy Software Applications |
References
- Pacholczyk, A.G. Radio Astrophysics. Nonthermal Processes in Galactic and Extragalactic Sources; W. H. Freeman: New York, NY, USA, 1970. [Google Scholar]
- Gabuzda, D.C.; Knuettel, S.; Bonafede, A. Evidence for a toroidal magnetic-field component in 5C 4.114 on kiloparsec scales. Astron. Astrophys. 2015, 583, A96. [Google Scholar] [CrossRef]
- Christodoulou, D.; Gabuzda, D.; Knuettel, S.; Contopoulos, I.; Kazanas, D.; Coughlan, C. Dominance of outflowing electric currents on decaparsec to kiloparsec scales in extragalactic jets. Astron. Astrophys. 2016. [Google Scholar] [CrossRef]
- Gabuzda, D.C.; Reichstein, A.R.; O’Neill, E.L. Are spine-sheath polarization structures in the jets of active galactic nuclei associated with helical magnetic fields? Mon. Not. R. Astron. Soc. 2014, 444, 172–184. [Google Scholar] [CrossRef]
- Gabuzda, D.C.; Knuettel, S.; Reardon, B. Transverse Faraday-rotation gradients across the jets of 15 active galactic nuclei. Mon. Not. R. Astron. Soc. 2015, 450, 2441–2450. [Google Scholar] [CrossRef]
- Bridle, A.H.; Fomalont, E.B.; Palimaka, J.J.; Willis, A.G. VLA observation of radio/optical knots in 3C 277.3 = Coma A. Astrophys. J. 1981, 248, 499–503. [Google Scholar] [CrossRef]
- Van Breugel, W.; Miley, G.; Heckman, T.; Butcher, H.; Bridle, A. Optical emission-line gas associated with the radio source 3C 277.3. Astrophys. J. 1985, 290, 496–500. [Google Scholar] [CrossRef]
- Taylor, A.R.; Stil, J.M.; Sunstrum, C. A Rotation Measure Image of the Sky. Astrophys. J. 2009, 702, 1230–1236. [Google Scholar] [CrossRef]
- Wegner, G.; Colless, M.; Saglia, R.P.; McMahan, J.R.K.; Davies, R.L.; Burstein, D.; Baggley, G. The peculiar motions of early-type galaxies in two distant regions—II. The spectroscopic data. Mon. Not. R. Astron. Soc. 1999, 305, 259–296. [Google Scholar] [CrossRef]
- Eilek, J.A.; Owen, F.N. Magnetic Fields in Cluster Cores: Faraday Rotation in A400 and A2634. Astrophys. J. 2002, 567, 202–220. [Google Scholar] [CrossRef]
- Contopoulos, I.; Christodoulou, D.M.; Kazanas, D.; Gabuzda, D.C. The Invariant Twist of Magnetic Fields in the Relativistic Jets of Active Galactic Nuclei. Astrophys. J. 2009, 702, L148–L152. [Google Scholar] [CrossRef]
| Project | MHz | MHz | Configuration | Approx Resolution | Observing Date | t h |
|---|---|---|---|---|---|---|
| VANB | 1413 | 25 | VLA A | 1.2″ | 18 March 1981 | 4.7 |
| VANB | 4885 | 50 | VLA B | 1.4″ | 1 June 1981 | 4.1 |
| AB348 | 14940 | 100 | VLA C | 2.0″ | 26 August 1985 | 6.2 |
| 13B-083 | 994–2006 | VLA B | 6.4″–3.2″ | 29 December 2013 | 1.8 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Knuettel, S.; Gabuzda, D.; O’Sullivan, S.P. Evidence for Toroidal B-Field Components in AGN Jets on Kiloparsec Scales. Galaxies 2017, 5, 61. https://doi.org/10.3390/galaxies5040061
Knuettel S, Gabuzda D, O’Sullivan SP. Evidence for Toroidal B-Field Components in AGN Jets on Kiloparsec Scales. Galaxies. 2017; 5(4):61. https://doi.org/10.3390/galaxies5040061
Chicago/Turabian StyleKnuettel, Sebastian, Denise Gabuzda, and Shane P. O’Sullivan. 2017. "Evidence for Toroidal B-Field Components in AGN Jets on Kiloparsec Scales" Galaxies 5, no. 4: 61. https://doi.org/10.3390/galaxies5040061
APA StyleKnuettel, S., Gabuzda, D., & O’Sullivan, S. P. (2017). Evidence for Toroidal B-Field Components in AGN Jets on Kiloparsec Scales. Galaxies, 5(4), 61. https://doi.org/10.3390/galaxies5040061






