Better Galactic Mass Models through Chemistry
Abstract
1. Introduction
2. Methods
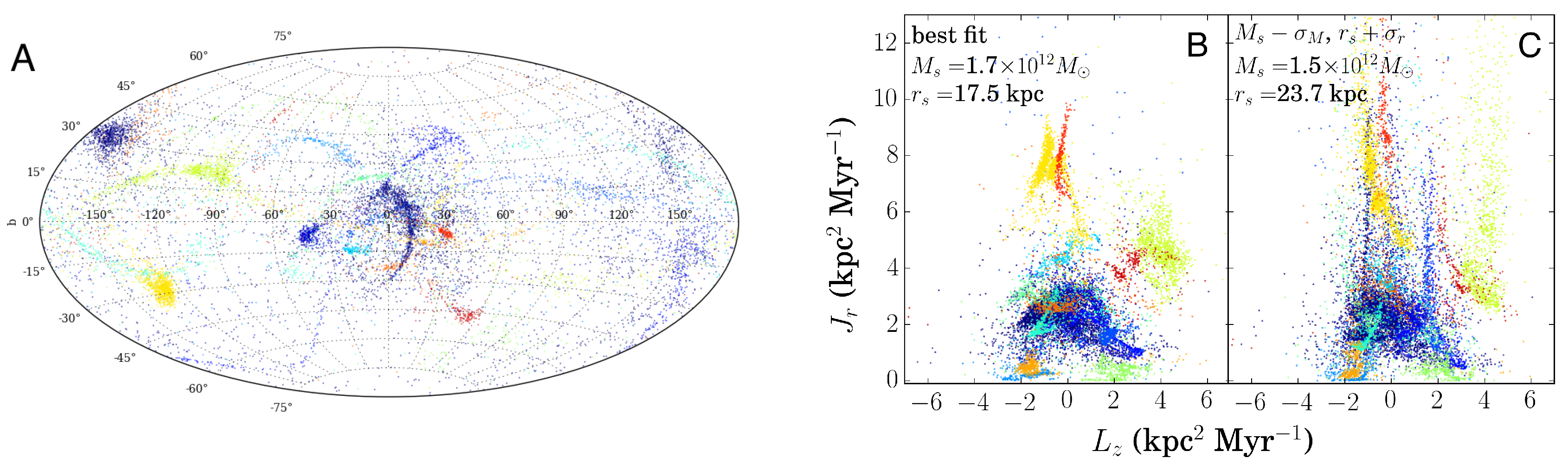
2.1. The Action Space of Stellar Orbits
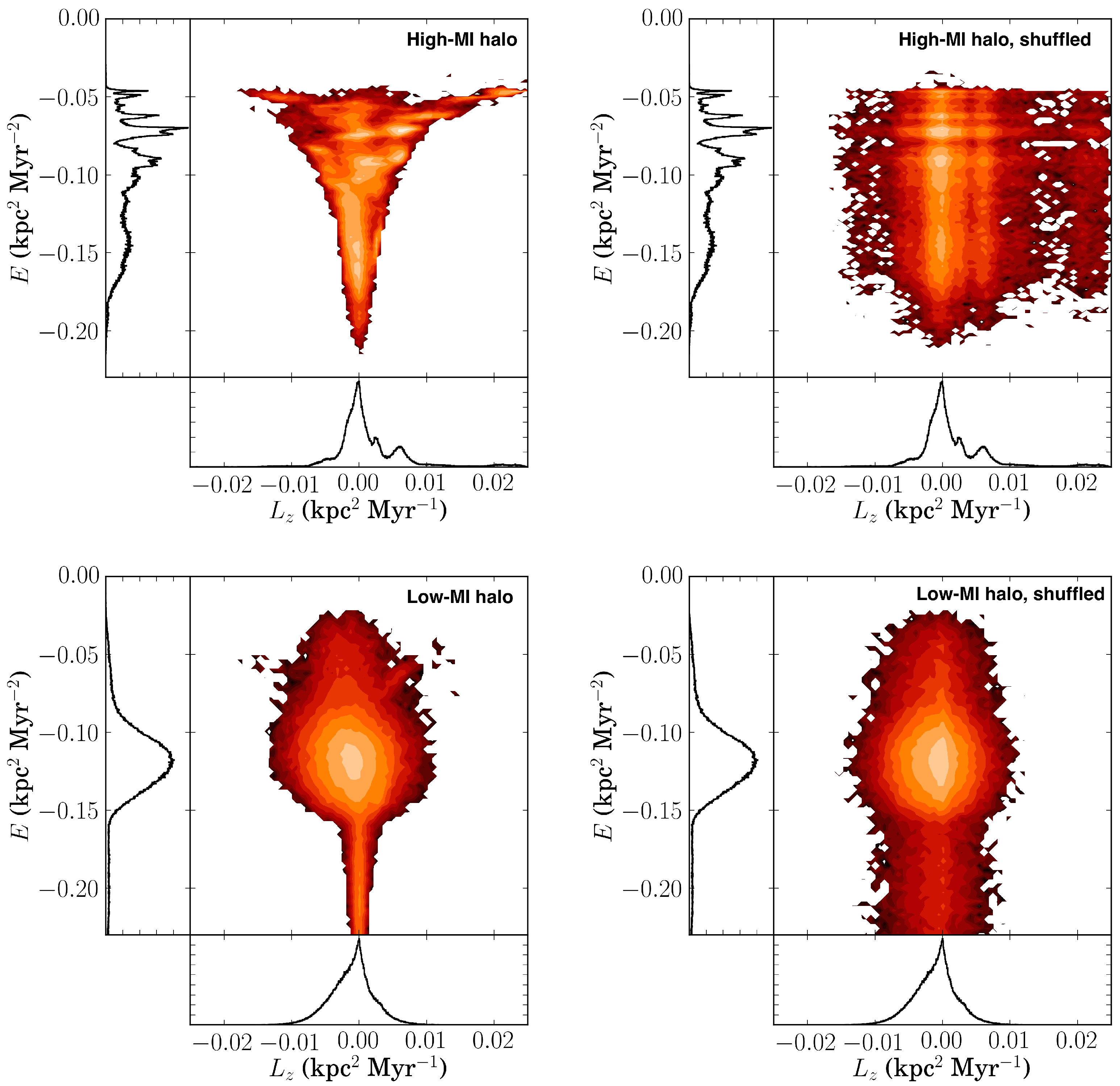
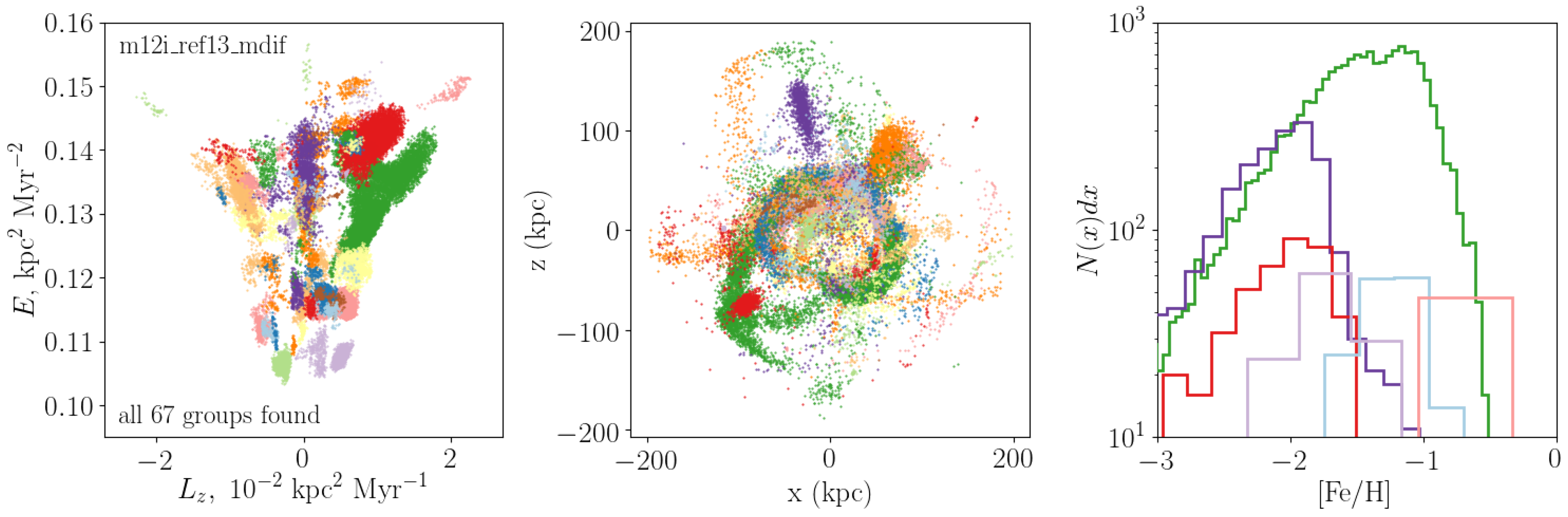
2.2. Measuring Clustering in Actions
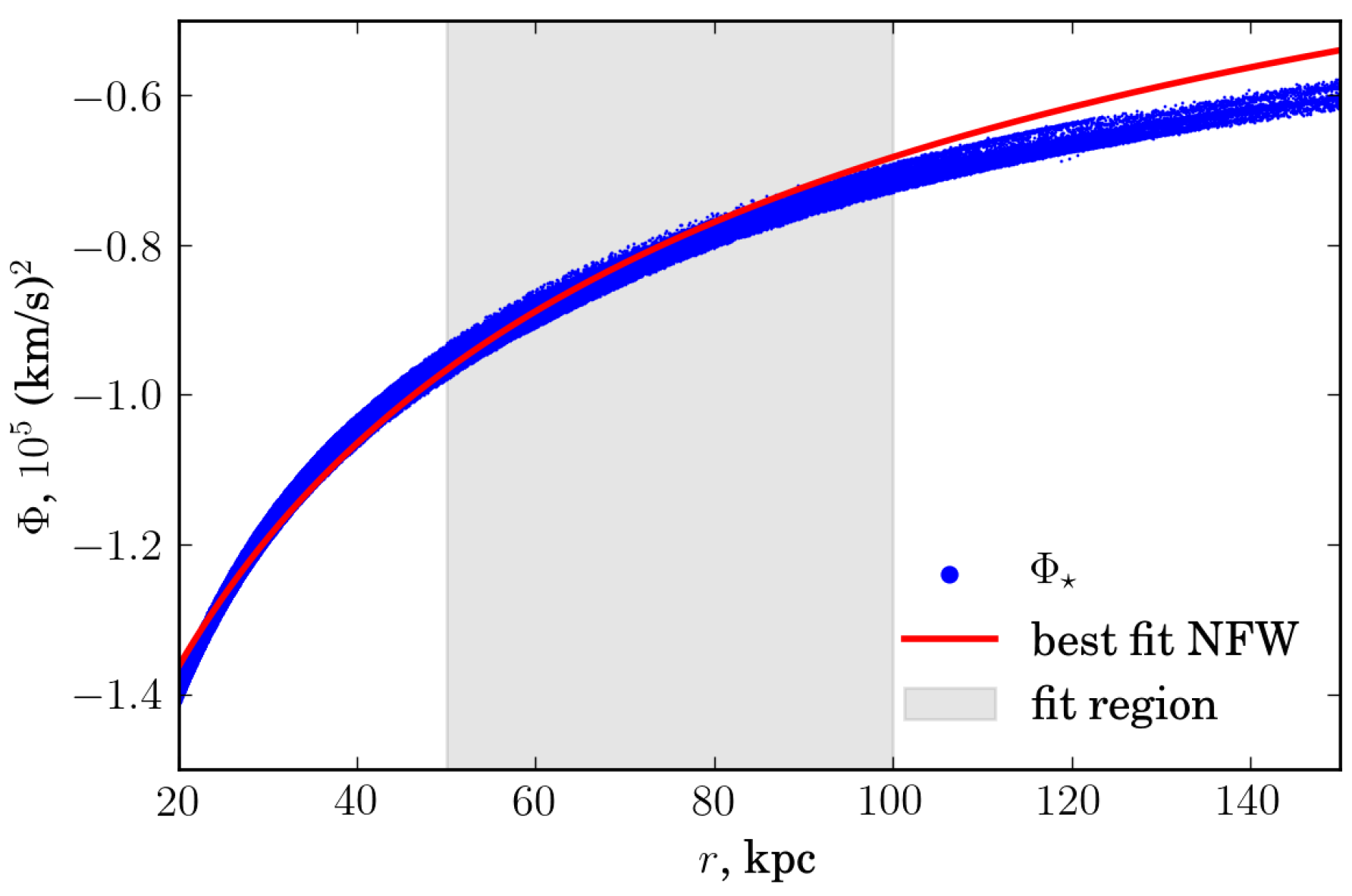
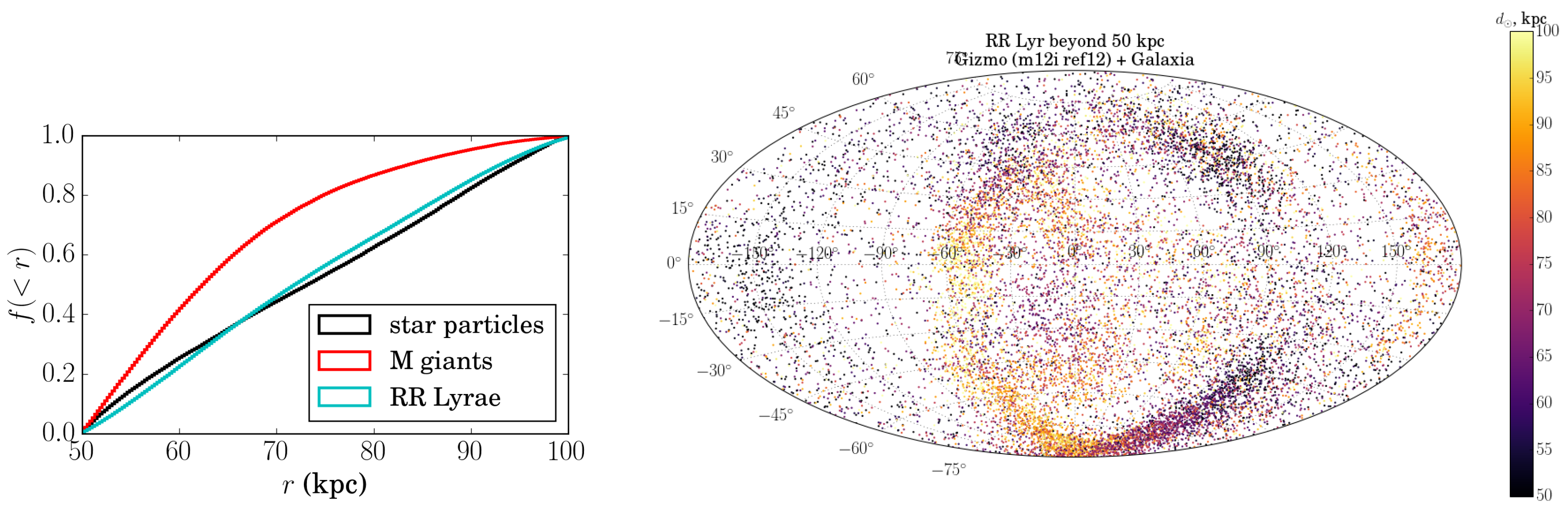
2.3. Simulating the Accreted Stellar Halo
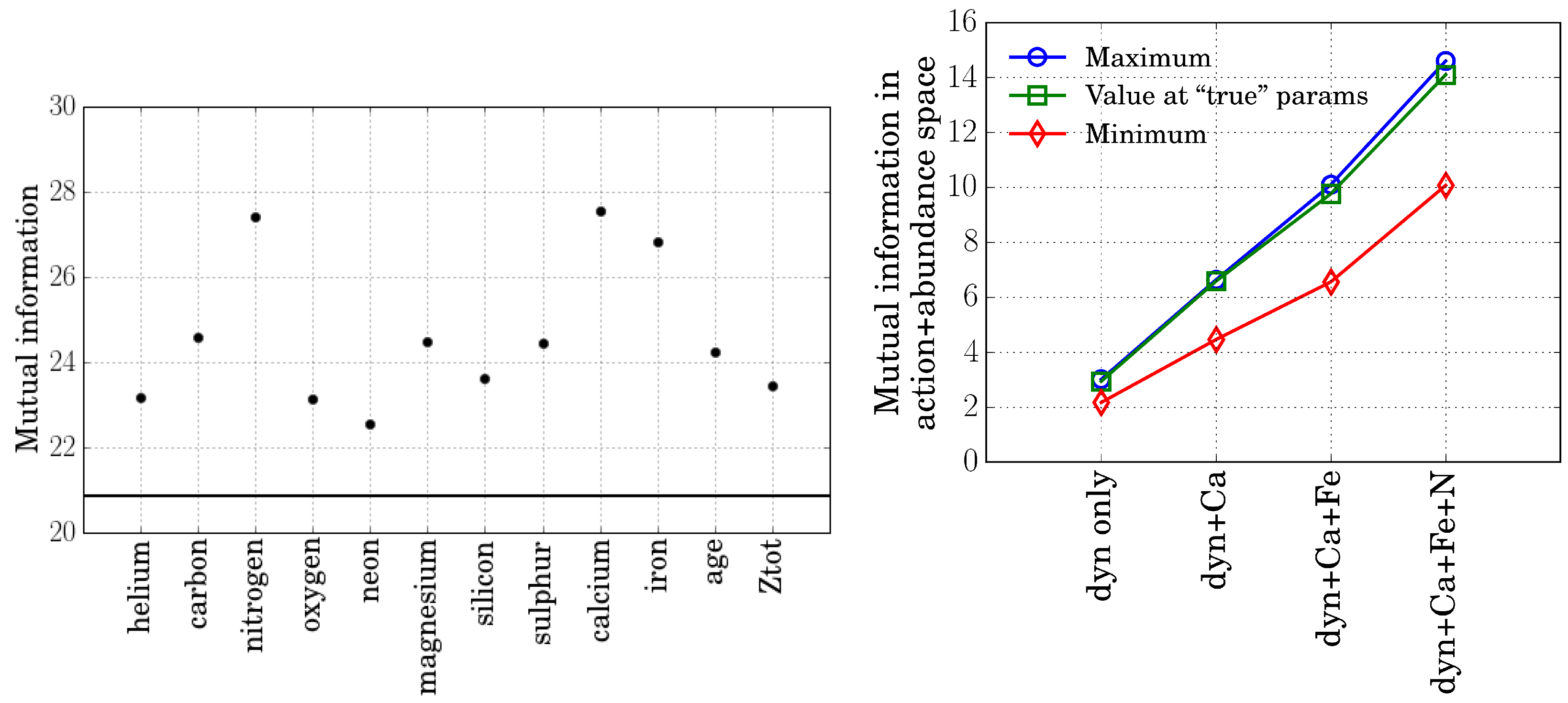
3. Results
4. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Chambers, K.C.; Magnier, E.A.; Metcalfe, N.; Flewelling, H.A.; Huber, M.E.; Waters, C.Z.; Denneau, L.; Draper, P.W.; Farrow, D.; Finkbeiner, D.P.; et al. The Pan-STARRS1 Surveys. arXiv 2016, arXiv:astro-ph.IM/1612.05560. [Google Scholar]
- LSST Science Collaboration; Abell, P.A.; Allison, J.; Anderson, S.F.; Andrew, J.R.; Angel, J.R.P.; Armus, L.; Arnett, D.; Asztalos, S.J.; Axelrod, T.S.; et al. LSST Science Book, Version 2.0. arXiv 2009, arXiv:astro-ph.IM/0912.0201. [Google Scholar]
- De Jong, R.S.; Bellido-Tirado, O.; Chiappini, C.; Depagne, É.; Haynes, R.; Johl, D.; Schnurr, O.; Schwope, A.; Walcher, J.; Dionies, F.; et al. 4MOST: 4-Metre Multi-Object Spectroscopic Telescope. In Proceedings of the SPIE Astronomical Instrumentation and Telescopes Conference, Amsterdam, The Netherlands, 1–6 July 2012; McLean, I.S., Ramsay, S.K., Takami, H., Eds.; SPIE: Bellingham, DC, USA, 2012; Volume 8446. [Google Scholar]
- Flaugher, B.; Bebek, C. The Dark Energy Spectroscopic Instrument (DESI). In Proceedings of the Ground-based and Airborne Instrumentation for Astronomy V, Montréal, QC, Canada, 22 June 2014; Ramsay, S.K., McLean, I.S., Takami, H., Eds.; SPIE: Bellingham, DC, USA, 2014; Volume 9147. [Google Scholar]
- Dalton, G.; Trager, S.C.; Abrams, D.C.; Carter, D.; Bonifacio, P.; Aguerri, J.A.L.; MacIntosh, M.; Evans, C.; Lewis, I.; Navarro, R.; et al. WEAVE: The next generation wide-field spectroscopy facility for the William Herschel Telescope. In Proceedings of the Ground-based and Airborne Instrumentation for Astronomy IV, Amsterdam, The Netherlands, 1 July 2012; Ramsay, S.K., Takami, H., Eds.; SPIE: Bellingham, DC, USA, 2012; Volume 8446. [Google Scholar]
- Chiba, M.; Cohen, J.; Wyse, R.F.G. Galactic Archaeology with the Subaru Prime Focus Spectrograph. In Proceedings of the International Astronomical Union, Honolulu, HI, USA, 3 August 2015; Bragaglia, A., Arnaboldi, M., Rejkuba, M., Romano, D., Eds.; IAU: Paris, France, 2016; Volume 317, pp. 280–281. [Google Scholar]
- Gaia Collaboration; Prusti, T.; de Bruijne, J.H.J.; Brown, A.G.A.; Vallenari, A.; Babusiaux, C.; Bailer-Jones, C.A.L.; Bastian, U.; Biermann, M.; Evans, D.W.; et al. The Gaia mission. Astron. Astrophys. 2016, 595, A1. [Google Scholar]
- Spergel, D.; Gehrels, D.; Baltay, C.; Bennett, D.; Breckinridge, J.; Donahue, M.; Dressler, A.; Gaudi, B.S.; Greene, T.; Guyon, O.; et al. Wide-Field InfrarRed Survey Telescope-Astrophysics Focused Telescope Assets WFIRST-AFTA 2015 Report. arXiv 2015, arXiv:1503.03757. [Google Scholar]
- Ness, M.; Hogg, D.W.; Rix, H.W.; Ho, A.Y.Q.; Zasowski, G. The Cannon: A data-driven approach to Stellar Label Determination. Astrophys. J. Suppl. Ser. 2015, 808, 21. [Google Scholar] [CrossRef]
- Alam, S.; Albareti, F.D.; Prieto, C.A.; Anders, F.; Anderson, S.F.; Andrews, B.H.; Armengaud, E.; Aubourg, E.; Bailey, S.; Bautista, J.E.; et al. The Eleventh and Twelfth Data Releases of the Sloan Digital Sky Survey: Final Data from SDSS-III. Astrophys. J. Suppl. Ser. 2015, 219, 27. [Google Scholar] [CrossRef]
- Martell, S.L.; Sharma, S.; Buder, S.; Duong, L.; Schlesinger, K.J.; Simpson, J.; Lind, K.; Ness, M.; Marshall, J.P.; Asplund, M.; et al. The GALAH survey: Observational overview and Gaia DR1 companion. Mon. Not. R. Astron. Soc. 2017, 465, 3203–3219. [Google Scholar] [CrossRef]
- Gilmore, G.; Randich, S.; Asplund, M.; Binney, J.; Bonifacio, P.; Drew, J.; Feltzing, S.; Ferguson, A.; Jeffries, R.; Micela, G.; et al. The Gaia-ESO Public Spectroscopic Survey. Messenger 2012, 147, 25–31. [Google Scholar]
- Sesar, B.; Hernitschek, N.; Dierickx, M.I.P.; Fardal, M.A.; Rix, H.W. The > 100 kpc Distant Spur of the Sagittarius Stream and the Outer Virgo Overdensity, as Seen in PS1 RR Lyrae Stars. arXiv 2017, arXiv:1706.10187. [Google Scholar] [CrossRef]
- Eadie, G.M.; Springford, A.; Harris, W.E. Bayesian Mass Estimates of the Milky Way: Including Measurement Uncertainties with Hierarchical Bayes. Astrophys. J. Suppl. Ser. 2017, 835, 167. [Google Scholar] [CrossRef]
- Law, D.R.; Majewski, S.R.; Johnston, K.V. Evidence for a Triaxial Milky Way Dark Matter Halo from the Sagittarius Stellar Tidal Stream. Astrophys. J. Suppl. Ser. 2009, 703, L67–L71. [Google Scholar] [CrossRef]
- Vera-Ciro, C.; Helmi, A. Constraints on the Shape of the Milky Way Dark Matter Halo from the Sagittarius Stream. Astrophys. J. Suppl. Ser. 2013, 773, L4. [Google Scholar] [CrossRef]
- Peñarrubia, J.; Gómez, F.A.; Besla, G.; Erkal, D.; Ma, Y.Z. A timing constraint on the (total) mass of the Large Magellanic Cloud. Mon. Not. R. Astron. Soc. 2016, 456, L54–L58. [Google Scholar] [CrossRef]
- Laporte, C.F.P.; Gómez, F.A.; Besla, G.; Johnston, K.V.; Garavito-Camargo, N. Response of the Milky Way’s disc to the Large Magellanic Cloud in a first infall scenario. arXiv 2016, arXiv:1608.04743. [Google Scholar]
- Mao, Y.Y.; Williamson, M.; Wechsler, R.H. The Dependence of Subhalo Abundance on Halo Concentration. Astrophys. J. Suppl. Ser. 2015, 810, 21. [Google Scholar] [CrossRef]
- Newberg, H.J.; Yanny, B.; Rockosi, C.; Grebel, E.K.; Rix, H.W.; Brinkmann, J.; Csabai, I.; Hennessy, G.; Hindsley, R.B.; Ibata, R.; et al. The Ghost of Sagittarius and Lumps in the Halo of the Milky Way. Astrophys. J. Suppl. Ser. 2002, 569, 245–274. [Google Scholar] [CrossRef]
- Bochanski, J.J.; Willman, B.; Caldwell, N.; Sanderson, R.; West, A.A.; Strader, J.; Brown, W. The Most Distant Stars in the Milky Way. Astrophys. J. Suppl. Ser. 2014, 790, L5. [Google Scholar] [CrossRef]
- Sanderson, R.E.; Secunda, A.; Johnston, K.V.; Bochanski, J.J. New views of the distant stellar halo. Mon. Not. R. Astron. Soc. 2017, in press. [Google Scholar] [CrossRef]
- Arnold, V.I.; Shandarin, S.F.; Zeldovich, I.B. The large scale structure of the universe. I - General properties One- and two-dimensional models. Geophys. Astrophys. Fluid Dyn. 1982, 20, 111–130. [Google Scholar] [CrossRef]
- Binney, J.; Tremaine, S. Galactic Dynamics, 2nd ed.; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Goldstein, H.; Poole, C.; Safko, J. Classical Mechanics, 3rd ed.; Addison Wesley: Boston, MA, USA, 2002. [Google Scholar]
- Sanderson, R.E.; Helmi, A.; Hogg, D.W. Action-space Clustering of Tidal Streams to Infer the Galactic Potential. Astrophys. J. Suppl. Ser. 2015, 801, 98. [Google Scholar] [CrossRef]
- Sanderson, R.E.; Hartke, J.; Helmi, A. Modeling the Gravitational Potential of a Cosmological Dark Matter Halo with Stellar Streams. Astrophys. J. Suppl. Ser. 2017, 836, 234. [Google Scholar] [CrossRef]
- Helmi, A.; White, S.D.M. Building up the stellar halo of the Galaxy. Mon. Not. R. Astron. Soc. 1999, 307, 495–517. [Google Scholar] [CrossRef]
- Helmi, A.; de Zeeuw, P.T. Mapping the substructure in the Galactic halo with the next generation of astrometric satellites. Mon. Not. R. Astron. Soc. 2000, 319, 657–665. [Google Scholar] [CrossRef]
- Sharma, S.; Johnston, K.V.; Majewski, S.R.; Muñoz, R.R.; Carlberg, J.K.; Bullock, J. Group Finding in the Stellar Halo Using M-giants in the Two Micron All Sky Survey: An Extended View of the Pisces Overdensity? Astrophys. J. Suppl. Ser. 2010, 722, 750–759. [Google Scholar] [CrossRef]
- Gómez, F.A.; Helmi, A.; Brown, A.G.A.; Li, Y.S. On the identification of merger debris in the Gaia era. Mon. Not. R. Astron. Soc. 2010, 408, 935–946. [Google Scholar] [CrossRef]
- Cooper, A.P.; Cole, S.; Frenk, C.S.; White, S.D.M.; Helly, J.; Benson, A.J.; De Lucia, G.; Helmi, A.; Jenkins, A.; Navarro, J.F.; et al. Galactic stellar haloes in the CDM model. Mon. Not. R. Astron. Soc. 2010, 406, 744–766. [Google Scholar] [CrossRef]
- Peñarrubia, J.; Koposov, S.E.; Walker, M.G. A Statistical Method for Measuring the Galactic Potential and Testing Gravity with Cold Tidal Streams. Astrophys. J. Suppl. Ser. 2012, 760, 2. [Google Scholar] [CrossRef]
- Magorrian, J. Bayes versus the virial theorem: Inferring the potential of a galaxy from a kinematical snapshot. Mon. Not. R. Astron. Soc. 2014, 437, 2230–2248. [Google Scholar] [CrossRef]
- Sanderson, R.E. Inferring the Galactic Potential with GAIA and Friends: Synergies with Other Surveys. Astrophys. J. Suppl. Ser. 2016, 818, 41. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On Information and Sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Sharma, S.; Johnston, K.V. A Group Finding Algorithm for Multidimensional Data Sets. Astrophys. J. Suppl. Ser. 2009, 703, 1061–1077. [Google Scholar] [CrossRef]
- Wetzel, A.R.; Hopkins, P.F.; Kim, J.H.; Faucher-Giguère, C.A.; Kereš, D.; Quataert, E. Reconciling Dwarf Galaxies with ΛCDM Cosmology: Simulating a Realistic Population of Satellites around a Milky Way-mass Galaxy. Astrophys. J. Lett. 2016, 827, L23. [Google Scholar] [CrossRef]
- Hopkins, P.F.; Wetzel, A.; Keres, D.; Faucher-Giguere, C.A.; Quataert, E.; Boylan-Kolchin, M.; Murray, N.; Hayward, C.C.; Garrison-Kimmel, S.; Hummels, C.; et al. FIRE-2 Simulations: Physics versus Numerics in Galaxy Formation. arXiv 2017, arXiv:1702.06148. [Google Scholar]
- Navarro, J.F.; Frenk, C.S.; White, S.D.M. The Structure of Cold Dark Matter Halos. Astrophys. J. Suppl. Ser. 1996, 462, 563. [Google Scholar] [CrossRef]
- Beaton, R.L.; Freedman, W.L.; Madore, B.F.; Bono, G.; Carlson, E.K.; Clementini, G.; Durbin, M.J.; Garofalo, A.; Hatt, D.; Jang, I.S.; et al. The Carnegie-Chicago Hubble Program. I. An Independent Approach to the Extragalactic Distance Scale Using Only Population II Distance Indicators. Astrophys. J. Suppl. Ser. 2016, 832, 210. [Google Scholar] [CrossRef]
- Sharma, S.; Bland-Hawthorn, J.; Johnston, K.V.; Binney, J. Galaxia: A Code to Generate a Synthetic Survey of the Milky Way. Astrophys. J. Suppl. Ser. 2011, 730, 3. [Google Scholar] [CrossRef]
- Bressan, A.; Marigo, P.; Girardi, L.; Salasnich, B.; Dal Cero, C.; Rubele, S.; Nanni, A. PARSEC: Stellar tracks and isochrones with the PAdova and TRieste Stellar Evolution Code. Mon. Not. R. Astron. Soc. 2012, 427, 127–145. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sanderson, R.E.; Wetzel, A.R.; Sharma, S.; Hopkins, P.F. Better Galactic Mass Models through Chemistry. Galaxies 2017, 5, 43. https://doi.org/10.3390/galaxies5030043
Sanderson RE, Wetzel AR, Sharma S, Hopkins PF. Better Galactic Mass Models through Chemistry. Galaxies. 2017; 5(3):43. https://doi.org/10.3390/galaxies5030043
Chicago/Turabian StyleSanderson, Robyn E., Andrew R. Wetzel, Sanjib Sharma, and Philip F. Hopkins. 2017. "Better Galactic Mass Models through Chemistry" Galaxies 5, no. 3: 43. https://doi.org/10.3390/galaxies5030043
APA StyleSanderson, R. E., Wetzel, A. R., Sharma, S., & Hopkins, P. F. (2017). Better Galactic Mass Models through Chemistry. Galaxies, 5(3), 43. https://doi.org/10.3390/galaxies5030043





