Distribution and Evolution of Metals in the Magneticum Simulations
Abstract
1. Introduction
2. Chemical Enrichment
2.1. Initial Mass Function
2.2. Lifetime Functions
2.3. Stellar Yields
2.4. Modeling the Enrichment Process
2.4.1. Type Ia Supernovae
2.4.2. Supernovae Type II, Low-, and Intermediate-Mass Stars
2.4.3. The Equations of Chemical Enrichment
3. The Magneticum Simulations
4. Metallicities from Magneticum in Comparison to Observations
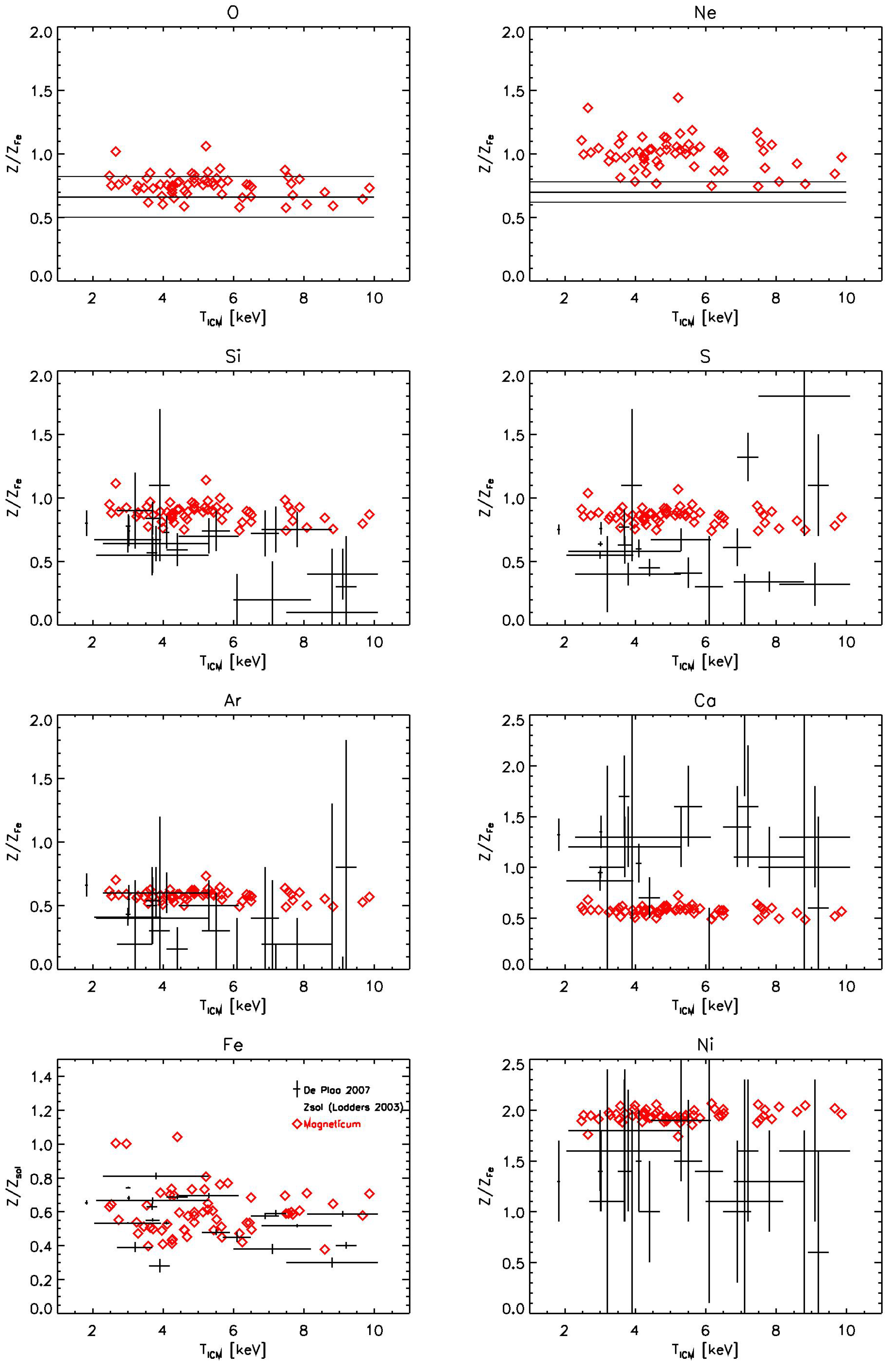
4.1. Galaxy Clusters: ICM Metallicities
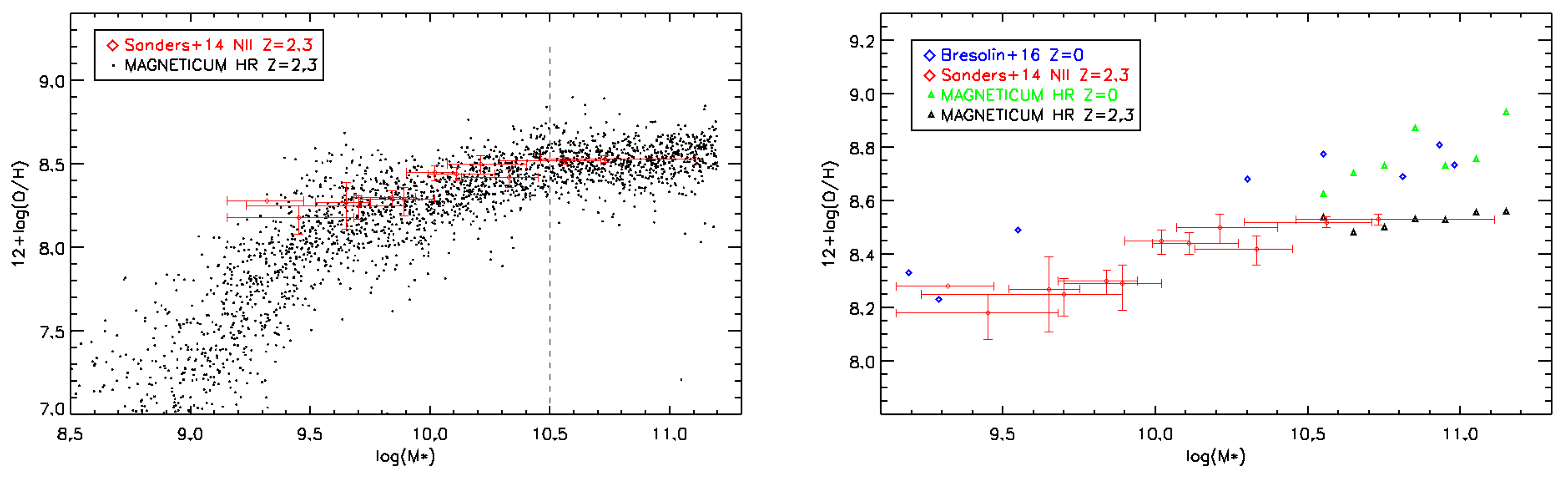
4.2. Galaxies: Gas Metallicities
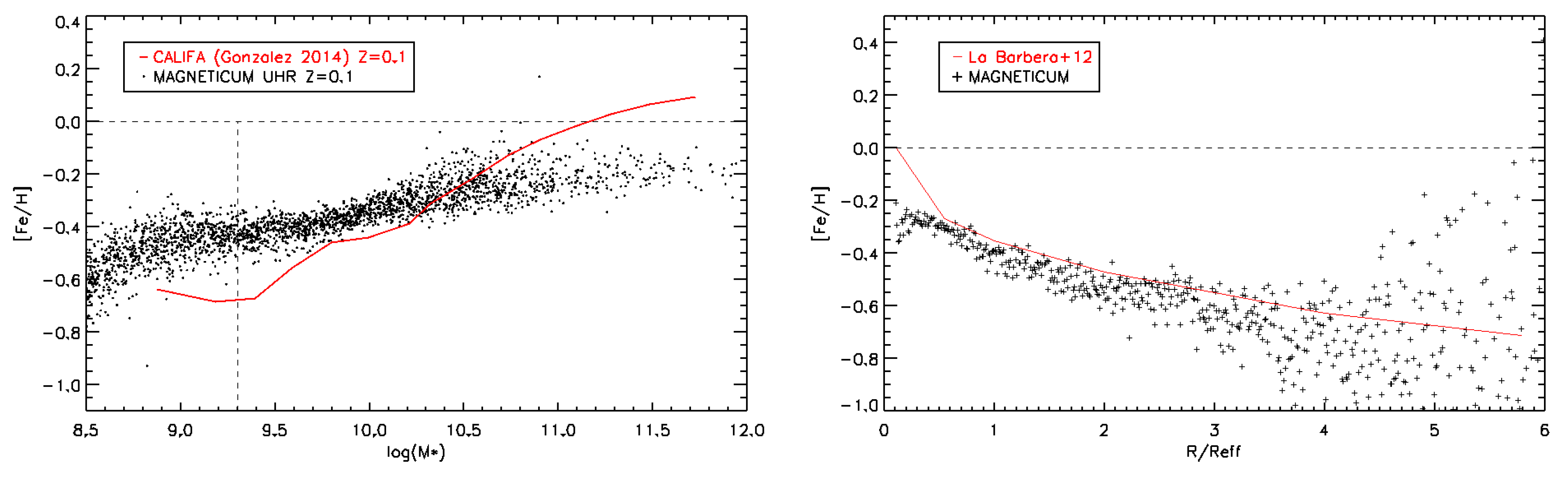
4.3. Galaxies: Stellar Metallicities
5. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Dolag, K. Hydrodynamic Methods for Cosmological Simulations. In The Encyclopedia of Cosmology; Fazio, G.G., Ed.; World Scientific: Singapore, 2017; Volume 2. [Google Scholar]
- Matteucci, F. The Chemical Evolution of the Galaxy; Springer: Houten, Netherlands, 2003. [Google Scholar]
- Borgani, S.; Fabjan, D.; Tornatore, L.; Schindler, S.; Dolag, K.; Diaferio, A. The Chemical Enrichment of the ICM from Hydrodynamical Simulations. Space Sci. Rev. 2008, 134, 379–403. [Google Scholar] [CrossRef]
- Salpeter, E.E. The Luminosity Function and Stellar Evolution. Astrophys. J. 1955, 121, 161–167. [Google Scholar] [CrossRef]
- Chabrier, G. Galactic Stellar and Substellar Initial Mass Function. Publ. Astron. Soc. Pac. 2003, 115, 763–795. [Google Scholar] [CrossRef]
- Padovani, P.; Matteucci, F. Stellar Mass Loss in Elliptical Galaxies and the Fueling of Active Galactic Nuclei. Astrophys. J. 1993, 416, 26. [Google Scholar] [CrossRef]
- Maeder, A.; Meynet, G. Grids of evolutionary models from 0.85 to 120 solar masses—Observational tests and the mass limits. Astron. Astrophys. 1989, 210, 155–173. [Google Scholar]
- Chiappini, C.; Matteucci, F.; Gratton, R. The Chemical Evolution of the Galaxy: The Two-Infall Model. Astrophys. J. 1997, 477, 765–780. [Google Scholar] [CrossRef]
- Karakas, A.; Lattanzio, J.C. Stellar Models and Yields of Asymptotic Giant Branch Stars. Publ. Astron. Soc. Pac. 2007, 24, 103–117. [Google Scholar] [CrossRef]
- Nomoto, K.; Kobayashi, C.; Tominaga, N. Nucleosynthesis in Stars and the Chemical Enrichment of Galaxies. Ann. Rev. Astron. Astrophys. 2013, 51, 457–509. [Google Scholar] [CrossRef]
- Thielemann, F.K.; Argast, D.; Brachwitz, F.; Hix, W.R.; Höflich, P.; Liebendörfer, M.; Martinez-Pinedo, G.; Mezzacappa, A.; Nomoto, K.; Panov, I. Supernova Nucleosynthesis and Galactic Evolution. In From Twilight to Highlight: The Physics of Supernovae; Hillebrandt, W., Leibundgut, B., Eds.; Springer: Berlin, Germany, 2003; p. 331. [Google Scholar]
- Greggio, L.; Renzini, A. The binary model for type I supernovae—Theoretical rates. Astron. Astrophys. 1983, 118, 217–222. [Google Scholar]
- Greggio, L. The rates of type Ia supernovae. I. Analytical formulations. Astron. Astrophys. 2005, 441, 1055–1078. [Google Scholar] [CrossRef]
- Matteucci, F.; Gibson, B.K. Chemical abundances in clusters of galaxies. Astron. Astrophys. 1995, 304, 11. [Google Scholar]
- Matteucci, F.; Greggio, L. Relative roles of type I and II supernovae in the chemical enrichment of the interstellar gas. Astron. Astrophys. 1986, 154, 279–287. [Google Scholar]
- Bocquet, S.; Saro, A.; Dolag, K.; Mohr, J.J. Halo mass function: baryon impact, fitting formulae, and implications for cluster cosmology. Mon. Not. R. Astron. Soc. 2016, 456, 2361–2373. [Google Scholar] [CrossRef]
- Pollina, G.; Hamaus, N.; Dolag, K.; Weller, J.; Baldi, M.; Moscardini, L. On the linearity of tracer bias around voids. Mon. Not. R. Astron. Soc. 2017, 469, 787–799. [Google Scholar] [CrossRef]
- Teklu, A.F.; Remus, R.S.; Dolag, K.; Beck, A.M.; Burkert, A.; Schmidt, A.S.; Schulze, F.; Steinborn, L.K. Connecting Angular Momentum and Galactic Dynamics: The Complex Interplay between Spin, Mass, and Morphology. Astrophys. J. 2015, 812, 29. [Google Scholar] [CrossRef]
- Remus, R.S.; Dolag, K.; Naab, T.; Burkert, A.; Hirschmann, M.; Hoffmann, T.L.; Johansson, P.H. The co-evolution of total density profiles and central dark matter fractions in simulated early-type galaxies. Mon. Not. R. Astron. Soc. 2017, 464, 3742–3756. [Google Scholar] [CrossRef]
- Hirschmann, M.; Dolag, K.; Saro, A.; Bachmann, L.; Borgani, S.; Burkert, A. Cosmological simulations of black hole growth: AGN luminosities and downsizing. Mon. Not. R. Astron. Soc. 2014, 442, 2304–2324. [Google Scholar] [CrossRef]
- Biffi, V.; Planelles, S.; Borgani, S.; Fabjan, D.; Rasia, E.; Murante, G.; Tornatore, L.; Dolag, K.; Granato, G.L.; Gaspari, M.; et al. The history of chemical enrichment in the intracluster medium from cosmological simulations. Mon. Not. R. Astron. Soc. 2017, 468, 531–548. [Google Scholar] [CrossRef]
- Santini, P.; Maiolino, R.; Magnelli, B.; Lutz, D.; Lamastra, Z.; Li Causi, G.; Eales, S.; Andreani, P.; Berta, S.; Buat, V.; et al. The evolution of the dust and gas content in galaxies. Astron. Astrophys. 2014, 562, A30. [Google Scholar] [CrossRef]
- De Plaa, J.; Werner, N.; Bleeker, J.A.M.; Vink, J.; Kaastra, J.S.; Méndez, M. Constraining supernova models using the hot gas in clusters of galaxies. Astron. Astrophys. 2007, 465, 345–355. [Google Scholar] [CrossRef]
- Teklu, A.F.; Remus, R.S.; Dolag, K.; Burkert, A. The Morphology-Density-Relation: Impact on the Satellite Fraction. ArXiv, 2017; arXiv:1702.06546. [Google Scholar]
- Sanders, R.L.; Shapley, A.E.; Kriek, M.; Reddy, N.A.; Freeman, W.R.; Coil, A.L.; Siana, B.; Mobasher, B.; Shivaei, I.; Price, S.H.; et al. The MOSDEF Survey: Mass, Metallicity, and Star-formation Rate at z ∼ 2.3. Astrophys. J. 2015, 799, 138. [Google Scholar] [CrossRef]
- Bresolin, F.; Kudritzki, R.; Urbaneja, M.A.; Gieren, W.; Ho, I.; Pietrzyński, G. Young stars and ionized nebulae in M83: Comparing chemical abundances at high metallicity. Astrophys. J. 2016, 830, 64–85. [Google Scholar] [CrossRef]
- González Delgado, R.M.; Cid Fernandes, R.; Garcia-Benito, R.; Perez, E.; de Amorim, A.L.; Cortijo-Ferrero, C.; Lacerda, E.A.D.; Lopez Fernandez, R.; Sanchez, S.F.; Vale Asari, N.; et al. Insights on the Stellar Mass-Metallicity Relation from the CALIFA Survey. Astrophys. J. 2014, 791, L16. [Google Scholar] [CrossRef]
- Remus, R.S.; Dolag, K.; Bachmann, L.K.; Beck, A.M.; Burkert, A.; Hirschmann, M.; Teklu, A. Disk Galaxies in the Magneticum Pathfinder Simulations. In Galaxies in 3D across the Universe, Proceedings of the International Astronomical Union (IAU) Symposium, Vienna, Austria, 7–11 July 2014; Ziegler, B.L., Combes, F., Dannerbauer, H., Verdugo, M., Eds.; Cambridge University Press: Cambridge, UK, 2015; Volume 309, pp. 145–148. [Google Scholar]
- Pastorello, N.; Forbes, D.A.; Foster, C.; Brodie, J.P.; Usher, C.; Romanowsky, A.J.; Strader, J.; Arnold, J.A. The SLUGGS survey: exploring the metallicity gradients of nearby early-type galaxies to large radii. Mon. Not. R. Astron. Soc. 2014, 442, 1003–1039. [Google Scholar] [CrossRef]
- La Barbera, F.; Ferreras, I.; de Carvalho, R.R.; Bruzual, G.; Charlot, S.; Pasquali, A.; Merlin, E. SPIDER—VII. Revealing the stellar population content of massive early-type galaxies out to 8Re. Mon. Not. R. Astron. Soc. 2012, 426, 2300–2317. [Google Scholar] [CrossRef]


| Simulation | Box0 | Box1 | Box2b | Box2 | Box3 | Box4 | ||
|---|---|---|---|---|---|---|---|---|
| Size [Mpc] | 3820 | 1300 | 910 | 500 | 180 | 68 | [] | [kpc/h] |
| mr | – | 5 | ||||||
| hr | – | – | 2 | |||||
| uhr | – | – | – | – | (z = 2) | 0.7 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dolag, K.; Mevius, E.; Remus, R.-S. Distribution and Evolution of Metals in the Magneticum Simulations. Galaxies 2017, 5, 35. https://doi.org/10.3390/galaxies5030035
Dolag K, Mevius E, Remus R-S. Distribution and Evolution of Metals in the Magneticum Simulations. Galaxies. 2017; 5(3):35. https://doi.org/10.3390/galaxies5030035
Chicago/Turabian StyleDolag, Klaus, Emilio Mevius, and Rhea-Silvia Remus. 2017. "Distribution and Evolution of Metals in the Magneticum Simulations" Galaxies 5, no. 3: 35. https://doi.org/10.3390/galaxies5030035
APA StyleDolag, K., Mevius, E., & Remus, R.-S. (2017). Distribution and Evolution of Metals in the Magneticum Simulations. Galaxies, 5(3), 35. https://doi.org/10.3390/galaxies5030035





