The Power of (Near) Simultaneous Multi-Frequency Observations for mm-VLBI and Astrometry
Abstract
:1. Introduction
2. Observations
3. Methods
4. Results
4.1. Increased Coherence Time for mm-VLBI
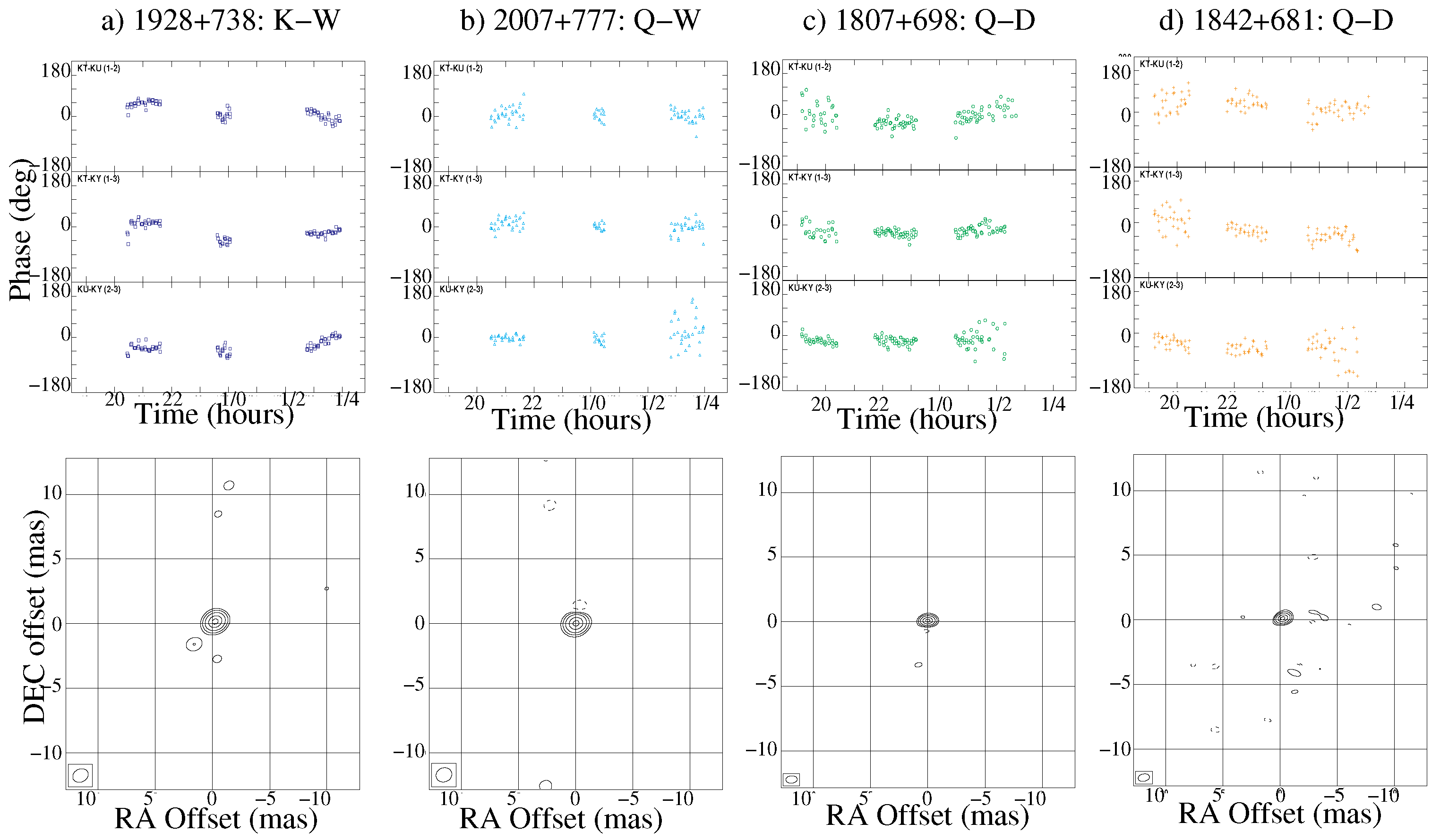
4.2. Astrometry at 22, 43, 87 and 130 GHz
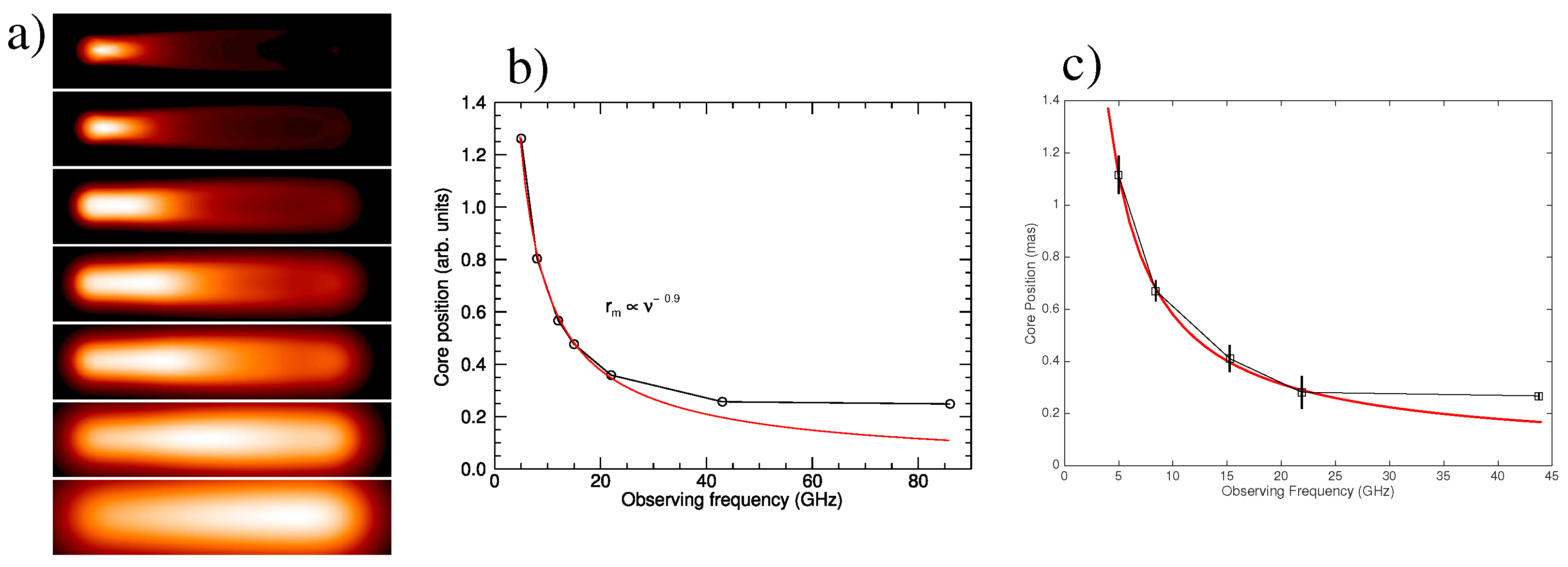
4.3. The Nature of the VLBI Core
5. Discussions
5.1. Demonstration of Multi-Frequency Calibration
5.2. Comparison of SFPR and MFPR to Other Methods
5.3. The Nature of the VLBI Core
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Porcas, R.W.; Rioja, M.J. VLBI phase-reference investigations at 86 GHz. In Proceedings of the 6th EVN Symposium, Bonn, Germany, 25–28 June 2002; Ros, E., Porcas, R.W., Lobanov, A.P., Zensus, J.A., Eds.; p. 65.
- Kim, H.G.; Han, S.T.; Minh, Y.C. Construction of the Korean VLBI Network (KVN). In Proceedings of the European VLBI Network on New Developments in VLBI Science and Technology, Toledo, Spain, 12–15 October 2004; Bachiller, R., Colomer, F., Desmurs, J.F., de Vicente, P., Eds.; pp. 281–284.
- Lee, S.S.; Petrov, L.; Byun, D.Y.; Kim, J.; Jung, T.; Song, M.G.; Oh, C.S.; Roh, D.G.; Je, D.H.; Wi, S.O.; et al. Early Science with the KVN: Evaluation of System Performance. Astrophys. J. 2014, 147, 77. [Google Scholar]
- Han, S.T.; Lee, J.W.; Kang, J.; Je, D.H.; Chung, M.H.; Wi, S.O.; Sasao, T.; Wylde, R. Millimeter-wave Receiver Optics for Korean VLBI Network. Int. J. Infrared Millim. Waves 2008, 29, 69–78. [Google Scholar] [CrossRef]
- Han, S.T.; Lee, J.W.; Kang, J.; Oh, C.S.; Byun, D.Y.; Je, D.H.; Chung, M.H.; Wi, S.O.; Song, M.; Kang, Y.W.; et al. Korean VLBI Network Receiver Optics for Simultaneous Multifrequency Observation: Evaluation. Publ. Astron. Soc. Pac. 2013, 125, 539–547. [Google Scholar] [CrossRef]
- Dodson, R.; Rioja, M. VLBA Scientific Memorandum n. 31: Astrometric calibration of mm-VLBI using “Source/Frequency Phase Referenced” observations. 2008. [Google Scholar]
- Rioja, M.; Dodson, R. High-precision Astrometric Millimeter Very Long Baseline Interferometry Using a New Method for Atmospheric Calibration. Astrophys. J. 2011, 141, 114. [Google Scholar] [CrossRef]
- Rioja, M.J.; Dodson, R.; Jung, T.; Sohn, B.W.; Byun, D.Y.; Agudo, I.; Cho, S.H.; Lee, S.S.; Kim, J.; Kim, K.T.; et al. Verification of the Astrometric Performance of the Korean VLBI Network, Using Comparative SFPR Studies with the VLBA at 14/7 mm. Astrophys. J. 2014, 148, 84. [Google Scholar] [CrossRef]
- Rioja, M.J.; Dodson, R.; Jung, T.; Sohn, B.W. The Power of Simultaneous Multi-Frequency Observations for mm-VLBI: Astrometry up to 130 GHz with the KVN. Astrophys. J. 2015, 150, 202. [Google Scholar]
- Marscher, A.P.; Jorstad, S.G.; D’Arcangelo, F.D.; Smith, P.S.; Williams, G.G.; Larionov, V.M.; Oh, H.; Olmstead, A.R.; Aller, M.F.; Aller, H.D.; et al. The inner jet of an active galactic nucleus as revealed by a radio-to-γ-ray outburst. Nature 2008, 452, 966–969. [Google Scholar] [CrossRef] [PubMed]
- Jorstad, S.G.; Marscher, A.P.; Smith, P.S.; Larionov, V.M.; Agudo, I.; Gurwell, M.; Wehrle, A.E.; Lähteenmäki, A.; Nikolashvili, M.G.; Schmidt, G.D.; et al. A Tight Connection between Gamma-Ray Outbursts and Parsec-scale Jet Activity in the Quasar 3C 454.3. Astrophys. J. 2013, 773, 147. [Google Scholar] [CrossRef]
- Casadio, C.; Gómez, J.L.; Jorstad, S.G.; Marscher, A.P.; Larionov, V.M.; Smith, P.S.; Gurwell, M.A.; Lähteenmäki, A.; Agudo, I.; Molina, S.N.; et al. A Multi-wavelength Polarimetric Study of the Blazar CTA 102 during a Gamma-Ray Flare in 2012. Astrophys. J. 2015, 813, 51. [Google Scholar] [CrossRef]
- Gómez, J.L.; Marti, J.M.A.; Marscher, A.P.; Ibanez, J.M.A.; Marcaide, J.M. Parsec-Scale Synchrotron Emission from Hydrodynamic Relativistic Jets in Active Galactic Nuclei. Astrophys. J. Lett. 1995, 449, L19. [Google Scholar] [CrossRef]
- Gómez, J.L.; Martí, J.M.; Marscher, A.P.; Ibáñez, J.M.; Alberdi, A. Hydrodynamical Models of Superluminal Sources. Astrophys. J. Lett. 1997, 482, L33–L36. [Google Scholar] [CrossRef]
- Daly, R.A.; Marscher, A.P. The gasdynamics of compact relativistic jets. Astrophys. J. 1988, 334, 539–551. [Google Scholar] [CrossRef]
- Blandford, R.D.; Königl, A. Relativistic jets as compact radio sources. Astrophys. J. 1979, 232, 34–48. [Google Scholar] [CrossRef]
- Königl, A. Relativistic jets as X-ray and gamma-ray sources. Astrophys. J. 1981, 243, 700–709. [Google Scholar] [CrossRef]
- Gómez, J.L.; Alberdi, A.; Marcaide, J.M. Synchrotron Emission from Bent Shocked Relativistic Jets—Part One—Bent Relativistic Jets. Astron. Astrophys. 1993, 274, 55–68. [Google Scholar]
- Lobanov, A.P. Ultracompact jets in active galactic nuclei. Astron. Astrophys. 1998, 330, 79–89. [Google Scholar]
- Lara, L.; Alberdi, A.; Marcaide, J.M.; Muxlow, T.W.B. The quasar 3C395 revisited: New VLBI observations and numerical simulations. Astron. Astrophys. 1994, 285, 393–403. [Google Scholar]
- Guirado, J.C.; Marcaide, J.M.; Alberdi, A.; Elosegui, P.; Ratner, M.I.; Shapiro, I.I.; Kilger, R.; Mantovani, F.; Venturi, T.; Rius, A.; et al. Proper Motion of Components in 4C 39.25. Astrophys. J. 1995, 110, 2586–2596. [Google Scholar] [CrossRef]
- Rioja, M.J.; Porcas, R.W. A phase-reference study of 1038+528A,B. Astron. Astrophys. 2000, 355, 552–563. [Google Scholar]
- Ros, E.; Marcaide, J.M.; Guirado, J.C.; Pérez-Torres, M.A. Absolute kinematics of radio source components in the complete S5 polar cap sample. I. Astron. Astrophys. 2001, 376, 1090–1105. [Google Scholar] [CrossRef]
- Martí-Vidal, I.; Marcaide, J.M.; Alberdi, A.; Pérez-Torres, M.A.; Ros, E.; Guirado, J.C. Detection of jet precession in the active nucleus of M 81. Astron. Astrophys. 2011, 533, A111. [Google Scholar] [CrossRef]
- Hada, K.; Doi, A.; Kino, M.; Nagai, H.; Hagiwara, Y.; Kawaguchi, N. An origin of the radio jet in M87 at the location of the central black hole. Nature 2011, 477, 185–187. [Google Scholar] [CrossRef] [PubMed]
- Kutkin, A.M.; Sokolovsky, K.V.; Lisakov, M.M.; Kovalev, Y.Y.; Savolainen, T.; Voytsik, P.A.; Lobanov, A.P.; Aller, H.D.; Aller, M.F.; Lahteenmaki, A.; et al. The core shift effect in the blazar 3C 454.3. Mon. Not. R. Astron. Soc. 2014, 437, 3396–3404. [Google Scholar] [CrossRef]
- Perucho, M.; Bosch-Ramon, V.; Khangulyan, D. 3D simulations of wind-jet interaction in massive X-ray binaries. Astron. Astrophys. 2010, 512, L4. [Google Scholar] [CrossRef]
- Gómez, J.L.; Marti, J.M.; Marscher, A.P.; Ibanez, J.M. Relativistic simulations of superluminal sources. Vistas Astron. 1997, 41, 79–85. [Google Scholar] [CrossRef]
- Mimica, P.; Aloy, M.A.; Agudo, I.; Martí, J.M.; Gómez, J.L.; Miralles, J.A. Spectral Evolution of Superluminal Components in Parsec-Scale Jets. Astrophys. J. 2009, 696, 1142–1163. [Google Scholar] [CrossRef]
- Dodson, R.; Rioja, M.J.; Molina, S.; Gómez, J. High-precision Astrometric Millimeter Very Long Baseline Interferometry Using a New Method for Multi-Frequency Calibration. Astron. J. 2017, 834, 177. [Google Scholar] [CrossRef]
- Dodson, R.; Rioja, M.J.; Jung, T.H.; Sohn, B.W.; Byun, D.Y.; Cho, S.H.; Lee, S.S.; Kim, J.; Kim, K.T.; Oh, C.S.; et al. Astrometrically Registered Simultaneous Observations of the 22 GHz H2O and 43 GHz SiO Masers toward R Leonis Minoris Using KVN and Source/Frequency Phase Referencing. Astrophys. J. 2014, 148, 97. [Google Scholar] [CrossRef]
- Hovatta, T.; Aller, M.F.; Aller, H.D.; Clausen-Brown, E.; Homan, D.C.; Kovalev, Y.Y.; Lister, M.L.; Pushkarev, A.B.; Savolainen, T. MOJAVE: Monitoring of Jets in Active Galactic Nuclei with VLBA Experiments. XI. Spectral Distributions. Astrophys. J. 2014, 147, 143. [Google Scholar] [CrossRef]
- Desmurs, J.F.; Bujarrabal, V.; Colomer, F.; Alcolea, J. VLBA observations of SiO masers: Arguments in favor of radiative pumping mechanisms. Astron. Astrophys. 2000, 360, 189–195. [Google Scholar]
- Cotton, W.D.; Mennesson, B.; Diamond, P.J.; Perrin, G.; du Foresto, V.C.; Chagnon, G.; van Langevelde, H.J.; Ridgway, S.; Waters, R.; Vlemmings, W.; et al. VLBA observations of SiO masers towards Mira variable stars. Astron. Astrophys. 2004, 414, 275–288. [Google Scholar] [CrossRef]
- Marscher, A.P.; Jorstad, S.G.; Gómez, J.L.; Aller, M.F.; Teräsranta, H.; Lister, M.L.; Stirling, A.M. Observational evidence for the accretion-disk origin for a radio jet in an active galaxy. Nature 2002, 417, 625–627. [Google Scholar] [CrossRef] [PubMed]
- Marscher, A.P.; Jorstad, S.G.; Larionov, V.M.; Aller, M.F.; Aller, H.D.; Lähteenmäki, A.; Agudo, I.; Smith, P.S.; Gurwell, M.; Hagen-Thorn, V.A.; et al. Probing the Inner Jet of the Quasar PKS 1510-089 with Multi-Waveband Monitoring During Strong Gamma-Ray Activity. Astrophys. J. Lett. 2010, 710, L126–L131. [Google Scholar] [CrossRef]
- Chatterjee, R.; Marscher, A.P.; Jorstad, S.G.; Markowitz, A.; Rivers, E.; Rothschild, R.E.; McHardy, I.M.; Aller, M.F.; Aller, H.D.; Lähteenmäki, A.; et al. Connection between the Accretion Disk and Jet in the Radio Galaxy 3C 111. Astrophys. J. 2011, 734, 43. [Google Scholar] [CrossRef]
- Fromm, C.M.; Perucho, M.; Ros, E.; Savolainen, T.; Zensus, J.A. On the location of the supermassive black hole in CTA 102. Astron. Astrophys. 2015, 576, A43. [Google Scholar] [CrossRef]
- Gómez, J.L.; Lobanov, A.P.; Bruni, G.; Kovalev, Y.Y.; Marscher, A.P.; Jorstad, S.G.; Mizuno, Y.; Bach, U.; Sokolovsky, K.V.; Anderson, J.M.; et al. Probing the Innermost Regions of AGN Jets and Their Magnetic Fields with RadioAstron. I. Imaging BL Lacertae at 21 Microarcsecond Resolution. Astrophys. J. 2016, 817, 96. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rioja, M.J.; Dodson, R.; Gómez, J.L.; Molina, S.N.; Jung, T.; Sohn, B.W. The Power of (Near) Simultaneous Multi-Frequency Observations for mm-VLBI and Astrometry. Galaxies 2017, 5, 9. https://doi.org/10.3390/galaxies5010009
Rioja MJ, Dodson R, Gómez JL, Molina SN, Jung T, Sohn BW. The Power of (Near) Simultaneous Multi-Frequency Observations for mm-VLBI and Astrometry. Galaxies. 2017; 5(1):9. https://doi.org/10.3390/galaxies5010009
Chicago/Turabian StyleRioja, María J., Richard Dodson, José L. Gómez, Sol N. Molina, Taehyun Jung, and Bong Won Sohn. 2017. "The Power of (Near) Simultaneous Multi-Frequency Observations for mm-VLBI and Astrometry" Galaxies 5, no. 1: 9. https://doi.org/10.3390/galaxies5010009
APA StyleRioja, M. J., Dodson, R., Gómez, J. L., Molina, S. N., Jung, T., & Sohn, B. W. (2017). The Power of (Near) Simultaneous Multi-Frequency Observations for mm-VLBI and Astrometry. Galaxies, 5(1), 9. https://doi.org/10.3390/galaxies5010009







