Abstract
Simultaneous or near-simultaneous observations at multiple frequency bands have the potential to overcome the fundamental limitation imposed by the atmospheric propagation in mm-VLBI observations. The propagation effects place a severe limit in the sensitivity achievable in mm-VLBI, reducing the time over which the signals can be coherently combined, and preventing the use of phase referencing and astrometric measurements. We present two demonstrations of the power of (near) simultaneous multi-frequency observations with the KVN and VLBA, and our recently developed analysis strategies to enable new measurements at mm-VLBI. The first case comprises simultaneous observations at 22, 43, 87 and 130 GHz of a group of five AGNs, the weakest of which is ∼200 mJy at 130 GHz, with angular separations ranging from 3.6 to 11 degrees, using the KVN. We analysed this data using the Frequency Phase Transfer (FPT) and the Source Frequency Phase Referencing (SFPR) techniques, which use the observations at a lower frequency to correct those at a higher frequency. The results of the analysis provide an empirical demonstration of the increase in the coherence times at 130 GHz from a few tens of seconds to about twenty minutes, with FPT, and up to many hours with SFPR. Moreover the astrometric analysis provides high precision relative position measurements between two frequencies, including, for the first time, astrometry at 130 GHz. The second case is a variation of the above, whereby adding dedicated wide-band cm-wavelength observations to measure the ionosphere eliminates the need for a second, calibrator, source. This addresses the scarcity of calibrators at mm-VLBI. We dubbed this technique Multi Frequency Phase Referencing (MFPR). We present bona fide astrometrically aligned VLBA images of BL Lacertae at 22 and 43 GHz using MFPR, which, combined with results from conventional phase referencing at cm-wavelengths, suggests the VLBI core has a recollimation shock that is revealed at mm-wavelengths. These shocks could be responsible for the γ-ray emission in blazar jets.
1. Introduction
VLBI at (sub)mm wavelengths (hereafter mm-VLBI) can result in the highest angular resolutions achieved in astronomy and has a unique access to emission regions that are inaccessible with any other approach or at longer wavelengths, because the compact areas of interest are often self-absorbed. Therefore it holds the potential to increase our understanding of the physical processes in e.g., Active Galactic Nuclei (AGN) and in the vicinity of super-massive Black Holes, and for studies of molecular transitions at high frequencies.
Nevertheless, the applications of mm-VLBI are not widespread. The observations become progressively more challenging as the wavelength gets shorter, because of the: limited telescope surface accuracy and aperture efficiency, receiver system temperatures and sensitivity, shorter atmospheric coherence times and the fact that sources are intrinsically weaker in general. Moreover phase referencing techniques, which are routinely used in cm-VLBI, fail to work beyond 43 GHz (excluding a single case at 86 GHz with the Very Long Baseline Array (VLBA) [1]). In this paper we will focus on two aspects that limit the potential of mm-VLBI observations: (1) achieving improved sensitivity through increased coherence times, to increase the number of targets; (2) achieving astrometry, and in particular for “bona fide” registration of images at multiple frequency bands, to reveal the physical processes in a number of fields of astronomy. The first case study presented in this paper uses observations with the Korean VLBI Network (KVN) [2,3]. The KVN is the first dedicated mm-VLBI array and addresses one of the fundamental limitations of the field, the atmospheric stability. It currently consists of three antennas operated by Korea Astronomy and Space Science Institute (KASI). The observing frequencies are centred at 22, 43, 87 and 130 GHz (i.e., K, Q, W and D bands). The baseline lengths between the antennas range between 300 and 500 km, which provide a spatial resolution ∼1 mas at the highest frequency band. The innovative multi-band receiver [4,5] of KVN is designed to mitigate the atmospheric propagation effects using simultaneous observations at multiple bands. The KVN combined with the Frequency Phase Transfer (FPT) and Source Frequency Phase Referencing (SFPR) data analysis techniques ([6,7,8,9] see also references therein) allows an effective increase of the coherence time, well beyond that imposed by tropospheric fluctuations, as well as high precision astrometric measurements, respectively, even at the highest frequencies.
The second case study is concerned with the nature of the VLBI core, in particular in blazars. Results from the VLBA-BU-BLAZAR program, show that most γ-ray flares are simultaneous within errors with the appearance of a new superluminal component or a major outburst in the core of the jet, which is defined as the bright, compact feature in the upstream end of the jet [10,11,12]. A burst in particle and magnetic energy density is therefore required when jet disturbances cross the radio core in order to produce γ-ray flares, which can naturally be explained by identifying the radio core with a recollimation shock [13,14,15]. Multi-wavelength observations of blazars therefore suggest that the radio core is a physical feature (recollimation shock) in the jet at a fixed location. On the other hand, the standard Blandford & Königl conical jet model hypothesises that the core is not a physical feature in the jet, but corresponds to the location at which the jet becomes optically thin, and therefore its position shifts with observing frequency [16,17,18,19]. This has been demonstrated using multi-frequency cm-VLBI phase-referencing for 3C 395, 4C 39.25, 1038+528, 3C 390.1, M 81, M 87 and 3C454.3 ([20,21,22,23,24,25,26] respectively).
A possible solution for this apparent contradiction is that, at low frequencies the core emission is downstream from the shock and follows the Blandford & Königl model, and at higher frequencies the jet is optically thin even close to the jet launch point so that the shock is revealed. High precision bona fide astrometry of the position of the radio core across a range of frequencies up to mm-wavelengths will shed light on this. For the BL Lac study presented here we use the Multi-Frequency Phase Referencing method, where the dispersive atmospheric and instrumental contributions are measured at other frequencies and removed before FPT calibration. As the FPT corrects the non-dispersive rapidly changing contributions, and the multi-frequency observations have removed the slowly changing dispersive terms, once again we can retrieve the astrometric measurement.
2. Observations
In March 5, 2014, we carried out simultaneous observations at four frequencies K, Q, W and D bands, with the three antennas of the KVN, towards 5 AGN target sources, for a total duration of 9 h. The target sources were selected based on two criteria: to have strong detections at W band, and angular separations in the sky ranging from a few, upto many degrees. The five selected sources (1803+784, 1807+698, 1842+681, 1928+738 and 2007+777) have angular separations among themselves that range between and . None of the sources had been observed previously with VLBI at 130 GHz.
The VLBA observations of BL Lac presented in this paper were carried out on 5 July 2013. The observations comprised blocks of conventional phase referencing observations at 5, 8, 15 and 22 GHz and blocks of MFPR observations at 22, 43 and 86 GHz. The former consisted of alternating observations between BL Lac and a calibrator source, with a switching cycle of ∼80 seconds, at each frequency; the latter, fast frequency switching observations, were just on BL Lac, between 22 and 43 GHz, and 22 and 86 GHz, with scans 30 s long. The MFPR blocks were bracketed by dedicated ionospheric calibration blocks, consisting of consecutive wide band observations between L, C and K-band receivers, with 40 s scans.
3. Methods
We carried out SFPR astrometric analysis of the four-band multi-frequency KVN dataset using AIPS. The details of SFPR analysis are presented elsewhere ([8], and references therein) and consists of two calibration steps. In the FPT step, the observations at the higher frequency bands () are calibrated using the simultaneous observations at a lower frequency band (), for each source. This is done for all frequency pairs that have an integer frequency ratio R (with R = ), which in turn is used to scale up the phase-calibration solutions from the lower frequency. This dual frequency calibration step eliminates the common non-dispersive residual errors (e.g., tropospheric propagation effects and inaccurate coordinates) in the complex visibility output of the correlator, providing increased signal coherence at the higher frequency. The SFPR step of the calibration removes the remaining dispersive residual errors (i.e., instrumental and ionospheric propagation effects) using the interleaving observations of another source. This two-step calibration retains the astrometric signature of any source position shifts between the two frequencies in the interferometric phase. The resultant calibrated visibilities, for a given frequency pair and a source pair, are dubbed SFPR-ed visibilities. The alternative approach is to measure and remove all contributions with additional measurements; this is the basis of MFPR. The Fourier transformation of the SFPR or MFPR datasets are the astrometric maps, which convey a bona fide astrometric measurement of the relative separation or shift between the position of the reference points in the images at the two frequencies.
To provide a prediction for the expected behaviour of a recollimation shock being revealed at high frequencies we used numerical simulations and the finite-volume code Ratpenat, which solves the equations of relativistic hydrodynamics ([27], and references therein). The jet is launched with a Lorentz factor of 7 and an initial over-pressure of 1.5 times that of the external medium, in order to obtain a recollimation shock. Using the hydrodynamical results as input, we have then computed the synchrotron emission at different observing frequencies (for details of the numerical model used see [13,28,29]), adjusting the model parameters so that the jet is optically thin at 86 and 43 GHz, and becomes optically thick at lower frequencies. A magnetic field in equipartition with the particle energy density is assumed. At cm-wavelengths (5 to 22 GHz) numerical simulations reproduce the opacity core-shift of a Blandford & Königl conical jet model, while at millimeter wavebands (43 and 86 GHz) the core position clearly departs from this behaviour, revealing the core as an optically thin recollimation shock at a fixed jet location.
4. Results
4.1. Increased Coherence Time for mm-VLBI
The rapid changes in the observed interferometric phases introduced by the tropospheric propagation effects set a severe limit on the coherence time for integration of the signal in observations at high frequencies, and therefore the sensitivity of those observations. A direct consequence of the effective tropospheric compensation achieved from simultaneous dual frequency observations is an increased coherence time and therefore sensitivity.
In order to quantify the increase in the coherence time, we have carried out a comparative study of the coherence times achieved with FPT and SFPR at 130 GHz. This is the highest frequency in our observations, where the propagation effects are most severe. To perform these tests we use the AIPS task CALIB on FPT-ed and SFPR-ed calibrated datasets of 1842+681 at = 130 GHz, with = 43 GHz and 1803+784 as the reference source, with a series of phase solution time intervals ranging from 0.5 to 480 min. In each case the phase solutions are applied and the calibrated visibility data Fourier inverted to produce a map. We use the fractional peak recovered flux quantity, defined as the ratio of the peak flux in this map and that from self-calibrated maps, as a measure of remaining phase errors in the analysis. The fractional peak recovered flux values in the maps decrease with increasing temporal solution intervals, as expected. The coherence time is defined as the solution interval at which the peak flux recovery is 60%, being equivalent to the rms residual phase being equal to 1 radian. Our analysis shows that the coherence time at 130 GHz is 20 min with FPT calibration. With SFPR calibration there is practically no limit in the coherence time; we could integrate up to 8-h, the whole duration of the experiment, with a mere ∼20% loss of peak flux. Note that the tropospheric coherence time at 130 GHz is some tens of seconds and that neither 1842+681 nor 2007+777 have direct detections at this frequency.
4.2. Astrometry at 22, 43, 87 and 130 GHz
The final outcome of the SFPR analysis is an SFPR map which conveys the astrometric information. Figure 1 shows a subset of the SFPR-ed maps obtained in the comprehensive analysis of KVN observations; they are the Fourier transform of the SFPR visibilities directly above in the same figure. The offset of the peak of brightness with respect to the center of the maps is a measurement of the relative position shift between the two frequency bands, for the two sources. The complete results from the SFPR astrometric analysis, comprising of the five frequency pairs and six source pairs, are summarized in Table 2 in Rioja et al. [9]. In Rioja et al. [9] we also present a detailed astrometric error analysis and a method for the decomposition of the relative astrometric measurements into the individual source position shifts required for the registration of images at multiple frequencies, up to 130 GHz. Table 5 in Rioja et al. [9] summarizes this along with the estimated registration errors, which range from 10 to 100 micro-arcseconds.
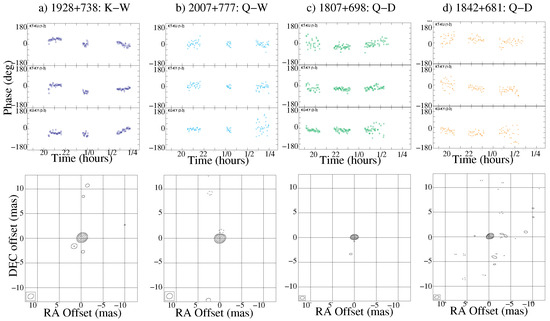
Figure 1.
Outcomes of Source Frequency Phase Referencing (SFPR) astrometric analysis: Upper Row: SFPR-ed residual visibility phases for a subset of source and frequency pairs. The target source and target frequency band (i.e., ), along with the angular separation to the reference source (in all cases 1803+784), the reference frequency band (i.e., ) and the frequency ratio R, in parenthesis, are as follows for each plot. From left to right: 1928+738 at W-band ( apart on the sky, K-band, R = 4); 2007+777 at W-band ( apart, Q-band, R = 2); 1807+698 at D-band ( apart, Q-band, R = 3); 1842+681 at D-band ( apart, Q-band, R = 3). Lower Row: SFPR-ed maps resulting from Fourier transformation of the SFPR-ed visibility phases directly above. From left to right: 1928+738 and 2007+777 at 87 GHz (W-band); 1807+698 and 1842+681 at 130 GHz (D-band). Peak fluxes are 2 Jy·beam, 266 mJy·beam, 415 mJy·beam and 216 mJy·beam, respectively. The contour levels in the maps start from 0.75% of the corresponding peak fluxes, respectively, and doubling thereafter in all cases. Each map includes a negative contour level at the same percent level of the peak flux as the first positive one. The beam size is indicated at the bottom left of the image.
4.3. The Nature of the VLBI Core
The results from the simulations are shown in Figure 2a,b. For comparison, the results from the high precision astrometric analysis of the VLBA observations of BL Lac are shown in Figure 2c. The measurements at 43 GHz, with respect to 22 GHz, are from MFPR; those at 22 GHz and lower frequencies are from conventional phase referencing.
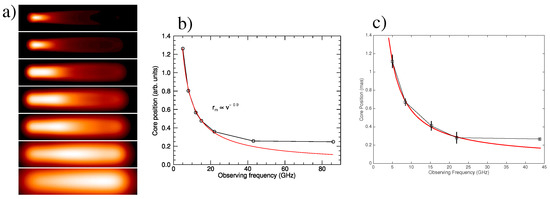
Figure 2.
(a) A sequence of simulated synchrotron total intensity images computed at 86, 43, 22, 15, 12, 8, and 5 GHz, respectively, using a relativistic hydrodynamical model of a jet with a recollimation shock; (b) Position of the simulated core as a function of frequency. The red curve indicates the best fit to the core positions between 5 and 22 GHz, which follows the canonical Blandford & Königl jet model. The 43 and 86 GHz data clearly deviate from the opacity core-shift curve, revealing the recollimation shock; (c) Astrometric core-shifts of BL Lac between 4.8 and 43 GHz, plotted as a function of frequency, adapted from Dodson et al. [30]. Overlaid in red is the model from the fitting of the cm-wavelength data (where κ is −0.99 and is 5.3 mas GHz).
5. Discussions
5.1. Demonstration of Multi-Frequency Calibration
Simultaneous multi-frequency observations offer an effective path to achieve increased sensitivity and precision astrometry in mm-VLBI, beyond the domain of standard techniques, such as phase referencing. The compensation of the fast phase changes imposed by the rapid tropospheric fluctuations in mm-VLBI, using observations at a lower frequency of the same source, results in an increased coherence time of up to 20 min at 130 GHz using FPT analysis, which increases the sensitivity by an order of magnitude. Moreover, when combined with the observations of another source, a bona fide astrometric measurement of the relative frequency dependent position-shift between the two frequencies can be estimated using the SFPR technique. This in turn results in an unlimited extension of the coherence time. The application of SFPR techniques has allowed the detection of weak sources that were not directly detected within the atmospheric coherence time (i.e., with self calibration) and we have measured frequency dependent position shifts between a range of frequencies from 22 up to 130 GHz with high precision, for each of the observed AGNs. We believe that these benefits would continue to apply beyond these frequencies.
5.2. Comparison of SFPR and MFPR to Other Methods
FPT requires fast switching, or simultaneous observations, of the two frequencies. Fast switching limits the maximum frequency for the method, as the rates become unmanageable. It is highly recommended that the frequencies are at an integer ratio ([31], but it is possible, with care, for non-integer ratios). SFPR requires two sources, which can both be detected at the lower frequency and at least one of which can be detected at the higher frequency (although the longer coherence time from the FPT helps with this step). For MFPR the main requirement is that the instrumental terms are stable and can be measured in the prime calibration step. Secondly, the ionospheric contributions should be measured through the curvature of the delay solutions across a wide frequency span, and preferably covering the lowest possible frequencies. For accurate (≤0.1 TECU) measurements 1.4 GHz must be included.
These are not very burdensome conditions, but they can limit the use. There exist a variety of other indirect methods used to register the images of AGNs and/or maser species at different frequencies. However the alternative methods have much more serious systematic problems. The application of these methods for compact sources and for sources with faint or smooth jets is clearly an issue. Therefore these methods can be unreliable or impossible to use in mm-VLBI, where in many cases only the compact core can be detected (see discussions in [32]).
In a similar fashion, some maser species can be assumed to form in a ring, and the centre of the ring can therefore act as a reference point [33], or one can identify a single component which appears similar in velocity and orientation with respect to the main body of emission and use that as the reference point across frequencies [34]. It is not hard to see the short-falls in such approaches and these different methods tend to produce incompatible conclusions. Phase referencing would provide a clear solution for such challenges but, as pointed out previously, conventional phase-referencing is not an option above 43 GHz.
Therefore SFPR/MFPR stands alone as a method that will allow for the unambiguous registration across wide frequency spans for mm-VLBI images, both for continuum and spectral line studies, because it provides a complete compensation of atmospheric propagation and instrumental effects. SFPR is widely applicable for many sources, since the calibrator source can be at a significant angular separation and slow source switching does not undermine the result. The method will work even at very high frequencies, making it particularly suitable for mm-VLBI observations. We note that systematic effects do need to be carefully taken into account, particularly when using a lower frequency of 22 GHz. MFPR does not require the second source, but has a greater calibration overhead.
5.3. The Nature of the VLBI Core
The nature of the VLBI core in AGNs continues to be elusive, with two sets of results, one suggesting that the radio core corresponds to a recollimation shock while the other implies that it marks the transition between the optically thick-thin jet regimes. For example M87 definitely follows the expected Blandford & Königl behaviour [25], but simultaneous observations at γ/X-rays, optical, infrared, and radio, together with mm-VLBI imaging, have shown that in several radio galaxies and blazars the core indeed is inferred to lie parsecs away from the central black hole [35,36,37,38]. Our astrometric measurements, shown in Figure 2c, suggest that the downstream recollimation shock has been detected in BL Lac (see also [39]), reproducing the expectations from simulations extremely closely [30].
Acknowledgments
We are grateful to all staff members and students in the KVN who helped to operate the array. The KVN is a facility operated by the Korea Astronomy and Space Science Institute. We acknowledge the support of the Australian DFAT Grant AKF-201400010. The work at IAA-CSIC is supported by the Spanish Ministerio de Economía y Competitividad grant AYA2013-40825-P. The VLBA is operated by National Radio Astronomy Observatory and is a facility of the National Science Foundation operated under cooperative agreement with Associated Universities Inc.
Author Contributions
Sol N. Molina and José L. Gómez designed the MFPR experiments; Taehyun Jung and Bong Won Sohn performed the SFPR experiments; María J. Rioja and Richard Dodson analyzed the data and wrote the paper
Conflicts of Interest
The authors declare no conflict of interest.
References
- Porcas, R.W.; Rioja, M.J. VLBI phase-reference investigations at 86 GHz. In Proceedings of the 6th EVN Symposium, Bonn, Germany, 25–28 June 2002; Ros, E., Porcas, R.W., Lobanov, A.P., Zensus, J.A., Eds.; p. 65.
- Kim, H.G.; Han, S.T.; Minh, Y.C. Construction of the Korean VLBI Network (KVN). In Proceedings of the European VLBI Network on New Developments in VLBI Science and Technology, Toledo, Spain, 12–15 October 2004; Bachiller, R., Colomer, F., Desmurs, J.F., de Vicente, P., Eds.; pp. 281–284.
- Lee, S.S.; Petrov, L.; Byun, D.Y.; Kim, J.; Jung, T.; Song, M.G.; Oh, C.S.; Roh, D.G.; Je, D.H.; Wi, S.O.; et al. Early Science with the KVN: Evaluation of System Performance. Astrophys. J. 2014, 147, 77. [Google Scholar]
- Han, S.T.; Lee, J.W.; Kang, J.; Je, D.H.; Chung, M.H.; Wi, S.O.; Sasao, T.; Wylde, R. Millimeter-wave Receiver Optics for Korean VLBI Network. Int. J. Infrared Millim. Waves 2008, 29, 69–78. [Google Scholar] [CrossRef]
- Han, S.T.; Lee, J.W.; Kang, J.; Oh, C.S.; Byun, D.Y.; Je, D.H.; Chung, M.H.; Wi, S.O.; Song, M.; Kang, Y.W.; et al. Korean VLBI Network Receiver Optics for Simultaneous Multifrequency Observation: Evaluation. Publ. Astron. Soc. Pac. 2013, 125, 539–547. [Google Scholar] [CrossRef]
- Dodson, R.; Rioja, M. VLBA Scientific Memorandum n. 31: Astrometric calibration of mm-VLBI using “Source/Frequency Phase Referenced” observations. 2008. [Google Scholar]
- Rioja, M.; Dodson, R. High-precision Astrometric Millimeter Very Long Baseline Interferometry Using a New Method for Atmospheric Calibration. Astrophys. J. 2011, 141, 114. [Google Scholar] [CrossRef]
- Rioja, M.J.; Dodson, R.; Jung, T.; Sohn, B.W.; Byun, D.Y.; Agudo, I.; Cho, S.H.; Lee, S.S.; Kim, J.; Kim, K.T.; et al. Verification of the Astrometric Performance of the Korean VLBI Network, Using Comparative SFPR Studies with the VLBA at 14/7 mm. Astrophys. J. 2014, 148, 84. [Google Scholar] [CrossRef]
- Rioja, M.J.; Dodson, R.; Jung, T.; Sohn, B.W. The Power of Simultaneous Multi-Frequency Observations for mm-VLBI: Astrometry up to 130 GHz with the KVN. Astrophys. J. 2015, 150, 202. [Google Scholar]
- Marscher, A.P.; Jorstad, S.G.; D’Arcangelo, F.D.; Smith, P.S.; Williams, G.G.; Larionov, V.M.; Oh, H.; Olmstead, A.R.; Aller, M.F.; Aller, H.D.; et al. The inner jet of an active galactic nucleus as revealed by a radio-to-γ-ray outburst. Nature 2008, 452, 966–969. [Google Scholar] [CrossRef] [PubMed]
- Jorstad, S.G.; Marscher, A.P.; Smith, P.S.; Larionov, V.M.; Agudo, I.; Gurwell, M.; Wehrle, A.E.; Lähteenmäki, A.; Nikolashvili, M.G.; Schmidt, G.D.; et al. A Tight Connection between Gamma-Ray Outbursts and Parsec-scale Jet Activity in the Quasar 3C 454.3. Astrophys. J. 2013, 773, 147. [Google Scholar] [CrossRef]
- Casadio, C.; Gómez, J.L.; Jorstad, S.G.; Marscher, A.P.; Larionov, V.M.; Smith, P.S.; Gurwell, M.A.; Lähteenmäki, A.; Agudo, I.; Molina, S.N.; et al. A Multi-wavelength Polarimetric Study of the Blazar CTA 102 during a Gamma-Ray Flare in 2012. Astrophys. J. 2015, 813, 51. [Google Scholar] [CrossRef]
- Gómez, J.L.; Marti, J.M.A.; Marscher, A.P.; Ibanez, J.M.A.; Marcaide, J.M. Parsec-Scale Synchrotron Emission from Hydrodynamic Relativistic Jets in Active Galactic Nuclei. Astrophys. J. Lett. 1995, 449, L19. [Google Scholar] [CrossRef]
- Gómez, J.L.; Martí, J.M.; Marscher, A.P.; Ibáñez, J.M.; Alberdi, A. Hydrodynamical Models of Superluminal Sources. Astrophys. J. Lett. 1997, 482, L33–L36. [Google Scholar] [CrossRef]
- Daly, R.A.; Marscher, A.P. The gasdynamics of compact relativistic jets. Astrophys. J. 1988, 334, 539–551. [Google Scholar] [CrossRef]
- Blandford, R.D.; Königl, A. Relativistic jets as compact radio sources. Astrophys. J. 1979, 232, 34–48. [Google Scholar] [CrossRef]
- Königl, A. Relativistic jets as X-ray and gamma-ray sources. Astrophys. J. 1981, 243, 700–709. [Google Scholar] [CrossRef]
- Gómez, J.L.; Alberdi, A.; Marcaide, J.M. Synchrotron Emission from Bent Shocked Relativistic Jets—Part One—Bent Relativistic Jets. Astron. Astrophys. 1993, 274, 55–68. [Google Scholar]
- Lobanov, A.P. Ultracompact jets in active galactic nuclei. Astron. Astrophys. 1998, 330, 79–89. [Google Scholar]
- Lara, L.; Alberdi, A.; Marcaide, J.M.; Muxlow, T.W.B. The quasar 3C395 revisited: New VLBI observations and numerical simulations. Astron. Astrophys. 1994, 285, 393–403. [Google Scholar]
- Guirado, J.C.; Marcaide, J.M.; Alberdi, A.; Elosegui, P.; Ratner, M.I.; Shapiro, I.I.; Kilger, R.; Mantovani, F.; Venturi, T.; Rius, A.; et al. Proper Motion of Components in 4C 39.25. Astrophys. J. 1995, 110, 2586–2596. [Google Scholar] [CrossRef]
- Rioja, M.J.; Porcas, R.W. A phase-reference study of 1038+528A,B. Astron. Astrophys. 2000, 355, 552–563. [Google Scholar]
- Ros, E.; Marcaide, J.M.; Guirado, J.C.; Pérez-Torres, M.A. Absolute kinematics of radio source components in the complete S5 polar cap sample. I. Astron. Astrophys. 2001, 376, 1090–1105. [Google Scholar] [CrossRef]
- Martí-Vidal, I.; Marcaide, J.M.; Alberdi, A.; Pérez-Torres, M.A.; Ros, E.; Guirado, J.C. Detection of jet precession in the active nucleus of M 81. Astron. Astrophys. 2011, 533, A111. [Google Scholar] [CrossRef]
- Hada, K.; Doi, A.; Kino, M.; Nagai, H.; Hagiwara, Y.; Kawaguchi, N. An origin of the radio jet in M87 at the location of the central black hole. Nature 2011, 477, 185–187. [Google Scholar] [CrossRef] [PubMed]
- Kutkin, A.M.; Sokolovsky, K.V.; Lisakov, M.M.; Kovalev, Y.Y.; Savolainen, T.; Voytsik, P.A.; Lobanov, A.P.; Aller, H.D.; Aller, M.F.; Lahteenmaki, A.; et al. The core shift effect in the blazar 3C 454.3. Mon. Not. R. Astron. Soc. 2014, 437, 3396–3404. [Google Scholar] [CrossRef]
- Perucho, M.; Bosch-Ramon, V.; Khangulyan, D. 3D simulations of wind-jet interaction in massive X-ray binaries. Astron. Astrophys. 2010, 512, L4. [Google Scholar] [CrossRef]
- Gómez, J.L.; Marti, J.M.; Marscher, A.P.; Ibanez, J.M. Relativistic simulations of superluminal sources. Vistas Astron. 1997, 41, 79–85. [Google Scholar] [CrossRef]
- Mimica, P.; Aloy, M.A.; Agudo, I.; Martí, J.M.; Gómez, J.L.; Miralles, J.A. Spectral Evolution of Superluminal Components in Parsec-Scale Jets. Astrophys. J. 2009, 696, 1142–1163. [Google Scholar] [CrossRef]
- Dodson, R.; Rioja, M.J.; Molina, S.; Gómez, J. High-precision Astrometric Millimeter Very Long Baseline Interferometry Using a New Method for Multi-Frequency Calibration. Astron. J. 2017, 834, 177. [Google Scholar] [CrossRef]
- Dodson, R.; Rioja, M.J.; Jung, T.H.; Sohn, B.W.; Byun, D.Y.; Cho, S.H.; Lee, S.S.; Kim, J.; Kim, K.T.; Oh, C.S.; et al. Astrometrically Registered Simultaneous Observations of the 22 GHz H2O and 43 GHz SiO Masers toward R Leonis Minoris Using KVN and Source/Frequency Phase Referencing. Astrophys. J. 2014, 148, 97. [Google Scholar] [CrossRef]
- Hovatta, T.; Aller, M.F.; Aller, H.D.; Clausen-Brown, E.; Homan, D.C.; Kovalev, Y.Y.; Lister, M.L.; Pushkarev, A.B.; Savolainen, T. MOJAVE: Monitoring of Jets in Active Galactic Nuclei with VLBA Experiments. XI. Spectral Distributions. Astrophys. J. 2014, 147, 143. [Google Scholar] [CrossRef]
- Desmurs, J.F.; Bujarrabal, V.; Colomer, F.; Alcolea, J. VLBA observations of SiO masers: Arguments in favor of radiative pumping mechanisms. Astron. Astrophys. 2000, 360, 189–195. [Google Scholar]
- Cotton, W.D.; Mennesson, B.; Diamond, P.J.; Perrin, G.; du Foresto, V.C.; Chagnon, G.; van Langevelde, H.J.; Ridgway, S.; Waters, R.; Vlemmings, W.; et al. VLBA observations of SiO masers towards Mira variable stars. Astron. Astrophys. 2004, 414, 275–288. [Google Scholar] [CrossRef]
- Marscher, A.P.; Jorstad, S.G.; Gómez, J.L.; Aller, M.F.; Teräsranta, H.; Lister, M.L.; Stirling, A.M. Observational evidence for the accretion-disk origin for a radio jet in an active galaxy. Nature 2002, 417, 625–627. [Google Scholar] [CrossRef] [PubMed]
- Marscher, A.P.; Jorstad, S.G.; Larionov, V.M.; Aller, M.F.; Aller, H.D.; Lähteenmäki, A.; Agudo, I.; Smith, P.S.; Gurwell, M.; Hagen-Thorn, V.A.; et al. Probing the Inner Jet of the Quasar PKS 1510-089 with Multi-Waveband Monitoring During Strong Gamma-Ray Activity. Astrophys. J. Lett. 2010, 710, L126–L131. [Google Scholar] [CrossRef]
- Chatterjee, R.; Marscher, A.P.; Jorstad, S.G.; Markowitz, A.; Rivers, E.; Rothschild, R.E.; McHardy, I.M.; Aller, M.F.; Aller, H.D.; Lähteenmäki, A.; et al. Connection between the Accretion Disk and Jet in the Radio Galaxy 3C 111. Astrophys. J. 2011, 734, 43. [Google Scholar] [CrossRef]
- Fromm, C.M.; Perucho, M.; Ros, E.; Savolainen, T.; Zensus, J.A. On the location of the supermassive black hole in CTA 102. Astron. Astrophys. 2015, 576, A43. [Google Scholar] [CrossRef]
- Gómez, J.L.; Lobanov, A.P.; Bruni, G.; Kovalev, Y.Y.; Marscher, A.P.; Jorstad, S.G.; Mizuno, Y.; Bach, U.; Sokolovsky, K.V.; Anderson, J.M.; et al. Probing the Innermost Regions of AGN Jets and Their Magnetic Fields with RadioAstron. I. Imaging BL Lacertae at 21 Microarcsecond Resolution. Astrophys. J. 2016, 817, 96. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).