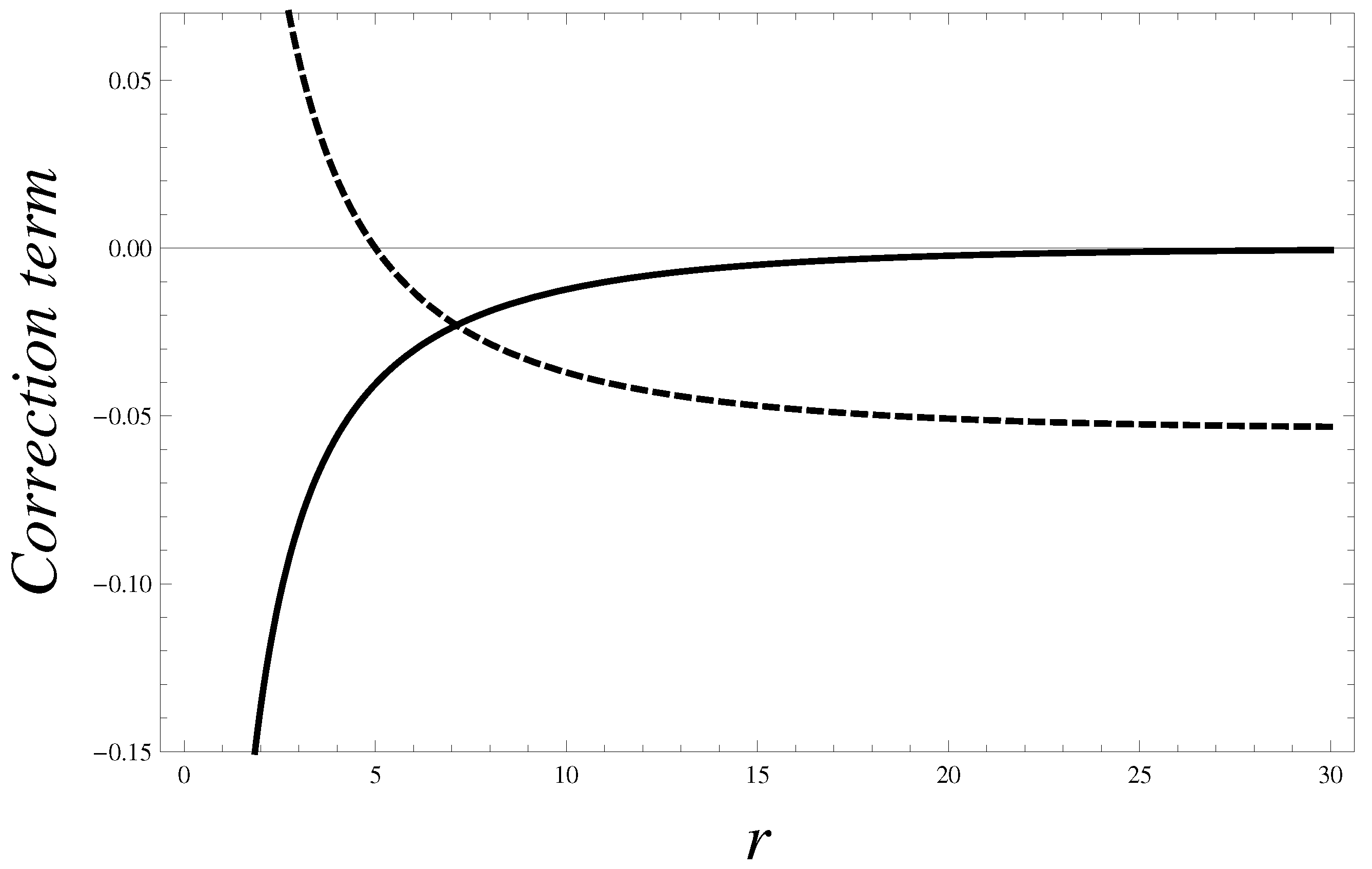1. Introduction
The today observed Universe appears spatially flat and undergoing an accelerated expansion. Several observational data probe this pictures [
1,
2,
3,
4,
5,
6] but two unrevealed ingredients are needed in order to achieve this dynamical scenario, namely Dark Matter (DM) at galactic and extragalactic scales and Dark Energy (DE) at cosmological scales. In particular, the dynamical evolution of self-gravitating structures can be figured out by the standard Newtonian gravity, but DM is needed to obtain agreement with observations [
7].
On the other hand, the effort to give a physical explanation to the today observed cosmic acceleration has attracted a lot of interest in the so-called Extended Theories of Gravity [
8,
9,
10], considered a viable mechanism to explain the cosmic acceleration by extending the geometric sector without introducing DM and DE. Other issues, at astrophysical level, can be framed in the same approach [
11] and then, apart the cosmological dynamics, a systematic analysis of such theories urges at short scale and in the weak field limit. Extended Theories of Gravity are then a new paradigm for gravitational physics aimed to address shortcomings coming out at ultra-violet and infra-red scales.
While it is very natural to extend General Relativity (GR) to theories with additional geometric degrees of freedom, recent attempts focused on the old idea of modifying the gravitational Lagrangian in taking into account generic functions of curvature invariants and leading to higher-order field equations. Despite of the positive results of GR, the study of possible modifications of Einstein’s theory has a long history which reaches back to the early 1920s [
12,
13,
14,
15,
16,
17,
18,
19]. The proposed early amendments of Einstein’s theory were aimed toward the unification of gravity with the other interactions of physics. Besides, the presence of Big Bang singularity, the flatness and horizon problems [
20] led to the statement that Cosmological Standard Model, based on GR and Standard Model of Particles, is inadequate to describe the universe in extreme regimes. From Quantum Field Theory point of view, GR is a
classical theory which does not work at fundamental level in order to achieve a full and comprehensive quantum description of spacetime and gravity.
Despite of modifications, the spirit of GR should be preserved since the only effective request is that the Hilbert-Einstein action is not given a priori. This is the reason why one can deals with
Extended Theories of Gravity and not with
Alternative Gravity. One of the possibilities is that gravitational interaction could act in different ways at different scales. In any case, the robust results of GR, at local and Solar System scales, have to be preserved for consistency (see [
21] for a detailed discussion). This is the case of
-gravity which reduces, in principle, to GR as soon as
.
On the other hand, the strong gravity regime [
22] is another way to check the viability of these theories. In general, the formation and the evolution of stars can be considered as suitable test-beds for Alternative Theories of Gravity. Considering the case of
-gravity, divergences stemming from the functional form of
may prevent the existence of relativistic stars in these theories [
23]. There are also numerical solutions corresponding to static star configurations with strong gravitational fields [
24,
25] where the choice of the equation of state is crucial for the existence of solutions.
Some observed stellar systems are incompatible with the standard models of stellar structure. We refer to anomalous neutron stars, the so called “magnetars” [
26] with masses larger than their expected Volkoff mass. It seems that, on particular length scales, the gravitational force is larger or smaller than the corresponding GR value [
27,
28].
A lot of research work is pointing out that physics of compact objects could be the
experimentum crucis to retain or rule out Alternative Theories of Gravity since precise observational data could give extremely good signatures for the models (see for example [
29,
30,
31,
32,
33,
34,
35,
36,
37,
38]).
Other motivations to modify gravity come from the issue of a full recovering of the Mach principle which leads to assume a varying gravitational coupling. The principle states that the local inertial frame is determined by the averaging process of motion of distant astronomical objects [
40]. This fact implies that the gravitational coupling can be scale-dependent and related to some scalar field. As a consequence, the concept of
inertia and the Equivalence Principle have to be revised. For example, the Brans-Dicke theory [
41] is a preliminary attempt to define an alternative theory of gravity: it takes into account a variable Newton gravitational coupling, whose dynamics is governed by a scalar field non-minimally coupled to the geometry. In such a way, Mach’s principle is better implemented [
41,
42,
43].
As already mentioned, corrections to the gravitational Lagrangian were already considered by several authors [
13,
16,
17] soon after the GR was proposed. From a conceptual viewpoint, there are no reason
a priori to restrict the gravitational Lagrangian to a linear function of the Ricci scalar, minimally coupled with matter [
44]. Since all curvature invariants are at least second order differential, the corrective terms in the field equations will be always at least fourth order. That is why one calls them higher order terms (with respect to GR).
Due to the increasing complexity of the field equations, the main amount of works is related to achieve some formally equivalent theories, where the reduction of the order of field equations can be obtained by considering metric and connections as independent fields [
44,
45,
46,
47,
48]. In addition, many authors exploited the formal relation to scalar-tensor theories to make some statements about the weak field regime [
49]. Moreover other authors discussed a systematic analysis of such theories in the low energy limit [
49,
50,
51,
52,
53,
54,
55,
56,
57,
58,
59]. In particular, Fourth Order Gravity has been studied in the Newtonian limit (weak field and small velocity) and in the Minkowskian limit (e.g., gravitational waves) [
60]. In the former case, one finds modifications of gravitational potential, while in the latter, massive gravitational wave modes come out [
61].
However, the weak field limit of such theories have to be tested against realistic self-gravitating structures. Galactic rotation curves, stellar hydrodynamics and gravitational lensing appear natural candidates as test-bed experiments [
62,
63,
64,
65].
In this paper, starting from Newtonian and post-Newtonian approximations of Extended Gravity, we match the outcomes with some typical astrophysical structures. The Newtonian limit of the general Fourth Order Gravity is considered by generalizing models with generic functions containing other curvature invariants, as Ricci square () and Riemann square (). The spherically symmetric solutions of metric tensor yet present Yukawa-like behaviors, but, in general, one has two characteristic lengths. The Gauss-Bonnet invariant , and the Weyl invariant can be reduced to the above cases.
The plan of the review is the following. In
Section 2 we summarize the basic ingredients of the Newtonian and the post-Newtonian limits [
56].
Section 3 is devoted to the Newtonian limit of Fourth Order Gravity [
57], while, in
Section 3.1, we discuss the solutions generated by pointlike sources with and without gauge conditions. A brief analysis of the free parameters of the theory is performed.
In
Section 4.1 we briefly review the classical hydrostatic problem for stellar structures and in
Section 4.2 we derive the modified Poisson equation in the framework of the Newtonian limit of
-gravity. Then the modified Lané-Emden equation is obtained in
Section 4.3. Analytic and numerical solutions are discussed [
66].
Galactic rotation curves are considered in
Section 5. The main properties of galactic metric are discussed and, in particular, the violation of the Gauss theorem due to the corrections to the Newtonian potential. In
Section 5.1, we discuss models for the mass distribution of galactic components. A qualitative and quantitative comparison between the experimental data and the theoretical predictions of rotation curve [
65] is obtained for our Galaxy and for NGC 3198 in
Section 5.2 by fixing numerically the free parameters of the theory. The motion of massive particles is discussed in
Section 5.3: analogies and differences between general Fourth Order Gravity and
-gravity are pointed out. Fourth Order Gravity is also considered with and without DM. The outcomes are compared with GR. The rotation curves results higher or lower than the same curves in GR, if the squared Ricci scalar contribution is dominant or not with respect to the contribution of the squared Ricci tensor. However, by modifying gravity, also the spatial description of DM could undergoes modifications and the free parameters of model assume different values.
Gravitational lensing is analyzed in the case of pointlike sources (
Section 6.1) and extended sources (
Section 6.2). An important outcome is found in the case of thin lenses: the bending of photons in
-gravity is the same as in GR [
67,
68]. If we add the squared Ricci tensor contribution, we obtain a shift of the image positions (
Section 6.3).
Finally we take into account the weak field limit of scalar-tensor gravity [
69] in the Jordan frame (
Section 7.1) and compare it with the analogous in the Einstein frame (
Section 7.2). Specifically, we consider how physical quantities, like gravitational potentials, derived in the Newtonian approximation for the same scalar-tensor theory, behave in the Jordan and in the Einstein frame. The approach allows to discriminate features that are invariant under conformal transformations and gives contributions in the debate of selecting the true physical frame.The particular case of
-gravity is considered in
Section 7.3.
Discussions and conclusions are drawn in
Section 8.
2. Newtonian and Post-Newtonian Approximations
It is worth discussing some general issues on the Newtonian and post-Newtonian limits. Basically there are some general features one has to take into account when approaching these limits, whatever the underlying theory of gravitation is.
If one consider a system of gravitationally interacting particles of mass
, the kinetic energy
will be, roughly, of the same order of magnitude as the typical potential energy
, with
,
, and
the typical average values of masses, separations, and velocities of these particles. As a consequence:
(for instance, a test particle in a circular orbit of radius
r about a central mass
M will have velocity
v given in Newtonian mechanics by the exact formula
).
The post-Newtonian approximation can be described as a method for obtaining the motion of the system to higher than first order (approximation which coincides with the Newtonian mechanics) with respect to the quantities and assumed small with respect to the squared light speed . This approximation is sometimes referred to as an expansion in inverse powers of the light speed.
The typical values of the Newtonian gravitational potential
U are nowhere larger than
in the Solar System (in geometrized units,
is dimensionless). On the other hand, planetary velocities satisfy the condition
, while (We consider here on the velocity
v in units of the light speed
c) the matter pressure
p experienced inside the Sun and the planets is generally smaller than the matter gravitational energy density
, in other words (Typical values of
are ∼
in the Sun and ∼
in the Earth [
70])
. Furthermore one must consider that even other forms of energy in the Solar System (compressional energy, radiation, thermal energy,
etc.) have small intensities and the specific energy density Π (the ratio of the energy density to the rest-mass density) is related to
U by
(Π is ∼
in the Sun and ∼
in the Earth [
70]). As matter of fact, one can consider that these quantities, as function of the velocity, give second order contributions
Therefore, the velocity
v gives
terms in the velocity expansions,
is of order
,
of
,
is of
, and so on. Considering these approximations, one has
and
Now, particles move along geodesics
where
is the relativistic distance. The Equation (5) can be written in details as
where the set of coordinates adopted is
. In the Newtonian approximation, that is vanishingly small velocities and only first-order terms in the difference between
and the Minkowski metric
, one obtains that the particle motion equations reduce to the standard result
The quantity
is of order
, so that the Newtonian approximation gives
to the order
, that is, to the order
. As a consequence if we would like to search for the post-Newtonian approximation, we need to compute
to the order
. Due to the Equivalence Principle and the differentiability of spacetime manifold, we expect that it should be possible to find out a coordinate system in which the metric tensor is nearly equal to the Minkowski one
, the correction being expandable in powers of
. In other words one has to consider the metric developed as follows (The Greek index runs from 0 to 3; the Latin index runs from 1 to 3)
where
is the Kronecker delta, and for the controvariant form of
, one has
In evaluating
we must take into account that the scale of distance and time, in our systems, are respectively set by
and
, thus the space and time derivatives should be regarded as being of order
Using the above approximations Equation (8) and Equation (9), we have, from the definition of Christoffel symbols
,
The Ricci tensor component are
with △ and ▽, respectively, the Laplacian and the gradient in flat space. The inverse of the metric tensor is defined by means of the equation
with
the Kronecker delta. The relations among the higher than first order terms turn out to be
Finally the Lagrangian of a particle in presence of a gravitational field can be expressed as proportional to the invariant distance
, thus we have :
which, to the
order, reduces to the classic Newtonian Lagrangian of a test particle
, where
. As matter of fact, post-Newtonian physics has to involve higher than
order terms in the Lagrangian.
An important remark concerns the odd-order perturbation terms or . Since, these terms contain odd powers of velocity or of time derivatives, they are related to the energy dissipation or absorption by the system. Nevertheless, the mass-energy conservations prevents the energy and mass losses and, as a consequence, prevents, in the Newtonian limit, terms of and orders in the Lagrangian. If one takes into account contributions higher than order, different theories give different predictions. GR, for example, due to the conservation of post-Newtonian energy, forbids terms of order; on the other hand, terms of order can appear and are related to the energy lost by means of the gravitational radiation.
On the matter side,
i.e., right-hand side of the field equations we start with the general definition of the energy-momentum tensor of a perfect fluid with additional energy Π
The explicit form of the energy-momentum tensor can be derived as follows
where
ρ is the density of energy.
3. The Newtonian Limit of -Gravity
Let us start with a general class of fourth order theories given by the action
where
f is an unspecified function of curvature invariants
,
and
. The term
is the minimally coupled ordinary matter contribution. In the metric approach, the field equations are obtained by varying Equation (18) with respect to
. We get
where
is the energy-momentum tensor of matter,
,
,
,
and
. The convention for Ricci’s tensor is
, while for the Riemann tensor is
. The affinities are the usual Christoffel symbols of the metric. The adopted signature is
(for details, see [
71]). The trace of field Equation (19) is the following
where
is the trace of energy-momentum tensor.
Some authors considered a linear Lagrangian containing not only
X,
Y and
Z but also the first power of curvature invariants
and
. Such a choice is justified because all curvature invariants have the same dimension (
) [
72]. Furthermore, this dependence on these two last invariants is only formal, since from the contracted Bianchi identity (
) we have only one independent invariant. In any linear theory of gravity (the function
f is linear) the terms
and
give us no contribution to the field equations, because they are four-divergences. However, if we consider a function of
or
by varying the action we still could have the four-divergences but we would have the contributions of sixth order differential. For our aim (we want to stay in framework of fourth order differential equations) the most general theory of fourth order is the action Equation (18).
The Newtonian limit analysis starts from the development Equation (8) of the metric tensor. Then we set the metric as
where we note that the presence of function
is superfluous here for our aim but it will be fundamental about the gravitational lensing. The curvature invariants
X,
Y,
Z become
The function
f can be developed as
and analogous relations for partial derivatives of
f are obtained. From the interpretation of stress-energy tensor components Equation (17) as energy density, momentum density and momentum flux, we have
,
and
at the various orders
where
denotes the term in
of order
. In particular
is the density of rest-mass, while
is the non-relativistic part of the energy density.
From the lowest order of field Equation (19) we have
Not only in
-gravity [
55,
56,
73] but also in
-theory a missing cosmological component in the action Equation (18) implies that the space-time is asymptotically Minkowskian. The Equation (19) and Equation (20) at
—order become (We used the properties:
and
)
By introducing the quantities
we get three differential equations for curvature invariant
,
- and
-component of Ricci tensor
The solution for curvature invariant
in third line of Equation (28) is
where
is the Green function of the field operator
. The solution for
, by remembering
, is
where
is the Green function of the field operator
.
The expression Equation (30) is the “modified” gravitational potential (here we have a factor 2) for
-gravity. The solution for the gravitational potential
has a Yukawa-like behaviors ([
55,
57]) depending by a characteristic lengths on whose it evolves.
The
-component of Ricci tensor in terms of metric tensor Equation (12) can be expressed by using the harmonic gauge condition (
) as
. Then the general solution for
from Equation (28), in the harmonic gauge, is
While if we hypothesize
(We choose a system of isotropic coordinates. Generally the set of coordinates
are called standard coordinates if the metric is expressed as
while if one has
the set
is called isotropic coordinates [
52,
75]) we have (without the validity of the harmonic gauge condition)
and the second field equation of Equation (28) becomes
Then the general solution for
from Equation (28) is
and the second line of Equation (32) is mathematically satisfied.
If we consider the trace of the second line of the set Equation (32) we have a mathematical constraint for the gravitational potentials Φ, Ψ
and we can affirm that only in GR the metric potentials are equals (or more generally their difference must be proportional to function
).
3.1. The Pointlike Solution
Let us consider a pointlike source with mass
M. The energy-momentum tensor Equation (17) is (we are not interesting to the internal structure)
where
is the mass density and
satisfies the condition
,
. Since Equation (21) the expression Equation (35) becomes
The energy-momentum tensor satisfies the relations
, where
is the Delta Dirac function. The expressions Equation (29), Equation (30) and Equation (33) are valid for any values of quantities
and
. However, when it wants to calculate the expression of the gravitational potential generated by a given mass distribution it is necessary to determine the algebraic sign of the parameters
and
, because from their signs the nature of Green functions
is determined. The possible choices of Green function, for spherically symmetric systems (
i.e.,
), are the following
where
. The first choice in Equation (37) corresponds to Yukawa-like behavior, while the second one to the oscillating case. However, the Green function for the negative squared mass is, in general, a linear combination of Cos and Sin with coefficients associated to the shift phase. For the sake of simplicity, we assumed here unitary coefficients. Both expressions are a generalization and/or an induced correction of the usual gravitational potential (
), and when
(
i.e.,
from the Equation (27)) we recover the field equations of GR. Independently of algebraic sign of
, one can introduce two scale lengths
. We note that in the case of
-gravity, we obtain only one scale length (
with
) on the which the Ricci scalar evolves [
55,
56,
57], but in
-gravity we have an additional scale length
on the which the Ricci tensor evolves.
If we choose
the curvature invariant
Equation (29) and the metric potentials Φ Equation (30) and Ψ Equation (33) are
where
is the Schwarzschild radius and the relativistic invariant is
The modified gravitational potential by
-gravity is further modified by the presence of functions of
and
. The curvature invariant
(the Ricci scalar) presents a massive propagation and when
we find the mass definition
and propagation mode with
disappear [
55,
56,
57]. Exponential and oscillating behaviors of solutions (37) are compatible with respect to the previous obtained outcomes in the Newtonian limit of
-gravity [
50,
51] . Indeed, in the case of a genuine
-gravity also the mass definition Equation (40) coincides again with the previous results.
The choice of parameters (Yukawa-like case for the Green function) is made also in [
72] and the constraint conditions on the derivatives of
f obtained here (
and
) are still compatible with respect to paper mentioned. Obviously the expressions Φ and Ψ in Equation (38) satisfy the constraint condition Equation (34).
The gravitational potential Φ, solution of Equation (59), has in general a Yukawa-like behavior depending on a characteristic length on which it evolves [
55,
76]. Then as it is evident the Gauss theorem is not valid (It is worth noticing that also if the Gauss theorem does not hold, the Bianchi identities are always valid so the conservation laws are guaranteed) since the force law is not
. The equivalence between a spherically symmetric distribution and point-like distribution is not valid and how the matter is distributed in the space is very important [
55,
56,
57,
58]. However, the field Equation (28) are linear and we can use the superposition principle. If we have a generic density mass
the potential Φ becomes
and in the case of a ball source with radius
ξ the potential Φ outside the source is
where
is a geometric factor depending on the form of source and satisfying the condition
.
Besides the Birkhoff theorem results modified at Newtonian level: the solution can be only factorized by a space-depending function and an arbitrary time-depending function [
56,
76]. Furthermore the correction to the gravitational potential is depending on the only first two derivatives of
f with rispect the
X and the first derivatives with rispect the
Y and
Z in the point
. This means that different analytical theories, from the third derivative perturbation terms on, admit the same Newtonian limit [
55,
56,
57].
For a right physical interpretation of Φ in Equation (38) we also impose the condition
. This is a necessary condition for a correct interpretation of attractive gravitational potential, in addition to the condition
for a well with a negative minimum in
. These conditions can be summarized in terms of scale lengths. In fact we find that the contribution induced by Ricci and Riemann square goes to zero faster than the contribution induced by Ricci scalar:
. In terms of Lagrangian it means that for any
-gravity the correction to Hilbert-Einstein Lagrangian depends more on the contributions of Ricci scalar (
) than ones of Ricci and Riemann square (
). Then, if we suppose
(for a right Newtonian limit), starting from the condition
we get a constraint on the derivatives of
f with respect to curvature invariants
In the case of
-gravity (
) we reobtain the same condition among the first and second derivatives of
f [
55,
56,
57,
58].
3.2. -Gravity and the Quadratic Lagrangian
The outcome Equation (38) can be obtained also by considering the so-called
Quadratic Lagrangian where
,
and
are constants. In this case, [
58] we find two characteristic lengths
,
and the Newtonian limit of theory implies as solution Equation (38). We can state, then, the Newtonian limit of any
-gravity can be reinterpreted by introducing the
Quadratic Lagrangian and the coefficients have to satisfy the following relations
A first considerations about Equation (44) is regarding the characteristic lengths induced by -gravity. The second length is originated from the presence, in the Lagrangian, of Ricci and Riemann tensor square, but also a theory containing only Ricci tensor square could show the same outcome (it is successful replacing the coefficients of Quadratic Lagrangian or renaming the function f). Obviously the same is valid also with the Riemann tensor square alone. Then a such modification of theory enables a massive propagation of Ricci Tensor and, as it is well known in the literature, a substitution of Ricci Scalar with any function of Ricci scalar enables a massive propagation of Ricci scalar. We can, then, affirm that an hypothesis of Lagrangian containing any function of only Ricci scalar and Ricci tensor square is not restrictive and only the experimental constraints can fix the arbitrary parameters.
A second consideration is starting from the Gauss - Bonnet invariant defined by the relation
[
77]. In fact the induced field equations satisfy in four dimensions the following condition
and by substituting them at Newtonian level (
) in the Equation (19) we find the field equations (ever at Newtonian Level) of
Quadratic Lagrangian which can be recasted as
The theory of gravity represented by the Lagrangian Equation (46) is the more general theory considering all invariant curvatures, but we have to take into account a degeneracy. In fact we have different
-gravity describing the same Newtonian Limit (see [
55,
56,
57,
58] for details). The solution of field equations or the observable quantities, as the galactic rotation curve, are parameterized by the derivatives of
f, then we have different functions
which admit the same physics in the weak field limit.
5. Rotation Curves of Galaxies
Another important astrophysical application of the above Newtonian limit of Fourth Order Gravity is related to the rotation curves of spiral galaxies. The approach can be considered also an alternative test for DM behavior.
In general, the motion of body embedded in the gravitational field is given by geodesic Equation (5) and in the Newtonian limit, formally, we obtain the classical structure of the motion Equation (7)
but the gravitational potential is given by Equation (38) or generally by Equation (41). The study of motion is very simple if we consider a particular symmetry of mass distribution
ρ, otherwise the analytical solutions are not available. Our aim is to evaluate the corrections to the classical motion in the easiest situation: the circular motion. In this case we do not consider the radial and vertical motion. The condition of stationary motion on the circular orbit is
where
is the velocity.
The distribution of mass can be modeled simply by introducing two sets of coordinates: the spherical coordinates
and the cylindrical coordinates
. An useful mathematical tool is the Gauss flux theorem for gravity:
The gravitational flux through any closed surface is proportional to the enclosed mass. The law is expressed in terms of the gravitational field. The gravitational field
is defined so that the gravitational force experienced by a particle with mass
m is
. Since the Newtonian mechanics satisfies this theorem and, by thinking to a spherical system of mass distribution, we get, from Equation (82), the equation
where
is the only mass enclosed in the sphere with radius
r. The Green function of the
-gravity (
), instead, does not satisfy the theorem [
58]. In this case we must consider directly the gravitational potential Equation (41) generated by using the superposition principle.
Apart the mathematical difficulties incoming from the research of gravitational potential for a given mass distribution, the non-validity of Gauss theorem implies, for example, that a sphere can not be reduced to a point (see solution Equation (42)). In fact the gravitational potential generated by a ball (also with constant density) is depending also on the Fourier transform of ball [
58]. However, our aim is to consider not the simple case of motion of body in the vacuum, but the more interesting case of motion in the matter. So we must leave any possibility of idealization and consider directly the calculation of the potential Equation (41).
Two remarks on the Equation (41) are needed. The two corrections have different algebraic sign, and in particular the Yukawa correction with implies a stronger gravitational force, while the second one (purely induced by Ricci and Riemann square) contributes with a repulsive force. By remembering that the motivations of extending the outcome of GR to new theories is supported by missing matter justifying the flat rotation curves of galaxies, the first correction is a nice candidate. A crucial point is given by the spatial range of correction. In fact the Yukawa corrections imply a massive propagation; then, more massive is the particle, shorter is the spatial range.
At last in Newtonian Mechanics the Gauss theorem gives us a spherically symmetric gravitational potential even if the spherically symmetric source is rotating. In GR as well as in Fourth Order Gravity, however, the rotating spherically symmetric source generates an axially symmetric space-time (the well known Kerr metric) and only if the source is at rest one has the space-time with the same symmetry (the well known Schwarzschild metric). Then the galaxy being a rotating system will generate an axially symmetric space-time while we are using the solution Equation (41). This aspect is not contradictory because the solutions are calculated in the Newtonian limit (
i.e.,
) and under this assumption the Kerr metric collapses into Schwarzschild metric. In fact we have
where
,
,
and
L is the angular momentum along the
z-axis.
5.1. Mass Models for Galaxies
From the point of view of morphology, a galaxy can be modeled by considering at least two components: the bulge and the disk. Obviously the galaxy is a more complicated structure and there are others components, but for our aim this idealization is satisfactory. The bulge, generally, can be represented easily with cylindrical coordinates (but in a more crude idealization it is like a ball), while the disk has a radius bigger than the thickness. However, we find that the rotation curve does not present the Keplerian behavior outside the matter, but the curve remain constant for any distance. Then we must formulate the existence of exotic matter that can justify the experimental observation. A simple discussion about the distribution of DM can be formulated by imposing the constant value of velocity in Equation (83) for large distances. In fact we find
A matter distribution as Equation (85) has a problem when we want to calculate the total mass. In fact if we have , the mass diverges. A such exotic behavior seems no-physical, but this outcome is only the consequence of constant rotation curve. In fact by increasing the distance also the mass must increase with the power law for any distance Equation (83). However, since the Gauss theorem holds in GR, the matter outside the sphere of integration does not contribute to the gravitational flux and then we do not have difference with respect to the ordinary matter.
The same arguments are not valid in -gravity: the non-viability of Gauss theorem implies that the range of integration of DM could cover all range and also the matter outside is considered. A cut off is needed now. Here then, for completeness, we consider that the galaxy is composed by three components: the bulge, the disk and an alone of DM.
It should be noted that the spatial behaviors of DM (generally spherically symmetric) are made only a posteriori: the cornerstones of rotation curves study are the GR and the distribution of ordinary matter. Only after this assumption the distribution of DM is such as to justify the gap between the theoretical prediction and the experimental observation.
Before jumping to analysis of rotation curves we want to resume the principal spatial distributions of mass in the three galactic components. In literature there are many forms of density, but it is possible to resume them as follows.
More realistic models are the ones with mass density depending also on the
z-coordinate for bulge and disk. Particularly one can consider the following choice
In this choice, suggested by Dehnen & Binney [
80], the bulge is described as a truncated power—law model (first line of Equation (86)) where
.
β,
γ,
q and
are the parameters. While for the disk, one adopted a double exponential where the total mass is
with
and
[
81]. Finally in the case of DM the density profile is the Navarro-Frenk-White model [
7,
82] where
,
and
are the virial mass and virial radius and
is a characteristic length. For the Milky Way
.
Leaving the axis-symmetry one can consider a more simple model: the spherical symmetry model. With this approach one has [
83,
84,
85]
where
,
,
,
,
,
, are the radii and the masses of bulge, disk and DM.
and
are dimensionless constants. The density profile of bulge considered is the well-known formula of de Vaucouleurs [
86].
A simpler model, resuming the previous ones, can be
where
is the Gamma function,
is a free parameter and
is the ratio of DM inside the sphere with radius
with respect to the total DM. The radius
and the mass
play conceptually the same role respectively of
and
. However, as before claimed, the hot point is the choice of DM model. Given all these models it is almost normal that there are many different estimates of DM. Therefore, the parameters of DM model may not be unique [
87].
5.2. Rotation Curves in -Gravity
We are interested to evaluate the circular velocity Equation (82) adopting the mass models Equation (88). So the potential Equation (41), by setting
, becomes
where Ξ is the distance on which we observe the rotation curve,
is the elliptic function and the modulus of distance is given by
The constant
a is a scale factor defined by the substitution
so all quantities are dimensionless. At last, by remembering
the circular speed Equation (82) in the galactic plan is given by
In the
Figure 2 and
Figure 3, we report the spatial behaviors of rotation curve induced by the bulge and disk component. The behavior for any component is compared in the framework of GR, Fourth Order Gravity (FOG), GR + DM and FOG + DM. The values of free parameters of model are in the first line in
Table 1 and refereing to Milky Way. The values of scale lengths
,
are set at
,
. In both components we note for
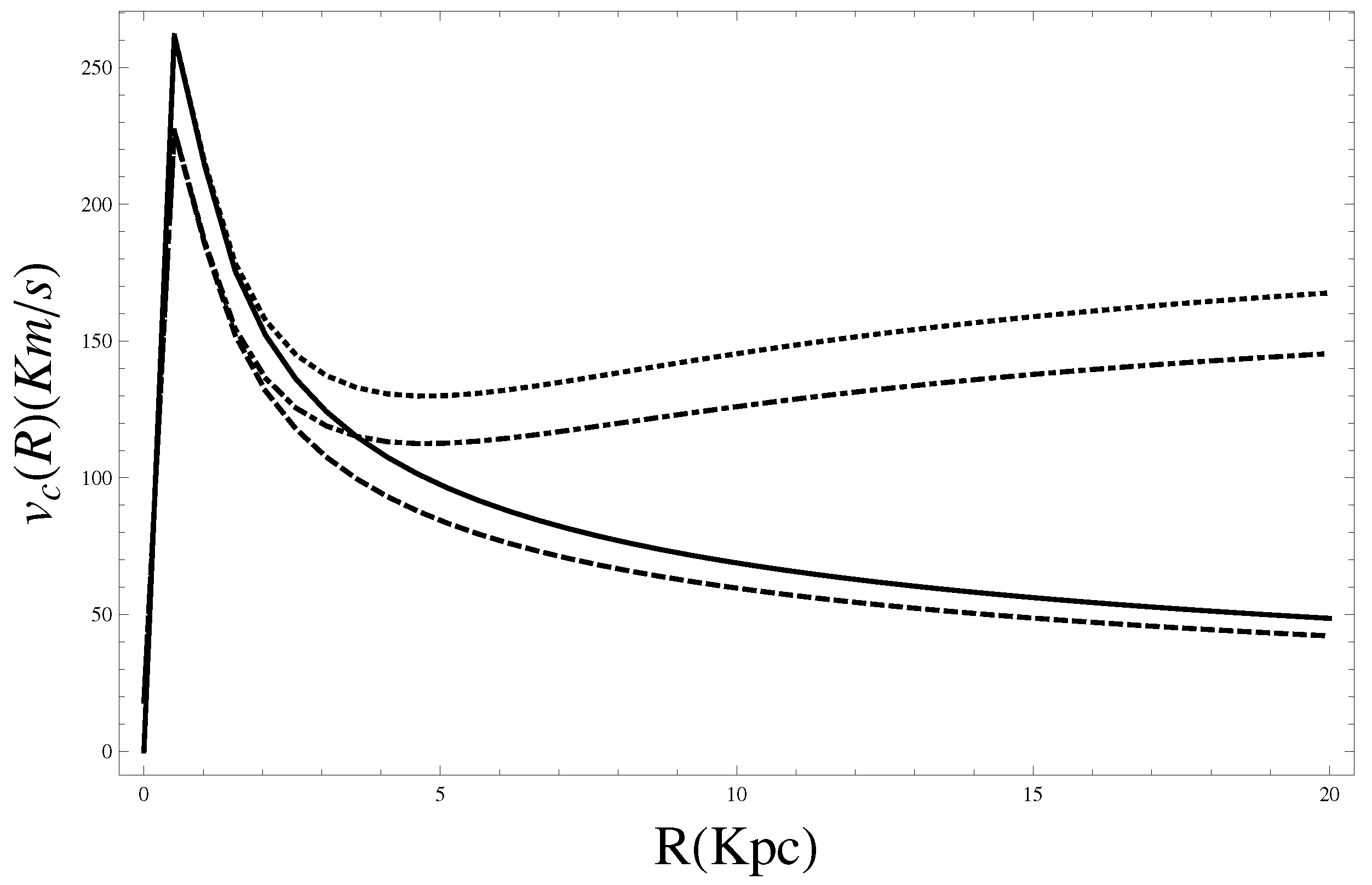
the Keplerian behavior, while it is missing only when we consider also the DM component. The shape of the rotation curve is similar to ones obtained by varying the total mass and scale radius. For a given scale radius, the peak velocity varies proportionally to a square root of the mass. For a fixed total mass, the peak-velocity position moves inversely proportionally to the scale radius, or along a Keplerian line.
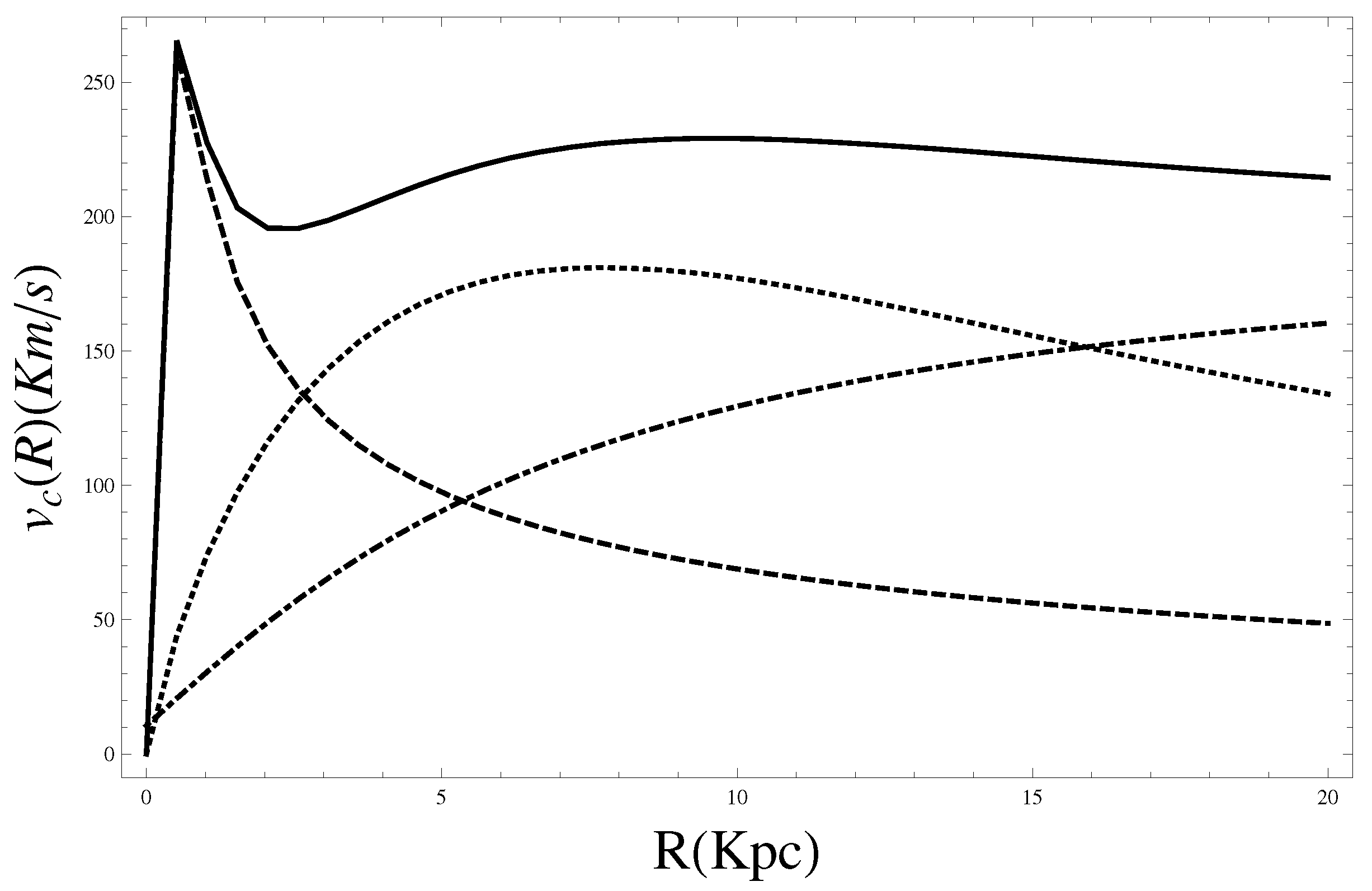
Figure 2.
The rotation curve induced by bulge component (first line of Equation (88)): GR (dashed line), GR + DM (dashed and dotted line), FOG (solid line) and FOG + DM (dotted line).
Figure 2.
The rotation curve induced by bulge component (first line of Equation (88)): GR (dashed line), GR + DM (dashed and dotted line), FOG (solid line) and FOG + DM (dotted line).
As it is known in literature
-gravity, and in particular
-gravity, mimics a partial contribution of DM. In fact the corrective term
contributes to enhance the attraction and thus the rotation curve must increase to balance the force. In the case of the other term, we have a correction
that contributes, being repulsive, to decrease the velocity. However, in both cases these terms are asymptotically null and
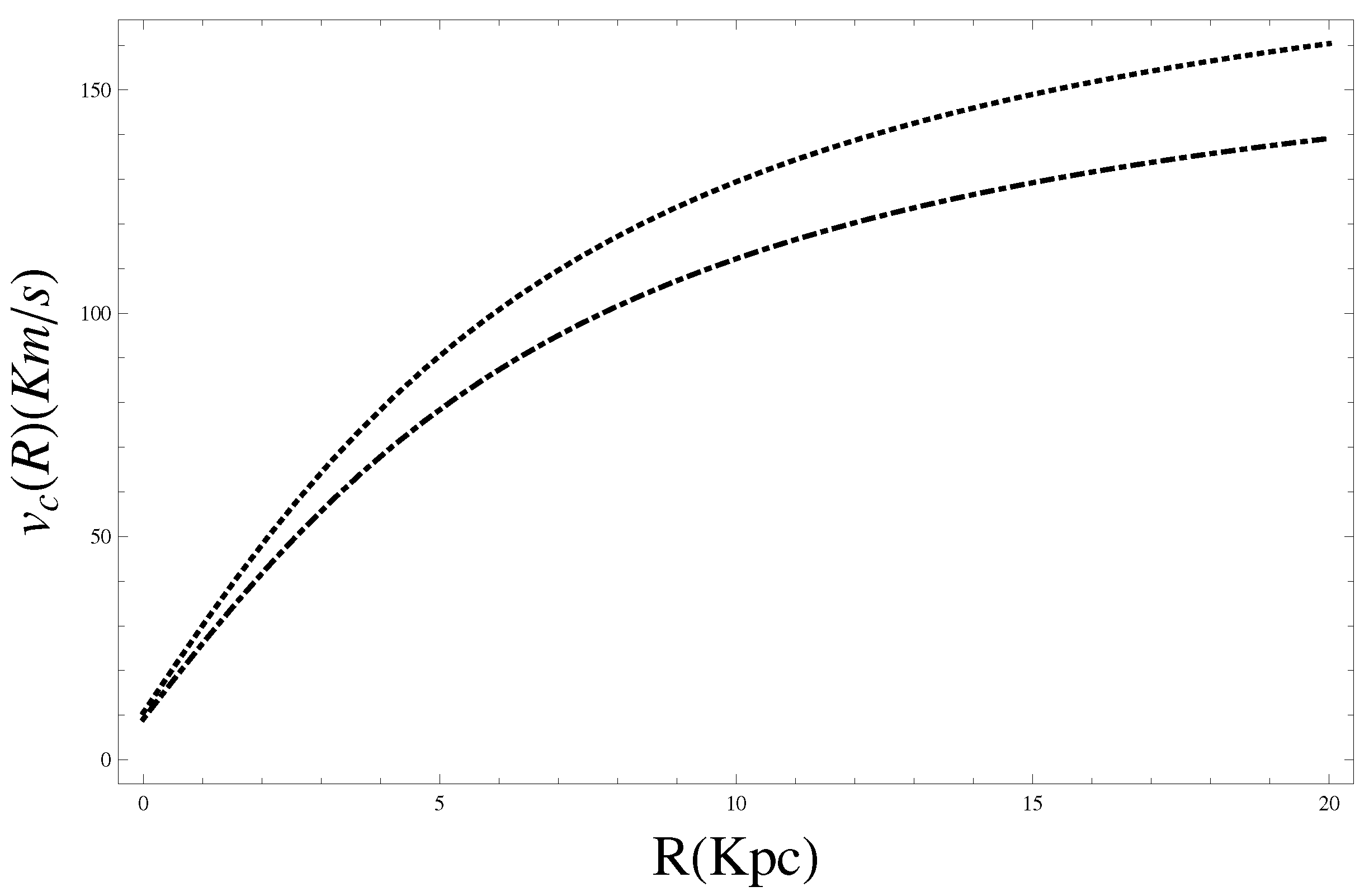
-gravity and GR must lead to the same result. Only with the addition of DM it is possible to raise the curve and have almost constant values. In the
Figure 4 we report the component of rotation curve induced by only auto-gravitating DM.
Figure 3.
The rotation curve induced by disk component (second line of Equation (88)): GR (dashed line), GR + DM (dashed and dotted line), FOG (solid line) and FOG + DM (dotted line).
Figure 3.
The rotation curve induced by disk component (second line of Equation (88)): GR (dashed line), GR + DM (dashed and dotted line), FOG (solid line) and FOG + DM (dotted line).
Table 1.
Parameters of models Equation Equation (88). The unity of mass is and .
Table 1.
Parameters of models Equation Equation (88). The unity of mass is and .
| Galaxy | | | γ | | | | | α | Ξ |
|---|
| Milky Way | 0.77 | 0.5 | 1.5 | 5.20 | 3.5 | 1.68 | 5.5 | 0.50 | 20 |
| NGC 3198 | 0 | / | / | 2.60 | 3.5 | 0.84 | 5.5 | 0.53 | 20 |
Figure 4.
The rotation curve induced by DM component (third line of Equation (88)): GR + DM (dashed and dotted line) and FOG + DM (dotted line).
Figure 4.
The rotation curve induced by DM component (third line of Equation (88)): GR + DM (dashed and dotted line) and FOG + DM (dotted line).
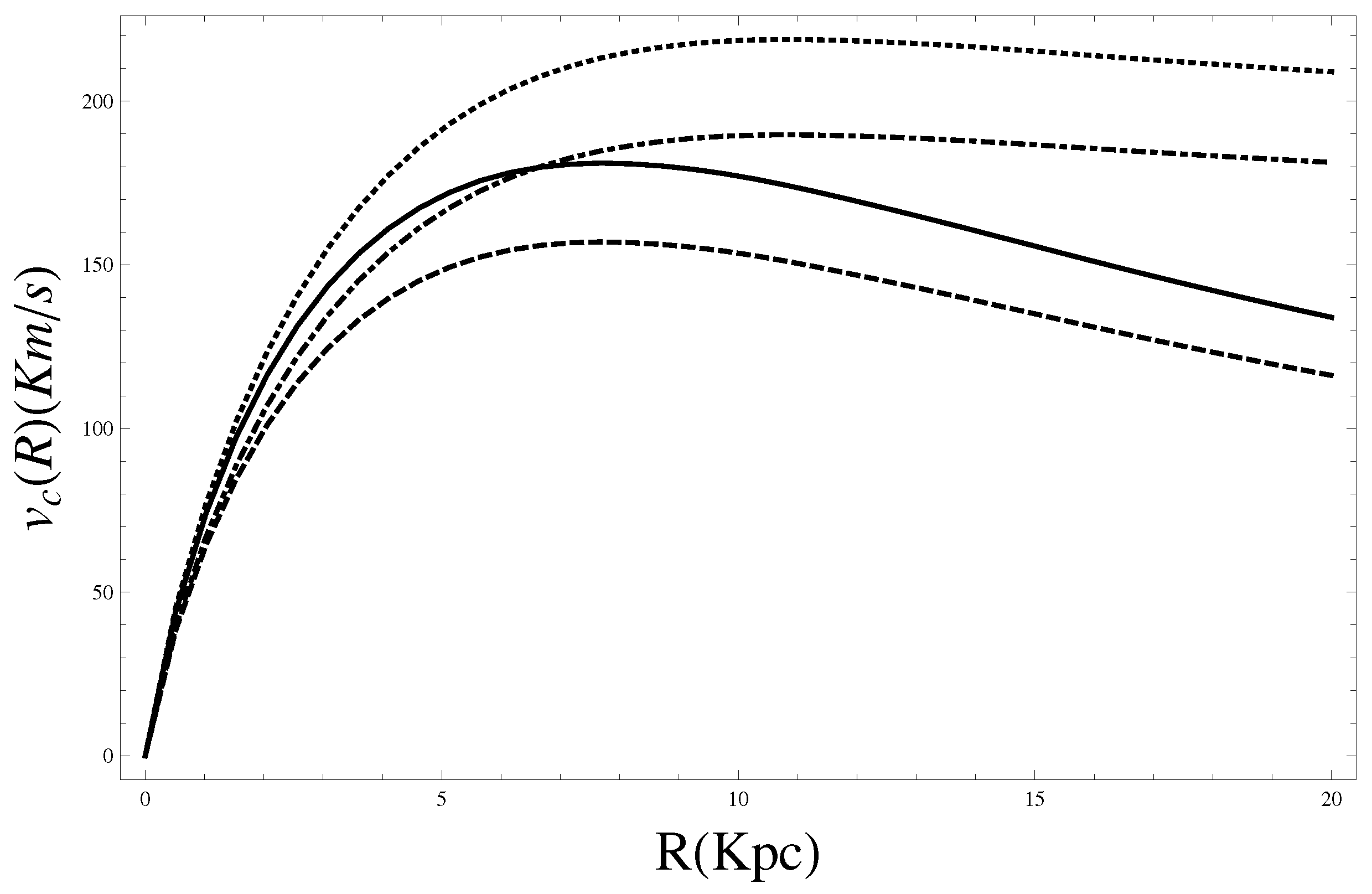
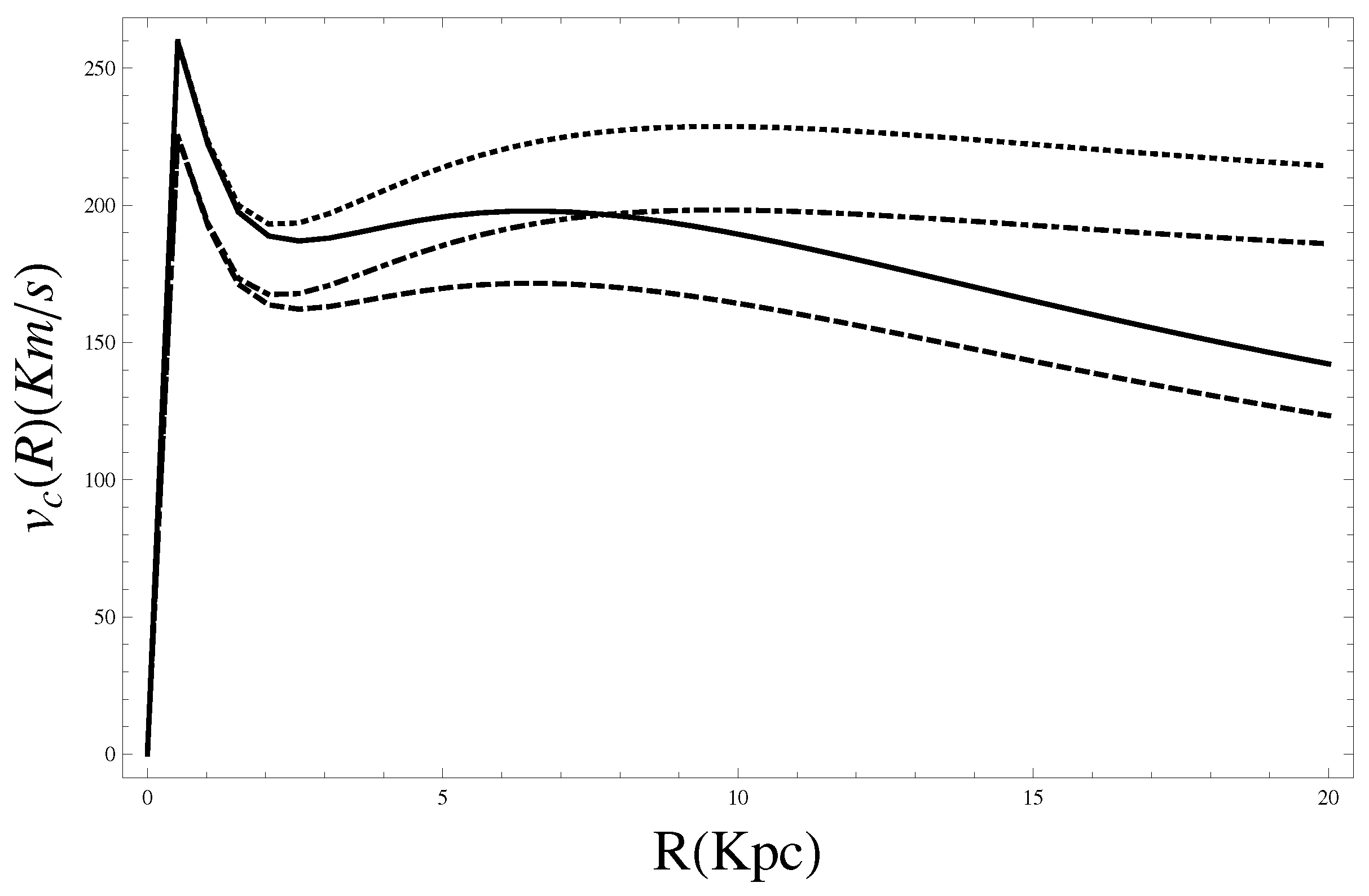
In
Figure 5 we show the global behavior (experimentally expected) of rotation curve compared with respect to the bulge, disk and DM component for the
-gravity. While in
Figure 6 there is the global rotation curve in the framework of GR, FOG, GR + DM and FOG + DM. At last in
Figure 7 we replicate the outcome of
Figure 6 but we inserted the value
. In this case the rotation curve induced by
-gravity allows lower values as previously we claimed.
Figure 5.
Comparison between the rotation curves of galactic components: bulge (dashed line), disk (dotted line), DM (dotted and dashed line) and the global galactic rotation curve (solid line). All curves have been valuated in the framework of FOG + DM.
Figure 5.
Comparison between the rotation curves of galactic components: bulge (dashed line), disk (dotted line), DM (dotted and dashed line) and the global galactic rotation curve (solid line). All curves have been valuated in the framework of FOG + DM.
Figure 6.
The global rotation curve in the framework of GR (dashed line), GR + DM (dashed and dotted line), FOG (solid line) and FOG + DM (dotted line). The values of “masses” are and .
Figure 6.
The global rotation curve in the framework of GR (dashed line), GR + DM (dashed and dotted line), FOG (solid line) and FOG + DM (dotted line). The values of “masses” are and .
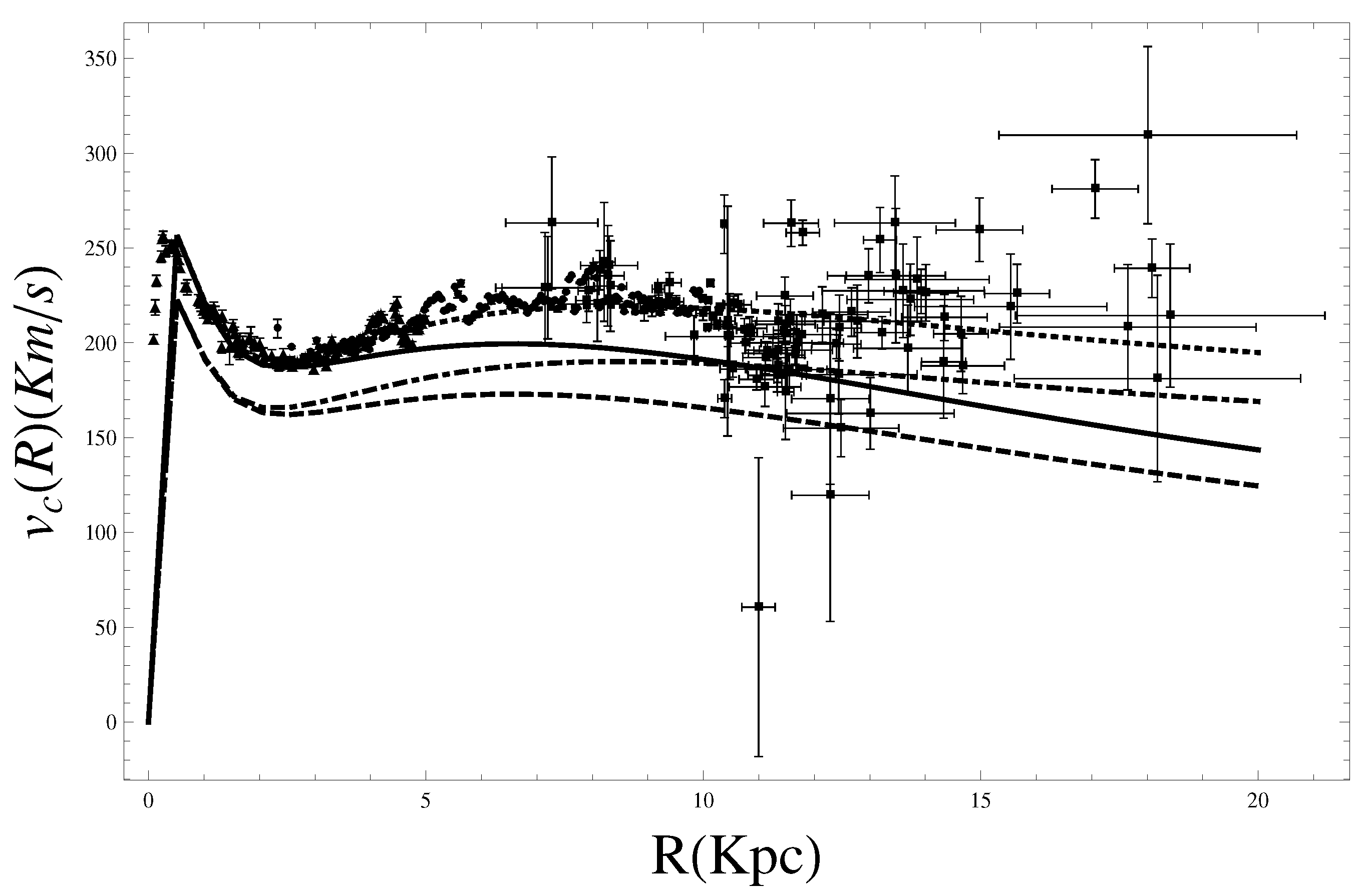
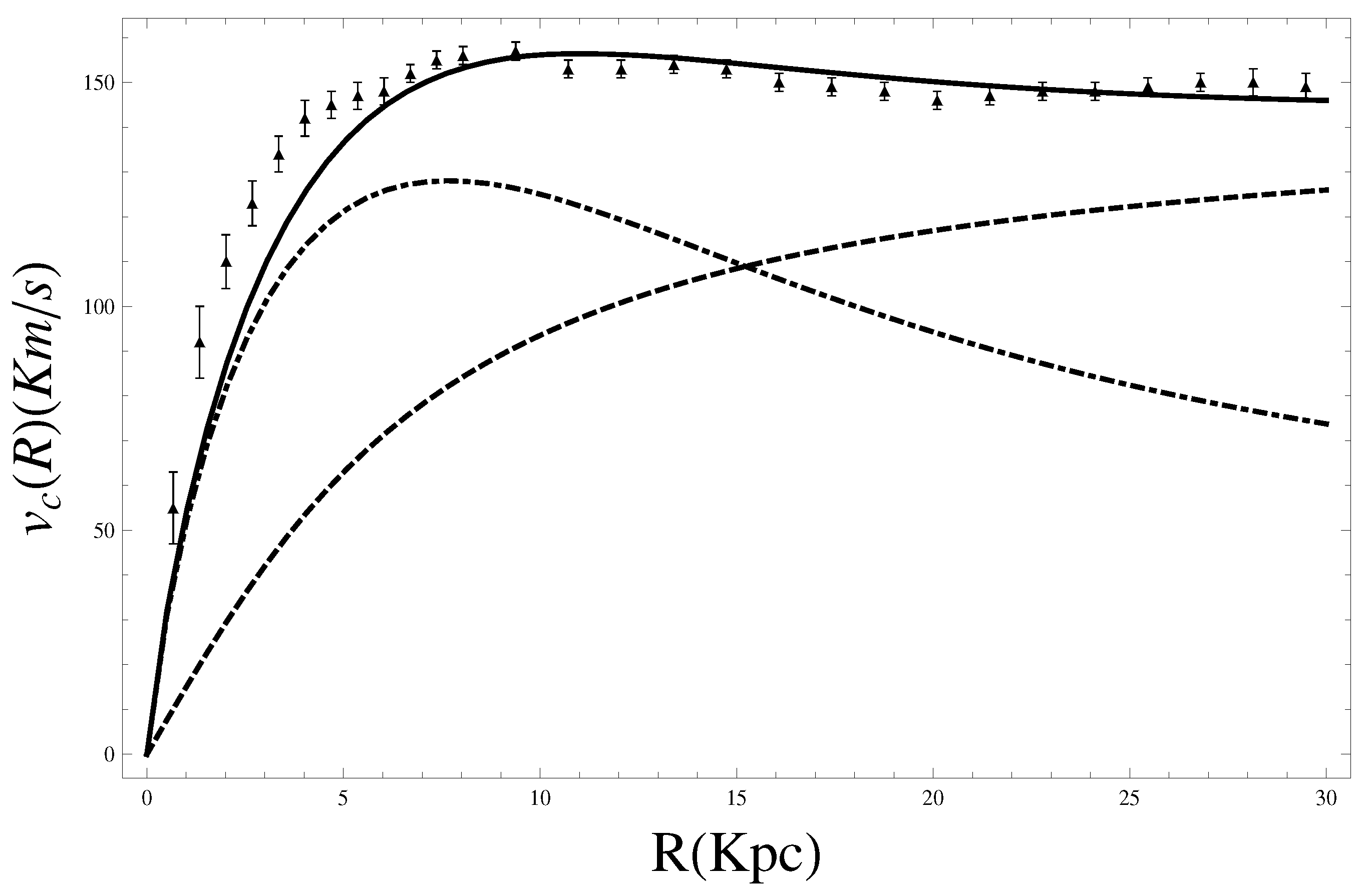
From the experimental point of view we used an updated rotation curve of Milky Way by integrating the existing data from the literature, and plot them in the same scale [
88]. The data used are available in a digitized [
89]. The unified rotation curve shows clearly the three dominant components: bulge, disk, and flat rotation due to the DM [
90,
91,
92,
93,
94,
95,
96,
97]. These data, finally, have been updated further by [
98]. The whole set of data are plotted in
Figure 8 and on them the theoretical rotation curve induced by
-gravity with DM has been superimposed. The values of best fit are shown in
Table 1 with
and
.
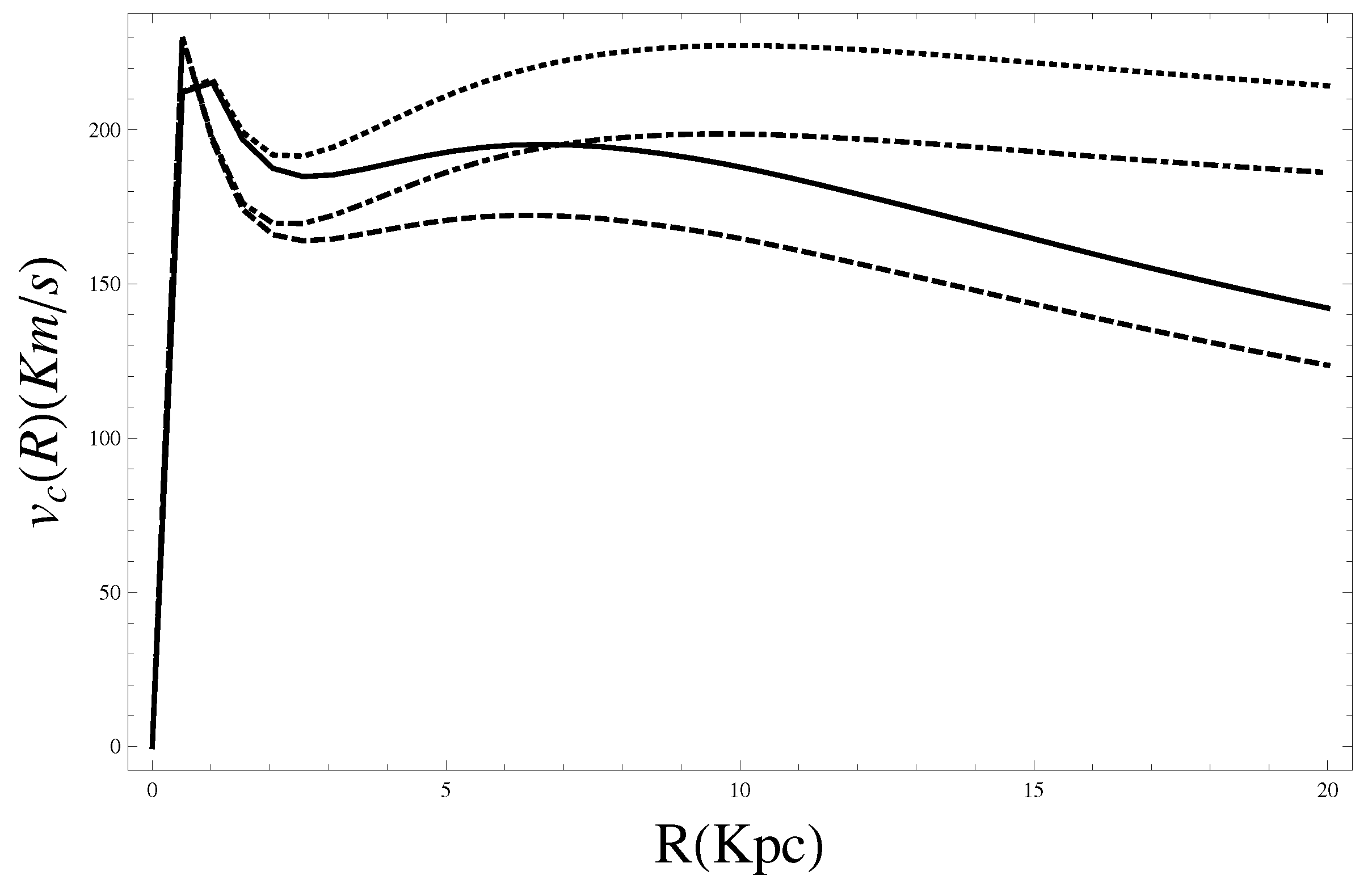
Figure 7.
The global rotation curve in the framework of GR (dashed line), GR + DM (dashed and dotted line), FOG (solid line) and FOG + DM (dotted line). The values of “masses” are and .
Figure 7.
The global rotation curve in the framework of GR (dashed line), GR + DM (dashed and dotted line), FOG (solid line) and FOG + DM (dotted line). The values of “masses” are and .
Figure 8.
Superposition of theoretical behaviors (GR (dashed line), GR + DM (dashed and dotted line), FOG (solid line), FOG + DM (dotted line)) on the experimental data for Milky Way. The mass model used is shown in Equation (88) and the values of parameters are in
Table 1. The values of “masses” are
and
.
Figure 8.
Superposition of theoretical behaviors (GR (dashed line), GR + DM (dashed and dotted line), FOG (solid line), FOG + DM (dotted line)) on the experimental data for Milky Way. The mass model used is shown in Equation (88) and the values of parameters are in
Table 1. The values of “masses” are
and
.
The same mass model Equation (88) has been considered also for the galaxy NGC 3198. This galaxy has been chosen since the bulge is missing. Then we set
in the Equation (89). In
Figure 9 we show the experimental data [
99] and the superposition of theoretical behavior. Also in this case we find a nice outcome for a new set of parameters shown in
Table 1, while the values of
and
are the same of Milky Way.
The initial aim, i.e., to extend the GR to a new class of theories, as we claimed in the introduction, is to justify the rotation curve without the DM component. From the previous outcomes, we see that even if the -gravity, or better a -gravity, admits a stronger attractive force, it is unable to realize our aim. Also in this framework we need Dark Matter. Obviously we need a smaller amount of DM on the middle distances, but for large distances we have the same problems of GR.
Figure 9.
Superposition of theoretical behaviors (GR (dashed line), GR + DM (dashed and dotted line), FOG (solid line), FOG + DM (dotted line)) on the experimental data for NGC 3198. The mass model used is shown in Equation (88) and the values of parameters are in
Table 1. The values of “masses” are
and
.
Figure 9.
Superposition of theoretical behaviors (GR (dashed line), GR + DM (dashed and dotted line), FOG (solid line), FOG + DM (dotted line)) on the experimental data for NGC 3198. The mass model used is shown in Equation (88) and the values of parameters are in
Table 1. The values of “masses” are
and
.
5.3. Rotation Curves in -Gravity and -Gravity
The problem of DM seems to have been solved in literature, in the framework of
-gravity, by considering the Lagrangian
with
[
59,
62]. In these papers the gravitational potential for a point-like source can be
where
is a characteristic length and
β is a dimensionless parameter. To recover the condition
one must have
. In the case
the GR is found.
We comment about the physical behavior of potential Equation (92) and we want to add some reflections considering the result of the rotation curve shown above. Before to analyze the mathematical properties of metric linked to potential Equation (92), we want to show the different values of correction to the Newtonian potential. In
Figure 10 we report the radial behavior of the corrections to
for the potentials Equation (38) and Equation (92) (to minimize the difference we considered only
-gravity). From the plot we note a discrepancy between the two corrections. The correction by
-gravity acts over distances much smaller, while the correction induced by
-gravity provides a potential nearly constant over large intervals and slowly goes to zero (
). For this aspect the potential Equation (92) does not need the DM component. Then with a procedure of fine tuning of
and
β it was possible to justify the experimental rotation curve for a wide class of galaxies [
62] when
. This choice was possible because there must be a relationship
so that the potential Equation (92) was compatible with respect to the field equations. These are the positive aspects of the potential Equation (92) used in [
59,
62].
Figure 10.
Comparison between the corrective terms induced by -gravity (, solid line) and -gravity (, dashed line). , and . The unities for and are arbitrary. The dashed curve shows a very slow ascent.
Figure 10.
Comparison between the corrective terms induced by -gravity (, solid line) and -gravity (, dashed line). , and . The unities for and are arbitrary. The dashed curve shows a very slow ascent.
We conclude this section by reviewing the fundamental weaknesses of
-gravity.
The potential Equation (92) presents an analogous behavior of potential Equation (38). In fact for one has then the correction is “repulsive” like one induced by Ricci tensor square, while for one has an attractive correction. Now by remembering the reason of extension of GR, now we have unlike a repulsive contribution for . If in -gravity we can delete the Ricci tensor square contribution and we have only the -gravity, in -gravity we must collapse only in GR.
The potential Equation (92) belongs to general class of solutions for
-gravity classified by a perturbative method [
58], but the solutions are
n-independent. Obviously the general solutions (it would be hard challenge to find them) are
n-dependent, but at first order with respect to the perturbative parameter and in the vacuum (This parameter is generally
, but the analysis is the same if we consider the dimensionless ratio
) the field equations are identically vanishing. So we say that the presence of matter has been not considered and the choice of arbitrary constant has been evaluated only by matching
-gravity with GR in the limit
. In fact by solving the field equations correctly in presence of matter (also with the point-like source) we would obtain solutions depending on the perturbative parameter and the technique is misplaced.
For these two aspects, but especially for the second point,
-gravity does not admit the Newtonian limit if
. The potential Equation (92) does not follow a correct framework when extending the GR to the new theories we want to generalize the Newtonian potential. Generally all theories without Ricci scalar in the Lagrangian suffer from the same problem. For example also
-gravity is in the same situation: is not possible to extend the solution in the matter [
58].
Although we have solutions as with additional asymptotically flat terms, it is not automatic the assertion that these solutions are the Newtonian limit of theory.
Let us analyze now the mathematical properties of the metric trying to justify the difference of spatial behaviors in
Figure 10. To simplify the calculation we choose the set of the standard coordinates. The metric Equation (21), from the expressions Equation (38), becomes (The set of standard coordinates is defined by the condition to obtain the standard definition of the circumference with radius
r. From the metric tensor Equation (21) we must impose the condition
for the new radial coordinate)
where
is the solid angle, while the element of distance linked to potential Equation (92) can be written as follows
where
is the the potential Equation (92) and
is the other potential missing in the paper [
62]. The metrics Equation (93) and Equation (38) represent the same space-time at first order of
. However, in their analysis the knowledge of last potential is useless because its contribution in the geodesic motion is at fourth order. By following the paradigm of weak field limit at small velocity [
55,
56,
57] for the
-gravity we find
where
and
are constants depending, respectively, on the value of
β and on the integral operation, while the Ricci scalar
R could be an arbitrary function. In fact it needs some comment about the index
n in the Ricci scalar. If
n is a integer number, then the Ricci scalar can assume any value and can be also a generic space depending function. More attention is needed if
n is a rational number. The field Equation (56) take into account up to third derivatives with respect to the Ricci scalar, then we must ensure that the function
and its derivatives are always well defined [
58]. In this case for
the solution Ricci flat (
) or space depending and asymptotically vanishing are excluded. Only solutions with constant values are allowed, but the algebraic sign is crucial. A such behavior is expected any time we have the condition
[
58]. Now in all these considerations we do not recover the condition
: then we have a theory which does not provide the Minkowskian limit. It is using the first perturbative contribution of a metric component (providing the flatness at infinity), while other contributions in the remaining metric components (negligible in the Newtonian limit) do not cover the same asymptotic limit. Then only for
we can have the flatness at infinity.
Then we could say that for the Minkowskian limit is recovered but a such perturbative approach can be performed only in the vacuum. The objection previously shown comes back. Up to third order ( or ) the geometrical side of field equation is identically null, but the matter side could not be null at first order ( or ).
The class of
-gravity are examples of theories where the weak field limit procedure does not generate automatically the Minkowskian limit. In fact only if we consider theories satisfying the condition
[
58], their weak field limit is compatible with the request of asymptotically flatness. Moreover
-gravity mimicking an additional source due to its scalar curvature [
55,
56,
60] we would have a constant matter that pervades all space giving us a justification of more intense gravitational potential. In addition if
we do not have the Minkowskian limit, but we can interpret the apparent mass, only from the experimental point of view, as DM. These aspects, then, can be a mathematical motivation for different shape of point-like gravitational potential, but also source of further attention.
8. Discussion and Conclusions
The weak field limit of Extended Theories of Gravity has been discussed in view of some relevant astrophysical issues. In particular, we have considered the hydrostatic equilibrium of stars, the galactic rotation curves and the gravitational lensing. Finally, we have analyzed the relations between the Jordan and Einstein frames in the same limit and focused our attention on the relations linking the gravitational potentials in both frames.
Specifically, we have considered theories containing generic functions of the Ricci scalar R, the squared Ricci tensor and the squared Riemann tensor . We obtain the analogy, in the Newtonian limit, with the so-called Quadratic Lagrangian containing the squared Ricci scalar and the squared Ricci tensor in addition to the linear term R. All contributions to the field equations related to the squared Riemann curvature invariant can be expressed by the other two curvature invariants (squared Ricci tensor and squared Ricci scalar) via the Gauss-Bonnet invariant. It is straightforward to show that the spherically symmetric solutions show a Yukawa-like dependence with two characteristic lengths. An important result is that, for generic Fourth Order Gravity models, two non-equivalent metric potentials come out. In the limit , only the Newtonian potential is present as it has to be in GR. The presence of two gravitational potentials, together with the non-validity of the Birkhoff and Gauss theorems, are the main differences between Fourth Order Gravity and GR.
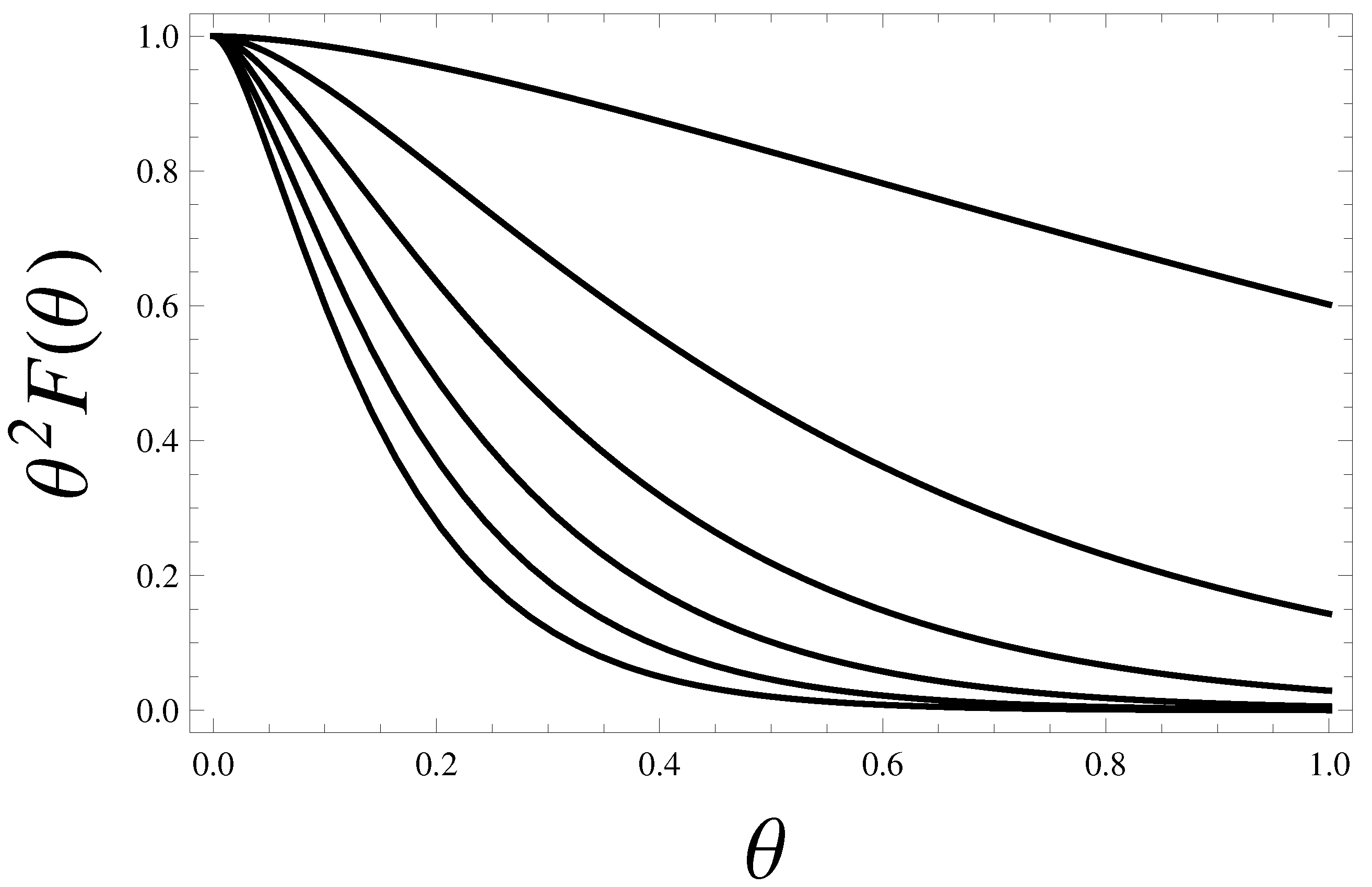
Coming to the astrophysical applications, we adopted a polytropic equation of state relating the mass density to the pressure and derived a
modified Lané-Emden equation whose solutions can be compared to the analogous solutions coming from GR. As soon as one considers the limit
, the standard hydrostatic equilibrium theory is fully recovered. Since the Gauss theorem is not valid in this context and the
modified Lané-Emden equation is an integro-differential equation, the mass distribution plays a crucial role. The correlation between two points in the star is given by a Yukawa-like term of the corresponding Green function. These feature opens the possibility to address the structure of anomalous stars that, in standard stellar theory could not be consistently achieved [
38].
As further astrophysical application, we have considered the rotation curves of spiral galaxies. Starting from the pointlike solutions and having formulated the expression of the rotation curves, we considered the principal galactic components (
i.e., the bulge, the disk and the halo). The theoretical curves have been compared with the experimental data. The rotation curves have been evaluated by considering the bulge and the DM component spherically symmetric and a circular disk symmetric with respect to a plane where the radius is larger than the thickness. Also in the case of Fourth Order Gravity with standard matter, we find that the rotation curve has the Keplerian behavior and only if one adds some DM component, a reliable matching with experimental data is achieved. However, the DM hypothesis gives rise to two serious problems: since the DM distribution is diverging when we consider the whole amount of mass, it is crucial the choice of the cut-off inside the integral. Another critical point is the choice of the mass model and the values of free parameters. These shortcomings can be consistently addressed by introducing a further scalar field as in [
108]. Such scalar field, however, can be reinterpreted in terms of curvature invariants [
108].
The gravitational lensing approach in Fourth Order Gravity has been pursued on two steps: firstly we considered a point-like source and the motion of photons. In the second step, we took into account the geodesic motion and reformulated the light deflection for a generic matter distribution. In the case of an axially symmetric matter distribution, we obtained the standard relation between the deflection angle and the orthogonal gradient of metric potentials. Otherwise, the angle is depending also on the travel direction of the photon. In particular, if there is a z-symmetry, the deflection angle does not depend explicitly on the parameters of Fourth Order Gravity. Starting from the definition of the masses, one have to note that the contribution of a generic function of the Ricci scalar is only in the missing parameter. Then -gravity admits the same geodesic trajectory of GR. If one wants to take into account corrections to GR, one needs to add a generic function of the squared Ricci tensor into the Hilbert-Einstein action. In this case, we find the deflection angle smaller than the one of GR. The mathematical motivation is a consequence of the algebraic sign of the parameter in front of the squared Ricci tensor. In fact it is different with respect to the GR term and we can interpret it as a “repulsive force” giving a lower curvature for the photon trajectory.
A similar result is found for the galactic rotation curve, where the contribution of the squared Ricci tensor gives a lower rotation velocity profile than the one derived from the weak field limit of GR. However, if we estimate the weight of the corrections induced by -gravity, we have a perfect agreement with the GR from the point of view of gravitational lensing. Only by adding in the action, we induce modifications in both gravitational lensing and galactic rotation profiles.
Finally, we have tackle the debate of selecting the physical frame by conformal transformations. Specifically, we have shown how the Newtonian limit behaves in the Jordan and in the Einstein frame. The general result is that Newtonian potentials, masses and other physical quantities can be compared in both frames once the perturbative analysis is correctly performed. The main result is that if such an analysis is carefully developed in a frame, the perturbative process can be controlled step by step leading to coherent results in both frames. In other words, also if the gauge invariance is broken, there is the possibility to control conformal quantities and fix the observables.