1. Introduction
Alternative theories of gravity (for reviews see [
1,
2]) have become more popular in recent years due to their ability to account for astrophysical observations without using dark matter (DM) and dark energy (DE). However, the cosmological constant-cold dark matter model (ΛCDM) remains the standard explanation of current astrophysical knowledge [
3].
Fourth-order conformal Weyl gravity (CG, for short, in the following) is the name given to an alternative gravitational theory, following the original work by Weyl [
4], not to be confused with other theories based on conformal invariance. It was shown that CG [
5,
6] can describe the rotation curves of galaxies without DM [
1,
7,
8,
9,
10,
11,
12] and can give rise to the accelerated expansion of the universe without resorting to DE [
1,
13].
A similar, but different approach to conformal cosmology was proposed by the current author in a series of papers [
14,
15,
16] introducing a model which was called kinematical conformal cosmology [
14] (KCC in the following) since it was based on purely kinematic considerations, without using any dynamical equation of state for the Universe. This model was able to account for the accelerated expansion of the Universe [
15] and might also be able to explain the origin of some gravitational anomalies, such as the Pioneer Anomaly [
16] and the Flyby Anomaly [
17].
Both models, the “standard” CG cosmology by Mannheim and KCC, were critically analyzed by Diaferio
et al. [
18] and compared to standard ΛCDM cosmology by applying a Bayesian approach to available astrophysical data from type Ia supernovae (SNIa) and gamma-ray bursts. Contrary to the authors’ expectations [
18], the results of this analysis showed that ΛCDM, Mannheim’s CG, and KCC can all describe the current astrophysical data equally well. Therefore, models based on conformal gravity can be considered viable alternatives to ΛCDM and are worthy of further investigation.
In addition, a recent study by Yang
et al. [
19] has tested Mannheim’s CG against recent astrophysical data from SNIa, determinations of the Hubble parameter at different redshift, and in relation to the “age problem” of the old quasar APM 08279+5255 at
. The outcome of this analysis is that CG can describe all these astrophysical data in a satisfactory manner and does not suffer from an age problem, as opposed to the case of ΛCDM.
Following this recent work, the goal of this paper is to test our KCC against the same astrophysical data used in Reference [
19] in order to ascertain whether KCC is still a viable cosmological model. In
Section 2, we begin by reviewing the main results of conformal gravity and KCC. In
Section 3, the main part of our paper, we will constrain the KCC parameters, by using the latest Union 2.1 SNIa data, and show that KCC can produce Hubble plots of the same quality as those obtained with standard ΛCDM. In
Section 4, we will compare the experimental data for the Hubble parameter, as a function of redshift
z, with KCC predictions and also briefly analyze the age problem in the context of KCC.
2. Conformal Gravity and Kinematical Conformal Cosmology
Conformal Gravity is based on the Weyl action:
where
,
is the conformal or Weyl tensor, and
is a dimensionless coupling constant.
is the unique general coordinate scalar action that is invariant under local conformal transformations:
. CG does not suffer from the cosmological constant problem and is renormalizable [
20]; it is a ghost-free theory [
21,
22], although it still faces some theoretical challenges ([
23,
24,
25,
26,
27,
28]).
The fourth-order CG field equations,
(where
is the Bach tensor—see [
1,
14] for full details), were studied in 1984 by Riegert [
29], who obtained the most general, spherically symmetric, static electrovacuum solution. The explicit form of this solution, for the practical case of a static, spherically symmetric source in CG,
i.e., the fourth-order analogue of the Schwarzschild exterior solution in General Relativity (GR), was then derived by Mannheim and Kazanas in 1989 [
5,
6]. This latter solution, in the case
(exterior solution), is described by the metric
with
The three integration constants in the last equation are as follows: can be considered the CG equivalent of the geometrized mass , where M is the mass of the (spherically symmetric) source and G is the universal gravitational constant; two additional parameters, and , are required by CG, while the standard Schwarzschild solution is recovered for in the equations above. The quadratic term indicates a background De Sitter spacetime, which is important only over cosmological distances, since κ has a very small value. Similarly, γ measures the departure from the Schwarzschild metric at smaller distances, since the term becomes significant over galactic distance scales.
The values of the CG parameters were first determined by Mannheim [
1] (Other estimates of these parameters exist in the literature. For example, in Reference [
30], constraints on the value of the
γ constant were obtained by studying the perihelion shift of planetary motion in CG.):
In our previous KCC publications [
14,
15] we have shown a different way to compute the CG parameters, obtaining values which differ by a few orders of magnitude from those above:
We will revise and update the values of these parameters in
Section 3 by constraining them with recent astrophysical data.
Mannheim
et al. ([
1,
7,
8,
9,
10,
11,
12] used the CG solutions in Equations (
2) and (
3) to perform extensive data fitting of galactic rotation curves without any DM contribution, with the values of
γ and
κ as in Equation (
4). Although the values of these CG parameters are very small, the linear and quadratic terms in Equation (
3) become significant over galactic and/or cosmological distances.
This also means that CG solutions (including those for other types of sources, see discussion in [
17]) are not asymptotically flat, thus raising the question of possible “gravitational redshift” effects at large distances. In fact, this was the main motivation for our “kinematical approach” to conformal cosmology: in regions far away from massive sources (for
) and also ignoring the term
, as suggested by the analysis of galactic rotation velocities,
simplifies to
This implies a possible gravitational redshift at large distances, analogous to the one experimentally observed in standard GR near massive sources such as the Earth, the Sun, or white dwarfs. This effect is related to the square-root of the ratio of the time-time components
of the metric at two different locations. In Reference [
14] we considered our current spacetime location (
;
) in relation to the spacetime location (
;
) of a distant galaxy which emits light at a time
t in the past that reaches us at present time
and appears to be redshifted in relation to the standard redshift parameter
z.
We then argued that this observed redshift could be due (in part, or totally) to the gravitational redshift effect mentioned above. If this effect were indeed the only source of the observed redshift, with the metric in Equation (
6), we would have:
In other words, if the CG metric in Equations (
2) and (
3) has a true physical meaning, as it seems to be the case from the detailed fitting of galactic rotational curves, it should also determine strong gravitational redshift at very large cosmological distances. (Equation (
6) is valid for regions far away from massive sources,
i.e., for
, where
M can be considered the mass of the largest structures in our Universe, such as galaxies, or clusters of galaxies. Therefore, the resulting characteristic distance
r represents the scale at which our kinematical approach is appropriate. For example, considering the estimated mass of a cluster, or a supercluster of galaxies, the resulting characteristic distance is approximately
, which shows that KCC mainly applies to the inter-galactic or cosmological scale.) As far as we are aware, this issue has never been raised in all current CG literature (except, of course, in our previous papers).
The CG metric in Equations (
2) and (
6) is actually conformal to the standard FRW metric (see details in [
5] or [
14]):
where
is the standard Robertson-Walker scale factor,
and
. As in our previous papers, we distinguish here between two sets of coordinates: the Static Standard Coordinates-SSC
used in Equations (
2), (
3), (
6) and (
7), as opposed to the FRW coordinates
—in bold—used in Equation (
8) (Similarly, bold type characters will be used for quantities referring to the FRW geometry, while normal type characters will be used with reference to the SSC coordinates. For example, the RW scale factor will be denoted here as
or
, respectively, in the two cases. In our previous papers we used
and
for the scale factor, but we now prefer to adopt the more common notation,
or
, in this work). Full details of the complete transformations between these coordinates can be found in our References [
14,
15].
This local conformal invariance induces a dependence of the length and time units on the local metric, so that the observed redshift can be interpreted as the ratio between the wavelength
of the radiation emitted by atomic transitions, at the time and location of the source, and the wavelength
of the same atomic transition measured here on Earth at current time. Since modern metrology defines our common units of length
and time
as being proportional respectively to the wavelength and to the period (inverse of the frequency
ν) of radiation emitted during certain atomic transitions, we can write the following “redshift equation”
connecting wavelengths
λ to unit-lengths
and frequencies
ν to unit-time intervals
(we also use
, with a constant speed of light
c).
Therefore, in KCC the observed redshift is due to the change of length and time units over cosmological spacetime, as opposed to the standard explanation of a pure expansion of the scale factor
. In view of this interpretation, and connecting together Equations (
7) and (
9), KCC is able to derive directly the scale factor as a function of space or time coordinates, without solving the dynamical field equations. In terms of SSC, we have:
or, using appropriate coordinate transformations, in terms of FRW coordinates:
with
All these scale-factor equations can also be written explicitly in terms of the time coordinates
t and
, as is usually done in standard cosmology, by computing the time it takes for a light signal, emitted at radial distance
r or
, to reach the observer at the origin. The detailed expressions for
and
, as well as all the connecting formulas between the different variables and conformal parameters, can be found in Reference [
14] (see
Table 1). Furthermore, from the plots of the KCC scale factors, such as
from Equation (
11), it can be seen that the observed redshift
is only possible for
, so that the other two cases,
, are actually ruled out.
The new CG dimensionless parameter
(for
) in Equation (
12) becomes the most important quantity in KCC (The parameter
δ in Equation (
12) is dimensionless only for
. For the
case, Equation (
11) simply becomes
. In this particular case, the coordinate
has dimensions of length, so this equation is still dimensionally correct (in this case the scale factor
becomes a dimensionless quantity, so that Equation (
8) is also correct). This is due to the particular form of the transformation between SSC and FRW coordinates, for the special
case. See
Section 3.1 in Reference [
14] for complete details.): it combines together the original CG parameters
γ and
κ, in view also of the relation between
k and
κ
already mentioned above. (In our previous papers, we considered the possibility that all these CG parameters might also be changing with spacetime coordinates. In particular, we supposed that the
δ parameter might play the role of a universal time and we used the zero subscript to denote the current values of all these parameters (
i.e.,
,
,
etc.). In this paper, we are just considering the current values of these parameters, so we simply write
δ,
γ,
κ,
etc.) It can be shown that
and that, for
, Equation (
11) yields the following direct relation between
and
z:
The plus-minus sign in the last equation indicates that there are two locations where : at the origin , and at a particular radial location which becomes of physical significance for . In fact, in this particular case, there is a region of negative redshift (i.e., a blueshift) for , followed by a standard redshift region at larger radial distances, for . This suggests that the (current) value of δ should be small and positive, so that the supposed blueshift region would be a small (practically undetectable) region around the observer: for example, a small region of the size of the Solar System, or similar.
In two of our previous papers [
15,
16] we actually suggested that this local blueshift region could have been the origin of the Pioneer Anomaly (PA—for a review, see [
31]) since “blueshifted” signals coming from the Pioneer spacecraft would appear to be equivalent to the observed anomalous acceleration. In view of this possible connection, the value of the
γ parameter in Equation (
5) was directly inferred from the Pioneer anomalous acceleration [
15,
16]; the value of the
δ parameter was then computed [
15] from the fitting of the SNIa data available at the time, and the values of the parameters
k and
κ were obtained through Equations (
12) and (
13). In summary, the values of the CG parameters were determined as follows (see also
Table 1 in Reference [
15]):
Although it is still possible that the PA might have a gravitational origin,
i.e., due to modifications of GR, it is now widely accepted that the cause of this anomaly is probably more mundane [
32]: thermal recoil forces originating from the spacecraft radioactive thermoelectric generators. Therefore, in the following sections we will perform a new computation of the CG parameters in Equation (
15), without using any more data related to the PA. We will begin, in the following section, by constraining our parameters using updated SNIa data.
3. KCC and Type Ia Supernovae
In order to constrain the CG parameters with recent SNIa data we need to redefine the luminosity distance in KCC, since this is the main cosmological distance used in this context. In this section we will expand upon concepts already introduced in Reference [
15] (more details about the definitions of distances in KCC can be found in this reference). We start by noticing that the new interpretation of the redshift discussed in the previous section (in particular, in Equation (
9)) implies that lengths and time intervals scale with redshift
z as:
where the subscript 0 indicates intervals of the given quantity associated with objects which share the same spacetime location of the observer at the origin (namely, here on Earth at
and at our current time
), while the subscript
z indicates intervals of the same quantity associated with objects at redshift
, as seen or measured by the same observer at the origin.
It should be emphasized that this change in lengths, or time intervals (as well as wavelengths, frequencies, and all other kinematical quantities derived from lengths and times), is due to the spacetime location of the object being studied (as measured by the redshift parameter z) and not to the “cosmic expansion” as in the standard cosmological model.
It is natural to assume that masses, energies, luminosities, and other dynamical quantities will follow similar scaling laws, but not necessarily the same as the one in Equation (
16). In Reference [
15] we assumed the following scaling laws for masses and energies (Mass and energy will scale in the same way, since
, with lengths and times scaling in the same manner, due to Equation (
16)):
where
is some arbitrary function of
, so that
.
As a consequence of these scaling laws, the “absolute luminosity”
L, or energy emitted per unit time, will scale as
where the meaning of the subscripts is the same as described above for the other quantities. Thus, KCC postulates a change in the absolute luminosity of a “standard candle”, which is intrinsically due to its spacetime location, while standard cosmology assumes an invariable absolute luminosity
L of the standard candle being considered.
Standard cosmology defines the luminosity distance as , with L and l being the absolute and apparent luminosities of the standard candle being used as a distance indicator; denotes the current value of the scale factor and the factor on the right-hand side of the equation originates from a dimming factor under the square root. This factor is due to the standard redshift of the photon frequency and also to a time dilation effect of the emission interval of photons.
KCC considers instead this
dimming factor as unphysical, so the
factor on the right-hand side of the standard luminosity distance equation is completely eliminated. In view also of our scaling law for luminosities in Equation (
18), and of Equation (
14), we then define the luminosity distance in KCC as (In the following equation we choose the positive sign in front of the square root to select the solution corresponding to past redshift,
for
, which is the correct choice for the following analysis of SNIa data)
Since this definition assumes an intrinsic dimming of the luminosity
with redshift
z, it leads to distance estimates which are dramatically different from those of standard cosmology for different values of
z (see the first three columns in
Table 2 of Reference [
15]).
To avoid this issue, an alternative definition could be employed, which would retain the concept of an invariable luminosity
of a standard candle, while including the other aspects of KCC. We can obtain this alternative luminosity distance
by modifying the previous equation as follows:
so that the right-hand side of the equation now depends explicitly on the still unknown function
. In
Table 2 of Reference [
15], it was shown that distances estimated using
are very close to those of standard cosmology (compare the values in the fourth column of this table with those in the third or fifth columns), so the KCC definition in Equation (
20) more closely agrees with the luminosity distance of standard cosmology.
We will see in the following that both definitions, in Equations (
19) and (
20), lead to the same results when applied to SNIa data, but they differ conceptually: the former assumes a variable absolute luminosity
of a standard candle, while the latter assumes an invariable absolute luminosity
, which is more in line with the standard interpretation.
Before we can apply these definitions to the analysis of SNIa data, we need to obtain an explicit form for the
function, which enters most of the KCC equations above. Expanding upon the arguments discussed in our previous work [
15], we can assume the following properties for this function:
- (1)
f is some arbitrary function of , with a “fixed point” at 1, that is, , or .
- (2)
f is a dimensionless quantity, so that Equations (
17)–(
20) are dimensionally correct.
- (3)
f is a function possibly built out of other expressions of KCC, which also depend on the factor .
Although the last property in the list above is just an educated guess, it suggests that the function
f might depend on the following KCC factor:
constructed as the (dimensionless) ratio between the luminosity distance in Equation (
19) and the reference distance
which corresponds to the value
of the radial coordinate (other than the origin) where we have
(see discussion after Equation (
14)). Therefore, as it was argued also in Reference [
15],
represents the ideal reference distance at which we should place a “standard candle” of given absolute luminosity
: at this location its luminosity is not affected by the scaling effect of Equation (
18), since
for
. In KCC
is the equivalent of the standard reference distance of 10 parsec, used for standard candles, such as supernovae.
Following the discussion above, the most general form of the function
that we will consider is:
where
α and
β are coefficients to be determined from SNIa data fitting. Again, the choice of the function
in the previous equation is just an educated guess, an “ansatz” based on the only two functions of
introduced in KCC: a function
, which generalizes the simple
scaling factor in Equation (
16), and a function
, which generalizes the inverse-square dependence of the apparent luminosity of a radiation source upon the (luminosity) distance between the observer and the source.
3.1. SNIa Data Fitting
In our previous work, we determined the CG parameters by using the SNIa data available at the time (292 SNIa data of the “gold-silver” set, see [
15] for details) and by considering the value of the Pioneer anomalous acceleration. As already mentioned, we will not use the PA data in this study, but we will use the latest compilation of SNIa data: the 580 supernovae from the Union 2.1 data set ([
33,
34,
35]).
The distance modulus
μ (difference between the apparent magnitude
m and the absolute magnitude
M) is usually computed, using Pogson’s law, in terms of the logarithm of the ratio between the apparent luminosity
(at redshift
z) and the reference apparent luminosity
(at the reference distance of choice). It can then be expressed in terms of absolute luminosities and distances, using the general relation
. We have:
where the subscript
z refers to quantities evaluated at redshift
, while the subscript
indicates the “reference” value of the quantity,
i.e., when the standard candle is placed at the reference distance.
As explained before, we have two possible choices for this reference distance: the traditional distance of 10 pc (since usually the absolute luminosity
L of a “standard candle” is defined as the apparent luminosity of the same object placed at 10 parsec) and the KCC reference distance
in Equation (
22) above, since this is the only location, other than the origin, where
.
Using this latter choice for the reference distance and combining Equation (
24) with Equations (
18), (
19), (
21) and (
23), we obtain explicitly:
an expression which can be used directly to fit SNIa data and determine the value of the three free parameters
α,
β, and
δ.
Using this last equation as a fitting formula for the Union 2.1 SNIa data, we obtained the following “best-fit” values for the free parameters:
Assuming that
α and
β are likely to be integer numbers, due to their role in the definition of the function
in Equation (
23), and close to the values reported in the previous equation, we repeated the fitting procedure, first by setting
:
then by fixing both
α and
β as follows:
All these fits have good statistical quality (
) and clearly confirm the results of our past SNIa data fitting [
15], where it was a priori postulated that
,
, and
δ was found to be as in Equation (
15). It can also be shown that our fitting formula in the second line of Equation (
25) can even be obtained by using the alternative definition of the luminosity distance
in Equation (
20), with appropriate changes in all formulas leading to Equation (
25). Thus, our SNIa data fitting procedure is valid even if we use
instead of
, which is equivalent to using a luminosity distance whose estimates are very close to those of standard cosmology.
In KCC, the values of the CG parameters
γ and
δ are also connected to the current value of the Hubble parameter:
in SSC or FRW coordinates, respectively, but with
for
[
15]. Since in this work we are not relying any longer on the PA data, we can now derive the value of
γ directly from the Hubble constant, using the previous equation.
The Union 2.1 SNIa data are consistent with the Hubble constant estimate by Riess
et al. [
36],
, from which we obtain
. However, the most commonly used estimate of the Hubble constant is from the Planck collaboration 2013 results [
37]:
therefore, in the rest of this paper we will consider the value of
γ above as the current KCC estimate.
It could be argued that, since the Union 2.1 SNIa data are based on the standard definitions for the luminosity distance, standard candles,
etc., it might be more appropriate to use
as a reference distance. This leads to a slightly different fitting formula, in view also of Equations (
19) and (
29):
which also includes the “normalized Hubble constant”
h as a fitting parameter. This dimensionless quantity is related to
as follows:
As in our previous fitting Formula (
25), we now have the option of leaving all four parameters (
α,
β,
δ, and
h) completely free, or to fix some of them, for example, by choosing integer values for
α and
β. If we leave all four parameters free, our best fit to Union 2.1 SNIa data yields:
in line with our previous estimate of the parameters in Equation (
26) and with our preferred value for
in Equation (
30). If we fix the value of the Hubble constant as in Equation (
30),
i.e.,
, and also set
,
, as it was done in Equation (
28), we obtain instead:
Comparing our results for
δ, in Equations (
28) and (
34), we see that our two possible fitting Formulas (
25) and (
31) produce consistent results for
, in line also with our previous determinations from Reference [
15], or in Equation (
15). In addition, our analysis confirms that the
function in Equation (
23) should be considered with
and
,
i.e.,
Although our two fitting formulas, Equations (
25) and (
31), both yield similar results, we have to choose one of the two methods for a final determination of the CG parameters. Since the former fitting formula assumes
, which is more consistent with the KCC model, while the latter formula assumes
, which is more consistent with standard cosmology, our final choice will be the first expression (as it was also done previously in Equation (43) of Reference [
15]).
Therefore, in view of Equations (
12), (
13), (
28), and (
30) our revised set of KCC parameters is the following:
and the function
is given in Equation (
35). In the next section we will plot our results and compare them with those of standard cosmology.
3.2. Union 2.1 Data and KCC Plots
As already mentioned at the beginning of
Section 3.1, our new KCC fits were performed with the latest Union 2.1 SNIa data (Also available in electronic form at:
http://supernova.lbl.gov/Union/) ([
33,
34,
35]). The Supernova Cosmology Project “Union2.1” SNIa compilation is an update of the previous “Union2” compilation, bringing together data for 833 supernovae, drawn from 19 datasets. Of these, 580 SNe pass usability cuts and are included in the data set. In
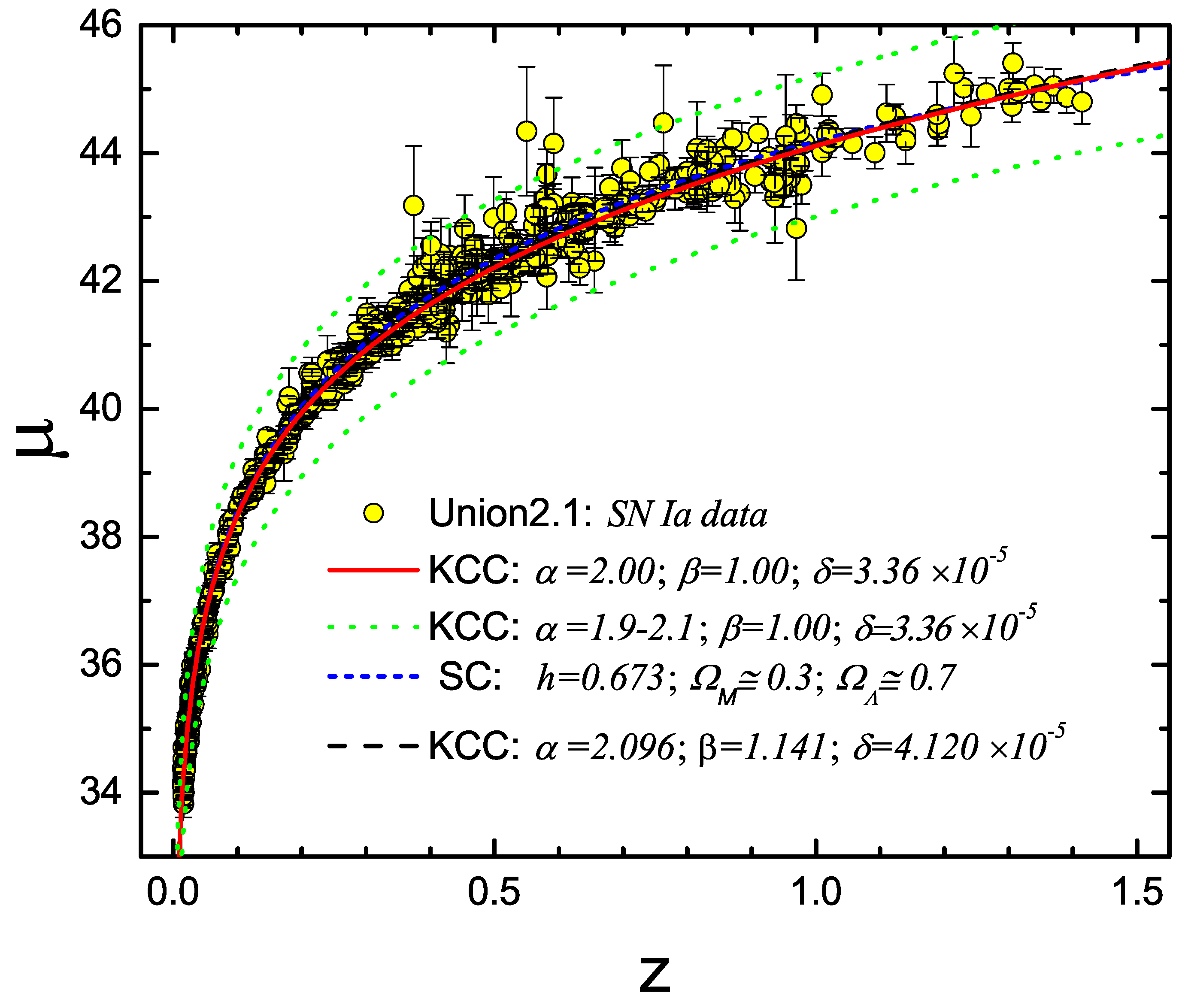
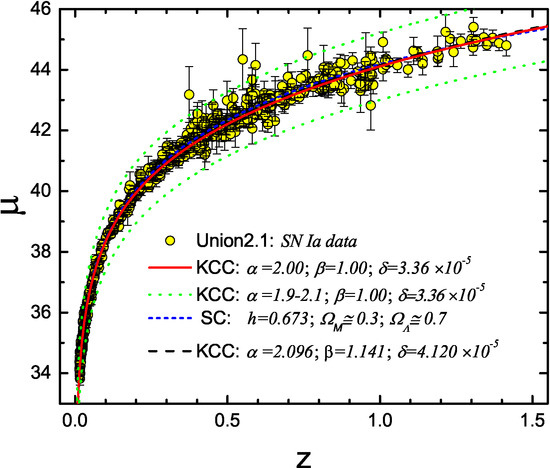
Figure 1 we plot these 580 data points (distance modulus
μvs. redshift
z) together with the standard cosmology (SC) Hubble plot (blue, short-dashed curve), obtained with standard values of the critical densities (
,
) and with the Hubble constant value in Equation (
30),
i.e.,
.
Figure 1.
Data from Union 2.1 SNIa set [
35] are fitted with Equation (
25). Our KCC fits (red-solid for fixed
α and
β; black long-dashed for variable
α and
β) show very good statistical quality (
) and are very close to the standard cosmology prediction (SC, blue short-dashed). Also shown (dotted-green curves) is the range of our KCC fitting curves for a variable
.
Figure 1.
Data from Union 2.1 SNIa set [
35] are fitted with Equation (
25). Our KCC fits (red-solid for fixed
α and
β; black long-dashed for variable
α and
β) show very good statistical quality (
) and are very close to the standard cosmology prediction (SC, blue short-dashed). Also shown (dotted-green curves) is the range of our KCC fitting curves for a variable
.
Our KCC fits are also presented in this figure: in red, solid curve, we show our main fit, using Equation (
25) and with the values of the parameters as in Equation (
28); the green-dotted curves show how our fits depend on changes of the
α parameter (in the range
), keeping the other parameters unchanged. Finally, the black, long-dashed curve is our KCC fit with the parameters as in Equation (
26),
i.e., when all the parameters are left free in the fitting procedure. This curve is practically the same as our main KCC fit in solid-red, and both KCC curves are very close to the standard cosmology theoretical prediction.
In
Figure 2 we reproduce the same data and the same fitting curves as in
Figure 1, but in the form of a standard Hubble plot, with logarithmic axis for redshift
z. In this way, all the fitting curves become almost straight lines and the differences between them can be better appreciated. Again, the two main KCC fits (red-solid and black-long dashed) are almost indistinguishable and only slightly different from the equivalent standard cosmology prediction (blue, short-dashed).
Similarly,
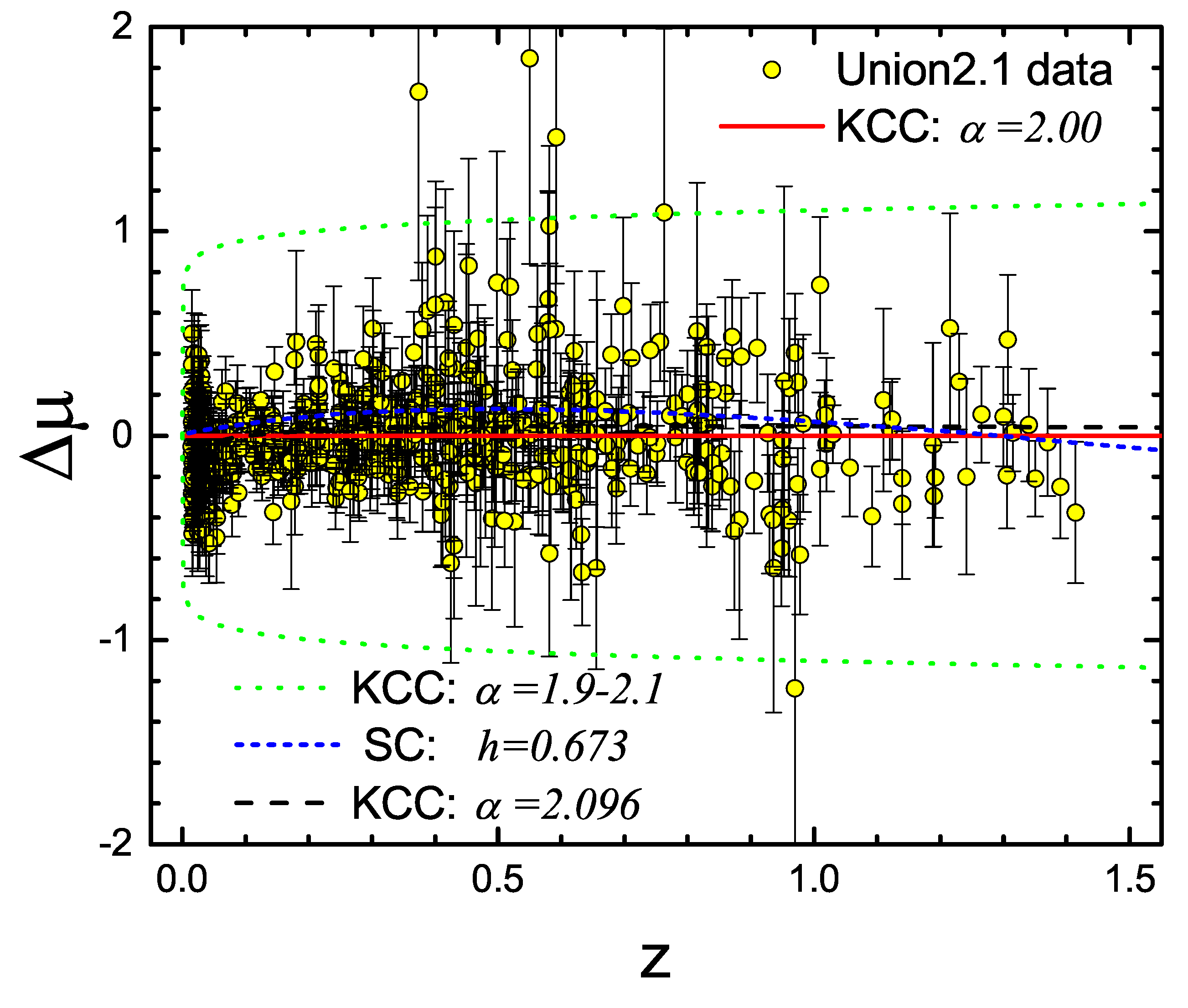
Figure 3 presents the same information in the form of residual values
, with the baseline represented by our main KCC fit (red-solid, with parameters as in Equation (
28)). In this figure it is easier to notice the small differences between our two KCC fits and the standard cosmology prediction. It is also evident that most of the SNIa data points fall within the
band.
Figure 2.
The same data and fitting curves presented in
Figure 1 are shown here in a standard Hubble plot, with logarithmic axis for the redshift
z. The meaning of the symbols and of the different plots is the same as in the previous figure.
Figure 2.
The same data and fitting curves presented in
Figure 1 are shown here in a standard Hubble plot, with logarithmic axis for the redshift
z. The meaning of the symbols and of the different plots is the same as in the previous figure.
Figure 3.
Data from Union 2.1 SNIa set [
35] are fitted with Equation (
25) and shown as residuals
. The baseline is represented by our main KCC fit (red-solid curve, with parameters as in Equation (
28)). The meaning of the other curves and symbols is the same as in the previous figures.
Figure 3.
Data from Union 2.1 SNIa set [
35] are fitted with Equation (
25) and shown as residuals
. The baseline is represented by our main KCC fit (red-solid curve, with parameters as in Equation (
28)). The meaning of the other curves and symbols is the same as in the previous figures.
The last study we performed, in connection with the Union 2.1 data, was related to the low-z behavior of our fitting formulas. As already discussed at length in [
15], we cannot effectively expand in powers of
z our luminosity distance
in Equation (
19), due to the very small value of the
δ parameter. Therefore, we just discard terms containing
δ in the same expression for
and retain only the leading term depending on
z:
Using this expression and
, from Equation (
22), in Equation (
25) and also assuming
, as suggested by previous fits, we have:
which becomes our “low-z” fitting formula.
To check this expression we selected 179 SNIa data from the Union 2.1 set with
and applied our fitting Formula (
38) to this data subset.
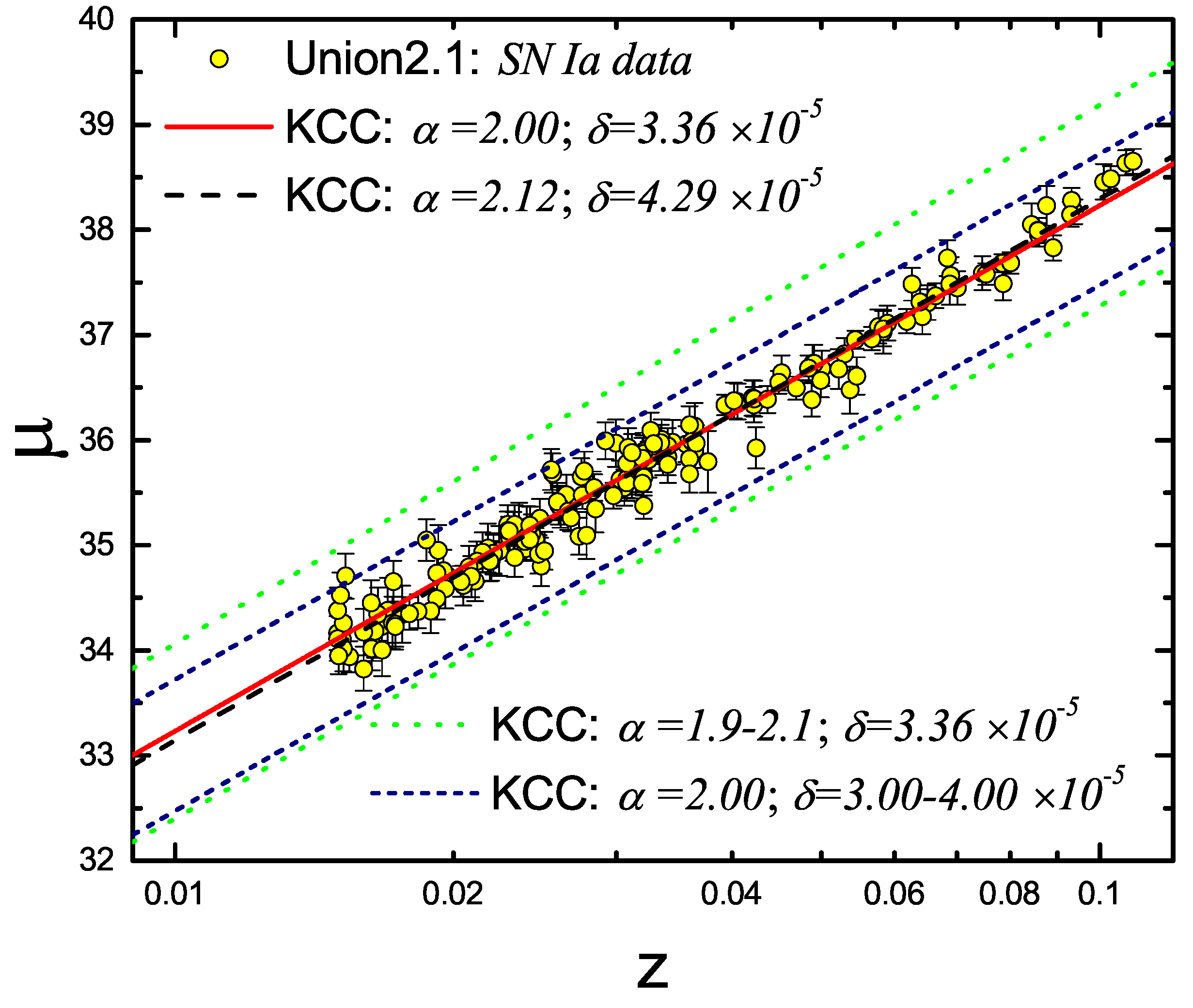
Figure 4 shows the results of this low-z fitting: our main KCC fit (red-solid curve), for a fixed
, yields
, essentially the same result as in Equation (
28) for the whole set of 580 supernovae. Leaving both parameters free (black, long-dashed curve) yields instead
,
, and the two KCC curves almost coincide. In this figure we also show how our low-z fit is sensitive to the value of
α in the range
(green-dotted curves) and to the value of
δ in the range
(blue, short-dashed curves).
Figure 4.
A subset of Union 2.1 SNIa data [
35], for
, is fitted with Equation (
38). Our low-z KCC fits (red-solid curves for fixed
α; black long-dashed curves for variable
α) yield essentially the same results as in the previous fits, which used the full range of values for
z. Also shown are the ranges of our KCC fitting curves, for a variable
(green-dotted curves) and for a variable
(blue, short-dashed curves).
Figure 4.
A subset of Union 2.1 SNIa data [
35], for
, is fitted with Equation (
38). Our low-z KCC fits (red-solid curves for fixed
α; black long-dashed curves for variable
α) yield essentially the same results as in the previous fits, which used the full range of values for
z. Also shown are the ranges of our KCC fitting curves, for a variable
(green-dotted curves) and for a variable
(blue, short-dashed curves).
In our previous work (see
Section 3.2 in [
15]) we also remarked that our low-z distance modulus expression in Equation (
38), for
, can be rewritten as
, so that it corresponds perfectly to the first terms of the standard cosmology expansion
, neglecting higher-order terms in
z. Comparing the right-hand sides of these two “low-z” expressions, we find a direct connection between the Hubble constant and the KCC
δ parameter:
having used our best estimate for
δ in Equation (
28) and with the speed of light given as
.
It is very remarkable that our KCC model and the related SNIa data fitting are able to obtain an estimate for the Hubble constant which is very close to th 2013 Planck collaboration value. We want to emphasize that our value for
δ in Equation (
28) came from the fitting formula in Equation (
25), which is independent of any assumed value for
.
Therefore, our value of
in Equation (
39) represents KCC’s direct evaluation of the Hubble constant, in agreement with current best estimates. We can recompute the value for
γ using
as
, which is essentially equivalent to our previous estimate in Equation (
30), based on the 2013 Planck collaboration value for
. Following these two estimates, our final value for
γ will be quoted as
, as already reported in Equation (
36).
4. KCC and Hubble Parameter Data
Another important test of our KCC model can be performed in relation with observed data for the Hubble parameter
, measured as a function of redshift. As it was done by Yang
et al. in their recent analysis [
19] of Mannheim’s CG, we will use here all the available data for
, obtained from different sources and with different methods, as reported in
Table 1 (When both statistical and systematic errors were quoted (as in [
38,
39]), we summed these errors in quadrature and reported the total error in the table).
Although different methods were used to obtain the data in this table, the most common argument relies on the fact that the Hubble parameter depends on the differential age of the Universe, as a function of redshift, in the form:
Therefore, a determination of , or more practically of the ratio between finite intervals of redshift and time, will lead to a direct measurement of .
In order to measure the time interval , we need to identify and use so-called “cosmic chronometers”, i.e., astrophysical objects, such as a galaxies, whose evolution follows a known fiducial model, so that these objects behave as “standard clocks” in the Universe.
Table 1.
Available Hubble parameter data H(z), from various sources, obtained with different methods.
Table 1.
Available Hubble parameter data H(z), from various sources, obtained with different methods.
| z | | Source | Method (See Text) |
|---|
| 0.0900 | 69 ± 12 | Jimenez et al. (2003) [40] | DA |
| 0.1700 | 83 ± 8 | Simon et al. (2005) [41] | DA |
| 0.2700 | 77 ± 14 | Simon et al. (2005) [41] | DA |
| 0.4000 | 95 ± 17 | Simon et al. (2005) [41] | DA |
| 0.9000 | 117 ± 23 | Simon et al. (2005) [41] | DA |
| 1.3000 | 168 ± 17 | Simon et al. (2005) [41] | DA |
| 1.4300 | 177 ± 18 | Simon et al. (2005) [41] | DA |
| 1.5300 | 140 ± 14 | Simon et al. (2005) [41] | DA |
| 1.7500 | 202 ± 40 | Simon et al. (2005) [41] | DA |
| 0.4800 | 97 ± 62 | Stern et al. (2010) [42] | DA |
| 0.8800 | 90 ± 40 | Stern et al. (2010) [42] | DA |
| 0.1791 | 75 ± 4 | Moresco et al. (2012) [38] | DA |
| 0.1993 | 75 ± 5 | Moresco et al. (2012) [38] | DA |
| 0.3519 | 83 ± 14 | Moresco et al. (2012) [38] | DA |
| 0.5929 | 104 ± 13 | Moresco et al. (2012) [38] | DA |
| 0.6797 | 92 ± 8 | Moresco et al. (2012) [38] | DA |
| 0.7812 | 105 ± 12 | Moresco et al. (2012) [38] | DA |
| 0.8754 | 125 ± 17 | Moresco et al. (2012) [38] | DA |
| 1.0370 | 154 ± 20 | Moresco et al. (2012) [38] | DA |
| 0.2400 | 79.69 ± 2.65 | Gaztaaga et al. (2009) [39] | BAO |
| 0.4300 | 86.45 ± 3.68 | Gaztaaga et al. (2009) [39] | BAO |
| 0.0700 | 69 ± 19.6 | Zhang et al. (2012) [43] | DA |
| 0.1200 | 68.6 ± 26.2 | Zhang et al. (2012) [43] | DA |
| 0.2000 | 72.9 ± 29.6 | Zhang et al. (2012) [43] | DA |
| 0.2800 | 88.8 ± 36.6 | Zhang et al. (2012) [43] | DA |
| 0.4400 | 82.6 ± 7.8 | Blake et al. (2012) [44] | BAO and GC |
| 0.6000 | 97.9 ± 6.1 | Blake et al. (2012) [44] | BAO and GC |
| 0.7300 | 97.3 ± 7.0 | Blake et al. (2012) [44] | BAO and GC |
| 0.3500 | 82.1 ± 5 | Chuang et al. (2012) [45] | GC |
Once this population of standard clocks has been found and dated, the “differential-age” technique can be used: the age difference
, and the corresponding redshift difference
, between two of these cosmic chronometers can be measured, thus determining
in view of Equation (
40). This differential age (DA) method has the advantage of not using any integrated cosmological quantity (such as the luminosity distance, which is expressed through an integral in standard cosmology), since these quantities depend on the integral of the expansion history, thus yielding less direct measurements of the expansion history itself.
Since the original proposal of this DA method [
40,
46], the best choice of “cosmic chronometers” was found to be a population of “red-envelope” galaxies: massive galaxies, harbored in high-density regions of galaxy clusters and containing the oldest stellar populations, which are now evolving only passively (
i.e., with very limited new star formation). The age of these passively evolving galaxies can then be used in connection with the DA technique explained above to measure
[
40,
41,
42]. A similar approach, also based on passively evolving galaxies, but more centered on a differential spectroscopic evolution of early-type galaxies as a function of redshift, was introduced by Moresco
et al. [
38,
47], yielding more data points, followed by the more recent work by Zhang
et al. [
43].
A different approach [
39] to the measurement of
considered instead the baryon acoustic oscillations (BAO) peak position as a standard ruler in the radial direction. This BAO method was later connected to the Alcock-Paczynski distortion from galaxy clustering (GC) in the WiggleZ Dark Energy Survey [
44], and one additional data point was recently obtained [
45] by using galaxy clustering data. All the measured data points for
are reported in
Table 1; we will now interpret these data in view of our kinematical conformal cosmology.
In KCC, the Hubble parameter is directly related to
z as follows (see Equation (10) in [
15]):
in view also of Equation (
29) and assuming
. At first, it seems impossible to fit the observational Hubble data (OHD) in
Table 1 with the formula on the right-hand side of the last equation, for
and
close to standard values. However, the OHD are obtained essentially from Equation (
40), or rather from the critical determination of the time interval
, which enters the denominator on the right-hand side of this equation.
Although the differential age methods used to obtain these OHD in the literature are slightly different (and even more different are the methods based on BAO and/or GC), they all rely heavily on time, distance, and spectroscopic determinations, based on standard cosmology. Since KCC allows for intrinsic scaling of lengths, time intervals, energies, luminosities, etc., as in Equations (
16) and (
18), we need to allow the presence of these scaling factors, such as powers of
and/or
, into our fitting Formula (
41).
In view also of the general form of
in Equation (
23), we generalize our fitting formula for
as:
where
l and
m are free parameters to be determined with our fitting procedure. The additional factor of
, introduced in the last equation, is justified in the same way as it was done in Equation (
23): it is just a reasonable “ansatz” based on the only two functions of
introduced in KCC. Of course, the new parameters
l and
m in Equation (
42) are not necessarily related to the similar
α and
β parameters used before with the SNIa data, since we are now fitting a different type of astrophysical data. In the last equation we also used our direct connection in Equation (
39) between
and
δ to avoid over-parametrizing this fitting formula.
We then used our revised Formula (
42) to fit the OHD in
Table 1, allowing up to three dimensionless parameters:
δ,
l, and
m. However, leaving all three parameters completely free does not lead to a satisfactory fit of the data, so we simply set
δ to our preferred value:
. Our best fit, considering
l and
m as free parameters, is:
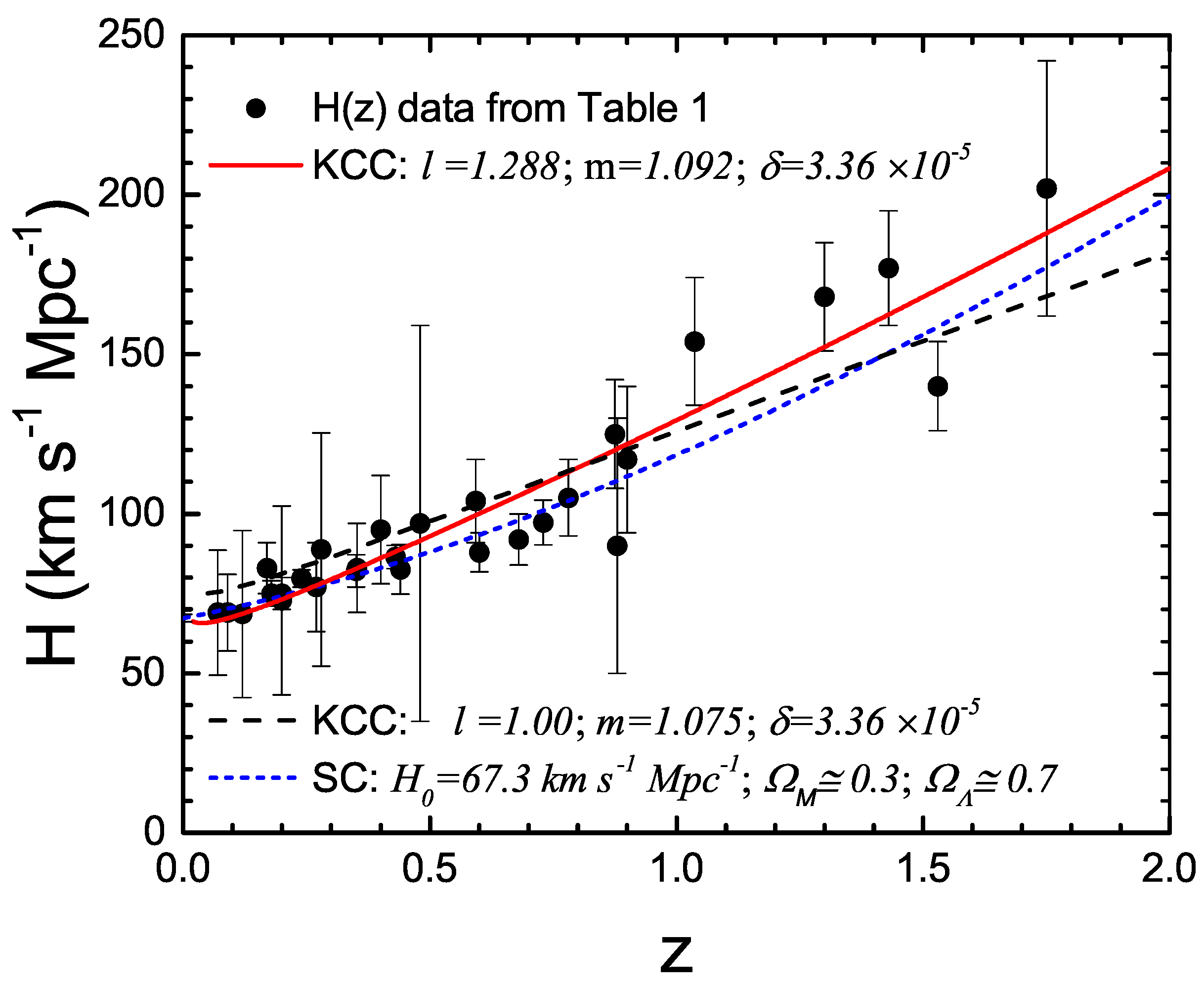
and is shown in
Figure 5 (red-solid curve), together with all the OHD from
Table 1. If we fix
l to be an integer value, close to the previous estimate, we obtain instead:
which is also shown in
Figure 5 (black, long-dashed curve). In the same figure, the standard cosmology prediction,
, is shown (blue, short-dashed curve) for
,
,
, and
.
The
value for the first parameter in our KCC fitting formula can be explained as originating from the scaling law of time intervals,
, applied to the measured value
which enters Equation (
40). In other words, the observed age differences at redshift
z are actually
intervals, but the age intervals entering Equation (
40) should be considered as
intervals, since standard cosmology does not allow for rescaled quantities. Thus, combining Equations (
40) and (
41), we have:
, where the
factor on the right-hand side is due to the rescaling of the time intervals.
Figure 5.
OHD from
Table 2 are fitted with our KCC Equation (
42), using values for the parameters as in Equation (
43) (red-solid curve), or as in Equation (
44) (black, long-dashed curve). Also shown is the standard cosmology prediction (blue, short-dashed curve).
Figure 5.
OHD from
Table 2 are fitted with our KCC Equation (
42), using values for the parameters as in Equation (
43) (red-solid curve), or as in Equation (
44) (black, long-dashed curve). Also shown is the standard cosmology prediction (blue, short-dashed curve).
Table 2.
Standard Cosmology and KCC estimates for the age of the Universe and of quasar APM 08279+5255.
Table 2.
Standard Cosmology and KCC estimates for the age of the Universe and of quasar APM 08279+5255.
| Model | Age of Universe | Age of Quasar |
|---|
| SC (, , ) | 14.0 Gyr | 1.34 Gyr |
| KCC—parameters from Equation (43) | 14.2 Gyr | 1.65 Gyr |
| KCC—parameters from Equation (44) | 15.8 Gyr | 2.45 Gyr |
The
value for the second parameter in our KCC fits is not so easily explained. This corresponds to a factor
on the right-hand side of our fitting Formula (
42), with
m close to unity. This could be due to the fact that the OHD are determined through spectroscopic measurements (involving the scaling factor
), or because the age determinations of the cosmic chronometers, such as the “red-envelope” galaxies, involve their luminosity distances, thus allowing for the KCC correction factor
to appear in our fitting formula.
In particular, age estimates are typically sensitive to the distance scale (see discussion in Reference [
48], pp. 62–63): a fractional change
in distance estimates will produce a change
in absolute luminosities and thus a fractional change
in age estimates, since the absolute luminosity of stars at the turn-off point in the main sequence is roughly inversely proportional to the age of the globular cluster being studied. In KCC the change in luminosity distance
is due to the difference between the revised
of Equation (
19) and the standard cosmology expression
, which assumes an invariable luminosity
.
Therefore, in view also of Equation (
35), a fractional change
might introduce a correcting factor
into our CG age estimates and ultimately yield a corresponding factor
on the right-hand side of our fitting Formula (
42), with
. Due to the complexity of the details related to the experimental measurements of the OHD, at this point we are unable to further explain the presence of this factor in our fitting formula for
.
Finally, we wish to comment on the “age problem” analyzed in Reference [
19], which was related to Mannheim’s CG. The issue being studied was a possible age problem for the old quasar APM 08279+5255 at
, as well as the current estimates of the age of the Universe. As already remarked in
Section 1, it was shown that CG does not suffer from an age problem, as it might be the case instead for standard cosmology (see again [
19] and references therein).
For a cosmological model where
is known explicitly, all age estimates are essentially obtained by integrating Equation (
40). For instance, the current age of the Universe
is:
assuming
at time zero and
at current time. More generally, the age of an astrophysical object (such as the old quasar mentioned above) which is observed at redshift
z, but whose formation occurred at earlier times, corresponding to a formation redshift
, is computed as:
In ΛCDM cosmology, using the standard expression for
with
,
,
, and
, the age of the Universe from Equation (
45) is computed as
, in line with estimates based on globular clusters, or other astrophysical objects. On the contrary, the quasar APM 08279+5255 is observed at
, with an estimated formation redshift
[
19]. Using Equation (
46), the standard cosmology age for this quasar would be
, causing a possible age problem, since the best estimated age for this quasar is
, with a
lower limit of
and an absolute lowest limit of
[
19].
As discussed at length in our previous work (see Section 4.5 in Reference [
14]), in KCC we have two possible time coordinates: the static standard coordinate
t related to our local unit of time, as opposed to the FRW coordinate
, where the former is essentially the conformal time of the latter. When using the former coordinate
t, the Universe does not appear to have initial or final singularities (thus, the age of the Universe would be infinite, if measured using this coordinate), while both singularities appear when using the latter coordinate
.
However, if we use FRW coordinates to estimate ages,
i.e., if we use
as in Equations (
41), (
45) and (
46), we would obtain extremely small estimates for the age of the Universe and for the age of the quasar being studied. This shows that age estimates in KCC are not directly comparable with age estimates in SC, in the same way that luminosity distances in KCC and SC are widely different, as already mentioned in
Section 3.
Once again, to reconcile the two different views, we must use the “revised” formula for
in Equation (
42) with the KCC parameters determined in Equation (
43), or Equation (
44). Using this formula and the related parameters in the age Equations (
45) and (
46) yields the results reported in
Table 2 (the corresponding SC results are also shown in this table).
As it can be seen from the values in this table, the KCC age of the Universe is, in both cases, in agreement with the accepted estimates. In KCC, there is also no apparent age problem for the Quasar APM 08279+5255: our first estimate () is greater than the lowest age limit of , while our second estimate () is larger than the best estimated age for this quasar of .