Thermodynamics of Rotating Black Holes and Black Rings: Phase Transitions and Thermodynamic Volume
Abstract
:1. Introduction
1.1. Canonical Ensemble and Phase Transitions
1.2. Thermodynamic Volume
1.3. Equation of State
2. Black Holes in 4d
2.1. Asymptotically Flat Black Holes
2.1.1. Schwarzschild Solution
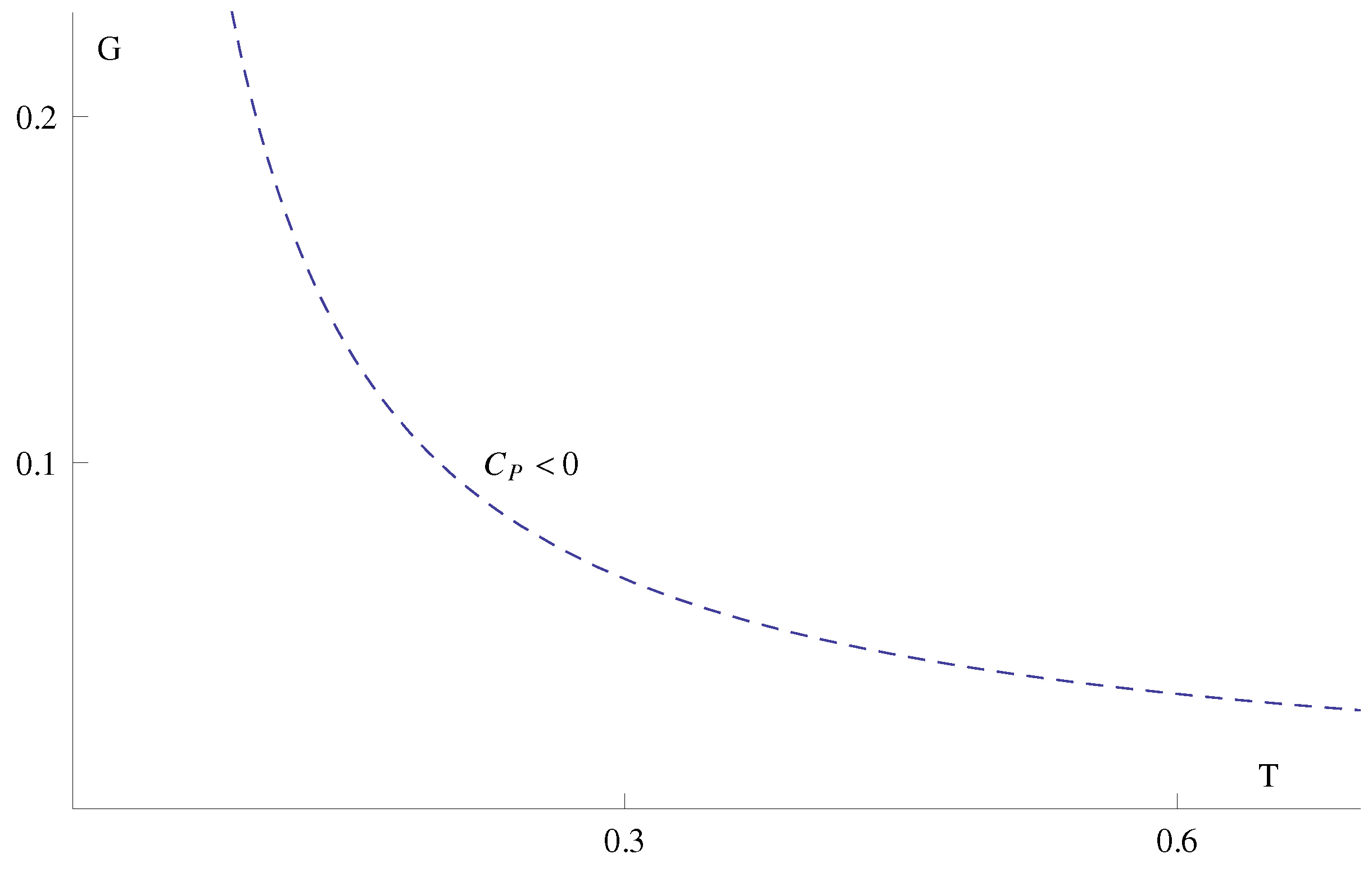
2.1.2. Charged Black Hole: Reissner–Nordström Solution
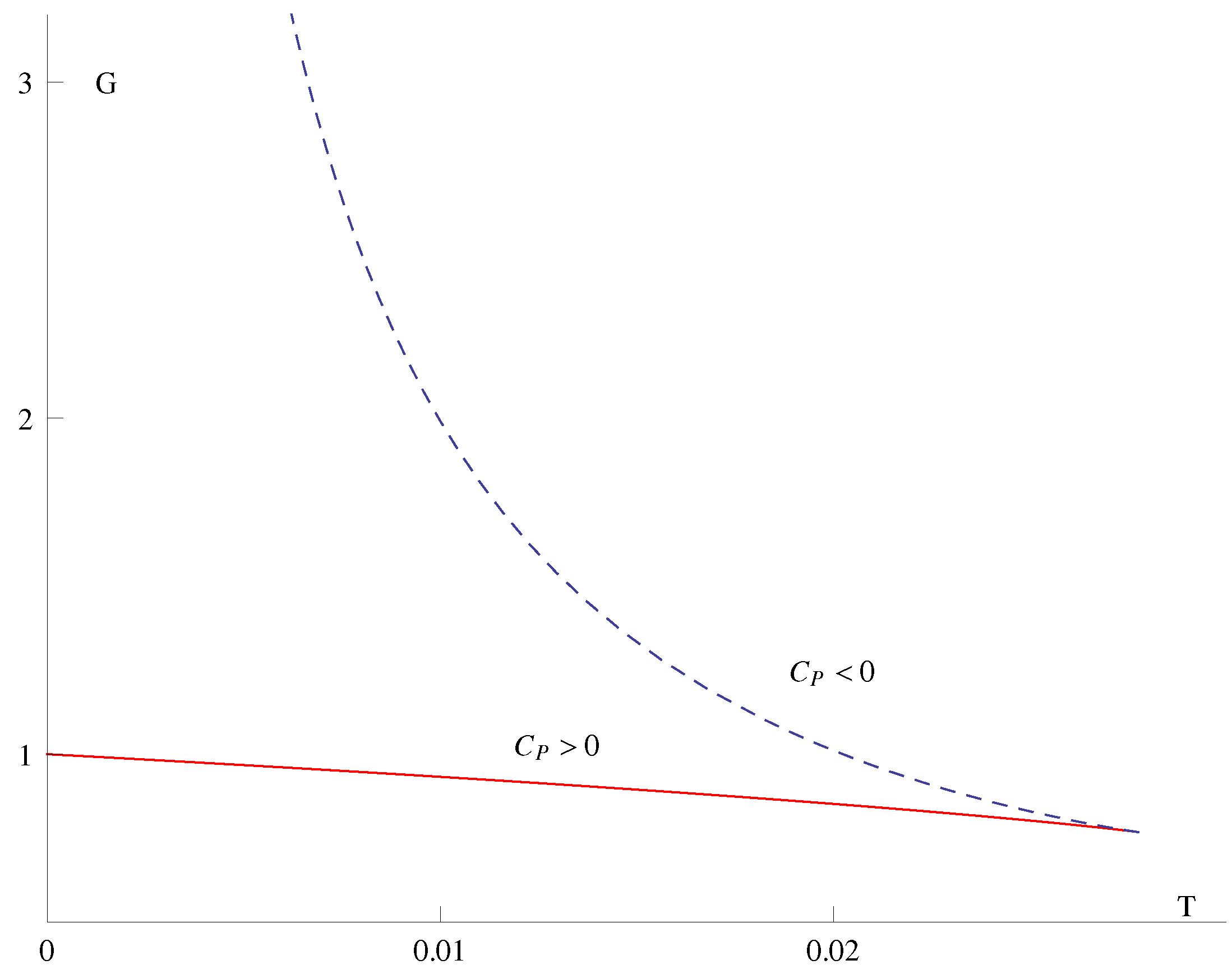
2.1.3. Rotating Black Hole: Kerr Solution
2.2. AdS Black Holes
2.2.1. Schwarzschild-AdS
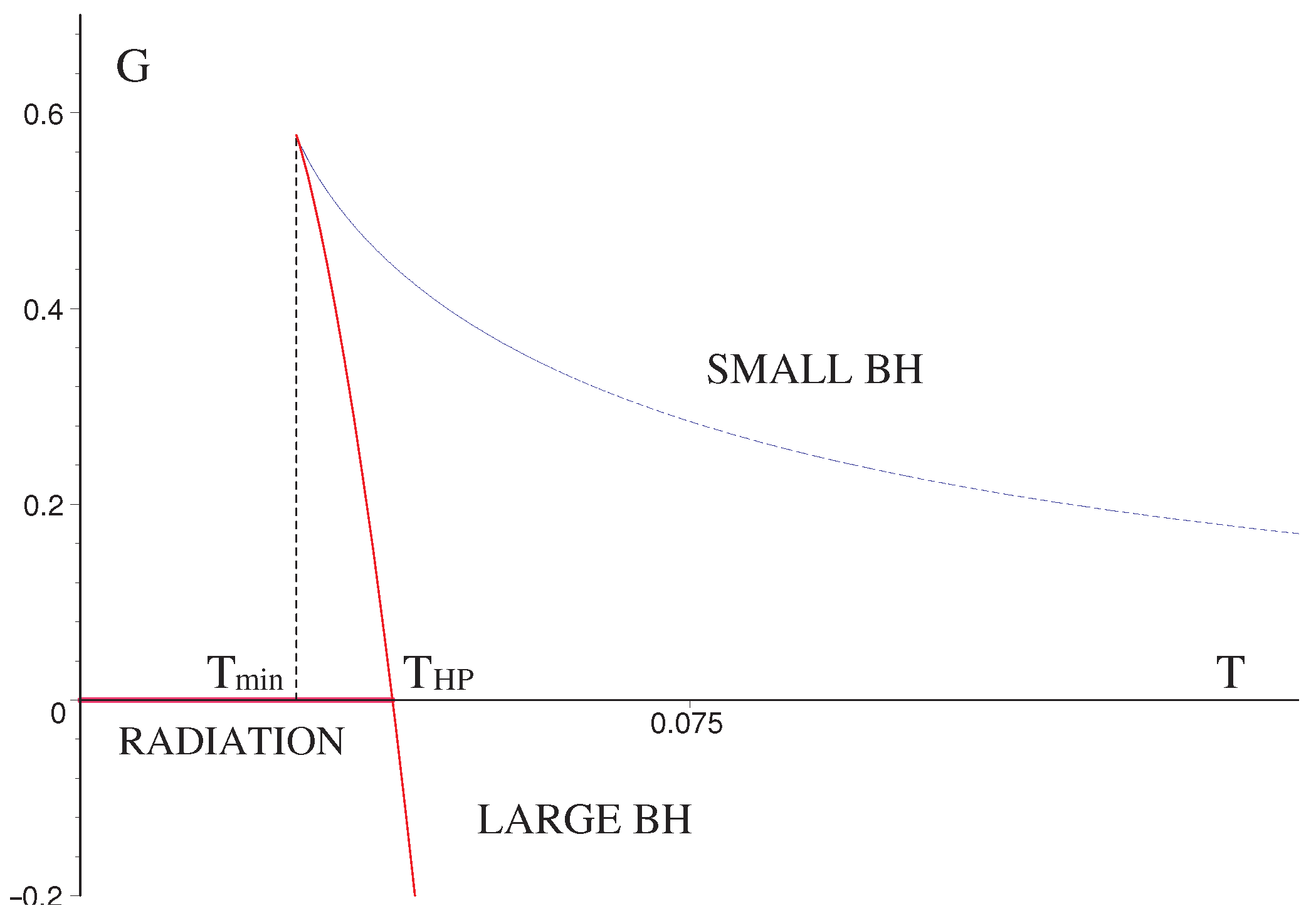
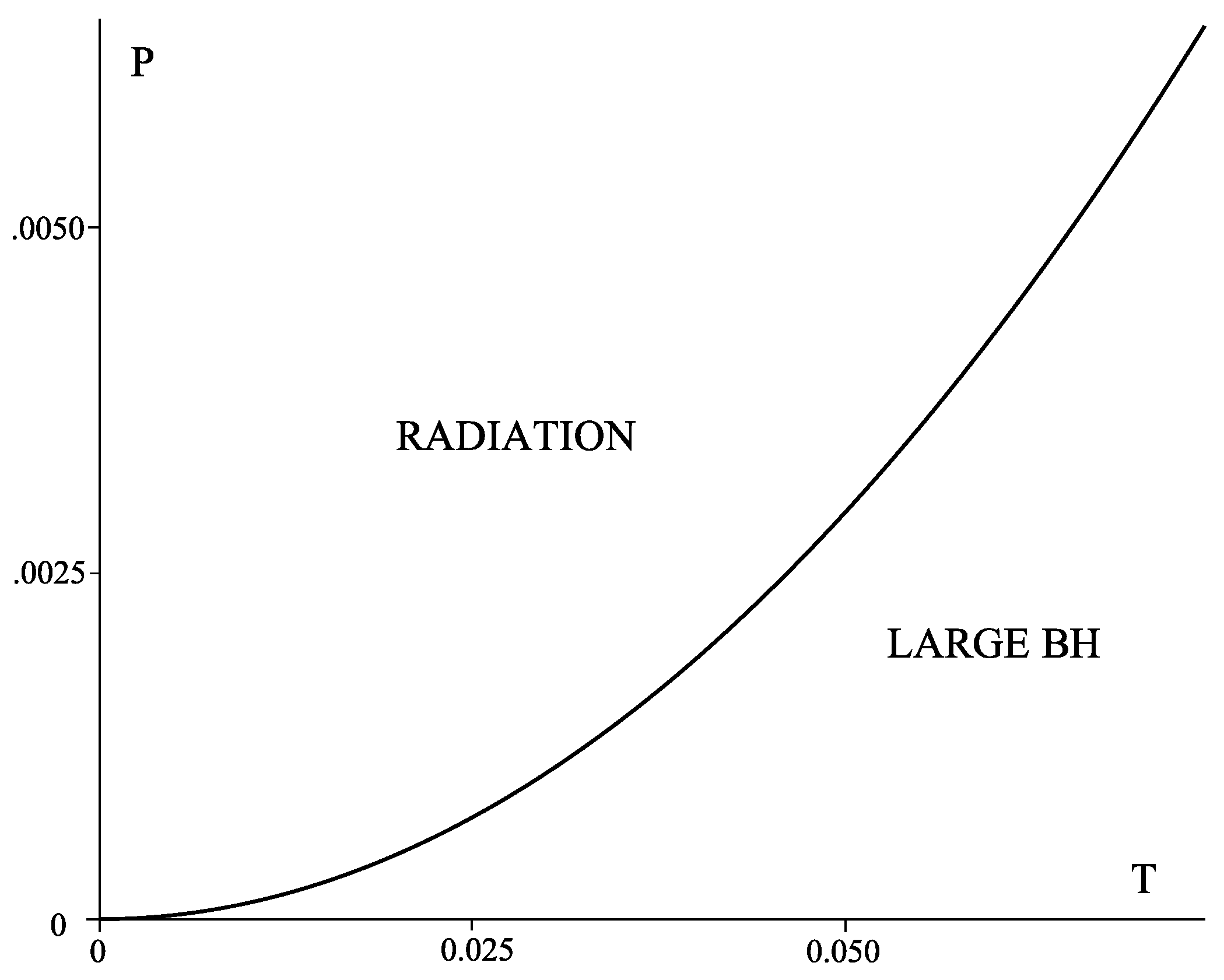
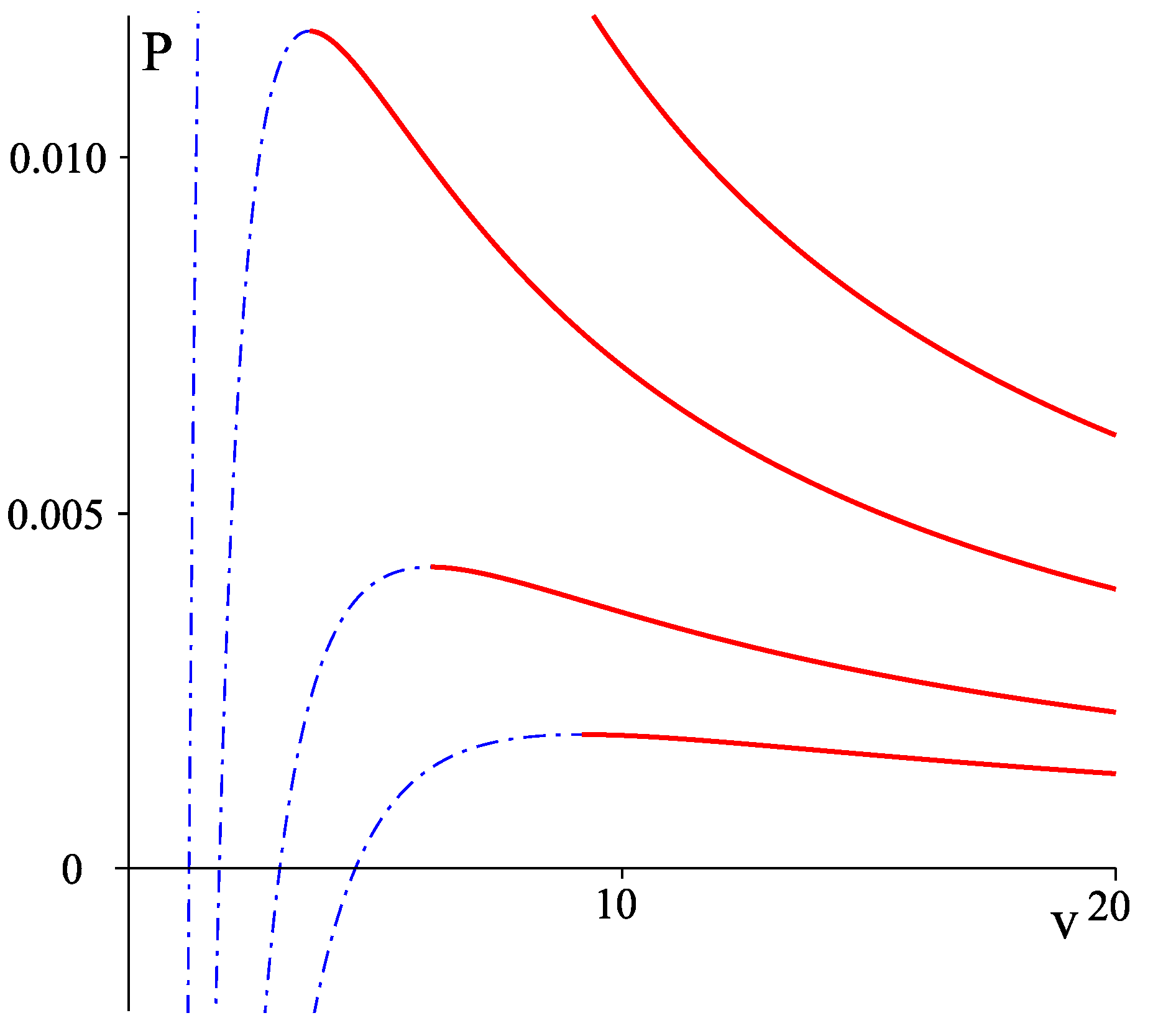
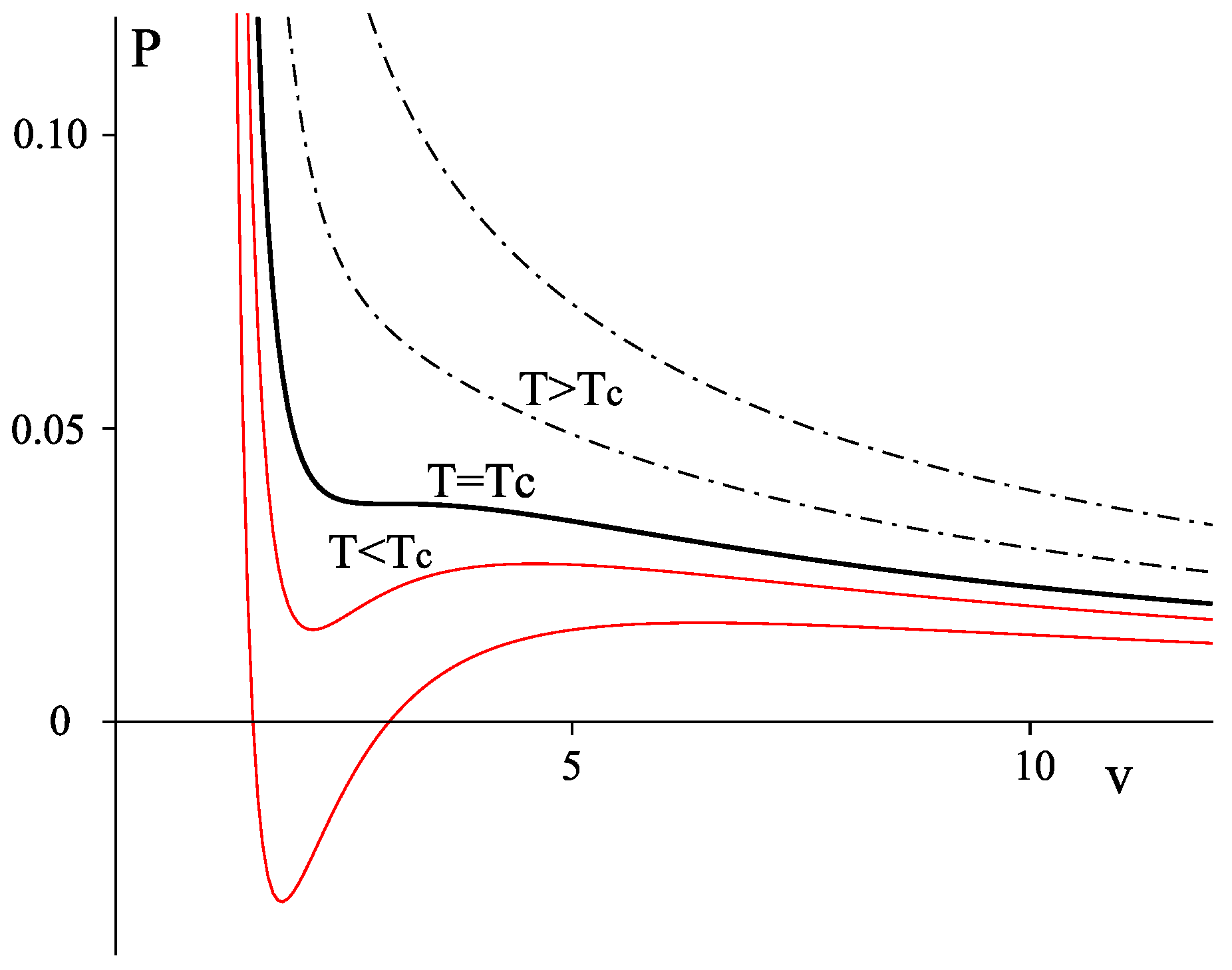
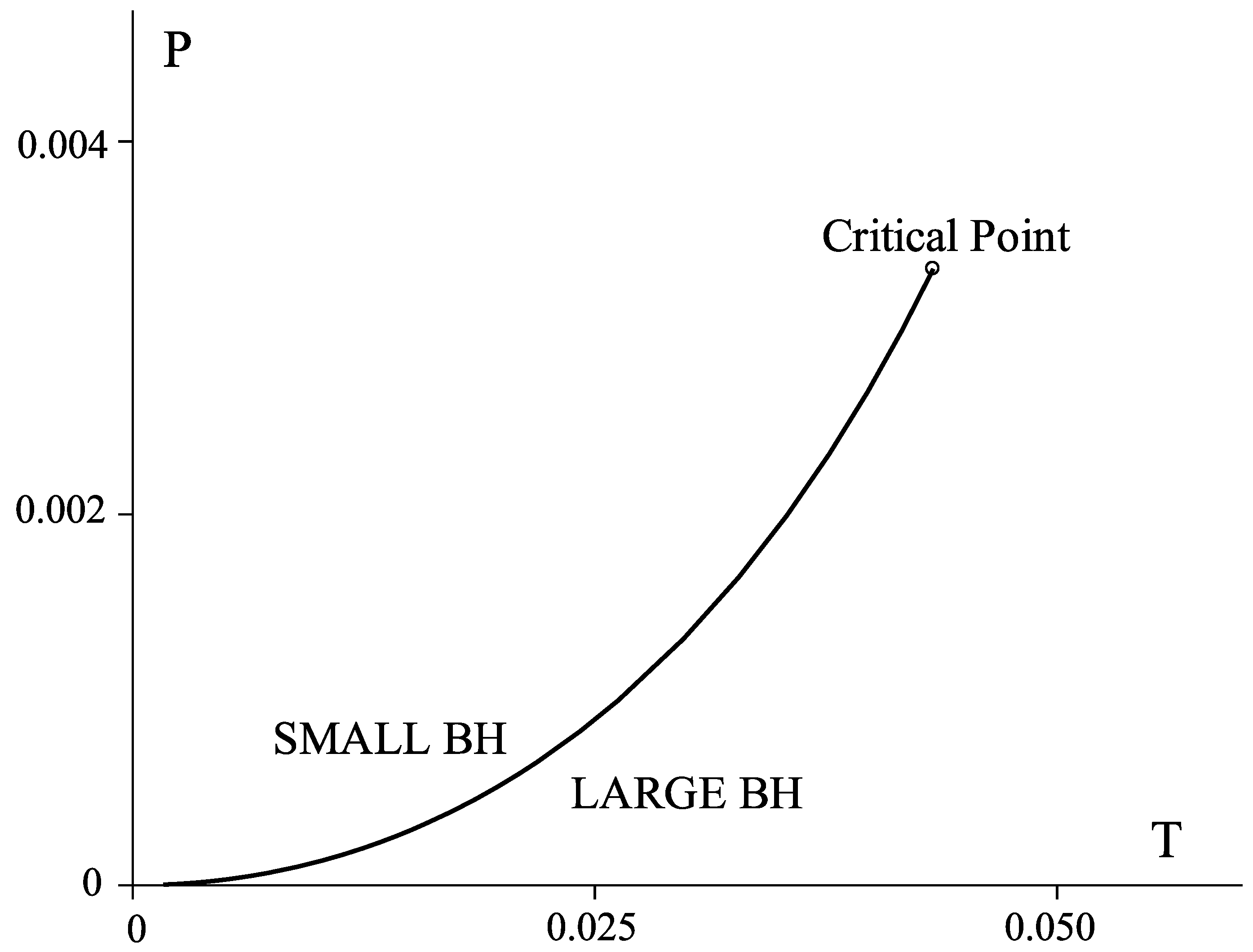
2.2.2. Charged AdS Black Hole

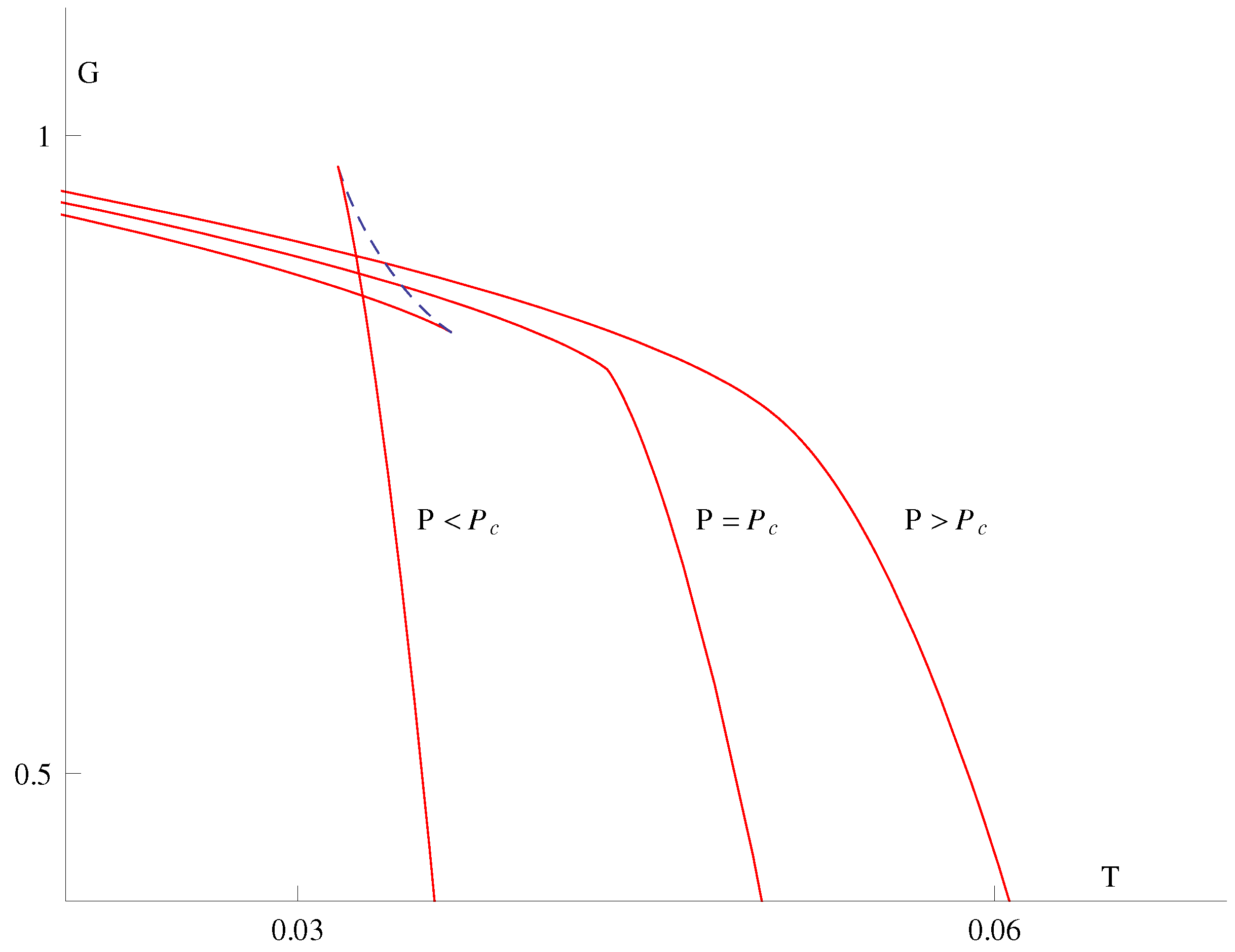
2.2.3. Kerr-AdS
3. Higher-Dimensional Kerr-AdS Black Hole Spacetimes
3.1. General Metrics
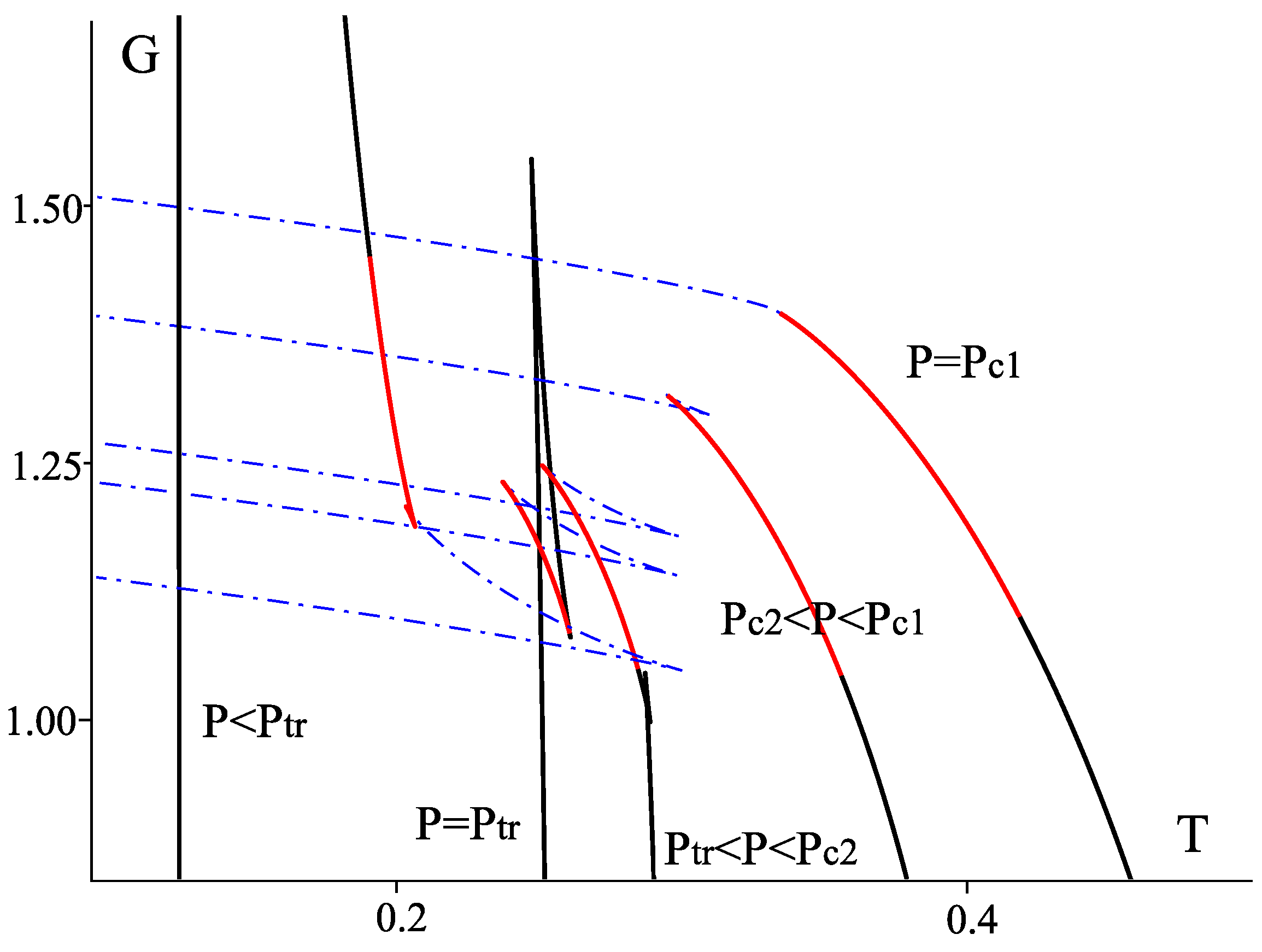
3.2. Classical Swallowtail
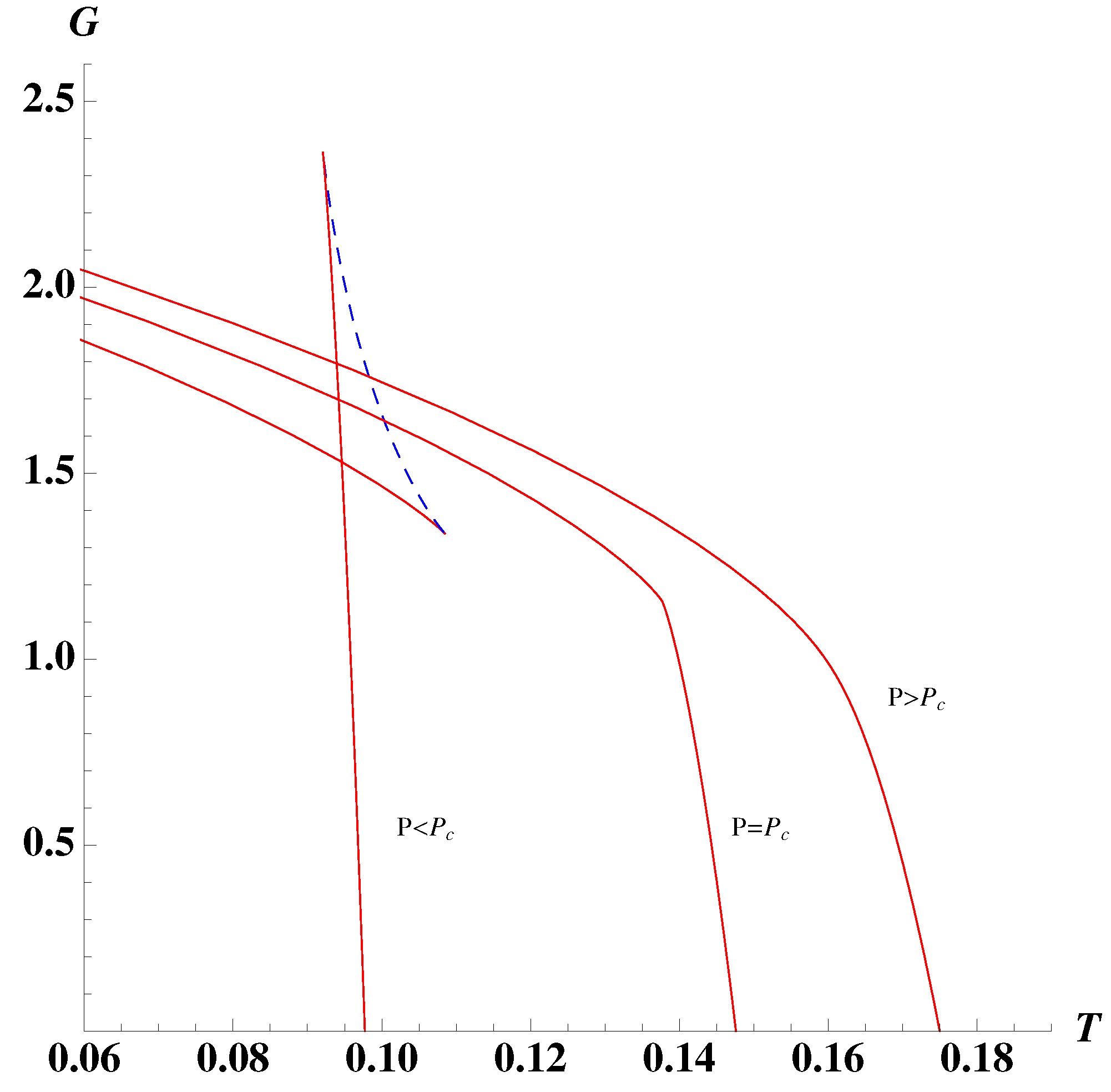
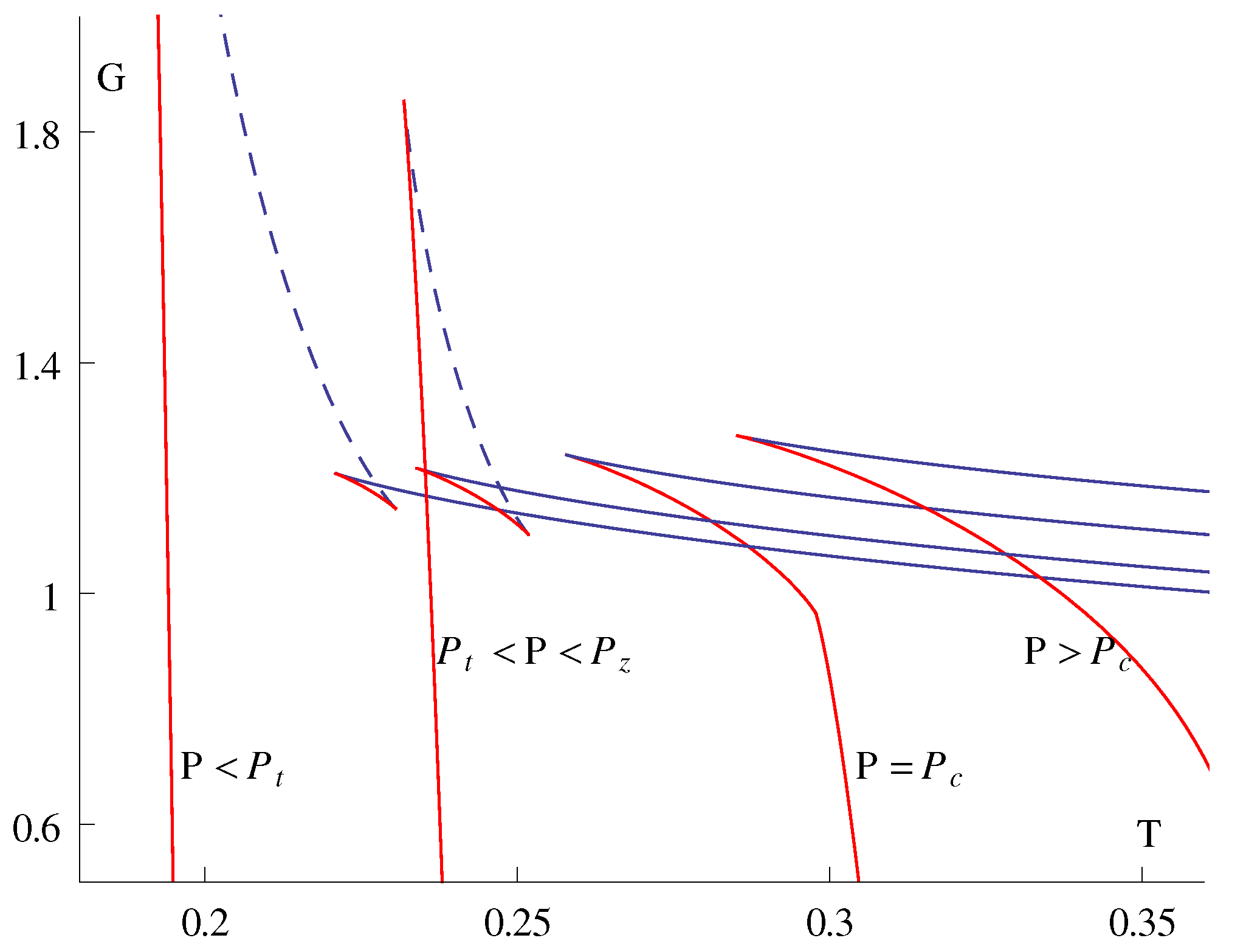
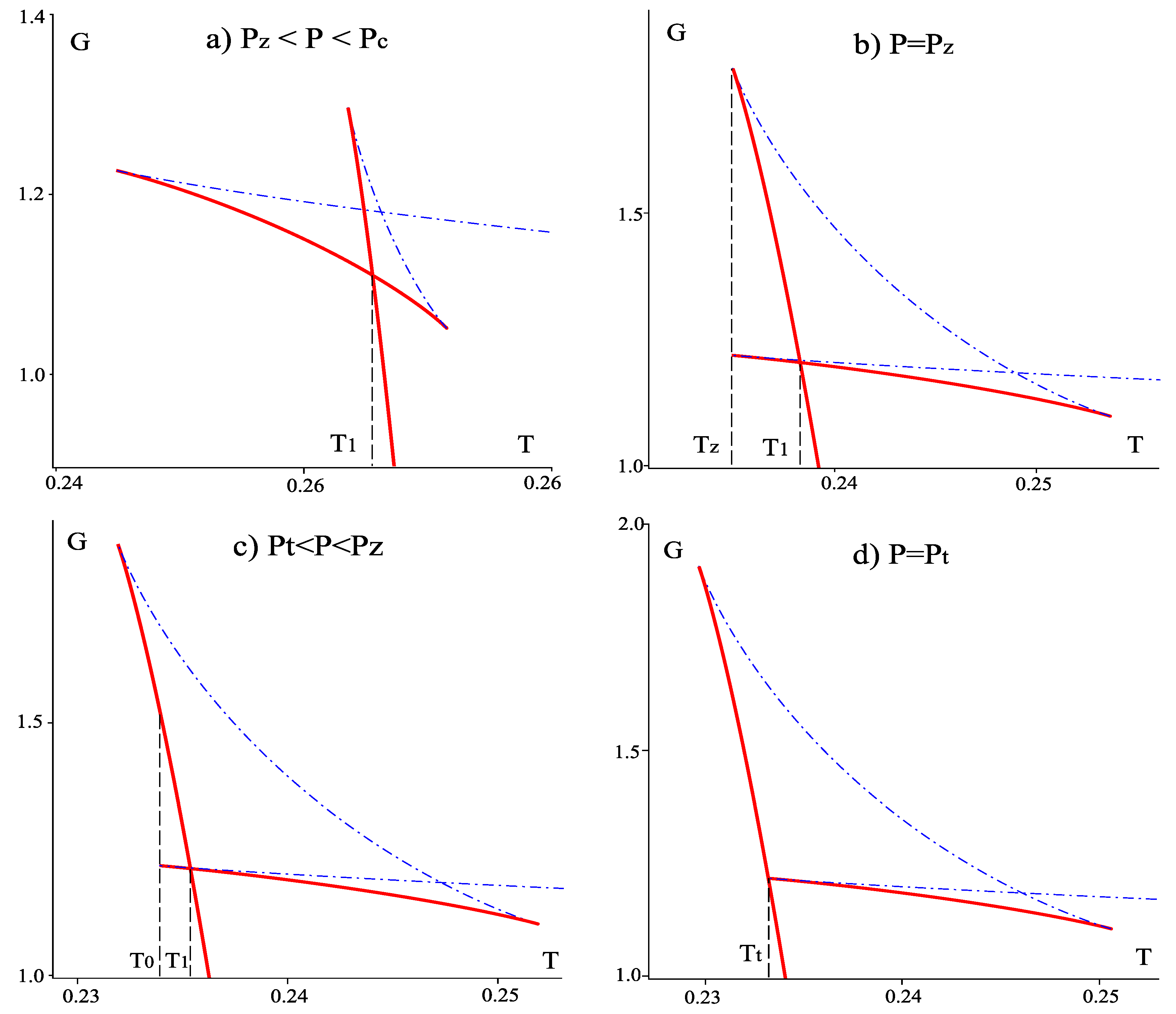
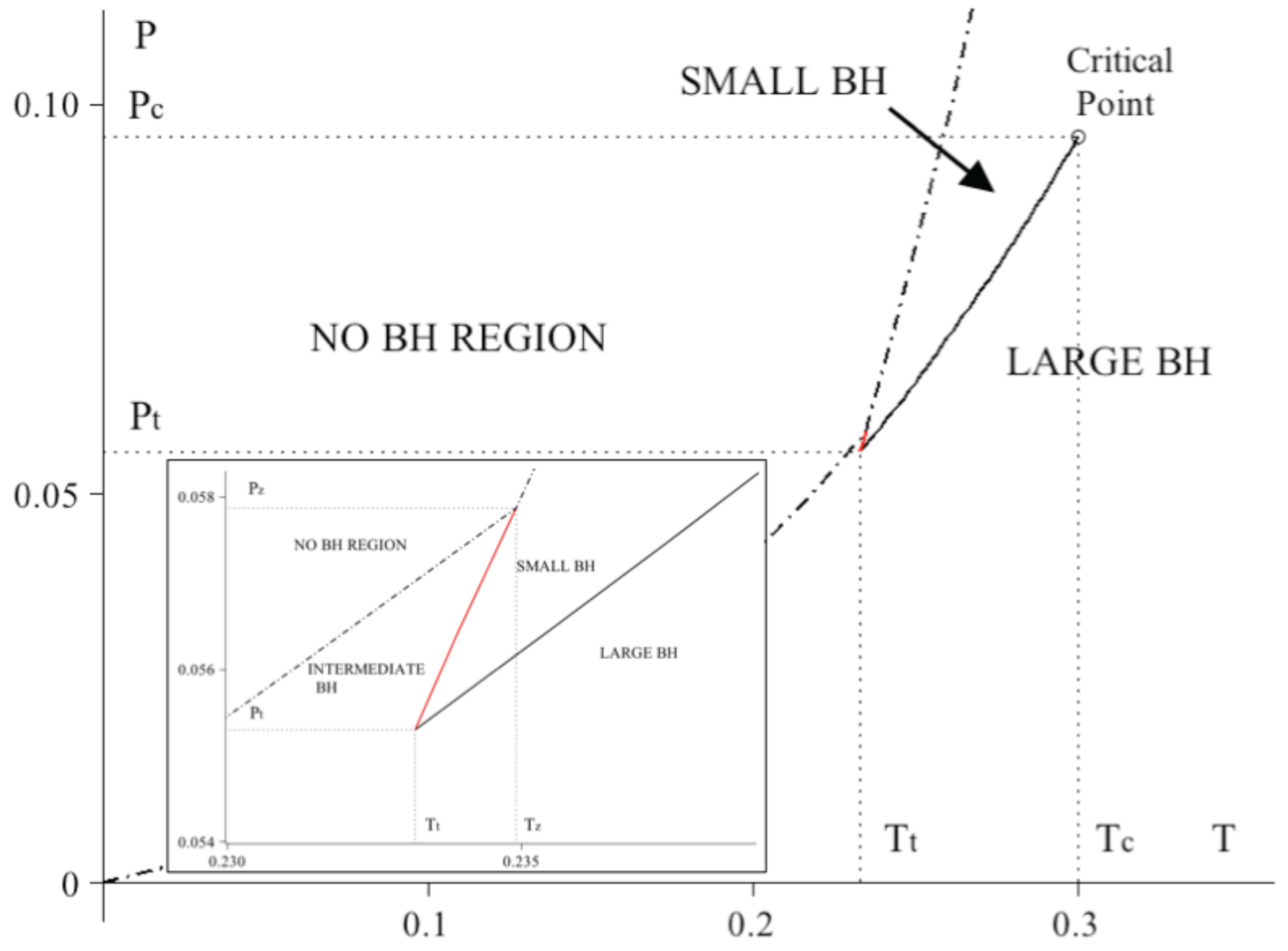
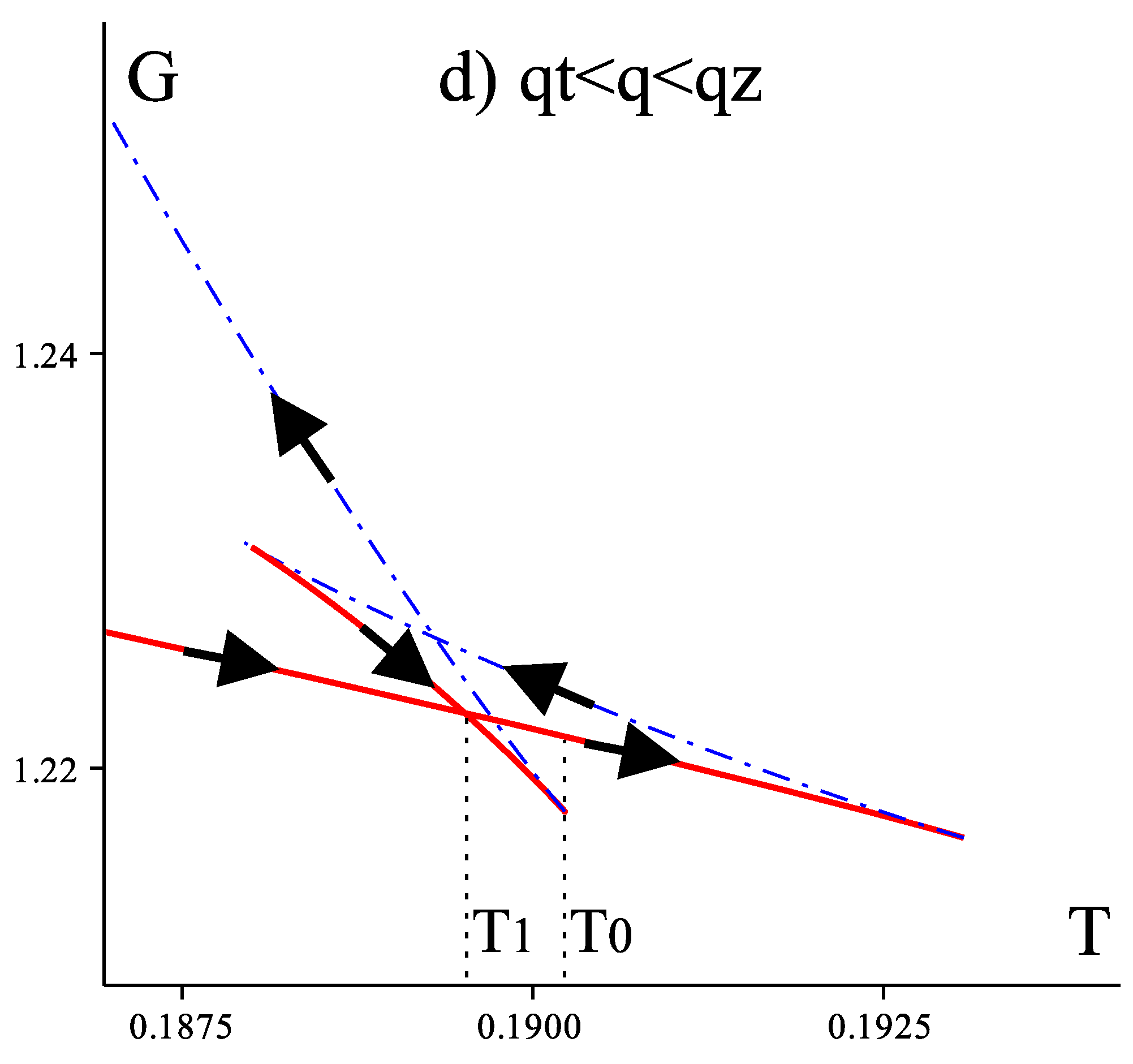
3.3. Reentrant Phase Transition
- (a)
- It is well known that in dimensions there is no “kinematic” limit on how fast the singly spinning Kerr-AdS black holes can rotate. However, fast spinning black holes are subject to various dynamical instabilities, such as ultraspinning instability, superradiant instability, or bar mode instability; these will be discussed in greater detail in Section 7. It turns out that black holes which participate in the reentrant phase transition are stable with respect to the ultraspinning instability: in Figure 12 c only the blue dashed curve with the smallest admits black holes subject to this instability. Unfortunately, this is no longer true for the superradiant and bar mode instability, which “compete” with the reentrant phase transition.
- (b)
- One may wonder why the reentrant phase transition, which is characteristic for multicomponent systems where various phenomena compete among each other to result in reentrance, should occur at all in a “homogeneous” system of one black hole. What are the competing phenomena in our case? A possible explanation is related to the ultraspinning regime. If so, this would also explain why we see reentrance in dimensions but not in or 5 where such a regime does not exist. It is well known that as we spin the spherical black hole faster and faster, its horizon flattens and the resulting object is in many respects similar to a black brane, see the next subsection. However, the thermodynamic behaviour of black branes is completely different from that of spherical black holes. It happens that small black holes that participate in the reentrant phase transition are “almost ultraspinning” and hence possess almost black brane behavior. For this reason it may be the competition between the black brane thermodynamic behavior and the black hole thermodynamic behavior which causes the ‘multicomponency’ and results in the reentrant phase transition.
- (c)
- We note that all the interesting behaviour leading to the reentrant phase transition occurs for a positive Gibbs free energy, i.e., below temperature . For this reason, one may expect that the thermal AdS (see Section 2) is actually preferred thermodynamic state in this region and the various black holes participating in the reentrant phase transition are actually metastable. If so, the reentrant phase transition may actually be destroyed and one would simply observe a Hawking–Page transition between thermal radiation and large black holes at . We stress that similar arguments also apply to the four-dimensional charged AdS black hole discussed in Section 2 and the corresponding “van der Waals” phase transition.
- (d)
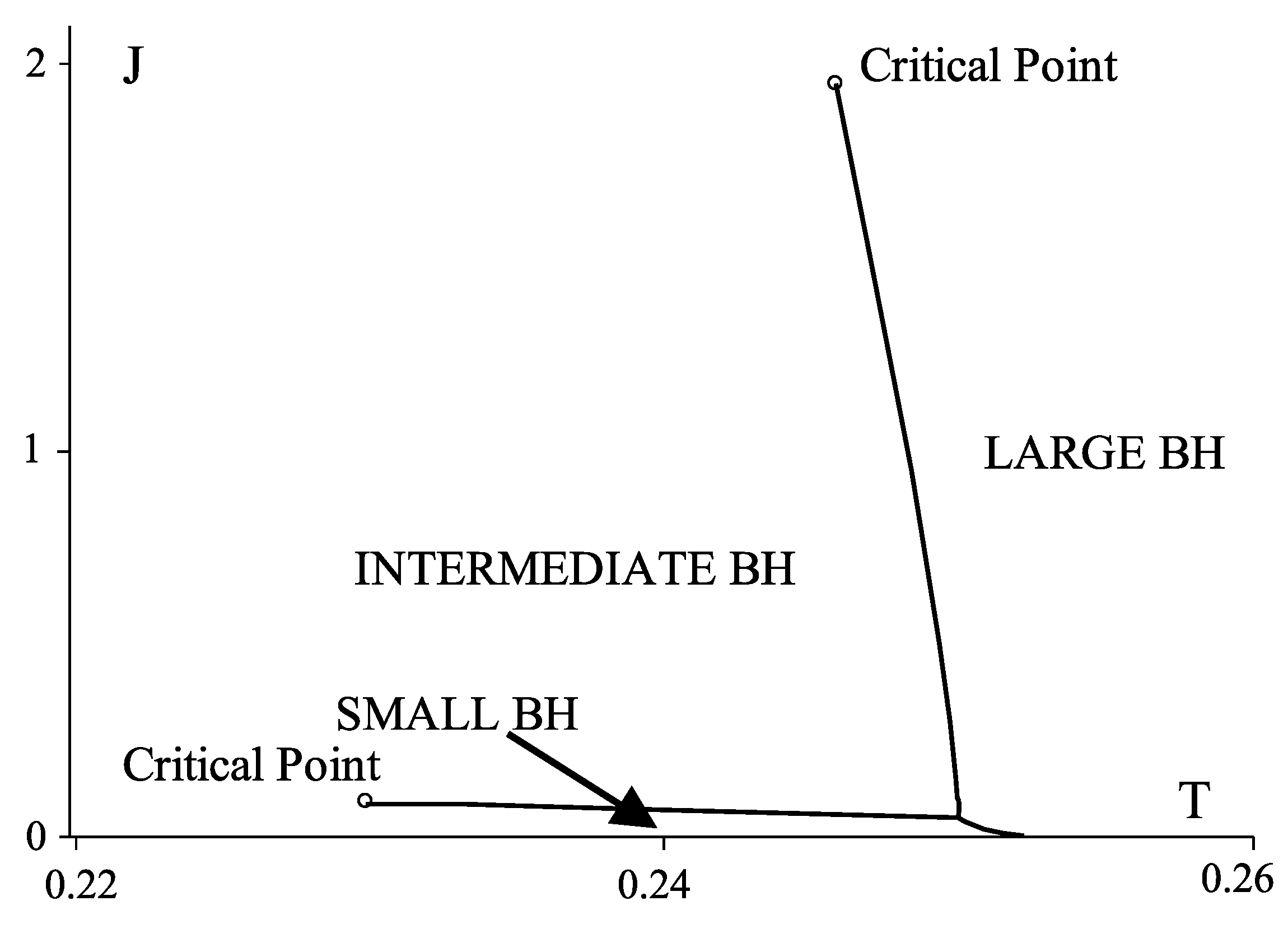
- The observed reentrant phase transition is well suited for the AdS/CFT interpretation. Although first observed [25] in the context of extended phase space thermodynamics, the existence of the reentrant phase transition does not require a variable cosmological constant. For any fixed value of Λ within the allowed range of pressure, the reentrant phase transition will take place. This opens up a possibility for an AdS/CFT interpretation—in particular in the dual CFT there will be a corresponding reentrant phase transition within the allowed range of N. In fact, we can fix the pressure and construct a phase diagram plotting J vs. T (Figure 15) showing that reentrant phase behaviour occurs. Hence in the dual CFT at this fixed pressure there will be a corresponding reentrant transition as the relative values of the quantities dual to the angular momenta are adjusted.
- (e)
- The existence of reentrant phase transitions in the context of black hole thermodynamics seems quite general. Similar phenomena have been observed in Born–Infeld black hole spacetimes [16]. We shall also see in Section 4, that reentrant phase transitions are observed for the asymptotically flat doubly-spinning Myers–Perry black holes of vacuum Einstein gravity. Hence, neither exotic matter nor a cosmological constant (and hence AdS/CFT correspondence) are required for this phenomenon to occur in black hole spacetimes.
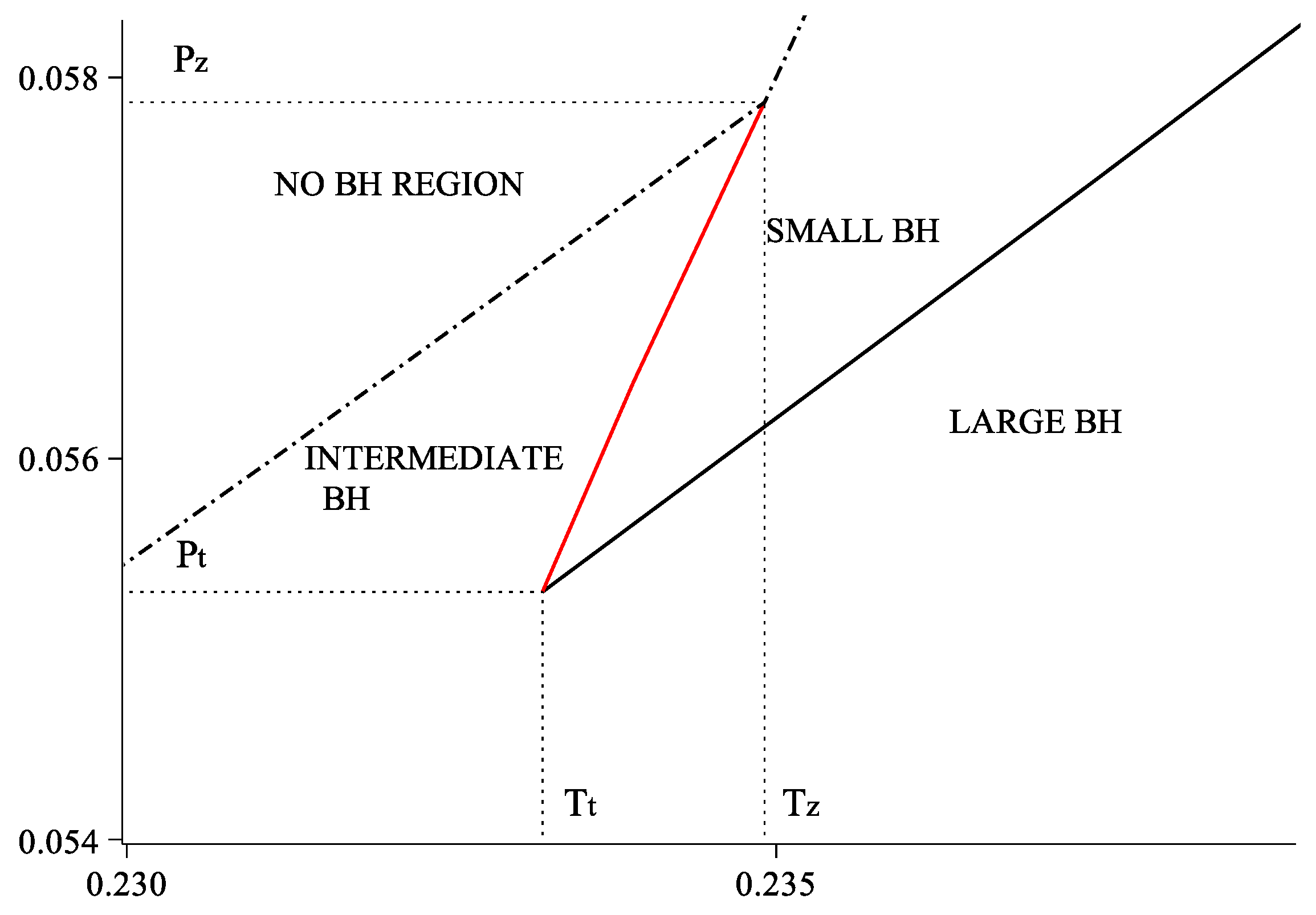
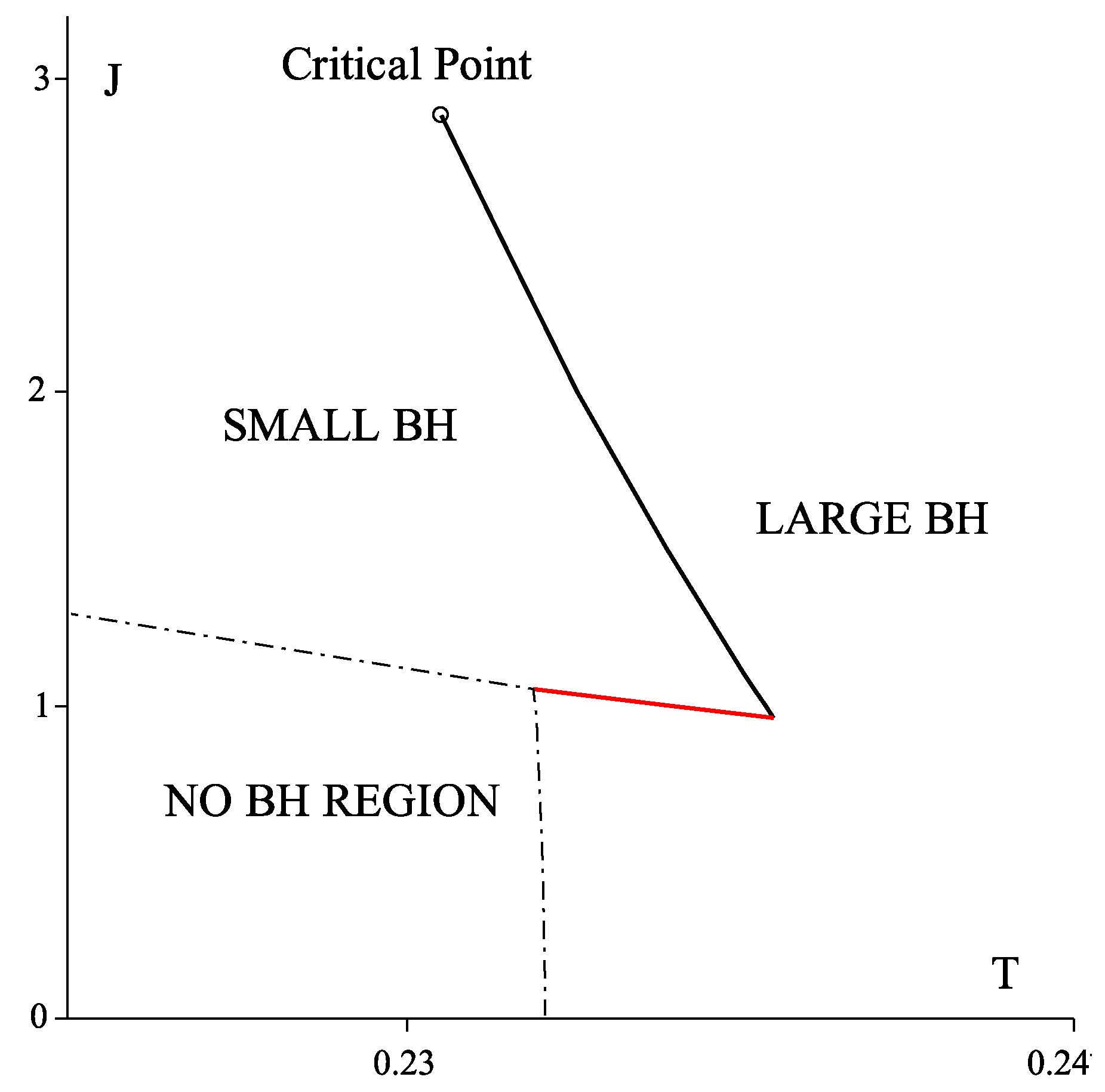
3.4. Equation of State
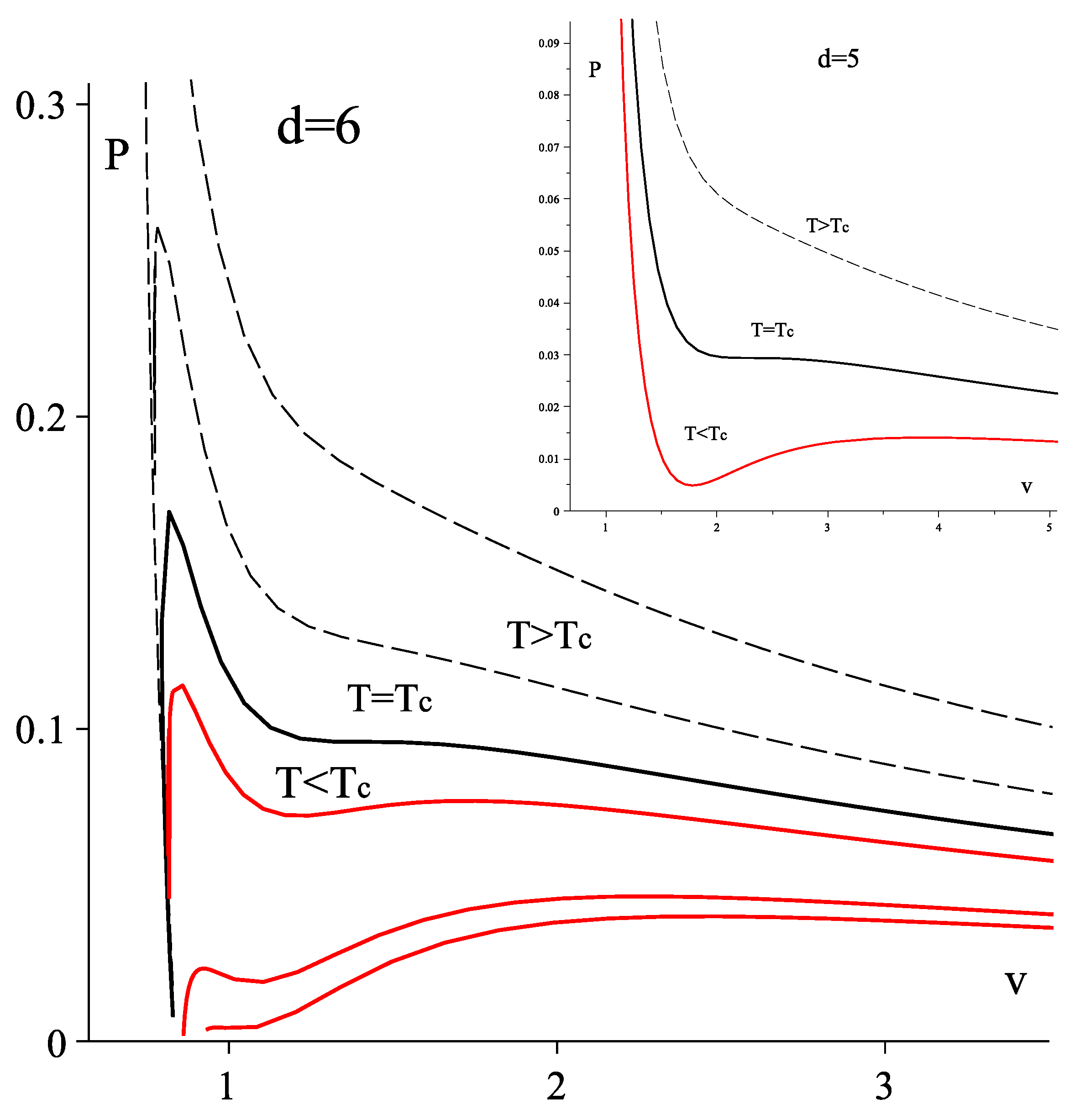
3.4.1. Slow Rotation Expansion
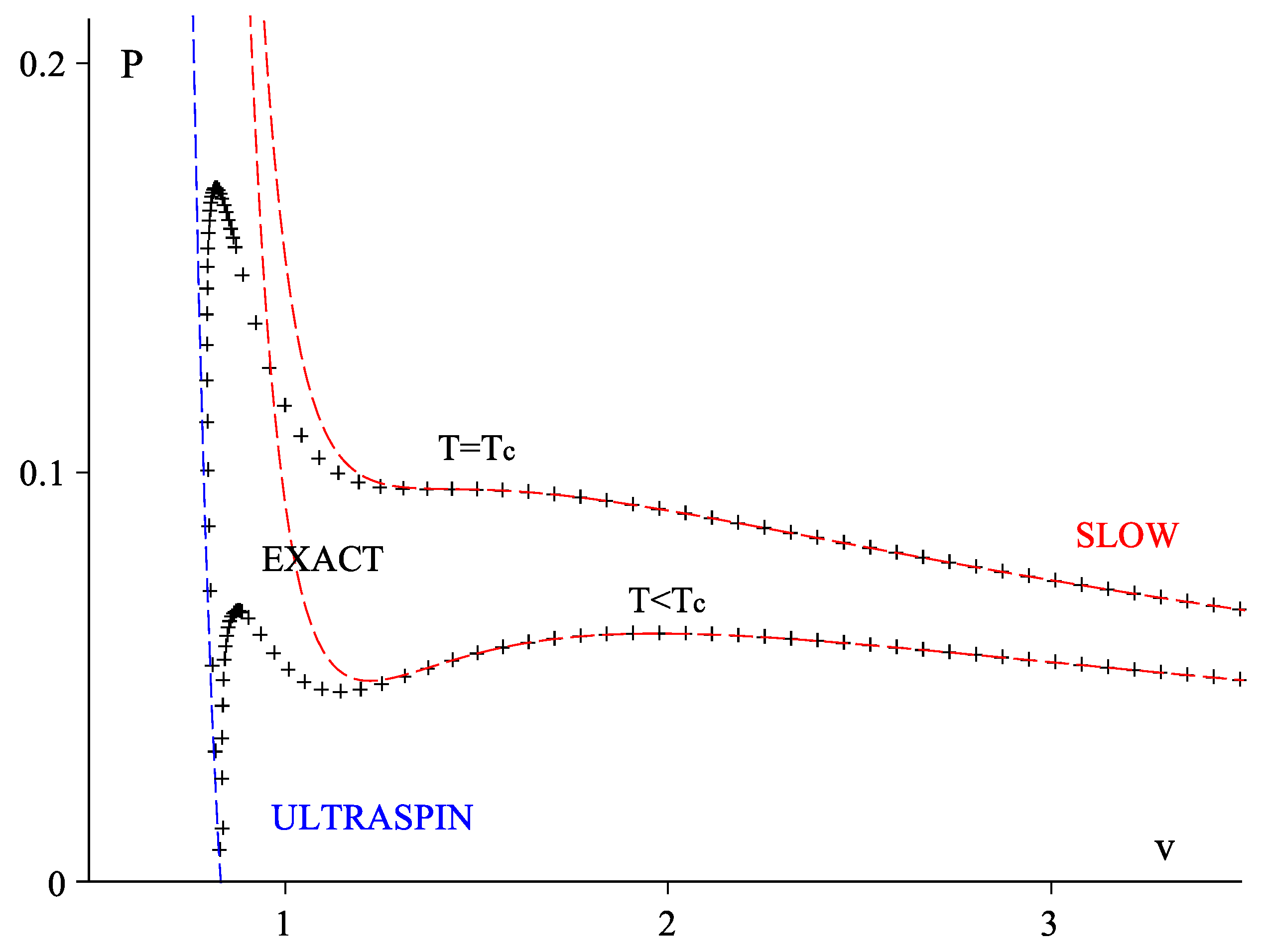
3.4.2. Critical Point
3.4.3. Remark on Exact Critical Exponents in
3.4.4. Ultraspinning Expansion
3.4.5. Ultraspinning Limit: Black Membranes
3.4.6. Equal Spinning AdS Black Holes
3.5. An Analogue of Triple Point and Solid/Liquid/Gas Phase Transition
3.5.1. Solid/Liquid Analogue
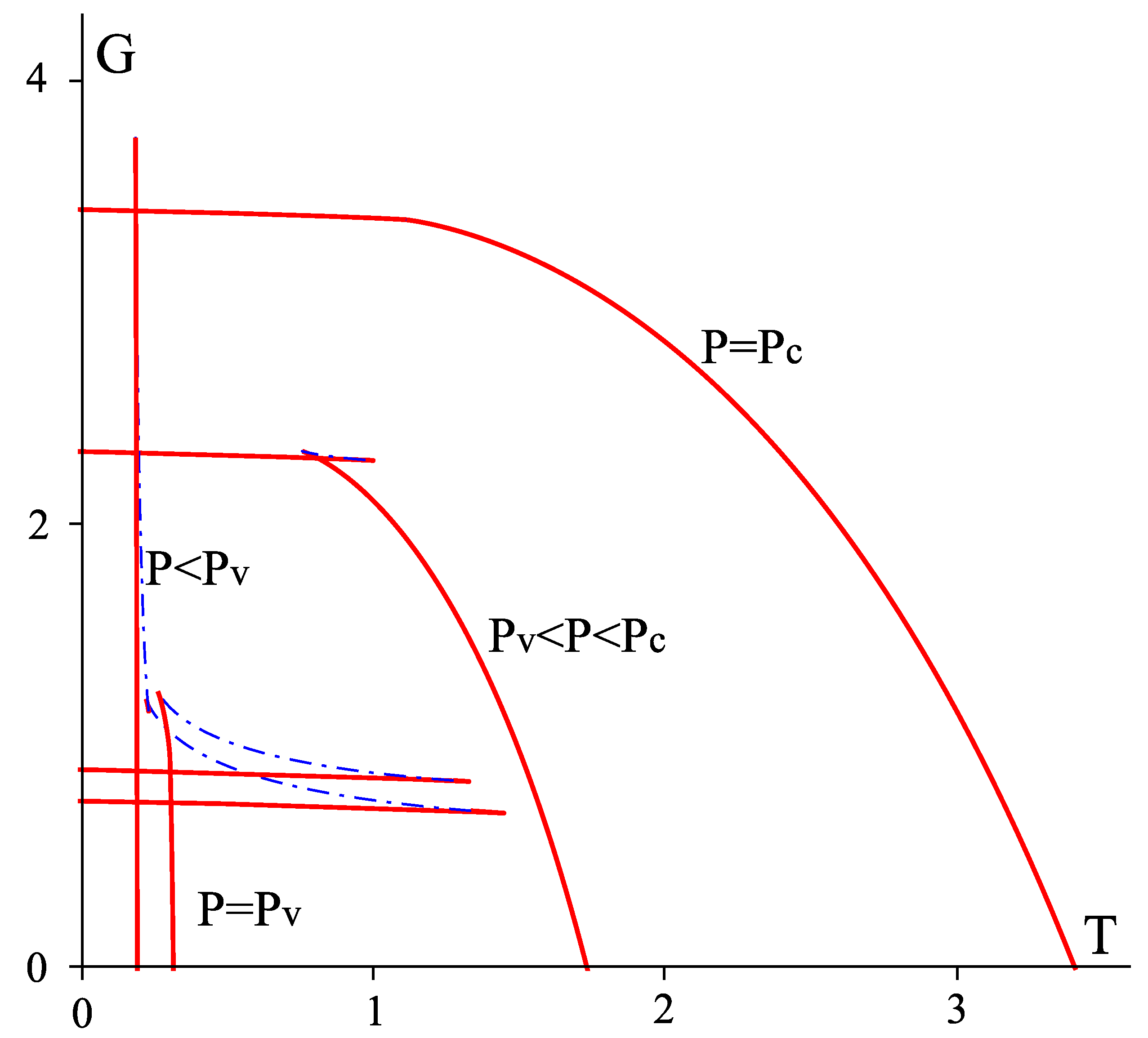
3.5.2. Triple Point and Solid/Liquid/Gas Analogue

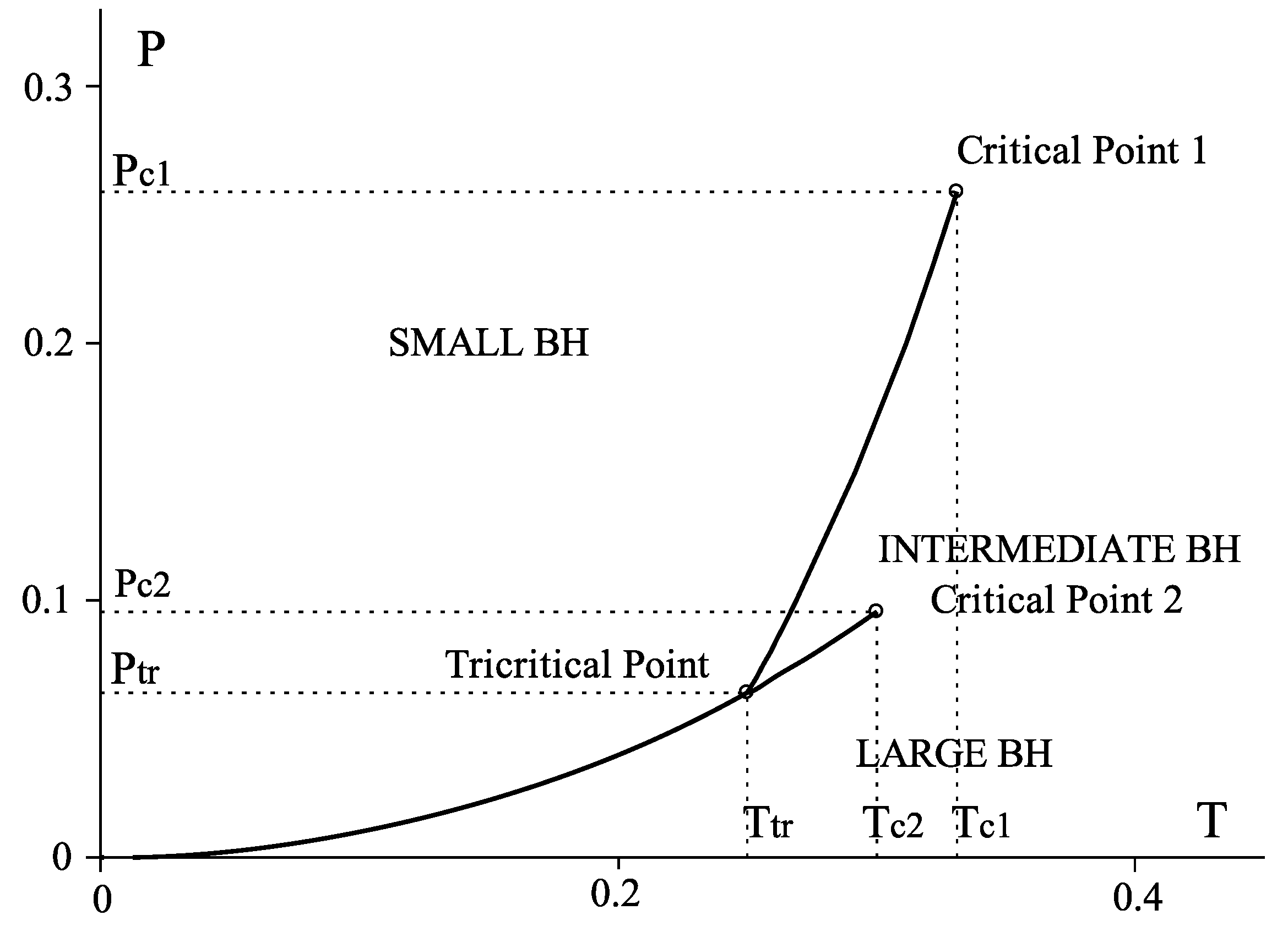

3.5.3. Van Der Waals Behavior
4. Myers–Perry Solutions
4.1. Five-Dimensional Case
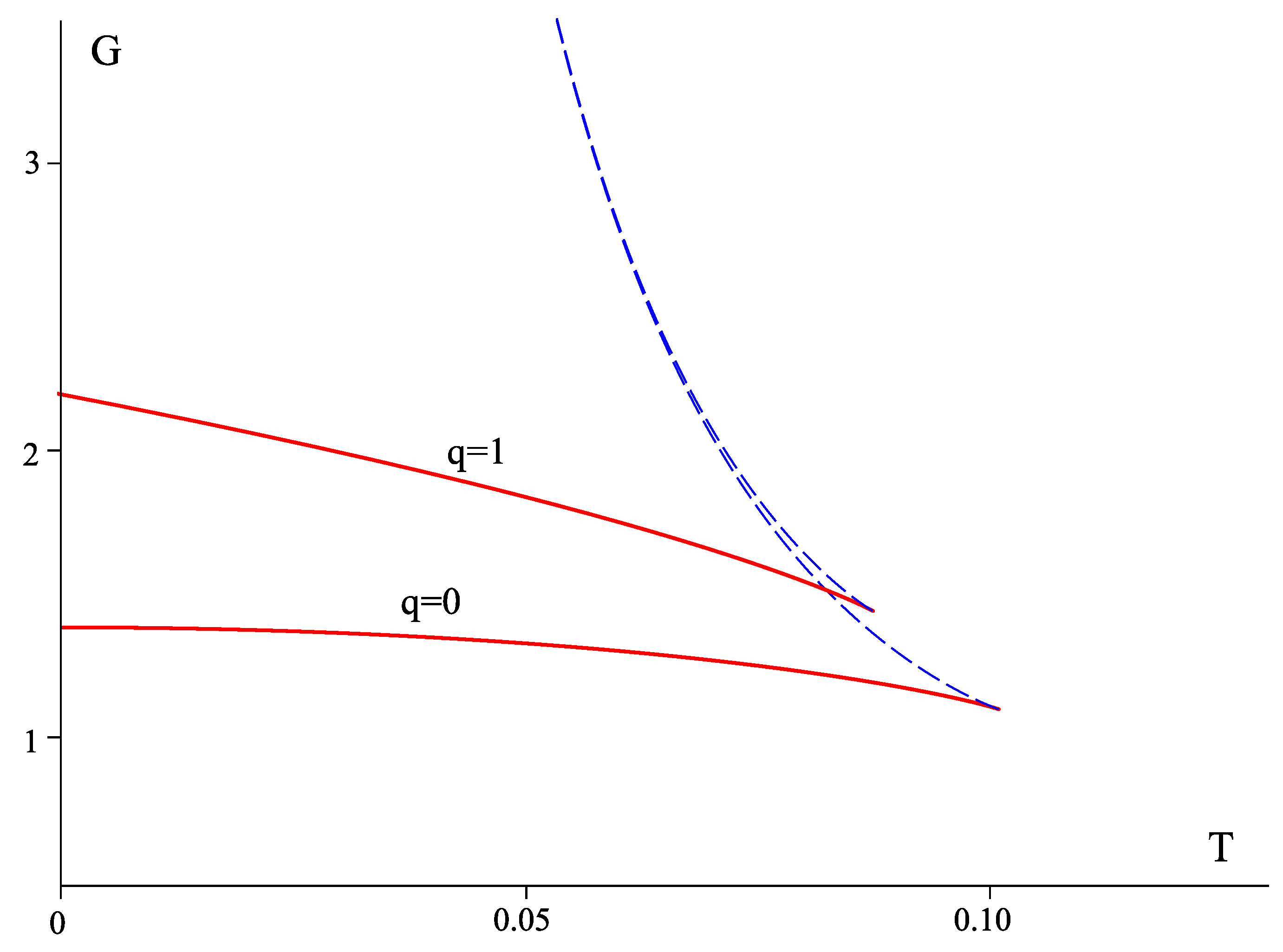
4.2. Reentrant Phase Transition
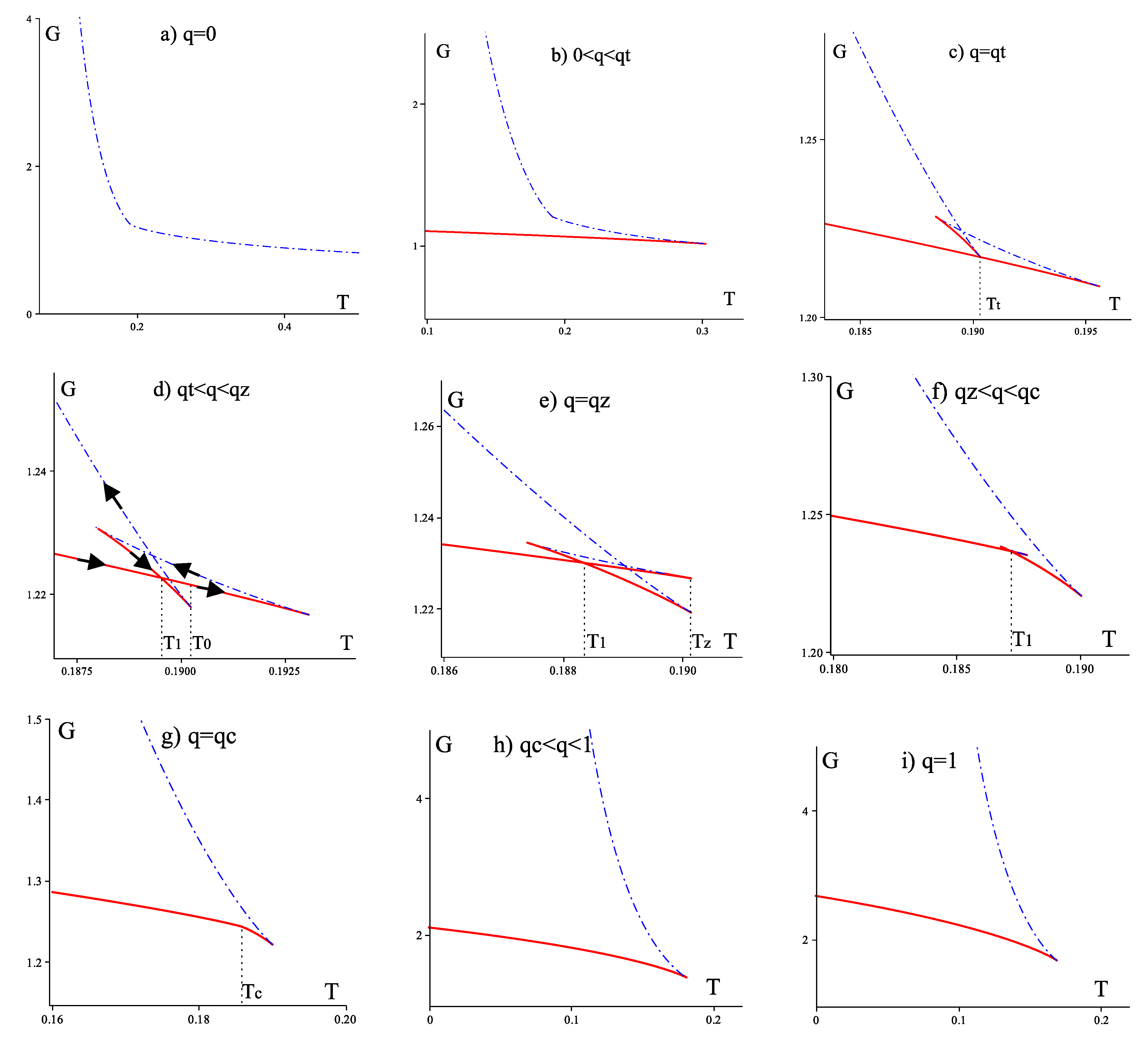
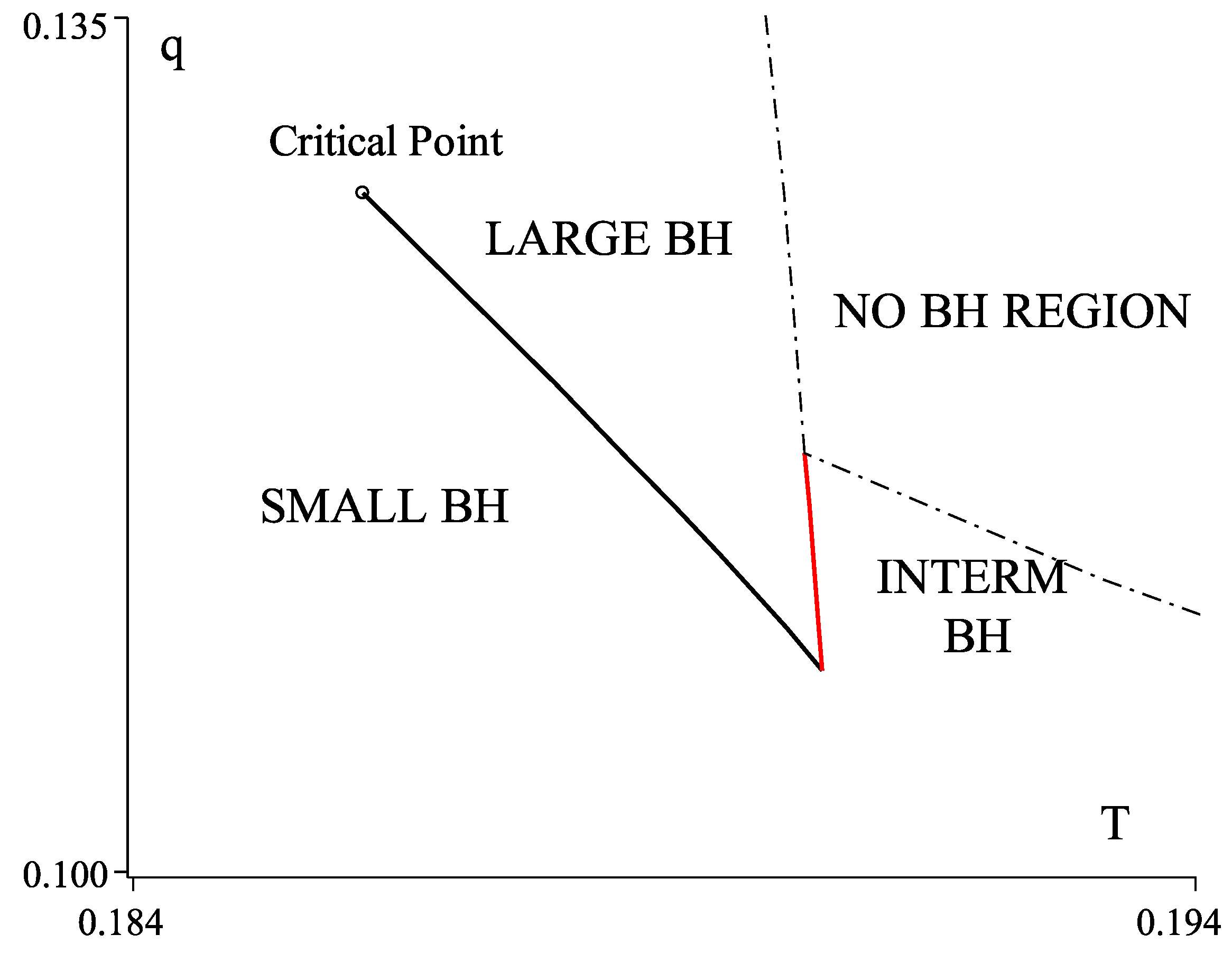
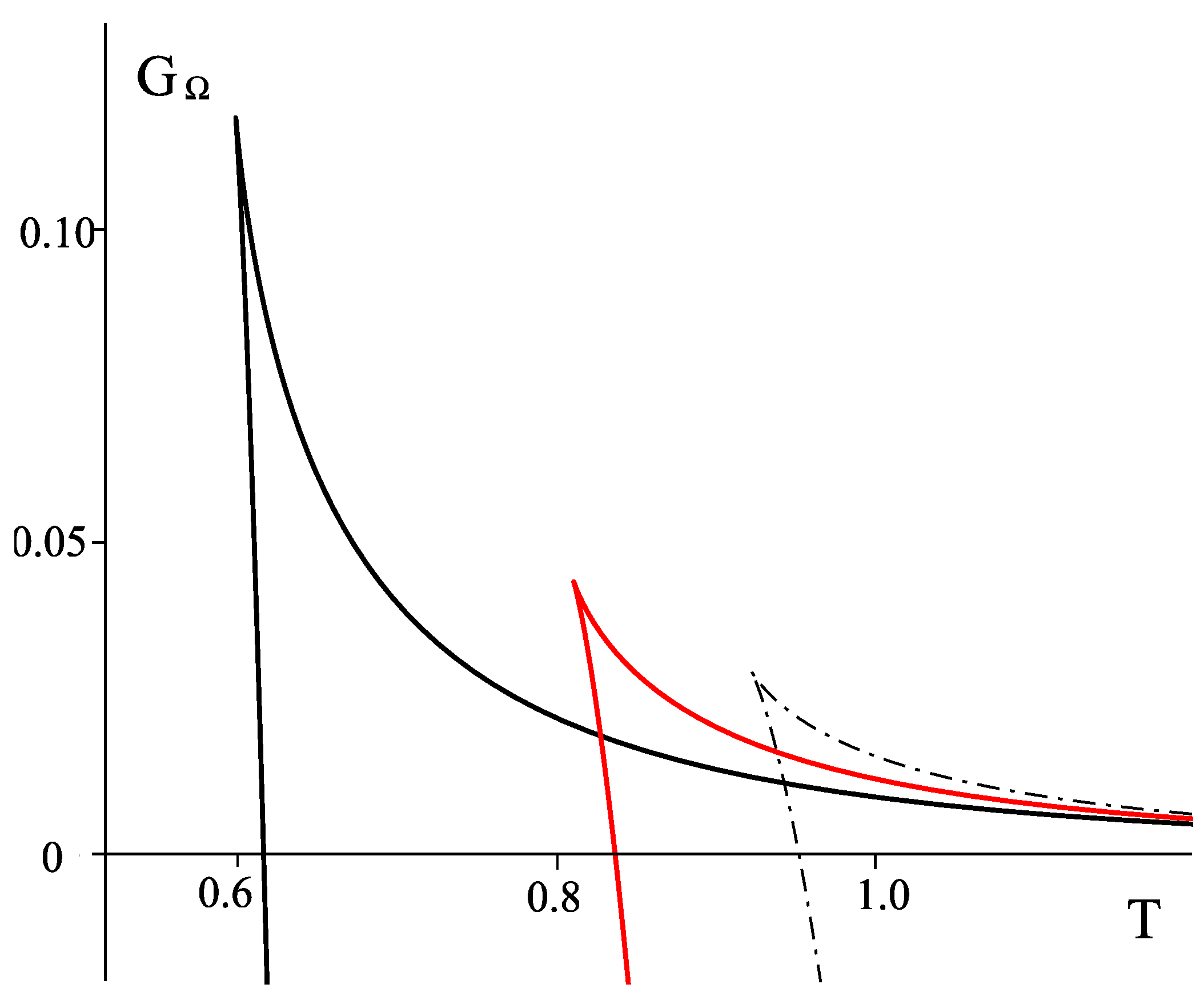
5. Five-Dimensional Black Rings and Black Saturns
5.1. Singly Spinning Black Ring

5.2. Black Saturn
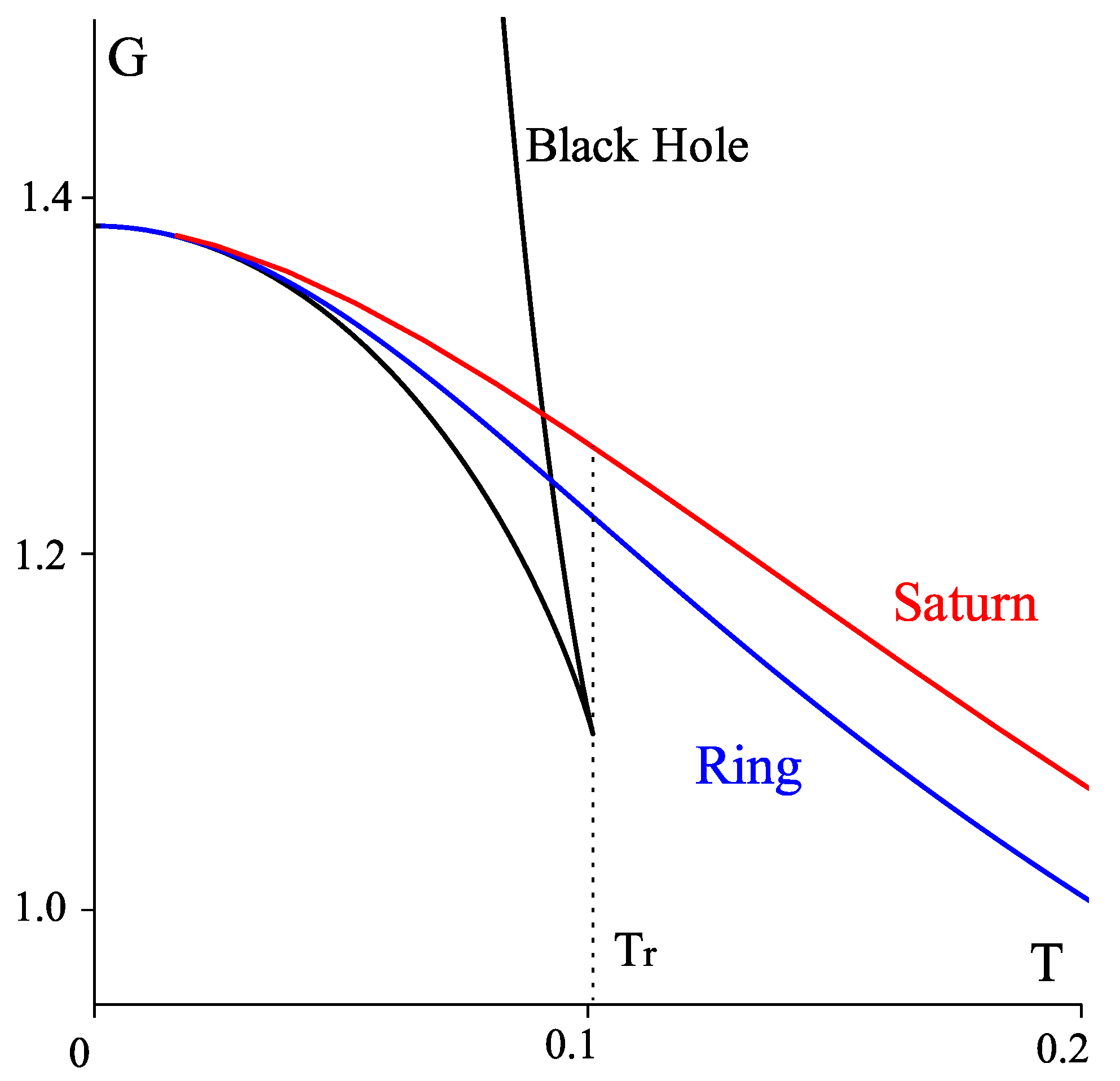
6. Thin Black Rings in AdS
6.1. Review of the Construction
6.2. Thermodynamics
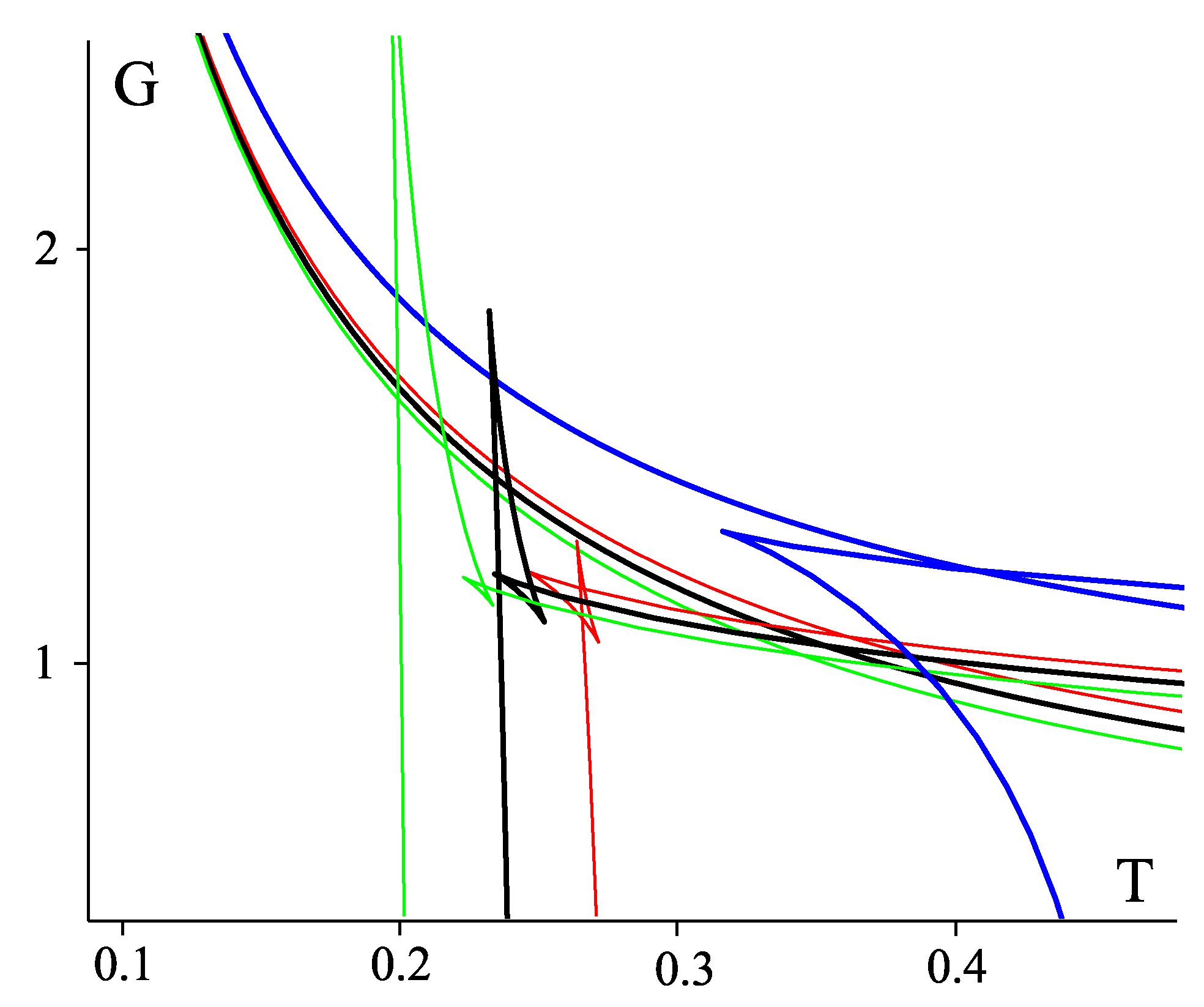
6.3. Thermodynamic Volume
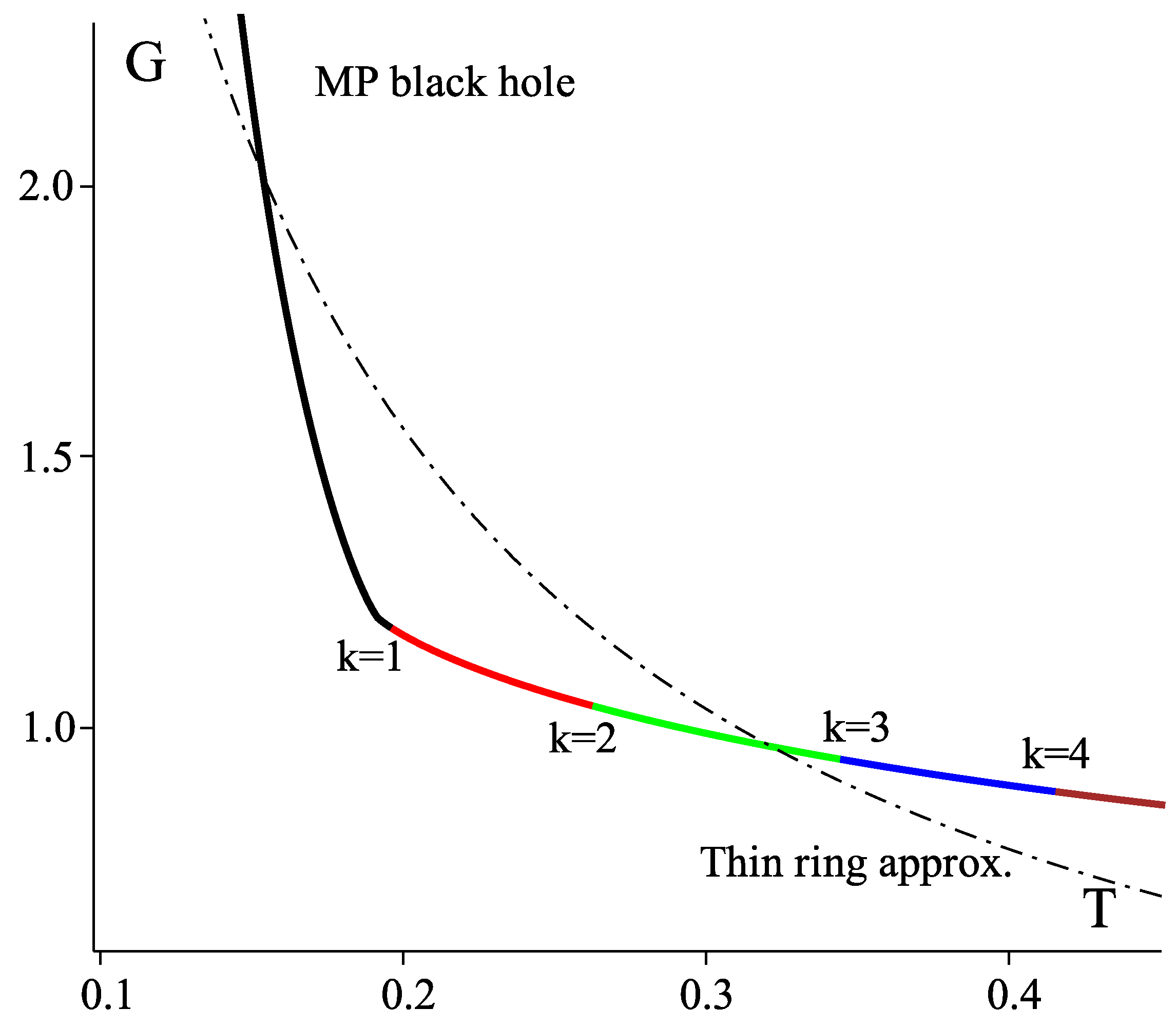
6.4. Isoperimetric Inequality
6.5. Equation of State
6.6. Ultraspinning Expansion

7. Beyond Thermodynamic Instabilities
7.1. Ultraspinning Instability
7.1.1. Bifurcations of Singly Spinning MP Black Holes
7.1.2. Thermodynamic Argument and Other Examples
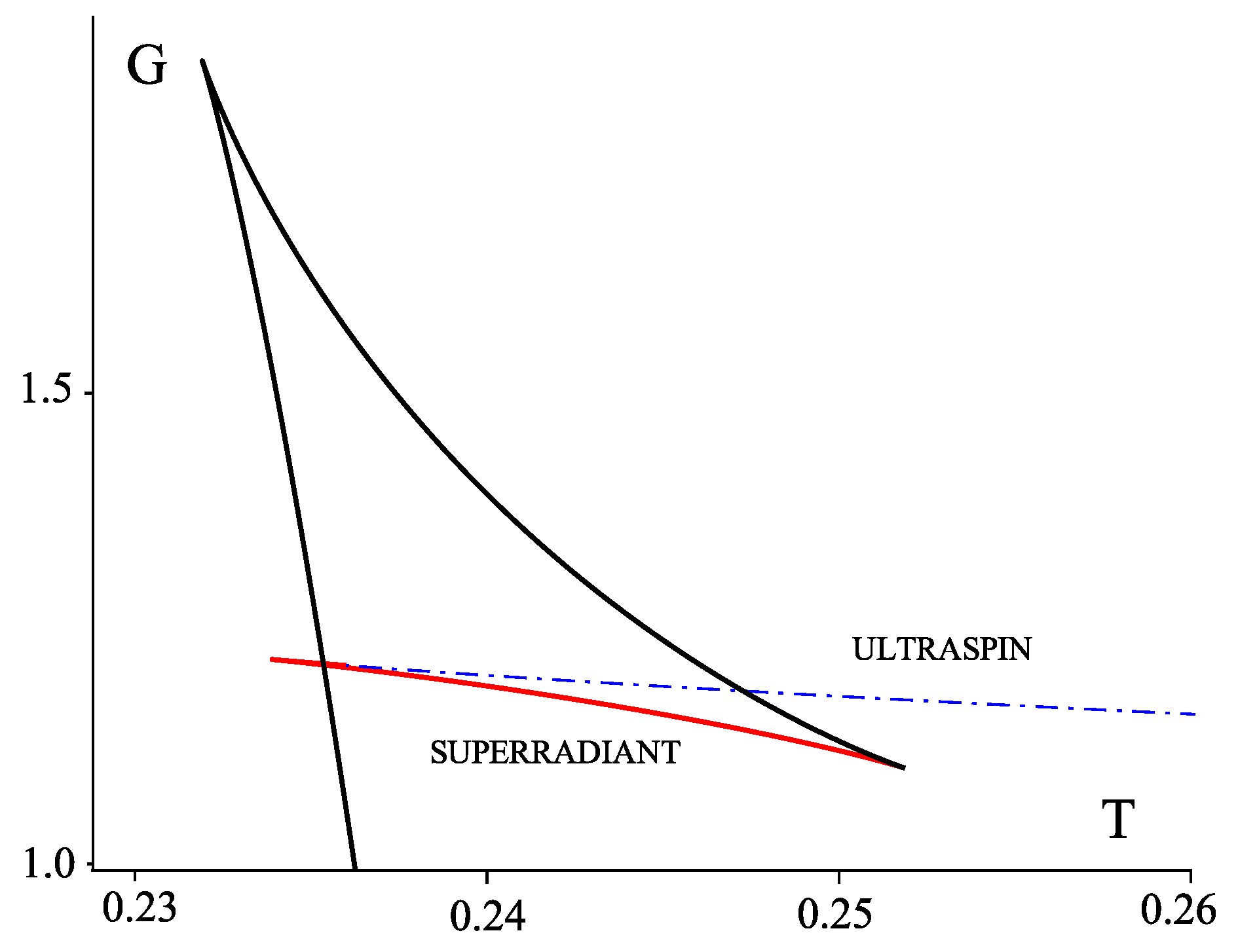
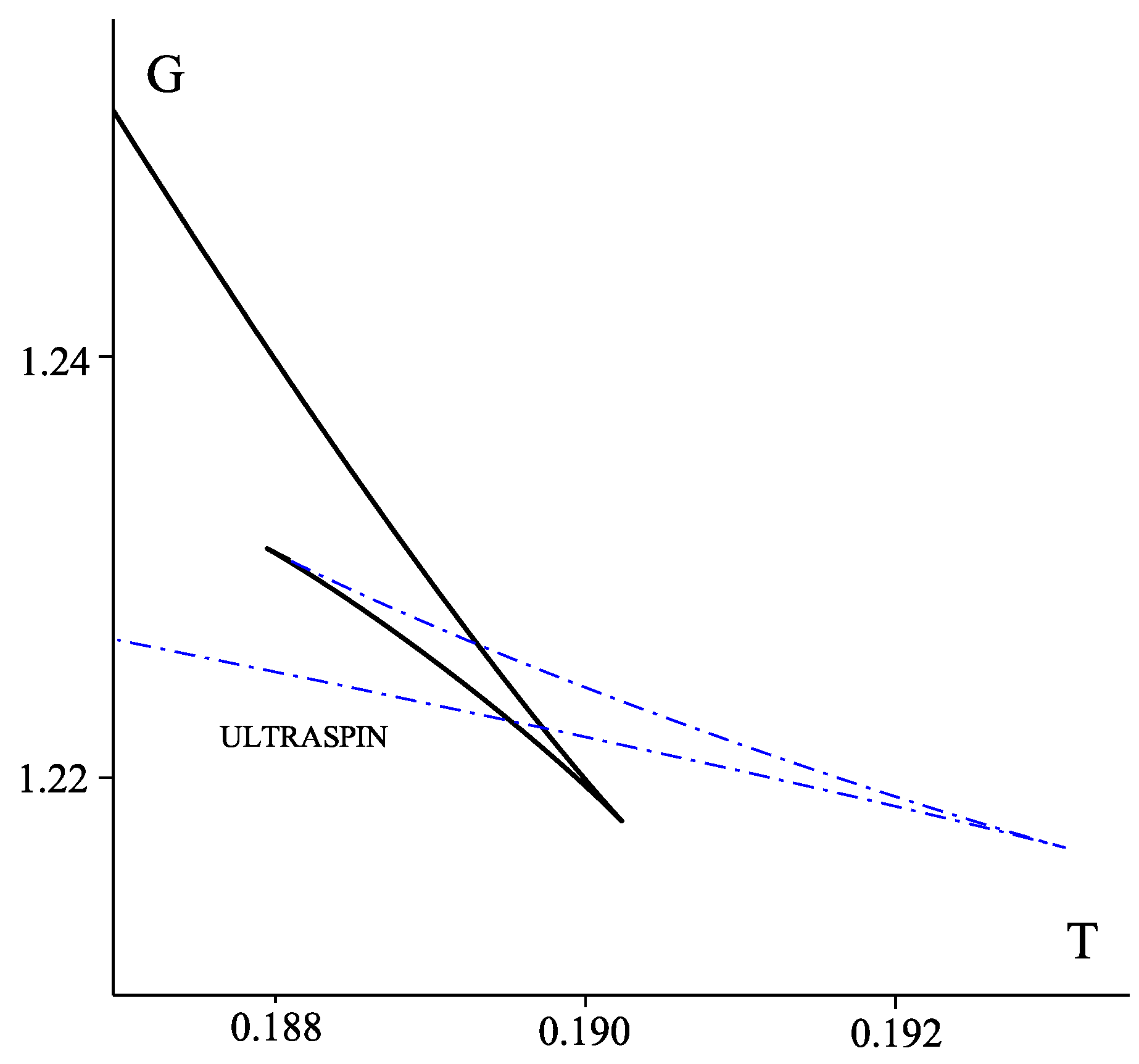
7.2. Superradiant Instabilities

8. Conclusions
Acknowledgments
Conflicts of Interest
References
- Hawking, S.; Page, D.N. Thermodynamics of black holes in anti-de sitter space. Commun. Math. Phys. 1983, 87, 577–588. [Google Scholar] [CrossRef]
- Kastor, D.; Ray, S.; Traschen, J. Enthalpy and the mechanics of AdS black holes. Class. Quant. Gravity 2009, 26, 195011. [Google Scholar] [CrossRef]
- Creighton, J.; Mann, R.B. Quasilocal thermodynamics of dilaton gravity coupled to gauge fields. Phys. Rev. D 1995, 52, 4569–4587. [Google Scholar]
- Caldarelli, M.M.; Cognola, G.; Klemm, D. Thermodynamics of Kerr-Newman-AdS black holes and conformal field theories. Class. Quant. Gravity 2000, 17, 399–420. [Google Scholar] [CrossRef]
- Dolan, B.P. The cosmological constant and black-hole thermodynamic potentials. Class. Quant. Gravity 2011, 28, 125020. [Google Scholar] [CrossRef]
- Dolan, B.P. Pressure and volume in the first law of black hole thermodynamics. Class. Quant. Gravity 2011, 28, 235017. [Google Scholar] [CrossRef]
- Dolan, B.P. Compressibility of rotating black holes. Phys. Rev. D 2011, 84, 127503. [Google Scholar] [CrossRef]
- Dolan, B.P. Where is the PdV Term in the Fist Law of Black Hole Thermodynamics? In Open Questions in Cosmology; Olmo, G.J., Ed.; InTech: Rijeka, Croatia, 2012. [Google Scholar]
- Dolan, B.P. The compressibility of rotating black holes in D-dimensions. Class. Quant. Gravity 2014, 31, 035022. [Google Scholar] [CrossRef]
- Cvetic, M.; Gibbons, G.; Kubiznak, D.; Pope, C. Black hole enthalpy and an entropy inequality for the thermodynamic volume. Phys. Rev. D 2011, 84, 024037. [Google Scholar] [CrossRef]
- Kastor, D.; Ray, S.; Traschen, J. Smarr formula and an extended first law for lovelock gravity. Class. Quant. Gravity 2010, 27, 235014. [Google Scholar] [CrossRef]
- Larranaga, A.; Cardenas, A. Geometric thermodynamics of schwarzschild-AdS black hole with a cosmological constant as state variable. J. Korean Phys. Soc. 2012, 60, 987–992. [Google Scholar] [CrossRef]
- Larranaga, A.; Mojica, S. Geometric thermodynamics of Kerr-AdS black hole with a cosmological constant as state variable. Abraham Zelmanov J. 2012, 5, 68–77. [Google Scholar]
- Gibbons, G. What is the shape of a black hole? AIP Conf. Proc. 2012, 1460, 90–100. [Google Scholar]
- Kubiznak, D.; Mann, R.B. P-V criticality of charged AdS black holes. J. High Energy Phys. 2012, 1207, 033. [Google Scholar] [CrossRef]
- Gunasekaran, S.; Kubiznak, D.; Mann, R. Extended phase space thermodynamics for charged and rotating black holes and Born-Infeld vacuum polarization. J. High Energy Phys. 2012, 1211, 110. [Google Scholar] [CrossRef]
- Belhaj, A.; Chabab, M.; El Moumni, H.; Sedra, M.B. On thermodynamics of AdS black holes in arbitrary dimensions. Chin. Phys. Lett. 2012, 29, 100401. [Google Scholar] [CrossRef]
- Lu, H.; Pang, Y.; Pope, C.N.; Vazquez-Poritz, J.F. AdS and lifshitz black holes in conformal and Einstein-Weyl gravities. Phys. Rev. D 2012, 86, 044011. [Google Scholar] [CrossRef]
- Smailagic, A.; Spallucci, E. Thermodynamical phases of a regular SAdS BH. Int. J. Mod. Phys. D 2013, 22, 1350010. [Google Scholar] [CrossRef]
- Spallucci, E.; Smailagic, A. Maxwell’s equal area law for charged Anti-de Sitter black holes. Phys. Lett. B 2013, 723, 436–441. [Google Scholar] [CrossRef]
- Hendi, S.; Vahidinia, M. P-V criticality of higher dimensional black holes with nonlinear source. Phys. Rev. D 2013, 88, 084045. [Google Scholar] [CrossRef]
- Chen, S.; Liu, X.; Liu, C.; Jing, J. P-V criticality of AdS black hole in f(R) gravity. Chin. Phys. Lett. 2013, 30, 060401. [Google Scholar] [CrossRef]
- Zhao, R.; Zhao, H.-H.; Ma, M.-S.; Zhang, L.-C. On the critical phenomena and thermodynamics of charged topological dilaton AdS black holes. Eur. Phys. J. C 2013, 73, 2645. [Google Scholar] [CrossRef]
- Belhaj, A.; Chabab, M.; El Moumni, H.; Sedra, M. Critical behaviors of 3D black holes with a scalar hair. ArXiv E-Prints 2013. [Google Scholar] [CrossRef]
- Altamirano, N.; Kubiznak, D.; Mann, R. Reentrant phase transitions in rotating antide Sitter black holes. Phys. Rev. D 2013, 88, 101502. [Google Scholar] [CrossRef]
- Altamirano, N.; Kubiznak, D.; Mann, R.B.; Sherkatghanad, Z. Kerr-AdS analogue of tricritical point and solid/liquid/gas phase transition. ArXiv E-Prints 2014. [Google Scholar]
- Cai, R.-G.; Cao, L.-M.; Li, L.; Yang, R.-Q. P-V criticality in the extended phase space of Gauss-Bonnet black holes in AdS space. J. High Energy Phys. 2013, 2013. [Google Scholar] [CrossRef]
- Belhaj, A.; Chabab, M.; Moumni, H.E.; Medari, L.; Sedra, M. The thermodynamical behaviors of kerr–newman AdS black holes. Chin. Phys. Lett. 2013, 30, 090402. [Google Scholar] [CrossRef]
- Spallucci, E.; Smailagic, A. Maxwell’s equal area law and the Hawking-Page phase transition. J. Gravity 2013, 2013, 525696. [Google Scholar] [CrossRef]
- Mo, J.-X.; Zeng, X.-X.; Li, G.-Q.; Jiang, X.; Liu, W.-B. A unified phase transition picture of the charged topological black hole in Horava-Lifshitz gravity. J. High Energy Phys. 2013, 2013, 056. [Google Scholar] [CrossRef]
- Xu, W.; Xu, H.; Zhao, L. Gauss-Bonnet coupling constant as a free thermodynamical variable and the associated criticality. ArXiv E-Prints 2013. [Google Scholar] [CrossRef]
- Mo, J.-X.; Liu, W.-B. Ehrenfest scheme for P-V criticality in the extended phase space of black holes. Phys. Lett. B 2013, 727, 336–339. [Google Scholar] [CrossRef]
- Zou, D.-C.; Zhang, S.-J.; Wang, B. Critical behavior of Born-Infeld AdS black holes in the extended phase space thermodynamics. ArXiv E-Prints 2013. [Google Scholar] [CrossRef]
- Ma, M.-S.; Zhao, H.-H.; Zhang, L.-C.; Zhao, R. Existence condition and phase transition of Reissner-Nordstro¨m-de Sitter black hole. ArXiv E-Prints 2013. [Google Scholar]
- Ulhoa, S.C.; Spaniol, E.P. On gravitational entropy of de Sitter universe. ArXiv E-Prints 2013. [Google Scholar]
- Castro, A.; Dehmami, N.; Giribet, G.; Kastor, D. On the universality of inner black hole mechanics and higher curvature gravity. J. High Energy Phys. 2013, 1307, 164. [Google Scholar] [CrossRef]
- El-Menoufi, B.M.; Ett, B.; Kastor, D.; Traschen, J. Gravitational tension and thermodynamics of planar AdS spacetimes. Class. Quantum Gravity 2013, 30, 155003. [Google Scholar] [CrossRef]
- Lu, H.; Pang, Y.; Pope, C. AdS dyonic black hole and its thermodynamics. J. High Energy Phys. 2013, 2013, 33. [Google Scholar] [CrossRef]
- Mo, J.-X.; Liu, W.-B. P-V Criticality of topological black holes in Lovelock-Born-Infeld gravity. ArXiv E-Prints 2013. [Google Scholar] [CrossRef]
- Dolan, B.; Kastor, D.; Kubiznak, D.; Mann, R.; Traschen, J. Thermodynamic volumes and isoperimetric inequalities for de sitter black holes. Phys. Rev. D 2013, 87, 104017. [Google Scholar] [CrossRef]
- Gibbons, G.W.; Hawking, S.W. Cosmological event horizons, thermodynamics, and particle creation. Phys. Rev. D 1977, 15, 2738–2751. [Google Scholar] [CrossRef]
- Hayward, S. Unified first law of black hole dynamics and relativistic thermodynamics. Class. Quantum Gravity 1998, 15, 3147–3162. [Google Scholar] [CrossRef]
- Padmanabhan, T. Classical and quantum thermodynamics of horizons in spherically symmetric space-times. Class. Quantum Gravity 2002, 19, 5387–5408. [Google Scholar] [CrossRef]
- Cai, R.-G. Cardy-verlinde formula and asymptotically de Sitter spaces. Phys. Lett. B 2002, 525, 331–336. [Google Scholar] [CrossRef]
- Cai, R.-G. Cardy-Verlinde formula and thermodynamics of black holes in de Sitter spaces. Nucl. Phys. B 2002, 628, 375–386. [Google Scholar] [CrossRef]
- Sekiwa, Y. Thermodynamics of de Sitter black holes: Thermal cosmological constant. Phys. Rev. D 2006, 73, 084009. [Google Scholar] [CrossRef]
- Urano, M.; Tomimatsu, A.; Saida, H. The mechanical first law of black hole spacetimes with a cosmological constant and its application to Schwarzschild-de Sitter spacetime. Class. Quantum Gravity 2009, 26, 105010. [Google Scholar] [CrossRef]
- Gibbons, G.; Perry, M.; Pope, C. Bulk/boundary thermodynamic equivalence, and the Bekenstein and cosmic-censorship bounds for rotating charged AdS black holes. Phys. Rev. D 2005, 72, 084028. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Lahiri, A. Mass function and particle creation in Schwarzschild-de Sitter spacetime. ArXiv E-Prints 2013. [Google Scholar] [CrossRef]
- Emparan, R.; Reall, H.S. Black holes in higher dimensions. Living Rev. Relativ. 2008, 11, 1–87. [Google Scholar] [CrossRef]
- Myers, R.C.; Perry, M.J. Black holes in higher dimensional space-times. Ann. Phys. 1986, 172, 304–347. [Google Scholar] [CrossRef]
- Weinberg, S. Does gravitation resolve the ambiguity among supersymmetry vacua? Phys. Rev. Lett. 1982, 48, 1776–1779. [Google Scholar] [CrossRef]
- Weinhold, F. Metric geometry of equilibrium thermodynamics. J. Chem. Phys. 1975, 63, 2479. [Google Scholar] [CrossRef]
- Weinhold, F. Metric geometry of equilibrium thermodynamics. II. Scaling, homogeneity, and generalized Gibbs-Duhem relations. J. Chem. Phys. 1975, 63, 2484. [Google Scholar] [CrossRef]
- Ruppeiner, G. Thermodynamics: A Riemannian geometric model. Phys. Rev. A 1979, 20, 1608–1613. [Google Scholar] [CrossRef]
- Ruppeiner, G. Riemannian geometry in thermodynamic fluctuation theory. Rev. Mod. Phys. 1995, 67, 605–659. [Google Scholar] [CrossRef]
- Quevedo, H. Geometrothermodynamics. J. Math. Phys. 2007, 48, 013506. [Google Scholar] [CrossRef]
- Liu, H.; Lu, H.; Luo, M.; Shao, K.-N. Thermodynamical metrics and black hole phase transitions. J. High Energy Phys. 2010, 1012, 54. [Google Scholar] [CrossRef]
- Monteiro, R.; Santos, J. Negative modes and the thermodynamics of Reissner-Nordstrom black holes. Phys. Rev. D 2009, 79, 064006. [Google Scholar] [CrossRef]
- Monteiro, R.; Perry, M.J.; Santos, J.E. Thermodynamic instability of rotating black holes. Phys. Rev. D 2009, 80, 024041. [Google Scholar] [CrossRef]
- Witten, E. Anti-de Sitter space, thermal phase transition, and confinement in gauge theories. Adv. Theor. Math. Phys. 1998, 2, 505–532. [Google Scholar]
- Chamblin, A.; Emparan, R.; Johnson, C.; Myers, R. Charged AdS black holes and catastrophic holography. Phys. Rev. D 1999, 60, 064018. [Google Scholar] [CrossRef]
- Chamblin, A.; Emparan, R.; Johnson, C.; Myers, R. Holography, thermodynamics and fluctuations of charged AdS black holes. Phys. Rev. D 1999, 60, 104026. [Google Scholar] [CrossRef]
- Cvetic, M.; Gubser, S. Phases of R charged black holes, spinning branes and strongly coupled gauge theories. J. High Energy Phys. 1999, 9904, 024. [Google Scholar] [CrossRef]
- Tsai, Y.-D.; Wu, X.; Yang, Y. Phase structure of kerr-AdS black hole. Phys. Rev. D 2012, 85, 044005. [Google Scholar] [CrossRef]
- Hristov, K.; Toldo, C.; Vandoren, S. Phase transitions of magnetic AdS4 black holes with scalar hair. Phys. Rev. D 2013, 88, 026019. [Google Scholar] [CrossRef]
- Johnson, C.V. Large N phase transitions, finite volume, and entanglement entropy. ArXiv E-Prints 2013. [Google Scholar] [CrossRef]
- Niu, C.; Tian, Y.; Wu, X.-N. Critical phenomena and thermodynamic geometry of RN-AdS black holes. Phys. Rev. D 2012, 85, 024017. [Google Scholar] [CrossRef]
- Poshteh, M.B.J.; Mirza, B.; Sherkatghanad, Z. Phase transition, critical behavior, and critical exponents of Myers-Perry black holes. Phys. Rev. D 2013, 88, 024005. [Google Scholar] [CrossRef]
- Wei, S.-W.; Liu, Y.-X. Critical phenomena and thermodynamic geometry of charged Gauss-Bonnet AdS black holes. Phys. Rev. D 2013, 87, 044014. [Google Scholar] [CrossRef]
- Dutta, S.; Jain, A.; Soni, R. Dyonic black hole and holography. J. High Energy Phys. 2013, 2013, 60. [Google Scholar] [CrossRef]
- Narayanan, T.; Kumar, A. Reentrant phase transitions in multicomponent liquid mixtures. Phys. Rep. 1994, 249, 135–218. [Google Scholar] [CrossRef]
- Maslov, V.P. Zeroth-order phase transitions. Math. Notes 2004, 76, 697–710. [Google Scholar] [CrossRef]
- Kubizňák, D.; Frolov, V.P. Hidden symmetry of higher dimensional Kerr-NUT-AdS spacetimes. Class. Quantum Gravity 2007, 24, 1–6. [Google Scholar] [CrossRef]
- Parikh, M. The Volume of black holes. Phys. Rev. D 2006, 73, 124021. [Google Scholar] [CrossRef]
- Ballik, W.; Lake, K. The volume of stationary black holes and the meaning of the surface gravity. ArXiv E-Prints 2010. [Google Scholar]
- Ballik, W.; Lake, K. The vector volume and black holes. Phys. Rev. D 2013, 88, 104038. [Google Scholar] [CrossRef]
- Emparan, R.; Harmark, T.; Niarchos, V.; Obers, N. Essentials of blackfold dynamics. J. High Energy Phys. 2010, 2010, 63. [Google Scholar] [CrossRef]
- Gregory, R.; Laflamme, R. Black strings and p-branes are unstable. Phys. Rev. Lett. 1993, 70, 2837–2840. [Google Scholar] [CrossRef] [PubMed]
- Gubser, S.S.; Mitra, I. Instability of charged black holes in anti-de Sitter space. ArXiv E-Prints 2000. [Google Scholar]
- Gubser, S.; Mitra, I. The Evolution of unstable black holes in anti-de Sitter space. J. High Energy Phys. 2001, 2001, 018. [Google Scholar] [CrossRef]
- Reall, H.S. Classical and thermodynamic stability of black branes. Phys. Rev. D 2001, 64, 044005. [Google Scholar] [CrossRef]
- Figueras, P.; Murata, K.; Reall, H.S. Black hole instabilities and local Penrose inequalities. Class. Quantum Gravity 2011, 28, 225030. [Google Scholar] [CrossRef]
- Hollands, S.; Wald, R.M. Stability of black holes and black branes. Commun. Math. Phys. 2013, 321, 629–680. [Google Scholar] [CrossRef]
- Goldenfeld, N. Lectures on Phase Transitions and the Renormalization Group; Westview Press: New York, NY, USA, 1992. [Google Scholar]
- Bertoldi, G.; Burrington, B.A.; Peet, A.W. Thermal behavior of charged dilatonic black branes in AdS and UV completions of Lifshitz-like geometries. Phys. Rev. D 2010, 82, 106013. [Google Scholar] [CrossRef]
- Berglund, P.; Bhattacharyya, J.; Mattingly, D. Charged dilatonic AdS black branes in arbitrary dimensions. J. High Energy Phys. 2012, 1208, 42. [Google Scholar] [CrossRef]
- Banerjee, R.; Modak, S.K.; Samanta, S. Second order phase transition and thermodynamic geometry in Kerr-AdS black hole. Phys. Rev. D 2011, 84, 064024. [Google Scholar] [CrossRef]
- Carlip, S.; Vaidya, S. Phase transitions and critical behavior for charged black holes. Class. Quantum Gravity 2003, 20, 3827–3838. [Google Scholar] [CrossRef]
- Gubser, S. Breaking an Abelian gauge symmetry near a black hole horizon. Phys. Rev. D 2008, 78, 065034. [Google Scholar] [CrossRef]
- Hartnoll, S.; Herzog, C.; Horowitz, G. Building a holographic superconductor. Phys. Rev. Lett. 2008, 101, 031601. [Google Scholar] [CrossRef] [PubMed]
- Hartnoll, S.A.; Herzog, C.; Horowitz, G. Holographic superconductors. J. High Energy Phys. 2008, 2008, 015. [Google Scholar] [CrossRef]
- Maeda, K.; Koga, J.-I.; Fujii, S. The final fate of instability of Reissner-Nordstro´m-anti-de Sitter black holes by charged complex scalar fields. ArXiv E-Prints 2010. [Google Scholar]
- Basu, P.; Bhattacharya, J.; Bhattacharyya, S.; Loganayagam, R.; Minwalla, S.; Umesh, A. Small hairy black holes in global AdS spacetime. J. High Energy Phys. 2010, 1010, 45. [Google Scholar] [CrossRef]
- Dias, O.; Figueras, P.; Minwalla, S.; Mitra, P.; Monteiro, R.; Santos, J. Hairy black holes and solitons in global AdS5. J. High Energy Phys. 2012, 1208, 117. [Google Scholar] [CrossRef]
- Horowitz, G. Introduction to holographic superconductors. Lect. Notes Phys. 2011, 828, 313–347. [Google Scholar]
- Hartmann, B. Stability of black holes and solitons in Anti-de Sitter space-time. ArXiv E-Prints 2013. [Google Scholar] [CrossRef]
- Hawking, S.; Reall, H. Charged and rotating AdS black holes and their CFT duals. Phys. Rev. D 2000, 61, 024014. [Google Scholar] [CrossRef]
- Sonner, J. A rotating holographic superconductor. Phys. Rev. D 2009, 80, 084031. [Google Scholar] [CrossRef]
- Dias, O.J.; Monteiro, R.; Reall, H.S.; Santos, J.E. A Scalar field condensation instability of rotating anti-de Sitter black holes. J. High Energy Phys. 2010, 2010, 36. [Google Scholar] [CrossRef]
- Cardoso, V.; Dias, O.C.; Hartnett, G.S.; Lehner, L.; Santos, J. Holographic thermalization, quasinormal modes and superradiance in Kerr-AdS. ArXiv E-Prints 2013. [Google Scholar] [CrossRef]
- Gibbons, G.W.; Lü, H.; Page, D.N.; Pope, C.N. Rotating black holes in higher dimensions with a cosmological constant. Phys. Rev. Lett. 2004, 93, 171102. [Google Scholar] [CrossRef] [PubMed]
- Gibbons, G.W.; Lü, H.; Page, D.N.; Pope, C.N. The general Kerr-de Sitter metrics in all dimensions. J. Geom. Phys. 2005, 53, 49–73. [Google Scholar] [CrossRef]
- Hawking, S.W.; Hunter, C.J.; Taylor-Robinson, M.M. Rotation and the AdS/CFT correspondence. Phys. Rev. D 1999, 59, 064005. [Google Scholar] [CrossRef]
- Frolov, V.P.; Kubizňák, D. Higher-dimensional black holes: Hidden symmetries and separation of variables. Class. Quantum Gravity 2008, 25, 154005. [Google Scholar] [CrossRef]
- Gibbons, G.; Perry, M.; Pope, C. The First law of thermodynamics for Kerr-anti-de Sitter black holes. Class. Quantum Gravity 2005, 22, 1503–1526. [Google Scholar] [CrossRef]
- Emparan, R.; Myers, R.C. Instability of ultra-spinning black holes. J. High Energy Phys. 2003, 2003, 025. [Google Scholar] [CrossRef]
- Armas, J.; Obers, N.A. Blackfolds in (Anti)-de Sitter Backgrounds. Phys. Rev. D 2011, 83, 084039. [Google Scholar] [CrossRef]
- Caldarelli, M.; Emparan, R.; Rodriguez, M.J. Black rings in (Anti)-deSitter space. J. High Energy Phys. 2008, 2008, 011. [Google Scholar] [CrossRef]
- Emparan, R.; Reall, H.S. A rotating black ring in five dimensions. Phys. Rev. Lett. 2002, 88, 101101. [Google Scholar] [CrossRef] [PubMed]
- Emparan, R. Rotating circular strings, and infinite nonuniqueness of black rings. J. High Energy Phys. 2004, 2004, 064. [Google Scholar] [CrossRef]
- Emparan, R.; Reall, H.S. Black rings. Class. Quantum Gravity 2006, 23, R169. [Google Scholar] [CrossRef]
- Elvang, H.; Emparan, R.; Figueras, P. Phases of five-dimensional black holes. J. High Energy Phys. 2007, 2007, 056. [Google Scholar] [CrossRef]
- Emparan, R.; Harmark, T.; Niarchos, V.; Obers, N.A.; Rodriguez, M. The phase structure of higher-dimensional black rings and black holes. J. High Energy Phys. 2007, 2007, 110. [Google Scholar] [CrossRef]
- Emparan, R.; Figueras, P. Multi-black rings and the phase diagram of higher-dimensional black holes. J. High Energy Phys. 2010, 2010, 022. [Google Scholar] [CrossRef]
- Elvang, H.; Emparan, R.; Virmani, A. Dynamics and stability of black rings. J. High Energy Phys. 2006, 2006, 074. [Google Scholar] [CrossRef]
- Elvang, H.; Figueras, P. Black saturn. J. High Energy Phys. 2007, 2007, 050. [Google Scholar] [CrossRef]
- Carter, B. Essentials of classical brane dynamics. Int. J. Theor. Phys. 2001, 40, 2099–2130. [Google Scholar] [CrossRef]
- Dias, O.; Figueras, P.; Monteiro, R.; Santos, J.E.; Emparan, R. Instability and new phases of higher-dimensional rotating black holes. Phys. Rev. D 2009, 80, 111701. [Google Scholar] [CrossRef]
- Dias, O.; Figueras, P.; Monteiro, R.; Reall, H.; Santos, J. An instability of higher-dimensional rotating black holes. J. High Energy Phys. 2010, 2010, 076. [Google Scholar] [CrossRef]
- Dias, O.; Figueras, P.; Monteiro, R.; Santos, J. Ultraspinning instability of rotating black holes. Phys. Rev. D 2010, 82, 104025. [Google Scholar] [CrossRef]
- Dias, O.; Figueras, P.; Monteiro, R.; Santos, J. Ultraspinning instability of anti-de Sitter black holes. J. High Energy Phys. 2010, 2010, 067. [Google Scholar] [CrossRef]
- Dias, O.; Monteiro, R.; Santos, J. Ultraspinning instability: The missing link. J. High Energy Phys. 2011, 2011, 139. [Google Scholar] [CrossRef]
- Cardoso, V.; Dias, O.; Lemos, J.P.S.; Yoshida, S. The black hole bomb and superradiant instabilities. Phys. Rev. D 2004, 70, 044039. [Google Scholar] [CrossRef]
- Cardoso, V.; Dias, O.J.C. Small Kerr-anti-de Sitter black holes are unstable. Phys. Rev. D 2004, 70, 084011. [Google Scholar] [CrossRef]
- Cardoso, V.; Dias, O.C.; Yoshida, S. Classical instability of Kerr-AdS black holes and the issue of final state. Phys. Rev. D 2006, 74, 044008. [Google Scholar] [CrossRef]
- Shibata, M.; Yoshino, H. Nonaxisymmetric instability of rapidly rotating black hole in five dimensions. Phys. Rev. D 2010, 81, 021501. [Google Scholar] [CrossRef]
- Shibata, M.; Yoshino, H. Bar-mode instability of rapidly spinning black hole in higher dimensions: Numerical simulation in general relativity. Phys. Rev. D 2010, 81, 104035. [Google Scholar] [CrossRef]
- Hartnett, G.S.; Santos, J.E. Non-axisymmetric instability of rotating black holes in higher dimensions. Phys. Rev. D 2013, 88, 041505. [Google Scholar] [CrossRef]
- Kleihaus, B.; Kunz, J.; Radu, E. Black rings in six dimensions. Phys. Lett. B 2013, 718, 1073–1077. [Google Scholar] [CrossRef]
- Dolan, B.P. On the thermodynamic stability of rotating black holes in higher dimensions—A comparison of thermodynamic ensembles. ArXiv E-Prints 2013. [Google Scholar]
- Detweiler, S. Klein–Gordon equation and rotating black holes. Phys. Rev. D 1980, 22, 2323–2326. [Google Scholar] [CrossRef]
- Dolan, S. Instability of the massive Klein-Gordon field on the Kerr spacetime. Phys. Rev. D 2007, 76, 084001. [Google Scholar] [CrossRef]
- Peca, C.; Lemos, J. Thermodynamics of Reissner-Nordstrom Anti-de Sitter black holes in the grand canonical ensemble. Phys. Rev. D 1999, 59, 124007. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Altamirano, N.; Kubizňák, D.; Mann, R.B.; Sherkatghanad, Z. Thermodynamics of Rotating Black Holes and Black Rings: Phase Transitions and Thermodynamic Volume. Galaxies 2014, 2, 89-159. https://doi.org/10.3390/galaxies2010089
Altamirano N, Kubizňák D, Mann RB, Sherkatghanad Z. Thermodynamics of Rotating Black Holes and Black Rings: Phase Transitions and Thermodynamic Volume. Galaxies. 2014; 2(1):89-159. https://doi.org/10.3390/galaxies2010089
Chicago/Turabian StyleAltamirano, Natacha, David Kubizňák, Robert B. Mann, and Zeinab Sherkatghanad. 2014. "Thermodynamics of Rotating Black Holes and Black Rings: Phase Transitions and Thermodynamic Volume" Galaxies 2, no. 1: 89-159. https://doi.org/10.3390/galaxies2010089
APA StyleAltamirano, N., Kubizňák, D., Mann, R. B., & Sherkatghanad, Z. (2014). Thermodynamics of Rotating Black Holes and Black Rings: Phase Transitions and Thermodynamic Volume. Galaxies, 2(1), 89-159. https://doi.org/10.3390/galaxies2010089




