Timing Analysis of Black Hole X-Ray Binaries with Insight-HXMT
Abstract
1. Introduction
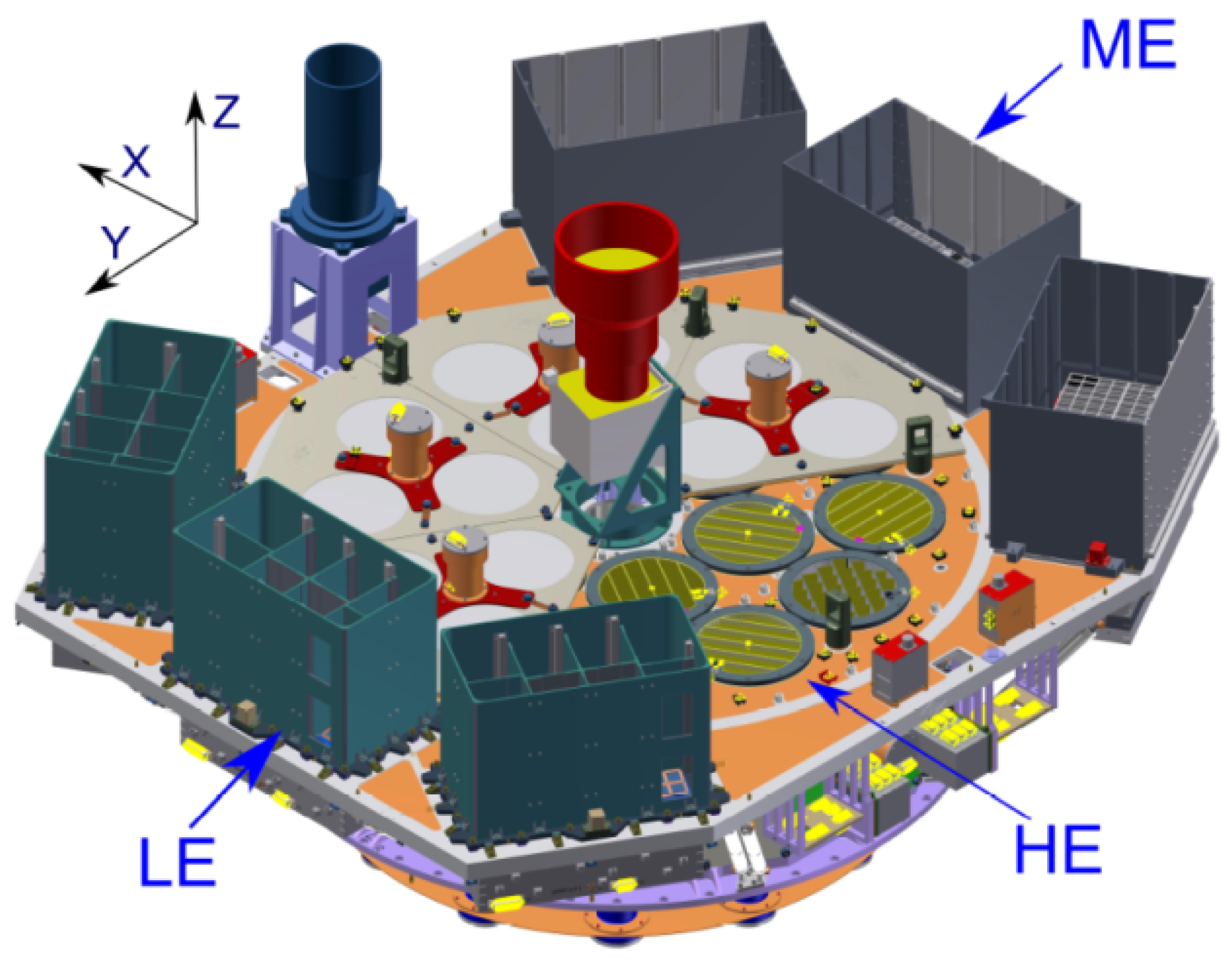
2. Instrument and Performance
3. Traditional Timing Analysis
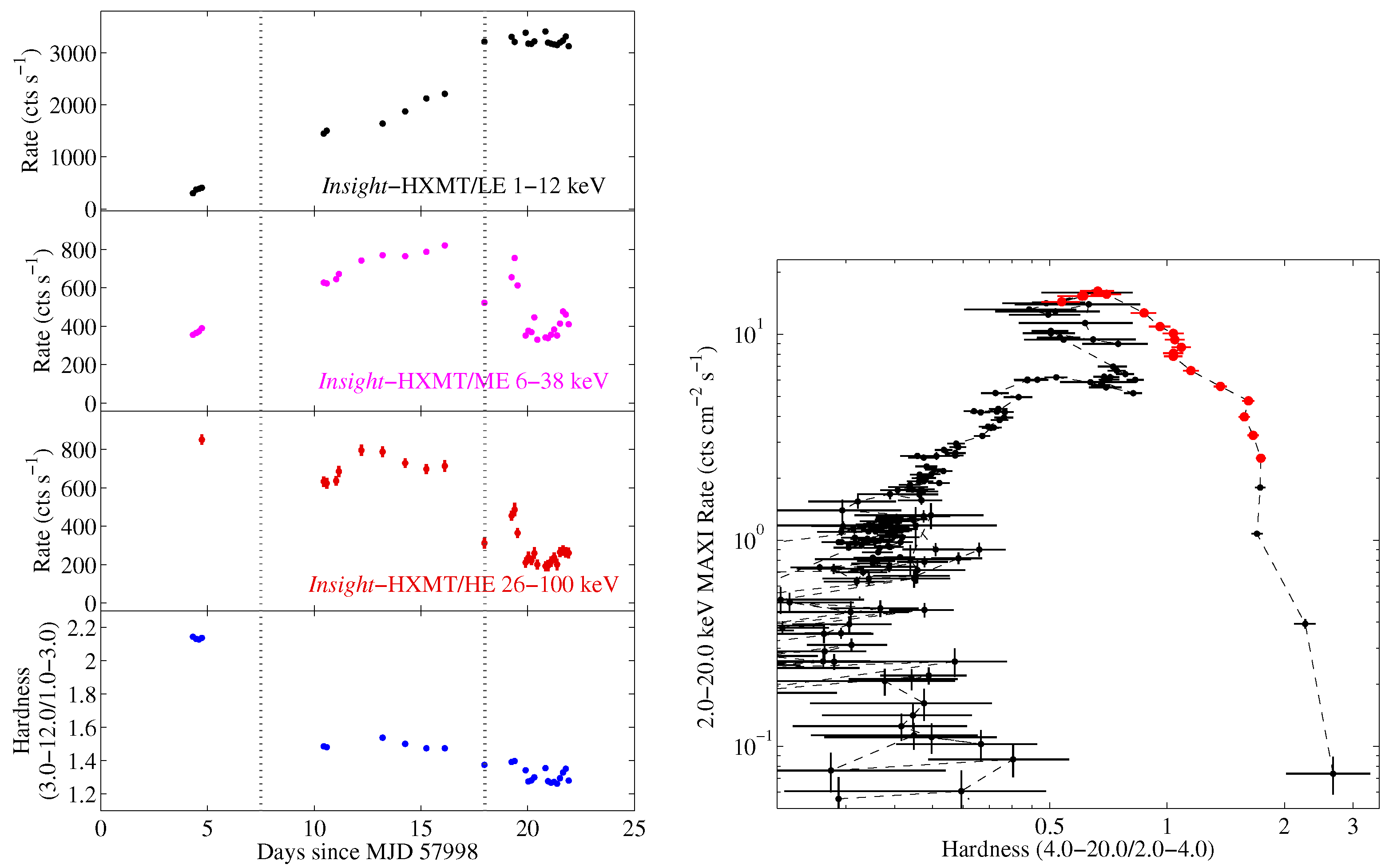
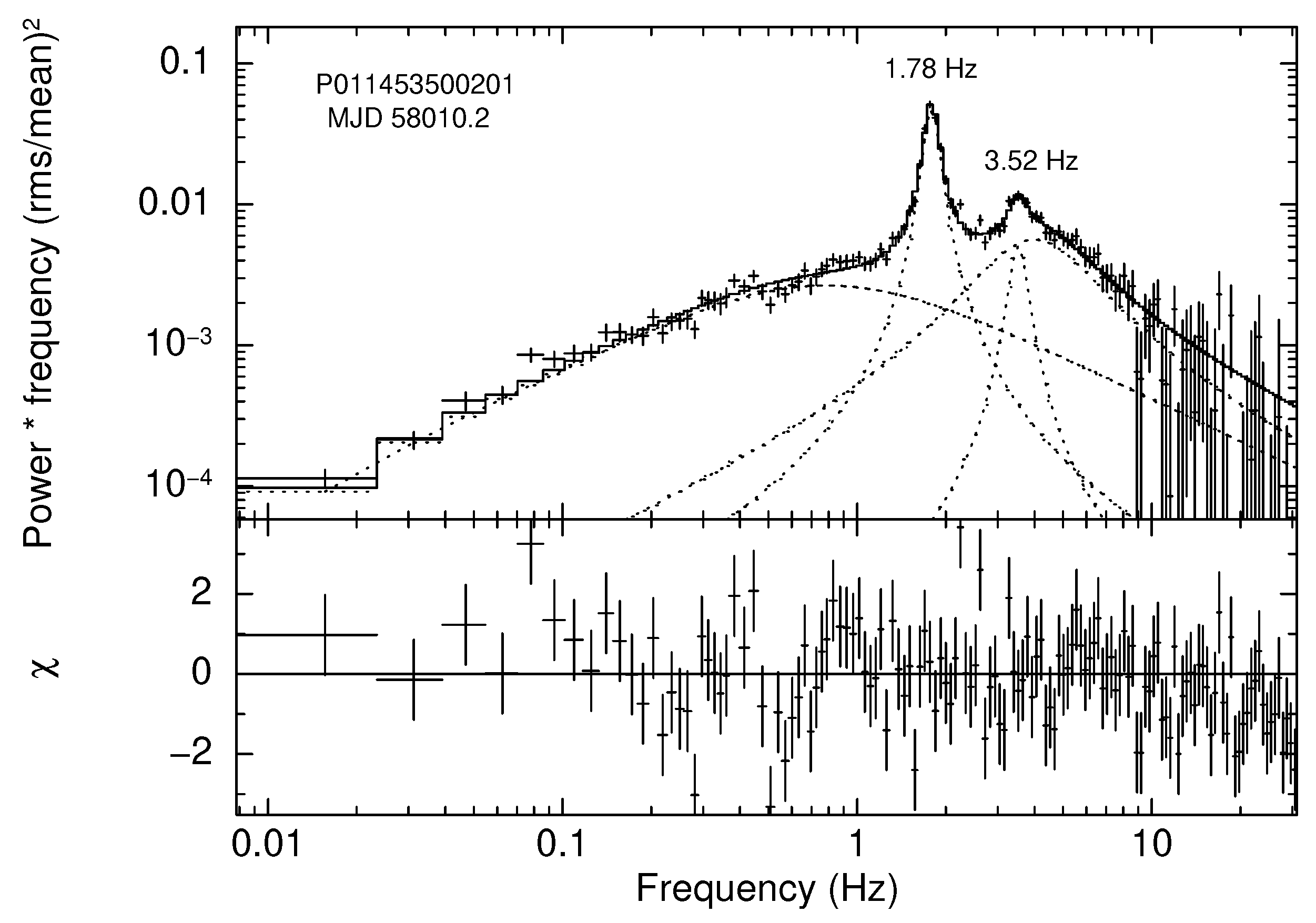
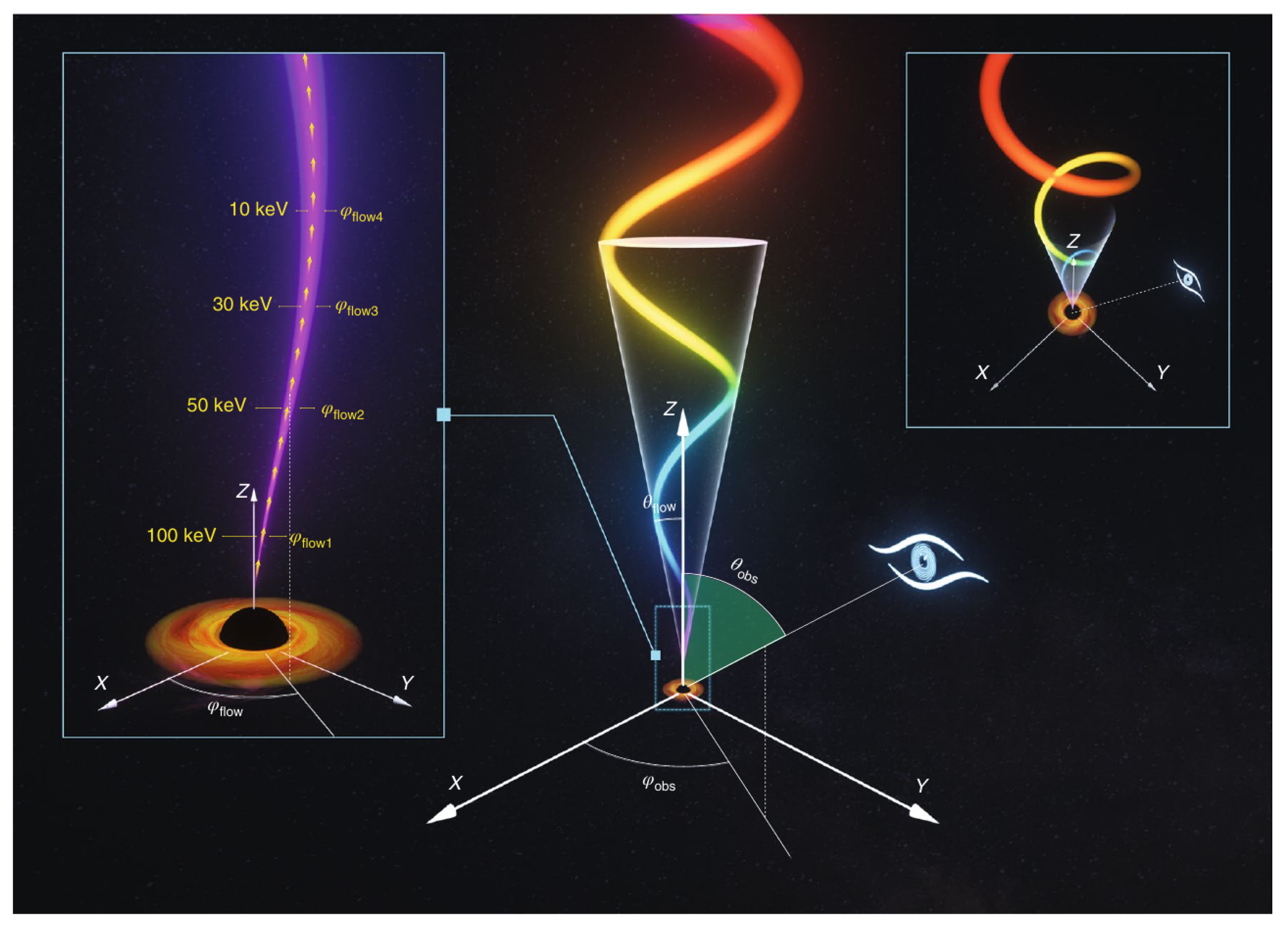
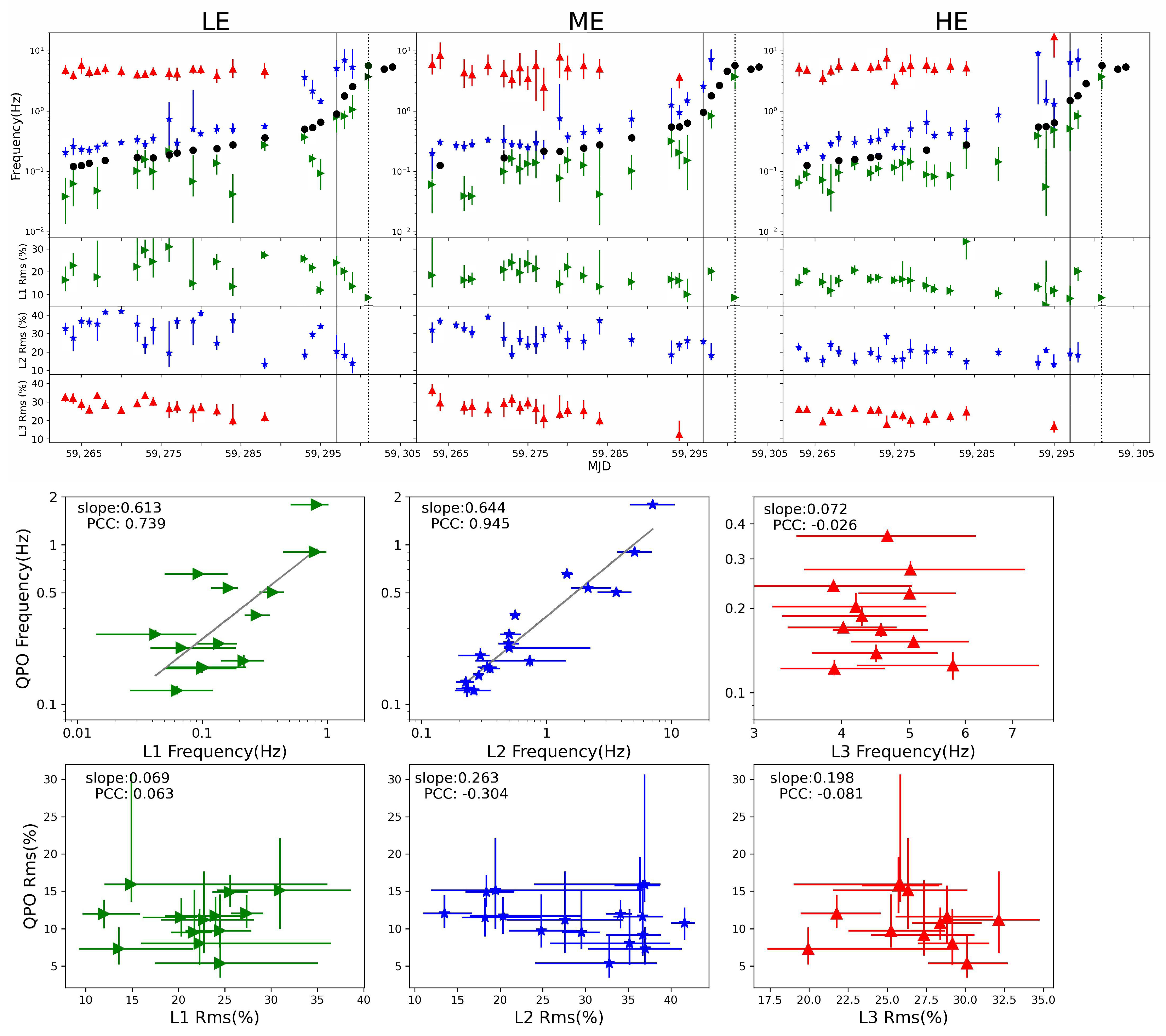
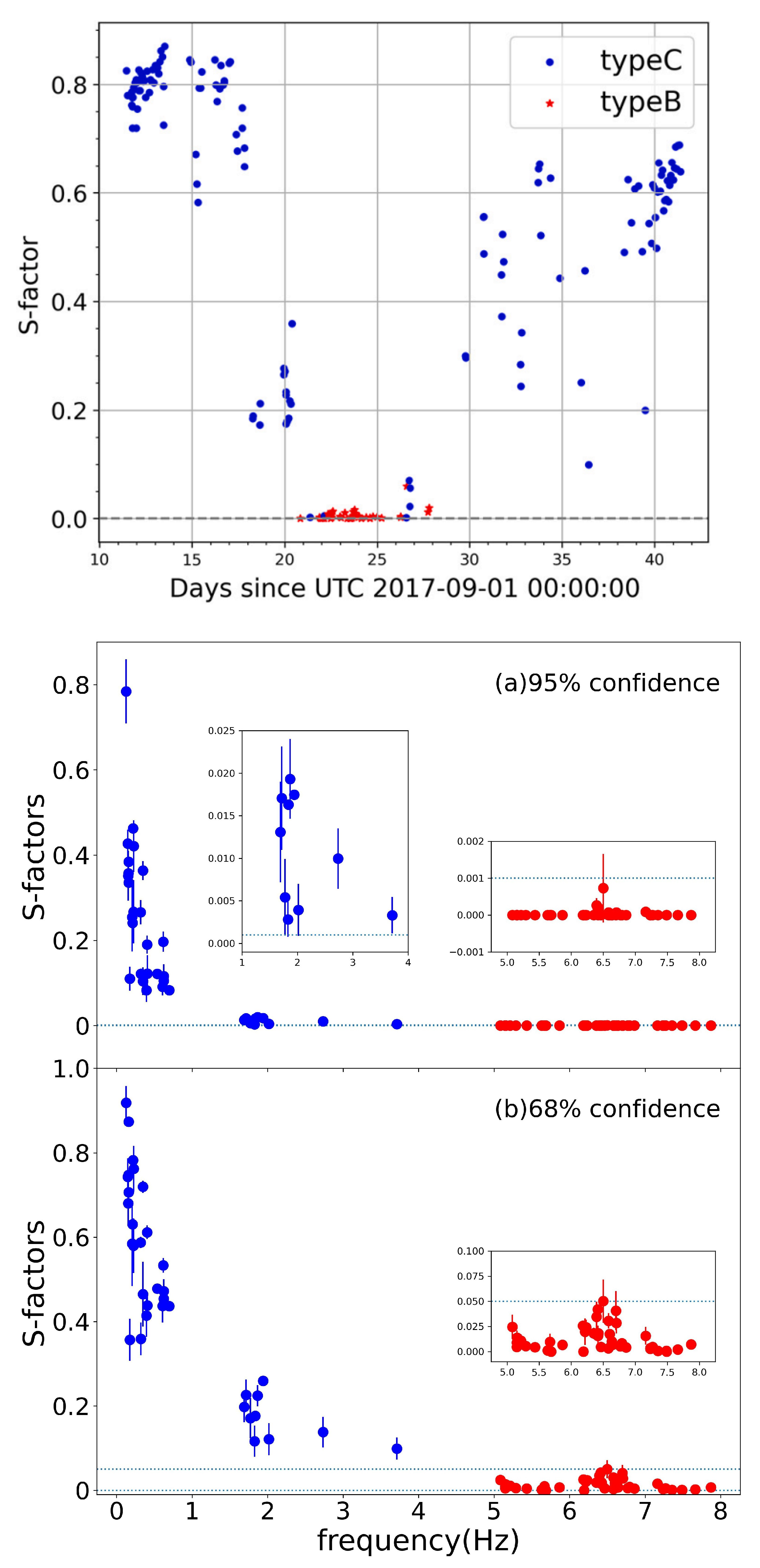
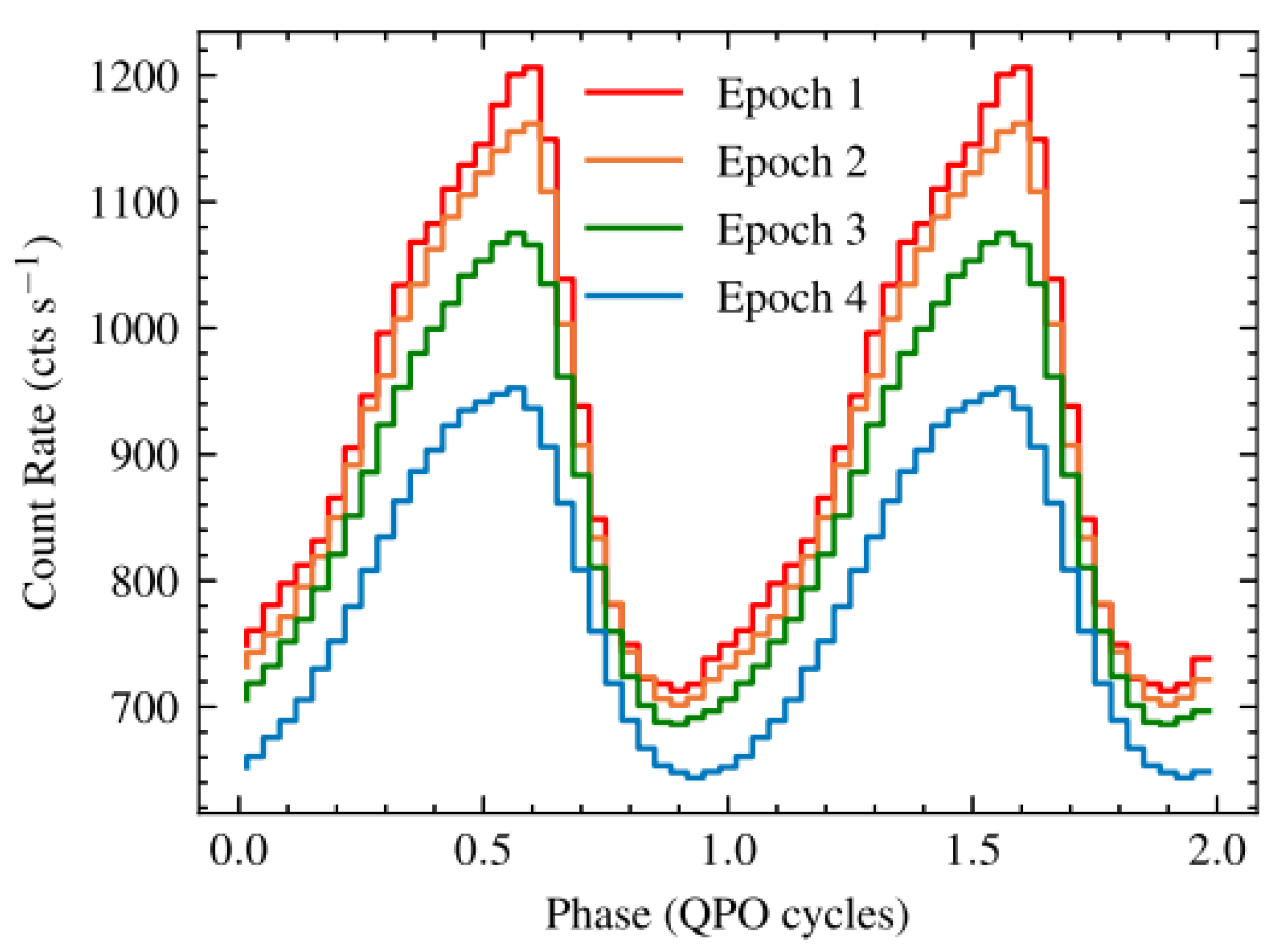
3.1. QPO Analysis
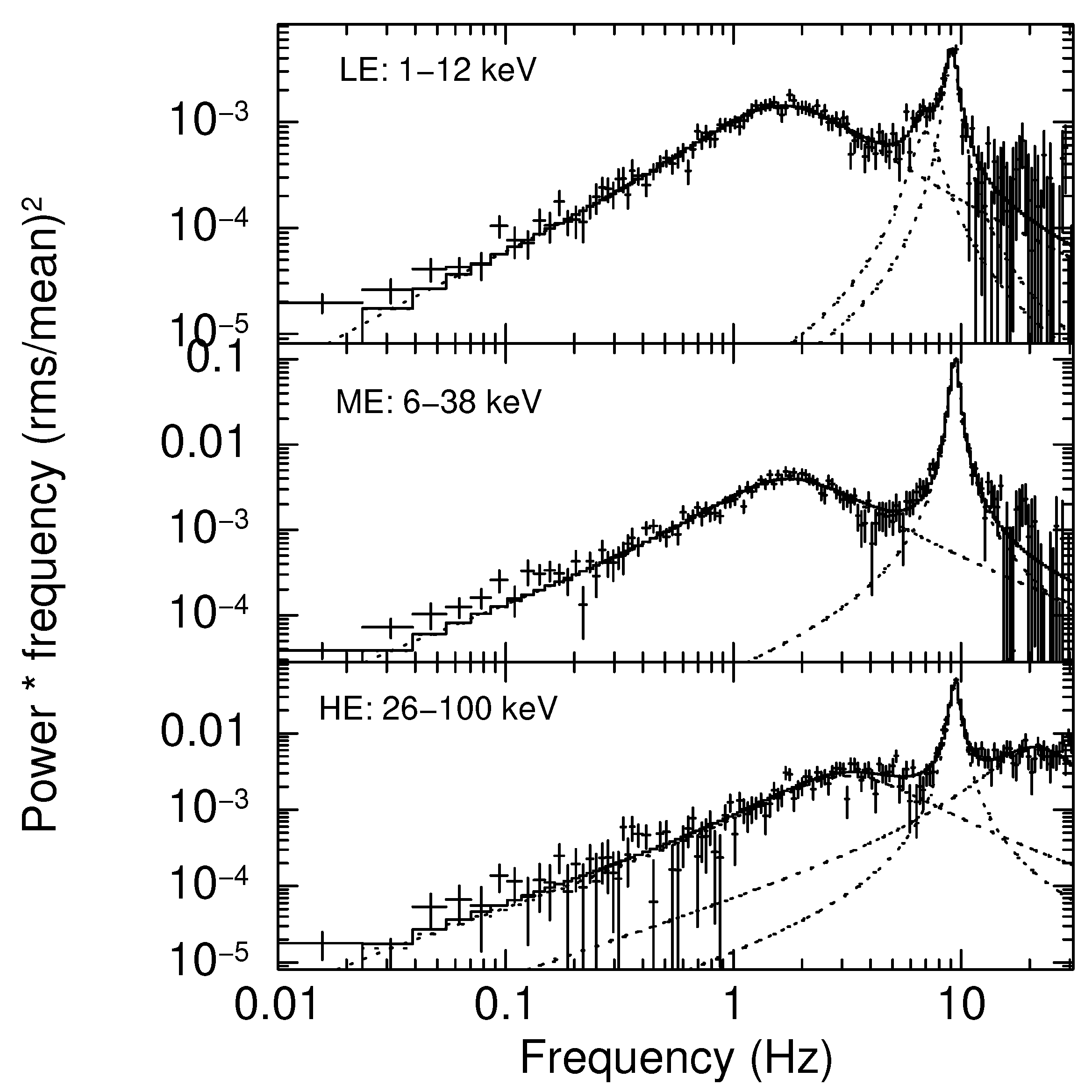
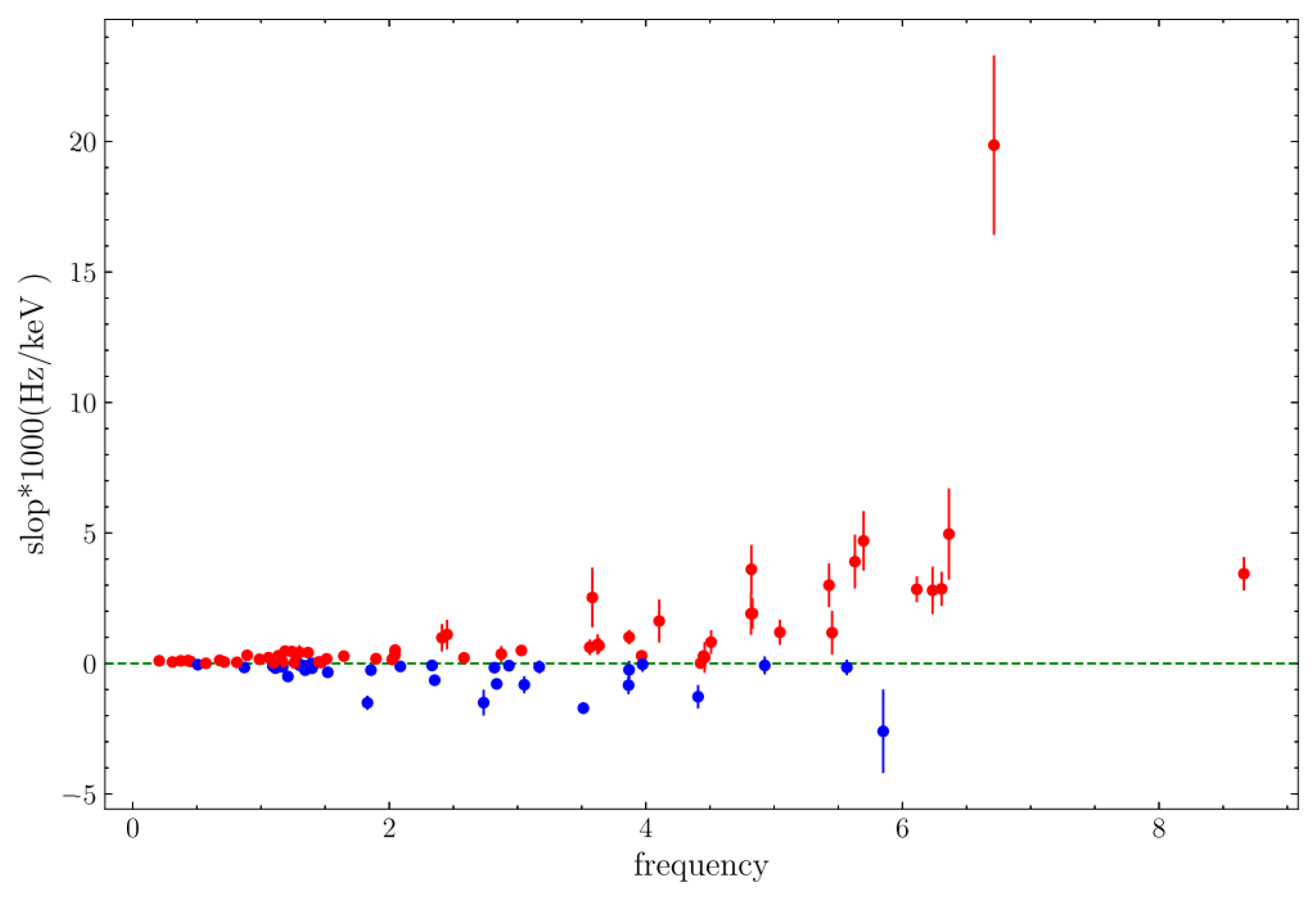
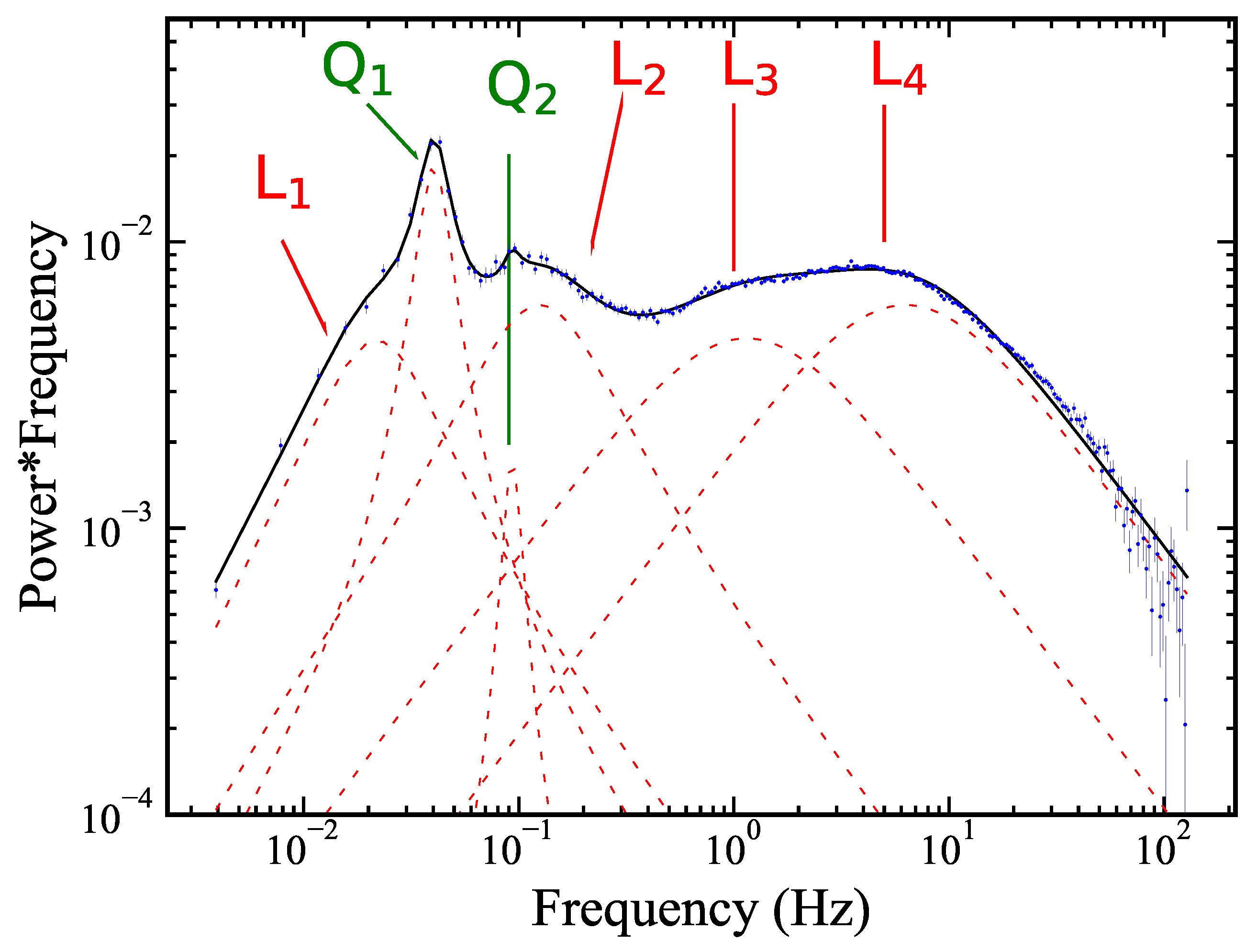
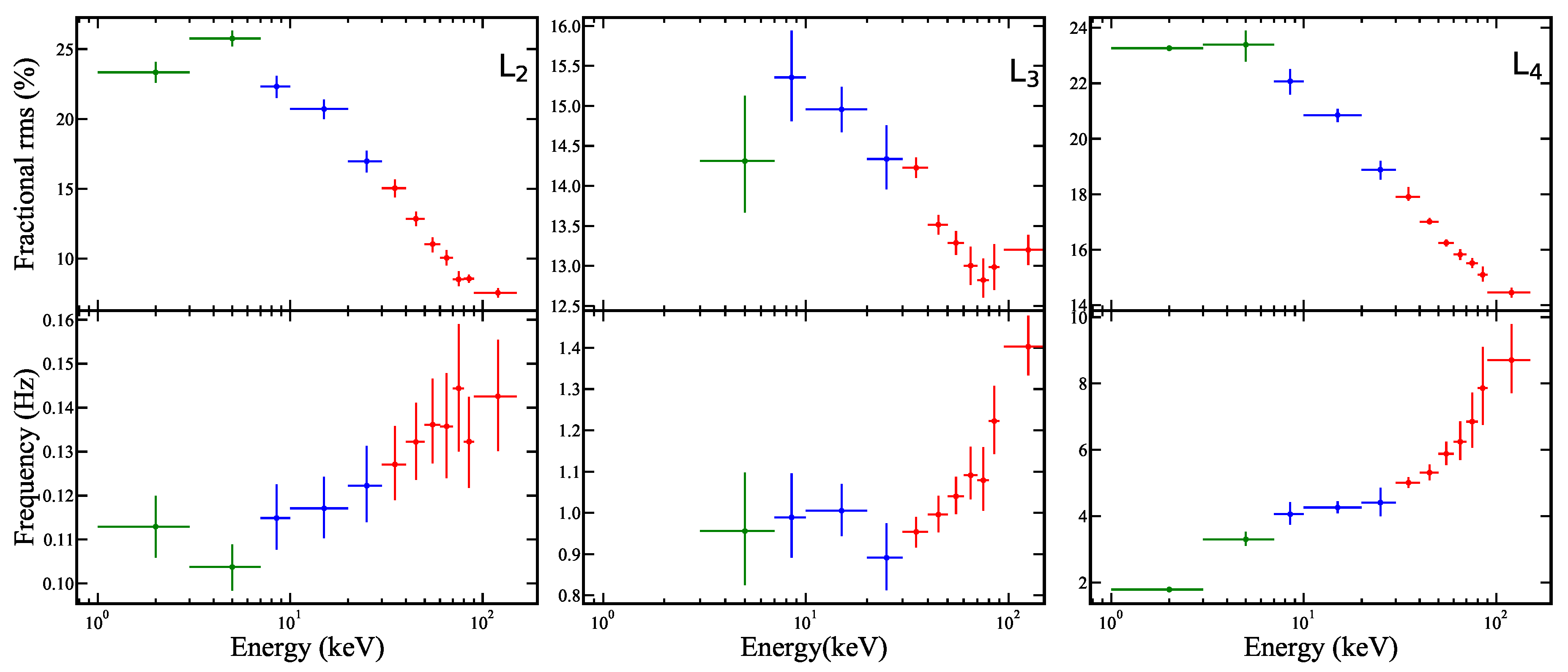
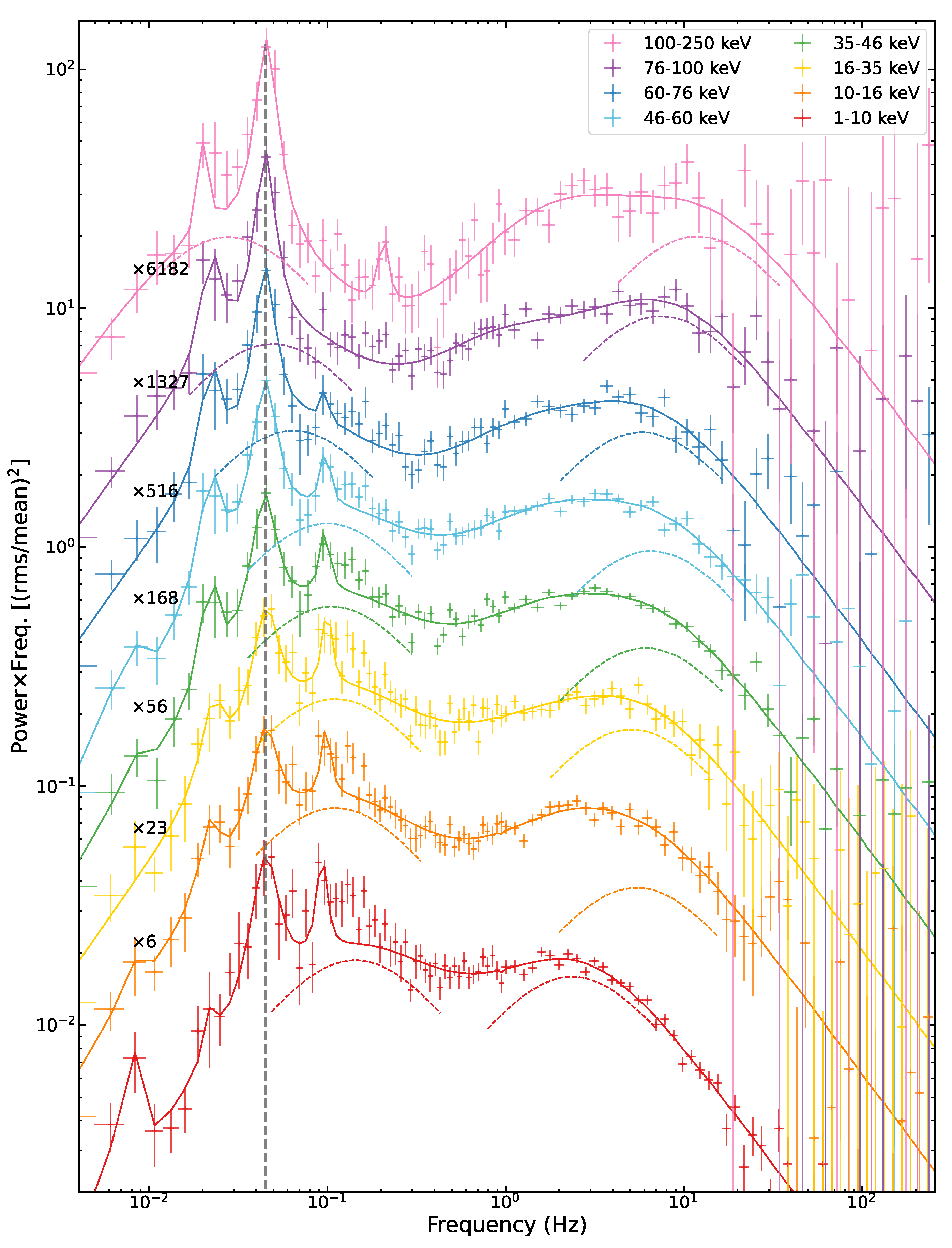
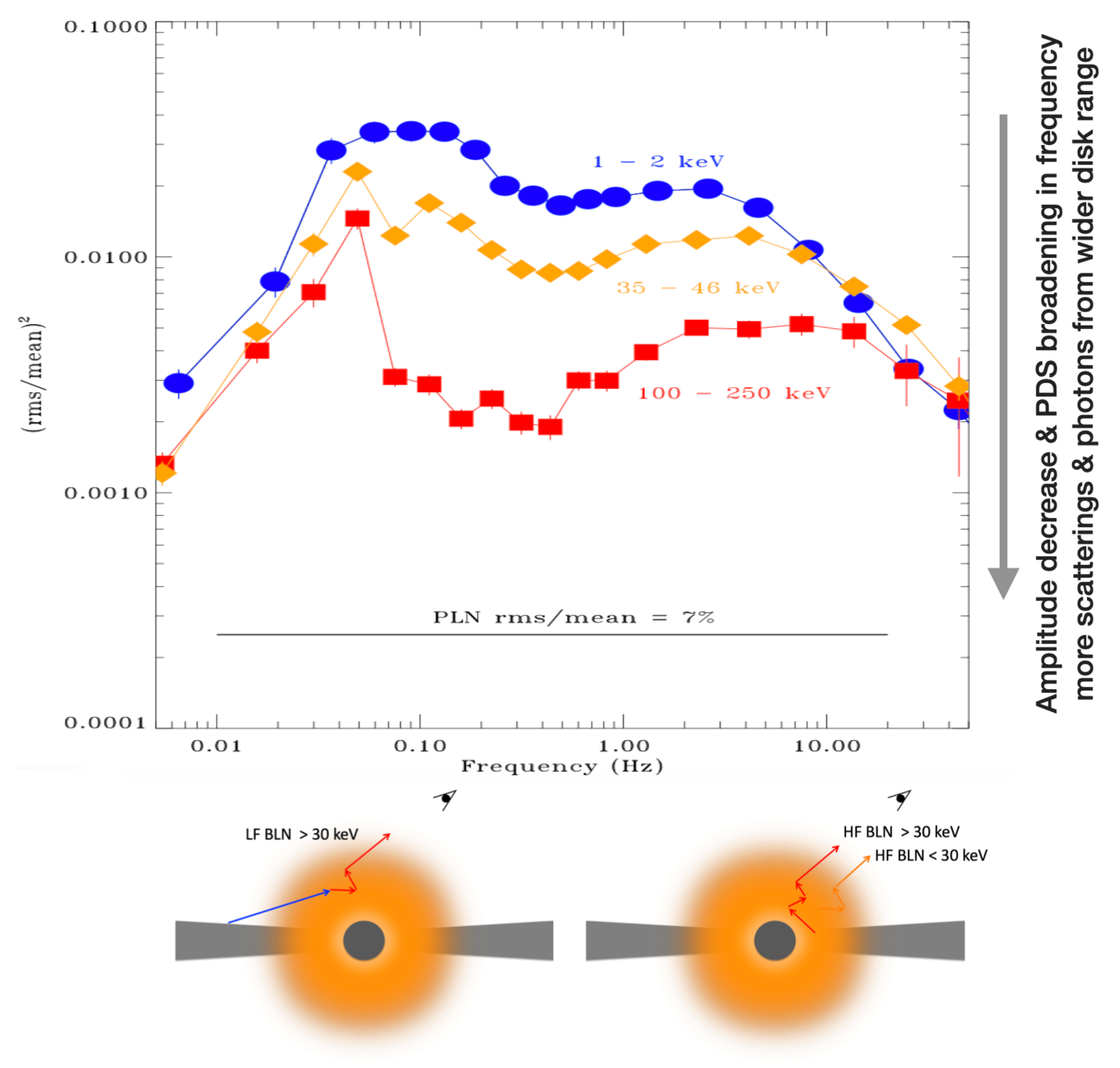
3.2. Broadband Noise Analysis
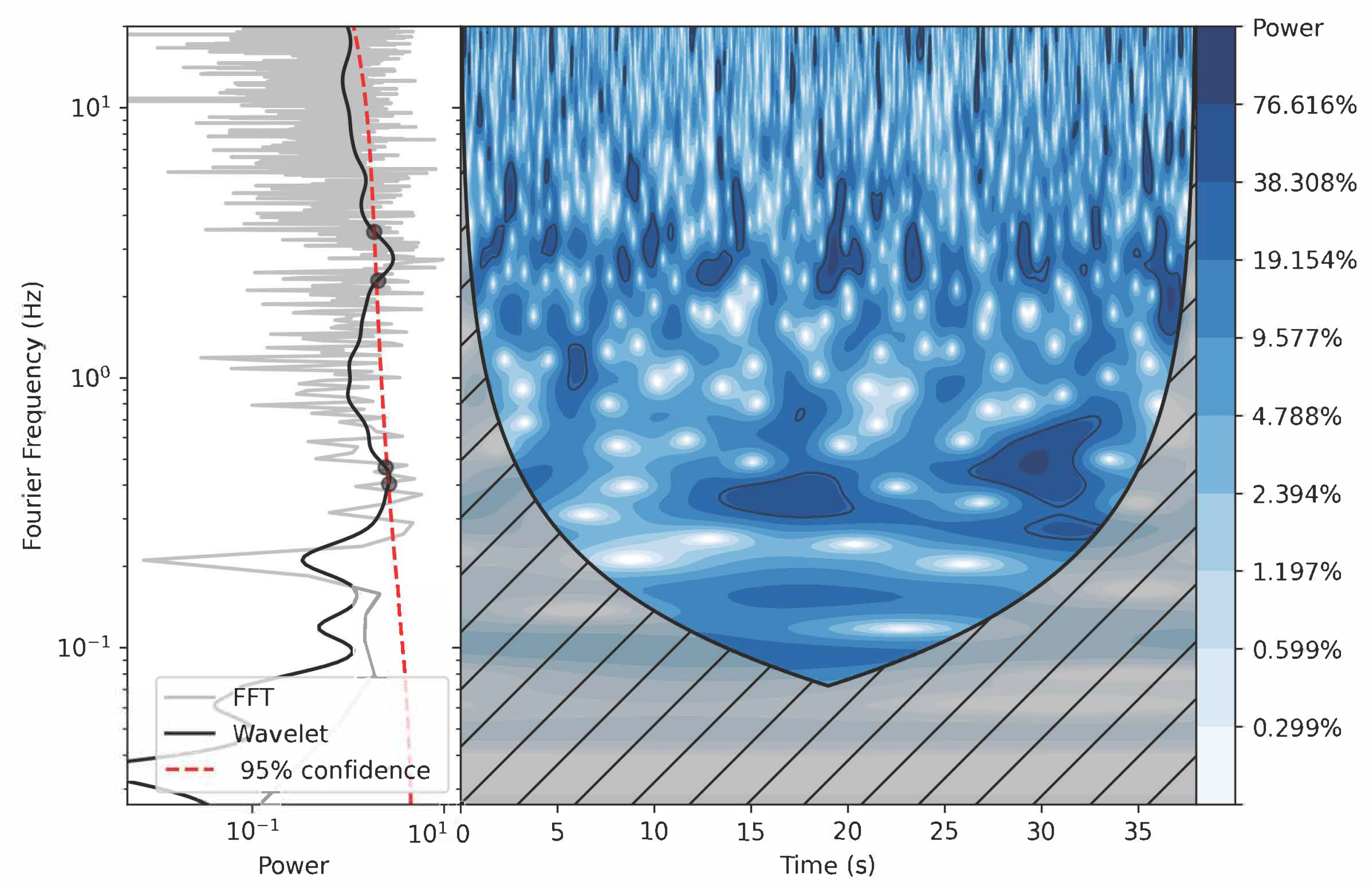
4. Wavelet Analysis
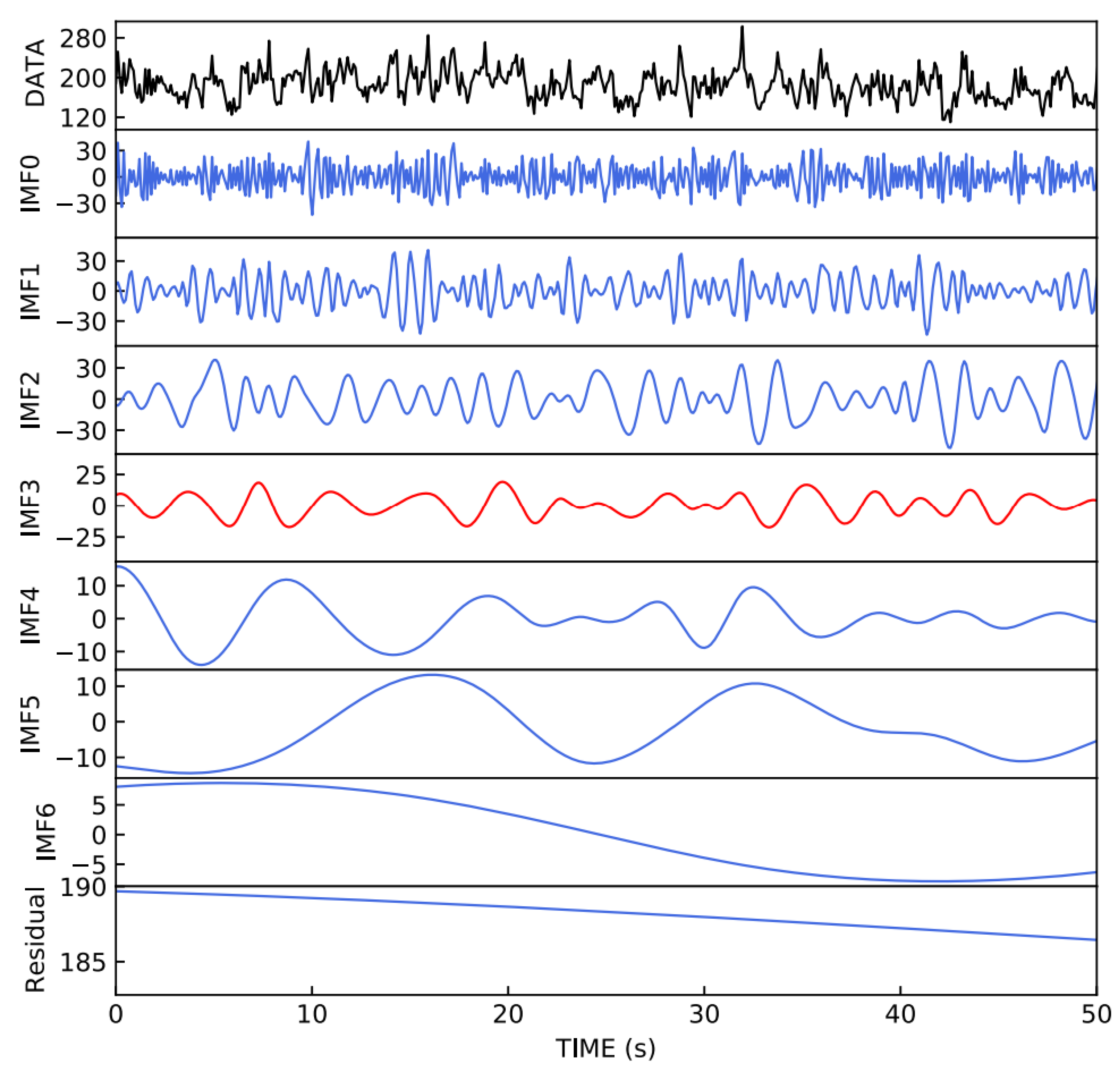
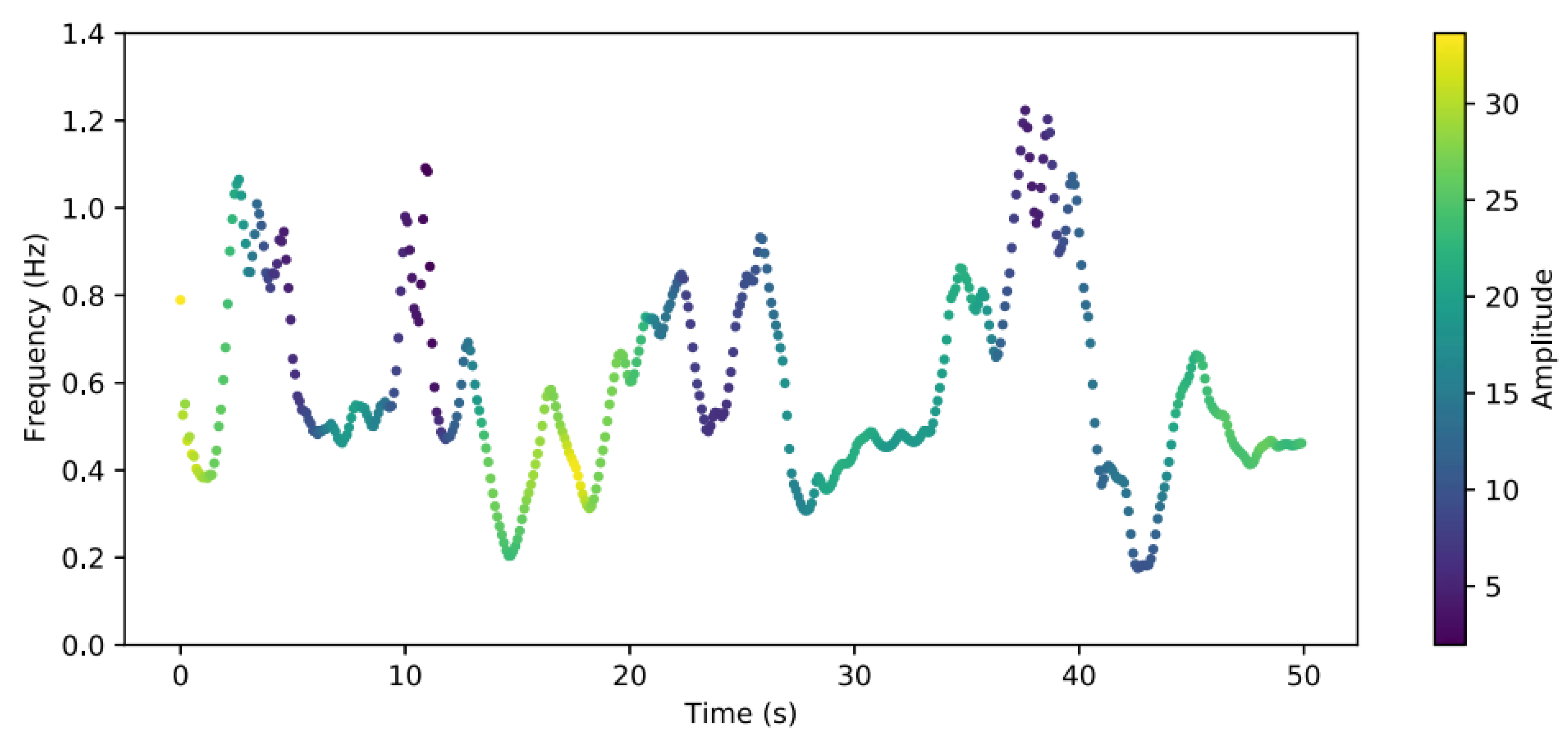
5. Hilbert-Huang Transform
- 1.
- Locate all the local extrema of the data , then construct the upper and lower envelopes by interpolating the local maxima and minima, respectively, using cubic splines.
- 2.
- Calculate the mean function by averaging the upper and lower envelopes, and subtract this mean from the data to obtain the first component: .
- 3.
- Check whether satisfies the criteria for an IMF. If it does not, treat as the new data and repeat steps (1) and (2) until an IMF is obtained.
- 4.
- Once the first IMF component is identified, define the residual . Repeat steps (1) to (3) on the residual signal until the residual becomes monotonic and no further IMFs can be extracted.
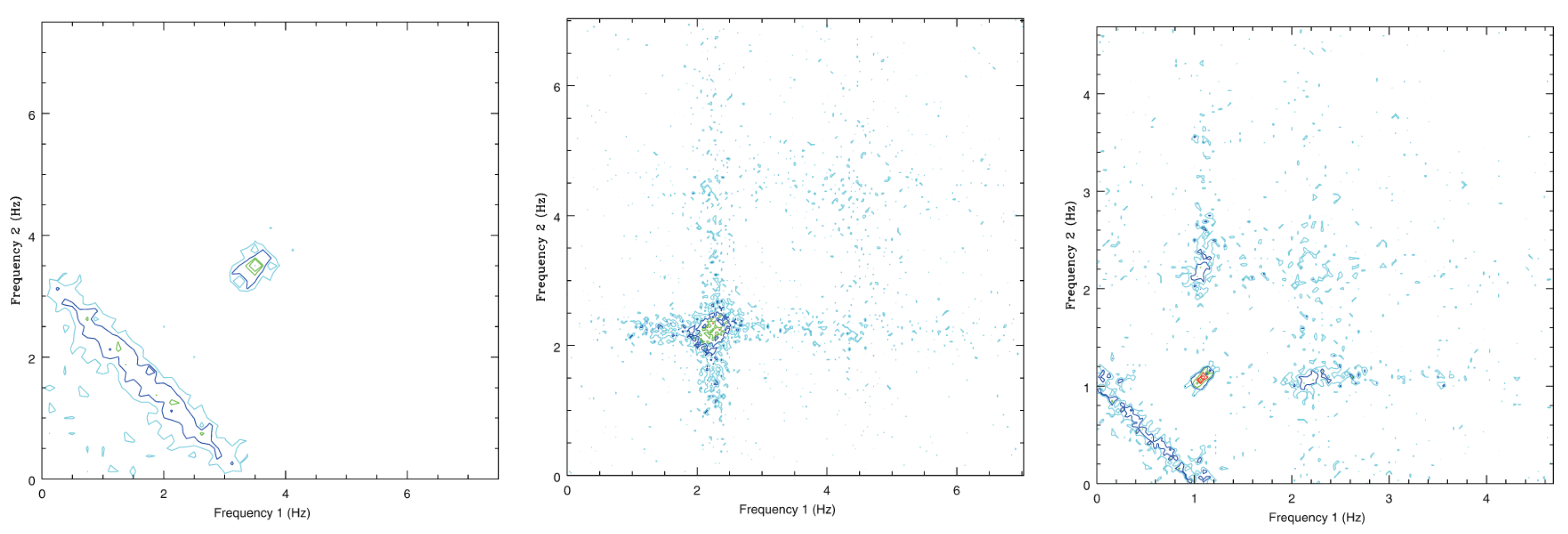
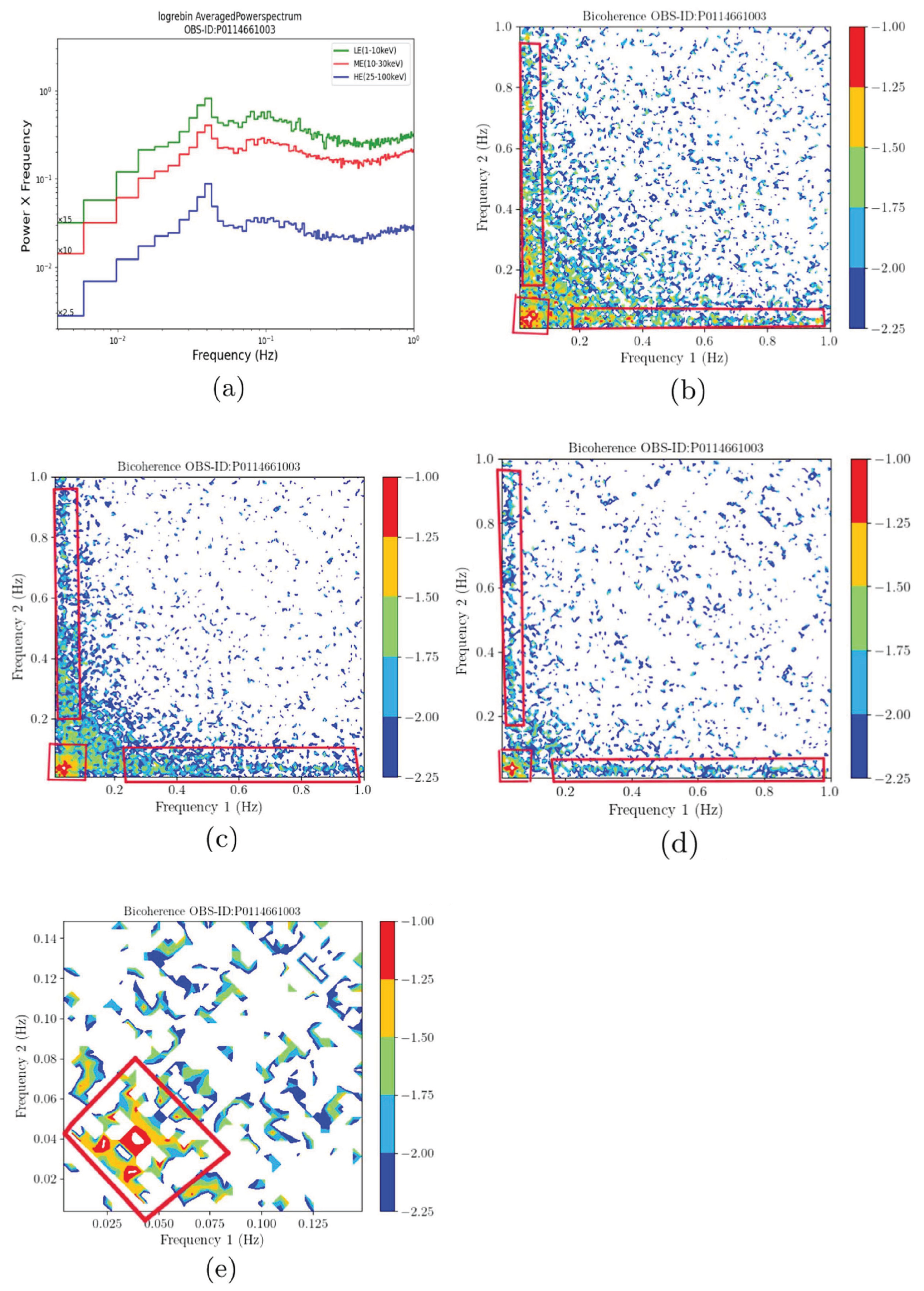
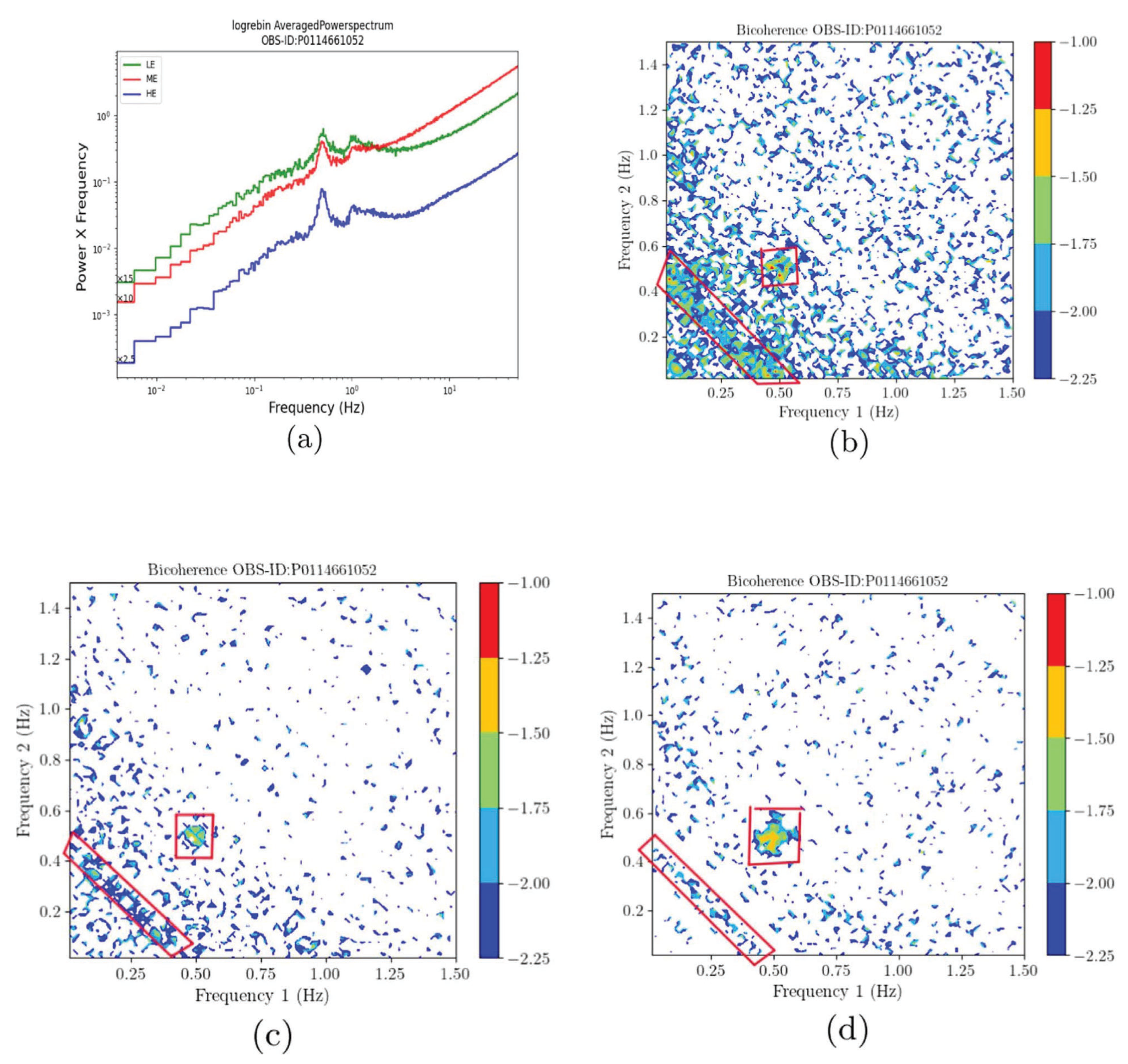
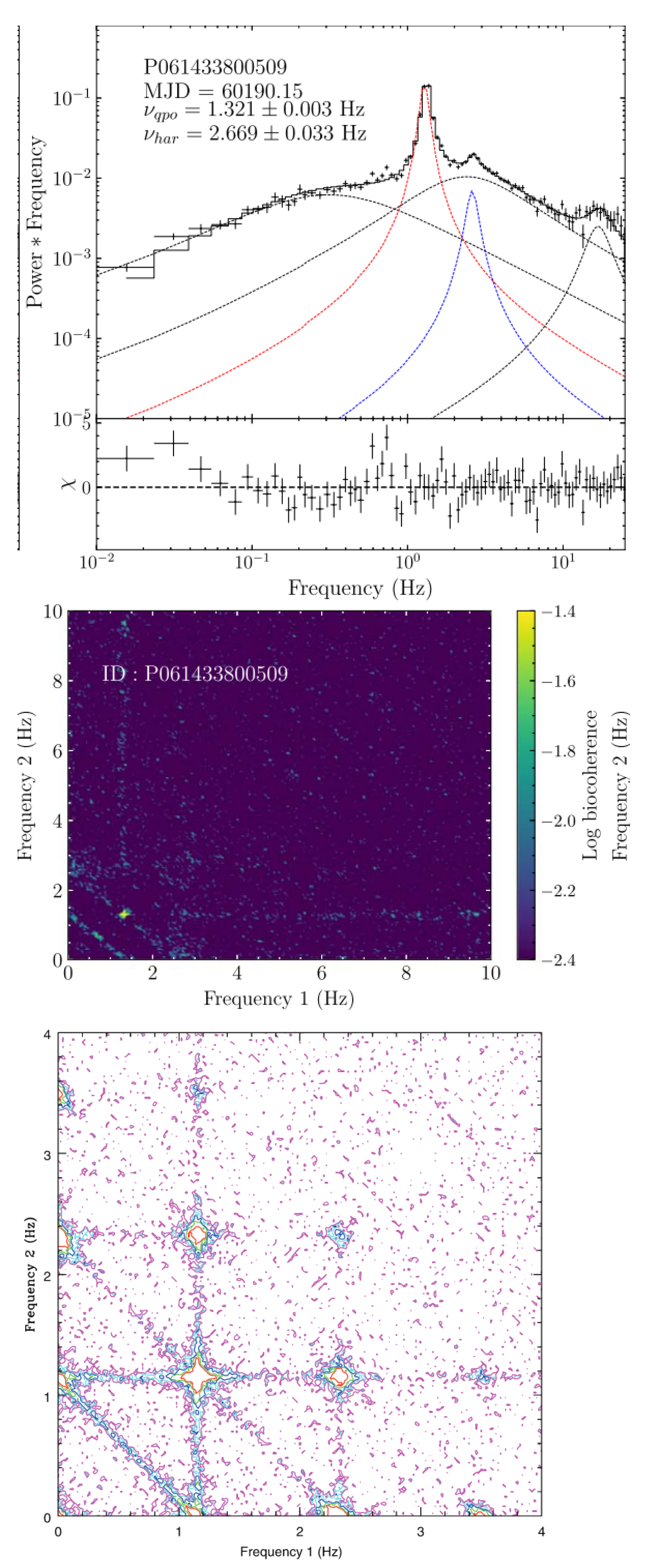
6. Bicoherence
7. Conclusions and Future Outlook
Funding
Data Availability Statement
Conflicts of Interest
| 1 | https://heasarc.gsfc.nasa.gov/docs/software/xspec/manual/node128.html accessed on 17 September 2025. |
References
- Remillard, R.A.; McClintock, J.E. X-ray properties of black-hole binaries. Annu. Rev. Astron. Astrophys. 2006, 44, 49–92. [Google Scholar] [CrossRef]
- Esin, A.A.; McClintock, J.E.; Narayan, R. Advection-dominated accretion and the spectral states of black hole X-ray binaries: Application to Nova Muscae 1991. Astrophys. J. 1997, 489, 865. [Google Scholar] [CrossRef]
- Fender, R.P.; Belloni, T.M.; Gallo, E. Towards a unified model for black hole X-ray binary jets. Mon. Not. R. Astron. Soc. 2004, 355, 1105–1118. [Google Scholar] [CrossRef]
- Basak, R.; Zdziarski, A.A. Spectral analysis of the XMM–Newton data of GX 339–4 in the low/hard state: Disc truncation and reflection. Mon. Not. R. Astron. Soc. 2016, 458, 2199–2214. [Google Scholar] [CrossRef]
- Sharma, R.; Jaleel, A.; Jain, C.; Pandey, J.C.; Paul, B.; Dutta, A. Spectral properties of MXB 1658–298 in the low/hard and high/soft state. Mon. Not. R. Astron. Soc. 2018, 481, 5560–5569. [Google Scholar] [CrossRef]
- Belloni, T.; Motta, S.; Bambi, C. Astrophysics of Black Holes: From Fundamental Aspects to Latest Developments; Astrophysics and Space Science Library; Springer: Berlin/Heidelberg, Germany, 2016; Volume 440. [Google Scholar]
- Wang, W. Observations of fast radio variations in microquasars by FAST. Chin. Phys. Lett. 2024, 41, 119701. [Google Scholar] [CrossRef]
- Casella, P.; Belloni, T.; Stella, L. The ABC of low-frequency quasi-periodic oscillations in black hole candidates: Analogies with Z sources. Astrophys. J. 2005, 629, 403. [Google Scholar] [CrossRef]
- Motta, S.; Casella, P.; Henze, M.; Muñoz-Darias, T.; Sanna, A.; Fender, R.; Belloni, T. Geometrical constraints on the origin of timing signals from black holes. Mon. Not. R. Astron. Soc. 2015, 447, 2059–2072. [Google Scholar] [CrossRef]
- Motta, S.E. Quasi periodic oscillations in black hole binaries. Astron. Nachrichten 2016, 337, 398–403. [Google Scholar] [CrossRef]
- Ingram, A.R.; Motta, S.E. A review of quasi-periodic oscillations from black hole X-ray binaries: Observation and theory. New Astron. Rev. 2019, 85, 101524. [Google Scholar] [CrossRef]
- Stella, L.; Vietri, M. Lense-Thirring precession and quasi-periodic oscillations in low-mass X-ray binaries. Astrophys. J. 1997, 492, L59. [Google Scholar] [CrossRef]
- Stella, L.; Vietri, M.; Morsink, S.M. Correlations in the quasi-periodic oscillation frequencies of low-mass X-ray binaries and the relativistic precession model. Astrophys. J. 1999, 524, L63. [Google Scholar] [CrossRef]
- Schnittman, J.D.; Homan, J.; Miller, J.M. A precessing ring model for low-frequency quasi-periodic oscillations. Astrophys. J. 2006, 642, 420. [Google Scholar] [CrossRef]
- Ingram, A.; Done, C.; Fragile, P.C. Low-frequency quasi-periodic oscillations spectra and Lense–Thirring precession. Mon. Not. R. Astron. Soc. Lett. 2009, 397, L101–L105. [Google Scholar] [CrossRef]
- Ingram, A.; Done, C. A physical model for the continuum variability and quasi-periodic oscillation in accreting black holes. Mon. Not. R. Astron. Soc. 2011, 415, 2323–2335. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G.P. A practical guide to wavelet analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Gendreau, K.C.; Arzoumanian, Z.; Adkins, P.W.; Albert, C.L.; Anders, J.F.; Aylward, A.T.; Baker, C.L.; Balsamo, E.R.; Bamford, W.A.; Benegalrao, S.S.; et al. The neutron star interior composition explorer (NICER): Design and development. In Proceedings of the Space Telescopes and Instrumentation 2016: Ultraviolet to Gamma Ray, Edinburgh, UK, 26 June–1 July 2016; SPIE: Bellingham, WA, USA, 2016; Volume 9905, pp. 420–435. [Google Scholar]
- Chen, X.; Wang, W. Different behaviors of wavelet results for type-B and type-C QPOs of MAXI J1535-571 based on NICER data. J. High Energy Astrophys. 2024, 41, 89–96. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Huang, N.E. Hilbert-Huang Transform and Its Applications; World Scientific: Singapore, 2014; Volume 16. [Google Scholar]
- Rilling, G.; Flandrin, P.; Goncalves, P. On empirical mode decomposition and its algorithms. In Proceedings of the IEEE-EURASIP Workshop on Nonlinear Signal and Image Processing, NSIP-03, Grado, Italy, 8–11 June 2003. [Google Scholar]
- Su, Y.H.; Chou, Y.; Hu, C.P.; Yang, T.C. Characterizing the Intermittency of the 4-Hz Quasi-Periodic Oscillation in XTE J1550-564 Using the Hilbert-Huang Transform. Astrophys. J. 2015, 815, 74. [Google Scholar] [CrossRef]
- Kim, Y.C.; Powers, E.J. Digital bispectral analysis and its applications to nonlinear wave interactions. IEEE Trans. Plasma Sci. 1979, 7, 120–131. [Google Scholar] [CrossRef]
- Fackrell, J.; McLaughlin, S. Detecting nonlinearities in speech sounds using the bicoherence. Proc.-Inst. Acoust. 1996, 18, 123–130. [Google Scholar]
- Maccarone, T.J.; Coppi, P.S. Higher order variability properties of accreting black holes. Mon. Not. R. Astron. Soc. 2002, 336, 817–825. [Google Scholar] [CrossRef]
- Belloni, T.; Psaltis, D.; van der Klis, M. A unified description of the timing features of accreting X-ray binaries. Astrophys. J. 2002, 572, 392. [Google Scholar] [CrossRef]
- Uttley, P.; McHardy, I.; Vaughan, S. Non-linear X-ray variability in X-ray binaries and active galaxies. Mon. Not. R. Astron. Soc. 2005, 359, 345–362. [Google Scholar] [CrossRef]
- Ingram, A.; Done, C. Modelling variability in black hole binaries: Linking simulations to observations. Mon. Not. R. Astron. Soc. 2012, 419, 2369–2378. [Google Scholar] [CrossRef]
- Mushtukov, A.A.; Lipunova, G.V.; Ingram, A.; Tsygankov, S.S.; Mönkkönen, J.; van der Klis, M. Broad-band aperiodic variability in X-ray pulsars: Accretion rate fluctuations propagating under the influence of viscous diffusion. Mon. Not. R. Astron. Soc. 2019, 486, 4061–4074. [Google Scholar] [CrossRef]
- Rapisarda, S.; Ingram, A.; van der Klis, M. Modelling hard and soft states of Cygnus X-1 with propagating mass accretion rate fluctuations. Mon. Not. R. Astron. Soc. 2017, 472, 3821–3832. [Google Scholar] [CrossRef]
- Turner, S.G.; Reynolds, C.S. Investigating the theory of propagating fluctuations with numerical models of stochastic accretion discs. Mon. Not. R. Astron. Soc. 2021, 504, 469–486. [Google Scholar] [CrossRef]
- You, B.; Cao, X.; Yan, Z.; Hameury, J.M.; Czerny, B.; Wu, Y.; Xia, T.; Sikora, M.; Zhang, S.N.; Du, P.; et al. Observations of a black hole X-Ray binary indicate formation of a magnetically arrested disk. Science 2023, 381, 961–964. [Google Scholar] [CrossRef] [PubMed]
- Peng, J.Q.; Zhang, S.; Wang, P.J.; Zhang, S.N.; Kong, L.D.; Chen, Y.P.; Shui, Q.C.; Ji, L.; Qu, J.L.; Tao, L.; et al. Back to Business: SLX 1746–331 after 13 Years of Silence. Astrophys. J. 2023, 955, 96. [Google Scholar] [CrossRef]
- Peng, J.Q.; Zhang, S.; Shui, Q.C.; Zhang, S.N.; Chen, Y.P.; Kong, L.D.; Yu, Z.L.; Ji, L.; Wang, P.J.; Ge, M.Y.; et al. NICER, NuSTAR, and Insight-HXMT Views to Black Hole X-Ray Binary SLX 1746–331. Astrophys. J. Lett. 2024, 965, L22. [Google Scholar] [CrossRef]
- Ma, R.; Soria, R.; Tao, L.; Zhang, W.; Qu, J.; Zhang, S.; Zhang, L.; Qiao, E.; Zhao, S.; Ge, M.; et al. The peculiar spectral evolution of the new X-ray transient MAXI J0637–430. Mon. Not. R. Astron. Soc. 2022, 514, 5238–5265. [Google Scholar] [CrossRef]
- Song, Y.; Jia, N.; Yang, J.; Feng, Y.; Gou, L.; Lu, T. The spin measurement of MAXI J1348-630 using the Insight-HXMT data. Mon. Not. R. Astron. Soc. 2023, 526, 6041–6051. [Google Scholar] [CrossRef]
- Wu, H.; Wang, W.; Sai, N.; Zhu, H.; Chen, J. A moderate spin for the black hole in X-ray binary MAXI J1348-630 revealed by Insight-HXMT. Mon. Not. R. Astron. Soc. 2023, 522, 4323–4331. [Google Scholar] [CrossRef]
- Chen, J.; Wang, W. The spin of a stellar black hole 4U 1543-47 determined by Insight-HXMT. Mon. Not. R. Astron. Soc. 2024, 527, 238–248. [Google Scholar] [CrossRef]
- Yorgancioglu, E.; Bu, Q.; Santangelo, A.; Tao, L.; Davis, S.; Vahdat, A.; Kong, L.; Piraino, S.; Zhou, M.; Zhang, S. Spin measurement of 4U 1543-47 with Insight-HXMT and NICER from its 2021 outburst-A test of accretion disk models at high luminosities. Astron. Astrophys. 2023, 677, A79. [Google Scholar] [CrossRef]
- Shui, Q.C.; Zhang, S.; Zhang, S.N.; Chen, Y.P.; Kong, L.D.; Wang, P.J.; Peng, J.Q.; Ji, L.; Santangelo, A.; Yin, H.X.; et al. A phase-resolved view of the low-frequency quasiperiodic oscillations from the black hole binary MAXI J1820+ 070. Astrophys. J. 2023, 957, 84. [Google Scholar] [CrossRef]
- Zhao, Q.C.; Tao, L.; Li, H.C.; Zhang, S.N.; Feng, H.; Ge, M.Y.; Ji, L.; Wang, Y.N.; Huang, Y.; Ma, X.; et al. The first polarimetric view on quasiperiodic oscillations in a black hole X-ray binary. Astrophys. J. Lett. 2024, 961, L42. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, S.; Lu, F.; Li, T.; Song, L.; Xu, Y.; Wang, H.; Qu, J.; Liu, C.; Chen, Y.; et al. The insight-HXMT mission and its recent progresses. In Proceedings of the Space Telescopes and Instrumentation 2018: Ultraviolet to Gamma Ray, Austin, TX, USA, 10–15 June 2018; SPIE: Bellingham, WA, USA, 2018; Volume 10699, pp. 434–455. [Google Scholar]
- Zhang, S.N.; Li, T.; Lu, F.; Song, L.; Xu, Y.; Liu, C.; Chen, Y.; Cao, X.; Bu, Q.; Chang, Z.; et al. Overview to the hard X-ray modulation telescope (Insight-HXMT) satellite. Sci. China Phys. Mech. Astron. 2020, 63, 249502. [Google Scholar] [CrossRef]
- Liu, C.; Zhang, Y.; Li, X.; Lu, X.; Chang, Z.; Li, Z.; Zhang, A.; Jin, Y.; Yu, H.; Zhang, Z.; et al. The High Energy X-ray telescope (HE) onboard the Insight-HXMT astronomy satellite. Sci. China Phys. Mech. Astron. 2020, 63, 249503. [Google Scholar] [CrossRef]
- Cao, X.; Jiang, W.; Meng, B.; Zhang, W.; Luo, T.; Yang, S.; Zhang, C.; Gu, Y.; Sun, L.; Liu, X.; et al. The Medium Energy X-ray telescope (ME) onboard the Insight-HXMT astronomy satellite. Sci. China Phys. Mech. Astron. 2020, 63, 249504. [Google Scholar] [CrossRef]
- Chen, Y.; Cui, W.; Li, W.; Wang, J.; Xu, Y.; Lu, F.; Wang, Y.; Chen, T.; Han, D.; Hu, W.; et al. The Low Energy X-ray telescope (LE) onboard the Insight-HXMT astronomy satellite. Sci. China Phys. Mech. Astron. 2020, 63, 249505. [Google Scholar] [CrossRef]
- Luo, Q.; Liao, J.Y.; Li, X.F.; Li, G.; Zhang, J.; Liu, C.Z.; Li, X.B.; Zhu, Y.; Li, C.K.; Huang, Y.; et al. Calibration of the instrumental response of Insight-HXMT/HE CsI detectors for gamma-ray monitoring. J. High Energy Astrophys. 2020, 27, 1–13. [Google Scholar] [CrossRef]
- Li, X.; Li, X.; Tan, Y.; Yang, Y.; Ge, M.; Zhang, J.; Tuo, Y.; Wu, B.; Liao, J.; Zhang, Y.; et al. In-flight calibration of the Insight-Hard X-ray Modulation Telescope. J. High Energy Astrophys. 2020, 27, 64–76. [Google Scholar] [CrossRef]
- Tuo, Y.; Li, X.; Ge, M.; Nie, J.; Song, L.; Xu, Y.; Zheng, S.; Lu, F.; Zhang, S.N.; Liu, C.; et al. In-orbit timing calibration of the insight-hard X-ray modulation telescope. Astrophys. J. Suppl. Ser. 2022, 259, 14. [Google Scholar] [CrossRef]
- Shu, Z.; Shuang-Nan, Z. Insight-HXMT Research Progress Since 2023. Chin. J. Space Sci. 2024, 44, 643–667. [Google Scholar] [CrossRef]
- Liao, J.Y.; Zhang, S.; Lu, X.F.; Zhang, J.; Li, G.; Chang, Z.; Chen, Y.P.; Ge, M.Y.; Guo, C.C.; Huang, R.; et al. Background model for the high-energy telescope of Insight-HXMT. J. High Energy Astrophys. 2020, 27, 14–23. [Google Scholar] [CrossRef]
- Guo, C.C.; Liao, J.Y.; Zhang, S.; Zhang, J.; Tan, Y.; Song, L.M.; Lu, F.J.; Cao, X.L.; Chang, Z.; Chen, Y.P.; et al. The background model of the medium energy X-ray telescope of Insight-HXMT. J. High Energy Astrophys. 2020, 27, 44–50. [Google Scholar] [CrossRef]
- Liao, J.Y.; Zhang, S.; Chen, Y.; Zhang, J.; Jin, J.; Chang, Z.; Chen, Y.P.; Ge, M.Y.; Guo, C.C.; Li, G.; et al. Background model for the low-energy telescope of Insight-HXMT. J. High Energy Astrophys. 2020, 27, 24–32. [Google Scholar] [CrossRef]
- Liao, J.Y.; Zhang, S.; Zhang, J.; Li, G.; Chang, Z.; Chen, Y.P.; Ge, M.Y.; Jin, J.; Lu, X.F.; You, Y.; et al. Five-year in-orbit background of Insight-HXMT. Radiat. Detect. Technol. Methods 2023, 7, 34–47. [Google Scholar] [CrossRef]
- Negoro, H.; Ishikawa, M.; Ueno, S.; Tomida, H.; Sugawara, Y.; Isobe, N.; Shimomukai, R.; Mihara, T.; Sugizaki, M.; Serino, M.; et al. MAXI/GSC discovery of a new hard X-ray transient MAXI J1535-571. Astron. Telegr. 2017, 10699, 1. [Google Scholar]
- Kennea, J.; Evans, P.; Beardmore, A.; Krimm, H.; Romano, P.; Yamaoka, K.; Serino, M.; Negoro, H. MAXI J1535-571: Swift detection and localization. Astron. Telegr. 2017, 10700, 1. [Google Scholar]
- Huang, Y.; Qu, J.; Zhang, S.; Bu, Q.; Chen, Y.; Tao, L.; Zhang, S.; Lu, F.; Li, T.; Song, L.; et al. INSIGHT-HXMT Observations of the New Black Hole Candidate MAXI J1535-571: Timing Analysis. Astrophys. J. 2018, 866, 122. [Google Scholar] [CrossRef]
- Miyamoto, S.; Kimura, K.; Kitamoto, S.; Dotani, T.; Ebisawa, K. X-ray variability of GX 339-4 in its very high state. Astrophys. J. Part 1 1991, 383, 784–807. [Google Scholar] [CrossRef]
- Van den Eijnden, J.; Ingram, A.; Uttley, P.; Motta, S.; Belloni, T.; Gardenier, D. Inclination dependence of QPO phase lags in black hole X-ray binaries. Mon. Not. R. Astron. Soc. 2017, 464, 2643–2659. [Google Scholar] [CrossRef]
- Xu, Y.; Harrison, F.A.; García, J.A.; Fabian, A.C.; Fürst, F.; Gandhi, P.; Grefenstette, B.W.; Madsen, K.K.; Miller, J.M.; Parker, M.L.; et al. Reflection spectra of the black hole binary candidate MAXI j1535-571 in the hard state observed by NuSTAR. Astrophys. J. Lett. 2018, 852, L34. [Google Scholar] [CrossRef]
- Wang, Y.; Ji, L.; Zhang, S.; Méndez, M.; Qu, J.; Maggi, P.; Ge, M.; Qiao, E.; Tao, L.; Zhang, S.; et al. The evolution of the broadband temporal features observed in the black-hole transient MAXI J1820+ 070 with insight-HXMT. Astrophys. J. 2020, 896, 33. [Google Scholar] [CrossRef]
- Liu, H.X.; Huang, Y.; Xiao, G.C.; Bu, Q.C.; Qu, J.L.; Zhang, S.; Zhang, S.N.; Jia, S.M.; Lu, F.J.; Ma, X.; et al. Timing analysis of the black hole candidate EXO 1846–031 with Insight-HXMT monitoring. Res. Astron. Astrophys. 2021, 21, 070. [Google Scholar] [CrossRef]
- Jin, Y.; Wang, W.; Chen, X.; Tian, P.; Liu, Q.; Zhang, P.; Wu, H.; Sai, N. Quasi-periodic Oscillations in GX 339-4 during the 2021 Outburst Observed with Insight-HXMT. Astrophys. J. 2023, 953, 33. [Google Scholar] [CrossRef] [PubMed]
- Ma, X.; Tao, L.; Zhang, S.N.; Zhang, L.; Bu, Q.C.; Ge, M.Y.; Chen, Y.P.; Qu, J.L.; Zhang, S.; Lu, F.J.; et al. Discovery of oscillations above 200 keV in a black hole X-ray binary with Insight-HXMT. Nat. Astron. 2021, 5, 94–102. [Google Scholar] [CrossRef]
- Ma, X.; Zhang, L.; Tao, L.; Bu, Q.; Qu, J.; Zhang, S.; Zhou, D.; Huang, Y.; Jia, S.; Song, L.; et al. A Detailed View of Low-frequency Quasi-periodic Oscillation in the Broadband 0.2–200 keV with Insight-HXMT and NICER. Astrophys. J. 2023, 948, 116. [Google Scholar] [CrossRef]
- Zhu, H.; Chen, X.; Wang, W. Timing analysis of the new black hole candidate MAXI J1803-298 with Insight–HXMT and NICER. Mon. Not. R. Astron. Soc. 2023, 523, 4394–4404. [Google Scholar] [CrossRef]
- Xu, Y.C.; Qu, J.L.; Méndez, M.; Ma, R.C.; Ji, L.; Zhang, L.; Huang, Y.; Bu, Q.C.; Song, L.M. Timing and Spectral Analysis of the Black Hole X-Ray Binary MAXI J1803-298 with Insight-HXMT Data. Res. Astron. Astrophys. 2024, 24, 065017. [Google Scholar] [CrossRef]
- Page, K.L.; Dichiara, S.; Gropp, J.D.; Krimm, H.A.; Parsotan, T.M.; Williams, M.A.; Neil Gehrels Swift Observatory Team. GRB 230824A: Swift detection of a burst. GCN 2023, 34537, 1. [Google Scholar]
- Negoro, H.; Serino, M.; Nakajima, M.; Kobayashi, K.; Tanaka, M.; Soejima, Y.; Kudo, Y.; Mihara, T.; Kawamuro, T.; Yamada, S.; et al. MAXI/GSC detection of a new hard X-ray transient Swift J1727.8-1613 (GRB 230824A). ATel 2023, 16205, 1. [Google Scholar]
- Castro-Tirado, A.; Sanchez-Ramirez, R.; Caballero-Garcia, M.; Perez-Garcia, I.; Fernandez-Garcia, E.; Guziy, S.; Hu, Y.D.; Blazek, M.; Hermelo, I.; Pinter, V.; et al. Optical spectroscopy of Swift J1727.8-1613 confirms a new low-mass X-ray binary hosting a black hole candidate. ATel 2023, 16208, 1. [Google Scholar]
- Miller-Jones, J.; Sivakoff, G.; Bahramian, A.; Russell, T. VLA radio detection of the new black hole X-ray binary candidate Swift J1727.8-1613. ATel 2023, 16211, 1. [Google Scholar]
- Sunyaev, R.; Mereminskiy, I.; Molkov, S.; Semena, A.; Arefiev, V.; Krivonos, R.; Levin, V.; Lutovinov, A.; Shtykovsky, A.; Tkachenko, A.Y. INTEGRAL and SRG/ART-XC observations of the rise of Swift J1727.8-1613. ATel 2023, 16217, 1. [Google Scholar]
- Palmer, D.M.; Parsotan, T.M. Swift J1727.8-1613 reaches 7.6 Crab with strong QPO in Hard X-rays. ATel 2023, 16215, 1. [Google Scholar]
- Sánchez, D.M.; Muñoz-Darias, T.; Padilla, M.A.; Casares, J.; Torres, M. Evidence for inflows and outflows in the nearby black hole transient Swift J1727.8-162. Astron. Astrophys. 2024, 682, L1. [Google Scholar] [CrossRef]
- Veledina, A.; Muleri, F.; Dovčiak, M.; Poutanen, J.; Ratheesh, A.; Capitanio, F.; Matt, G.; Soffitta, P.; Tennant, A.F.; Negro, M.; et al. Discovery of X-Ray Polarization from the Black Hole Transient Swift J1727.8-1613. ApJL 2023, 958, L16. [Google Scholar] [CrossRef]
- Ingram, A.; Bollemeijer, N.; Veledina, A.; Dovčiak, M.; Poutanen, J.; Egron, E.; Russell, T.D.; Trushkin, S.A.; Negro, M.; Ratheesh, A.; et al. Tracking the X-Ray Polarization of the Black Hole Transient Swift J1727.8-1613 during a State Transition. Astrophys. J. 2024, 968, 76. [Google Scholar] [CrossRef]
- Peng, J.Q.; Zhang, S.; Shui, Q.C.; Zhang, S.N.; Kong, L.D.; Chen, Y.P.; Wang, P.J.; Ji, L.; Qu, J.L.; Tao, L.; et al. NICER, NuSTAR, and Insight-HXMT Views to the Newly Discovered Black Hole X-Ray Binary Swift J1727.8-1613. Astrophys. J. Lett. 2024, 960, L17. [Google Scholar] [CrossRef]
- Yu, W.; Bu, Q.C.; Zhang, S.N.; Liu, H.X.; Zhang, L.; Ducci, L.; Tao, L.; Santangelo, A.; Doroshenko, V.; Huang, Y.; et al. Timing analysis of the newly discovered black hole candidate Swift J1727.8-1613 with Insight-HXMT. Mon. Not. R. Astron. Soc. 2024, 529, 4624–4632. [Google Scholar] [CrossRef]
- Psaltis, D.; Belloni, T.; van der Klis, M. Correlations in quasi-periodic oscillation and noise frequencies among neutron star and black hole X-ray binaries. Astrophys. J. 1999, 520, 262. [Google Scholar] [CrossRef]
- Zhu, H.; Wang, W. Energy Dependence of the Low-frequency Quasiperiodic Oscillations in Swift J1727.8-1613. Astrophys. J. 2024, 968, 106. [Google Scholar] [CrossRef]
- Yang, Z.X.; Zhang, L.; Zhang, S.N.; Tao, L.; Zhang, S.; Ma, R.; Bu, Q.C.; Huang, Y.; Liu, H.X.; Yu, W.; et al. A timing view of the additional high-energy spectral component discovered in the black hole candidate Swift J1727.8-1613. Astrophys. J. Lett. 2024, 970, L33. [Google Scholar] [CrossRef]
- Stiele, H.; Yu, W. Energy dependence of the band-limited noise in black hole X-ray binaries. Mon. Not. R. Astron. Soc. 2015, 452, 3666–3678. [Google Scholar] [CrossRef]
- Belloni, T.; Motta, S.; Munoz-Darias, T. Black hole transients. Bull. Astr. Soc. India 2011, 39, 409. [Google Scholar]
- Yu, W.; Zhang, W. Energy-dependent Power Spectral States and Origin of Aperiodic Variability in Black Hole Binaries. Astrophys. J. 2013, 770, 135. [Google Scholar] [CrossRef]
- Stiele, H.; Yu, W. Detection of distinct power spectra in soft and hard X-ray bands in the hard state of GRS 1915+ 105. Mon. Not. R. Astron. Soc. 2014, 441, 1177–1185. [Google Scholar] [CrossRef]
- Yang, Z.X.; Zhang, L.; Bu, Q.C.; Huang, Y.; Liu, H.X.; Yu, W.; Wang, P.; Tao, L.; Qu, J.; Zhang, S.; et al. The accretion flow geometry of MAXI J1820+ 070 through broadband noise research with insight hard X-ray modulation telescope. Astrophys. J. 2022, 932, 7. [Google Scholar] [CrossRef]
- Gao, C.; Yan, Z.; Yu, W. Low-frequency quasi-periodic oscillation in MAXI J1820+ 070: Revealing distinct Compton and reflection contributions. Mon. Not. R. Astron. Soc. 2023, 520, 5544–5551. [Google Scholar] [CrossRef]
- Gao, C.; Yu, W.; Yan, Z. On the Broadening of the Characteristic Frequency Range towards Higher Photon Energies in the X-ray Variability of the Black Hole Transient MAXI J1820+ 070. arXiv 2024, arXiv:2409.06414. [Google Scholar] [CrossRef]
- Jin, Y.J.; Chen, X.; Zhu, H.F.; Jiang, Z.J.; Wang, W. Broad-band noises in GX 339-4 during the 2021 outburst observed with Insight-HXMT and NICER. Astron. Astrophys. 2025, 697, A120. [Google Scholar] [CrossRef]
- Done, C.; Gierliński, M.; Kubota, A. Modelling the behaviour of accretion flows in X-ray binaries: Everything you always wanted to know about accretion but were afraid to ask. Astron. Astrophys. Rev. 2007, 15, 1–66. [Google Scholar] [CrossRef]
- Kato, S.; Fukue, J.; Mineshige, S. Black-Hole Accretion Disks: Towards a New Paradigm; Kyoto University Press: Kyoto, Japan, 2008. [Google Scholar]
- Kawamura, T.; Axelsson, M.; Done, C.; Takahashi, T. A full spectral-timing model to map the accretion flow in black hole binaries: The low/hard state of MAXI J1820+ 070. Mon. Not. R. Astron. Soc. 2022, 511, 536–552. [Google Scholar] [CrossRef]
- Xu, Y.; Harrison, F.A.; Tomsick, J.A.; Barret, D.; Gandhi, P.; García, J.A.; Miller, J.M.; Uttley, P.; Walton, D.J. Broadband X-Ray Spectral and Timing Analyses of the Black Hole Binary Candidate Swift J1658.2-4242: Rapid Flux Variation and the Turn-on of a Transient QPO. Astrophys. J. 2019, 879, 93. [Google Scholar] [CrossRef]
- Sriram, K.; Rao, A.; Choi, C. Study of a sudden QPO transition event in the black hole source XTE J1550-564. Astrophys. J. 2016, 823, 67. [Google Scholar] [CrossRef]
- Zhang, L.; Altamirano, D.; Uttley, P.; García, F.; Méndez, M.; Homan, J.; Steiner, J.; Alabarta, K.; Buisson, D.; Remillard, R.; et al. NICER uncovers the transient nature of the type-B quasi-periodic oscillation in the black hole candidate MAXI J1348-630. Mon. Not. R. Astron. Soc. 2021, 505, 3823–3843. [Google Scholar] [CrossRef]
- Sriram, K.; Harikrishna, S.; Choi, C. Spectro-temporal Studies of Rapid Transition of the Quasi-periodic Oscillations in the Black Hole Source H1743-322. Astrophys. J. 2021, 911, 127. [Google Scholar] [CrossRef]
- Ding, Y.; Wang, W.; Zhang, P.; Bu, Q.; Cai, C.; Cao, X.; Zhi, C.; Chen, L.; Chen, T.; Chen, Y.; et al. QPOs and orbital elements of X-ray binary 4U 0115+ 63 during the 2017 outburst observed by Insight-HXMT. Mon. Not. R. Astron. Soc. 2021, 503, 6045–6058. [Google Scholar] [CrossRef]
- Chen, X.; Wang, W.; You, B.; Tian, P.; Liu, Q.; Zhang, P.; Ding, Y.; Qu, J.; Zhang, S.; Song, L.; et al. Wavelet analysis of MAXI J1535-571 with Insight-HXMT. Mon. Not. R. Astron. Soc. 2022, 513, 4875–4886. [Google Scholar] [CrossRef]
- Tian, P.; Zhang, P.; Wang, W.; Wang, P.; Sun, X.; Liu, J.; Zhang, B.; Dai, Z.; Yuan, F.; Zhang, S.; et al. Subsecond periodic radio oscillations in a microquasar. Nature 2023, 621, 271–275. [Google Scholar] [CrossRef]
- Chen, X.; Wang, W.; Tian, P.; Zhang, P.; Liu, Q.; Wu, H.; Sai, N.; Huang, Y.; Song, L.; Qu, J.; et al. Wavelet analysis of the transient QPOs in MAXI J1535-571 with Insight-HXMT. Mon. Not. R. Astron. Soc. 2022, 517, 182–191. [Google Scholar] [CrossRef]
- Jin, Y.; Chen, X.; Zhu, H.; Jiang, Z.; Zhang, L.; Wang, W. Wavelet analysis of low-frequency quasi-periodic oscillations in MAXI J1803-298 observed with Insight-HXMT and NICER. Mon. Not. R. Astron. Soc. 2024, 535, 207–216. [Google Scholar] [CrossRef]
- García, F.; Méndez, M.; Karpouzas, K.; Belloni, T.; Zhang, L.; Altamirano, D. A two-component Comptonization model for the type-B QPO in MAXI J1348-630. Mon. Not. R. Astron. Soc. 2021, 501, 3173–3182. [Google Scholar] [CrossRef]
- Bellavita, C.; García, F.; Méndez, M.; Karpouzas, K. vKompth: A variable Comptonization model for low-frequency quasi-periodic oscillations in black hole X-ray binaries. Mon. Not. R. Astron. Soc. 2022, 515, 2099–2109. [Google Scholar] [CrossRef]
- Peirano, V.; Méndez, M.; García, F.; Belloni, T. Dual-corona Comptonization model for the type-b quasi-periodic oscillations in GX 339-4. Mon. Not. R. Astron. Soc. 2023, 519, 1336–1348. [Google Scholar] [CrossRef]
- Wang, W.; Chen, J.; Tian, P.; Ho, L.C.; Sun, X.; Wang, P.; Zhang, B.; Zheng, Z.; Chen, X.; Zhang, P.; et al. Quasi-periodic oscillations of GHz-band polarization in a black hole. Nat. Commun. 2025, 16, 5139. [Google Scholar] [CrossRef]
- Hu, C.P.; Chou, Y.; Yang, T.C.; Su, Y.H. Tracking the Evolution of the Quasi-Periodic Oscillation in RE J1034+396 Using the Hilbert–Huang Transform. Astrophys. J. 2014, 788, 31. [Google Scholar]
- Hu, C.P.; Lin, L.C.C.; Pan, K.C.; Li, K.L.; Yen, C.C.; Kong, A.K.; Hui, C. A comprehensive analysis of the gravitational wave events with the stacked Hilbert–Huang transform: From compact binary coalescence to supernova. Astrophys. J. 2022, 935, 127. [Google Scholar] [CrossRef]
- Hsieh, H.E.; Chou, Y. Phase-resolved Analyses of Millihertz Quasi-periodic Oscillations in 4U 1636-53 using the Hilbert–Huang Transform. Astrophys. J. 2020, 900, 116. [Google Scholar] [CrossRef]
- Dai, X.; Kong, L.; Ji, L.; Zhou, M.; Shui, Q.; Wang, P.; Zhang, S.; Santangelo, A. Unveiling the rebrightening mechanism of GRS 1915+ 105: Insights from a change in the quasi-periodic oscillations and from a wind analysis. Astron. Astrophys. 2024, 692, A117. [Google Scholar] [CrossRef]
- Huang, N.E.; Wu, Z. A review on Hilbert-Huang transform: Method and its applications to geophysical studies. Rev. Geophys. 2008, 46, RG2006. [Google Scholar] [CrossRef]
- Yu, W.; Bu, Q.C.; Yang, Z.X.; Liu, H.X.; Zhang, L.; Huang, Y.; Zhou, D.K.; Qu, J.L.; Zhang, S.N.; Zhang, S.; et al. Hilbert–Huang Transform Analysis of Quasiperiodic Oscillations in MAXI J1820+ 070. Astrophys. J. 2023, 951, 130. [Google Scholar] [CrossRef]
- Spada, M.; Ghisellini, G.; Lazzati, D.; Celotti, A. Internal shocks in the jets of radio-loud quasars. Mon. Not. R. Astron. Soc. 2001, 325, 1559–1570. [Google Scholar] [CrossRef]
- Boettcher, M.; Dermer, C.D. Timing signatures of the internal-shock model for blazars. Astrophys. J. 2010, 711, 445. [Google Scholar] [CrossRef]
- Yang, W.; Wang, W.; Epili, P.R. Evidence for a Cyclotron Absorption Line and Spectral Transition in EXO 2030+ 375 during the 2021 Giant Outburst. Astrophys. J. 2024, 969, 107. [Google Scholar] [CrossRef]
- Liu, Q.; Wang, W.; Santangelo, A.; Kong, L.; Ji, L.; Ducci, L. Temporal and spectral variations of the X-ray pulsar Cen X-3 observed by NuSTAR. Astron. Astrophys. 2024, 687, A210. [Google Scholar] [CrossRef]
- Shui, Q.C.; Zhang, S.; Peng, J.Q.; Zhang, S.N.; Chen, Y.P.; Ji, L.; Kong, L.D.; Feng, H.; Yu, Z.L.; Wang, P.J.; et al. Phase-resolved Spectroscopy of Low-frequency Quasiperiodic Oscillations from the Newly Discovered Black Hole X-Ray Binary Swift J1727.8-1613. Astrophys. J. 2024, 973, 59. [Google Scholar] [CrossRef]
- Shui, Q.C.; Zhang, S.; Zhang, S.N.; Chen, Y.P.; Kong, L.D.; Peng, J.Q.; Ji, L.; Wang, P.J.; Chang, Z.; Zhuo, L.Y.; et al. Recovery of High-energy Low-frequency Quasiperiodic Oscillations from Black Hole X-Ray Binary MAXI J1535-571 with a Hilbert–Huang Transform Method. Astrophys. J. Lett. 2024, 965, L7. [Google Scholar] [CrossRef]
- Maccarone, T.J.; Uttley, P.; Van Der Klis, M.; Wijnands, R.A.; Coppi, P.S. Coupling between QPOs and broad-band noise components in GRS 1915+ 105. Mon. Not. R. Astron. Soc. 2011, 413, 1819–1827. [Google Scholar] [CrossRef][Green Version]
- Arur, K.; Maccarone, T. Non-linear variability of quasi-periodic oscillations in GX 339-4. Mon. Not. R. Astron. Soc. 2019, 486, 3451–3458. [Google Scholar][Green Version]
- Ding, Q.; Ji, L.; Bu, Q.C.; Dong, T.; Chang, J. Nonlinear variability observed with Insight-HXMT in MAXI J1820+ 070 and MAXI J1535-571. Res. Astron. Astrophys. 2023, 23, 085024. [Google Scholar] [CrossRef]
- Zhu, Z.; Chen, X.; Wang, W. The bicoherence study of quasi-periodic oscillations in MAXI J1535-571. Mon. Not. R. Astron. Soc. 2024, 529, 4602–4610. [Google Scholar] [CrossRef]
- Zhu, H.; Wang, W.; Zhu, Z. The Bicoherence Analysis of Type-C Quasiperiodic Oscillations in Swift J1727.8-1613. Astrophys. J. 2024, 974, 303. [Google Scholar] [CrossRef]
- Méndez, M.; Peirano, V.; García, F.; Belloni, T.; Altamirano, D.; Alabarta, K. Unveiling hidden variability components in accreting X-ray binaries using both the Fourier power and cross-spectra. Mon. Not. R. Astron. Soc. 2024, 527, 9405–9430. [Google Scholar] [CrossRef]
- Qu, J.; Lu, F.; Lu, Y.; Song, L.; Zhang, S.; Ding, G.; Wang, J. The energy dependence of the centroid frequency and phase lag of the quasi-periodic oscillations in GRS 1915+ 105. Astrophys. J. 2010, 710, 836. [Google Scholar] [CrossRef]
- Lin, Z.; Wang, Y.; del Palacio, S.; Méndez, M.; Zhang, S.N.; Russell, T.D.; Ji, L.; Zhang, J.; Zhang, L.; Altamirano, D.; et al. Unraveling the Hybrid Origins of the X-Ray Nonthermal Emission from IGR J17091-3624. Astrophys. J. 2024, 974, 79. [Google Scholar] [CrossRef]
- Bellavita, C.; Méndez, M.; García, F.; Ma, R.; König, O. The nature of an imaginary quasi-periodic oscillation in the soft-to-hard transition of MAXI J1820+ 070. Astron. Astrophys. 2025, 696, A128. [Google Scholar] [CrossRef]
- Jin, P.; Méndez, M.; García, F.; Altamirano, D.; Zhang, G.; Rout, S.K. Timing analysis of the black-hole candidate Swift J1727.8-1613: Detection of a dip-like feature in the high-energy cross spectrum. arXiv 2025, arXiv:2504.20717. [Google Scholar] [CrossRef]
- Fogantini, F.A.; García, F.; Méndez, M.; König, O.; Wilms, J. A hidden quasi-periodic oscillation in Cygnus X-1 revealed by NICER. Astron. Astrophys. 2025, 696, A237. [Google Scholar] [CrossRef]
- Yuan, W.; Zhang, C.; Chen, Y.; Ling, Z. The Einstein probe mission. In Handbook of X-Ray and Gamma-Ray Astrophysics; Springer: Berlin/Heidelberg, Germany, 2022; pp. 1–30. [Google Scholar]
- Zhang, W.; Yuan, W.; Ling, Z.; Chen, Y.; Rea, N.; Rau, A.; Cai, Z.; Cheng, H.; Zelati, F.C.; Dai, L.; et al. Einstein Probe discovery of EP240408a: A peculiar X-ray transient with an intermediate timescale. Sci. China Phys. Mech. Astron. 2025, 68, 219511. [Google Scholar] [CrossRef]
- van Dalen, J.N.; Levan, A.J.; Jonker, P.G.; Malesani, D.B.; Izzo, L.; Sarin, N.; Quirola-Vásquez, J.; Sánchez, D.M.; de Ugarte Postigo, A.; van Hoof, A.P.; et al. The Einstein Probe Transient EP240414a: Linking fast X-Ray transients, gamma-ray bursts, and luminous fast blue optical transients. Astrophys. J. Lett. 2025, 982, L47. [Google Scholar] [CrossRef]
- Marino, A.; Yang, H.; Zelati, F.C.; Rea, N.; Guillot, S.; Jaisawal, G.; Maitra, C.; Ness, J.U.; Haberl, F.; Kuulkers, E.; et al. Einstein Probe Discovery of EP J005245. 1-722843: A Rare Be–White Dwarf Binary in the Small Magellanic Cloud? Astrophys. J. Lett. 2025, 980, L36. [Google Scholar] [CrossRef]
- Liu, Y.; Sun, H.; Xu, D.; Svinkin, D.; Delaunay, J.; Tanvir, N.; Gao, H.; Zhang, C.; Chen, Y.; Wu, X.F.; et al. Soft X-ray prompt emission from the high-redshift gamma-ray burst EP240315a. Nat. Astron. 2025, 9, 564–576. [Google Scholar] [CrossRef]







| Method | Advantages | Applications/Notes |
|---|---|---|
| Fourier Analysis | High frequency resolution; computationally efficient; commonly used method | QPO frequency, rms, phase lag extraction; limited in capturing short-term variations |
| Wavelet Analysis | Good time-frequency localization; detects transients | Tracking short-term frequency changes; sensitive to mother wavelet choice |
| HHT | Adaptive for nonlinear, non-stationary data; instantaneous frequency and phase | QPO signal extraction; modulation and phase studies; noise sensitive |
| Bicoherence Analysis | Quantifies nonlinear phase coupling; reveals frequency interactions | Studies QPO and noise coupling; requires high Signal-to-Noise Ratio; less common |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, H.; Wang, W. Timing Analysis of Black Hole X-Ray Binaries with Insight-HXMT. Galaxies 2025, 13, 111. https://doi.org/10.3390/galaxies13050111
Zhu H, Wang W. Timing Analysis of Black Hole X-Ray Binaries with Insight-HXMT. Galaxies. 2025; 13(5):111. https://doi.org/10.3390/galaxies13050111
Chicago/Turabian StyleZhu, Haifan, and Wei Wang. 2025. "Timing Analysis of Black Hole X-Ray Binaries with Insight-HXMT" Galaxies 13, no. 5: 111. https://doi.org/10.3390/galaxies13050111
APA StyleZhu, H., & Wang, W. (2025). Timing Analysis of Black Hole X-Ray Binaries with Insight-HXMT. Galaxies, 13(5), 111. https://doi.org/10.3390/galaxies13050111






