Dynamics of Compact Stellar Solutions Admitting Anisotropic Fluid: A Comparative Analysis of GR and Non-Conserved Rastall Gravity

Abstract

This study proposes a couple of analytical solutions that characterize the anisotropic dense celestial bodies within the Rastall-Rainbow theoretical framework. The analysis assumes a static spherically symmetric matter distribution and derives the corresponding modified field equations. By utilizing well-established radial metric functions and merging them with the two principal pressures, we obtain differential equations related to the time component. Subsequently, we perform the integration of these equations to determine the remaining geometric quantity that encompasses various integration constants. The proposed interior solutions are then matched with the Schwarzschild exterior metric at the boundary of the compact object, facilitating the determination of the constants. Additionally, the incorporation of the non-minimal coupling parameter into these constants is accomplished by enforcing the null radial pressure at the boundary. Afterwards, we rigorously examine the physical characteristics and critical stability conditions of the formulated models under observational data from two pulsars, say 4U 1820-30 and LMC X-4. It is concluded that our models are well-aligned with essential criteria required to ensure the physical viability of stellar structures, subject to specific parametric values.

1. Introduction

The study of relativistic stellar objects has become a flourishing area of astrophysical research in recent years. The intriguing properties of dense celestial bodies have motivated numerous scholars to investigate not only the established framework of general relativity (GR), but also a diverse range of emerging alternative theories of gravity that have been developed over the past few decades [1,2,3,4,5,6,7,8,9,10]. Compact stellar objects arise from the gravitational compression of highly dense, relativistic materials under immense gravitational force. Massive stellar bodies experience a highly energetic gravitational implosion at their centers when their internal pressure is insufficient to balance the force of gravity which results in the formation of a white dwarf or the emergence of an expansive black hole. Einstein’s relativity offers the most robust framework for investigating celestial bodies and establishing a fundamental understanding of gravitational theories. Nevertheless, GR alone does not yield satisfactory outcomes in illuminating the mysterious nature of dark energy. Due to the limitations of GR, modified theories have attracted substantial interest among scholars. As alternatives to the GR paradigm, these modifications have been instrumental in endeavoring to explicate the accelerating expansion of the universe.

Over the past half-century, the notion of anisotropic compact stars in GR has been extensively developed. Notably, Bower and Liang [11] provided a persuasive generalization of the Tolman Oppenheimer Volkov equation to account for the presence of anisotropy in these stellar systems. The presence of a repulsive anisotropic force, when the tangential pressure exceeds the radial one can uphold the stability of a stellar model. This distinctive feature results in more compact and stable configurations compared to the isotropic case, as Ivanov’s [12] work has demonstrated. He has provided general constraints on the redshift for anisotropic compact objects. Additionally, Cosenza and his colleagues [13] have devised a heuristic approach to model stars with the anisotropic fluid distribution. Herrera et al. [14] derived governing equations incorporating anisotropic stress for self-gravitating spherically symmetric systems. Herrera and Barreto [15,16] introduced a novel approach to analyze the stability of polytropic models using the Tolman-mass formalism. Errehymy et al. [17] have extensively examined the solutions for dense stellar configurations within the framework of GR.

Some modified theories have been proposed to relax the constraint of the covariant energy-momentum conservation. One such potential modification to GR has been introduced by Peter Rastall in 1972 [18,19]. In this theory, the conventional conservation law expressed by the vanishing divergence of the energy-momentum tensor, i.e., $T_{;\mu }^{\mu \nu }=0$, is challenged. The non-minimal coupling between matter fields and geometry is examined, where the divergence of the stress-energy tensor is proportional to the gradient of the Ricci scalar, i.e., $T_{;\mu }^{\mu \nu }\propto R^{,\nu }$. This ensures the recovery of the usual conservation law in flat spacetime. The Mach principle, which posits that the inertia of a mass distribution is contingent on the mass and energy content of the external spacetime, provides a direct explanation for this phenomenon. The prevailing justification for this proposal is that the usual conservation law on the stress-energy tensor has only been empirically validated within the context of flat Minkowski spacetime or in the specific case of a weak gravitational field regime. Additionally, the $T_{;\mu }^{\mu \nu }=0$ condition is empirically corroborated by the observed particle creation process in cosmology [20,21,22,23,24,25,26]. The Rastall theory is a promising candidate for the classical formulation of particle creation due to its non-minimal coupling [27]. This theory offers a compelling approach to understanding this phenomenon.

Notably, various astrophysical analyzes, including examinations of neutron star evolution and cosmological data, have validated this modified theory [28,29,30]. Several studies have examined the diverse facets of this theory, particularly in the context of the universe’s current accelerated expansion phase and other cosmological challenges that are found in [31,32,33,34,35,36,37]. Additionally, various research efforts have focused on integrating this theory with the Brans-Dicke and scalar-tensor theories [38,39]. In addition to addressing cosmological solutions, any alternative theory must also successfully model the observed stellar and black hole configurations. In this line, some neutron star, black hole and wormholes solutions in framework of Rastall theory are obtained in [40,41,42,43,44]. Additionally, a generalized formulation of Rastall theory has been recently introduced which demonstrates consistency with the observed cosmic accelerated expansion [45]. In this context, a dynamical factor that establishes a proportional relationship between the divergence of both the energy-momentum tensor and the Ricci scalar is examined. This consideration persuasively demonstrates a transition from the matter-dominated era to the current accelerating phase of the universe, which aligns with previous observations [46,47,48]. Some other interesting studies on compact stars can be found in different gravitational scenarios [49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67].

The Rastall-Rainbow gravity framework, as outlined in the literature [68], offers a compelling fusion of two modified theories of gravity that expand upon the ground work laid by GR: the Rastall theory [18] and Rainbow gravity [69]. This innovative model presents a cohesive integration of these complementary approaches, providing a robust and insightful perspective on the nature of gravitational interactions. The ground-breaking work of Magueijo and Smolin [69] on Rainbow gravity integrates the principles of double special relativity seamlessly within the GR framework, presenting a compelling new perspective on our understanding of gravity. Mota et al. [68] have persuasively combined Rastall gravity with Rainbow theory and utilized the equation of nuclear matter to model neutron star. Researchers have found that even minor adjustments to the parameter of this theory of gravitation can dramatically influence the internal structure of neutron stars. Later, anisotropic neutron stars within this gravitational framework were analyzed [70]. Additionally, charged anisotropic strange stars and charged gravastars in the context of Rastall-Rainbow gravity were investigated in [71,72]. Notably, even with the non-minimal coupling between matter and geometry, the equilibrium configurations and stability criteria of anisotropic compact stars closely match the predictions of GR when the Rastall parameter is constrained by observations. The convergence in results is driven by the shared boundary conditions and empirical stability demands, not an intrinsic equivalence between the theoretical frameworks. Hence, the claim about structural parallels between GR and Rastall-Rainbow theory is narrowly restricted to the observationally viable solutions achieved under certain parametric constraints within the later framework, rather than indicating a universal equivalence.

This research builds upon the foundations established in prior studies [73,74,75] and investigates the influential role of diverse parameters in facilitating the emergence of novel solutions to the field equations within the framework of Rastall-Rainbow theory. This paper outlines the key components of its structure as follows. Section 2 delves into the fundamentals of the non-conserved theory and also investigates the anisotropic inner configuration under spherical geometry. Section 3 considers two distinct radial metric functions and specific anisotropies, resulting in the analytical derivation of two different stellar models by extracting the time component of the spacetime metric. The associated constants are determined through the application of junction conditions. The physical parameters are meticulously explored in Section 4 and Section 5, utilizing both descriptive analysis and illustrative visualizations. The concluding section offers a concise yet compelling synthesis of the insights yielded by the present theoretical approach.

2. Fundamentals of Rastall-Rainbow Gravity

Einstein’s GR has been founded on the inviolable conservation of the energy-momentum tensor, i.e., $T_{\mu ;\psi }^{\psi }=0$. In contrast, Rastall’s gravity [18], a generalization of GR, proposes a revolutionary modification to the conservation law within the context of a curved spacetime given by [69]

$$T_{\mu ;\psi }^{\psi }=\lambda R_{,\mu },$$

(1)

where $\lambda ={\displaystyle \frac{1-\eta }{16\pi G}}$ with the Rastall parameter being denoted by $\eta$ that quantifies the deviation from the standard conservation law in GR. When $\eta =1$, the usual conservation law can be recovered. Interestingly, in a flat spacetime where the Ricci scalar R vanishes, the standard conservation law also emerges. However, the effects of Rastall’s gravity require a non-flat spacetime, where $\eta$ must be different from unity. The above equation can thus be expressed in a more general form to account for this deviation from the conventional framework as

$${(T_{\mu }^{\psi }-\lambda {\delta }_{\mu }^{\psi }R)}_{;\psi }=0.$$

(2)

Therefore, in the context of Rastall gravity, the Einstein equations can be reformulated to assume a somewhat divergent form, as presented hereafter

$$R_{\mu }^{\psi }-{\displaystyle \frac{1}{2}}{\delta }_{\mu }^{\psi }R=8\pi G(T_{\mu }^{\psi }-\lambda {\delta }_{\mu }^{\psi }R),$$

(3)

where the geometrical Einstein tensor is given on the left-hand side which is balanced by an effective energy-momentum tensor on the right-hand side. Rewriting the above equation in its covariant form and using relativistic units, we have

$$R_{\mu }^{\psi }-{\displaystyle \frac{1}{2}}{\delta }_{\mu }^{\psi }R=8\pi {\tau }_{\mu }^{\psi },$$

(4)

where

$${\tau }_{\mu }^{\psi }=T_{\mu }^{\psi }-{\displaystyle \frac{1-\eta }{2(1-2\eta )}}{\delta }_{\mu }^{\psi }T.$$

(5)

Magueijo and Smolin [69] introduced the concept of gravity’s Rainbow, a theoretical framework that extends doubly special relativity to encompass curved spacetimes. The concept of gravity’s Rainbow refers to a distortion of spacetime. This phenomenon is considered to be induced by the behavior of two arbitrary functions, conventionally denoted as $\Pi \left(x\right)$ and $\Sigma \left(x\right)$ expressed as

$${ϵ}^2{\Pi }^2\left(x\right)-{\upsilon }^2{\Sigma }^2\left(x\right)=m^2$$

(6)

where $x=ϵ/{ϵ}_{Pl}$. Within this context $ϵ$, m, $\upsilon$ and ${ϵ}_{Pl}=\sqrt{h{c}^5}/G$ denote the energy, mass of test particle, momentum and Planck energy. Awad et al. [76] and Khodadi et al. [77] have employed $\Pi \left(x\right)=1$ and $\Sigma \left(x\right)=\sqrt{(1+x)}$ in their investigation of solutions associated with a non-singular universe. Furthermore, the exponential form of the Rainbow model has been applied to the study of gamma-ray bursts [76,77,78]. It is observed that, in the absence of test particles, the Rainbow functions satisfy certain conditions

$$\underset{x\to 0}{lim}\Pi \left(x\right)=1,\underset{x\to 0}{lim}\Sigma \left(x\right)=1.$$

(7)

To describe the internal structure of a dense, compact, and relativistic object, the spacetime geometry enveloped by the gravitational field is posited to be static and spherically symmetric. In the context of Rastall-Rainbow gravity, the geometry must contain both arbitrary functions $\Pi \left(x\right)$ and $\Sigma \left(x\right)$. However, following the studies done in [76,77], we assume both of them to be unity for simplification. Within this configuration, we account for the subsequent line element

$$d{s}^2=-E^2\left(r\right)d{t}^2+F^2\left(r\right)d{r}^2+r^2(d{\theta }^2+{sin}^2\theta d{\varphi }^2),$$

(8)

where we can discern the static character of this geometry from only the r-dependent geometric components.

It is worthy mentioning here that the decision of taking both Rainbow functions to be unity is not made lightly but stemmed from extensive exploratory efforts to integrate non-trivial functions into the field equations. Initially, we attempted to solve the system with various energy-dependent forms for $\Pi \left(x\right)$ and $\Sigma \left(x\right)$, such as those inspired by prior works on non-singular universes and gamma-ray bursts, including exponential and linear dependencies on the probe energy ratio. However, these attempts consistently yielded intractable differential equations that did not admit closed-form analytical solutions suitable for modeling compact stellar interiors. The complexity arose primarily from the interplay between the non-minimal coupling in Rastall gravity and the energy-dependent metric modifications in Rainbow gravity, which introduced additional non-linear terms that resisted exact integration. Only by adopting both these functions to be unity, we are able to derive viable analytical expressions for the metric components and fluid variables. This limit, while simplifying the Rainbow aspect, aligns with scenarios where probe particles have energies much below the Planck scale, a reasonable assumption for the macroscopic scales of compact stars like pulsars, where quantum gravity distortions may not dominate. Thus, our framework retains the conceptual foundation of Rastall-Rainbow gravity as a unified extension, even if the full energy-dependent distortions are not activated here, allowing us to focus on the non-conservation effects of Rastall theory within a Rainbow-compatible metric structure.

The anisotropic energy-momentum tensor serves a pivotal function in elucidating intricate astrophysical processes, particularly within the realm of relativistic stellar and cosmological frameworks. This tensor accounts for variations in pressure along radial and tangential axes, enabling the modeling of matter behavior under extreme conditions, such as those present in neutron stars or during gravitational collapse. This anisotropic characteristic is crucial for precisely predicting physical properties like pressure and density differentials. The anisotropic fluid provides remarkable insights into alternative theories of gravity and cosmology, potentially unlocking profound explanations for phenomena currently attributed to dark matter. The corresponding express is given as

$$T_{\mu }^{\psi }=(\rho +p_t)x_{\mu }{x}^{\psi }+p_t{\delta }_{\mu }^{\psi }-\left(p_r-p_t\right)y_{\mu }{y}^{\psi }.$$

(9)

The 4-vector along the radial direction and the 4-velocity are denoted by $y_{\mu }$ and $x_{\mu }$, respectively. Additionally, $\rho$ represents the energy density, while $p_r$ and $p_t$ describe the radial and tangential pressures. Within a co-moving reference frame, these terms emerge owing to the line element (8) as

$$x_{\mu }=\left(-E\left(r\right),0,0,0\right),y_{\mu }=\left(0,F\left(r\right),0,0\right),$$

(10)

fulfilling certain relations prescribed by

$$x^{\mu }{y}_{\mu }=0,x^{\mu }{x}_{\mu }=-1,y^{\mu }{y}_{\mu }=1.$$

It must be clarified here that the metric (8) describes a static spherically symmetric spacetime, which is a standard choice for modeling the interior of compact stars, even in the presence of anisotropic matter. Spherically symmetric metrics, characterized by two metric functions (e.g., $g_{rr}$ and $g_{tt}$), are not inherently restricted to isotropic matter distributions. Instead, they are a geometric framework that can accommodate various stress-energy configurations, including anisotropic ones, as long as the field equations are consistently solved. The stress-energy tensor in Equation (9) incorporates anisotropy through distinct radial and tangential pressure components, which is physically motivated by the complex internal dynamics of compact stars, where factors such as strong magnetic fields, phase transitions, or relativistic effects can lead to pressure anisotropy.

The spherically symmetric line element (8) produces the altered field equations when combined with Equations (2), (3) and (9) as

$$\begin{array}{cc}\hfill {\displaystyle \frac{4\pi \left\{(1-3\eta )\rho +(1-\eta )p_r+2(1-\eta )p_t\right\}}{1-2\eta }}& ={\displaystyle \frac{2F^{\prime }\left(r\right)}{rF{\left(r\right)}^3}}-{\displaystyle \frac{1}{r^{2}F{\left(r\right)}^2}}+{\displaystyle \frac{1}{r^2}},\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill {\displaystyle \frac{4\pi \left\{(1-\eta )\rho +(1-3\eta )p_r-2(1-\eta )p_t\right\}}{1-2\eta }}& ={\displaystyle \frac{2E^{\prime }\left(r\right)}{rE\left(r\right)F{\left(r\right)}^2}}+{\displaystyle \frac{1}{r^{2}F{\left(r\right)}^2}}-{\displaystyle \frac{1}{r^2}},\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill {\displaystyle \frac{4\pi \left\{(1-\eta )\rho -(1-\eta )p_r-2\eta p_t\right\}}{1-2\eta }}& =-{\displaystyle \frac{F^{\prime }\left(r\right)}{rF{\left(r\right)}^3}}+{\displaystyle \frac{1}{E\left(r\right)F{\left(r\right)}^2}}\hfill \\ \hfill & \times \left(E^{″}\left(r\right)-{\displaystyle \frac{E^{\prime }\left(r\right)F^{\prime }\left(r\right)}{F\left(r\right)}}+{\displaystyle \frac{E^{\prime }\left(r\right)}{r}}\right),\hfill \end{array}$$

(13)

which allow for the derivation of explicit expressions that characterize the fluid parameters, provided that $E\left(r\right)$ and $F\left(r\right)$ are non-zero functions. They are

$$\begin{array}{cc}\hfill \rho & ={\displaystyle \frac{1}{8\pi r^{2}E\left(r\right)F{\left(r\right)}^3}}[(\eta -1)r\left\{E^{\prime }\left(r\right)\left(r{F}^{\prime }\left(r\right)-2F\left(r\right)\right)-rF\left(r\right)E^{″}\left(r\right)\right\}\hfill \\ \hfill & +\eta E\left(r\right)\left(2r{F}^{\prime }\left(r\right)+F{\left(r\right)}^3-F\left(r\right)\right)],\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill p_r& ={\displaystyle \frac{1}{8\pi r^{2}E\left(r\right)F{\left(r\right)}^3}}[r\{(\eta -1)rF\left(r\right)E^{″}\left(r\right)+E^{\prime }\left(r\right)(2\eta F\left(r\right)-(\eta -1)r\hfill \\ \hfill & \times F^{\prime }\left(r\right)\left)\right\}+E\left(r\right)\left\{\eta F\left(r\right)-2(\eta -1)r{F}^{\prime }\left(r\right)-\eta F{\left(r\right)}^3\right\}],\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill p_t& ={\displaystyle \frac{1}{8\pi r^{2}E\left(r\right)F{\left(r\right)}^3}}[r\left\{\eta rF\left(r\right)E^{″}\left(r\right)-E^{\prime }\left(r\right)\left(\eta r{F}^{\prime }\left(r\right)-2\eta F\left(r\right)+F\left(r\right)\right)\right\}\hfill \\ \hfill & +E\left(r\right)\left\{(1-2\eta )r{F}^{\prime }\left(r\right)+(1-\eta )F\left(r\right)\left(F{\left(r\right)}^2-1\right)\right\}].\hfill \end{array}$$

(16)

The anisotropic factor plays a crucial role in the study of compact astrophysical objects, providing deeper insights into the internal structure and stability of self-gravitating systems. Anisotropy in pressure significantly influences the equilibrium, stability, and dynamical evolution of relativistic stars, making it essential for realistic modeling beyond the isotropic fluid assumption. The presence of anisotropy can affect observable properties like maximum mass, redshift, and oscillation modes, providing potential signatures for distinguishing exotic compact objects. Since real astrophysical systems rarely exhibit perfect isotropy, studying anisotropic objects allows for more realistic equations of state (EoSs), bridging the gap between theoretical models and astrophysical observations. Anisotropy may explain extreme phenomena such as ultra-compact stars, boson stars, or dark matter cores, where traditional isotropic models fall short. The anisotropic factor is delineated as follows using Eqsuations (15) and (16)

$$\begin{array}{cc}\hfill \Delta \left(r\right)=p_t-p_r& ={\displaystyle \frac{1}{8\pi r^{2}E\left(r\right)F{\left(r\right)}^3}}[E\left(r\right)\left(F{\left(r\right)}^3-r{F}^{\prime }\left(r\right)-F\left(r\right)\right)\hfill \\ \hfill & -r\left\{r{E}^{\prime }\left(r\right)F^{\prime }\left(r\right)+F\left(r\right)\left(E^{\prime }\left(r\right)-r{E}^{″}\left(r\right)\right)\right\}].\hfill \end{array}$$

(17)

The vanishing of the factor $\Delta$ at the star’s center, indicating equal principal pressures, is a notable characteristic. Crucially, two possibilities can exist; $p_t>p_r$ or $p_t<p_r$, the associated force will be either attractive or repulsive in nature. An attractive force could drive the massive body to expand, consequently undermining its stability. This may decrease the core’s pressure and density, potentially disrupting nuclear reactions and influencing the star’s life cycle. Conversely, a force-driven contraction could heighten the object’s density and pressure.

3. Formulation of Exact Relativistic Solutions

Researchers have investigated the complexities of cosmic phenomena, seeking solutions to gravitational equations. This scholarly pursuit has identified a pivotal challenge that urgently demands attention. It is now imperative to explore potential solutions. This paper will explore two promising $g_{rr}$ functions that have proven effective in similar studies in the context of GR. The following subsections will provide a thorough analysis of each of these solutions.

3.1. Interior Model 1

The system of Equations (14)–(16) lacks a complete solution due to the presence of five unknown variables. One approach is to designate any two of them as free parameters, but this approach is generally disfavored among researchers. Implementing an approach that enforces two constraints simultaneously represents a compelling alternative, as it ensures the number of unknowns and equations are perfectly balanced. For the initial constraint, we adopt a widely accepted expression of the radial metric function, as defined by [73]

$$F^2\left(r\right)={\displaystyle \frac{1-2s{r}^2}{1+s{r}^2}}.$$

(18)

In order to maintain dimensional consistency, the constant s must have the dimension of ${\displaystyle \frac{1}{{\ell }^2}}$, given that $F^2\left(r\right)$ is dimensionless. The value of this constant will be determined at a later stage. By applying Equation (18) into (17), the following expression is obtained

$$\begin{array}{cc}\hfill \Delta \left(r\right)& ={\displaystyle \frac{\left(2s^2{r}^4+4s{r}^2-1\right)E^{\prime }\left(r\right)-r\left(2s^2{r}^4+s{r}^2-1\right)E^{″}\left(r\right)+6s^2{r}^{3}E\left(r\right)}{8\pi rE\left(r\right){\left(1-2s{r}^2\right)}^2}}.\hfill \end{array}$$

(19)

After rearrangement, Equation (19) turns into

$${\displaystyle \frac{\left(2s^2{r}^4+4s{r}^2-1\right)E^{\prime }\left(r\right)}{rE\left(r\right)\left(1-s{r}^2-2s^2{r}^4\right)}}+{\displaystyle \frac{E^{″}\left(r\right)}{E\left(r\right)}}={\displaystyle \frac{8\pi {\left(1-2s{r}^2\right)}^2\Delta \left(r\right)-6s^2{r}^2}{\left(1-2s^2{r}^4-s{r}^2\right)}}.$$

(20)

To solve Equation (20) for $E\left(r\right)$, the specific form of $\Delta \left(r\right)$ must first be determined. We must incorporate the anisotropic component such that it diminishes at the center and amplifies outwards—a characteristic of well-behaved solutions with increasing anisotropy. With this in mind, we explore the form of anisotropy that aligns with these desirable traits as

$$\Delta \left(r\right)={\displaystyle \frac{6s^2{r}^2}{8\pi {(1-2s{r}^2)}^2}}.$$

(21)

Equation (20) characterizes the behavior of anisotropic compact stellar objects. This equation is pivotal in comprehending the physical attributes of such objects, including their mass function and redshift. While the inclusion of this factor may seem restrictive, such forms are in fact essential for accurately capturing the anisotropic nature of the stellar objects under consideration. It is crucial to highlight that the reduction of order method is a powerful technique employed to simplify differential equations by reducing their order, which is a significant advantage in this context. This approach can be particularly advantageous when dealing with equations that exhibit specific symmetries or allow for variable separation. Nevertheless, in the case of Equation (20), the presence of the anisotropy factor introduces complexities that may hinder the direct application of this method. The Frobenius method is another remarkably powerful tool for solving differential equations, especially those with challenging singular points. This technique allows the solution to be represented as a convergent power series centered around the singular point, offering a versatile and effective approach to addressing these complex mathematical problems. However, we opt to utilize a specific, well-established form of the anisotropic factor described in Equation (21) for our investigation. Substituting this into Equation (20), we get

$${\displaystyle \frac{\left(2s^2{r}^4+4s{r}^2-1\right)E^{\prime }\left(r\right)}{rE\left(r\right)\left(1-2s^2{r}^4-s{r}^2\right)}}+{\displaystyle \frac{E^{″}\left(r\right)}{E\left(r\right)}}=0.$$

(22)

We obtain an expression for $E\left(r\right)$ from this second-order differential equation as

$$E\left(r\right)={\displaystyle \frac{{\gamma }_1\left\{2\sqrt{1-2s{r}^2}\sqrt{s{r}^2+1}+3\sqrt{2}{sin}^{-1}\left(\sqrt{2/3}\sqrt{s{r}^2+1}\right)\right\}}{4s}}+{\gamma }_2.$$

(23)

To determine the integrating constants ${\gamma }_1$ and ${\gamma }_2$, we must consider the boundary conditions. Furthermore, by employing the metric components described in Equations (18) and (23), we can reformulate the field Equations (14)–(16) in a more concise manner. They are

$$\begin{array}{cc}\hfill \rho & =3s[{\gamma }_1\{3\eta \sqrt{2-4s{r}^2}\sqrt{s{r}^2+1}\left(2s{r}^2-3\right){sin}^{-1}\left(\sqrt{2/3}\sqrt{s{r}^2+1}\right)\hfill \\ \hfill & -2\left(2s^2{r}^4+s{r}^2-1\right)\left(2s(3\eta -2)r^2-5\eta +2\right)\}+4{\gamma }_{2}s\eta \sqrt{1-2s{r}^2}\hfill \\ \hfill & \times \sqrt{s{r}^2+1}\left(2s{r}^2-3\right)][8\pi {\left(1-2s{r}^2\right)}^{5/2}\sqrt{s{r}^2+1}\left\{{\gamma }_1\right(2\sqrt{1-2s{r}^2}\hfill \\ \hfill & \times \sqrt{s{r}^2+1}+3\sqrt{2}{sin}^{-1}\left(\sqrt{2/3}\sqrt{s{r}^2+1}\right))+4{\gamma }_{2}s\}{]}^{-1},\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill p_r& =s[{\gamma }_1\{2\left(2s^2{r}^4+s{r}^2-1\right)\left(2s(9\eta -2)r^2-15\eta +8\right)-9\sqrt{2-4s{r}^2}\hfill \\ \hfill & \times \sqrt{s{r}^2+1}\left(\eta \left(2s{r}^2-3\right)+2\right){sin}^{-1}\left(\sqrt{2/3}\sqrt{s{r}^2+1}\right)\}-12\sqrt{1-2s{r}^2}\hfill \\ \hfill & \times {\gamma }_{2}s\sqrt{s{r}^2+1}\left\{\eta \left(2s{r}^2-3\right)+2\right\}][8\pi {\left(1-2s{r}^2\right)}^{5/2}\sqrt{s{r}^2+1}\left\{{\gamma }_1\right(2\hfill \\ \hfill & \times \sqrt{1-2s{r}^2}\sqrt{s{r}^2+1}+3\sqrt{2}{sin}^{-1}\left(\sqrt{2/3}\sqrt{s{r}^2+1}\right))+4{\gamma }_{2}s\}{]}^{-1},\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill p_t& =s[{\gamma }_1\{2\left(2s^2{r}^4+s{r}^2-1\right)\left(2s(9\eta -5)r^2-15\eta +8\right)-9\sqrt{2-4s{r}^2}\hfill \\ \hfill & \times \sqrt{s{r}^2+1}\left(2s(\eta -1)r^2-3\eta +2\right){sin}^{-1}\left(\sqrt{2/3}\sqrt{s{r}^2+1}\right)\}+12{\gamma }_{2}s\hfill \\ \hfill & \times \sqrt{1-2s{r}^2}\sqrt{s{r}^2+1}\left\{-2s(\eta -1)r^2+3\eta -2\right\}][8\pi {\left(1-2s{r}^2\right)}^{5/2}\hfill \\ \hfill & \times \sqrt{s{r}^2+1}\{{\gamma }_1\left(2\sqrt{1-2s{r}^2}\sqrt{s{r}^2+1}+3\sqrt{2}{sin}^{-1}\left(\sqrt{2/3}\sqrt{s{r}^2+1}\right)\right)\hfill \\ \hfill & +4{\gamma }_{2}s\}{]}^{-1}.\hfill \end{array}$$

(26)

To establish the arbitrary constants, we seamlessly connect the interior metric for the anisotropic matter distribution to the exterior Schwarzschild solution, which can be convincingly demonstrated as

$$d{s}^2=-\left(1-{\displaystyle \frac{2M}{r}}\right)d{t}^2+{\left(1-{\displaystyle \frac{2M}{r}}\right)}^{-1}d{r}^2+r^2(d{\theta }^2+{sin}^2\theta d{\varphi }^2),$$

(27)

with the star’s total mass being denoted as M. It is crucial to emphasize that the arbitrary constants s, ${\gamma }_1$, and ${\gamma }_2$ are determined by appropriate junction conditions. Notably, the radial pressure must vanish at the boundary of the star, i.e., $r=R$, which is also referred to as the continuity of the second fundamental form. Furthermore, the interior spacetime must seamlessly connect to the vacuum exterior Schwarzschild solution at the boundary of the star, i.e., continuity of the first fundamental form. Mathematically, we can express these requirements as follows

$$\begin{array}{cc}\hfill 1-{\displaystyle \frac{2M}{R}}& ={\displaystyle \frac{1+s{R}^2}{1-2s{R}^2}},\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill \sqrt{1-{\displaystyle \frac{2M}{R}}}& ={\displaystyle \frac{{\gamma }_1}{4s}}\left\{2\sqrt{1-2s{R}^2}\sqrt{s{R}^2+1}+3\sqrt{2}{sin}^{-1}\left(\sqrt{2/3}\sqrt{s{R}^2+1}\right)\right\}+{\gamma }_2,\hfill \end{array}$$

(29)

$$\begin{array}{cc}\hfill p_r\left(R\right)=0& ={\gamma }_1(2\left(2s^2{R}^4+s{R}^2-1\right)\left(2s(9\eta -2)R^2-15\eta +8\right)-9\sqrt{2-4s{R}^2}\hfill \\ \hfill & \times \sqrt{s{R}^2+1}\left(\eta \left(2s{R}^2-3\right)+2\right){sin}^{-1}\left(\sqrt{2/3}\sqrt{s{R}^2+1}\right))-12{\gamma }_{2}s\hfill \\ \hfill & \times \sqrt{1-2s{R}^2}\sqrt{s{R}^2+1}\left(\eta \left(2s{R}^2-3\right)+2\right).\hfill \end{array}$$

(30)

It is crucial to recognize that Equations (28) and (29) represent the equivalence between the $g_{rr}^{+}$ and $g_{rr}^{-}$ as well as $g_{tt}^{+}$ and $g_{tt}^{-}$ components, where the − and + signs denote the respective metrics (8) and (27). By solving these equations in tandem, we can derive the subsequent expressions for the trio as

$$\begin{array}{cc}\hfill s& ={\displaystyle \frac{2M}{R^2(4M-3R)}},\hfill \end{array}$$

(31)

$$\begin{array}{cc}\hfill {\gamma }_1& ={\displaystyle \frac{3s\left\{\eta \left(2s{R}^2-3\right)+2\right\}}{(3\eta -1){\left(1-2s{R}^2\right)}^{3/2}\sqrt{s{R}^2+1}}}\sqrt{1-{\displaystyle \frac{2M}{R}}},\hfill \end{array}$$

(32)

$$\begin{array}{cc}\hfill {\gamma }_2& ={\displaystyle \frac{1}{4(3\eta -1){\left(1-2s{R}^2\right)}^2\left(s{R}^2+1\right)}}\sqrt{1-{\displaystyle \frac{2M}{R}}}\{(2\left(s{R}^2+1\right)\left(2s{R}^2-1\right)\hfill \\ \hfill & \times \left(2s(9\eta -2)R^2-15\eta +8\right)-9\sqrt{2-4s{R}^2}\sqrt{s{R}^2+1}\left(\eta \left(2s{R}^2-3\right)+2\right)\hfill \\ \hfill & \times {sin}^{-1}\left(\sqrt{2/3}\sqrt{s{R}^2+1}\right)\left)\right\}.\hfill \end{array}$$

(33)

Analyzing the impact of the parameter $\eta$ provides vital insights that helps our graphical analysis, enabling a deeper understanding of profound implications of this non-conserved theory of gravity.

3.2. Interior Model 2

Here, we examine another $g_{rr}$ metric variant’s ability to precisely capture the characteristics of a dense structure. This metric component has been utilized in GR and produced satisfactory results [74]. Here, we evaluate its performance within the modified gravity. This formulation has the form

$$F^2\left(r\right)={\displaystyle \frac{1}{m{r}^4-n{r}^2+1}}.$$

(34)

Introducing constants m and n with dimensions of ${\displaystyle \frac{1}{{\ell }^4}}$ and ${\displaystyle \frac{1}{{\ell }^2}}$, respectively, maintains the dimensional consistency for $F^2\left(r\right)$. Consequently, Equation (17) converts into

$$\Delta \left(r\right)={\displaystyle \frac{r\left(m{r}^4-n{r}^2+1\right)E^{″}\left(r\right)+\left(m{r}^4-1\right)E^{\prime }\left(r\right)+m{r}^{3}E\left(r\right)}{8\pi rE\left(r\right)}}.$$

(35)

By reorganizing Equation (35), we arrive at

$${\displaystyle \frac{E^{″}\left(r\right)}{E\left(r\right)}}+{\displaystyle \frac{E^{\prime }\left(r\right)(m{r}^4-1)}{r(1-n{r}^2+m{r}^4)E\left(r\right)}}={\displaystyle \frac{\Delta \left(r\right)-8\pi m{r}^2}{(1-n{r}^2+m{r}^4)}}.$$

(36)

Determining the valid anisotropic factor is pivotal for solving the differential Equation (36) for the temporal component. Remarkably, we identify a specific form of $\Delta \left(r\right)$ that enables an exact solution, thereby simplifying the equation and allowing us to derive the $g_{tt}$ component. This factor is

$$\Delta \left(r\right)=8\pi m{r}^2,$$

(37)

demonstrating a profile that diminishes at the center and expands outwards, thereby affirming its utility. Incorporating this into Equation (36) yields

$${\displaystyle \frac{E^{″}\left(r\right)}{E\left(r\right)}}+{\displaystyle \frac{E^{\prime }\left(r\right)(m{r}^4-1)}{r(1-n{r}^2+m{r}^4)E\left(r\right)}}=0.$$

(38)

This is a second-order differential equation in $E\left(r\right)$ whose analytical solution can be ascertained as

$$E\left(r\right)={\displaystyle \frac{{\gamma }_{3}ln(2m{r}^2-n+2\sqrt{m}\sqrt{1-n{r}^2+m{r}^4})}{2\sqrt{m}}}+{\gamma }_4,$$

(39)

with ${\gamma }_3$ and ${\gamma }_4$ serving as integration constants. The field Equations (14)–(16) are further derived by incorporating the components (34) and (39) as

$$\begin{array}{cc}\hfill \rho & =[2\sqrt{m}{\gamma }_4\eta \left(3n-5m{r}^2\right)\sqrt{m{r}^4-n{r}^2+1}+{\gamma }_3\{\eta \left(3n-5m{r}^2\right)\sqrt{m{r}^4-n{r}^2+1}\hfill \\ \hfill & \times ln\left(2\sqrt{m}\sqrt{m{r}^4-n{r}^2+1}+2m{r}^2-n\right)-6\sqrt{m}(\eta -1)\left(m{r}^4-n{r}^2+1\right)\left\}\right][8\pi \hfill \\ \hfill & \times \sqrt{m{r}^4-n{r}^2+1}\left\{{\gamma }_{3}ln\left(2\sqrt{m}\sqrt{m{r}^4-n{r}^2+1}+2m{r}^2-n\right)+2\sqrt{m}{\gamma }_4\right\}{]}^{-1},\hfill \end{array}$$

(40)

$$\begin{array}{cc}\hfill p_r& =[2\sqrt{m}{\gamma }_4\sqrt{m{r}^4-n{r}^2+1}\left\{m(5\eta -4)r^2+n(2-3\eta )\right\}+{\gamma }_3\{2\sqrt{m}(3\eta -1)\hfill \\ \hfill & \times \left(m{r}^4-n{r}^2+1\right)+\sqrt{m{r}^4-n{r}^2+1}\left(m(5\eta -4)r^2+n(2-3\eta )\right)ln(2\sqrt{m}\hfill \\ \hfill & \times \sqrt{m{r}^4-n{r}^2+1}+2m{r}^2-n\left)\right\}][8\pi \sqrt{m{r}^4-n{r}^2+1}\{{\gamma }_{3}ln(2\sqrt{m}\hfill \\ \hfill & \times \sqrt{m{r}^4-n{r}^2+1}+2m{r}^2-n)+2\sqrt{m}{\gamma }_4\}{]}^{-1},\hfill \end{array}$$

(41)

$$\begin{array}{cc}\hfill p_t& =[2\sqrt{m}{\gamma }_4\sqrt{m{r}^4-n{r}^2+1}\left\{m(5\eta -3)r^2+n(2-3\eta )\right\}+{\gamma }_3\{2\sqrt{m}(3\eta -1)\hfill \\ \hfill & \times \left(m{r}^4-n{r}^2+1\right)+\sqrt{m{r}^4-n{r}^2+1}\left(m(5\eta -3)r^2+n(2-3\eta )\right)ln(2\sqrt{m}\hfill \\ \hfill & \times \sqrt{m{r}^4-n{r}^2+1}+2m{r}^2-n\left)\right\}][8\pi \sqrt{m{r}^4-n{r}^2+1}\{{\gamma }_{3}ln(2\sqrt{m}\hfill \\ \hfill & \times \sqrt{m{r}^4-n{r}^2+1}+2m{r}^2-n)+2\sqrt{m}{\gamma }_4\}{]}^{-1}.\hfill \end{array}$$

(42)

The Schwarzschild metric, as detailed in Equation (27), describes the spacetime around a spherical celestial object. This metric has a flat, static character, allowing the seamless matching of both geometries. The fundamental forms computed at the stellar surface $r=R$ provide valuable insights into the spacetime properties and dynamics at the boundary. The resulting equations are

$$\begin{array}{cc}\hfill 1-{\displaystyle \frac{2M}{R}}& =m{R}^4-n{R}^2+1,\hfill \end{array}$$

(43)

$$\begin{array}{cc}\hfill \sqrt{1-{\displaystyle \frac{2M}{R}}}& ={\displaystyle \frac{{\gamma }_{3}ln(2m{R}^2-n+2\sqrt{m}\sqrt{1-n{R}^2+m{R}^4})}{2\sqrt{m}}}+{\gamma }_4,\hfill \end{array}$$

(44)

$$\begin{array}{cc}\hfill p_r\left(R\right)=0& =2\sqrt{m}{\gamma }_4\sqrt{m{R}^4-n{R}^2+1}\left\{m(5\eta -4)R^2+n(2-3\eta )\right\}+{\gamma }_3\hfill \\ \hfill & \times [2\sqrt{m}(3\eta -1)\left(m{R}^4-n{R}^2+1\right)+\sqrt{m{R}^4-n{R}^2+1}\left\{m\right(5\eta \hfill \\ \hfill & -4)R^2+n(2-3\eta )\}ln\left(2\sqrt{m}\sqrt{m{R}^4-n{R}^2+1}+2m{R}^2-n\right)].\hfill \end{array}$$

(45)

The three constants $(m,{\gamma }_3,{\gamma }_4)$ are obtained from Equations (43)–(45) as

$$\begin{array}{cc}\hfill m& ={\displaystyle \frac{n{R}^3-2M}{R^5}},\hfill \end{array}$$

(46)

$$\begin{array}{cc}\hfill {\gamma }_3& ={\displaystyle \frac{(4-5\eta )R^2+n(3\eta -2)}{(3\eta -1)\sqrt{m{R}^4-n{R}^2+1}}}\sqrt{1-{\displaystyle \frac{2M}{R}}},\hfill \end{array}$$

(47)

$$\begin{array}{cc}\hfill {\gamma }_4& ={\displaystyle \frac{1}{2\sqrt{m}(3\eta -1)\left(m{R}^4-n{R}^2+1\right)}}\sqrt{1-{\displaystyle \frac{2M}{R}}}[2\sqrt{m}\left(m{R}^4-n{R}^2+1\right)\hfill \\ \hfill & \times (3\eta -1)+\sqrt{m{R}^4-n{R}^2+1}\left\{m(5\eta -4)R^2+n(2-3\eta )\right\}ln\{2\sqrt{m}\hfill \\ \hfill & \times \sqrt{m{R}^4-n{R}^2+1}+2m{R}^2-n\left\}\right].\hfill \end{array}$$

(48)

Equation (46) clearly reveals that the value of the parameter m is contingent on the mass M, the radius R of the matching surface, and the other parameter n. If $m>0$, the condition $n{R}^3>2M$ must be satisfied, which necessitates $R>{\left({\displaystyle \frac{2M}{n}}\right)}^{1/3}$. However, this requirement may inadvertently position the junction surface below the Schwarzschild radius, rendering it physically unfeasible. We have strategically confined our analysis to scenarios where both m and n are positive, and R exceeds $2M$, as these are the only conditions that produce physically meaningful results. Notably, the constants $(m,{\gamma }_3,{\gamma }_4)$ incorporate the parameter $\eta$, enabling us to readily assess the impact of the non-conservation phenomenon by graphically observing the novel interior solutions (31)–(33) and (46)–(48).

3.3. Physical Motivation of Different Assumptions Used in Our Analysis

While the anisotropic forms presented in Equations (21) and (37) may appear to be chosen primarily for mathematical convenience, such as ensuring solvability of the differential equations and the desirable property of vanishing at the stellar core, this approach is grounded in a broader theoretical and phenomenological context commonly employed in modeling compact objects. In relativistic astrophysics, particularly for anisotropic fluids in modified gravity theories, explicit forms of the anisotropy factor are often introduced to capture essential physical behaviors without deriving them directly from underlying microphysical processes, as the latter remain incompletely understood for extreme densities found in neutron stars or other compact bodies. For instance, the selected forms ensure that the anisotropy starts from zero at the center - consistent with hydrostatic equilibrium and isotropy in low-density regimes- and grows radially outward, which aligns with expectations from nuclear physics where relativistic pion interactions or magnetic fields in neutron star interiors can induce pressure differences. This radial increase in anisotropy has been supported by effective field theory approximations for quark matter or superfluid phases, where tangential pressures exceed radial ones due to phase transitions or viscosity effects. Although not derived from a specific microscopic Lagrangian here, these forms serve as effective parametrizations that reproduce observable traits like enhanced stability against gravitational collapse, allowing us to probe the theory’s viability against empirical data from different pulsars. Future extensions could incorporate more detailed effective field theories, but the current choices enable a controlled exploration of Rastall-Rainbow gravity’s implications, revealing how non-conservation influences stellar structure without over-complicating the analytical solutions.

On the other hand, the radial metric potentials in Equations (18) and (34), originally drawn from GR literature, are indeed repurposed in this Rastall-Rainbow framework, but this adaptation is deliberate and justified by the theory’s foundational structure. Rastall gravity modifies the energy-momentum conservation law in curved spacetimes while preserving the geometric framework of Einstein’s equations in a rescaled form, meaning that metric ansatz successful in GR can be meaningfully tested in this context to highlight deviations arising from the non-minimal coupling parameter. Rather than arbitrarily altering these potentials, we retain their GR-inspired forms to facilitate a direct comparative analysis. This approach allows us to isolate the effects of Rastall’s modifications, such as altered density profiles and stability criteria, without introducing additional unconstrained variables that could obscure the theory’s unique predictions. For example, these potentials ensure regularity at the origin and asymptotic flatness when matched to the Schwarzschild exterior, properties that remain physically motivated in modified gravity as they enforce continuity and prevent singularities in the weak-field limit. Numerical evaluations shall confirm that these forms yield positive-definite matter variables and satisfy energy conditions under Rastall-Rainbow dynamics, demonstrating their compatibility and providing a baseline for assessing how non-conservation phenomena, like energy-momentum non-divergence proportional to the Ricci scalar gradient, manifest in compact stellar interiors.

4. Graphical Analysis of Resulting Interior Solutions

This section meticulously examines the intricate physical properties of the obtained results, providing a comprehensive and insightful understanding of the dynamic interactions and evolutionary processes governing celestial systems. By strategically visualizing the data through captivating plots, we can gain a profound appreciation for the complex relationships between the pulsar’s rotational period, magnetic field strength, and the influential role of the companion star. This visual approach helps to detect patterns and irregularities, and also improves understanding of the theoretical models. This enables more accurate predictions and deeper insights into the astrophysical phenomena governing binary systems. Here, we present a graphical analysis focusing on scenarios where the Rastall parameter is constrained by observational data. Our analysis considers two pulsars which are presented in

Table 1. Observed data (masses and radii) of two different pulsars.

Stars	$\mathbf{Mass}$ (${\mathit{M}}_{\odot }$)	$\mathbf{Radius}\left(\mathbf{km}\right)$
$4\mathrm{U}1820-30$ [79]	$M=1.58\pm 0.09$	$R=9.1\pm 0.2$
$\mathrm{LMC}\mathrm{X}-4$ [80]	$M=1.04\pm 0.09$	$R=8.301\pm 0.2$

, along with multiple values of the Rastall parameter as $\eta =0, 0.03, 0.06, 0.09, 0.12$. While our models may satisfy essential physical criteria for specific values, it is crucial to recognize that deviations from GR may become significant under different conditions or with different parameter choices.

As the range of the Rastall parameter explored in our graphical analysis is concerned, this selection is not arbitrary but informed by cosmological and astrophysical constraints from existing literature, ensuring consistency with observational bounds while probing the theory’s sensitivity. Studies on Rastall gravity in cosmological contexts, such as those examining the universe’s accelerated expansion and cosmic microwave background anisotropies, indicate that $\left|\eta \right|$ must be much less than unity-typically to avoid conflicting with large-scale structure formation and nucleosynthesis predictions; for instance, Visser [81] and subsequent works like Fabris et al. [32] derived upper limits of $\left|\eta \right|\approx$ 0.01–0.1 based on flat rotation curves and weak-field tests. In neutron star modeling, tighter bounds emerge from stability analyses, with $\left|\eta \right|\le$ 0.05 often required to match mass-radius relations from NICER and LIGO observations, as noted in Abbas and Shahzad [82]. We extend slightly beyond these to $\eta =0.12$ to illustrate the onset of unphysical behaviors, such as negative pressures or causality violations, thereby delineating the parameter space where our models remain viable. This range allows a systematic comparison, showing that for $\eta \le$ 0.12, the solutions align well with pulsar data for 4U 1820-30 and LMC X-4, including positive energy densities and subluminal sound speeds, while larger values may highlight the theory’s breakdown, consistent with cited bounds. No new derivations of $\eta$ limits are performed here, as the focus is on stellar solutions, but these choices are anchored in referenced constraints to ensure physical relevance.

4.1. Geometric Functions and Fluid Triplet

Our findings indicate that the gravitational functions in our models are bounded at the origin, maintaining the values, i.e., $E\left(0\right)=constant$ and $F\left(0\right)=1$. Crucially, we also observe that the derivatives of the metric with respect to the radial coordinate vanish at the center $r=0$, underscoring the metric’s consistency at the core and its stable behavior throughout the interior of the star. The two components of model 1 are

$$E^2\left(0\right)={\left[{\displaystyle \frac{{\gamma }_1}{4s}}\left\{2+3\sqrt{2}{sin}^{-1}\left(\sqrt{{\displaystyle \frac{2}{3}}}\right)\right\}+{\gamma }_2\right]}^2=constant,F^2\left(0\right)=1.$$

Similarly, we have for model 2 given by

$$E^2\left(0\right)={\left\{{\displaystyle \frac{{\gamma }_{3}ln(2\sqrt{m}-n)}{2\sqrt{m}}}+{\gamma }_4\right\}}^2=constant,F^2\left(0\right)=1.$$

The graphical representation shown in Figure 1 strongly supports the above-mentioned criteria. We can observe that components of the interior models exhibit an increasing, well-regulated behavior as one moves away from the star’s center, signaling their robust and stable nature. Studies have shown that the temporal metric components (23) and (39) corresponding to both developed models display an inverse relation with the parameter $\eta$. Although monotonically increasing metric components are generally anticipated for physical reasons, such as ensuring stability and acceptable energy/pressure profiles, the inherent complexity of the model, particularly in the realm of modified gravity theories, can occasionally give rise to counterintuitive behaviors. Nonetheless, these non-intuitive aspects do not necessarily undermine the overall validity of the model.

Maintaining a physically viable model requires well-defined and consistent matter variables throughout the structure. Crucially, for a stable model, all the fluid terms must remain positive within the star, and these critical quantities must also stay finite at the center. As illustrated in Figure 2, the density remains positive across the entire domain, exhibiting a gradual decline from its peak value at the center towards the outer edge. Increasing the model parameter considerably amplifies the central density. Notably, the central density of the pulsar 4U 1820-30 substantially exceeds that of LMC X-4 in both interior models. In contrast with the other model, the first model generates significantly denser stellar interiors for both pulsars. Additionally, the radial pressure exhibits a pronounced decline from its peak value at the center towards the boundary, and becomes zero at the boundary, yet the tangential pressure persists with a non-zero value. As illustrated in the same Figure, the increasing anisotropy within the configuration strongly suggests that the anisotropic force is directed outward. The anisotropic fluid distribution appears to give rise to a repulsive force that leads to a more concentrated arrangement of objects, in contrast with the isotropic distribution. An increase in the value of $\eta$ leads to greater anisotropy within the interior fluid, suggesting that the developed models exhibit prolonged stability in Rastall theory compared to GR.

4.2. Gradient

A viable model of the anisotropic compact star should demonstrate that the energy density and pressure reach their peak at the center and then steadily decline towards the star’s surface. This behavior is crucial for the model’s feasibility as a representation of the actual compact star. Specific conditions, namely regularity constraints require thorough examination in the present context. They are

$${\left({\displaystyle \frac{d\rho }{dr}}\right)}_{r=0}=0={\left({\displaystyle \frac{d{p}_r}{dr}}\right)}_{r=0},{\left({\displaystyle \frac{d^2\rho }{d{r}^2}}\right)}_{r=0}<0,{\left({\displaystyle \frac{d^2{p}_r}{d{r}^2}}\right)}_{r=0}<0.$$

It is important to note that the derivatives of $p_t$ at the center is contingent upon the anisotropy (as described in Equations (21) and (37)) and may not invariably be negative. The graphical analysis in Figure 3 conclusively demonstrates that these conditions are met by both interior models, which exhibit a zero value at $r=0$ and a steadily decreasing profile moving outward. However, incorporating the plots of second derivatives in this article does not appear to be necessary.

4.3. Equation of State and Viability Check

The EoS is a crucial relationship between energy density and pressure that characterizes dense stellar objects. The EoS is essential for predicting the physical behavior of substances under different environmental conditions, as it establishes important connections between these key parameters. This enables the robust modeling and comprehensive analysis of complex systems spanning an extensive range of scales, from the microscopic to the cosmological realms. The barotropic EoS can be represented through a multitude of functional formulations, encompassing a wide range of possibilities such as linear, quadratic, polytropic, and beyond. Within the scope of the current analysis, the EoS parameters are precisely defined as

$${\omega }_r={\displaystyle \frac{p_r}{\rho }},{\omega }_t={\displaystyle \frac{p_t}{\rho }}.$$

(49)

The parameters ought to remain within a range of $[0,1]$, as any significant deviations would be viewed as an unconventional configuration. These parameters are visually depicted in Figure 4 for a couple of compact stellar objects, substantiating their feasibility.

When examining the structural characteristics of our solution, we underscore the critical energy conditions that directly relate to the energy-momentum tensor of matter. The most promising types are weak (WECs), null (NECs), strong (SECs) and dominant (DECs). Within the anisotropic fluid setup, these aspects are characterized by

$NECs:\rho +p_r\ge 0,\rho +p_t\ge 0$,

$WECs:\rho \ge 0,\rho +p_r\ge 0,\rho +p_t\ge 0$,

$DECs:\rho \pm p_r\ge 0,\rho \pm p_t\ge 0$,

$SECs:\rho +p_r\ge 0,\rho +p_t\ge 0,\rho +p_r+2p_t\ge 0$.

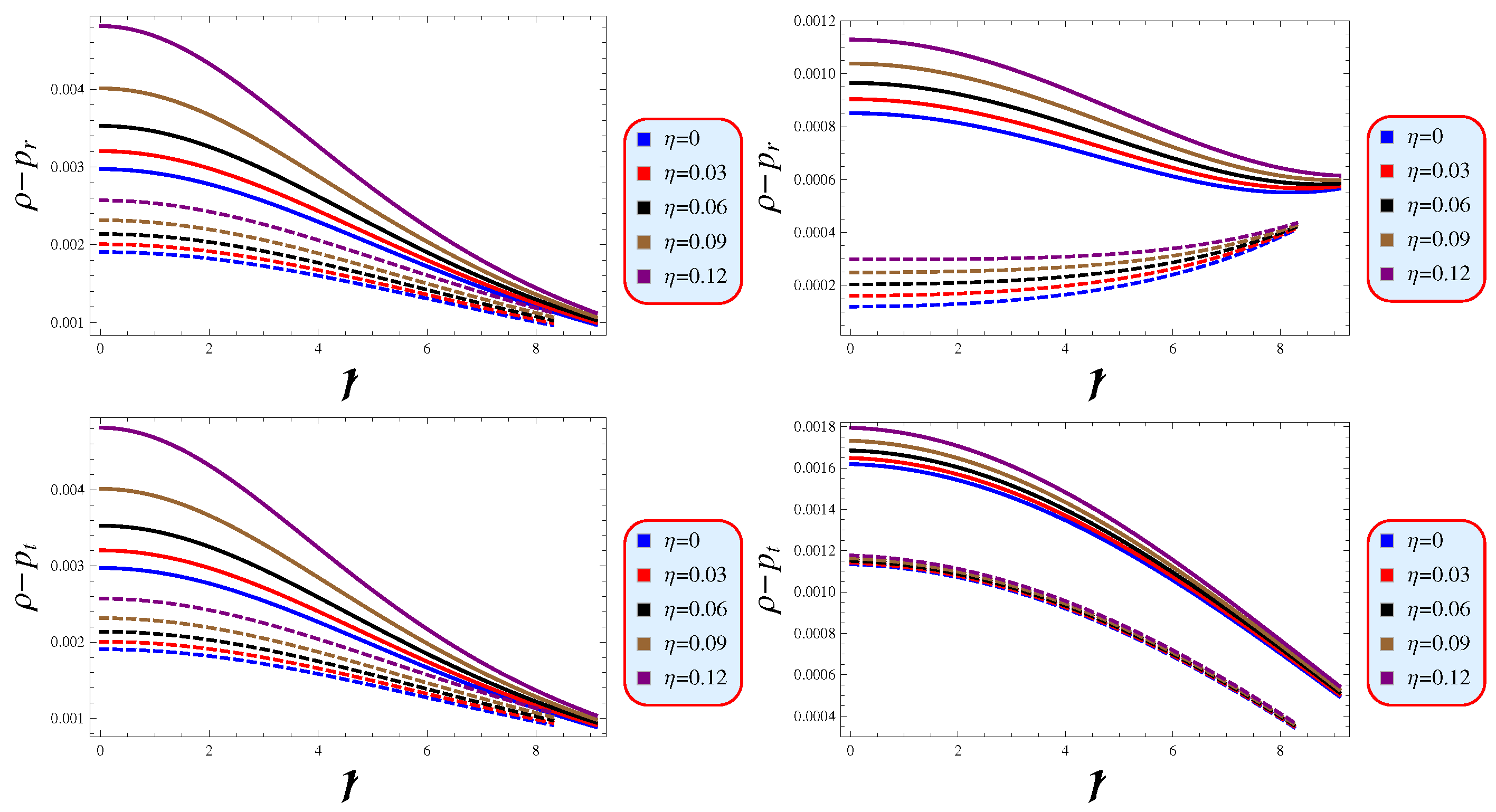
• The NECs stipulate that an observer traveling along a null geodesic will measure the energy density in their local environment to be positive. The WECs mandate that the energy density, as observed by any timelike observer, must remain positive at all times. The SECs provide compelling evidence that the observer consistently detects a positive trace of the tidal tensor [83]. The DECs steadfastly affirm that, irrespective of the observer’s viewpoint, the local energy density is perceived as inherently non-negative, and the local energy flow vector is constrained to non-spacelike behavior [84]. Figure 5 shows that the DECs are satisfied for both models, implying that ordinary matter is present within their interiors.

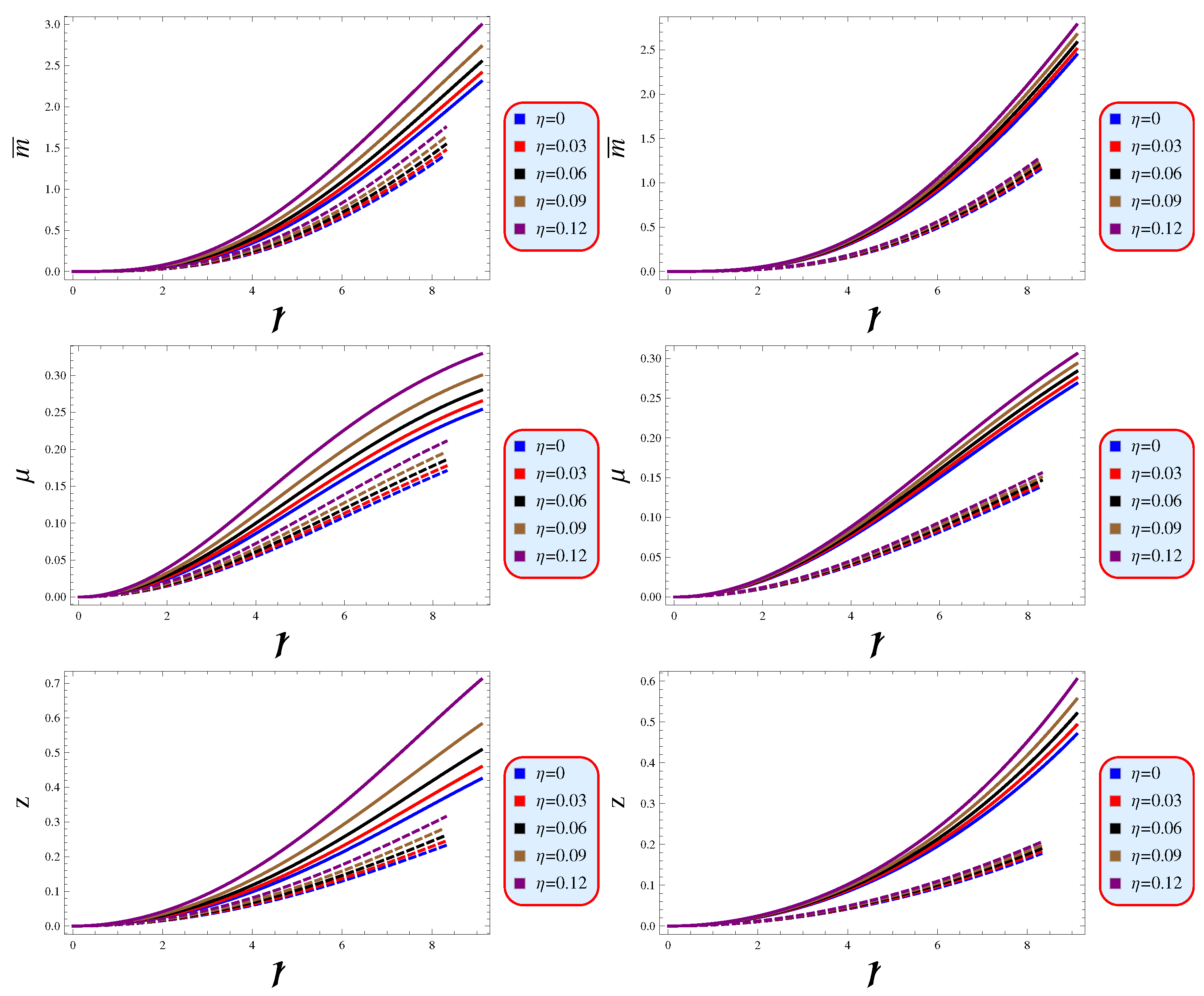
4.4. Spherical Mass Function and Its Relying Factors

The total mass enclosed within a sphere of radius r can be determined using the following expression

$$\overline{m}\left(r\right)={\displaystyle \frac{1}{2}}{\int }_0^r{r}^2\rho \left(r\right)dr⟹{\overline{m}}^{\prime }\left(r\right)={\displaystyle \frac{1}{2}}{r}^2\rho \left(r\right).$$

(50)

The specific solution can be deduced by carefully examining the complexities within the field equations or the given context. Unfortunately, in the present case, the exact solution to the aforementioned equation remains elusive. Accordingly, we solve it numerically using a suitable initial condition, i.e., $\overline{m}\left(0\right)=0$. To align with the matching conditions outlined in Equations (28)–(33) and (43)–(48), it is crucial that the mass function reaches its peak at the star’s boundary. The star’s total mass is a crucial parameter that fundamentally defines its physical characteristics.

The steady increase of the mass function throughout the stellar interior aligns seamlessly with both theoretical predictions and boundary requirements. The gravitational mass enclosed within a given radius r for relativistic compact objects is represented by the mass function, which intrinsically grows radially outward due to the increasing contribution of matter. This is a crucial aspect to consider in the modeling of such relativistic systems. This analysis compellingly shows that the function adheres to the established relativistic criteria given as

• Zero at the center, i.e., $\overline{m}\left(0\right)=0$,
• Positively increasing which implies ${\displaystyle \frac{d\overline{m}}{dr}}>0$, ∀ $r\in (0,R)$,
• Continuous at boundary, i.e., ${lim}_{r\to R_{-}}\overline{m}\left(r\right)=M$ (Schwarzschild mass).

The junction conditions at the surface ensure a seamless transition between the interior and exterior metrics, preserving the continuity of the mass function. As illustrated in Figure 6, the resulting mass distribution demonstrates a well-suited pattern. As the radius r approaches zero, the function diminishes, suggesting the absence of a concentrated mass at the origin. Conversely, as r increases, the function shows a persistently rising trend, implying that the mass becomes increasingly dispersed and concentrated as the radius expands. We investigate the mass function for diverse parameter values to pinpoint physically meaningful scenarios where the mass function attains a peak. This function further shows (i) a smooth and continuous transition in the exterior mass value at the boundary $r=R$, (ii) the continuity of the first derivative at the interface is crucial, and (iii) the positive density profile, ensuring that the derivative of the mass with respect to the radius remains greater than zero $({\displaystyle \frac{d\overline{m}}{dr}}>0)$ throughout the interior region. The distinct peak at the boundary is firmly explained by our specific application of the Darmois junction conditions. The radial derivative of the mass function at $r=R$ is intimately linked to the surface density through Equation (50), which maintains a finite and well-defined form within our physical models. Our theoretical models demonstrate mathematical coherence with the field equations and physical plausibility concerning dense matter configurations. This rigorous analysis guarantees that our models adhere to the anticipated behavior of compact stellar bodies.

The size, mass, and degree of compactness of an object profoundly influence its gravitational interactions and overall structural resilience. Celestial bodies with exceptional density, like neutron stars, exhibit extraordinary gravitational properties as a result of their remarkable compactness. Buchdahl’s seminal work [85] has demonstrated that for a stable compact structure, this dimensionless factor can be mathematically defined as $\mu \left(r\right)={\displaystyle \frac{m\left(r\right)}{r}}<0.44$. This finding is a crucial constraint that must be satisfied for the system to maintain structural stability.

Photons originating from massive celestial objects undergo redshift, shifting to longer, less energetic wavelengths. This phenomenon arises from the intense gravitational pull of these objects, which profoundly alters the passage of time. As light escapes the powerful gravitational influence, its energy diminishes, leading to the observed redshift. The mathematical formula elegantly captures this effect is

$$z=-1+{\left\{1-2\mu \left(r\right)\right\}}^{-{\displaystyle \frac{1}{2}}}.$$

(51)

The heightened compactness of the object leads to an augmented surface redshift. An analysis of the anisotropic matter distribution demonstrates that the redshift reaches remarkably high values, up to $5.211$, at the surface [12]. The profile shown in Figure 6 exhibits a well-behaved nature for both these factors. Notably, the non-conserved energy-momentum tensor inherent to Rastall gravity can yield highly significant characteristics.

4.5. Moment of Inertia

A critical feature to be examined, particularly in the study of rotational dynamics is the moment of inertia which is proportional to the square of the stellar radius. This is a measure of an object’s resistance to changes in its rotational motion, is influenced by the distribution of mass around the axis of rotation. As the total mass of an object increases, its moment of inertia typically rises, assuming the mass distribution remains consistent. However, the exact relationship can vary significantly depending on how the mass is distributed relative to the axis of rotation. Its formula is [86]

$$I={\displaystyle \frac{2}{5}}\left[\left(1+{\displaystyle \frac{M}{R}}\right)M{R}^2\right],$$

(52)

where the total mass is calculated via Equation (50). The formula for the moment of inertia in Bejger and Haensel’s work [86] has been derived within the framework of GR, specifically for strange stars. However, the empirical nature of this formula makes it somewhat versatile, as it is based on general principles of stellar structure rather than being strictly tied to the specifics of Einstein’s field equations. While the underlying gravitational theory differs, the physical principles governing the rotation and angular momentum of compact stars remain similar. The moment of inertia is a measure of how mass is distributed within the star, and this distribution is influenced by the star’s internal structure and composition rather than solely by the gravitational theory. Therefore, as long as the stellar models in Rastall theory exhibit similar structural characteristics to those in GR (e.g., spherically symmetric matter distribution, comparable density profiles), the empirical formula can serve as a reasonable approximation. It should also be clarified that our adoption of this approximation is intended as a first-order estimate to facilitate a comparative analysis between GR and the modified gravity scenario, rather than a definitive exact computation. This formula is an empirical approximation based on numerical integrations of slowly rotating neutron star models in GR, where the compactness parameter plays a central role in capturing deviations from the classical rigid-body moment of inertia. In our study, we employ this form because the exterior spacetime in both GR and Rastall-Rainbow gravity is matched to the vacuum Schwarzschild metric at the stellar boundary, ensuring that the total mass and radius are consistently defined and observationally constrained in a manner agnostic to the interior theory specifics.

An acceptable behavior of this factor involves its direct relationship with the total mass. This is seen to increase as the mass M increases and depicted in Figure 7, indicating the significance of our models. For rotating stars, the increase in moment of inertia against the parameter $\eta$ affects the star’s rotational dynamics, potentially influencing phenomena like gravitational wave emission or the stability of rapidly rotating stars. Further, the variation in moment of inertia due to the parameter $\eta$ can be used to interpret astrophysical observations, such as those related to neutron star mergers or pulsar timing. This relationship also helps to constrain the EoS of neutron stars.

5. Stability Analysis

Understanding the stability of computed stellar solutions is critical for studying compact celestial bodies, as it validates the physical soundness of these stellar entities. This investigation examines the stability of compact stars to understand their response to disturbances. Researchers can determine the conditions that may lead to catastrophic changes in these stellar objects or maintain their stability using various mathematical techniques. The following subsections will explore several of these analytical approaches.

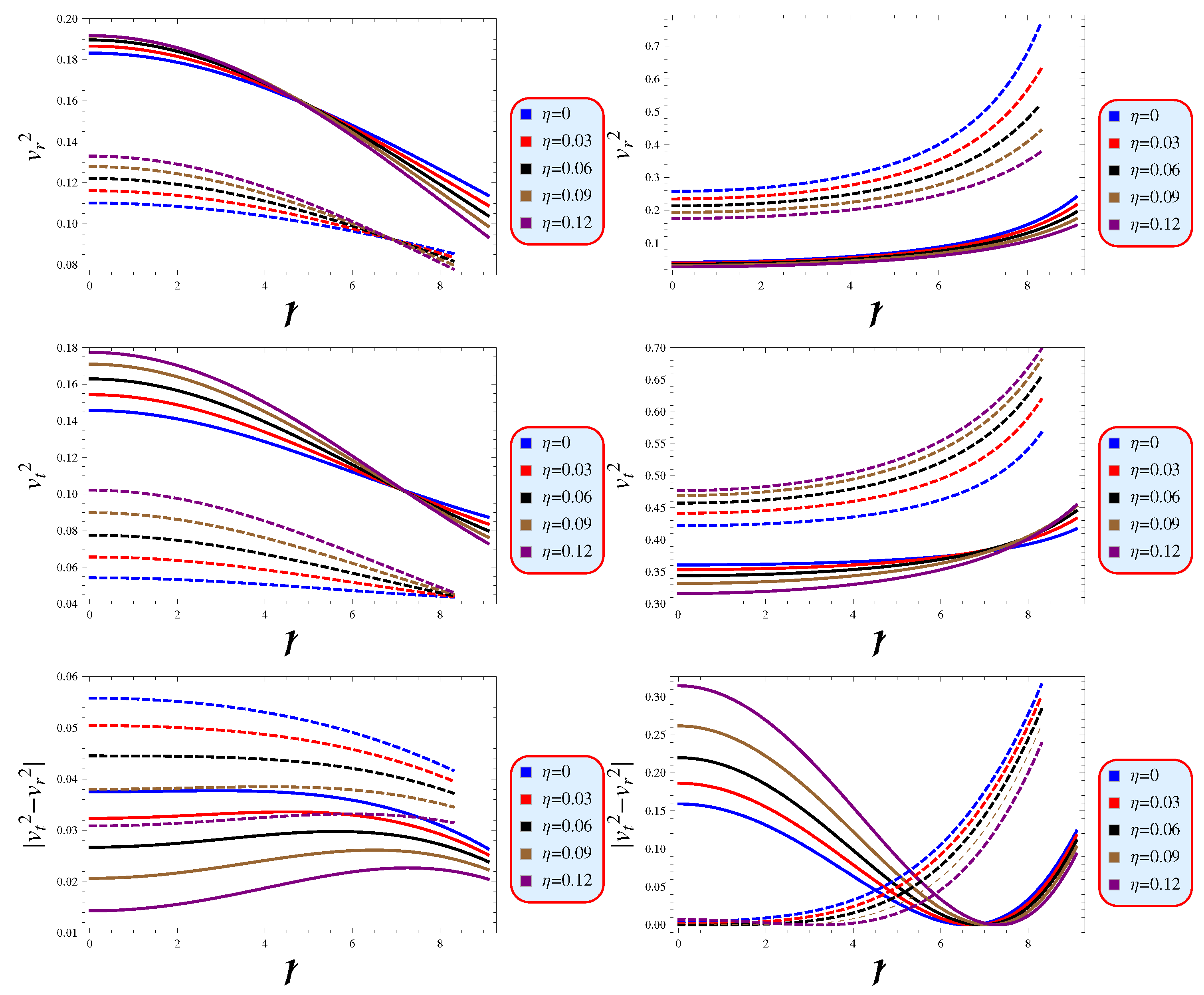
5.1. Sound Speed

To ensure the physical stability of a star with the anisotropic fluid, the radial and transverse speeds of sound within the matter distribution must be bounded to not exceed the speed of light, a fundamental requirement known as the causality condition [87]. Mathematically, they are

$$0\le v_r^2={\displaystyle \frac{d{p}_r}{d\rho }}\le 1,0\le v_t^2={\displaystyle \frac{d{p}_t}{d\rho }}\le 1.$$

As depicted in Figure 8, our models convincingly show that the propagation speed of sound waves in both directions is less than unity, signifying their inherent stability.

Analyzing the cracking phenomenon is an effective way to study the stability of anisotropic configurations. The fundamental premise is that the fluid components exhibit accelerated relative motion on either side of the cracking point. Cracking is a crucial technique to examine the behavior of a fluid distribution as it departs from equilibrium. The concept of cracking encompasses the tendency of a configuration to divide at a specific point within its distribution, without collapsing or expanding. Herrera [88] pioneered the investigation of the cracking concept for anisotropic matter distributions in self-gravitating compact objects. His requirement for viable stellar models is that the sound speeds must adhere to causality constraints. Building upon this, Abreu et al. [87] revisited the concept of Herrera’s cracking and devised a range to pinpoint potentially stable anisotropic compact objects. Their insightful analysis revealed that for a model to be potentially stable, it must satisfy the following

$$0\le |v_t^2-v_r^2|\le 1.$$

This condition is graphically depicted in Figure 8, and our formulated models are found to satisfy the stability criterion across the entire range of Rastall parameter. Consequently, these models exhibit unwavering stability under both the approaches, irrespective of the parametric values.

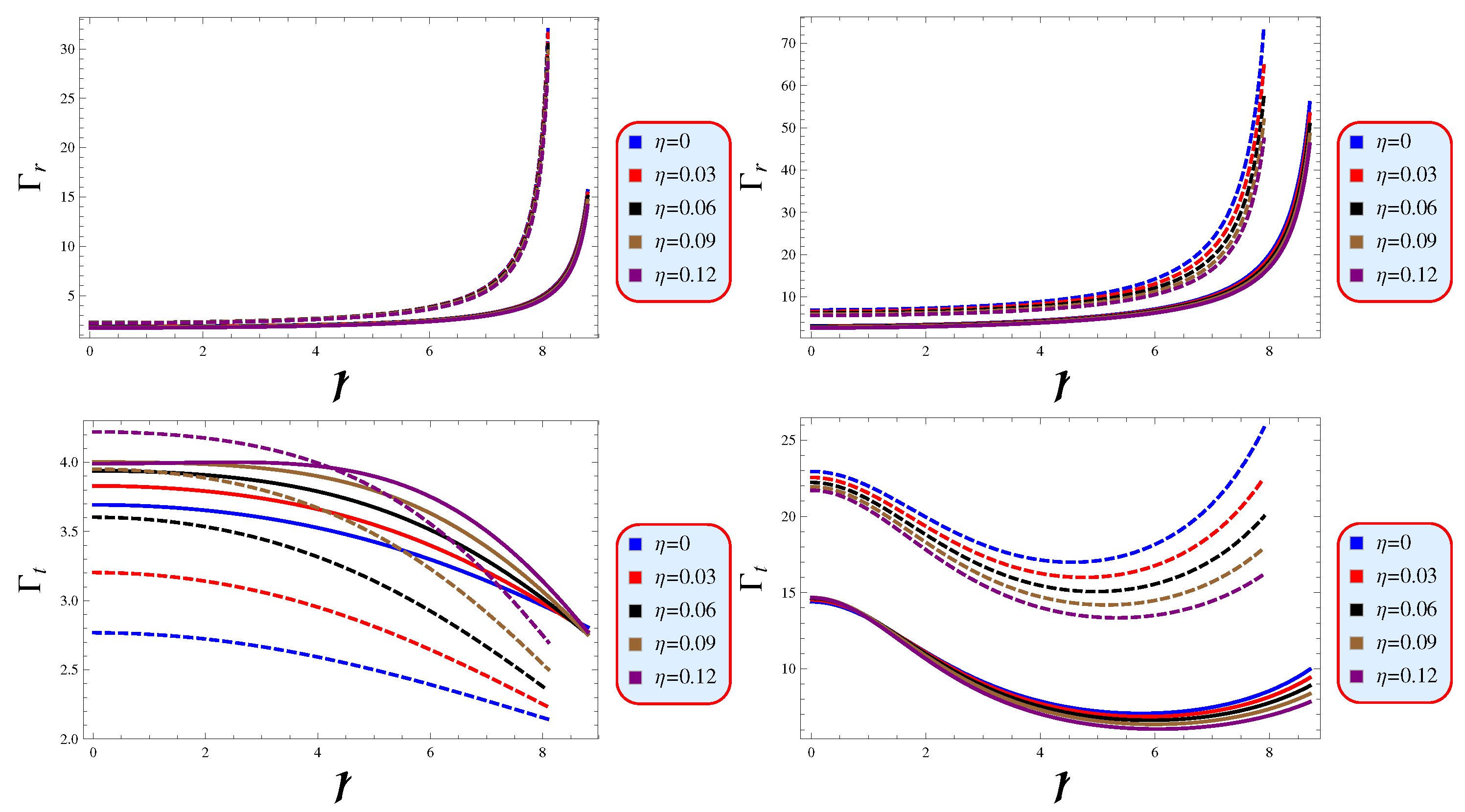
5.2. Adiabatic Index

The adiabatic index is a key thermodynamic property that shows how substances act when temperature and pressure change without heat exchange. It connects specific heat at constant pressure and volume, giving insights into energy conversion and gas compressibility which ultimately affects sound travel. The index reflects the complex ties between molecular degrees of freedom and energy conservation in adiabatic processes, making it a vital property with wide-ranging effects. This is described in the following way

$${\Gamma }_r={\displaystyle \frac{\rho +p_r}{p_r}}{\displaystyle \frac{d{p}_r}{d\rho }},{\Gamma }_t={\displaystyle \frac{\rho +p_t}{p_t}}{\displaystyle \frac{d{p}_t}{d\rho }}.$$

The proposed models demonstrate an encouraging pattern for ${\Gamma }_r$ and ${\Gamma }_t$ (which must be greater than 4/3 for stability [89]) in Figure 9, indicating the stability of both models. This underscores the advantages of the current theory over GR for achieving stable configurations.

It should be mentioned that our current analysis focuses on static equilibrium configurations and the adiabatic index as a stability criterion, as is standard in studies of compact stars. However, we contend that this focus is justified given the complexity of the Rastall-Rainbow framework, where the non-conservation of the energy-momentum tensor introduces additional degrees of freedom compared to GR. The perturbations beyond the adiabatic index, such as radial oscillation modes or non-radial perturbations, could be explored in future work by adapting techniques like those used in GR for polytropic models [15,16]. While such an analysis is beyond the scope of the current paper due to the analytical complexity of the modified field equations, our models satisfy essential stability criteria, such as positive energy density, vanishing radial pressure at the boundary, and well-behaved metric functions. These ensure that the solutions are physically viable and provide a stable foundation for further dynamical studies.

5.3. Comparative Analysis with General Relativity and Other Modified Theories

We acknowledge that, in GR (equivalent to $\eta =0$ in our models), the mass-radius relations for the pulsars 4U 1820-30 and LMC X-4 would adhere strictly to the Tolman-Oppenheimer-Volkoff (TOV) equation without non-conservation terms. In our Rastall-modified setup, the effective TOV-like equilibrium arises from the altered field Equations (14)–(16), incorporating $\eta$-dependent corrections that allow for higher central densities and enhanced anisotropy for $\eta >0$. For instance, with $\eta =0.12$, the central density for 4U 1820-30 increases by approximately 15–20% compared to the GR limit ($\eta$ = 1), potentially supporting more massive configurations before instability sets in. Similarly, the compactness parameter shows subtle enhancements (up to 5–10% for the considered values), which we quantify using the observational data in Table 1: for 4U 1820-30, $M/R\approx 0.256$ in GR versus 0.268–0.275 in our models for $\eta =$ 0.06–0.12, implying stronger gravitational redshifts. These differences are further highlighted in the stability analysis, where the adiabatic index exceeds 4/3 more robustly in the Rastall case, and the cracking instability threshold remains satisfied over a broader parameter range. Such quantitative metrics demonstrate that, while structurally similar under boundary constraints, our models predict distinct astrophysical signatures, e.g., altered mass-radius curves that could be testable against future pulsar observations, underscoring the non-trivial impact of the non-conserved framework over standard GR.

Studies such as those by Astashenok et al. [90] have explored neutron star models in $f\left(R\right)$ gravity, particularly using the form $f\left(R\right)=R+\alpha R^2$, where $\alpha$ is a coupling constant. Unlike our Rastall-Rainbow framework, $f\left(R\right)$ gravity preserves the conservation of the energy-momentum tensor, and the additional curvature terms arise from the modified action rather than a direct matter-geometry coupling. They found that $f\left(R\right)$ models can increase the maximum mass of neutron stars compared to GR, allowing for configurations that support observed high-mass pulsars (e.g., PSR J0348+0432). Our Rastall-Rainbow solutions similarly predict enhanced stability for compact stars due to the anisotropic factor, which introduces a repulsive force when tangential pressure exceeds radial pressure. However, the mechanism differs: in $f\left(R\right)$ gravity, the increased mass limit arises from modified gravitational dynamics due to higher-order curvature terms, whereas in our models, the non-conservation parameter $\eta$ modifies the effective energy-momentum tensor, mimicking an additional pressure component that enhances stability. Graphically, our models show that increasing $\eta$ amplifies central density and anisotropy, a feature analogous to the increased compactness in $f\left(R\right)$ models but driven by non-conservation rather than curvature modifications. This distinction highlights the unique role of non-conservation in our framework, which aligns with cosmological particle creation processes and offers a complementary perspective to $f\left(R\right)$ gravity’s curvature-driven effects.

Horbatsch and Burgess [91] and Doneva et al. [92] have investigated neutron star solutions in scalar-tensor gravity, particularly in the context of Brans-Dicke theory and its generalizations. In these models, the scalar field can lead to spontaneous scalarization, a phenomenon where the scalar field develops a non-trivial configuration inside the star, significantly affecting its structure and stability. For instance, Doneva and his colleagues demonstrated that scalar-tensor theories can predict neutron stars with higher maximum masses and distinct oscillation modes compared to GR, particularly for certain values of the scalar field coupling parameter. In contrast, our Rastall-Rainbow framework does not introduce a dynamical scalar field but instead modifies the field equations through the non-conservation law and Rainbow functions. The Rastall parameter $\eta$ in our models plays a role analogous to the scalar field coupling by altering the effective stress-energy tensor, which influences the pressure and density profiles. However, unlike scalar-tensor theories, where the scalar field can lead to non-perturbative effects like scalarization, our models rely on the static, spherically symmetric geometry and the anisotropic fluid to capture the internal dynamics of compact stars.

Another key point of comparison is the treatment of observational constraints. In $f\left(R\right)$ gravity, studies like those by Astashenok et al. [93] have shown that neutron star models must be carefully tuned to satisfy constraints from gravitational wave observations (e.g., GW170817), which limit deviations from GR in the strong-field regime. Similarly, scalar-tensor theories are constrained by binary pulsar timing and gravitational wave data, as discussed by Freire et al. [94], which require the scalar field coupling to be small to avoid significant deviations from GR predictions. Our Rastall-Rainbow models are tested against observational data from pulsars 4U 1820-30 and LMC X-4, ensuring that the metric functions and fluid variables remain physically viable. The Rastall parameter $\eta$ is varied within a particular range to explore its impact on the stellar structure, and our results show that small deviations from GR produce stable configurations that align with observed pulsar properties. Unlike $f\left(R\right)$ and scalar-tensor theories, which face stringent constraints from weak-field tests (e.g., solar system observations), Rastall gravity’s non-conservation is more pronounced in high-curvature regimes like stellar cores, making it particularly suited for studying compact objects. This feature allows our models to mimic dark energy-like effects in the stellar core, where the non-conservation parameter introduces an effective negative pressure that enhances stability, a phenomenon not directly replicated in $f\left(R\right)$ or scalar-tensor frameworks.

6. Conclusions

This research establishes analytical solutions to the gravitational field equations describing anisotropic spherically symmetric configurations within the Rastall-Rainbow theoretical framework. The study began by assuming a static spherical spacetime which facilitates the derivation of modified equations of motion governing the dynamics of the anisotropic interior. In order to obtain a non-singular solution, we were compelled to impose a constraint owing to the existence of five unknown variables: metric functions, two pressures and energy density. These variables were systematically deduced from a rigorous set of four foundational equations, comprising three non-zero components of the gravitational field equations and the condition for anisotropy. By employing a strategic approach, we have considered two distinct, singularity-free values for the radial component of the metric. This has culminated in the formulation of two differential equations, which are expressed up to the second order in terms of the temporal coefficient. Our analysis has then incorporated specialized pressure anisotropies to support the solvability of these equations. Crucially, these anisotropies must diminish at the core and grow as the radial distance increases. This mathematical exploration led to the development of two distinct compact interior models. We subsequently utilized the Schwarzschild metric at the boundary $r=R$ to determine the relevant constants pertaining to the metric components.

Investigating the fundamental properties of our models involves carefully assessing the consistency of matter variables, energy constraints, and the system’s stability through multiple key analytical approaches. These rigorous examinations are essential for validating the integrity and viability of our theoretical framework. Our analysis has focused on a specific range of $\eta =\{0,0.03,0.06,0.09,0.12\}$, along with observational data from two pulsars, 4U 1820-30 and LMC X-4. In the following, we provide a complete summary of the key aspects of our investigation.

• The metric functions have been demonstrated to be well-defined, positive and regular throughout the internal region. Additionally, they displaye a constant value at the center and an increasing trend towards the outer edge, which allows for the construction of a dense compact models (Figure 1).
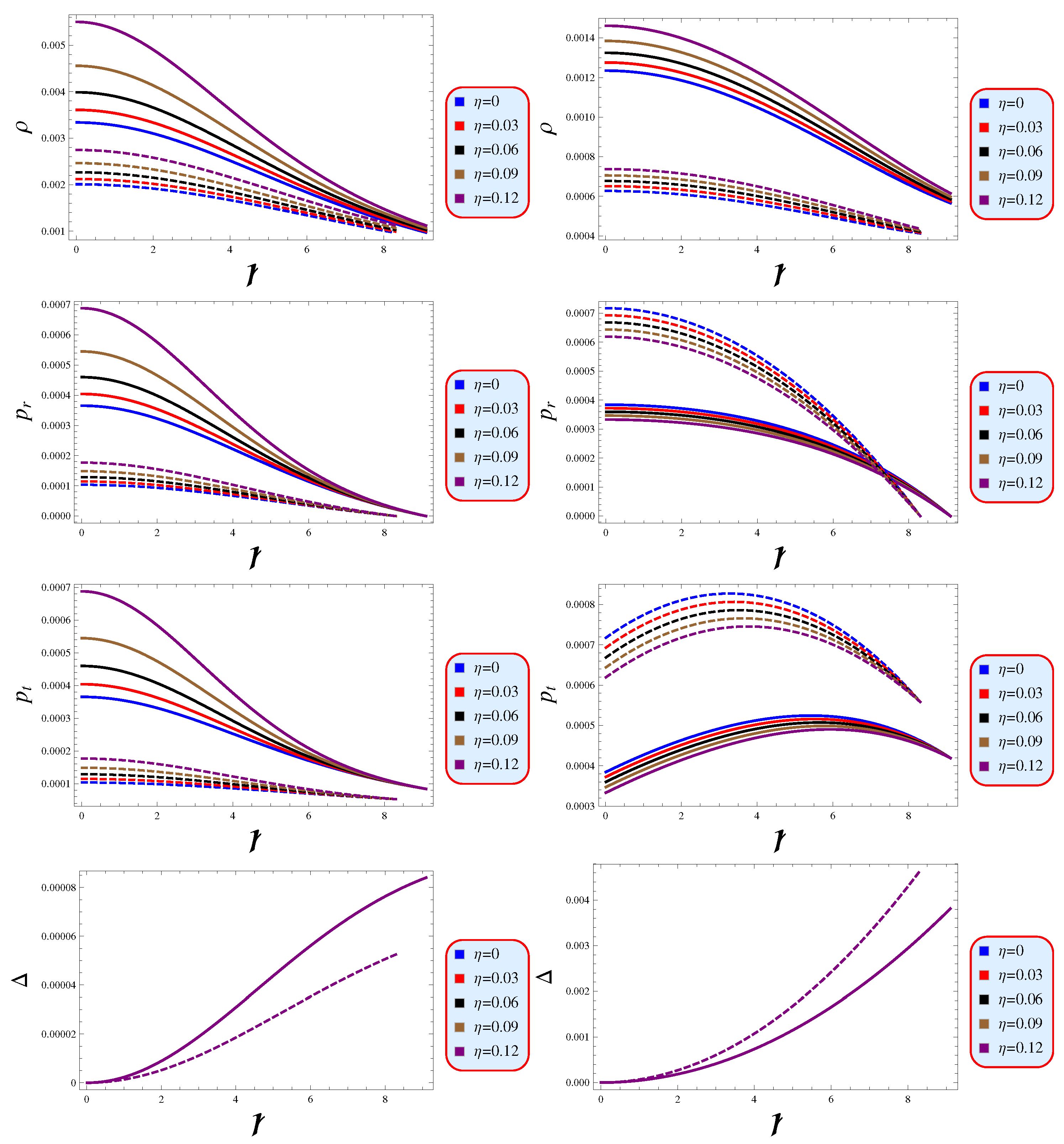
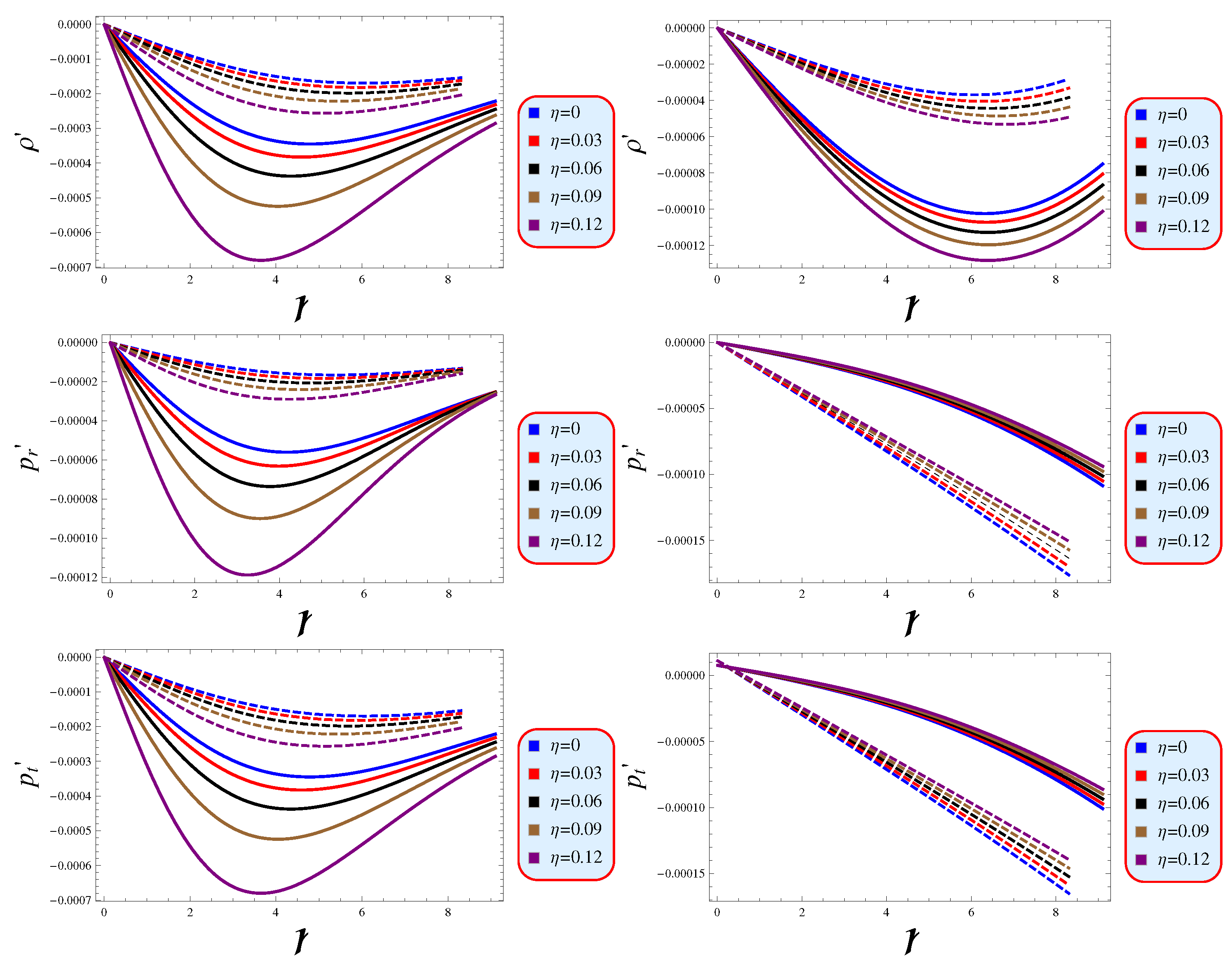
• The compact stellar object must demonstrate a positive energy density profile that gradually decreases from the densely concentrated center towards the surface. The radial pressure exhibits a consistently declining trend as one moves closer to the surface, as demonstrated and confirmed in Figure 2. The positive anisotropy observed in this Figure suggests that the anisotropic force acts in an outward direction, thereby contributing to the modeling of a stable configuration. Additionally, the regularity conditions have been verified (Figure 3).
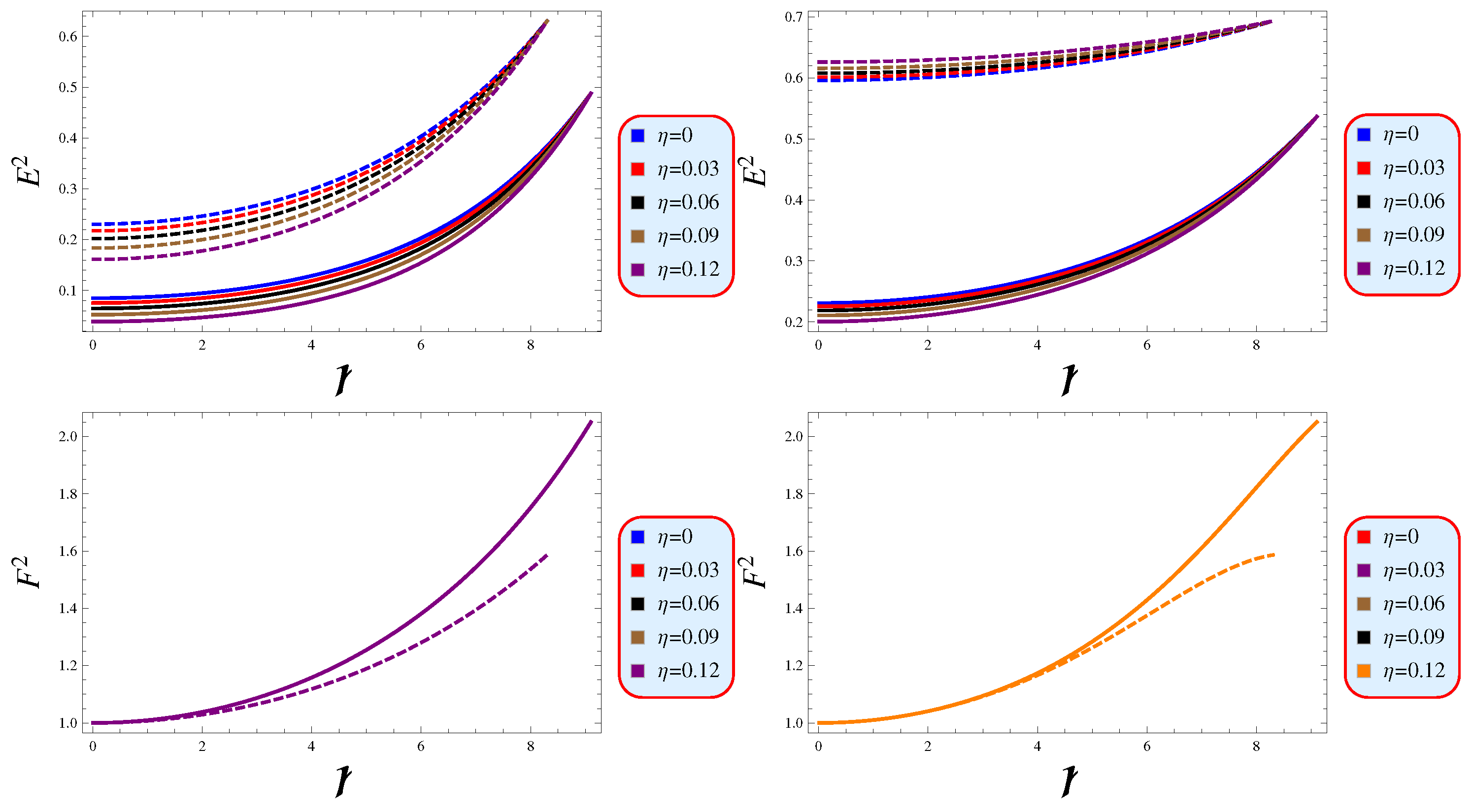
• The EoS is a pivotal component in comprehensively evaluating the intrinsic characteristics of any stellar structure. This direct linear correlation between pressure and density, as illustrated in Figure 4, is essential for developing a profound understanding of these celestial bodies. Any viable physical model must strictly adhere to the prescribed bounds based on its pressures and density, which are claimed as energy conditions. We have carefully examined and determined that our models fully satisfy these requirements (Figure 5).
• Figure 6 shows that the mass function and compactness increase consistently as the radius grows, ultimately attaining their peak values at the surface. Additionally, the redshift reaches its maximum value at the surface and decreases towards the center. The rotational dynamics is also discussed in Figure 7.
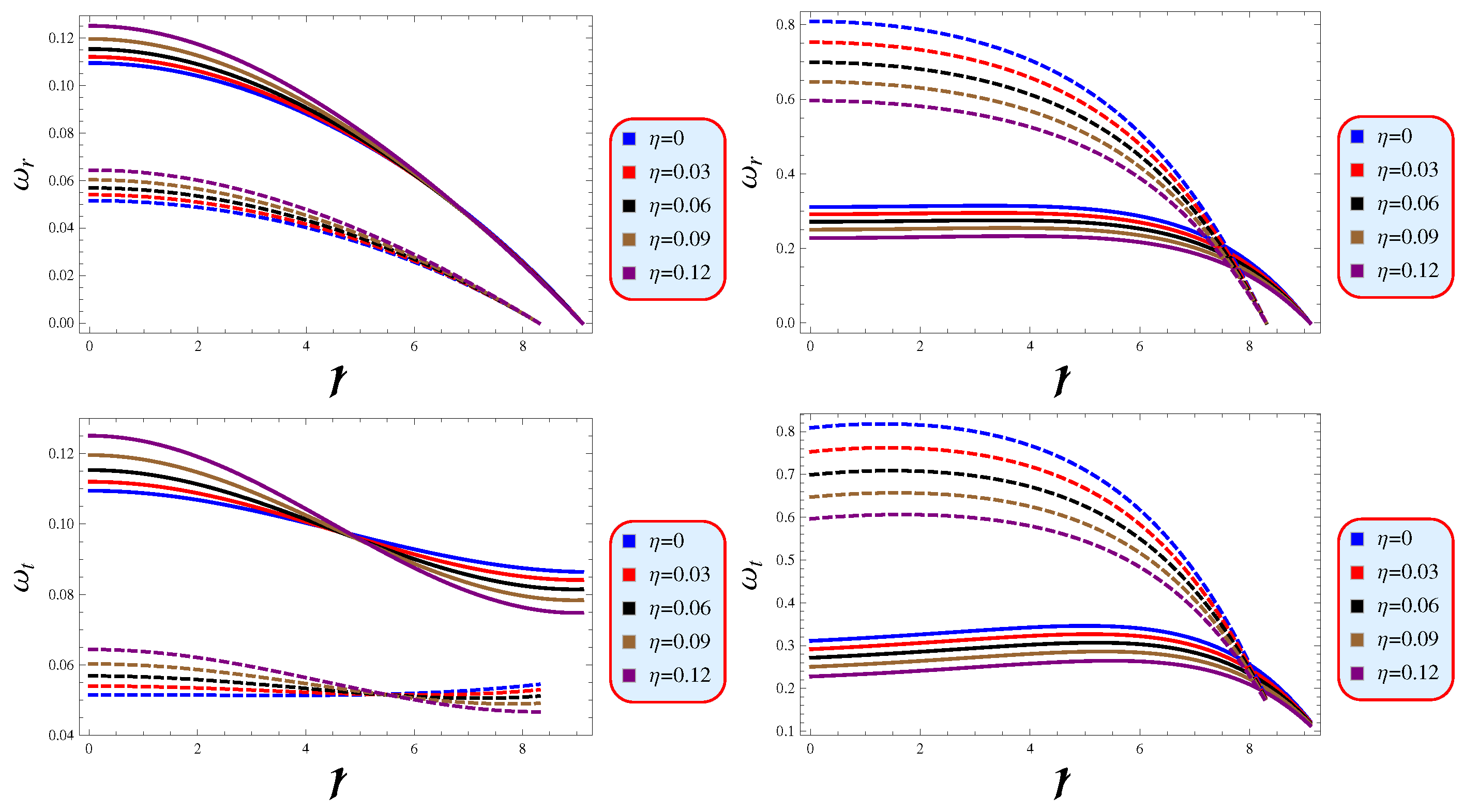
• Our models successfully satisfied the causality and cracking conditions, as evidenced by both the individual sound speeds and their absolute difference being less than 1 (Figure 8). Additionally, the adiabatic index, as depicted in Figure 9, demonstrates that the tangential and radial components exceed the critical value of 4/3, thereby providing a robust verification of the stability of our proposed models.
• In Rastall gravity, the non-conservation of the energy-momentum tensor implies that matter and geometry are coupled non-minimally, allowing energy exchange between the matter fields and the gravitational field. In cosmological contexts, this non-conservation has been shown to mimic the effects of dark energy by driving accelerated expansion. In stellar cores, where densities and curvature are extremely high, this non-conservation can manifest as an effective modification to the pressure and density profiles, analogous to an additional energy component. For instance, the Rastall parameter influences the fluid variables in our models, leading to enhanced anisotropy and altered stability properties compared to GR. This can be interpreted as a dark energy-like effect, where the non-conserved energy-momentum contributes to a repulsive force, potentially stabilizing the star against gravitational collapse.
• When the parameter $\eta$ is set to zero, our findings converge with those of GR.

This study underscores the profound implications of Rastall-Rainbow gravity in modeling anisotropic compact stars, demonstrating its capacity to yield physically viable solutions that align with observational constraints. The significance of our models, validated through geometric consistency, energy conditions, and stability criteria, highlights the theory’s potential to address unresolved questions in high-density astrophysical regimes. However, the interplay of anisotropy, non-conservation, and rainbow deformation invites deeper exploration—particularly in dynamical settings, multi-messenger astrophysics, or quantum gravitational corrections. Beyond the specific results for pulsars 4U 1820-30 and LMC X-4, which demonstrate physical viability and stability under constrained Rastall parameters, these findings have significant implications for astrophysical phenomena such as neutron star mergers. Neutron star mergers involve extreme gravitational and matter interactions, where anisotropic effects and deviations from GR could manifest prominently. The anisotropic fluid models developed in our work suggest that the non-minimal coupling between matter and geometry, as proposed by Rastall gravity, may influence the internal structure of merging neutron stars. Specifically, the increased stability induced by anisotropic pressure in our models could lead to more compact configurations, potentially affecting the merger dynamics, such as the threshold mass for prompt black hole formation or the emission profiles of gravitational waves. By providing a framework where the Rastall parameter modulates the degree of non-conservation, our models allow for testable predictions about how deviations from GR might alter the EoS during mergers, which could be probed through future observations by gravitational wave detectors like LIGO-Virgo-KAGRA. This connection underscores the relevance of our findings to multi-messenger astronomy, where combined electromagnetic and gravitational wave signals from neutron star mergers can constrain modified gravity theories.

Furthermore, our results carry implications for probing the interface between classical gravity and quantum gravity. The Rastall-Rainbow framework, by incorporating energy-dependent modifications to spacetime geometry, offers a semi-classical approach that bridges GR with potential quantum gravitational effects. While our study focuses on macroscopic stellar structures, the non-conserved nature of the energy-momentum tensor in Rastall gravity aligns with theoretical efforts to model particle creation and quantum effects in curved spacetimes. These effects are particularly relevant in high-energy regimes, such as those near compact objects or during the early universe. Our models, which successfully reproduce physically viable stellar configurations, suggest that Rastall-Rainbow gravity could serve as a testing ground for quantum gravity-inspired modifications. For instance, the dependence of our solutions on the Rainbow functions, even when simplified to unity for analytical tractability, hints at the potential to incorporate energy-scale variations that mimic quantum gravitational corrections. Future work could extend this framework to rotating configurations, inflationary cosmology, or hybrid star scenarios, where the synergy of modified gravity and exotic matter may unveil new phenomena. Such advancements would not only refine our understanding of compact objects but also test the limits of gravitational theories beyond GR, paving the way for ground-breaking discoveries in fundamental physics.