Mass Loss in Be Stars: News from Two Fronts
Abstract
1. Introduction
1.1. Defining the Object: Be Stars
1.2. Mass Loss in Be Stars
2. Mass Loss Front
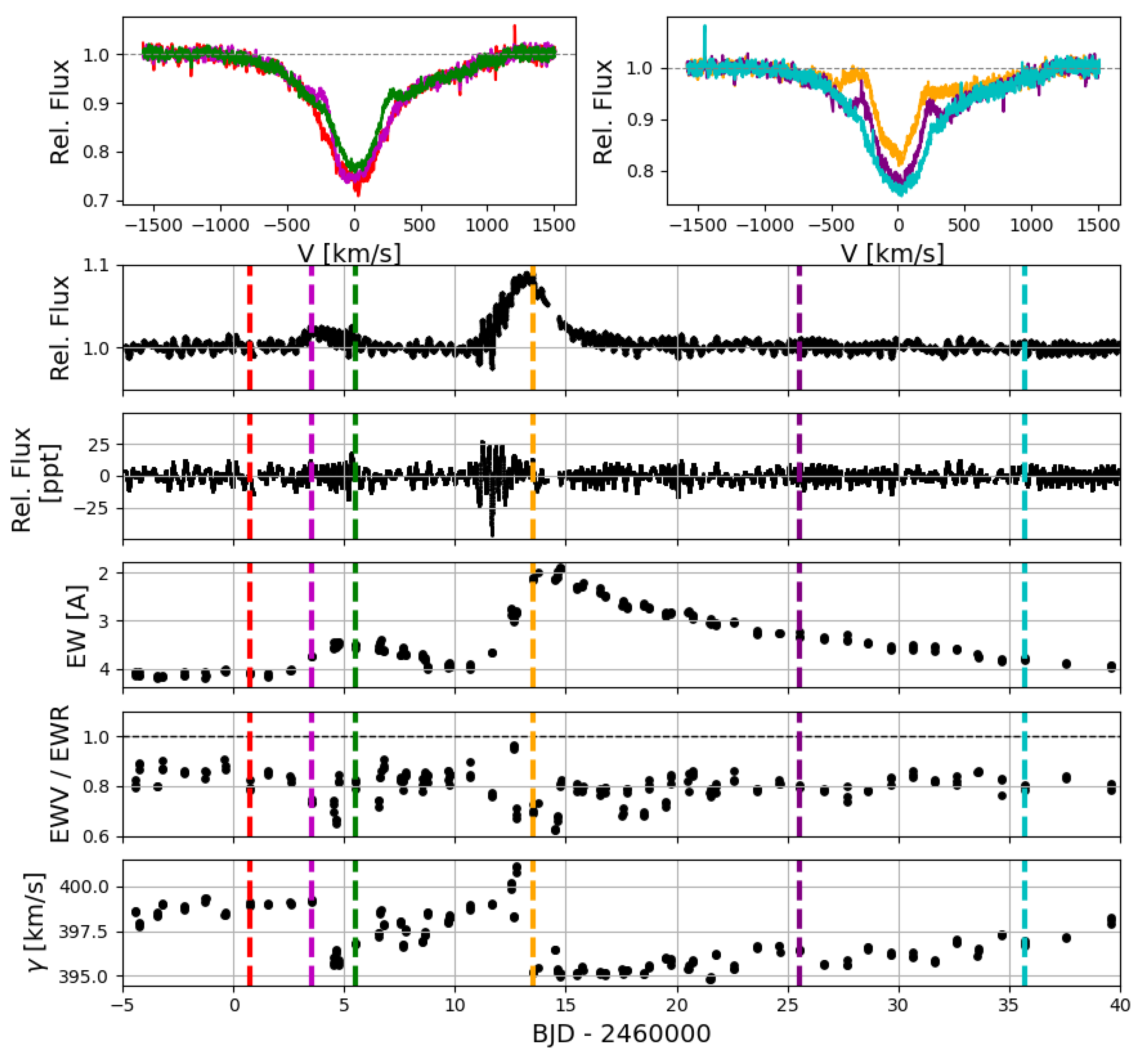
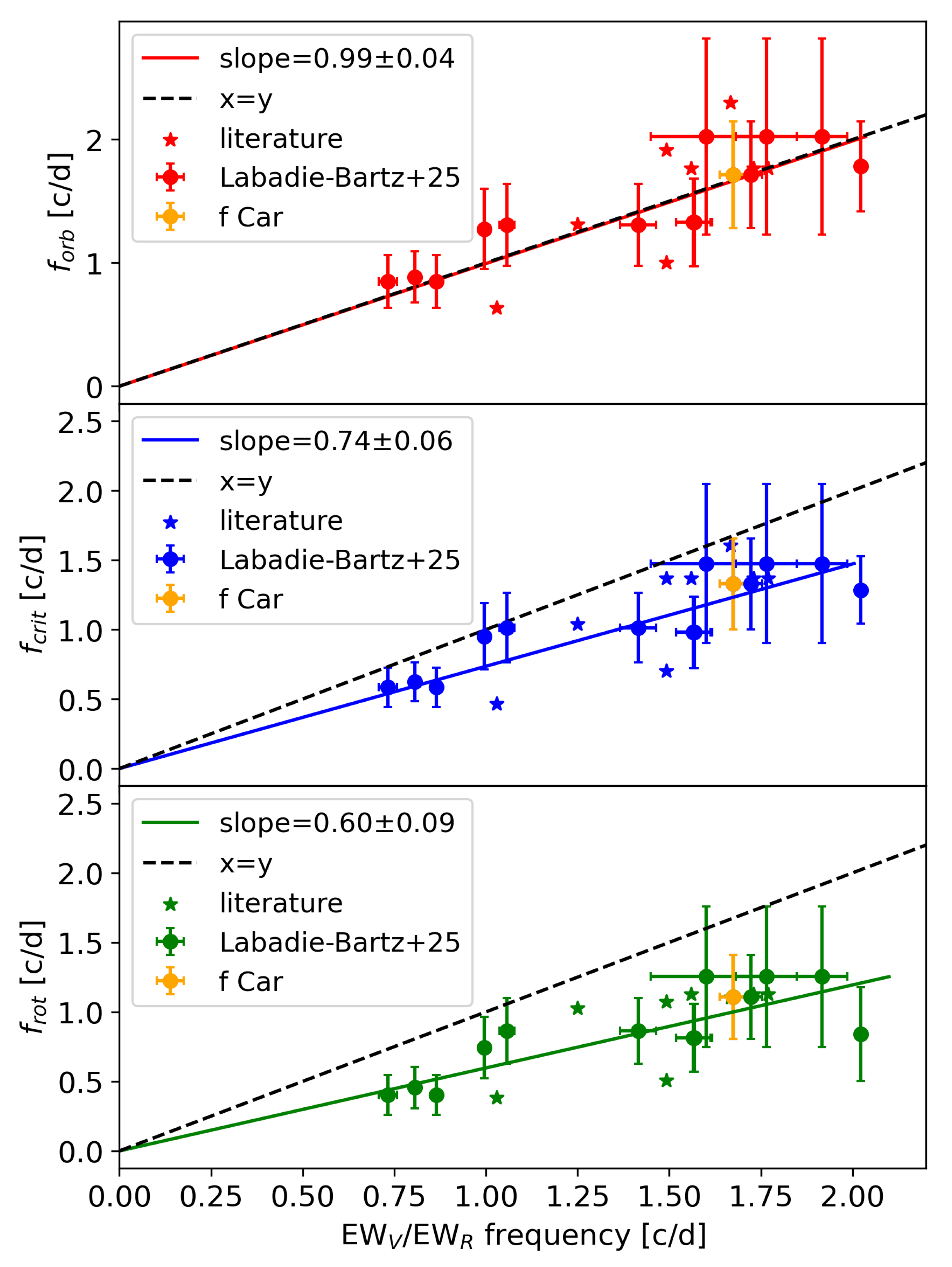
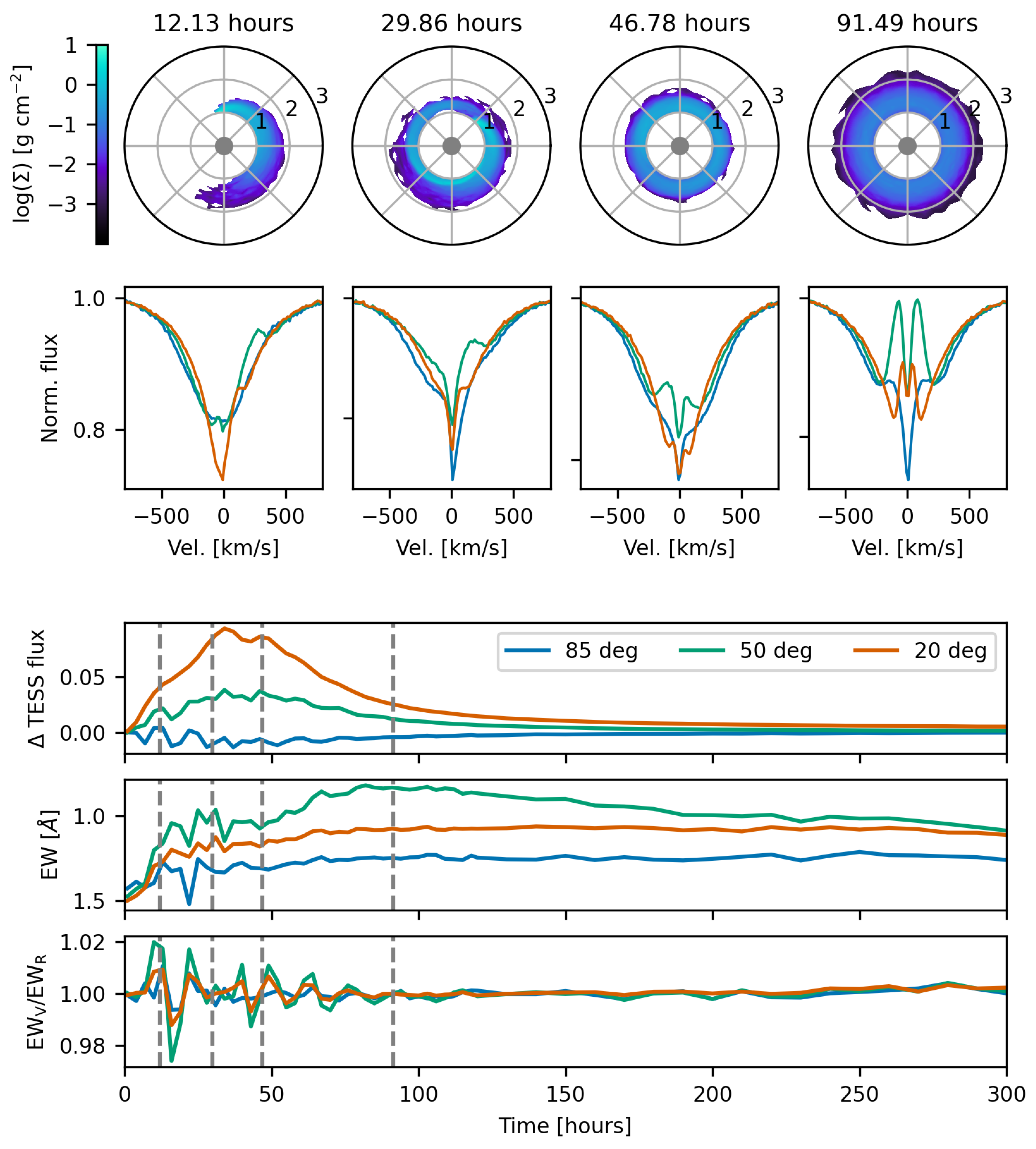
Recent Modeling Advancements
3. Disk Front
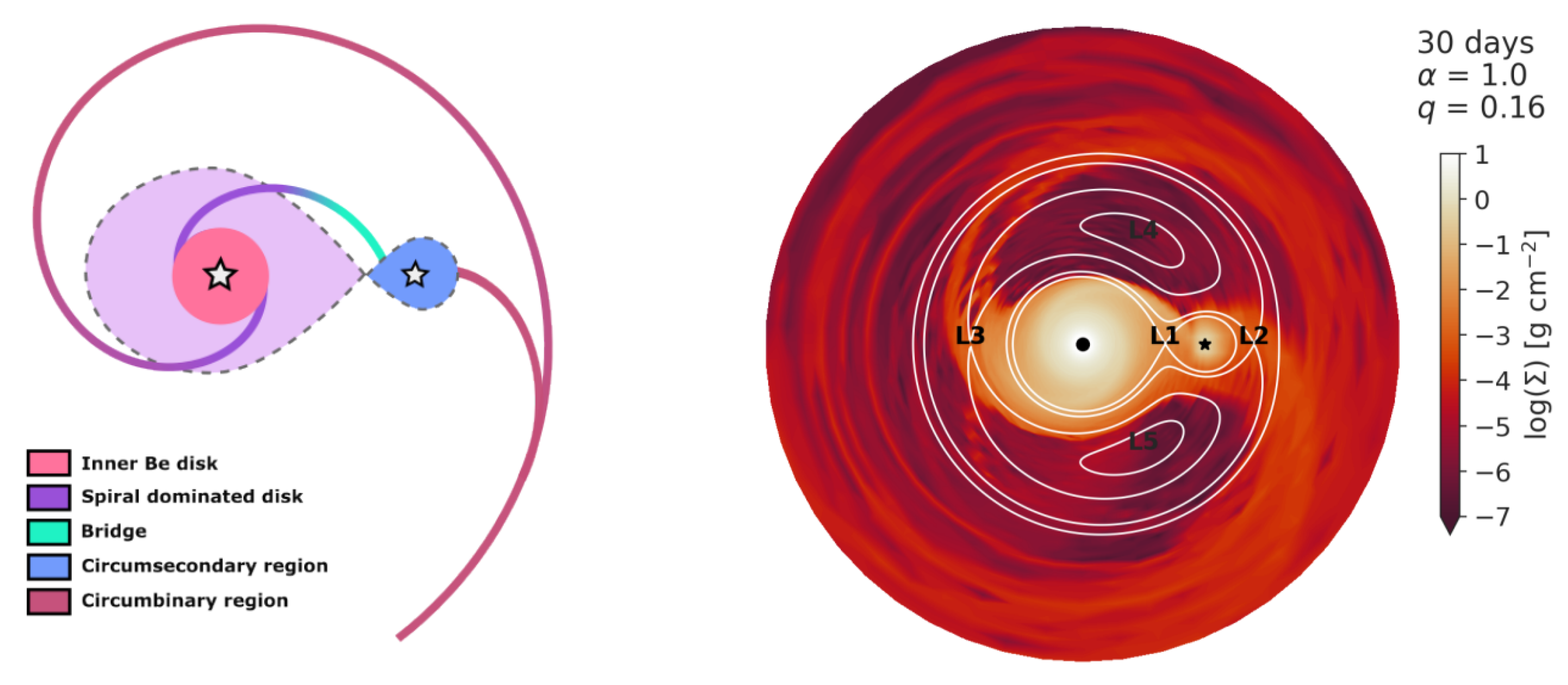
- 1.
- Inner Be disk—This is the region closest to the Be star, and is the least perturbed by the presence of the secondary. It behaves much like the classical VDD, with near-axisymmetry and quasi-Keplerian rotation [70]. Nevertheless, the tidal torque from the companion induces the so-called accumulation effect, where material piles up in the inner disk due to the inhibition of outward angular momentum transport. This leads to a shallower surface density profile. Observationally, this results in enhanced V-band flux, different He and Fe emission line strengths, and increased polarization levels.
- 2.
- Spiral-dominated disk—Beyond a few stellar radii, the companion’s gravitational potential excites large-scale two-armed spiral density waves. These structures are dynamically active, produce significant radial velocity fluctuations, and break axisymmetry. The spiral arms arise from orbital perturbations; they are tightly wound in high-viscosity disks and more open in low-viscosity systems [67]. This region can cause cyclic V/R variations in the Balmer lines and changes in the line profiles. A prime example is the locked V/R variations found in Aqr [71] and several other Be stars [72].
- 3.
- Bridge—As one of the spiral arms extends into the Roche lobe of the secondary, a stream of material is channeled directly towards the companion. This narrow elongated structure—dubbed the bridge—acts as a conduit for angular momentum and mass exchange between the Be disk and the secondary’s immediate environment. Its presence may lead to transient emission components or asymmetries in spectral lines.
- 4.
- Circumsecondary region—Material entering the companion’s Roche lobe is not instantly removed, as in previous simulations; instead, it accumulates and circularizes into a rotationally supported structure, effectively forming a small circumsecondary disk. The presence of this region is critical for understanding low-level accretion phenomena, including the possibility of faint X-ray signatures, and may offer indirect observational clues about hidden companions. Emission from this structure has been already detected in a handful of objects, such as HD 55606 [73], as well as by spectro-interferometry for HR 2142 [74].
- 5.
- Circumbinary region—Not all of the material entering the Roche lobe is accreted; a significant portion exits the lobe behind the companion, joining the trailing spiral arm and forming a large-scale one-armed spiral that wraps around the entire binary system. This circumbinary spiral is dynamically decoupled from the inner disk and constitutes the only part of the ejected matter that ultimately escapes the gravitational influence of the system. It may manifest as infrared or radio excess (see, e.g., [75]).
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | V/R stands for the ratio between the blue- and red-shifted peaks in a two-peaked line profile. |
| 2 | In the Roche approximation [57], the critical radius is defined as the maximum equatorial radius of a stable fast-spinning star, and is 50% larger than the polar radius. |
References
- Strafella, F.; Pezzuto, S.; Corciulo, G.G.; Bianchini, A.; Vittone, A.A. Stellar Winds in Herbig Ae/Be Stars. Astrophys. J. 1998, 505, 299–314. [Google Scholar] [CrossRef]
- Kudritzki, R.P.; Puls, J. Winds from Hot Stars. Annu. Rev. Astron. Astrophys. 2000, 38, 613–666. [Google Scholar] [CrossRef]
- Castor, J.I.; Abbott, D.C.; Klein, R.I. Radiation-driven winds in Of stars. Astrophys. J. 1975, 195, 157–174. [Google Scholar] [CrossRef]
- Pauldrach, A.; Puls, J.; Kudritzki, R.P. Radiation-driven winds of hot luminous stars. Improvements of the theory and first results. Astron. Astrophys. 1986, 164, 86–100. [Google Scholar]
- Vink, J.; Bocchino, F.; Damiani, F.; Kaastra, J.S. An unresolved X-ray source inside the supernova remnant RCW 86. Astron. Astrophys. 2000, 362, 711–714. [Google Scholar]
- Vink, J.S.; de Koter, A.; Lamers, H.J.G.L.M. Mass-loss predictions for O and B stars as a function of metallicity. Astron. Astrophys. 2001, 369, 574–588. [Google Scholar] [CrossRef]
- van Loon, J.T.; Cioni, M.R.L.; Zijlstra, A.A.; Loup, C. An empirical formula for the mass-loss rates of dust-enshrouded red supergiants and oxygen-rich Asymptotic Giant Branch stars. Astron. Astrophys. 2005, 438, 273–289. [Google Scholar] [CrossRef]
- Humphreys, R.M.; Davidson, K. The Luminous Blue Variables: Astrophysical Geysers. Publ. Astron. Soc. Pac. 1994, 106, 1025. [Google Scholar] [CrossRef]
- Nugis, T.; Lamers, H.J.G.L.M. Mass-loss rates of Wolf-Rayet stars as a function of stellar parameters. Astron. Astrophys. 2000, 360, 227–244. [Google Scholar]
- Rivinius, T.; Carciofi, A.C.; Martayan, C. Classical Be stars. Rapidly rotating B stars with viscous Keplerian decretion disks. aapr 2013, 21, 69. [Google Scholar] [CrossRef]
- Zorec, J.; Frémat, Y.; Domiciano de Souza, A.; Royer, F.; Cidale, L.; Hubert, A.M.; Semaan, T.; Martayan, C.; Cochetti, Y.R.; Arias, M.L.; et al. Critical study of the distribution of rotational velocities of Be stars. I. Deconvolution methods, effects due to gravity darkening, macroturbulence, and binarity. Astron. Astrophys. 2016, 595, A132. [Google Scholar] [CrossRef]
- Labadie-Bartz, J.; Carciofi, A.C.; Henrique de Amorim, T.; Rubio, A.; Luiz Figueiredo, A.; Ticiani dos Santos, P.; Thomson-Paressant, K. Classifying Be Star Variability with TESS. I. The Southern Ecliptic. Astron. J. 2022, 163, 226. [Google Scholar] [CrossRef]
- Bodenheimer, P. Rapidly Rotating Stars. VII. Effects of Angular Momentum on Upper-Main Models. Astrophys. J. 1971, 167, 153. [Google Scholar] [CrossRef]
- Pols, O.R.; Cote, J.; Waters, L.B.F.M.; Heise, J. The formation of Be stars through close binary evolution. Astron. Astrophys. 1991, 241, 419–438. [Google Scholar]
- Ekström, S.; Meynet, G.; Maeder, A.; Barblan, F. Evolution towards the critical limit and the origin of Be stars. Astron. Astrophys. 2008, 478, 467–485. [Google Scholar] [CrossRef]
- Sana, H.; de Mink, S.E.; de Koter, A.; Langer, N.; Evans, C.J.; Gieles, M.; Gosset, E.; Izzard, R.G.; Le Bouquin, J.B.; Schneider, F.R.N. Binary Interaction Dominates the Evolution of Massive Stars. Science 2012, 337, 444. [Google Scholar] [CrossRef]
- Hastings, B.; Langer, N.; Wang, C.; Schootemeijer, A.; Milone, A.P. Stringent upper limit on Be star fractions produced by binary interaction. Astron. Astrophys. 2021, 653, A144. [Google Scholar] [CrossRef]
- Bodensteiner, J.; Shenar, T.; Sana, H. Investigating the lack of main-sequence companions to massive Be stars. Astron. Astrophys. 2020, 641, A42. [Google Scholar] [CrossRef]
- Dodd, J.M.; Oudmaijer, R.D.; Radley, I.C.; Vioque, M.; Frost, A.J. Gaia uncovers difference in B and Be star binarity at small scales: Evidence for mass transfer causing the Be phenomenon. Mon. Not. R. Astron. Soc. 2024, 527, 3076–3086. [Google Scholar] [CrossRef]
- Preece, H.P.; Hamers, A.S.; Battich, T.; Rajamuthukumar, A.S. Forming hot subluminous stars from hierarchical triples—I. The role of an outer tertiary on formation channels. Mon. Not. R. Astron. Soc. 2022, 517, 2111–2120. [Google Scholar] [CrossRef]
- Granada, A.; Ekström, S.; Georgy, C.; Krtička, J.; Owocki, S.; Meynet, G.; Maeder, A. Populations of rotating stars. II. Rapid rotators and their link to Be-type stars. Astron. Astrophys. 2013, 553, A25. [Google Scholar] [CrossRef]
- Hastings, B.; Wang, C.; Langer, N. The single star path to Be stars. Astron. Astrophys. 2020, 633, A165. [Google Scholar] [CrossRef]
- Zhao, X.; Fuller, J. Centrifugally driven mass-loss and outbursts of massive stars. Mon. Not. R. Astron. Soc. 2020, 495, 249–265. [Google Scholar] [CrossRef]
- Georgy, C.; Ekström, S.; Granada, A.; Meynet, G.; Mowlavi, N.; Eggenberger, P.; Maeder, A. Populations of rotating stars. I. Models from 1.7 to 15 Msun at Z = 0.014, 0.006, and 0.002 with Ω/Ωcrit between 0 and 1. Astron. Astrophys. 2013, 553, A24. [Google Scholar] [CrossRef]
- Rímulo, L.R.; Carciofi, A.C.; Vieira, R.G.; Rivinius, T.; Faes, D.M.; Figueiredo, A.L.; Bjorkman, J.E.; Georgy, C.; Ghoreyshi, M.R.; Soszyński, I. The life cycles of Be viscous decretion discs: Fundamental disc parameters of 54 SMC Be stars. Mon. Not. R. Astron. Soc. 2018, 476, 3555–3579. [Google Scholar] [CrossRef]
- Corsaro, E.; Mathur, S.; García, R.A.; Gaulme, P.; Pinsonneault, M.; Stassun, K.; Stello, D.; Tayar, J.; Trampedach, R.; Jiang, C.; et al. Metallicity effect on stellar granulation detected from oscillating red giants in open clusters. Astron. Astrophys. 2017, 605, A3. [Google Scholar] [CrossRef]
- Bjorkman, J.E.; Cassinelli, J.P. Equatorial Disk Formation around Rotating Stars Due to Ram Pressure Confinement by the Stellar Wind. Astrophys. J. 1993, 409, 429. [Google Scholar] [CrossRef]
- Owocki, S.P.; Cranmer, S.R.; Gayley, K.G. Inhibition FO Wind Compressed Disk Formation by Nonradial Line-Forces in Rotating Hot-Star Winds. Astrophys. J. Lett. 1996, 472, L115. [Google Scholar] [CrossRef]
- Cranmer, S.R.; Owocki, S.P. The Effect of Oblateness and Gravity Darkening on the Radiation Driving in Winds from Rapidly Rotating B Stars. Astrophys. J. 1995, 440, 308. [Google Scholar] [CrossRef]
- Grady, C.A.; Bjorkman, K.S.; Snow, T.P. Highly Ionized Stellar Winds in Be Stars: The Evidence for Aspect Dependence. Astrophys. J. 1987, 320, 376. [Google Scholar] [CrossRef]
- Kee, N.D.; Owocki, S.; Sundqvist, J.O. Line-driven ablation of circumstellar discs—I. Optically thin decretion discs of classical Oe/Be stars. Mon. Not. R. Astron. Soc. 2016, 458, 2323–2335. [Google Scholar] [CrossRef] [PubMed]
- Kee, N.D.; Owocki, S.; Kuiper, R. Line-driven ablation of circumstellar discs—II. Analysing the role of multiple resonances. Mon. Not. R. Astron. Soc. 2018, 474, 847–853. [Google Scholar] [CrossRef]
- Martayan, C.; Frémat, Y.; Hubert, A.M.; Floquet, M.; Zorec, J.; Neiner, C. Effects of metallicity, star-formation conditions, and evolution in B and Be stars. II. Small Magellanic Cloud, field of NGC 330. Astron. Astrophys. 2007, 462, 683–694. [Google Scholar] [CrossRef]
- Cassinelli, J.P.; Brown, J.C.; Maheswaran, M.; Miller, N.A.; Telfer, D.C. A Magnetically Torqued Disk Model for Be Stars. Astrophys. J. 2002, 578, 951–966. [Google Scholar] [CrossRef]
- Rogers, T.M.; Lin, D.N.C.; McElwaine, J.N.; Lau, H.H.B. Internal Gravity Waves in Massive Stars: Angular Momentum Transport. Astrophys. J. 2013, 772, 21. [Google Scholar] [CrossRef]
- Owocki, S. Formation and Evolution of Disks around Classical Be Stars. Astron. Soc. Pac. Conf. Ser. 2006, 355, 219. [Google Scholar]
- Baade, D. Does 28 CMa have a photometric period differing from its spectroscopic period ? Astron. Astrophys. 1982, 110, L15–L17. [Google Scholar]
- Rivinius, T.; Baade, D.; Štefl, S. Non-radially pulsating Be stars. Astron. Astrophys. 2003, 411, 229–247. [Google Scholar] [CrossRef]
- Rivinius, T.; Baade, D.; Stefl, S.; Stahl, O.; Wolf, B.; Kaufer, A. Stellar and circumstellar activity of the Be star MU Centauri. I. Line emission outbursts. Astron. Astrophys. 1998, 333, 125–140. [Google Scholar]
- Baade, D.; Rivinius, T.; Pigulski, A.; Carciofi, A.C.; Martayan, C.; Moffat, A.F.J.; Wade, G.A.; Weiss, W.W.; Grunhut, J.; Handler, G.; et al. Short-term variability and mass loss in Be stars. I. BRITE satellite photometry of η and μ Centauri. Astron. Astrophys. 2016, 588, A56. [Google Scholar] [CrossRef]
- Lee, U.; Osaki, Y.; Saio, H. Viscous excretion discs around Be stars. Mon. Not. R. Astron. Soc. 1991, 250, 432–437. [Google Scholar] [CrossRef]
- Haubois, X.; Carciofi, A.C.; Rivinius, T.; Okazaki, A.T.; Bjorkman, J.E. Dynamical Evolution of Viscous Disks around Be Stars. I. Photometry. Astrophys. J. 2012, 756, 156. [Google Scholar] [CrossRef]
- Okazaki, A.T.; Bate, M.R.; Ogilvie, G.I.; Pringle, J.E. Viscous effects on the interaction between the coplanar decretion disc and the neutron star in Be/X-ray binaries. Mon. Not. R. Astron. Soc. 2002, 337, 967–980. [Google Scholar] [CrossRef]
- Carciofi, A.C.; Bjorkman, J.E.; Otero, S.A.; Okazaki, A.T.; Štefl, S.; Rivinius, T.; Baade, D.; Haubois, X. The First Determination of the Viscosity Parameter in the Circumstellar Disk of a Be Star. Astrophys. J. Lett. 2012, 744, L15. [Google Scholar] [CrossRef]
- Haubois, X.; Mota, B.C.; Carciofi, A.C.; Draper, Z.H.; Wisniewski, J.P.; Bednarski, D.; Rivinius, T. Dynamical Evolution of Viscous Disks around Be Stars. II. Polarimetry. Astrophys. J. 2014, 785, 12. [Google Scholar] [CrossRef]
- Marr, K.C.; Jones, C.E.; Carciofi, A.C.; Rubio, A.C.; Mota, B.C.; Ghoreyshi, M.R.; Hatfield, D.W.; Rímulo, L.R. The Be Star 66 Ophiuchi: 60 Years of Disk Evolution. Astrophys. J. 2021, 912, 76. [Google Scholar] [CrossRef]
- Rubio, A.C.; Carciofi, A.C.; Ticiani, P.; Mota, B.C.; Vieira, R.G.; Faes, D.M.; Genaro, M.; de Amorim, T.H.; Klement, R.; Araya, I.; et al. Bayesian sampling with BeAtlas, a grid of synthetic Be star spectra I. Recovering the fundamental parameters of α Eri and β CMi. Mon. Not. R. Astron. Soc. 2023, 526, 3007–3036. [Google Scholar] [CrossRef]
- Figueiredo, A.L.; Carciofi, A.C.; Labadie-Bartz, J.; Pinho, M.L.; de Amorin, T.H.; dos Santos, P.T.; Soszyński, I.; Udalski, A. Be star demographics: A comprehensive study of thousands of lightcurves in the Magellanic Clouds. arXiv 2025, arXiv:2505.08714. [Google Scholar] [CrossRef]
- Ricker, G.R.; Winn, J.N.; Vanderspek, R.; Latham, D.W.; Bakos, G.Á.; Bean, J.L.; Berta-Thompson, Z.K.; Brown, T.M.; Buchhave, L.; Butler, N.R.; et al. Transiting Exoplanet Survey Satellite (TESS). J. Astron. Telesc. Instruments Syst. 2015, 1, 014003. [Google Scholar] [CrossRef]
- Siverd, R.J.; Brown, T.M.; Barnes, S.; Bowman, M.K.; De Vera, J.; Foale, S.; Harbeck, D.R.; Henderson, T.; Hygelund, J.; Kirby, A.; et al. NRES: The network of robotic echelle spectrographs. In Proceedings of the SPIE Astronomical Telescopes + Instrumentation, Austin, TX, USA, 10–15 June 2018; Volume 10702, p. 107026C. [Google Scholar] [CrossRef]
- Vieira, R.G.; Carciofi, A.C.; Bjorkman, J.E. The pseudo-photosphere model for the continuum emission of gaseous discs. Mon. Not. R. Astron. Soc. 2015, 454, 2107–2119. [Google Scholar] [CrossRef]
- Zamanov, R.K.; Stoyanov, K.A.; Stefanov, S.Y.; Bode, M.F.; Minev, M.S. Optical spectroscopy of Be stars: Peak separation of Balmer emission lines. Astron. Nachr. 2023, 344. [Google Scholar] [CrossRef]
- Labadie-Bartz, J.; Carciofi, A.C.; Rubio, A.C.; Baade, D.; Siverd, R.; Arcos, C.; Figueiredo, A.L.; Nazé, Y.; Neiner, C.; Rivinius, T.; et al. The birth of Be star disks I. From localized ejection to circularization. arXiv 2025, arXiv:2504.07571. [Google Scholar] [CrossRef]
- Slettebak, A. BE Stars as Rotating Stars: Observations (review Paper). Symp. Int. Astron. Union 1976, 70, 123–136. [Google Scholar] [CrossRef]
- Hanuschik, R.W.; Kozok, J.R.; Kaiser, D. High-resolution emission-line spectroscopy of Be stars. III—Balmer line profiles. Astron. Astrophys. 1988, 189, 147–162. [Google Scholar]
- Štefl, S.; Baade, D.; Rivinius, T.; Otero, S.; Stahl, O.; Budovičová, A.; Kaufer, A.; Maintz, M. Stellar and circumstellar activity of the Be star omega CMa. I. Line and continuum emission in 1996–2002. Astron. Astrophys. 2003, 402, 253–265. [Google Scholar] [CrossRef]
- Roche, E. Recherches sur les atmospheres des cometes. Ann. L’Obs. Paris 1859, 5, 353–393. [Google Scholar]
- Carciofi, A.C.; Magalhães, A.M.; Leister, N.V.; Bjorkman, J.E.; Levenhagen, R.S. Achernar: Rapid Polarization Variability as Evidence of Photospheric and Circumstellar Activity. Astrophys. J. Lett. 2007, 671, L49–L52. [Google Scholar] [CrossRef]
- Carciofi, A.C.; Bjorkman, J.E. Non-LTE Monte Carlo Radiative Transfer. I. The Thermal Properties of Keplerian Disks around Classical Be Stars. Astrophys. J. 2006, 639, 1081–1094. [Google Scholar] [CrossRef]
- Carciofi, A.C.; Bjorkman, J.E. Non-LTE Monte Carlo Radiative Transfer. II. Nonisothermal Solutions for Viscous Keplerian Disks. Astrophys. J. 2008, 684, 1374–1383. [Google Scholar] [CrossRef]
- Rubio, A.C.; Carciofi, A.C.; Baade, D.; Labadie-Bartz, J.; de Amorim, T.H. The birth of Be star disks — II. SPH models of localized mass ejections. in preparation 2025. [Google Scholar]
- Carciofi, A.C. The circumstellar discs of Be stars. Proc. Int. Astron. Union 2010, 6, 325–336. [Google Scholar] [CrossRef]
- Rubio, A.C.; Carciofi, A.C.; Bjorkman, J.E.; de Amorim, T.H.; Okazaki, A.T.; Suffak, M.W.; Jones, C.E.; Candido, P.P. High-spatial-resolution simulations of Be star disks in binary systems: I. Structure and kinematics of coplanar disks. Astron. Astrophys. 2025, 698, 309. [Google Scholar] [CrossRef]
- Panoglou, D.; Carciofi, A.C.; Vieira, R.G.; Cyr, I.H.; Jones, C.E.; Okazaki, A.T.; Rivinius, T. Be discs in binary systems—I. Coplanar orbits. Mon. Not. R. Astron. Soc. 2016, 461, 2616–2629. [Google Scholar] [CrossRef]
- Cyr, I.H.; Jones, C.E.; Panoglou, D.; Carciofi, A.C.; Okazaki, A.T. Be discs in binary systems—II. Misaligned orbits. Mon. Not. R. Astron. Soc. 2017, 471, 596–605. [Google Scholar] [CrossRef]
- Panoglou, D.; Faes, D.M.; Carciofi, A.C.; Okazaki, A.T.; Baade, D.; Rivinius, T.; Borges Fernandes, M. Be discs in coplanar circular binaries: Phase-locked variations of emission lines. Mon. Not. R. Astron. Soc. 2018, 473, 3039–3050. [Google Scholar] [CrossRef]
- Cyr, I.H.; Jones, C.E.; Carciofi, A.C.; Steckel, C.; Tycner, C.; Okazaki, A.T. Spiral density enhancements in Be binary systems. Mon. Not. R. Astron. Soc. 2020, 497, 3525–3536. [Google Scholar] [CrossRef]
- Suffak, M.; Jones, C.E.; Carciofi, A.C. Growth and dissipation of Be star discs in misaligned binary systems. Mon. Not. R. Astron. Soc. 2022, 509, 931–944. [Google Scholar] [CrossRef]
- Suffak, M.W.; Jones, C.E.; Carciofi, A.C. Investigating Kozai-Lidov oscillations and disc tearing in Be star discs. Mon. Not. R. Astron. Soc. 2025, 536, 2234–2259. [Google Scholar] [CrossRef]
- Wheelwright, H.E.; Bjorkman, J.E.; Oudmaijer, R.D.; Carciofi, A.C.; Bjorkman, K.S.; Porter, J.M. Probing the properties of Be star discs with spectroastrometry and NLTE radiative transfer modelling: β CMi. Mon. Not. R. Astron. Soc. 2012, 423, L11–L15. [Google Scholar] [CrossRef]
- Zharikov, S.V.; Miroshnichenko, A.S.; Pollmann, E.; Danford, S.; Bjorkman, K.S.; Morrison, N.D.; Favaro, A.; Guarro Fló, J.; Terry, J.N.; Desnoux, V.; et al. Doppler tomography of the circumstellar disk of π Aquarii. Astron. Astrophys. 2013, 560, A30. [Google Scholar] [CrossRef]
- Miroshnichenko, A.S.; Chari, R.; Danford, S.; Prendergast, P.; Aarnio, A.N.; Andronov, I.L.; Chinarova, L.L.; Lytle, A.; Amantayeva, A.; Gabitova, I.A.; et al. Searching for Phase-Locked Variations of the Emission-Line Profiles in Binary Be Stars. Galaxies 2023, 11, 83. [Google Scholar] [CrossRef]
- Chojnowski, S.D.; Labadie-Bartz, J.; Rivinius, T.; Gies, D.; Panoglou, D.; Borges Fernandes, M.; Wisniewski, J.P.; Whelan, D.G.; Mennickent, R.E.; McMillan, R.; et al. The Remarkable Be+sdOB Binary HD 55606. I. Orbital and Stellar Parameters. Astrophys. J. 2018, 865, 76. [Google Scholar] [CrossRef]
- Klement, R.; Rivinius, T.; Gies, D.R.; Baade, D.; Mérand, A.; Monnier, J.D.; Schaefer, G.H.; Lanthermann, C.; Anugu, N.; Kraus, S.; et al. The CHARA Array Interferometric Program on the Multiplicity of Classical Be Stars: New Detections and Orbits of Stripped Subdwarf Companions. Astrophys. J. 2024, 962, 70. [Google Scholar] [CrossRef]
- Klement, R.; Carciofi, A.C.; Rivinius, T.; Ignace, R.; Matthews, L.D.; Torstensson, K.; Gies, D.; Vieira, R.G.; Richardson, N.D.; Domiciano de Souza, A.; et al. Prevalence of SED Turndown among Classical Be Stars: Are All Be Stars Close Binaries? Astrophys. J. 2019, 885, 147. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carciofi, A.C.; Bolzan, G.P.P.; Querido, P.R.; Rubio, A.C.; Labadie-Bartz, J.; de Amorim, T.H.; Fonseca Silva, A.C.; Schiavolim, V.L. Mass Loss in Be Stars: News from Two Fronts. Galaxies 2025, 13, 77. https://doi.org/10.3390/galaxies13040077
Carciofi AC, Bolzan GPP, Querido PR, Rubio AC, Labadie-Bartz J, de Amorim TH, Fonseca Silva AC, Schiavolim VL. Mass Loss in Be Stars: News from Two Fronts. Galaxies. 2025; 13(4):77. https://doi.org/10.3390/galaxies13040077
Chicago/Turabian StyleCarciofi, Alex C., Guilherme P. P. Bolzan, Pâmela R. Querido, Amanda C. Rubio, Jonathan Labadie-Bartz, Tajan H. de Amorim, Ariane C. Fonseca Silva, and Vittória L. Schiavolim. 2025. "Mass Loss in Be Stars: News from Two Fronts" Galaxies 13, no. 4: 77. https://doi.org/10.3390/galaxies13040077
APA StyleCarciofi, A. C., Bolzan, G. P. P., Querido, P. R., Rubio, A. C., Labadie-Bartz, J., de Amorim, T. H., Fonseca Silva, A. C., & Schiavolim, V. L. (2025). Mass Loss in Be Stars: News from Two Fronts. Galaxies, 13(4), 77. https://doi.org/10.3390/galaxies13040077





