Unveiling the Evolution of MWC 728: Non-Conservative Mass Transfer in an FS CMa Binary
Abstract
1. Introduction
2. Fundamental Parameters of the System
3. Method and Numerical Input
- α
- is the fraction of the transferred mass removed as isotropic wind from the donor;
- β
- is the fraction isotropically re-emitted near the accretor (hot boundary layer and outflow);
- δ
- is the fraction fed into a circumbinary torus located at , where a is the instantaneous orbital separation of the binary, carrying a specific angular momentum of ;
- ηacc
- is the mass-accretion efficiency: the fraction of the transferred mass that is effectively accreted by the secondary (accretor), computed as [33].
- Donor wind (α). Two regimes imposed boundaries on the expected isotropic wind from the Roche-filling star.(i) When the donor was a B7-type star, the Vink formulation predicted that [26], i.e., relative to the peak mass-transfer rate adopted in the grid.(ii) After the Algol reversal, the donor was an F-type subgiant; a Reimers-style scaling gave an even weaker [36], implying .Both limits lie well below the non-spherical channels (, ), so we adopt a single constant value, . Tests with –0.03 change the orbital period by , confirming its negligible effect.
- Re-emission from the gainer (β). Three-dimensional simulations show that gainers rotating at re-emit 40– of the incident stream [37]. For the accretor with and , the Roche-corrected expression gives . The observed projected rotation velocity is , and with the binary inclination [11], the equatorial (true) rotation speed, obtained via , is . This places the accretor well within the simulated high-rotation regime, so we adopt the representative value .
- Circumbinary torus (δ, γ). The SED of MWC 728 shows a smooth, featureless infrared excess and exceeds the combined stellar photospheres by more than an order of magnitude [11]. Free–free emission from a Be-type envelope cannot reproduce such a broad hump, whereas radiative-transfer models with a warm, optically thick circumbinary dust reservoir match both the slope and the absolute flux level [38]. SPH calculations that include dust formation further show that 10–20% of the transferred mass can settle into a long-lived torus at – [39]. For MWC 728, the observed IR luminosity is reproduced for –0.18 and a lever-arm factor of .
4. Results
5. Conclusions
- Fundamental parameters: a 5000-cycle Monte-Carlo propagation yields , , , and , confirming a hot B7 IV accretor ( K) and a cool G-type donor ( K).
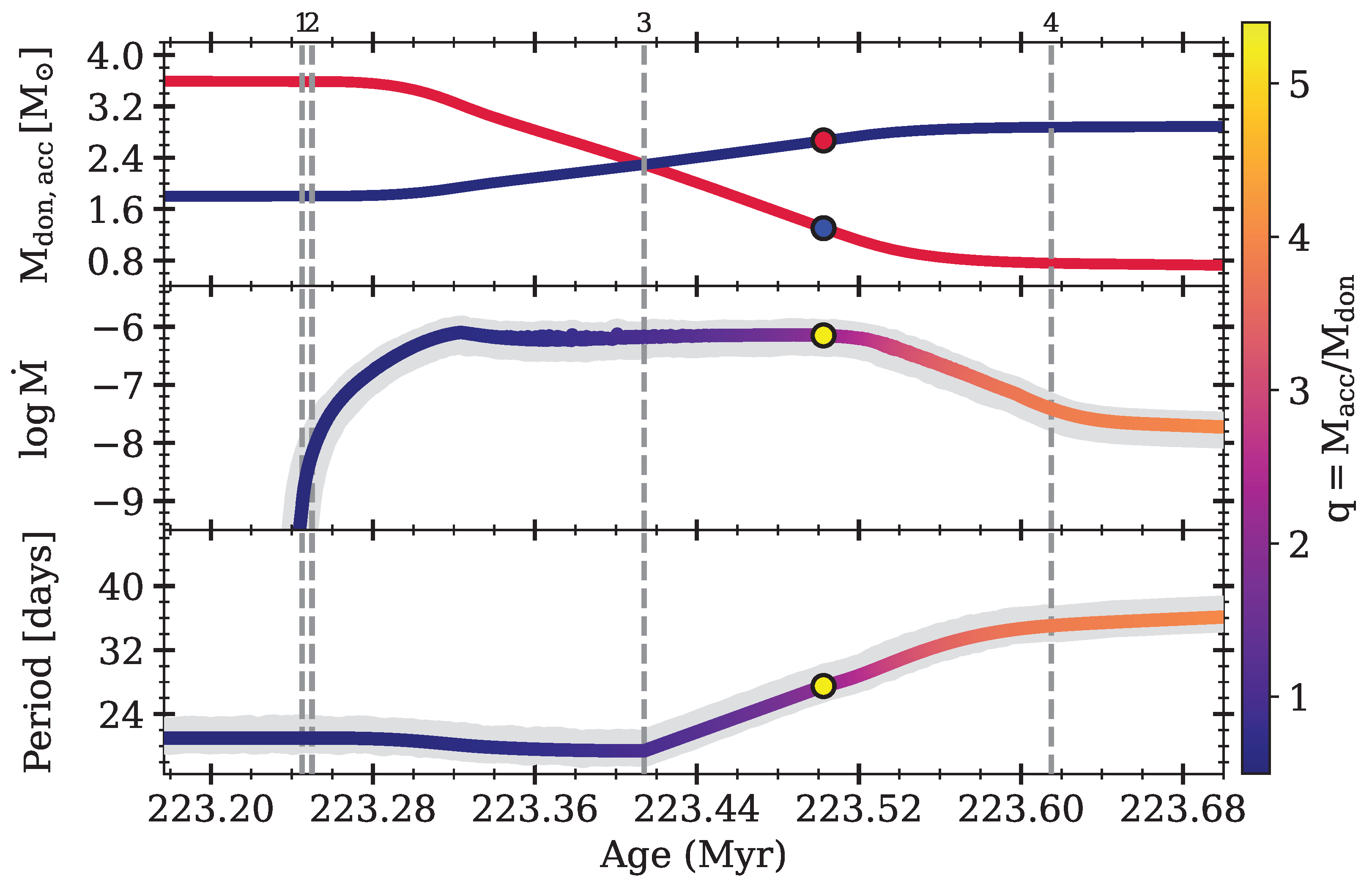
- Binary evolution: The best-fit MESA track starts with , , and d and evolves through thermally driven, moderately non-conservative Roche-lobe overflow. Mass loss fractions of , , , and reproduce the dusty torus and expand the orbit to the observed d. At Myr, the model matches the present-day masses (, ), the ratio , and an ongoing transfer rate of .
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
References
- Miroshnichenko, A.S.; Zharikov, S.V.; Manset, N.; Khokhlov, S.A.; Nodyarov, A.S.; Klochkova, V.G.; Danford, S.; Kuratova, A.K.; Mennickent, R.; Chojnowski, S.D.; et al. Recent Progress in Finding Binary Systems with the B[e] Phenomenon. Galaxies 2023, 11, 36. [Google Scholar] [CrossRef]
- Lamers, H.J.G.L.M.; Zickgraf, F.J.; de Winter, D.; Houziaux, L.; Zorec, J. An improved classification of B[e]-type stars. Astron. Astrophys. 1998, 340, 117–128. [Google Scholar]
- Miroshnichenko, A.S. Toward Understanding the B[e] Phenomenon. I. Definition of the Galactic FS CMa Stars. Astrophys. J. 2007, 667, 497–504. [Google Scholar] [CrossRef][Green Version]
- Barsukova, E.A.; Burenkov, A.N.; Goranskij, V.P.; Zharikov, S.V.; Iliev, L.; Manset, N.; Metlova, N.V.; Miroshnichenko, A.S.; Moiseeva, A.V.; Nedialkov, P.L.; et al. B[e] Star CI Camelopardalis in the Optical Range. Astrophys. Bull. 2023, 78, 1–24. [Google Scholar] [CrossRef]
- Varga, J.; Gerják, T.; Ábrahám, P.; Chen, L.; Gabányi, K.; Kóspál, Á. Dust evolution in the circumstellar disc of the unclassified B[e] star HD 50138. Mon. Not. R. Astron. Soc. 2019, 485, 3112–3123. [Google Scholar] [CrossRef]
- Khokhlov, S.A.; Miroshnichenko, A.S.; Zharikov, S.V.; Manset, N.; Arkharov, A.A.; Efimova, N.; Klimanov, S.; Larionov, V.M.; Kusakin, A.V.; Kokumbaeva, R.I.; et al. Toward Understanding the B[e] Phenomenon. VII. AS 386, a Single-lined Binary with a Candidate Black Hole Component. Astrophys. J. 2018, 856, 158. [Google Scholar] [CrossRef]
- Miroshnichenko, A.S.; Zharikov, S.V. FS CMa Type Binaries. In The Physics of Evolved Stars: A Conference Dedicated to the Memory of Olivier Chesneau; EAS Publications Series; EDP Sciences: Les Ulis, France, 2015; Volume 71–72, pp. 181–186. [Google Scholar] [CrossRef]
- de la Fuente, D.; Najarro, F.; Trombley, C.; Davies, B.; Figer, D.F. First detections of FS Canis Majoris stars in clusters. Evolutionary state as constrained by coeval massive stars. Astron. Astrophys. 2015, 575, A10. [Google Scholar] [CrossRef]
- Moranchel-Basurto, A.; Korčáková, D.; Chametla, R.O. 2.5D magnetohydrodynamic models of circumstellar discs around FS CMa post-mergers-I. Non-stationary accretion stage. Mon. Not. R. Astron. Soc. 2023, 523, 5554–5564. [Google Scholar] [CrossRef]
- Merrill, P.W.; Burwell, C.G. Second Supplement to the Mount Wilson Catalogue and Bibliography of Stars of Classes B and a whose Spectra have Bright Hydrogen Lines. Astrophys. J. 1949, 110, 387. [Google Scholar] [CrossRef]
- Miroshnichenko, A.S.; Zharikov, S.V.; Danford, S.; Manset, N.; Korčáková, D.; Kříček, R.; Šlechta, M.; Omarov, C.T.; Kusakin, A.V.; Kuratov, K.S.; et al. Toward Understanding the B[e] Phenomenon. V. Nature and Spectral Variations of the MWC 728 Binary System. Astrophys. J. 2015, 809, 129. [Google Scholar] [CrossRef]
- Bailer-Jones, C.A.L.; Rybizki, J.; Fouesneau, M.; Demleitner, M.; Andrae, R. Estimating Distances from Parallaxes. V. Geometric and Photogeometric Distances to 1.47 Billion Stars in Gaia Early Data Release 3. Archit. J. 2021, 161, 147. [Google Scholar] [CrossRef]
- Gaia Collaboration; Brown, A.G.A.; Vallenari, A.; Prusti, T.; de Bruijne, J.H.J.; Babusiaux, C.; Biermann, M.; Creevey, O.L.; Evans, D.W.; Eyer, L.; et al. Gaia Early Data Release 3. Summary of the contents and survey properties. Astron. Astrophys. 2021, 649, A1. [Google Scholar] [CrossRef]
- Lindegren, L.; Hernández, J.; Bombrun, A.; Klioner, S.; Bastian, U.; Ramos-Lerate, M.; de Torres, A.; Steidelmüller, H.; Stephenson, C.; Hobbs, D.; et al. Gaia Data Release 2. The astrometric solution. Astron. Astrophys. 2018, 616, A2. [Google Scholar] [CrossRef]
- El-Badry, K. How to use Gaia parallaxes for stars with poor astrometric fits. arXiv 2025, arXiv:arXiv:2504.11528. [Google Scholar] [CrossRef]
- Green, G.M.; Schlafly, E.; Zucker, C.; Speagle, J.S.; Finkbeiner, D. A 3D Dust Map Based on Gaia, Pan-STARRS 1, and 2MASS. Astrophys. J. 2019, 887, 93. [Google Scholar] [CrossRef]
- Pecaut, M.J.; Mamajek, E.E. Intrinsic Colors, Temperatures, and Bolometric Corrections of Pre-main-sequence Stars. Astrophys. J. Suppl. 2013, 208, 9. [Google Scholar] [CrossRef]
- Paxton, B.; Bildsten, L.; Dotter, A.; Herwig, F.; Lesaffre, P.; Timmes, F. Modules for Experiments in Stellar Astrophysics (MESA). Astrophys. J. Suppl. 2011, 192, 3. [Google Scholar] [CrossRef]
- Paxton, B.; Cantiello, M.; Arras, P.; Bildsten, L.; Brown, E.F.; Dotter, A.; Mankovich, C.; Montgomery, M.H.; Stello, D.; Timmes, F.X.; et al. Modules for Experiments in Stellar Astrophysics (MESA): Planets, Oscillations, Rotation, and Massive Stars. Astrophys. J. Suppl. 2013, 208, 4. [Google Scholar] [CrossRef]
- Paxton, B.; Marchant, P.; Schwab, J.; Bauer, E.B.; Bildsten, L.; Cantiello, M.; Dessart, L.; Farmer, R.; Hu, H.; Langer, N.; et al. Modules for Experiments in Stellar Astrophysics (MESA): Binaries, Pulsations, and Explosions. Astrophys. J. Suppl. 2015, 220, 15. [Google Scholar] [CrossRef]
- Paxton, B.; Schwab, J.; Bauer, E.B.; Bildsten, L.; Blinnikov, S.; Duffell, P.; Farmer, R.; Goldberg, J.A.; Marchant, P.; Sorokina, E.; et al. Modules for Experiments in Stellar Astrophysics (MESA): Convective Boundaries, Element Diffusion, and Massive Star Explosions. Astrophys. J. Suppl. 2018, 234, 34. [Google Scholar] [CrossRef]
- Paxton, B.; Smolec, R.; Schwab, J.; Gautschy, A.; Bildsten, L.; Cantiello, M.; Dotter, A.; Farmer, R.; Goldberg, J.A.; Jermyn, A.S.; et al. Modules for Experiments in Stellar Astrophysics (MESA): Pulsating Variable Stars, Rotation, Convective Boundaries, and Energy Conservation. Astrophys. J. Suppl. 2019, 243, 10. [Google Scholar] [CrossRef]
- Jermyn, A.S.; Bauer, E.B.; Schwab, J.; Farmer, R.; Ball, W.H.; Bellinger, E.P.; Dotter, A.; Joyce, M.; Marchant, P.; Mombarg, J.S.G.; et al. Modules for Experiments in Stellar Astrophysics (MESA): Time-dependent Convection, Energy Conservation, Automatic Differentiation, and Infrastructure. Astrophys. J. Suppl. 2023, 265, 15. [Google Scholar] [CrossRef]
- Vaidman, N.L.; Miroshnichenko, A.S.; Zharikov, S.V.; Khokhlov, S.A.; Agishev, A.T.; Yermekbayev, B.S. Fundamental Parameters and Evolutionary Scenario of HD 327083. Galaxies 2025, 13, 47. [Google Scholar] [CrossRef]
- Asplund, M.; Grevesse, N.; Sauval, A.J.; Scott, P. The Chemical Composition of the Sun. Annu. Rev. Astron. Astrophys. 2009, 47, 481–522. [Google Scholar] [CrossRef]
- Vink, J.S.; de Koter, A.; Lamers, H.J.G.L.M. Mass-loss predictions for O and B stars as a function of metallicity. Astron. Astrophys. 2001, 369, 574–588. [Google Scholar] [CrossRef]
- de Jager, C.; Nieuwenhuijzen, H.; van der Hucht, K.A. Mass loss rates in the Hertzsprung-Russell diagram. Astron. Astrophys. Suppl. Ser. 1988, 72, 259–289. [Google Scholar]
- Beasor, E.R.; Davies, B.; Smith, N.; van Loon, J.T.; Gehrz, R.D.; Figer, D.F. A new mass-loss rate prescription for red supergiants. Mon. Not. R. Astron. Soc. 2020, 492, 5994–6006. [Google Scholar] [CrossRef]
- Björklund, R.; Sundqvist, J.O.; Singh, S.M.; Puls, J.; Najarro, F. New predictions for radiation-driven, steady-state mass-loss and wind-momentum from hot, massive stars. III. Updated mass-loss rates for stellar evolution. Astron. Astrophys. 2023, 676, A109. [Google Scholar] [CrossRef]
- Crowther, P.A.; Lennon, D.J.; Walborn, N.R. Physical parameters and wind properties of galactic early B supergiants. Astron. Astrophys. 2006, 446, 279–293. [Google Scholar] [CrossRef]
- Smith, N. Mass Loss: Its Effect on the Evolution and Fate of High-Mass Stars. Annu. Rev. Astron. Astrophys. 2014, 52, 487–528. [Google Scholar] [CrossRef]
- Kolb, U.; Ritter, H. A comparative study of the evolution of a close binary using a standard and an improved technique for computing mass transfer. Astron. Astrophys. 1990, 236, 385–392. [Google Scholar]
- Soberman, G.E.; Phinney, E.S.; van den Heuvel, E.P.J. Stability criteria for mass transfer in binary stellar evolution. Astron. Astrophys. 1997, 327, 620–635. [Google Scholar] [CrossRef]
- Eggleton, P.P. Aproximations to the radii of Roche lobes. Astrophys. J. 1983, 268, 368–369. [Google Scholar] [CrossRef]
- Ritter, H. Turning on and off mass transfer in cataclysmic binaries. Astron. Astrophys. 1988, 202, 93–100. [Google Scholar]
- Reimers, D. Observational evidence for mass-loss from K giants, G and K supergiants. Astron. Astrophys. 1977, 57, 395–400. [Google Scholar]
- Deschamps, R.; Siess, L.; Davis, P.J.; Jorissen, A. Critically-rotating accretors and non-conservative evolution in Algols. Astron. Astrophys. 2013, 557, A40. [Google Scholar] [CrossRef]
- Kraus, S.; Hofmann, K.H.; Menten, K.M.; Schertl, D.; Weigelt, G.; Wyrowski, F.; Meilland, A.; Perraut, K.; Petrov, R.; Robbe-Dubois, S.; et al. A hot compact dust disk around a massive young stellar object. Nature 2010, 466, 339–342. [Google Scholar] [CrossRef][Green Version]
- Pejcha, O.; Metzger, B.D.; Tomida, K. Cool and luminous transients from mass-losing binary stars. Mon. Not. R. Astron. Soc. 2016, 455, 4351–4372. [Google Scholar] [CrossRef]
- Artymowicz, P.; Lubow, S.H. Dynamics of Binary-Disk Interaction. I. Resonances and Disk Gap Sizes. Astrophys. J. 1994, 421, 651. [Google Scholar] [CrossRef]
- Hut, P. Tidal evolution in close binary systems. Astron. Astrophys. 1981, 99, 126–140. [Google Scholar]
- Zahn, J.P. Tidal friction in close binary systems. Astron. Astrophys. 1977, 57, 383–394. [Google Scholar]
- Zahn, J.P. Tidal evolution of close binary stars. I - Revisiting the theory of the equilibrium tide. Astron. Astrophys. 1989, 220, 112–116. [Google Scholar]
- Böhm-Vitense, E. Über die Wasserstoffkonvektionszone in Sternen verschiedener Effektivtemperaturen und Leuchtkräfte. Mit 5 Textabbildungen. Z. FÜR Astrophys. 1958, 46, 108. [Google Scholar]
- Claret, A. Theoretical tidal evolution constants for stellar models from the pre-main sequence to the white dwarf stage. Apsidal motion constants, moment of inertia, and gravitational potential energy. Astron. Astrophys. 2023, 674, A67. [Google Scholar] [CrossRef]
- Herwig, F. The evolution of AGB stars with convective overshoot. Astron. Astrophys. 2000, 360, 952–968. [Google Scholar] [CrossRef]
- Claret, A.; Torres, G. The Dependence of Convective Core Overshooting on Stellar Mass: A Semi-empirical Determination Using the Diffusive Approach with Two Different Element Mixtures. Astrophys. J. 2017, 849, 18. [Google Scholar] [CrossRef]
- Tauris, T.M.; van den Heuvel, E.P.J. Formation and evolution of compact stellar X-ray sources. In Compact Stellar X-Ray Sources; Lewin, W.H.G., van der Klis, M., Eds.; Cambridge University Press: Cambridge, UK, 2006; Volume 39, pp. 623–665. [Google Scholar] [CrossRef]
- Webbink, R.F. The evolution of low-mass close binary systems. III. 1.50 M sun: Unsteady mass loss and shrinking secondaries. Astrophys. J. 1977, 211, 486–498. [Google Scholar] [CrossRef]
- Shao, Y.; Li, X.D. On the Formation of Be Stars through Binary Interaction. Astrophys. J. 2014, 796, 37. [Google Scholar] [CrossRef]
- Chen, X.; Han, Z. Mass transfer from a giant star to a main-sequence companion and its contribution to long-orbital-period blue stragglers. Mon. Not. R. Astron. Soc. 2008, 387, 1416–1430. [Google Scholar] [CrossRef]
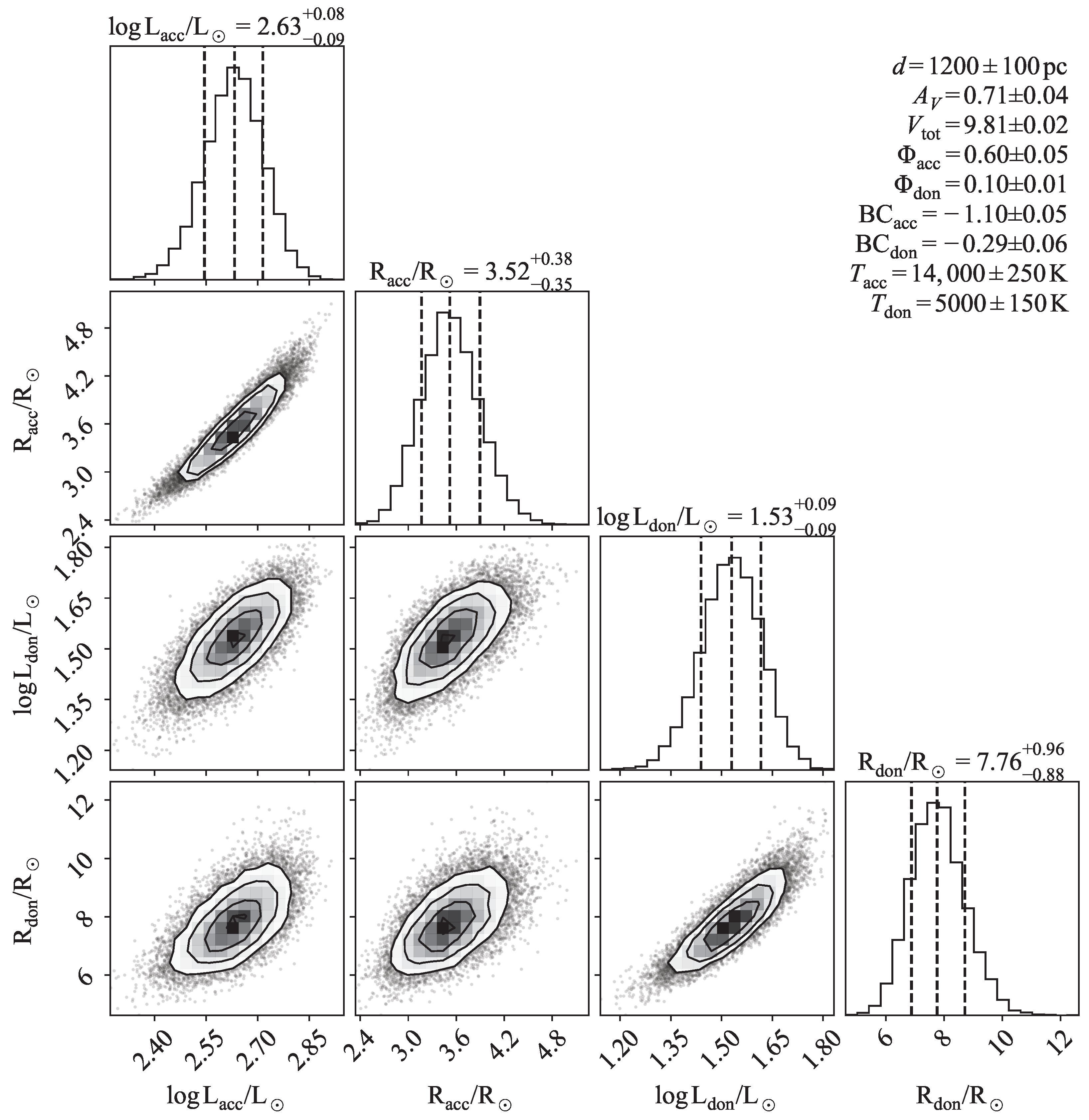

| Parameter | Accretor | Donor |
|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vaidman, N.L.; Khokhlov, S.A.; Agishev, A.T. Unveiling the Evolution of MWC 728: Non-Conservative Mass Transfer in an FS CMa Binary. Galaxies 2025, 13, 78. https://doi.org/10.3390/galaxies13040078
Vaidman NL, Khokhlov SA, Agishev AT. Unveiling the Evolution of MWC 728: Non-Conservative Mass Transfer in an FS CMa Binary. Galaxies. 2025; 13(4):78. https://doi.org/10.3390/galaxies13040078
Chicago/Turabian StyleVaidman, Nadezhda L., Serik A. Khokhlov, and Aldiyar T. Agishev. 2025. "Unveiling the Evolution of MWC 728: Non-Conservative Mass Transfer in an FS CMa Binary" Galaxies 13, no. 4: 78. https://doi.org/10.3390/galaxies13040078
APA StyleVaidman, N. L., Khokhlov, S. A., & Agishev, A. T. (2025). Unveiling the Evolution of MWC 728: Non-Conservative Mass Transfer in an FS CMa Binary. Galaxies, 13(4), 78. https://doi.org/10.3390/galaxies13040078






