Very-High-Energy Gamma-Ray Observations as a Probe to the Nature of Dark Matter and Prospects for MACE
Abstract
1. Introduction
2. Weakly Interacting Massive Particles
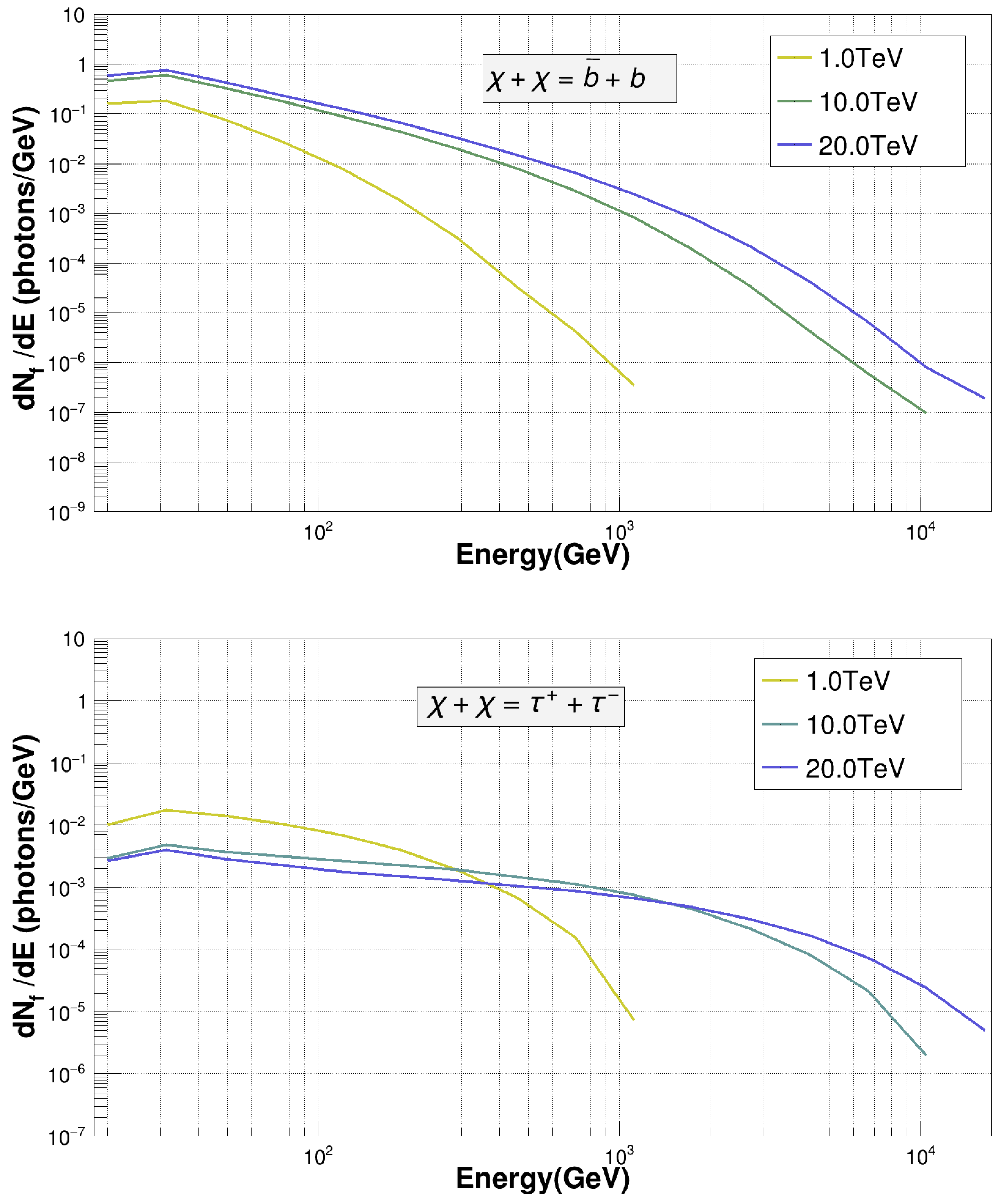
3. Gamma-Ray Signal from WIMPs
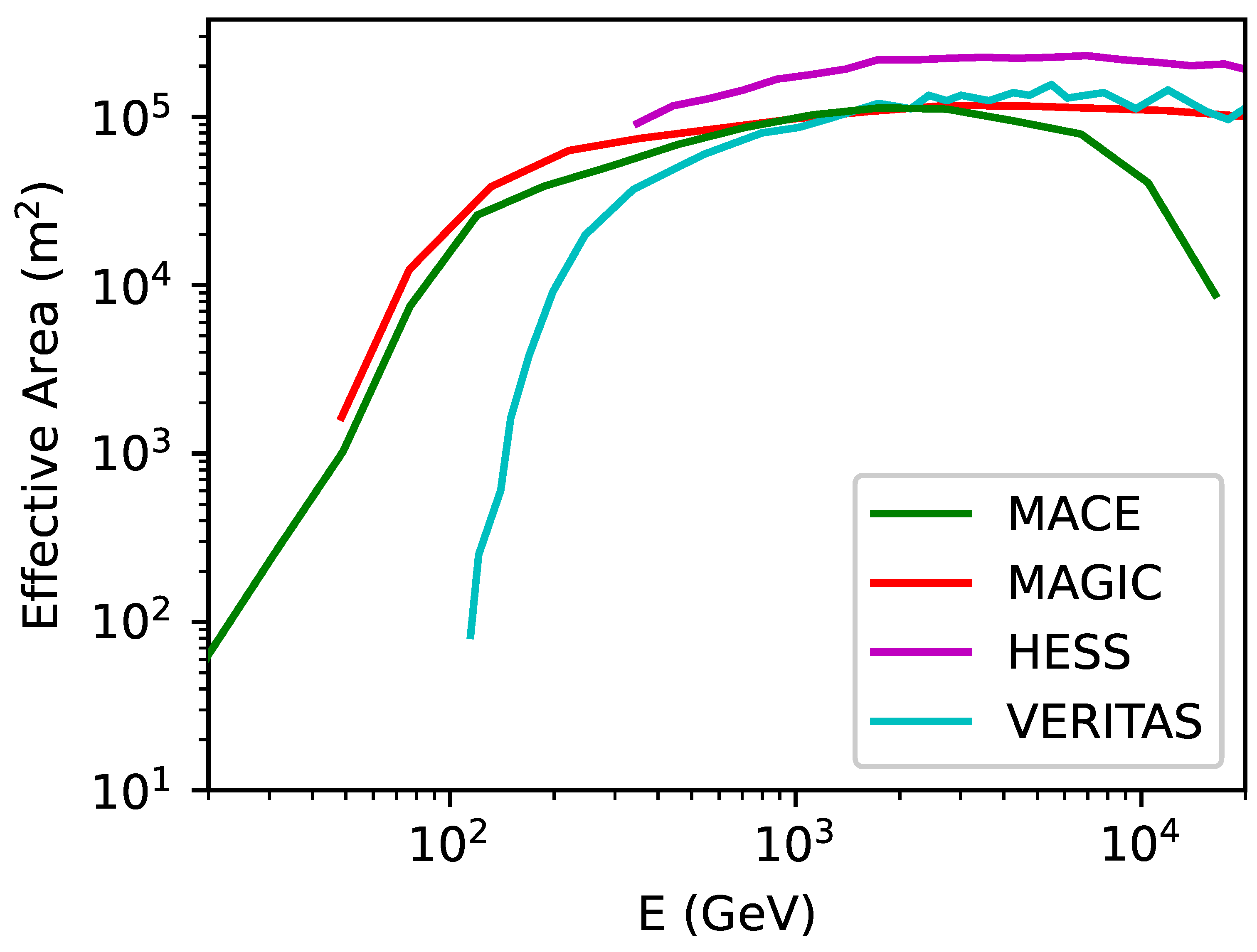
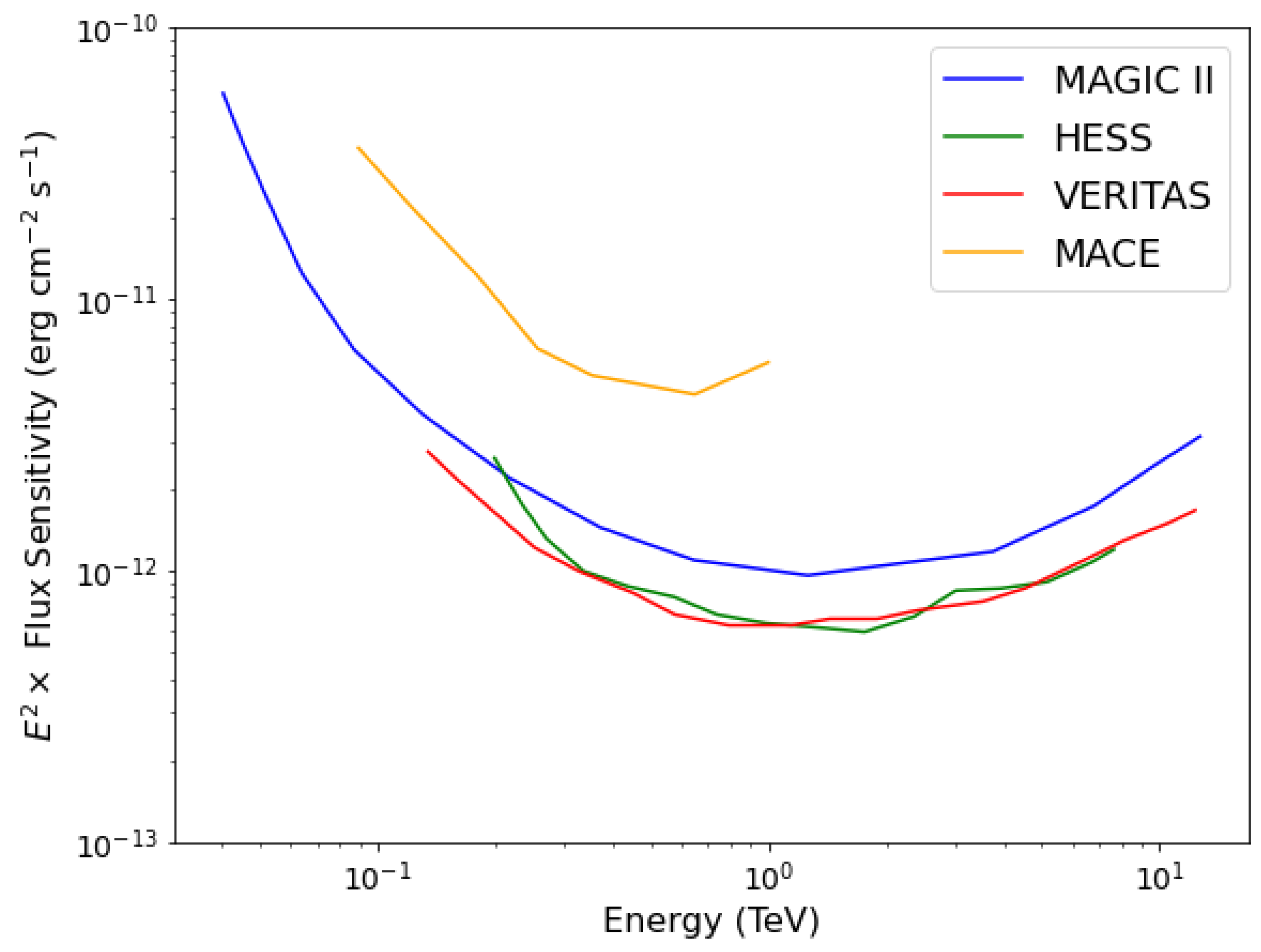
4. Opportunity for MACE
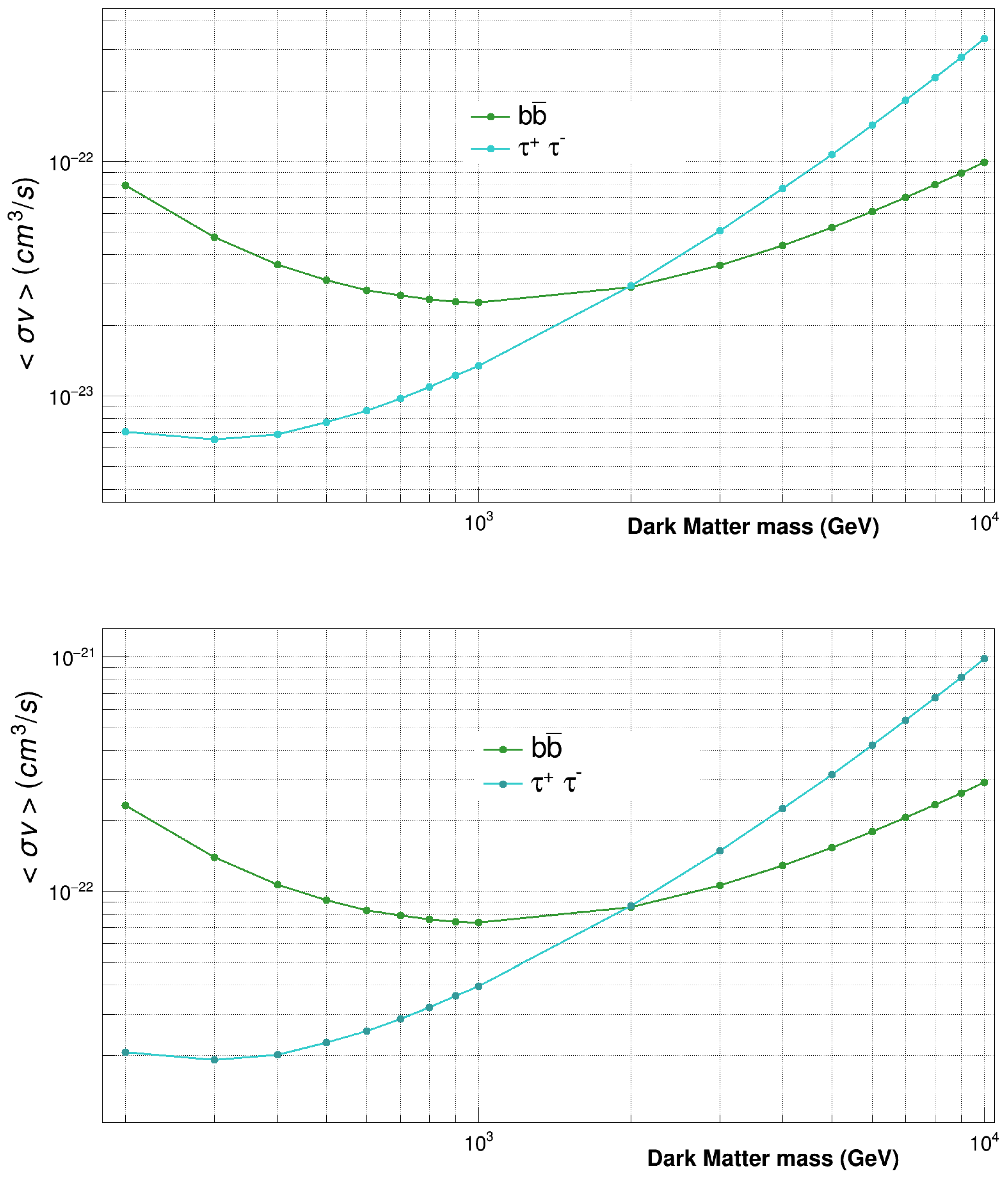
4.1. Expectations for MACE
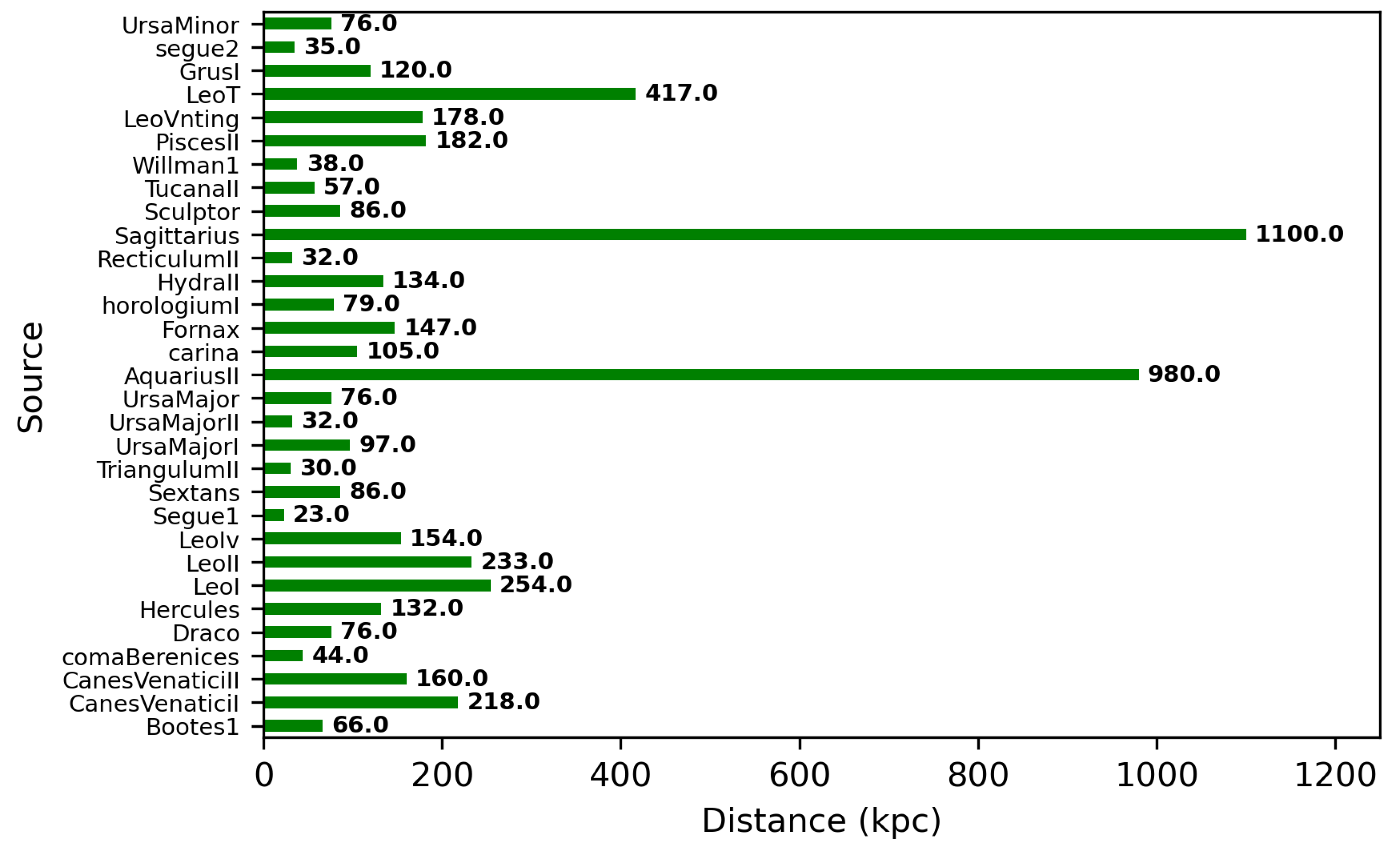
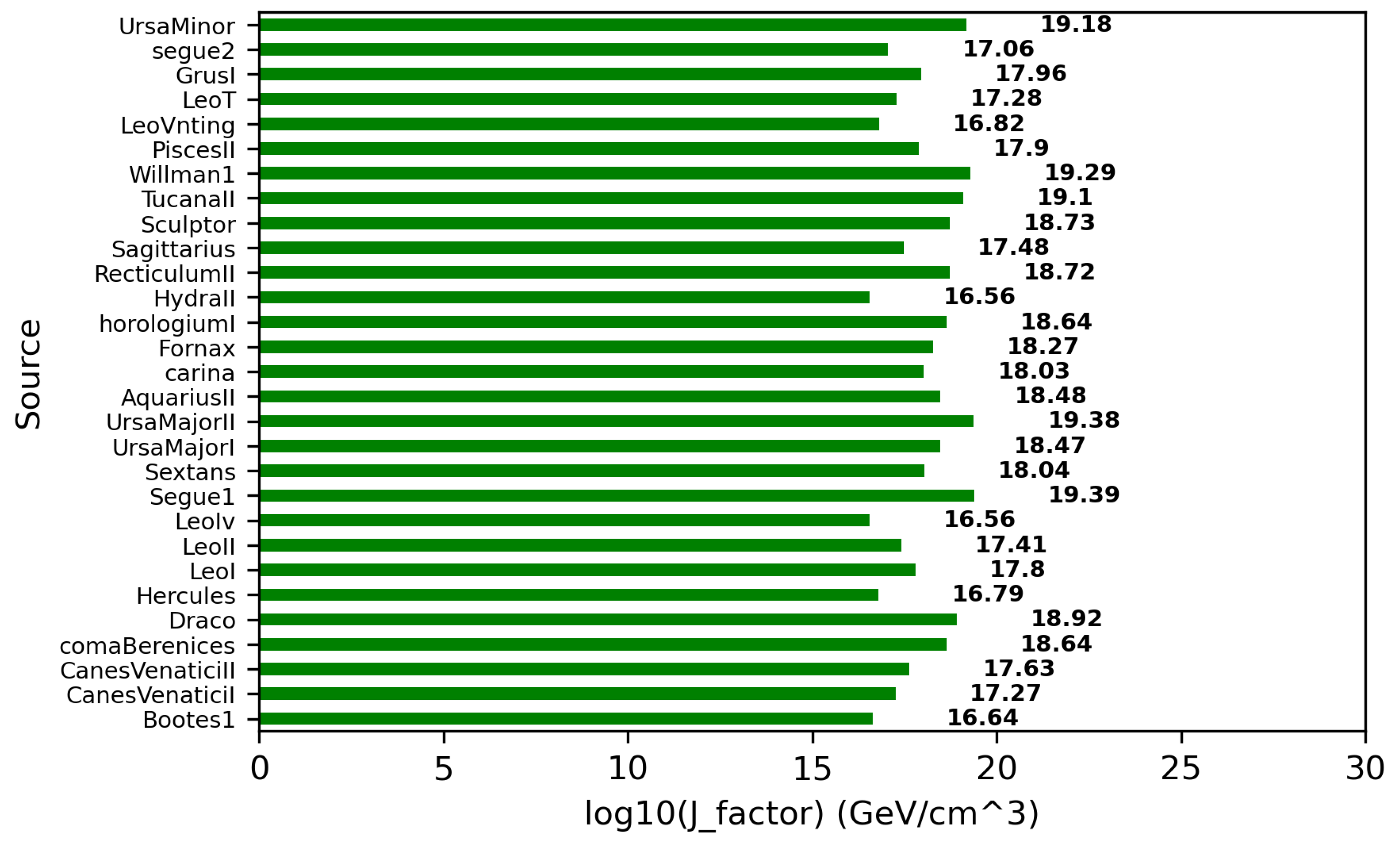
4.2. Plausible Targets
5. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bennett, C.L.; Halpern, M.; Hinshaw, G.; Jarosik, N.; Kogut, A.; Limon, M.; Meyer, S.S.; Page, L.; Spergel, D.N.; Tucker, G.S.; et al. First-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Preliminary Maps and Basic Results. Astrophys. J. Suppl. Ser. 2003, 148, 1. [Google Scholar] [CrossRef]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.B.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. Astron. J. 1998, 116, 1009. [Google Scholar] [CrossRef]
- Weinberg, D.H.; Mortonson, M.J.; Eisenstein, D.J.; Hirata, C.; Riess, A.G.; Rozo, E. Observational probes of cosmic acceleration. Phys. Rep. 2013, 530, 87. [Google Scholar]
- Abbott, T.M.; Aguena, M.; Alarcon, A.; Allam, S.; Alves, O.; Amon, A.; Andrade-Oliveira, F.; Annis, J.; Avila, S.; Bacon, D.; et al. Dark Energy Survey Year 3 results: Cosmological constraints from galaxy clustering and weak lensing. Phys. Rev. D 2022, 105, 023520. [Google Scholar] [CrossRef]
- Weinberg, S. The cosmological constant problem. Rev. Mod. Phys. 1989, 61, 1–23. [Google Scholar] [CrossRef]
- Trimble, V. Existence and nature of dark matter in the universe. Ann. Rev. Astron. Astrophys. 1987, 25, 425–472. [Google Scholar] [CrossRef]
- Guth, A.H. Inflationary universe: A possible solution to the horizon and flatness problems. Phys. Rev. D 1981, 23, 347–356. [Google Scholar] [CrossRef]
- Poincare, H. The Milky Way and the Theory of Gases. Pop. Astron. 1906, 14, 475–488. [Google Scholar]
- Zwicky, F. The Redshift of Extragalactic Nebulae. Helv. Phys. Acta 1933, 6, 110–127. [Google Scholar]
- Zwicky, F. On the Masses of Nebulae and of Clusters of Nebulae. Astrophys. J. 1937, 86, 217. [Google Scholar] [CrossRef]
- Freeman, K.C. On the Disks of Spiral and S0 Galaxies. Astrophys. J. 1970, 160, 811. [Google Scholar] [CrossRef]
- Rogstad, D.H.; Shostak, G.S. Gross Properties of Five Scd Galaxies as Determined from 21-CENTIMETER Observations. Astrophys. J. 1972, 1756, 315. [Google Scholar] [CrossRef]
- Roberts, M.S. Radio Observations of Neutral Hydrogen in Galaxies. In Galaxies and the Universe; University of Chicago Press: Chicago, IL USA, 1975; p. 309. [Google Scholar]
- Boveia, A.; Doglioni, C. Dark Matter Searches at Colliders. Annu. Rev. Nucl. Part. Sci. 2018, 68, 429–459. [Google Scholar] [CrossRef]
- Workman, R.L.; Burkert, V.D.; Crede, V.; Klempt, E.; Thoma, U.; Tiator, L.; Agashe, K.; Aielli, G.; Allanach, B.C.; Amsler, C.; et al. Review of Particle Physics. Prog. Theor. Exp. Phys. 2022, 083C01. [Google Scholar] [CrossRef]
- Jungman, G.; Kamionkowski, M.; Griest, K. Supersymmetric dark matter. Phys. Rep. 1996, 267, 195–373. [Google Scholar] [CrossRef]
- Harigaya, K.; Mukaida, K.; Yamada, M. Dark matter production during the thermalization era. J. High Energy Phys. 2019, 2019, 59. [Google Scholar] [CrossRef]
- Steigman, G.; Dasgupta, B.; Beacom, J.F. Precise relic WIMP abundance and its impact on searches for dark matter annihilation. Phys. Rev. D 2012, 86, 023506. [Google Scholar] [CrossRef]
- Bertone, G.; Hooper, D.; Silk, J. Particle dark matter: Evidence, candidates and constraints. Phys. Rep. 2005, 405, 279–390. [Google Scholar] [CrossRef]
- Griest, K.; Kamionkowski, M. Unitarity limits on the mass and radius of dark-matter particles. Phys. Rev. Lett. 1990, 64, 615. [Google Scholar] [CrossRef]
- Roszkowski, L.; Sessolo, E.M.; Trojanowski, S. WIMP dark matter candidates and searches—Current status and future prospects. Rep. Prog. Phys. 2018, 81, 066201. [Google Scholar] [CrossRef] [PubMed]
- Hochberg, Y.; Kuflik, E.; Murayama, H. Twin Higgs model with strongly interacting massive particle dark matter. Phys. Rev. D 2019, 99, 015005. [Google Scholar] [CrossRef]
- Gaskins, J.M. A review of indirect searches for particle dark matter. Contp. Phys. 2016, 57, 496–525. [Google Scholar] [CrossRef]
- Gondolo, P.; Edsjö, J.; Ullio, P.; Bergström, L.; Schelke, M.; Baltz, E.A. DarkSUSY: Computing supersymmetric dark matter properties numerically. J. Cosm. Astrop. Phys. 2004, 0407, 008. [Google Scholar] [CrossRef]
- Belanger, G.; Boudjema, F.; Pukhov, A.; Semenov, A. micrOMEGAs: Version 1.3. Comput. Phys. Commun. 2016, 174, 577–604. [Google Scholar] [CrossRef]
- Tesla, E.J.; Stefano, P. Fitting the Gamma-Ray Spectrum from Dark Matter with DMFIT: GLAST and the Galactic Center Region. J. Cosm. Astrop. Phys. 2008, 0811, 003. [Google Scholar]
- Cirelli, M.; Corcella, G.; Hektor, A.; Hütsi, G.; Kadastik, M.; Panci, P.; Raidal, M.; Sala, F.; Strumia, A. PPPC 4 DM ID: A Poor Particle Physicist Cookbook for Dark Matter Indirect Detection. J. Cosm. Astrop. Phys. 2011, 11032, 051. [Google Scholar] [CrossRef]
- Sjostrand, T.; Ask, S.; Christiansen, J.R.; Corke, R.; Desai, N.; Ilten, P.; Mrenna, S.; Prestel, S.; Rasmussen, C.O.; Skands, P.Z. An Introduction to PYTHIA 8.2. Comput. Phys. Commun. 2015, 191, 159–177. [Google Scholar] [CrossRef]
- Ambrogi, F.; Arina, C.; Backović, M.; Heisig, J.; Maltoni, F.; Mantani, L.; Mattelaer, O.; Mohlabeng, G. MadDM v.3.0: A comprehensive tool for dark matter studies. Phys. Dark Univ. 2019, 24, 100249. [Google Scholar] [CrossRef]
- Bauer, C.W.; Rodd, N.L.; Webber, B.R. Dark matter spectra from the electroweak to the Planck scale. J. High Energy Phys. 2021, 2021, 121. [Google Scholar] [CrossRef]
- Evans, N.W.; Ferrer, F.; Sarkar, S. A travel guide to the dark matter annihilation signal. Phys. Rev. D 2004, 69, 123501. [Google Scholar] [CrossRef]
- Singh, K.K. Gamma-ray astronomy with the imaging atmospheric Cherenkov telescopes in India. J. Astrophys. Astron. 2022, 43, 3. [Google Scholar] [CrossRef]
- Yadav, K.K.; Chouhan, N.; Thubstan, R.; Norlha, S.; Hariharan, J.; Borwankar, C.; Chandra, P.; Dhar, V.K.; Mankuzhyil, N.; Godambe, S.; et al. Commissioning of the MACE gamma-ray telescope at Hanle, Ladakh, India. Curr. Sci. 2022, 123, 1428. [Google Scholar] [CrossRef]
- Borwankar, C.; Sharma, M.; Hariharan, J.; Venugopal, K.; Godambe, S.; Mankuzhyil, N.; Chandra, P.; Khurana, M.; Sarkar, D.; Dar, Z.A.; et al. Observations of the Crab Nebula with MACE (major atmospheric Cherenkov experiment). Astropart. Phys. 2024, 159, 102960. [Google Scholar]
- Godambe, S.; Mankuzhiyil, N.; Borwankar, C.; Ghosal, B.; Tolamatti, A.; Pal, M.; Chandra, P.; Khurana, M.; Pandey, P.; Dar, Z.A.; et al. Very High-energy Gamma-Ray Episodic Activity of Radio Galaxy NGC 1275 in 2022–2023 Measured with MACE. Astrophys. J. Lett. 2024, 974, L31. [Google Scholar] [CrossRef]
- Tolamatti, A.; Garg, A.; Pathania, A.; Singh, K.; Borwankar, C.; Khurana, M.; Chandra, P.; Shukla, A.; Godiyal, S.; Godambe, S.; et al. Search for very high energy gamma-ray emission from a sample of high redshift blazars with MACE. J. High Energy Phys. 2025, 45, 241–249. [Google Scholar] [CrossRef]
- Borwankar, C.; Bhatt, N.; Bhattacharyya, S.; Rannot, R.; Tickoo, A.; Koul, R.; Thoudam, S. Simulation studies of MACE-I: Trigger rates and energy thresholds. Astropart. Phys. 2016, 84, 97–106. [Google Scholar] [CrossRef]
- Singh, K.K.; Yadav, K.K. 20 years of Indian gamma ray astronomy using imaging Cherenkov telescopes and road ahead. Universe 2021, 7, 96. [Google Scholar] [CrossRef]
- Khurana, M.; Singh, K.K.; Godiyal, S.; Yadav, K.K. Effects of the moonlight on the operating parameters of the MACE γ-ray telescope: A feasibility study. J. Astrophys. Astron. 2022, 43, 12. [Google Scholar] [CrossRef]
- Khurana, M.; Yadav, K.K.; Chandra, P.; Singh, K.K.; Pathania, A.; Borwankar, C. PyMAP: Python-Based Data Analysis Package with a New Image Cleaning Method to Enhance the Sensitivity of MACE Telescope. Galaxies 2025, 13, 14. [Google Scholar] [CrossRef]
- Tolamatti, A.; Singh, K.K.; Yadav, K.K. Feasibility study of observing γ-ray emission from high redshift blazars using the MACE telescope. J. Astrophys. Astron. 2022, 43, 49. [Google Scholar] [CrossRef]
- Merritt, D.; Milosavljević, M.; Verde, L.; Jimenez, R. Dark Matter Spikes and Annihilation Radiation from the Galactic Center. Phys. Rev. Lett. 2002, 88, 191301. [Google Scholar] [CrossRef] [PubMed]
- Ackermann, M.; Albert, A.; Anderson, B.; Atwood, W.B.; Baldini, L.; Barbiellini, G.; Bastieri, D.; Bechtol, K.; Bellazzini, R.; Bissaldi, E.; et al. Searching for Dark Matter Annihilation from Milky Way Dwarf Spheroidal Galaxies with Six Years of Fermi Large Area Telescope Data. Phys. Rev. Lett. 2015, 115, 231301. [Google Scholar] [CrossRef]
- Sánchez-Conde, M.A.; Cannoni, M.; Zandanel, F.; Gómez, M.; Prada, F. Dark matter searches with Cherenkov telescopes: Nearby dwarf galaxies or local galaxy clusters? J. Cosmo. Astropart. Phys. 2011, 2011, 011. [Google Scholar] [CrossRef]
- Grcevich, J.; Putman, M.E. HI in Local Group Dwarf Galaxies and Stripping by the Galactic Halo. Astrophys. J. 2009, 696, 385–395. [Google Scholar] [CrossRef]
- Strigari, L.E. Galactic Searches for Dark Matter. Phys. Rep. 2013, 531, 1. [Google Scholar] [CrossRef]
- Read, J.I.; Walker, M.G.; Steger, P. Dark matter heats up in dwarf galaxies. Mon. Not. R. Astron. Soc. 2019, 484, 1401–1420. [Google Scholar] [CrossRef]
- Hayashi, K.; Chiba, M.; Ishiyama, T. Diversity of Dark Matter Density Profiles in the Galactic Dwarf Spheroidal Satellites. Astrophys. J. 2020, 904, 45. [Google Scholar] [CrossRef]
- Navarro, J.F.; Frenk, C.S.; White, S.D.M. A Universal Density Profile from Hierarchical Clustering. Astrophys. J. 1997, 490, 493–508. [Google Scholar] [CrossRef]
- Khurana, M.; Pathania, A.; Singh, K.K.; Borwankar, C.; Netrakanti, P.K.; Yadav, K.K. Prospects of detecting gamma-ray signal of dark matter interaction with the MACE telescope. Proc. Sci. 2023, ICRC2023, 1412. [Google Scholar]
- Ackermann, M.; Ajello, M.; Albert, A.; Atwood, W.B.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; Bechtol, K.; Bellazzini, R.; et al. Constraining Dark Matter Models from a Combined Analysis of Milky Way Satellites with the Fermi Large Area Telescope. Phys. Rev. Lett. 2011, 107, 241302. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Liang, Y.-F.; Fan, Y.-Z. Search for gamma-ray emission from the 12 nearby dwarf spheroidal galaxies with 12 years of Fermi-LAT data. Phys. Rev. D 2021, 104, 083037. [Google Scholar] [CrossRef]
- Acciari, V.A.; Ansoldi, S.; Antonelli, L.; Engels, A.A.; Artero, M.; Asano, K.; Baack, D.; Babić, A.; Baquero, A.; de Almeida, U.B.; et al. Combined searches for dark matter in dwarf spheroidal galaxies observed with the MAGIC telescopes, including new data from Coma Berenices and Draco. Phys. Dark Universe 2022, 35, 100912. [Google Scholar] [CrossRef]
- Acharyya, A.; Adams, C.B.; Bangale, P.; Bartkoske, J.T.; Batista, P.; Benbow, W.; Christiansen, J.L.; Chromey, A.J.; Duerr, A.; Errando, M.; et al. Indirect search for dark matter with a combined analysis of dwarf spheroidal galaxies from VERITAS. Phys. Rev. D 2024, 110, 063034. [Google Scholar] [CrossRef]
- Abramowski, A.; Acero, F.; Aharonian, F.; Akhperjanian, A.; Anton, G.; Barnacka, A.; de Almeida, U.B.; Bazer-Bachi, A.; Becherini, Y.; Becker, J.; et al. H.E.S.S. constraints on dark matter annihilations towards the sculptor and carina dwarf galaxies. Astropart. Phys. 2011, 34, 608–616. [Google Scholar] [CrossRef]
- Cao, Z.; Aharonian, F.; An, Q.; Axikegu; Bai, Y.X.; Bao, Y.W.; Bastieri, D.; Bi, X.J.; Bi, Y.J.; Cai, J.T.; et al. Constraints on Ultraheavy Dark Matter Properties from Dwarf Spheroidal Galaxies with LHAASO Observations. Phys. Rev. Lett. 2024, 133, 061001. [Google Scholar] [CrossRef]
- Ackermann, M.; Ajello, M.; Atwood, W.B.; Baldini, L.; Barbiellini, G.; Bastieri, D.; Bechtol, K.; Bellazzini, R.; Blandford, R.D.; Bloom, E.D.; et al. Constraints on the Galactic Halo Dark Matter from Fermi-LAT Diffuse Measurements. Astrophys. J. 2012, 761, 91. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khurana, M.; Singh, K.K.; Pathania, A.; Netrakanti, P.K.; Yadav, K.K. Very-High-Energy Gamma-Ray Observations as a Probe to the Nature of Dark Matter and Prospects for MACE. Galaxies 2025, 13, 53. https://doi.org/10.3390/galaxies13030053
Khurana M, Singh KK, Pathania A, Netrakanti PK, Yadav KK. Very-High-Energy Gamma-Ray Observations as a Probe to the Nature of Dark Matter and Prospects for MACE. Galaxies. 2025; 13(3):53. https://doi.org/10.3390/galaxies13030053
Chicago/Turabian StyleKhurana, Mani, Krishna Kumar Singh, Atul Pathania, Pawan Kumar Netrakanti, and Kuldeep Kumar Yadav. 2025. "Very-High-Energy Gamma-Ray Observations as a Probe to the Nature of Dark Matter and Prospects for MACE" Galaxies 13, no. 3: 53. https://doi.org/10.3390/galaxies13030053
APA StyleKhurana, M., Singh, K. K., Pathania, A., Netrakanti, P. K., & Yadav, K. K. (2025). Very-High-Energy Gamma-Ray Observations as a Probe to the Nature of Dark Matter and Prospects for MACE. Galaxies, 13(3), 53. https://doi.org/10.3390/galaxies13030053






