Semi-Empirical Estimates of the Cosmic Planet Formation Rate
Abstract
1. Introduction
2. Semi-Empirical Modeling
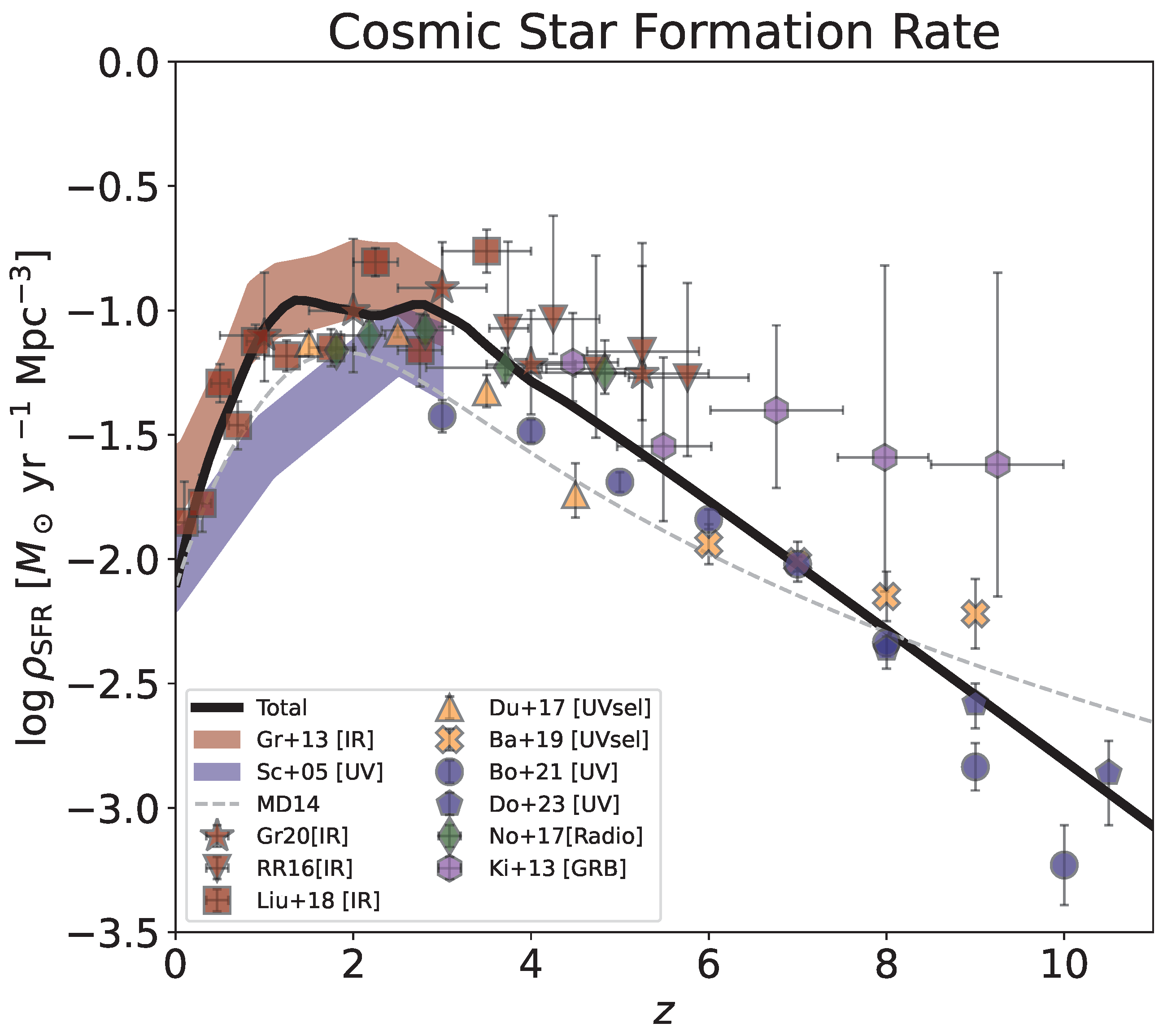
2.1. Galaxy Formation Side
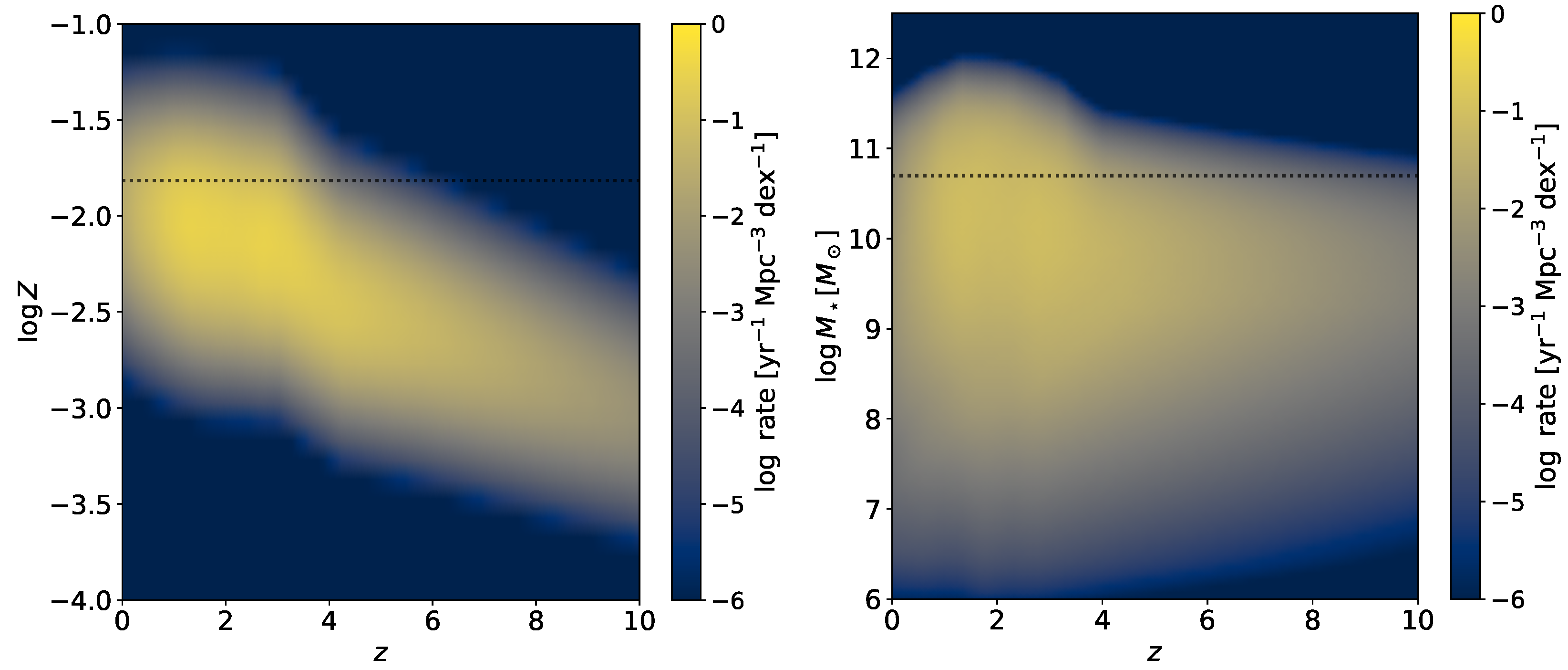
2.2. Stellar and Planetary Side
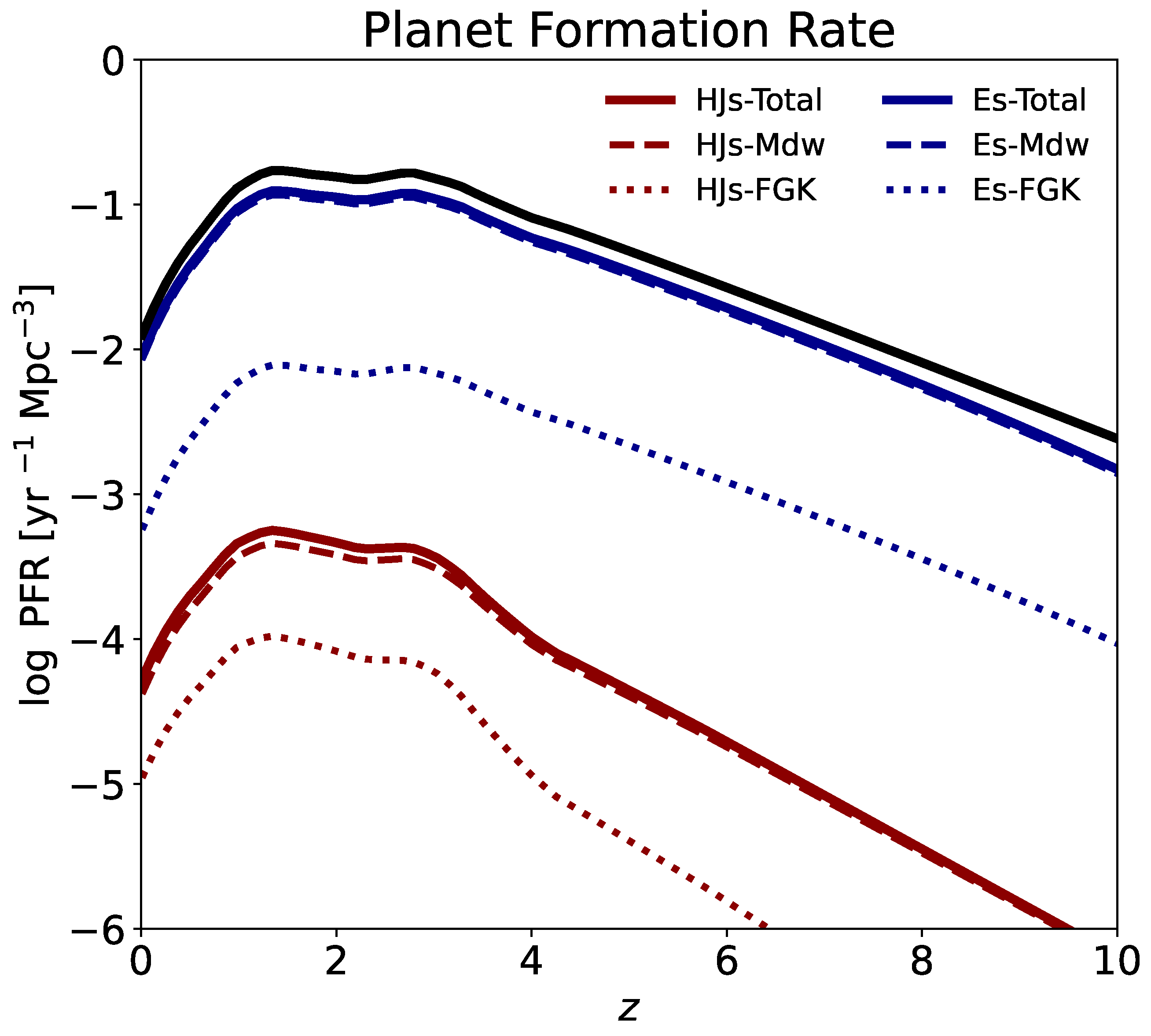
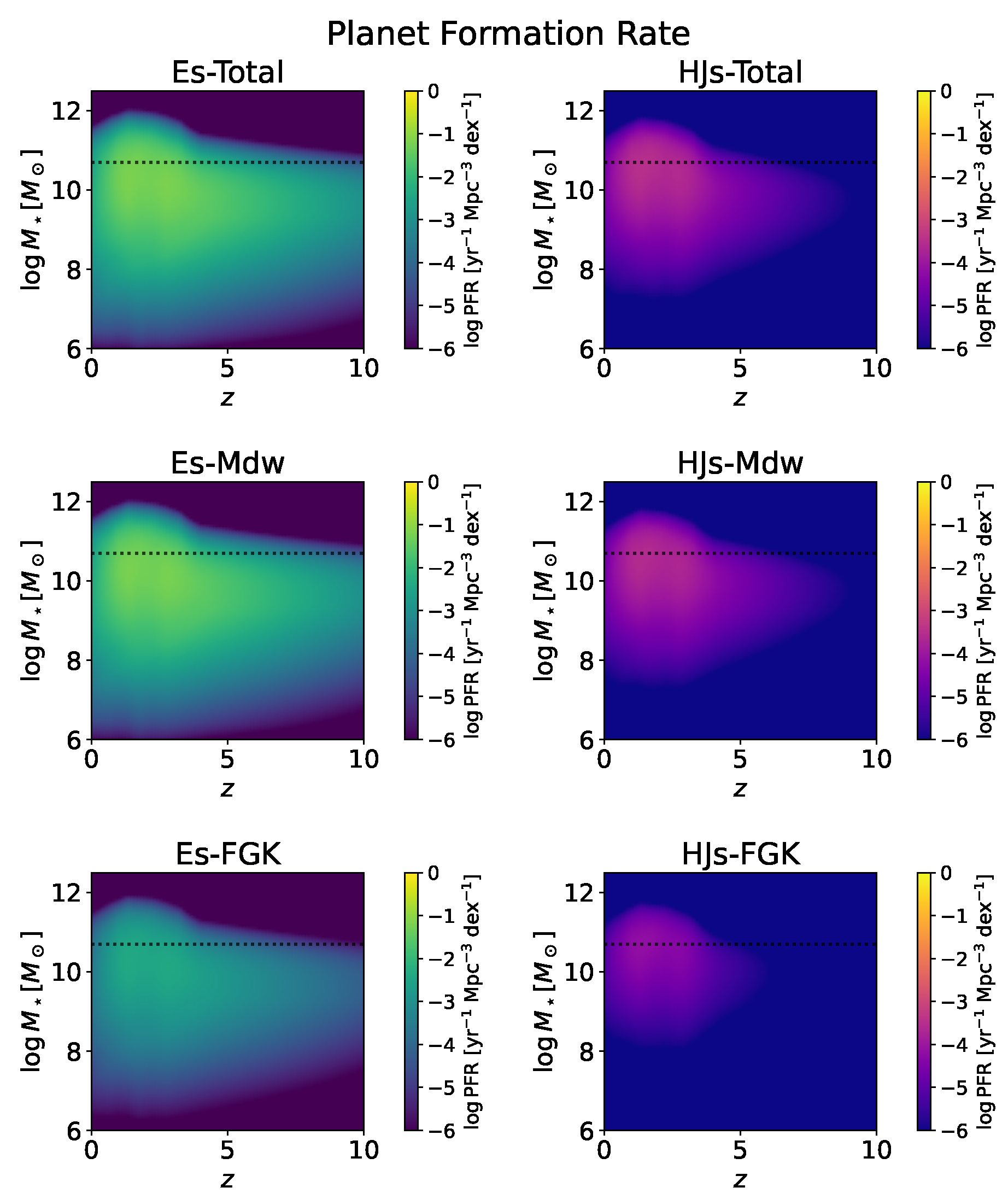
2.3. Planet Formation Rate
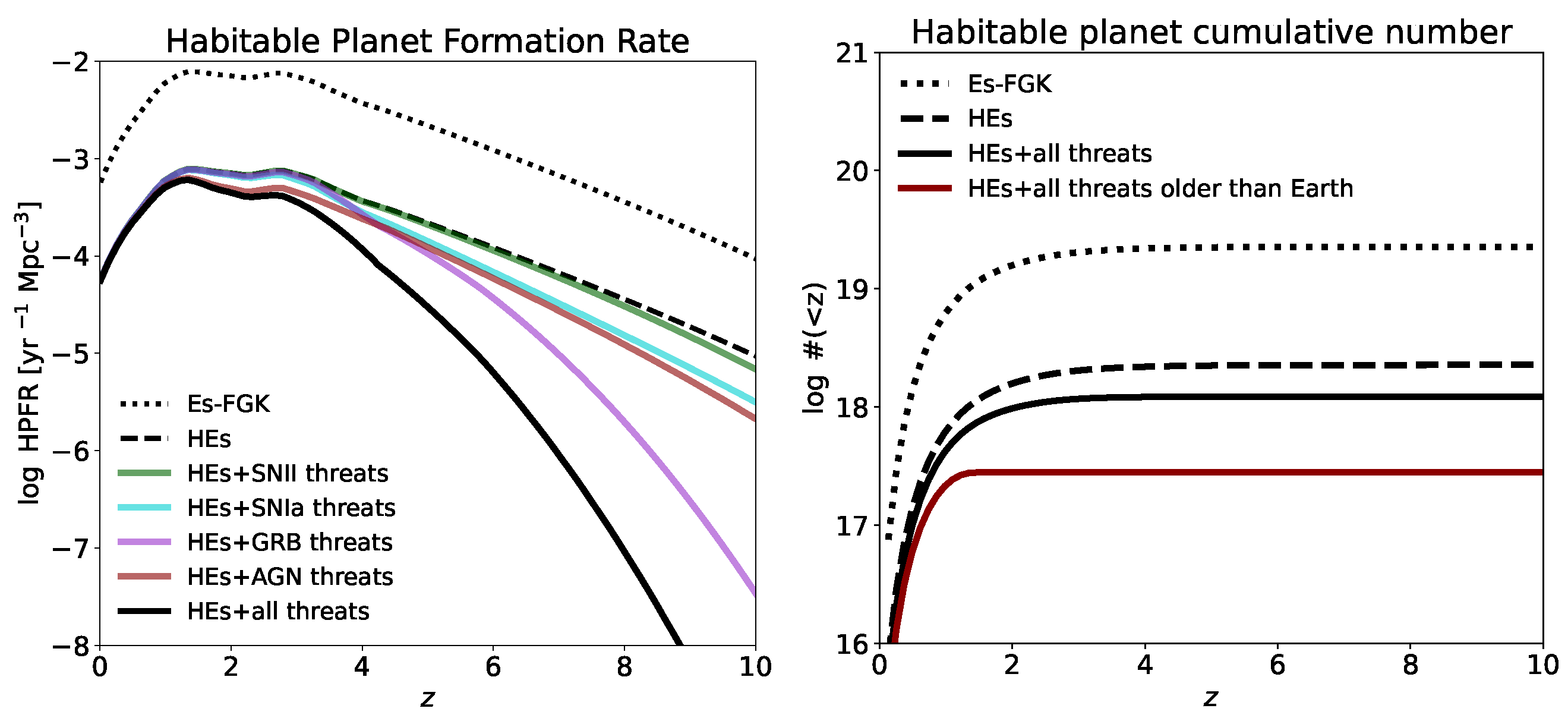
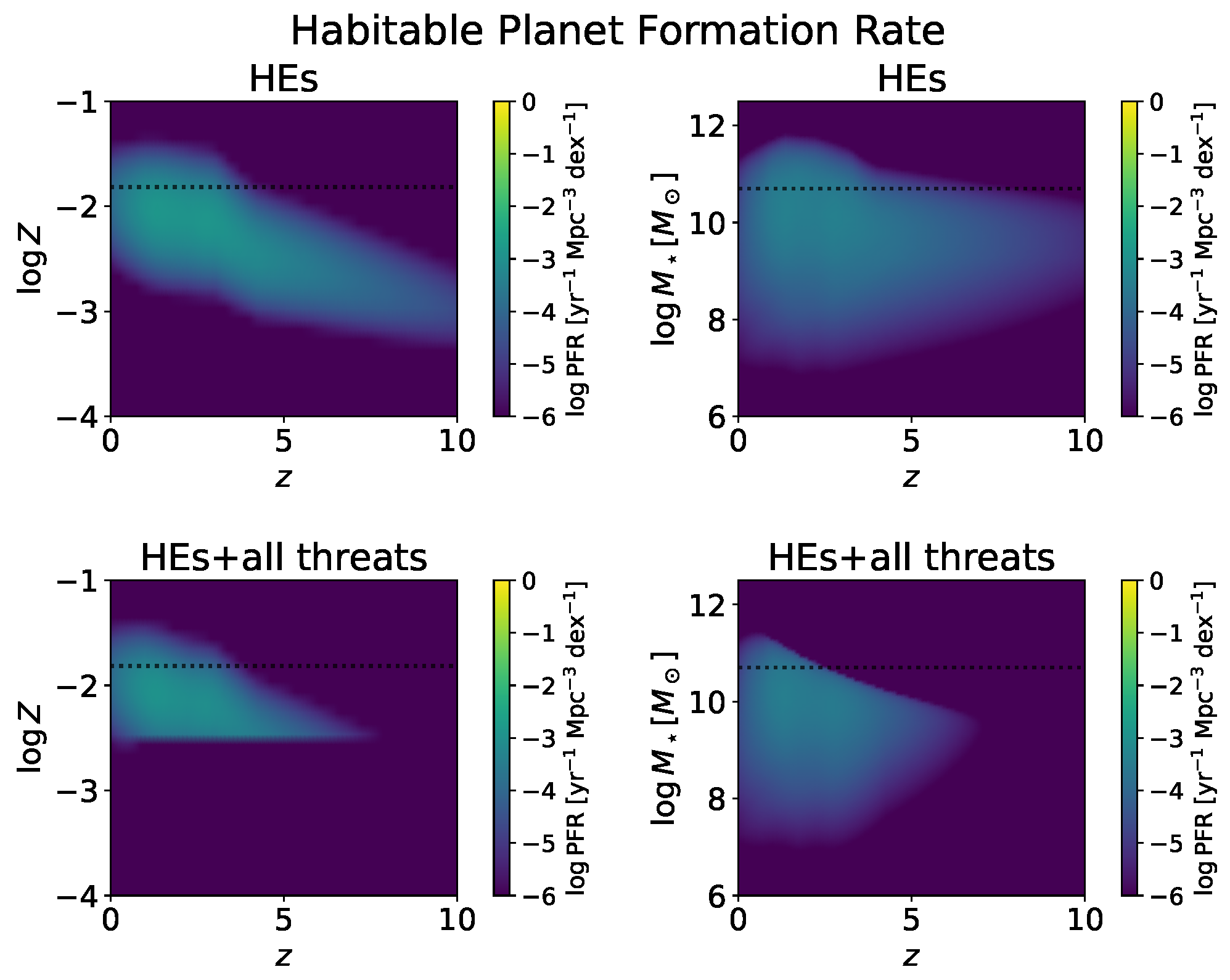
3. Results
4. Discussion: Habitability and Threatening Sources
5. Summary
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lineweaver, C.H. An Estimate of the Age Distribution of Terrestrial Planets in the Universe: Quantifying Metallicity as a Selection Effect. Icarus 2001, 151, 307–313. [Google Scholar] [CrossRef]
- Fischer, D.A.; Valenti, J. The Planet-Metallicity Correlation. Astrophys. J. 2005, 622, 1102–1117. [Google Scholar] [CrossRef]
- Sousa, S.G.; Santos, N.C.; Mayor, M.; Udry, S.; Casagrande, L.; Israelian, G.; Pepe, F.; Queloz, D.; Monteiro, M.J.P.F.G. Spectroscopic parameters for 451 stars in the HARPS GTO planet search program. Stellar [Fe/H] and the frequency of exo-Neptunes. Astron. Astrophys. 2008, 487, 373–381. [Google Scholar] [CrossRef]
- Johnson, J.L.; Li, H. The First Planets: The Critical Metallicity for Planet Formation. Astrophys. J. 2012, 751, 81. [Google Scholar] [CrossRef]
- Gaidos, E.; Mann, A.W. M Dwarf Metallicities and Giant Planet Occurrence: Ironing Out Uncertainties and Systematics. Astrophys. J. 2014, 791, 54. [Google Scholar] [CrossRef]
- Buchhave, L.A.; Latham, D.W.; Johansen, A.; Bizzarro, M.; Torres, G.; Rowe, J.F.; Batalha, N.M.; Borucki, W.J.; Brugamyer, E.; Caldwell, C.; et al. An abundance of small exoplanets around stars with a wide range of metallicities. Nature 2012, 486, 375–377. [Google Scholar] [CrossRef] [PubMed]
- Petigura, E.A.; Marcy, G.W.; Winn, J.N.; Weiss, L.M.; Fulton, B.J.; Howard, A.W.; Sinukoff, E.; Isaacson, H.; Morton, T.D.; Johnson, J.A. The California-Kepler Survey. IV. Metal-rich Stars Host a Greater Diversity of Planets. Astron. J. 2018, 155, 89. [Google Scholar] [CrossRef]
- Thompson, S.E.; Coughlin, J.L.; Hoffman, K.; Mullally, F.; Christiansen, J.L.; Burke, C.J.; Bryson, S.; Batalha, N.; Haas, M.R.; Catanzarite, J.; et al. Planetary Candidates Observed by Kepler. VIII. A Fully Automated Catalog with Measured Completeness and Reliability Based on Data Release 25. Astrophys. J. Suppl. 2018, 235, 38. [Google Scholar] [CrossRef] [PubMed]
- Zhu, W. Influence of Stellar Metallicity on Occurrence Rates of Planets and Planetary Systems. Astrophys. J. 2019, 873, 8. [Google Scholar] [CrossRef]
- Lu, C.X.; Schlaufman, K.C.; Cheng, S. An Increase in Small-planet Occurrence with Metallicity for Late-type Dwarf Stars in the Kepler Field and Its Implications for Planet Formation. Astron. J. 2020, 160, 253. [Google Scholar] [CrossRef]
- Zhu, W.; Dong, S. Exoplanet Statistics and Theoretical Implications. Annu. Rev. Astron. Astrophys. 2021, 59, 291–336. [Google Scholar] [CrossRef]
- Bello-García, A.; Passegger, V.M.; Ordieres-Meré, J.; Schweitzer, A.; Caballero, J.A.; González-Marcos, A.; Ribas, I.; Reiners, A.; Quirrenbach, A.; Amado, P.J.; et al. The CARMENES search for exoplanets around M dwarfs. A deep transfer learning method to determine Teff and [M/H] of target stars. Astron. Astrophys. 2023, 673, A105. [Google Scholar] [CrossRef]
- Gore, R.; Giacalone, S.; Dressing, C.D.; Turtelboom, E.V.; Schroeder, A.; Fortenbach, C.D.; Hardegree-Ullman, K.K.; Zink, J.K.; Mayo, A.W.; Schlieder, J.E.; et al. Metallicities and Refined Stellar Parameters for 52 Cool Dwarfs with Transiting Planets and Planet Candidates. Astrophys. J. Suppl. 2024, 271, 48. [Google Scholar] [CrossRef]
- Kewley, L.J.; Ellison, S.L. Metallicity Calibrations and the Mass-Metallicity Relation for Star-forming Galaxies. Astrophys. J. 2008, 681, 1183–1204. [Google Scholar] [CrossRef]
- Mannucci, F.; Cresci, G.; Maiolino, R.; Marconi, A.; Gnerucci, A. A fundamental relation between mass, star formation rate and metallicity in local and high-redshift galaxies. Mon. Not. R. Astron. Soc. 2010, 408, 2115–2127. [Google Scholar] [CrossRef]
- Andrews, B.H.; Martini, P. The Mass-Metallicity Relation with the Direct Method on Stacked Spectra of SDSS Galaxies. Astrophys. J. 2013, 765, 140. [Google Scholar] [CrossRef]
- Zahid, H.J.; Kashino, D.; Silverman, J.D.; Kewley, L.J.; Daddi, E.; Renzini, A.; Rodighiero, G.; Nagao, T.; Arimoto, N.; Sanders, D.B.; et al. The FMOS-COSMOS Survey of Star-forming Galaxies at z~1.6. II. The Mass-Metallicity Relation and the Dependence on Star Formation Rate and Dust Extinction. Astrophys. J. 2014, 792, 75. [Google Scholar] [CrossRef]
- Hunt, L.; Dayal, P.; Magrini, L.; Ferrara, A. Coevolution of metallicity and star formation in galaxies to z ≃ 3.7 - I. A Fundamental Plane. Mon. Not. R. Astron. Soc. 2016, 463, 2002–2019. [Google Scholar] [CrossRef]
- Maiolino, R.; Mannucci, F. De re metallica: The cosmic chemical evolution of galaxies. Astron. Astrophys. Rev. 2019, 27, 3. [Google Scholar] [CrossRef]
- Curti, M.; Mannucci, F.; Cresci, G.; Maiolino, R. The mass-metallicity and the fundamental metallicity relation revisited on a fully Te-based abundance scale for galaxies. Mon. Not. R. Astron. Soc. 2020, 491, 944–964. [Google Scholar] [CrossRef]
- Boco, L.; Lapi, A.; Chruslinska, M.; Donevski, D.; Sicilia, A.; Danese, L. Evolution of Galaxy Star Formation and Metallicity: Impact on Double Compact Object Mergers. Astrophys. J. 2021, 907, 110. [Google Scholar] [CrossRef]
- Chruślińska, M.; Nelemans, G.; Boco, L.; Lapi, A. The impact of the FMR and starburst galaxies on the (low metallicity) cosmic star formation history. Mon. Not. R. Astron. Soc. 2021, 508, 4994–5027. [Google Scholar] [CrossRef]
- Curti, M.; D’Eugenio, F.; Carniani, S.; Maiolino, R.; Sandles, L.; Witstok, J.; Baker, W.M.; Bennett, J.S.; Piotrowska, J.M.; Tacchella, S.; et al. The chemical enrichment in the early Universe as probed by JWST via direct metallicity measurements at z ∼ 8. Mon. Not. R. Astron. Soc. 2023, 518, 425–438. [Google Scholar] [CrossRef]
- Nakajima, K.; Ouchi, M.; Isobe, Y.; Harikane, Y.; Zhang, Y.; Ono, Y.; Umeda, H.; Oguri, M. JWST Census for the Mass-Metallicity Star Formation Relations at z = 4–10 with Self-consistent Flux Calibration and Proper Metallicity Calibrators. Astrophys. J. Suppl. 2023, 269, 33. [Google Scholar] [CrossRef]
- Gonzalez, G.; Brownlee, D.; Ward, P. The Galactic Habitable Zone: Galactic Chemical Evolution. Icarus 2001, 152, 185–200. [Google Scholar] [CrossRef]
- Lineweaver, C.H.; Fenner, Y.; Gibson, B.K. The Galactic Habitable Zone and the Age Distribution of Complex Life in the Milky Way. Science 2004, 303, 59–62. [Google Scholar] [CrossRef] [PubMed]
- Gowanlock, M.G.; Patton, D.R.; McConnell, S.M. A Model of Habitability within the Milky Way Galaxy. Astrobiology 2011, 11, 855–873. [Google Scholar] [CrossRef] [PubMed]
- Behroozi, P.; Peeples, M.S. On the history and future of cosmic planet formation. Mon. Not. R. Astron. Soc. 2015, 454, 1811–1817. [Google Scholar] [CrossRef]
- Gobat, R.; Hong, S.E. Evolution of galaxy habitability. Astron. Astrophys. 2016, 592, A96. [Google Scholar] [CrossRef][Green Version]
- Zackrisson, E.; Calissendorff, P.; González, J.; Benson, A.; Johansen, A.; Janson, M. Terrestrial Planets across Space and Time. Astrophys. J. 2016, 833, 214. [Google Scholar] [CrossRef]
- Forgan, D.; Dayal, P.; Cockell, C.; Libeskind, N. Evaluating galactic habitability using high-resolution cosmological simulations of galaxy formation. Int. J. Astrobiol. 2017, 16, 60–73. [Google Scholar] [CrossRef]
- Stanway, E.R.; Hoskin, M.J.; Lane, M.A.; Brown, G.C.; Childs, H.J.T.; Greis, S.M.L.; Levan, A.J. Exploring the cosmic evolution of habitability with galaxy merger trees. Mon. Not. R. Astron. Soc. 2018, 475, 1829–1842. [Google Scholar] [CrossRef]
- Whitmire, D.P. The habitability of large elliptical galaxies. Mon. Not. R. Astron. Soc. 2020, 494, 3048–3052. [Google Scholar] [CrossRef]
- Balbi, A.; Hami, M.; Kovačević, A. The Habitability of the Galactic Bulge. Life 2020, 10, 132. [Google Scholar] [CrossRef] [PubMed]
- Madau, P. Beyond the Drake Equation: A Time-dependent Inventory of Habitable Planets and Life-bearing Worlds in the Solar Neighborhood. Astrophys. J. 2023, 957, 66. [Google Scholar] [CrossRef]
- Boettner, C.; Dayal, P.; Trebitsch, M.; Libeskind, N.; Rice, K.; Cockell, C.; Tieleman, B.I. Populating the Milky Way. Characterising planet demographics by combining galaxy formation simulations and planet population synthesis models. Astron. Astrophys. 2024, 686, A167. [Google Scholar] [CrossRef]
- Aversa, R.; Lapi, A.; de Zotti, G.; Shankar, F.; Danese, L. Black Hole and Galaxy Coevolution from Continuity Equation and Abundance Matching. Astrophys. J. 2015, 810, 74. [Google Scholar] [CrossRef]
- Moster, B.P.; Naab, T.; White, S.D.M. EMERGE—An empirical model for the formation of galaxies since z ∼ 10. Mon. Not. R. Astron. Soc. 2018, 477, 1822–1852. [Google Scholar] [CrossRef]
- Behroozi, P.; Wechsler, R.H.; Hearin, A.P.; Conroy, C. UNIVERSEMACHINE: The correlation between galaxy growth and dark matter halo assembly from z = 0–10. Mon. Not. R. Astron. Soc. 2019, 488, 3143–3194. [Google Scholar] [CrossRef]
- Grylls, P.J.; Shankar, F.; Zanisi, L.; Bernardi, M. A statistical semi-empirical model: Satellite galaxies in groups and clusters. Mon. Not. R. Astron. Soc. 2019, 483, 2506–2523. [Google Scholar] [CrossRef]
- Hearin, A.P.; Ramachandra, N.; Becker, M.R.; DeRose, J. Differentiable Predictions for Large Scale Structure with SHAMNet. Open J. Astrophys. 2022, 5, 3. [Google Scholar] [CrossRef]
- Drakos, N.E.; Villasenor, B.; Robertson, B.E.; Hausen, R.; Dickinson, M.E.; Ferguson, H.C.; Furlanetto, S.R.; Greene, J.E.; Madau, P.; Shapley, A.E.; et al. Deep Realistic Extragalactic Model (DREaM) Galaxy Catalogs: Predictions for a Roman Ultra-deep Field. Astrophys. J. 2022, 926, 194. [Google Scholar] [CrossRef]
- Fu, H.; Shankar, F.; Ayromlou, M.; Dickson, M.; Koutsouridou, I.; Rosas-Guevara, Y.; Marsden, C.; Brocklebank, K.; Bernardi, M.; Shiamtanis, N.; et al. Testing the key role of the stellar mass-halo mass relation in galaxy merger rates and morphologies via DECODE, a novel Discrete statistical sEmi-empiriCal mODEl. Mon. Not. R. Astron. Soc. 2022, 516, 3206–3233. [Google Scholar] [CrossRef]
- Boco, L.; Lapi, A.; Shankar, F.; Fu, H.; Gabrielli, F.; Sicilia, A. TwO Parameters Semi Empirical Model (TOPSEM): Galaxy Evolution and Bulge/Disk Dicothomy from Two-stage Halo Accretion. Astrophys. J. 2023, 954, 97. [Google Scholar] [CrossRef]
- Zhang, H.; Behroozi, P.; Volonteri, M.; Silk, J.; Fan, X.; Hopkins, P.F.; Yang, J.; Aird, J. TRINITY I: Self-consistently modelling the dark matter halo-galaxy-supermassive black hole connection from z = 0–10. Mon. Not. R. Astron. Soc. 2023, 518, 2123–2163. [Google Scholar] [CrossRef]
- Lapi, A.; Boco, L. Semi-empirical Models of Galaxy Formation and Evolution. In Encyclopedia of Astrophysics; Elsevier: Amsterdam, The Netherlands, 2024. [Google Scholar]
- Planck Collaboration; Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; et al. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar] [CrossRef]
- Chabrier, G. Galactic Stellar and Substellar Initial Mass Function. Publ. Astron. Soc. Pac. 2003, 115, 763–795. [Google Scholar] [CrossRef]
- Weaver, J.R.; Davidzon, I.; Toft, S.; Ilbert, O.; McCracken, H.J.; Gould, K.M.L.; Jespersen, C.K.; Steinhardt, C.; Lagos, C.D.P.; Capak, P.L.; et al. COSMOS2020: The galaxy stellar mass function: The assembly and star formation cessation of galaxies at 0.2 < z < 7.5. Astron. Astrophys. 2023, 677, A184. [Google Scholar] [CrossRef]
- Popesso, P.; Concas, A.; Cresci, G.; Belli, S.; Rodighiero, G.; Inami, H.; Dickinson, M.; Ilbert, O.; Pannella, M.; Elbaz, D. The main sequence of star-forming galaxies across cosmic times. Mon. Not. R. Astron. Soc. 2023, 519, 1526–1544. [Google Scholar] [CrossRef]
- Gruppioni, C.; Pozzi, F.; Rodighiero, G.; Delvecchio, I.; Berta, S.; Pozzetti, L.; Zamorani, G.; Andreani, P.; Cimatti, A.; Ilbert, O.; et al. The Herschel PEP/HerMES luminosity function—I. Probing the evolution of PACS selected Galaxies to z = 4. Mon. Not. R. Astron. Soc. 2013, 432, 23–52. [Google Scholar] [CrossRef]
- Schiminovich, D.; Ilbert, O.; Arnouts, S.; Milliard, B.; Tresse, L.; Le Fèvre, O.; Treyer, M.; Wyder, T.K.; Budavári, T.; Zucca, E.; et al. The GALEX-VVDS Measurement of the Evolution of the Far-Ultraviolet Luminosity Density and the Cosmic Star Formation Rate. Astrophys. J. Lett. 2005, 619, L47–L50. [Google Scholar] [CrossRef]
- Gruppioni, C.; BEthermin, M.; Loiacono, F.; Le Fèvre, O.; Capak, P.; Cassata, P.; Faisst, A.L.; Schaerer, D.; Silverman, J.; Yan, L.; et al. The ALPINE-ALMA [CII] survey: The nature, luminosity function, and star formation history of dusty galaxies up to z = 6. Astron. Astrophys. 2020, 643, A8. [Google Scholar] [CrossRef]
- Rowan-Robinson, M.; Oliver, S.; Wang, L.; Farrah, D.; Clements, D.L.; Gruppioni, C.; Marchetti, L.; Rigopoulou, D.; Vaccari, M. The star formation rate density from z = 1 to 6. Mon. Not. R. Astron. Soc. 2016, 461, 1100–1111. [Google Scholar] [CrossRef]
- Liu, D.; Daddi, E.; Dickinson, M.; Owen, F.; Pannella, M.; Sargent, M.; Béthermin, M.; Magdis, G.; Gao, Y.; Shu, X.; et al. “Super-deblended” Dust Emission in Galaxies. I. The GOODS-North Catalog and the Cosmic Star Formation Rate Density out to Redshift 6. Astrophys. J. 2018, 853, 172. [Google Scholar] [CrossRef]
- Dunlop, J.S.; McLure, R.J.; Biggs, A.D.; Geach, J.E.; Michałowski, M.J.; Ivison, R.J.; Rujopakarn, W.; van Kampen, E.; Kirkpatrick, A.; Pope, A.; et al. A deep ALMA image of the Hubble Ultra Deep Field. Mon. Not. R. Astron. Soc. 2017, 466, 861–883. [Google Scholar] [CrossRef]
- Bhatawdekar, R.; Conselice, C.J.; Margalef-Bentabol, B.; Duncan, K. Evolution of the galaxy stellar mass functions and UV luminosity functions at z = 6–9 in the Hubble Frontier Fields. Mon. Not. R. Astron. Soc. 2019, 486, 3805–3830. [Google Scholar] [CrossRef]
- Oesch, P.A.; Bouwens, R.J.; Illingworth, G.D.; LabbE, I.; Stefanon, M. The Dearth of z = 10 Galaxies in All HST Legacy Fields—The Rapid Evolution of the Galaxy Population in the First 500 Myr*. Astrophys. J. 2018, 855, 105. [Google Scholar] [CrossRef]
- Bouwens, R.J.; Oesch, P.A.; Stefanon, M.; Illingworth, G.; LabbE, I.; Reddy, N.; Atek, H.; Montes, M.; Naidu, R.; Nanayakkara, T.; et al. New Determinations of the UV Luminosity Functions from z 9 to 2 Show a Remarkable Consistency with Halo Growth and a Constant Star Formation Efficiency. Astron. J. 2021, 162, 47. [Google Scholar] [CrossRef]
- Donnan, C.T.; McLeod, D.J.; Dunlop, J.S.; McLure, R.J.; Carnall, A.C.; Begley, R.; Cullen, F.; Hamadouche, M.L.; Bowler, R.A.A.; Magee, D.; et al. The evolution of the galaxy UV luminosity function at redshifts z = 8–15 from deep JWST and ground-based near-infrared imaging. Mon. Not. R. Astron. Soc. 2022, 518, 6011–6040. [Google Scholar] [CrossRef]
- Novak, M.; Smolčić, V.; Delhaize, J.; Delvecchio, I.; Zamorani, G.; Baran, N.; Bondi, M.; Capak, P.; Carilli, C.L.; Ciliegi, P.; et al. The VLA-COSMOS 3 GHz Large Project: Cosmic star formation history since z 5. Astron. Astrophys. 2017, 602, A5. [Google Scholar] [CrossRef]
- Kistler, M.D.; Yuksel, H.; Hopkins, A.M. The Cosmic Star Formation Rate from the Faintest Galaxies in the Unobservable Universe. arXiv 2013, arXiv:1305.1630. [Google Scholar] [CrossRef]
- Madau, P.; Dickinson, M. Cosmic Star-Formation History. Annu. Rev. Astron. Astrophys. 2014, 52, 415–486. [Google Scholar] [CrossRef]
- Horneck, G.; Rettberg, P. (Eds.) Complete Course in Astrobiology; Wiley, VCH Verlag: Weinheim, Germany, 2007. [Google Scholar]
- Longstaff, A. Astrobiology, An Introduction; CRC Press by Taylor & Francis: Boca Raton, FL, USA, 2015. [Google Scholar]
- Rothery, D.A.; Gilmour, I.; Sephton, M.A.; Anand, M. (Eds.) An Introduction to Astrobiology; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Kolb, V.M. (Ed.) Handbook of Astrobiology; CRC Press by Taylor & Francis: Boca Raton, FL, USA, 2021. [Google Scholar]
- Rasio, F.A.; Ford, E.B. Dynamical instabilities and the formation of extrasolar planetary systems. Science 1996, 274, 954–956. [Google Scholar] [CrossRef] [PubMed]
- Lin, D.N.C.; Ida, S. On the Origin of Massive Eccentric Planets. Astrophys. J. 1997, 477, 781–791. [Google Scholar] [CrossRef]
- Marzari, F.; Nagasawa, M.; Goździewski, K. Planet-planet scattering in presence of a companion star. Mon. Not. R. Astron. Soc. 2022, 510, 5050–5061. [Google Scholar] [CrossRef]
- Suzuki, D.; Bennett, D.P.; Sumi, T.; Bond, I.A.; Rogers, L.A.; Abe, F.; Asakura, Y.; Bhattacharya, A.; Donachie, M.; Freeman, M.; et al. The Exoplanet Mass-ratio Function from the MOA-II Survey: Discovery of a Break and Likely Peak at a Neptune Mass. Astrophys. J. 2016, 833, 145. [Google Scholar] [CrossRef]
- Bourrier, V.; Lecavelier des Etangs, A.; Ehrenreich, D.; Sanz-Forcada, J.; Allart, R.; Ballester, G.E.; Buchhave, L.A.; Cohen, O.; Deming, D.; Evans, T.M.; et al. Hubble PanCET: An extended upper atmosphere of neutral hydrogen around the warm Neptune GJ 3470b. Astron. Astrophys. 2018, 620, A147. [Google Scholar] [CrossRef]
- Holtzman, J.A.; Shetrone, M.; Johnson, J.A.; Allende Prieto, C.; Anders, F.; Andrews, B.; Beers, T.C.; Bizyaev, D.; Blanton, M.R.; Bovy, J.; et al. Abundances, Stellar Parameters, and Spectra from the SDSS-III/APOGEE Survey. Astron. J. 2015, 150, 148. [Google Scholar] [CrossRef]
- Stanton, T.M.; Cullen, F.; McLure, R.J.; Shapley, A.E.; Arellano-Córdova, K.Z.; Begley, R.; Amorín, R.; Barrufet, L.; Calabrò, A.; Carnall, A.C.; et al. The NIRVANDELS Survey: The stellar and gas-phase mass-metallicity relations of star-forming galaxies at z = 3.5. arXiv 2024, arXiv:2405.00774. [Google Scholar] [CrossRef]
- Maiolino, R.; Nagao, T.; Grazian, A.; Cocchia, F.; Marconi, A.; Mannucci, F.; Cimatti, A.; Pipino, A.; Ballero, S.; Calura, F.; et al. AMAZE. I. The evolution of the mass-metallicity relation at z > 3. Astron. Astrophys. 2008, 488, 463–479. [Google Scholar] [CrossRef]
- Kasting, J.F.; Whitmire, D.P.; Reynolds, R.T. Habitable Zones around Main Sequence Stars. Icarus 1993, 101, 108–128. [Google Scholar] [CrossRef] [PubMed]
- Kopparapu, R.K.; Ramirez, R.M.; SchottelKotte, J.; Kasting, J.F.; Domagal-Goldman, S.; Eymet, V. Habitable Zones around Main-sequence Stars: Dependence on Planetary Mass. Astrophys. J. Lett. 2014, 787, L29. [Google Scholar] [CrossRef]
- Petigura, E.A.; Howard, A.W.; Marcy, G.W. Prevalence of Earth-size planets orbiting Sun-like stars. Proc. Natl. Acad. Sci. USA 2013, 110, 19273–19278. [Google Scholar] [CrossRef] [PubMed]
- Dressing, C.D.; Charbonneau, D. The Occurrence of Potentially Habitable Planets Orbiting M Dwarfs Estimated from the Full Kepler Dataset and an Empirical Measurement of the Detection Sensitivity. Astrophys. J. 2015, 807, 45. [Google Scholar] [CrossRef]
- Adibekyan, V.; Figueira, P.; Santos, N.C. Which Type of Planets do We Expect to Observe in the Habitable Zone? Orig. Life Evol. Biosph. 2016, 46, 351–359. [Google Scholar] [CrossRef]
- Bryson, S.; Kunimoto, M.; Kopparapu, R.K.; Coughlin, J.L.; Borucki, W.J.; Koch, D.; Aguirre, V.S.; Allen, C.; Barentsen, G.; Batalha, N.M.; et al. The Occurrence of Rocky Habitable-zone Planets around Solar-like Stars from Kepler Data. Astron. J. 2021, 161, 36. [Google Scholar] [CrossRef]
- Luger, R.; Barnes, R. Extreme Water Loss and Abiotic O2Buildup on Planets throughout the Habitable Zones of M Dwarfs. Astrobiology 2015, 15, 119–143. [Google Scholar] [CrossRef] [PubMed]
- Sengupta, S. An Upper Limit on the Ratio Between the Extreme Ultraviolet and the Bolometric Luminosities of Stars Hosting Habitable Planets. J. Astrophys. Astron. 2016, 37, 11. [Google Scholar] [CrossRef][Green Version]
- Shields, A.L.; Ballard, S.; Johnson, J.A. The habitability of planets orbiting M-dwarf stars. Phys. Rep. 2016, 663, 1. [Google Scholar] [CrossRef]
- Wandel, A. On the Biohabitability of M-dwarf Planets. Astrophys. J. 2018, 856, 165. [Google Scholar] [CrossRef]
- Chen, H.; Wolf, E.T.; Zhan, Z.; Horton, D.E. Habitability and Spectroscopic Observability of Warm M-dwarf Exoplanets Evaluated with a 3D Chemistry-Climate Model. Astrophys. J. 2019, 886, 16. [Google Scholar] [CrossRef]
- do Amaral, L.N.R.; Barnes, R.; Segura, A.; Luger, R. The Contribution of M-dwarf Flares to the Thermal Escape of Potentially Habitable Planet Atmospheres. Astrophys. J. 2022, 928, 12. [Google Scholar] [CrossRef]
- Modi, A.; Estrela, R.; Valio, A. Impact of M-dwarf stellar wind and photoevaporation on the atmospheric evolution of small planets. Mon. Not. R. Astron. Soc. 2023, 525, 5168–5179. [Google Scholar] [CrossRef]
- Seager, S.; Bains, W.; Hu, R. Biosignature Gases in H2-dominated Atmospheres on Rocky Exoplanets. Astrophys. J. 2013, 777, 95. [Google Scholar] [CrossRef]
- Bergsten, G.J.; Pascucci, I.; Mulders, G.D.; Fernandes, R.B.; Koskinen, T.T. The Demographics of Kepler’s Earths and Super-Earths into the Habitable Zone. Astron. J. 2022, 164, 190. [Google Scholar] [CrossRef]
- Murgas, F.; Castro-González, A.; Pallé, E.; Pozuelos, F.J.; Millholland, S.; Foo, O.; Korth, J.; Marfil, E.; Amado, P.J.; Caballero, J.A.; et al. Two super-Earths at the edge of the habitable zone of the nearby M dwarf TOI-2095. Astron. Astrophys. 2023, 677, A182. [Google Scholar] [CrossRef]
- Prantzos, N. On the “Galactic Habitable Zone”. Space Sci. Rev. 2008, 135, 313–322. [Google Scholar] [CrossRef]
- Carigi, L.; García-Rojas, J.; Meneses-Goytia, S. Chemical Evolution and the Galactic Habitable Zone of M31. Rev. Mex. Astron. Astrofisica 2013, 49, 253–273. [Google Scholar] [CrossRef]
- Melott, A.L.; Thomas, B.C.; Kachelrieß, M.; Semikoz, D.V.; Overholt, A.C. A Supernova at 50 pc: Effects on the Earth’s Atmosphere and Biota. Astrophys. J. 2017, 840, 105. [Google Scholar] [CrossRef] [PubMed]
- Brunton, I.R.; O’Mahoney, C.; Fields, B.D.; Melott, A.L.; Thomas, B.C. X-ray-luminous Supernovae: Threats to Terrestrial Biospheres. Astrophys. J. 2023, 947, 42. [Google Scholar] [CrossRef]
- Thomas, B.C.; Yelland, A.M. Terrestrial Effects of Nearby Supernovae: Updated Modeling. Astrophys. J. 2023, 950, 41. [Google Scholar] [CrossRef]
- Thomas, B.C.; Jackman, C.H.; Melott, A.L.; Laird, C.M.; Stolarski, R.S.; Gehrels, N.; Cannizzo, J.K.; Hogan, D.P. Terrestrial Ozone Depletion due to a Milky Way Gamma-Ray Burst. Astrophys. J. Lett. 2005, 622, L153–L156. [Google Scholar] [CrossRef]
- Piran, T.; Jimenez, R. Possible Role of Gamma Ray Bursts on Life Extinction in the Universe. Phys. Rev. Lett. 2014, 113, 231102. [Google Scholar] [CrossRef]
- Spinelli, R.; Ghirlanda, G. The Impact of GRBs on Exoplanetary Habitability. Universe 2023, 9, 60. [Google Scholar] [CrossRef]
- Gonzalez, G. Habitable Zones in the Universe. Orig. Life Evol. Biosph. 2005, 35, 555–606. [Google Scholar] [CrossRef] [PubMed]
- Balbi, A.; Tombesi, F. The habitability of the Milky Way during the active phase of its central supermassive black hole. Sci. Rep. 2017, 7, 16626. [Google Scholar] [CrossRef] [PubMed]
- Ambrifi, A.; Balbi, A.; Lingam, M.; Tombesi, F.; Perlman, E. The impact of AGN outflows on the surface habitability of terrestrial planets in the Milky Way. Mon. Not. R. Astron. Soc. 2022, 512, 505–516. [Google Scholar] [CrossRef]
- Garofalo, D. Advanced Life Peaked Billions of Years Ago According to Black Holes. Galaxies 2023, 11, 66. [Google Scholar] [CrossRef]
- Pacetti, E.; Balbi, A.; Lingam, M.; Tombesi, F.; Perlman, E. The impact of tidal disruption events on galactic habitability. Mon. Not. R. Astron. Soc. 2020, 498, 3153–3157. [Google Scholar] [CrossRef]
- Gehrels, N.; Laird, C.M.; Jackman, C.H.; Cannizzo, J.K.; Mattson, B.J.; Chen, W. Ozone Depletion from Nearby Supernovae. Astrophys. J. 2003, 585, 1169–1176. [Google Scholar] [CrossRef]
- Melott, A.L.; Thomas, B.C. Astrophysical Ionizing Radiation and Earth: A Brief Review and Census of Intermittent Intense Sources. Astrobiology 2011, 11, 343–361. [Google Scholar] [CrossRef]
- Dartnell, L.R. Ionizing Radiation and Life. Astrobiology 2011, 11, 551–582. [Google Scholar] [CrossRef]
- Lingam, M.; Ginsburg, I.; Bialy, S. Active Galactic Nuclei: Boon or Bane for Biota? Astrophys. J. 2019, 877, 62. [Google Scholar] [CrossRef]
- Spinelli, R.; Borsa, F.; Ghirlanda, G.; Ghisellini, G.; Haardt, F. The ultraviolet habitable zone of exoplanets. Mon. Not. R. Astron. Soc. 2023, 522, 1411–1418. [Google Scholar] [CrossRef]
- Dayal, P.; Cockell, C.; Rice, K.; Mazumdar, A. The Quest for Cradles of Life: Using the Fundamental Metallicity Relation to Hunt for the Most Habitable Type of Galaxy. Astrophys. J. Lett. 2015, 810, L2. [Google Scholar] [CrossRef]
- Bressan, A.; Marigo, P.; Girardi, L.; Salasnich, B.; Dal Cero, C.; Rubele, S.; Nanni, A. PARSEC: Stellar tracks and isochrones with the PAdova and TRieste Stellar Evolution Code. Mon. Not. R. Astron. Soc. 2012, 427, 127–145. [Google Scholar] [CrossRef]
- Gabrielli, F.; Boco, L.; Ghirlanda, G.; Salafia, O.S.; Salvaterra, R.; Spera, M.; Lapi, A. Constraining the Initial-Mass Function via Stellar Transients. Universe 2024. submitted. [Google Scholar]
- Heger, A.; Fryer, C.L.; Woosley, S.E.; Langer, N.; Hartmann, D.H. How Massive Single Stars End Their Life. Astrophys. J. 2003, 591, 288–300. [Google Scholar] [CrossRef]
- Drake, F.D. Project Ozma. Phys. Today 1961, 14, 40. [Google Scholar] [CrossRef]
- Maccone, C. The Statistical Drake Equation. Acta Astronaut. 2010, 67, 1366–1383. [Google Scholar] [CrossRef]
- Spiegel, D.S.; Turner, E.L. Bayesian analysis of the astrobiological implications of life’s early emergence on Earth. Proc. Natl. Acad. Sci. USA 2012, 109, 395–400. [Google Scholar] [CrossRef] [PubMed]
- Vakoch, D.A.; Dowd, M.F.; Drake, F. The Drake Equation; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Loeb, A.; Batista, R.A.; Sloan, D. Relative likelihood for life as a function of cosmic time. J. Cosmol. Astropart. Phys. 2016, 2016, 040. [Google Scholar] [CrossRef][Green Version]
- Lineweaver, C.H. The ‘Oumuamua Controversy: Bayesian Priors and the Evolution of Technological Intelligence. Astrobiology 2022, 22, 1419–1428. [Google Scholar] [CrossRef] [PubMed]
- Mieli, E.; Valli, A.M.F.; Maccone, C. Astrobiology: Resolution of the statistical Drake equation by Maccone’s lognormal method in 50 steps. Int. J. Astrobiol. 2023, 22, 428–537. [Google Scholar] [CrossRef]
- Frank, A.; Sullivan, W.T., III. A New Empirical Constraint on the Prevalence of Technological Species in the Universe. Astrobiology 2016, 16, 359–362. [Google Scholar] [CrossRef] [PubMed]
- Lingam, M.; Loeb, A. Life in the Cosmos: From Biosignatures to Technosignatures; Harvard University Press: Cambridge, MA, USA, 2021. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lapi, A.; Boco, L.; Perrotta, F.; Massardi, M. Semi-Empirical Estimates of the Cosmic Planet Formation Rate. Galaxies 2024, 12, 49. https://doi.org/10.3390/galaxies12040049
Lapi A, Boco L, Perrotta F, Massardi M. Semi-Empirical Estimates of the Cosmic Planet Formation Rate. Galaxies. 2024; 12(4):49. https://doi.org/10.3390/galaxies12040049
Chicago/Turabian StyleLapi, Andrea, Lumen Boco, Francesca Perrotta, and Marcella Massardi. 2024. "Semi-Empirical Estimates of the Cosmic Planet Formation Rate" Galaxies 12, no. 4: 49. https://doi.org/10.3390/galaxies12040049
APA StyleLapi, A., Boco, L., Perrotta, F., & Massardi, M. (2024). Semi-Empirical Estimates of the Cosmic Planet Formation Rate. Galaxies, 12(4), 49. https://doi.org/10.3390/galaxies12040049






