Abstract
We perform new measurements of the expansion rate and the sound horizon at the end of the baryon decoupling, and derive constraints on cosmic key parameters in the framework of the CDM model, wCDM model, non-flat CDM model and the phenomenological emergent dark energy (PEDE) model. We keep and completely free, and use the recent Dark Energy Spectroscopic Instrument (DESI) Year 1 and Dark Energy Survey (DES) Year 6 BAO measurements in the effective redshift range , combined with the compressed form of the Pantheon sample of Type Ia supernovae, the latest 34 observational measurements based on the differential age method, and the recent measurement from SH0ES 2022 as an additional Gaussian prior. Combining BAO data with the observational measurements, and the Pantheon SNe Ia data, we obtain km , Mpc in flat CDM model, km , Mpc in PEDE model. The spatial curvature is , and the dark energy equation of state is , consistent with a cosmological constant. We apply the Akaike information and the Bayesian information criterion test to compare the four models, and see that the PEDE model performs better.
1. Introduction
Observational experiments [1,2] have provided precise estimates of the key parameters of the standard cosmological model CDM. Early measurements [1] estimated the value of the Hubble constant at km with an uncertainty of less than 1 km . However, measurements in our local neighborhood of the Hubble constant [3,4,5,6,7] have been improved through the use of cepheid stars in a distance ladder method, leading to a more precise measurement of as km [7]. Despite the success of the CDM model in explaining the current Universe, the measurements of late-time [7] and early-time accelerated cosmic expansion [1] are in tension, with a discrepancy of 4–5.7. This tension suggests that either the measurements have systematic and calibration issues, or the standard cosmological model needs to be extended with new physics. As a result, various alternative cosmological models have been proposed to address the inconsistencies between cosmological surveys [8,9,10,11,12,13,14,15,16,17,18,19,20]. In the opposite directions, many observational studies have been made to provide estimates of the expansion rate, such as quasar lensing [21,22], gravitational-wave events [23,24,25], fast radio bursts (FRBs) [26,27], Megamaser [28,29,30], red giant branch tip method (TRGs) [31,32,33], BAOs [34], etc. [35]. Novel measurements of the Hubble constant independent of the CMB surveys and distance ladder measurements have been performed. A dark siren measurement of the Hubble constant with the LIGO/Virgo gravitational wave event GW190412 and DESI galaxies combined with the bright standard siren measurement from GW170817 estimates km [36]. DECam Local Volume Exploration Survey (DELVE) analyses combined with gravitational wave events from the first three LIGO/Virgo observing runs estimates km [37]. Speaking of Baryon Acoustic Oscillations (BAOs), whose measurements from the Dark Energy Spectroscopic Instrument (DESI) and the Dark Energy Survey (DES) play a key role in our analysis, they are sound waves traveling in the primordial plasma, frozen at the recombination epoch. The BAOs surveys gather data on , , , , and , with as the comoving sound horizon at the baryon decoupling . The Hubble constant and the sound horizon are tightly linked, connecting the early- and late-time universe. The sound horizon is determined by early universe conditions and observations from Planck 2018 [1]. An alternative approach to calibrating involves combining BAO data with observations at low redshifts.
In this work, we present the constraints of cosmological key parameters, highlighting measurements of the Hubble constant and the cosmic sound horizon at the baryon decoupling , where we set the characteristic scale of BAO as a free parameter in the framework of different cosmologies. Without regarding any assumption of the early time physics, we combine the measurement of Baryon Acoustic Oscillations (BAO) in galaxy, quasar, and Lyman- forest tracers for the first year of observations from the Dark Energy Spectroscopic Instrument (DESI) [38], the BAO measurement for the sixth year of observations from the Dark Energy Survey (DES) [39], the SNe-Ia Pantheon compilation data [40], the observational data (OHD), and the latest measurement of the Hubble constant performed by SH0ES 2022 as an additional Gaussian prior [7]. The paper is structured as follows: Section 2 presents the cosmological models under study, where will set constraints on cosmic key parameters. Section 3 summarizes our data and methodology. Results on cosmological parameters and constraints are given in Section 4. Finally, we present our discussion and conclusion in Section 5.
2. Theoretical Background
2.1. Flat CDM Model
The cold dark matter (CDM) model takes the dark energy equation-of-state (EoS) as the cosmological constant with , acting as a negative pressure to counteract the effect of gravity. The Friedmann equation for this model is expressed as
where we can set , with EoS . The Friedmann Equation (1) depends on the free parameters , , . The term is the expansion rate that is the ratio , where is the Hubble parameter at redshift z and is the Hubble constant measured at present time.
2.2. Non-Flat CDM Model
In the CDM model, we depart from the assumption of spatial flatness by introducing a variable curvature parameter . In the framework of a Friedmann–Lemaître–Robertson–Walker (FLRW) background, this is analogous to allowing the dark energy density to vary independently from the matter density , while maintaining a constant dark-energy EoS with . The Friedmann equation for this model is expressed as
2.3. wCDM Model
The cosmological model wCDM assumes a constant EoS w. The Friedmann equation for wCDM model is expressed as
where Equation (3) depends on the free parameters , , , and w. Despite the success of the cosmological constant fitting existing data very well, the small value of relative to the theoretical estimations based on particle physics poses a conflict. This requires going beyond CDM, where dark energy has dynamic-time dependence, hence proposing cosmological models with dark energy EoS parameterized.
2.4. Phenomenological Emergent Dark Energy (PEDE) Model
Generally, the parameterization of a given dark energy EoS w can be a function of redshift z or the scale factor of the FLRW metric universe, noticing that , where is the present value of the scale factor. Here, we consider a dynamical dark energy EoS w parameterization called the phenomenological emergent dark energy (PEDE) model. This model introduces a dark energy density, written as
where . From the PEDE model, we can write the Friedmann equation in terms of the expansion function as
where Equation (5) depend on free parameters , , . This dark energy model with zero degrees of freedom as the CDM model acts with no presence in early times, and emerges at later times. We must recall that the PEDE model does not generalize the CDM model. The EoS of this model lies in the phantom region () in the past and present (), and approximates to the cosmological constant () in the far future [18].
3. Data and Methodology
In order to estimate and place constraints on the cosmological key parameters in the framework of different cosmologies that we have described above, we use the following observational data sets: the recent BAO measurements performed by DESI year 1, DES year 6, observational data (OHD), the Pantheon Sample, and the local measurement of the Hubble constant labeled as R22.
BAO measurements depend on the sound horizon at the epoch of baryon decoupling at in the standard model. It is given by
where the sound speed is a function of the baryon to photon densities ratio, and is the expansion rate function in terms of our present-day density fraction , , , and . The sound horizon is the characteristic scale to calibrate BAO observations, where it is often settled a prior of the CMB measurement. In this analysis, we remove the prior from CMB Planck satellite and set as a free parameter. The BAO measurements from surveys of galaxies, quasars and Lyman- forest are given by the observables , , and . The transverse comoving distance and the volume angle-average length that quantifies the average of distances measured along are linked to the expansion rate function by
We use the recent BAO measurements from DESI year 1 data release (DESI DR1) and DES year 6 (DESY6) result, which are performed at a series of redshifts, allowing constrains on the cosmic key parameters. The DESI DR1 and DESY6 BAO data points are listed in Table 1 with their corresponding redshifts , observables, measurements, and errors.

Table 1.
We present the recent 13 BAO measurements from the Dark Energy Spectroscopic Instrument (DESI) year 1 data release and Dark Energy Survey (DES) year 6, on which we perform our analysis.
In this analysis, we do not take into account the OHD obtained from the measurement of BAO. We only make use of the OHD from differential age method proposed in Ref. [41]. Table 2 shows an updated compilation of OHD covering a total of 34 data points given by the differential age method [41]. We also make use of the Pantheon compilation of 1048 SNe Ia in the redshift range [40] and the Hubble constant estimation from the SH0ES team yielding to the Gaussian prior km at CL (R22) [7]. To perform our cosmological analysis, we use a nested sampling algorithm tailored for high-dimensional parameter space called Polychord, developed by Handley et al. [42] with the GetDist v1.5.1 [43], as performed in [44,45]. Lastly, we compare our different cosmological models using the Akaike information criterion (AIC) and the Bayesian information Criterion (BIC). The AIC criterion is defined as [46]
where is the maximum likelihood of the data taken into consideration in which we take the full dataset without the Riess 2022 prior, is the total number of data points, and k is the numbers of parameters. For large , our expression is reduced to
which is the standard form of the AIC criterion [46]. On the other hand, the Bayesian information criterion is defined as [47]

Table 2.
We present an update of all 34 measurements (in units of km ) obtained with the differential age method and their associated errors on which we perform our analysis. It is noted that all these measurements are independent, since they come from different datasets.
4. Analysis and Results
To obtain our results, aside from the BAO measurements listed in Table 1 obtained by DESI and DES, we use the Pantheon data given in [40], the latest observational measurements using the differential age method containing 34 data points listed in Table 2, and the latest Hubble constant measurement, labeled as R22 [7]. We consider the combination of BAO + OHD + Pantheon datasets as the full dataset.
4.1. Flat CDM Model
We present cosmological constraints for the flat CDM model, where , . We set , , , and as free parameters with the following prior: , , (km ) , and (Mpc) . The recent measurement of the Hubble constant km is included into our study as an additional prior, labeled as R22. In Figure 1 our results are depicted at and confidence levels for the posterior distribution in the , , and , and contour planes of the standard model of cosmology CDM. In Table 3 are listed our results. Regarding the BAO data alone, the matter density is estimated at C.L. , giving a smaller value than the one estimated by Planck 2018 [1], but this has been reported in other studies [38,58,59]. In addition, when we remove DESY6 BAO data point and consider DESI BAO data alone, the matter density is estimated at C.L. . The center panel summarizes the constraints in plane obtained from the combination of BAO data with R22 prior, and other datasets. All combinations prefer somehow higher values of and lower ones of matter density than the ones estimated by Planck [1]. However, they fall in the range of agreement with the values estimated by DESI collaboration [38]. In the right panel, it is noted that combining BAO with OHD and Pantheon or with R22 prior, we break the degeneracy in the contour plane. The joint analysis of BAO, OHD, and Pantheon, where we refer it as our full dataset, gives the constraint of Hubble constant km and sound horizon at the baryon decoupling Mpc. By adding Riess 2022 prior for , the fit gives km (which is closer to the value measured by SH0ES team 2022 [7]) and Mpc. Verde et al. [60] finds Mpc. Lemos et al. Ref. [61] estimates the values of the BAO scale range with the binning method 141.45 Mpc 159.44 Mpc and for the Gaussian method 143.35 Mpc 161.59 Mpc. The various methods used to measure reveal a significant difference between early and late-time observations, similar to the discrepancy seen in values. An interesting observation is that excluding the Riess 2022 prior leads to and results that align more closely with those from the Planck survey [1].
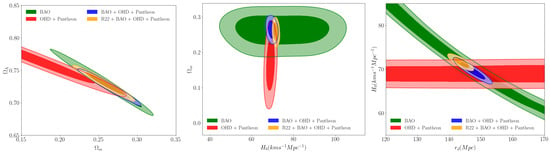
Figure 1.
(Left panel): Marginalized posterior cosmic constraints on dark energy parameter density and matter density . (Center panel): Marginalized posterior cosmic constraints on matter parameter density and the Hubble constant , obtained from combining BAO with external data used to calibrate the BAO characteristic scale . (Right panel): Marginalized posterior constraints on the sound horizon at the baryon decoupling and the Hubble constant , which shows that R22 prior breaks the degeneracy between and .
4.2. Non-Flat CDM Model
In the non-flat CDM model, we allow the parameter of curvature to vary with the prior and . For the other priors, they are the same as for flat CDM model. In Figure 2, we show the and confidence levels for the posterior distribution of the cosmic parameters of our interest and the mean parameter values and C.L. uncertainties derived from the combinations of data sets are listed in Table 4.
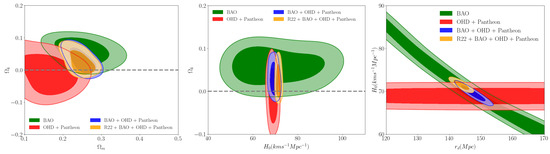
Figure 2.
Constraints on different cosmic parameters in the non-flat CDM model. (Left panel): and marginalized posterior cosmic constraints on - plane. (Center panel): and marginalized posterior cosmic constraints on - plane. (Right panel): and marginalized posterior constraints on the sound horizon at the baryon decoupling and the Hubble constant , which shows that R22 prior breaks the degeneracy between and .

In this model, BAO measurements from DESI DR1 and DES Year 6 alone thus measure the parameters (, ), finding the following constraints values of , . Referring to curvature, we find . For the full dataset, we estimate the values of , , and at km , Mpc, , respectively. The value of for all data combinations as listed in Table 4 do not take a negative spatial curvature (), which is similar to the DESI result [38] and different from the results obtained by Planck for CMB alone [1]. The estimated results are very close to zero, so they do not rule out a flat universe.
4.3. wCDM Model
In Figure 3, we show the and confidence levels for the posterior distribution of the cosmic parameters of our interest and the mean parameter values and C.L. uncertainties derived from the combinations of data sets are listed in Table 5.
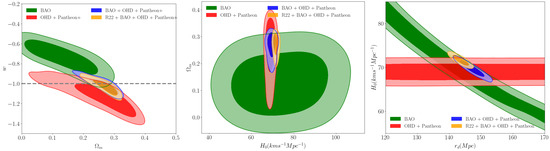
Figure 3.
(Left panel): and marginalized posterior cosmic constraints on -w plane. (Center panel): and marginalized posterior cosmic constraints on - plane. (Right panel): and marginalized posterior constraints on the sound horizon at the baryon decoupling and the Hubble constant , which shows that R22 prior breaks the degeneracy between and .

In the left panel of Figure 3 we show the constraints on and w derived from the latest DESI and DES BAO measurements and combinations, while the center and right panel show the corresponding bounds on and . In the plane , we find for the full dataset , , while combining the full dataset with the R22 prior for , the constraint on w leads to . Therefore, we observe that the dark energy equation of state we obtain for the full dataset is in agreement with the value estimated by the CMB Planck satellite [1], which results in , consistent with a cosmological constant. However, when we consider BAO alone and BAO + R22, the equation of state is away from the cosmological constant, which result in , , respectively. Although these results are obtained in the wCDM model, they are consistent with the results from DESI collaboration [38] when the equation of state is allowed to vary with time where DESI data prefer solutions and , but this will require further investigation. Referring to the center and right panel in Figure 3, we observe that the sound horizon at the baryon decoupling and the Hubble constant regarding the full dataset tend to be in agreement with the values estimated by Planck [1], while combining the full dataset with R22 prior for , we find Mpc, which is consistent with other results performed by Pogosian et al., Nunes et al., and Verde et al. [58,60,62].
4.4. Phenomenological Emergent Dark Energy Model
Motivated by the current issues of cosmological observations of the accelerated cosmic expansion, a new model which proposes dark energy with no effective presence in the past and emerging at later times has caught the attention [18]. This dark energy model with zero degrees of freedom (similar to the CDM) is called phenomenological emergent dark energy. We show our results in Figure 4, in which we show the and confidence levels for the posterior distribution of the cosmic parameters of our interest and the mean parameter values and C.L. uncertainties derived from the combinations of data sets are listed in Table 6.
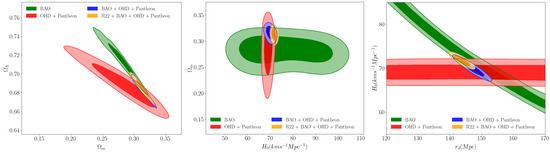
Figure 4.
Constraints on different cosmic parameters in the PEDE model. (Left panel): and marginalized posterior cosmic constraints on - plane. (Center panel): and marginalized posterior cosmic constraints on - plane. (Right panel): and marginalized posterior constraints on the sound horizon at the baryon decoupling and the Hubble constant , which shows that R22 prior breaks the degeneracy between and .

In BAO data alone, the matter density parameter results in , which is consistent with the value obtained by DESI () [38]. However, the full dataset gives the value of and , which are in excellent agreement with those obtained by Planck [1]. Additionally, the Hubble constant is found to be higher at km , which falls between the Planck and SH0ES 2022 measurements of the Hubble constant and is found to be in agreement with measurements from the tip of the red giant branch performed by Freeman et al. [31,32,33]. By incorporating the R22 prior for , the fit gives a result in accord with the value obtained by SH0ES 2022 [7], while the sound horizon is lower in comparison with Planck: km and Mpc. Additionally, the matter and dark energy densities also are in agreement with the values reported by Planck [1], and we do not see a tension in these parameters as it was reported by Shafieloo et al. [18].
5. Discussion
In this work, we have provided new measurements on the Hubble constant and sound horizon using the recent BAO measurements from different tracers of the matter density in seven redshift bins performed by the Dark Energy Spectroscopic Instrument DESI year 1 data release [38], the angular diameter distance measurement obtained with the Baryonic Acoustic Oscillation feature from galaxy clustering in the completed Dark Energy Survey, consisting of six years (Y6) of observations [39], the observational data, the Pantheon SNe Ia sample, and the R22 prior.
For the full dataset, we determine the Hubble constant and sound horizon values to be km , in the standard flat CDM model, km , in the non-flat CDM, and km , in the flat wCDM model. The most interesting results are in the phenomenological emergent dark energy PEDE model: combining the full dataset with the R22 prior for , the matter density parameter is , the dark energy density parameter , the Hubble constant km , and the sound horizon , alleviating the tension from those measured in combination with the CMB full dataset [18]. This is important, as this PEDE model results from our data align with cosmological observations at low [38] and high redshifts [1], which can be a good alternative to explain the effective behavior of dark energy in comparison with the cosmological constant . The DESI collaboration has recently presented findings suggesting a potential deviation from the standard model of cosmology, CDM, at the 3.9 level [38]. Utilizing the first-year data release from DESI, combined with additional cosmological datasets, several recent studies have explored the characteristics of dark energy and applied constraints to its behavior [63,64,65,66,67,68]. These investigations have involved the use of parameterized models, such as the Chevallier–Polarski–Linder (CPL) model, quintessence, Chaplying gas model, and Taylor-expanded dark models, among others. However, the adequacy of the recent DESI year 1 data release in rejecting the standard cosmological model remains uncertain. Consequently, forthcoming DESI data releases will be essential for comprehensively characterizing the evolution of dark energy.
Comparing our models, we calculate the AIC and BIC for the PEDE, flat CDM, non-flat CDM, and wCDM models. The results are listed in Table 7. Table 7 shows that the lowest values of AIC and BIC correspond to the PEDE model, as well as AIC and BIC having negative values. Therefore, the PEDE model performs better than the reference model flat CDM model and the rest of the models. Consequently, making the comparison of our results with other studies, we see that our values are consistent with DESI collaboration official results [38] for the same models studied there by the inclusion of the observation measurements (OHD) and R22 prior and the exclusion of the CMB full dataset. As for the PEDE model, the tension remaining in the estimation of the matter density reported in [18] vanishes by incorporating the BAO measurements performed by DESI and DES disregarding the CMB full dataset. In conclusion, the BAO information obtained by DESI and DES demonstrates an enormous power for deriving values and constraints of the cosmological parameters when combined with other estimations for the sound horizon and Hubble constant.

Table 7.
The table presents the values of Akaike information criterion (AIC), the Bayesian information criterion (BIC), and the differences of AIC and BIC for each model by taking flat CDM model as our reference model.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data underlying this article is already given with references during the analysis of this work.
Acknowledgments
We would like to thank CONAHCYT for sponsoring this project.
Conflicts of Interest
The author declares no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Planck Collaboration. Planck 2018 Results—VI. Cosmological Parameters. Astron. Astrophys. 2020, A6, 641. [Google Scholar]
- Bennett, C.L.; Larson, D.; Weil, J.L.; Jarosik, N.; Hinshaw, G.; Odegard, N.; Smith, K.M.; Hill, R.S.; Gold, B.; Halpern, M.; et al. Nine-year Wilkinson microwave anisotropy probe (WMAP) observations: Final maps and results. Astrophys. J. Suppl. Ser. 2013, 208, 20. [Google Scholar] [CrossRef]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gillil, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. Astron. J. 1998, 116, 1009. [Google Scholar] [CrossRef]
- Riess, A.G.; Macri, L.; Casertano, S.; Lampeitl, H.; Ferguson, H.C.; Filippenko, A.V.; Jha, S.W.; Li, W.; Chornock, R. A 3% solution: Determination of the Hubble constant with the Hubble space telescope and wide field camera 3. Astron. J. 2011, 730, 119. [Google Scholar] [CrossRef]
- Riess, A.G.; Macri, L.M.; Hoffmann, S.L.; Scolnic, D.; Casertano, S.; Filippenko, A.V.; Tucker, B.E.; Reid, M.J.; Jones, D.O.; Silverman, J.M.; et al. A 2.4% determination of the local value of the Hubble constant. Astron. J. 2016, 826, 56. [Google Scholar] [CrossRef]
- Riess, A.G.; Casertano, S.; Yuan, W.; Macri, L.M.; Scolnic, D. Large Magellanic Cloud Cepheid Standards Provide a 1% Foundation for the Determination of the Hubble Constant and Stronger Evidence for Physics beyond ΛCDM. Astron. J. 2019, 876, 55. [Google Scholar] [CrossRef]
- Riess, A.G.; Yuan, W.; Macri, L.M.; Scolnic, D.; Brout, D.; Casertano, S.; Jones, D.O.; Murakami, Y.; Anand, G.S.; Breuval, L.; et al. A Comprehensive Measurement of the Local Value of the Hubble Constant with 1 km/s/Mpc Uncertainty from the Hubble Space Telescope and the SH0ES Team. Astrophys. J. Lett. 2022, 934, L7. [Google Scholar] [CrossRef]
- Huang, Q.G.; Wang, K. How the dark energy can reconcile Planck with local determination of the Hubble constant. Eur. Phys. J. 2016, 76, 506. [Google Scholar] [CrossRef]
- Di Valentino, E.; Melchiorri, A.; Silk, J. Reconciling Planck with the local value of H0 in extended parameter space. Phys. Lett. B 2016, 761, 242–246. [Google Scholar] [CrossRef]
- Xu, L.; Huang, Q.G. Detecting the neutrinos mass hierarchy from cosmological data. Sci. China Phys. Mech. Astron. 2018, 61, 039521. [Google Scholar] [CrossRef]
- Yang, W.; Pan, S.; Di Valentino, E.; Saridakis, E.N.; Chakraborty, S. Observational constraints on one-parameter dynamical dark-energy parametrizations and the H0 tension. Phys. Rev. D 2019, 99, 043543. [Google Scholar] [CrossRef]
- Poulin, V.; Smith, T.L.; Karwal, T.; Kamionkowsk, M. Early Dark Energy can Resolve the Hubble Tension. Phys. Rev. Lett. 2019, 122, 221301. [Google Scholar] [CrossRef] [PubMed]
- Vagnozzi, S. New physics in light of the H0 tension: An alternative view. Phys. Rev. D 2020, 102, 023518. [Google Scholar] [CrossRef]
- Liu, M.; Huang, Z.; Luo, X.; Miao, H.; Singh, N.K.; Huang, L. Can non-standard recombination resolve the Hubble tension? Sci. China Phys. Mech. Astron. 2020, 63, 290405. [Google Scholar] [CrossRef]
- Ding, Q.; Nakama, T.; Wang, Y. A gigaparsec-scale local void and the Hubble tension. Sci. China Phys. Mech. Astron. 2020, 63, 290403. [Google Scholar] [CrossRef]
- Ryan, J.; Chen, Y.; Ratra, B. Baryon acoustic oscillation, Hubble parameter, and angular size measurement constraints on the Hubble constant, dark energy dynamics, and spatial curvature. Mon. Not. R. Astron. Soc. 2019, 488, 3844–3856. [Google Scholar] [CrossRef]
- Zhao, G.B.; Raveri, M.; Pogosian, L.; Wang, Y.; Crittenden, R.G.; Handley, W.J.; Percival, W.J.; Beutler, F.; Brinkmann, J.; Chuang, C.; et al. Dynamical dark energy in light of the latest observations. Nat. Astron. 2017, 1, 627–632. [Google Scholar] [CrossRef]
- Li, X.; Shafieloo, A. A Simple Phenomenological Emergent Dark Energy Model can Resolve the Hubble Tension. Astrophys. J. Lett. 2019, 883, L3. [Google Scholar] [CrossRef]
- Di Valentino, E. Investigating Cosmic Discordance. Astrophys. J. Lett. 2021, 908, L9. [Google Scholar] [CrossRef]
- Haitao, M.; Zhiqi, H. The H0 Tension in Non-flat QCDM Cosmology. Astron. J. 2018, 868, 20. [Google Scholar]
- Millon, M.; Galan, A.; Courbin, F.; Treu, T.; Suyu, S.H.; Ding, X.; Birrer, S.; Chen, G.C.-F.; Shajib, A.J.; Sluse, D.; et al. An exploration of systematic uncertainties in the inference of H0 from time-delay cosmography. Astron. Astrophys. 2020, 639, A101. [Google Scholar] [CrossRef]
- Wong, K.C.; Suyu, S.H.; Chen, G.C.-F.; Rusu, C.E.; Millon, M.; Sluse, D.; Bonvin, V.; Fassnacht, C.D.; Taubenberger, S.; Auger, M.W.; et al. H0LiCOW—XIII. A 2.4 percent measurement of H0 from lensed quasars: 5.3σ tension between early- and late-Universe probes. Mon. Not. R. Astron. Soc. 2020, 498, 1420–1439. [Google Scholar] [CrossRef]
- Mooley, K.P.; Deller, A.T.; Gottlieb, O.; Nakar, E.; Hallinan, G.; Bourke, S.; Frail, D.A.; Horesh, A.; Corsi, A.; Hotokezaka, K. Superluminal motion of a relativistic jet in the neutron-star merger GW170817. Nature 2018, 561, 355–359. [Google Scholar] [CrossRef] [PubMed]
- The LIGO Scientific Collaboration and The Virgo Collaboration; The 1M2H Collaboration; The Dark Energy Camera GW-EM Collaboration and the DES Collaboration; The DLT40 Collaboration; The Las Cumbres Observatory Collaboration; The VINROUGE Collaboration; The MASTER Collaboration. A gravitational-wave standard siren measurement of the Hubble constant. Nature 2017, 551, 85–88. [Google Scholar] [CrossRef] [PubMed]
- Hotokezaka, K.; Nakar, E.; Gottlieb, O.; Nissanke, S.; Masuda, K.; Hallinan, G.; Mooley, K.P.; Deller, A.T. A Hubble constant measurement from the superluminal motion of the jet in GW170817. Nat. Astron. 2019, 3, 940–944. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, G.-Q.; Wang, F.-Y. An 8 percent determination of the Hubble constant from localized fast radio bursts. Mon. Not. R. Astron. Soc. Lett. 2022, 515, L1–L5. [Google Scholar] [CrossRef]
- James, C.W.; Ghosh, E.M.; Prochaska, J.X.; Bannister, K.W.; Bhari, S.; Day, C.K.; Deller, A.T.; Glowacki, M.; Gordon, A.C.; Heintz, K.E.; et al. A measurement of Hubble’s Constant using Fast Radio Bursts. Mon. Not. R. Astron. Soc. 2022, 516, 4862–4881. [Google Scholar] [CrossRef]
- Pesce, D.W.; Braatz, J.A.; Reid, M.J.; Riess, A.G.; Scolnic, D.; Condon, J.J.; Gao, F.; Henkel, C.; Impellizzeri, C.M.V.; Kuo, C.Y.; et al. The Megamaser Cosmology Project. XIII. Combined Hubble Constant Constraints. Astrophys. J. Lett. 2020, 891, L1. [Google Scholar] [CrossRef]
- Reid, J.; Pesce, D.W.; Riess, A.G. An Improved Distance to NGC 4258 and Its Implications for the Hubble Constant. Astrophys. J. Lett. 2019, 886, L27. [Google Scholar] [CrossRef]
- Kuo, C.Y.; Braatz, J.A.; Lo, K.Y.; Reid, M.J.; Suyu, S.H.; Pesce, D.W.; Condon, J.J.; Henkel, C.; Impellizzeri, C.M.V. The Megamaser Cosmology Project. VI. Observations of NGC 6323. Astron. J. 2015, 800, 26. [Google Scholar] [CrossRef]
- Freedman, W.L.; Madore, B.F.; Hatt, D.; Hoyt, T.J.; Jang, I.S.; Beaton, R.L.; Burns, C.R.; Lee, M.G.; Monson, A.J.; Neeley, J.R.; et al. The Carnegie-Chicago Hubble Program. VIII. An Independent Determination of the Hubble Constant Based on the Tip of the Red Giant Branch. Astron. J. 2019, 882, 34. [Google Scholar] [CrossRef]
- Freedman, W.L.; Madore, B.F.; Hoyt, T.; Jang, I.S.; Beaton, R.; Lee, M.G.; Monson, A.; Neeley, J.; Jeffrey, R. Calibration of the Tip of the Red Giant Branch. Astron. J. 2020, 891, 57. [Google Scholar] [CrossRef]
- Freedman, W.L. Measurements of the Hubble Constant: Tensions in Perspective. Astron. J. 2021, 919, 16. [Google Scholar] [CrossRef]
- Addison, G.E.; Watts, D.J.; Bennett, C.L.; Halpern, M.; Hinshaw, G.; Weil, J.L. Elucidating ΛCDM: Impact of Baryon Acoustic Oscillation Measurements on the Hubble Constant Discrepancy. Astron. J. 2021, 853, 119. [Google Scholar] [CrossRef]
- Moresco, M.; Amati, L.; Amendola, L.; Birrer, S.; Blakeslee, J.P.; Cantiello, M.; Cimatti, A.; Darling, J.; Valle, M.D.; Fishbach, M.; et al. Unveiling the Universe with emerging cosmological probes. Living Rev. Relativ. 2022, 25, 6. [Google Scholar]
- Ballard, W.; Palmese, A.; Magaña, I.; BenZvi, S.; Moon, J.; Ross, A.J.; Rossi, G.; Aguilar, J.; Ahlen, S.; Blum, R.; et al. A dark siren measurement of the Hubble constant with the LIGO/Virgo gravitational wave event GW190412 and DESI galaxies. arXiv 2023, arXiv:2311.13062. [Google Scholar] [CrossRef]
- Alfradique, V.; Bom, C.R.; Palmese, A.; Teixeira, G.; Santana-Silva, L.; Drlica-Wagner, A.; Riley, A.H.; Rossi, G.; Martínez-Vázquez, C.E.; Sand, D.J.; et al. A dark siren measurement of the Hubble constant using gravitational wave events from the first three LIGO/Virgo observing runs and DELVE. Mon. Not. R. Astron. Soc. 2024, 528, 3249–3259. [Google Scholar] [CrossRef]
- DESI Collaboration. DESI 2024 VI: Cosmological Constraints from the Measurements of Baryon Acoustic Oscillations. arXiv 2024, arXiv:2404.03002. [Google Scholar]
- DES Collaboration. Dark Energy Survey: A 2.1% measurement of the angular Baryonic Acoustic Oscillation scale at redshift zeff = 0.85 from the final dataset. arXiv 2024, arXiv:2402.10696. [Google Scholar]
- Scolnic, D.M.; Jones, D.O.; Rest, A.; Pan, Y.C.; Chornock, R.; Foley, R.J.; Huber, M.E.; Kessler, R.; Narayan, G.; Riess, A.G.; et al. The Complete Light-curve Sample of Spectroscopically Confirmed SNe Ia from Pan-STARRS1 and Cosmological Constraints from the Combined Pantheon Sample. Astron. J. 2018, 859, 101. [Google Scholar] [CrossRef]
- Jimenez, R.; Loeb, A. Constraining Cosmological Parameters Based on Relative Galaxy Ages. Astrophys. J. 2002, 573, 37. [Google Scholar] [CrossRef]
- Handley, W.J.; Hobson, M.P.; Lasenby, A.N. POLYCHORD: Nested sampling for cosmology. Mon. Not. R. Astron. Soc. Lett. 2015, 450, L61–L65. [Google Scholar] [CrossRef]
- Lewis, A. GetDist: A Python package for analysing Monte Carlo samples. Instrumentation and Methods for Astrophysics. arXiv 2019, arXiv:1910.13970. [Google Scholar]
- Lozano Torres, J.A. Testing Cosmic Acceleration from the Late-Time Universe. Astronomy 2023, 2, 300–314. [Google Scholar] [CrossRef]
- Kazantzidis, L.; Perivolaropoulos, L. Evolution of the fσ8 tension with the Planck15/ΛCDM determination and implications for modified gravity theories. Phys. Rev. D 2018, 97, 103503. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control. 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the Dimension of a Model. Ann. Statist. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Cong, Z.; Han, Z.; Shuo, Y.; Siqi, L.; Tong-Jie, Z.; Yan-Chun, S. Four new observational H(z) data from luminous red galaxies in the Sloan Digital Sky Survey data release seven. Res. Astron. Astrophys. 2014, 14, 1221. [Google Scholar]
- Simon, J.; Verde, L.; Jimenez, R. Constraints on the redshift dependence of the dark energy potential. Phys. Rev. D 2005, 71, 123001. [Google Scholar] [CrossRef]
- Moresco, M.; Cimatti, A.; Jimenez, R.; Pozzetti, L.; Zamorani, G.; Bolzonella, M.; Dunlop, J.; Lamareille, F.; Mignoli, M.; Pearce, H.; et al. Improved constraints on the expansion rate of the Universe up to z ≈ 1.1 from the spectroscopic evolution of cosmic chronometers. J. Cosmol. Astropart. Phys. 2012, 8, 6. [Google Scholar] [CrossRef]
- Moresco, M.; Pozzetti, L.; Cimatti, A.; Jimenez, R.; Maraston, C.; Verde, L.; Thomas, D.; Citro, A.; Tojeiro, R.; Wilkinson, D. A 6 percent measurement of the Hubble parameter at z ≈ 0.45: Direct evidence of the epoch of cosmic re-acceleration. J. Cosmol. Astropart. Phys. 2016, 5, 14. [Google Scholar] [CrossRef]
- Ratsimbazafy, A.L.; Loubser, S.I.; Crawford, S.M.; Cress, C.M.; Bassett, B.A.; Nichol, R.C.; Väisänen, P. Age-dating luminous red galaxies observed with the Southern African Large Telescope. Mon. Not. R. Astron. Soc. 2017, 467, 3239–3254. [Google Scholar] [CrossRef]
- Stern, D.; Jimenez, R.; Verde, L.; Kamionkowski, M.; Stanford, S.A. Cosmic chronometers: Constraining the equation of state of dark energy. I: H(z) measurements. J. Cosmol. Astropart. Phys. 2010, 2, 8. [Google Scholar] [CrossRef]
- Borghi, N.; Moresco, M.; Cimatti, A. Toward a Better Understanding of Cosmic Chronometers: A New Measurement of H(z) at z ≈ 0.7. Astrophys. J. Lett. 2022, 928, L4. [Google Scholar] [CrossRef]
- Jiao, K.; Borghi, N.; Moresco, M.; Zhang, T.-J. New Observational H(z) Data from Full-spectrum Fitting of Cosmic Chronometers in the LEGA-C Survey. Astrophys. J. Suppl. Ser. 2023, 265, 48. [Google Scholar] [CrossRef]
- Tomasetti, E.; Borghi, N.; Moresco, M.; Jiao, K.; Cimmatti, A.; Pozzetti, L.; Carnall, A.C.; McLure, R.J.; Pentericci, L. A new measurement of the expansion history of the Universe at z = 1.26 with cosmic chronometers in VANDELS. Astron. Astrophys. 2023, 265, 48. [Google Scholar] [CrossRef]
- Moresco, M. Raising the bar: New constraints on the Hubble parameter with cosmic chronometers at z ≈ 2. Astrophys. J. Suppl. Ser. 2023, A96, 18. [Google Scholar] [CrossRef]
- Nunes, R.C.; Yadav, S.K.; Jesus, J.F.; Bernui, A. Cosmological parameter analyses using transversal BAO data. Mon. Not. R. Astron. Soc. 2020, 497, 2133–2141. [Google Scholar] [CrossRef]
- Nunes, R.C.; Bernui, A. BAO signatures in the 2-point angular correlations and the Hubble tension. Eur. Phys. J. C. 2020, 80, 1025. [Google Scholar] [CrossRef]
- Verde, L.; Bernal, J.L.; Heavens, A.F.; Jimenez, R. The length of the low-redshift standard ruler. Mon. Not. R. Astron. Soc. 2017, 467, 731–736. [Google Scholar] [CrossRef][Green Version]
- Lemos, T.; Ruchika; Carvalho, J.C.; Alcaniz, J. Low-redshift estimates of the absolute scale of baryon acoustic oscillations. Eur. Phys. J. C 2023, 83, 495. [Google Scholar] [CrossRef]
- Pogosian, L.; Zhao, G.-B.; Jedamzik, K. Recombination-independent Determination of the Sound Horizon and the Hubble Constant from BAO. Astrophys. J. Lett. 2020, 904, L7. [Google Scholar] [CrossRef]
- Luongo, O.; Muccino, M. Model independent cosmographic constraints from DESI 2024. arXiv 2024, arXiv:2404.07070. [Google Scholar] [CrossRef]
- Carloni, Y.; Luongo, O.; Muccino, M. Does dark energy really revive using DESI 2024 data. arXiv 2024, arXiv:2404.12068. [Google Scholar]
- Liu, G.; Wang, Y.; Zhao, W. Impact of LRG1 and LRG2 in DESI 2024 BAO data on dark energy evolution. arXiv 2024, arXiv:2407.04385. [Google Scholar]
- Giare, W.; Najafi, M.; Pan, S.; Di Valentino, E.; Firouzjaee, J.T. Robust Preference for Dynamical Dark Energy in DESI BAO and SN Measurements. arXiv 2024, arXiv:2407.16689. [Google Scholar]
- Dinda, B.R.; Maartens, R. Model-agnostic assessment of dakr energy after DESI DR1 BAO. arXiv 2024, arXiv:2407.17252. [Google Scholar]
- Jiang, J.-Q.; Giare, W.; Gariazzo, S.; Dainotti, M.G.; Di Valentino, E.; Mena, O.; Pedrotti, D.; Santos da Costa, S.; Vagnozzi, S. Neutrino cosmology after DESI: Tightest mass upper limits, preference for the normal ordering, and tension with terrestrial observations. arXiv 2024, arXiv:2407.18047. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).