X-ray Polarimetry of X-ray Pulsars
Abstract
1. Introduction
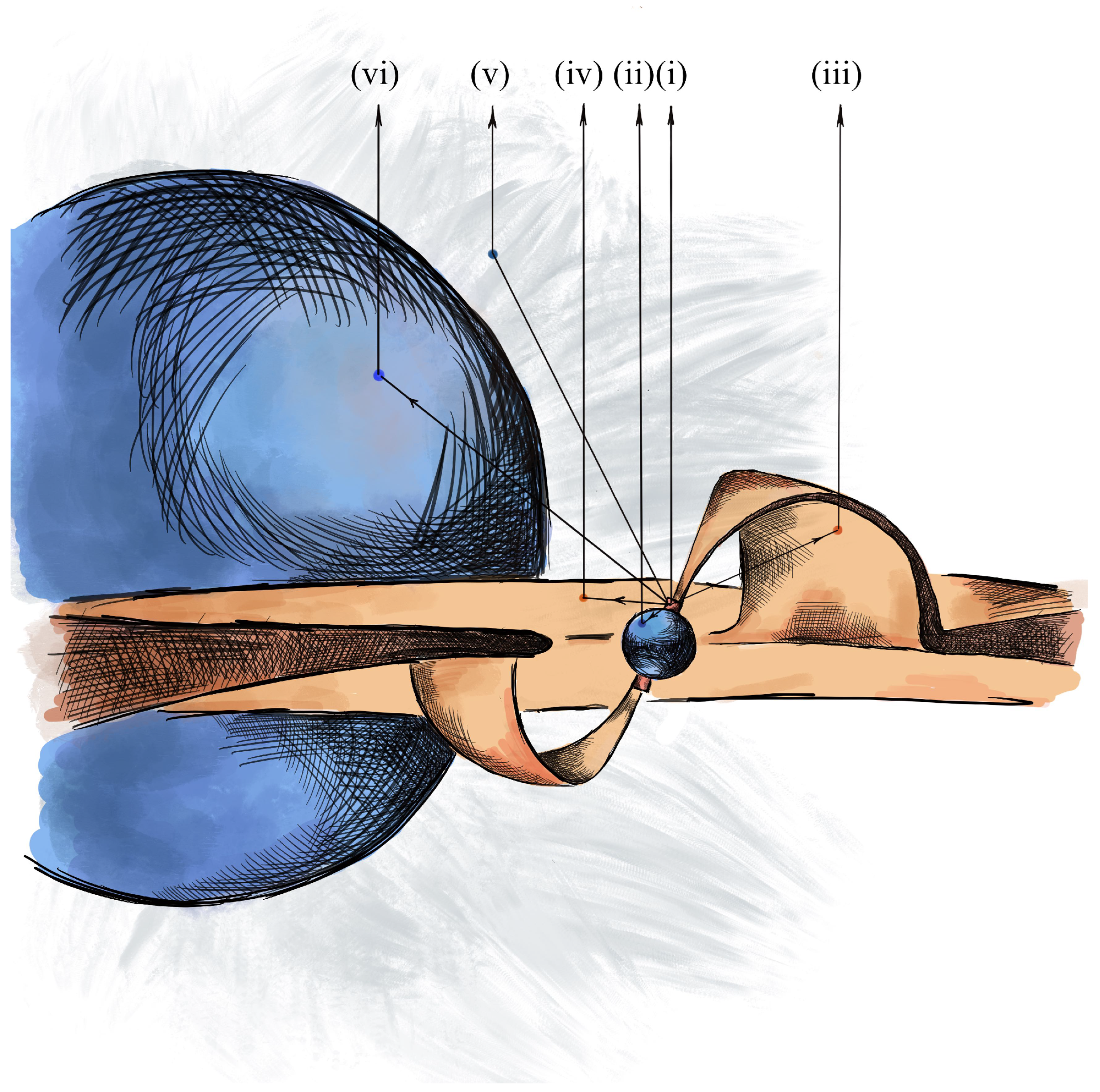
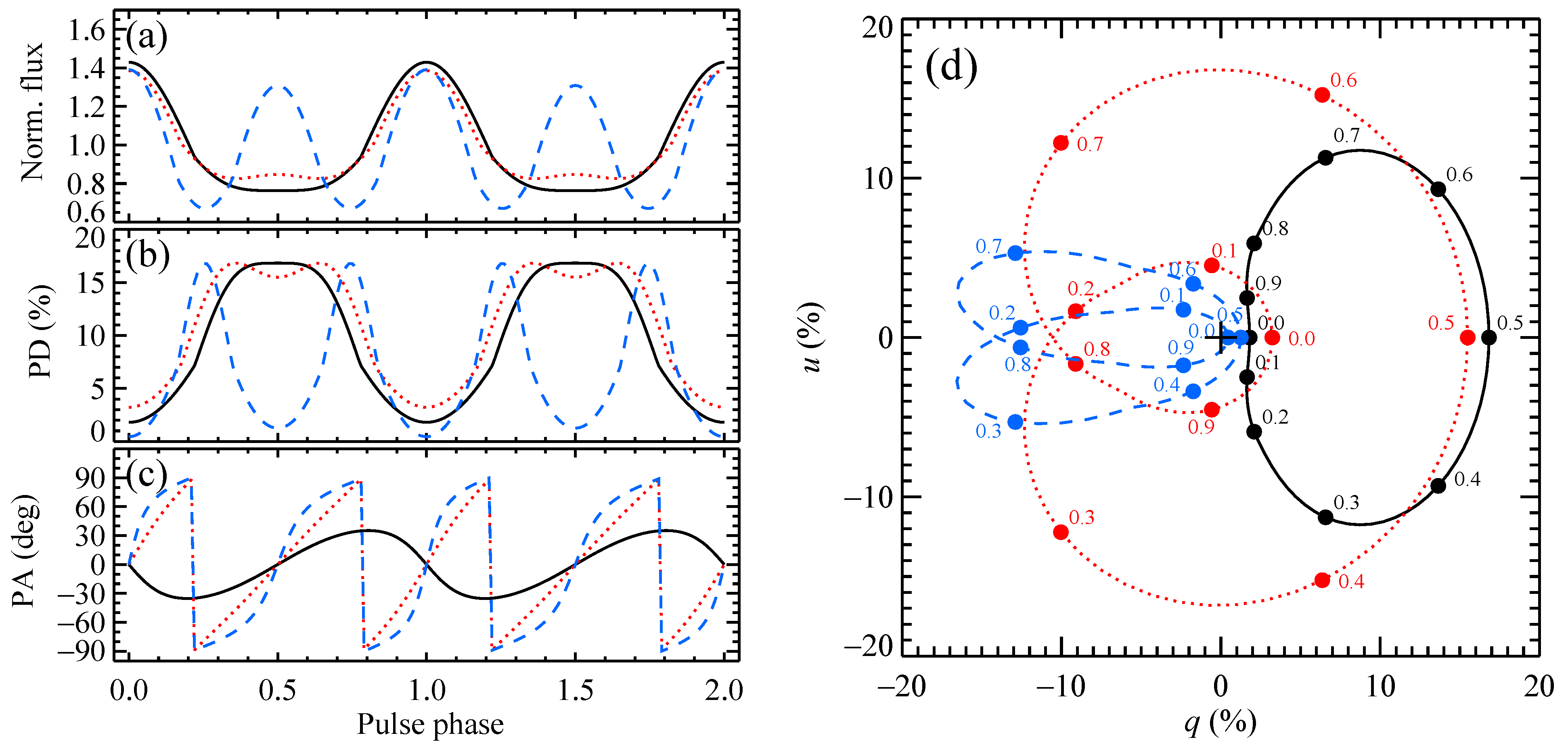
2. Rotating Vector Model
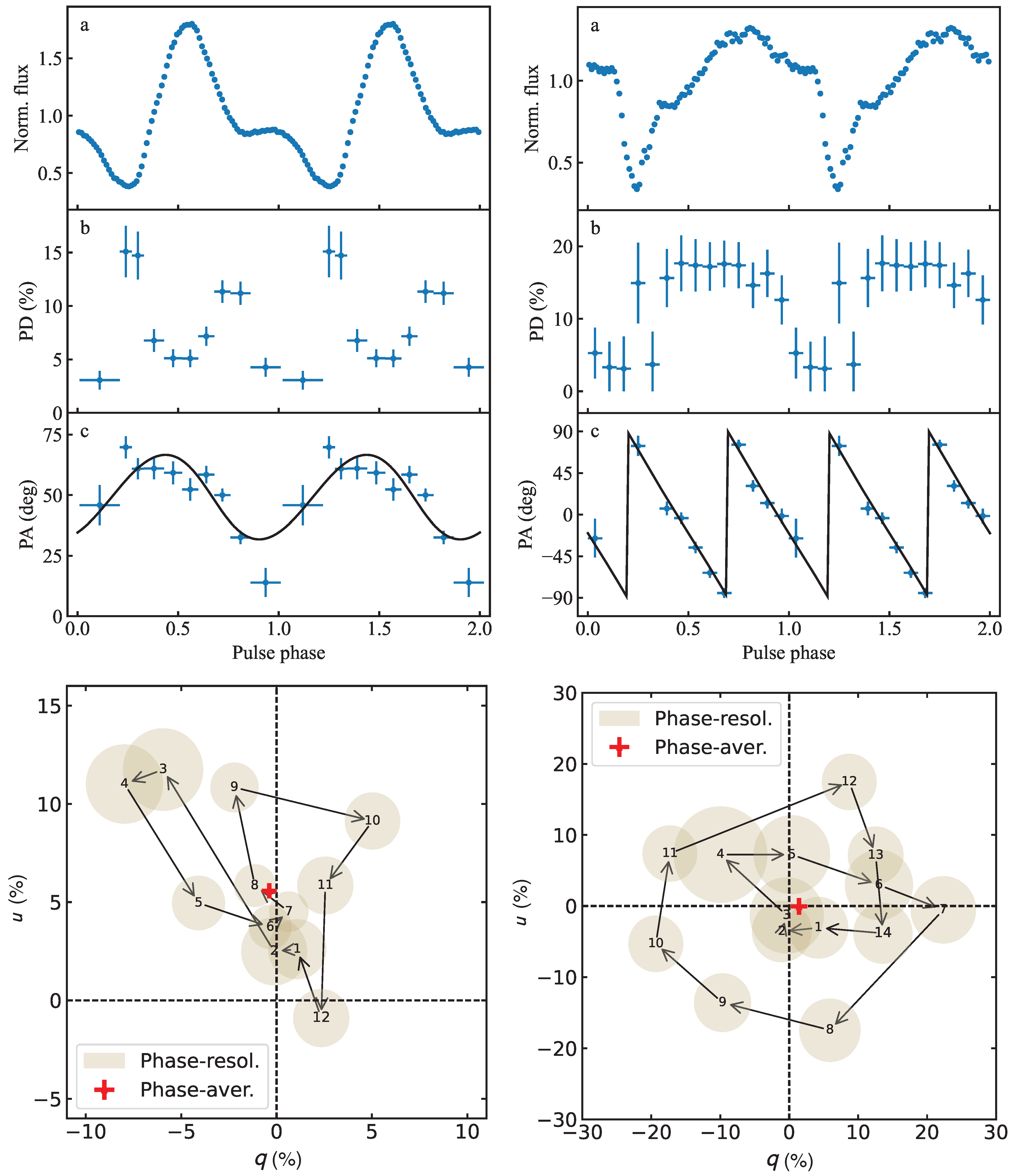
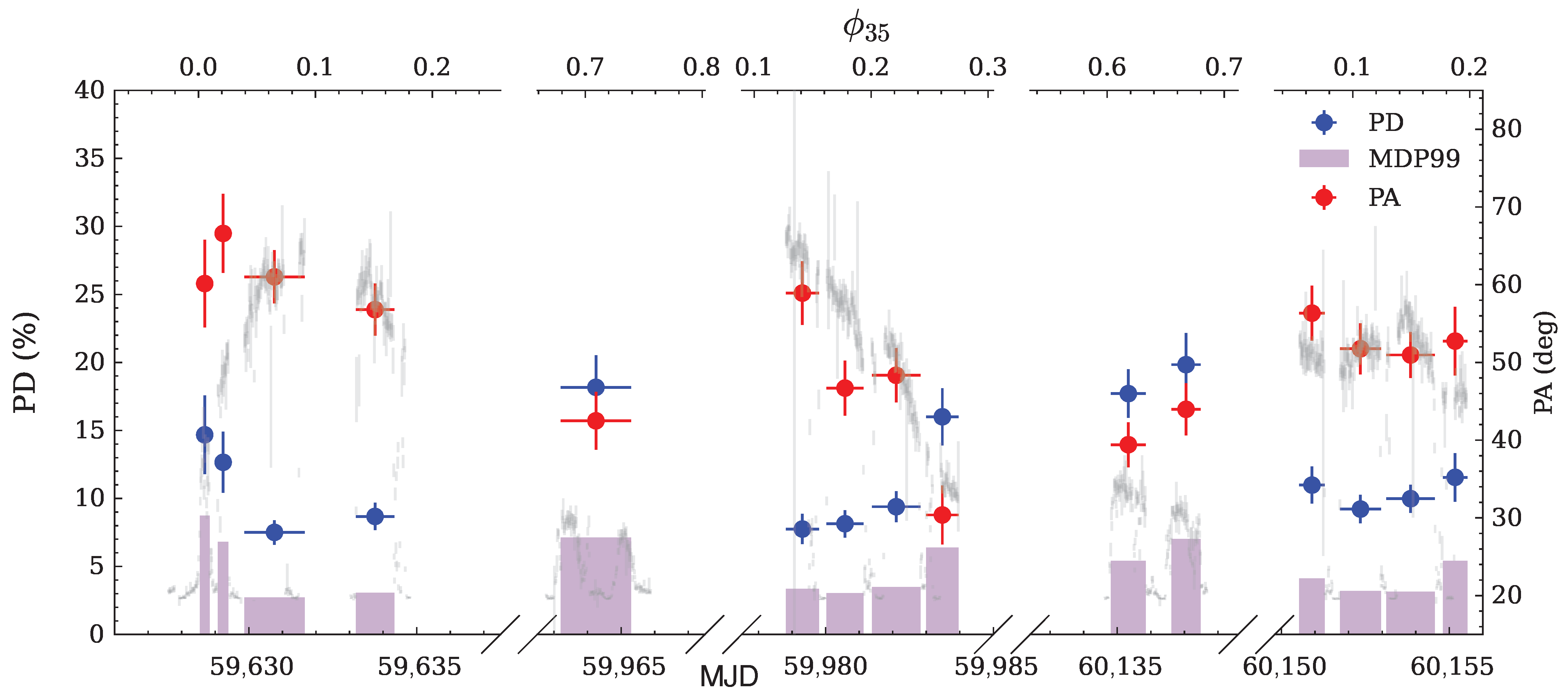
3. X-ray Pulsars Observed by IXPE
4. Summary
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| IXPE | Imaging X-ray Polarimetry Explorer |
| XRP | X-ray pulsar |
| NS | Neutron star |
| PD | Polarization degree |
| PA | Polarization angle |
| RVM | Rotating vector model |
| CRSF | Cyclotron resonance spectral feature |
References
- Mushtukov, A.; Tsygankov, S. Accreting strongly magnetised neutron stars: X-ray Pulsars. In Handbook of X-ray and Gamma-ray Astrophysics; Bambi, C., Santangelo, A., Eds.; Springer: Singapore, 2024; pp. 4105–4176. [Google Scholar] [CrossRef]
- Basko, M.M.; Sunyaev, R.A. The limiting luminosity of accreting neutron stars with magnetic fields. Mon. Not. R. Astron. Soc. 1976, 175, 395–417. [Google Scholar] [CrossRef]
- Becker, P.A.; Klochkov, D.; Schönherr, G.; Nishimura, O.; Ferrigno, C.; Caballero, I.; Kretschmar, P.; Wolff, M.T.; Wilms, J.; Staubert, R. Spectral formation in accreting X-ray pulsars: Bimodal variation of the cyclotron energy with luminosity. Astron. Astrophys. 2012, 544, A123. [Google Scholar] [CrossRef]
- Mushtukov, A.A.; Suleimanov, V.F.; Tsygankov, S.S.; Poutanen, J. The critical accretion luminosity for magnetized neutron stars. Mon. Not. R. Astron. Soc. 2015, 447, 1847–1856. [Google Scholar] [CrossRef]
- Gnedin, Y.N.; Pavlov, G.G. The transfer equations for normal waves and radiation polarization in an anisotropic medium. Sov. J. Exp. Theor. Phys. 1974, 38, 903–908. [Google Scholar]
- Gnedin, Y.N.; Pavlov, G.G.; Shibanov, Y.A. The effect of vacuum birefringence in a magnetic field on the polarization and beaming of X-ray pulsars. Sov. Astron. Lett. 1978, 4, 117–119. [Google Scholar]
- Harding, A.K.; Lai, D. Physics of strongly magnetized neutron stars. Rep. Prog. Phys. 2006, 69, 2631–2708. [Google Scholar] [CrossRef]
- Mushtukov, A.A.; Nagirner, D.I.; Poutanen, J. Compton scattering S matrix and cross section in strong magnetic field. Phys. Rev. D 2016, 93, 105003. [Google Scholar] [CrossRef]
- Nagel, W. Radiative transfer in a strongly magnetized plasma. I—Effects of anisotropy. II—Effects of Comptonization. Astrophys. J. 1981, 251, 278–296. [Google Scholar] [CrossRef]
- Nagel, W. Radiative Transfer in a Strongly Magnetized Plasma—Part Two—Effects of Comptonization. Astrophys. J. 1981, 251, 288–296. [Google Scholar] [CrossRef]
- Kaminker, A.D.; Pavlov, G.G.; Shibanov, I.A. Radiation from a Strongly Magnetized Plasma—The Case of Predominant Scattering. Astrophys. Space Sci. 1982, 86, 249–297. [Google Scholar] [CrossRef]
- Meszaros, P.; Nagel, W. X-ray pulsar models. I. Angle-dependent cyclotron line formation and comptonization. Astrophys. J. 1985, 298, 147–160. [Google Scholar] [CrossRef]
- Meszaros, P.; Nagel, W. X-ray pulsar models. II. Comptonized spectra and pulse shapes. Astrophys. J. 1985, 299, 138–153. [Google Scholar] [CrossRef]
- Kii, T. X-ray polarization from accreting strongly magnetized neutron stars: Case studies for the X-ray pulsars 4U 1626-67 and Hercules X-1. Publ. Astron. Soc. Jpn. 1987, 39, 781–800. [Google Scholar]
- Meszaros, P.; Novick, R.; Szentgyorgyi, A.; Chanan, G.A.; Weisskopf, M.C. Astrophysical Implications and Observational Prospects of X-ray Polarimetry. Astrophys. J. 1988, 324, 1056–1067. [Google Scholar] [CrossRef]
- Mushtukov, A.A.; Suleimanov, V.F.; Tsygankov, S.S.; Portegies Zwart, S. Spectrum formation in X-ray pulsars at very low mass accretion rate: Monte Carlo approach. Mon. Not. R. Astron. Soc. 2021, 503, 5193–5203. [Google Scholar] [CrossRef]
- Sokolova-Lapa, E.; Gornostaev, M.; Wilms, J.; Ballhausen, R.; Falkner, S.; Postnov, K.; Thalhammer, P.; Fürst, F.; García, J.A.; Shakura, N.; et al. X-ray emission from magnetized neutron star atmospheres at low mass-accretion rates. I. Phase-averaged spectrum. Astron. Astrophys. 2021, 651, A12. [Google Scholar] [CrossRef]
- Caiazzo, I.; Heyl, J. Polarization of accreting X-ray pulsars. I. A new model. Mon. Not. R. Astron. Soc. 2021, 501, 109–128. [Google Scholar] [CrossRef]
- González-Caniulef, D.; Zane, S.; Turolla, R.; Wu, K. Atmosphere of strongly magnetized neutron stars heated by particle bombardment. Mon. Not. R. Astron. Soc. 2019, 483, 599–613. [Google Scholar] [CrossRef]
- Mushtukov, A.A.; Tsygankov, S.S.; Poutanen, J.; Doroshenko, V.; Salganik, A.; Costa, E.; Di Marco, A.; Heyl, J.; La Monaca, F.; Lutovinov, A.A.; et al. X-ray polarimetry of X-ray pulsar X Persei: Another orthogonal rotator? Mon. Not. R. Astron. Soc. 2023, 524, 2004–2014. [Google Scholar] [CrossRef]
- Silver, E.H.; Weisskopf, M.C.; Kestenbaum, H.L.; Long, K.S.; Novick, R.; Wolff, R.S. The first search for X-ray polarization in the Centaurus X-3 and Hercules X-1 pulsars. Astrophys. J. 1979, 232, 248–254. [Google Scholar] [CrossRef]
- Abarr, Q.; Baring, M.; Beheshtipour, B.; Beilicke, M.; de Geronimo, G.; Dowkontt, P.; Errando, M.; Guarino, V.; Iyer, N.; Kislat, F.; et al. Observations of a GX 301-2 Apastron Flare with the X-Calibur Hard X-ray Polarimeter Supported by NICER, the Swift XRT and BAT, and Fermi GBM. Astrophys. J. 2020, 891, 70. [Google Scholar] [CrossRef]
- Weisskopf, M.C.; Soffitta, P.; Baldini, L.; Ramsey, B.D.; O’Dell, S.L.; Romani, R.W.; Matt, G.; Deininger, W.D.; Baumgartner, W.H.; Bellazzini, R.; et al. The Imaging X-ray Polarimetry Explorer (IXPE): Pre-Launch. J. Astron. Telesc. Instrum. Syst. 2022, 8, 026002. [Google Scholar] [CrossRef]
- Soffitta, P.; Baldini, L.; Bellazzini, R.; Costa, E.; Latronico, L.; Muleri, F.; Del Monte, E.; Fabiani, S.; Minuti, M.; Pinchera, M.; et al. The Instrument of the Imaging X-ray Polarimetry Explorer. Astron. J. 2021, 162, 208. [Google Scholar] [CrossRef]
- Radhakrishnan, V.; Cooke, D.J. Magnetic Poles and the Polarization Structure of Pulsar Radiation. Astrophys. Lett. 1969, 3, 225. [Google Scholar]
- Komesaroff, M.M. Possible Mechanism for the Pulsar Radio Emission. Nature 1970, 225, 612–614. [Google Scholar] [CrossRef]
- Pavlov, G.G.; Shibanov, Y.A. Influence of vacuum polarization by a magnetic field on the propagation of electromagnetic waves in a plasma. Sov. J. Exp. Theor. Phys. 1979, 49, 741. [Google Scholar]
- Heyl, J.S.; Shaviv, N.J. Polarization evolution in strong magnetic fields. Mon. Not. R. Astron. Soc. 2000, 311, 555–564. [Google Scholar] [CrossRef]
- Heyl, J.S.; Shaviv, N.J. QED and the high polarization of the thermal radiation from neutron stars. Phys. Rev. D 2002, 66, 023002. [Google Scholar] [CrossRef]
- Taverna, R.; Turolla, R.; Gonzalez Caniulef, D.; Zane, S.; Muleri, F.; Soffitta, P. Polarization of neutron star surface emission: A systematic analysis. Mon. Not. R. Astron. Soc. 2015, 454, 3254–3266. [Google Scholar] [CrossRef]
- Heyl, J.; Caiazzo, I. Strongly Magnetized Sources: QED and X-ray Polarization. Galaxies 2018, 6, 76. [Google Scholar] [CrossRef]
- Taverna, R.; Turolla, R. X-ray Polarization from Magnetar Sources. Galaxies 2024, 12, 6. [Google Scholar] [CrossRef]
- Poutanen, J. Relativistic rotating vector model for X-ray millisecond pulsars. Astron. Astrophys. 2020, 641, A166. [Google Scholar] [CrossRef]
- Loktev, V.; Salmi, T.; Nättilä, J.; Poutanen, J. Oblate Schwarzschild approximation for polarized radiation from rapidly rotating neutron stars. Astron. Astrophys. 2020, 643, A84. [Google Scholar] [CrossRef]
- Poutanen, J. Accurate analytic formula for light bending in Schwarzschild metric. Astron. Astrophys. 2020, 640, A24. [Google Scholar] [CrossRef]
- Tsygankov, S.S.; Doroshenko, V.; Poutanen, J.; Heyl, J.; Mushtukov, A.A.; Caiazzo, I.; Di Marco, A.; Forsblom, S.V.; González-Caniulef, D.; Klawin, M.; et al. The X-ray Polarimetry View of the Accreting Pulsar Cen X-3. Astrophys. J. Lett. 2022, 941, L14. [Google Scholar] [CrossRef]
- Doroshenko, V.; Poutanen, J.; Tsygankov, S.S.; Suleimanov, V.F.; Bachetti, M.; Caiazzo, I.; Costa, E.; Di Marco, A.; Heyl, J.; La Monaca, F.; et al. Determination of X-ray pulsar geometry with IXPE polarimetry. Nat. Astron. 2022, 6, 1433–1443. [Google Scholar] [CrossRef]
- Heyl, J.; Doroshenko, V.; González-Caniulef, D.; Caiazzo, I.; Poutanen, J.; Mushtukov, A.; Tsygankov, S.S.; Kirmizibayrak, D.; Bachetti, M.; Pavlov, G.G.; et al. Complex rotational dynamics of the neutron star in Hercules X-1 revealed by X-ray polarization. Nat. Astron. 2024, in press. [CrossRef]
- Marshall, H.L.; Ng, M.; Rogantini, D.; Heyl, J.; Tsygankov, S.S.; Poutanen, J.; Costa, E.; Zane, S.; Malacaria, C.; Agudo, I.; et al. Observations of 4U 1626-67 with the Imaging X-ray Polarimetry Explorer. Astrophys. J. 2022, 940, 70. [Google Scholar] [CrossRef]
- Forsblom, S.V.; Poutanen, J.; Tsygankov, S.S.; Bachetti, M.; Di Marco, A.; Doroshenko, V.; Heyl, J.; La Monaca, F.; Malacaria, C.; Marshall, H.L.; et al. IXPE Observations of the Quintessential Wind-accreting X-ray Pulsar Vela X-1. Astrophys. J. Lett. 2023, 947, L20. [Google Scholar] [CrossRef]
- Tsygankov, S.S.; Doroshenko, V.; Mushtukov, A.A.; Poutanen, J.; Di Marco, A.; Heyl, J.; La Monaca, F.; Forsblom, S.; Malacaria, C.; Marshall, H.L.; et al. X-ray pulsar GRO J1008-57 as an orthogonal rotator. Astron. Astrophys. 2023, A48. [Google Scholar] [CrossRef]
- Malacaria, C.; Heyl, J.; Doroshenko, V.; Tsygankov, S.S.; Poutanen, J.; Forsblom, S.V.; Capitanio, F.; Di Marco, A.; Du, Y.; Ducci, L.; et al. A polarimetric-oriented X-ray stare at the accreting pulsar EXO 2030+375. Astron. Astrophys. 2023, 675, A29. [Google Scholar] [CrossRef]
- Suleimanov, V.F.; Forsblom, S.V.; Tsygankov, S.S.; Poutanen, J.; Doroshenko, V.; Doroshenko, R.; Capitanio, F.; Di Marco, A.; González-Caniulef, D.; Heyl, J.; et al. X-ray polarimetry of the accreting pulsar GX 301-2. Astron. Astrophys. 2023, 678, A119. [Google Scholar] [CrossRef]
- Doroshenko, V.; Poutanen, J.; Heyl, J.; Tsygankov, S.S.; Caiazzo, I.; Turolla, R.; Veledina, A.; Weisskopf, M.C.; Forsblom, S.V.; González-Caniulef, D.; et al. Complex variations in X-ray polarization in the X-ray pulsar LS V +44 17/RX J0440.9+4431. Astron. Astrophys. 2023, 677, A57. [Google Scholar] [CrossRef]
- Poutanen, J.; Tsygankov, S.S.; Doroshenko, V.; Forsblom, S.V.; Jenke, P.; Kaaret, P.; Berdyugin, A.V.; Blinov, D.; Kravtsov, V.; Liodakis, I.; et al. Studying geometry of the ultraluminous X-ray pulsar Swift J0243.6+6124 using X-ray and optical polarimetry. arXiv 2024, arXiv:2405.08107. [Google Scholar] [CrossRef]
- Forsblom, S.V.; Tsygankov, S.S.; Poutanen, J.; Doroshenko, V.; Mushtukov, A.A.; Ng, M.; Ravi, S.; Marshall, H.L.; Di Marco, A.; La Monaca, F.; et al. Probing the polarized emission from SMC X-1: The brightest X-ray pulsar observed by IXPE. arXiv 2024, arXiv:2406.08988. [Google Scholar] [CrossRef]
- Zhao, Q.C.; Li, H.C.; Tao, L.; Feng, H.; Zhang, S.N.; Walter, R.; Ge, M.Y.; Tong, H.; Ji, L.; Zhang, L.; et al. Polarization perspectives on Hercules X-1: Further constraining the geometry. Mon. Not. R. Astron. Soc. 2024, 531, 3935–3949. [Google Scholar] [CrossRef]
- Neumann, M.; Avakyan, A.; Doroshenko, V.; Santangelo, A. XRBcats: Galactic High Mass X-ray Binary Catalogue. Astron. Astrophys. 2023, 677, A134. [Google Scholar] [CrossRef]
- Avakyan, A.; Neumann, M.; Zainab, A.; Doroshenko, V.; Wilms, J.; Santangelo, A. XRBcats: Galactic low-mass X-ray binary catalogue. Astron. Astrophys. 2023, 675, A199. [Google Scholar] [CrossRef]
- Staubert, R.; Trümper, J.; Kendziorra, E.; Klochkov, D.; Postnov, K.; Kretschmar, P.; Pottschmidt, K.; Haberl, F.; Rothschild, R.E.; Santangelo, A.; et al. Cyclotron lines in highly magnetized neutron stars. Astron. Astrophys. 2019, 622, A61. [Google Scholar] [CrossRef]
- Kolesnikov, D.; Shakura, N.; Postnov, K. Evidence for neutron star triaxial free precession in Her X-1 from Fermi/GBM pulse period measurements. Mon. Not. R. Astron. Soc. 2022, 513, 3359–3367. [Google Scholar] [CrossRef]
- Sunyaev, R.A.; Titarchuk, L.G. Comptonization of low-frequency radiation in accretion disks Angular distribution and polarization of hard radiation. Astron. Astrophys. 1985, 143, 374–388. [Google Scholar] [CrossRef]
- Piccinni, O.J. Status and Perspectives of Continuous Gravitational Wave Searches. Galaxies 2022, 10, 72. [Google Scholar] [CrossRef]
- Wette, K. Searches for continuous gravitational waves from neutron stars: A twenty-year retrospective. Astropart. Phys. 2023, 153, 102880. [Google Scholar] [CrossRef]


| Name | Spin Period a,b | Orbital Period a,b | Distance a,b | Luminosity c | CRSF d | IXPE |
|---|---|---|---|---|---|---|
| [s] | [d] | [kpc] | [erg s−1] | [keV] | Reference | |
| Cen X-3 | 4.8 | 2.09 | 6.07 | 28 | [36] | |
| Her X-1 | 1.24 | 1.7 | 7.09 | ∼ | 37 | [37,38] |
| 4U 1626-67 | 7.7 | 0.02875 | 15.08 | 37, 61? | [39] | |
| Vela X-1 | 283 | 8.96 | 1.87 | 25, 53 | [40] | |
| GRO J1008-57 | 93.5 | 249.5 | 3.21 | 78 | [41] | |
| EXO 2030+375 | 41.31 | 46.02 | 2.08 | 36/63? | [42] | |
| X Persei | 837.67 | 250.3 | 0.63 | 29 | [20] | |
| GX 301-2 | 696.0 | 41.59 | 3.54 | 37/50 | [43] | |
| LS V +44 17 | 202.5 | 155.0 | 2.29 | ≤ | 32 | [44] |
| Swift J0243.6+6124 | 9.87 | 28.3 | 5.2 | 146 | [45] | |
| SMC X-1 | 0.717 | 3.892 | 61 | – | [46] |
| Name | [deg] | [deg] | [deg] |
|---|---|---|---|
| Cen X-3 | 70.2 (fixed) | ||
| Her X-1 (main-on) | |||
| Her X-1 (short-on) | |||
| GRO J1008-57 | |||
| EXO 2030+375 | |||
| X Persei | |||
| GX 301-2 | 135 | ||
| LS V +44 17/Obs. 1 | |||
| LS V +44 17/Obs. 2 | |||
| LS V +44 17 a | |||
| Swift J0243/Obs. 1 | |||
| Swift J0243/Obs. 2 | |||
| Swift J0243/Obs. 3 | |||
| Swift J0243 a | |||
| SMC X-1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Poutanen, J.; Tsygankov, S.S.; Forsblom, S.V. X-ray Polarimetry of X-ray Pulsars. Galaxies 2024, 12, 46. https://doi.org/10.3390/galaxies12040046
Poutanen J, Tsygankov SS, Forsblom SV. X-ray Polarimetry of X-ray Pulsars. Galaxies. 2024; 12(4):46. https://doi.org/10.3390/galaxies12040046
Chicago/Turabian StylePoutanen, Juri, Sergey S. Tsygankov, and Sofia V. Forsblom. 2024. "X-ray Polarimetry of X-ray Pulsars" Galaxies 12, no. 4: 46. https://doi.org/10.3390/galaxies12040046
APA StylePoutanen, J., Tsygankov, S. S., & Forsblom, S. V. (2024). X-ray Polarimetry of X-ray Pulsars. Galaxies, 12(4), 46. https://doi.org/10.3390/galaxies12040046






