Abstract
The Event Horizon Telescope (EHT) Collaboration has successfully produced images of two supermassive black holes, enabling novel tests of black holes and their accretion flows on horizon scales. The EHT has so far published total intensity and linear polarization images, while upcoming images may include circular polarization, rotation measure, and spectral index, each of which reveals different aspects of the plasma and space-time. The next-generation EHT (ngEHT) will greatly enhance these studies through wider recorded bandwidths and additional stations, leading to greater signal-to-noise, orders of magnitude improvement in dynamic range, multi-frequency observations, and horizon-scale movies. In this paper, we review how each of these different observables informs us about the underlying properties of the plasma and the spacetime, and we discuss why polarimetric studies are well-suited to measurements with sparse, long-baseline coverage.
1. Simulating Black Hole Accretion Flows
The Event Horizon Telescope (EHT) collaboration has produced the first images of supermassive black holes (SMBHs), ushering in a new era of spatially resolved astrophysics at the event horizon [1,2,3,4,5,6,7,8,9,10,11,12,13,14]. The images have been very constraining for general relativistic magnetohydrodynamics (GRMHD) models, which evolve plasma in a Kerr spacetime under the assumptions of ideal MHD. EHT science has focused mainly on constraining three free parameters: spin, the magnetic field state, and , which is related to the ion-to-electron temperature ratio [5,8,13]. The SMBH spin, which we will denote as , is the dimensionless angular momentum of a SMBH described by a Kerr metric that can vary between . A SMBH’s spin reflects its recent assembly history and affects its accretion and feedback processes see [15]. Meanwhile, the accretion flow’s magnetic field structure may vary between “MAD” and “SANE” states. In a Magnetically Arrested Disk (MAD), the magnetic flux at the horizon saturates, and the magnetic fields grow dynamically important, resulting in azimuthal asymmetries including flux eruption events [16,17,18]. This contrasts with “Standard and Normal Evolution” (SANE), where the magnetic fields remain turbulent and dynamically unimportant [19,20]. Finally, the ratio of the ion to electron temperature in different regions is highly uncertain, since the mean free path of the particles is much larger than the size of the system, and ions are heated more efficiently [21,22,23]. EHT studies have encapsulated this uncertainty with the post-processing parameters and , which describe the asymptotic ion to electron temperature ratio at low and high plasma , respectively, [24], where is the ratio of gas to magnetic pressure. Less thoroughly studied parameters include the electron distribution function (eDF) [13,25,26,27,28], the detailed particle composition of the plasma [29,30,31], and the tilt of a potentially misaligned disk [32,33], which are the subject of many recent and ongoing studies.
In this paper, we review how properties of the spacetime and the plasma become imprinted onto multifrequency polarimetric observables accessible to the EHT and ngEHT. In Figure 1, we plot a single GRMHD snapshot, ray-traced at 214 and 228 GHz with ipole [34] and scaled to Sagittarius A*. This particular model is a MAD model with , 1, and a viewing angle of . To date, the EHT has produced total intensity maps for both M87* and Sgr A* and a linear polarization map of M87*. The remaining maps have yet to be generated for EHT data, and will be explained in detail in this paper. In brief, circular polarization may arise from both Faraday conversion and intrinsically emitted synchrotron, e.g., [35], and is especially sensitive to the details of the underlying magnetic field geometry [36,37,38] and plasma composition [29,30,39]. Meanwhile, the spectral index is the logarithmic derivative of the flux or intensity with respect to frequency, ; , which helps break degeneracies between number density, temperature, and magnetic field strength [40,41]. Finally, rotation measure is the derivative of the electric vector position angle (EVPA or ) with respect to observing wavelength squared , which encodes Faraday rotation. Since colder electrons Faraday rotate more efficiently, the RM offers a glimpse into a colder population of electrons, which may exist at large number densities but may be too cold to contribute significantly to the intensity [42,43,44]. As discussed in the other contributions to this special issue, the ngEHT will enable access to these observables with higher image dynamic range than currently published EHT results (increasing from ∼10 to ≳103), improved spatial resolution (decreasing from about 20 μas to ∼10–15 μas), and time-resolved images of the dynamical activity in both M87* and Sgr A* over hundreds-to-thousands of gravitational timescales. This will result in movies of both the accretion disks and relativistic jets near SMBHs. In this article, we discuss what physical information each of these maps carry.
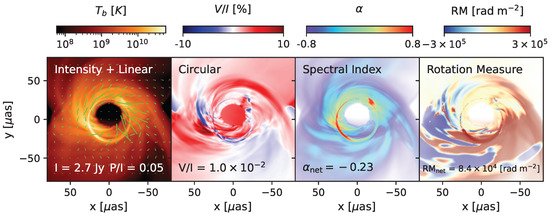
Figure 1.
A single GRMHD snapshot ray-traced and scaled to Sgr A* properties, with three decades in dynamic range shown. In the leftmost panel, ticks representing the linear polarization have lengths scaled proportionally to the total linearly polarized intensity. To date, total intensity maps have been produced for both Sgr A* and M87*, a linear polarization map has been produced for M87*, and the remaining observables have yet to be generated for either source. In the era of ngEHT, we will have access to each of these observables with improved dynamic range and time-domain information, which will greatly inform models of the black hole accretion flow. Note that finite spatial resolution and other data corruptions have not been taken into account.
2. Total Intensity and Spectral Index
In the millimeter, we observe Sgr A* and M87* near the peak of emission from synchrotron radiation, where the flow transitions from optically thick to optically thin. Here, the emissivity scales approximately as , where n is the electron number density, B is the magnetic field strength, and is the electron temperature2 (in units of the electron rest mass energy). Each of these quantities can vary by orders of magnitude among different models, and thus even the total flux is informative for jointly constraining these parameters. To match the total flux of a given system, the fluid in ideal GRMHD simulations can be rescaled via , , and , where u is the internal energy and is a scalar. After doing so, both MAD and SANE simulations are capable of matching the total flux of EHT sources at a single frequency, as well as broad image characteristics such as the image size [5,13]. However, this rescaling causes SANE simulations to typically have orders of magnitude larger number density than MADs, due to their intrinsically weaker magnetic fields and lower temperatures [8,13]. Consequently, any additional observables sensitive to these variables immediately help break degeneracies and distinguish between models.
For example, the degeneracies between n, B, and can be partially resolved with the spectral index, . Spectral index is mainly sensitive to the optical depth as well as the temperature and magnetic field strength in the combination (on which the critical synchrotron frequency is dependent), e.g., [45]. Ricarte et al. [41] show that GRMHD models span a wide range of spectral indices, and that SANE models typically exhibit more negative spectral indices than MADs at a fixed optical depth due to their lower temperatures. Although lacking by construction in ideal GRMHD simulations, spectral index can also provide insight into synchrotron cooling processes that affect the temperature.
In the ngEHT era, multi-frequency VLBI will enable spatially resolved spectral index maps. Since the most important parameters (, B, and ) all decline with radius, spectral index maps should generically grow more negative as radius increases. Equivalently, the image becomes smaller as the frequency grows larger, e.g., [46]. One example from Ricarte et al. [41] is shown in Figure 2: a MAD simulation of Sgr A* with , , and a non-thermal “kappa” electron distribution function3 with [47,48], inclined at . The true spectral index map across 214 to 228 GHz is shown in the top central panel, while a one-zone analytic prediction is shown in the top right, using a eDF combined with the plasma variables computed in the bottom row. To obtain the analytic prediction, each pixel is treated as a one-zone model using plasma properties computed via an emissivity-weighted average along the geodesic. In this simulation, both and B decline with radius, but stays in a relatively narrow range. Thus, the decline of with radius can be attributed to a decline in and B. Models also exhibit a generic spike in in the photon ring, whose geodesics plunge into regions with strong magnetic fields and acquire a larger optical depth due to their longer path lengths in the emitting region.
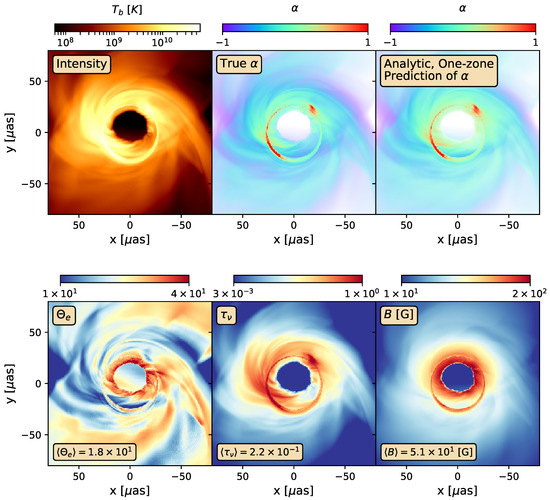
Figure 2.
Intensity and spectral index map of a MAD model of Sgr A* adapted from Figure 4 of [41]. The top left panel plots total intensity in log scale averaged between 214 and 228 GHz, the top center panel plots the spectral index across this bandwidth calculated by ray tracing the image at two different frequencies, and the top right panel plots an analytic prediction of the spectral index in each pixel obtained by combining the three quantities in the bottom panel: electron temperature, optical depth, and magnetic field strength, each computed by performing an emissivity-weighted average long each geodesic. The excellent agreement between the true spectral index map and the analytic prediction illustrates the power of spectral index maps to jointly constrain these plasma quantities.
3. Linear Polarization
In flat space, a uniform parcel of synchrotron emitting optically thin plasma intrinsically produces a linear polarization fraction of , with an orientation perpendicular to its magnetic field projected onto the plane perpendicular to the photon wave-vector, e.g., [49]. The observed orientation of this linear polarization gets modified by two effects: achromatic effects of propagation through the curved space-time, and chromatic “Faraday” effects of propagation through a magnetized plasma (recent theoretical investigations in the vicinity of a black hole include [50,51,52,53]). Both rotate and potentially scramble the electric vector position angle (EVPA, or ). Thus, resolved images of linear polarization can inform us about the magnetic field geometry, the magnitude of Faraday effects, and potentially the space-time itself. In Figure 3, we plot the linear polarization pattern of a ring of emission moving clockwise on the sky around a Schwarzschild black hole using the model of Narayan et al. [51]. Here, only the direct () sub-image is included. The ring is located at a radius of and has a Gaussian width of . The angular momentum vector of the ring projected onto the sky has a position angle of East of North and is viewed at an inclination of , consistent with that of M87* [54]. In the toroidal and radial field cases, the resulting linear polarization pattern is simply perpendicular to the magnetic fields projected onto the line-of-sight. In the idealized vertical case, the EVPA pattern becomes more sensitive to the direction of the fluid’s motion [8].

Figure 3.
Polarization pattern of a ring of emission around a Schwarzschild black hole threaded with magnetic fields of different geometries: toroidal, radial, and vertical adapted from Figure 3 of [8]. The toroidal and radial magnetic field cases clearly illustrate the fact that synchrotron emission is polarized perpendicular to the magnetic field projected onto the sky. The orientation of the ticks in the vertical field case encodes the direction of the fluid’s motion [8], chosen here to be clockwise on the sky. These maps were computed using the analytic ring model of Narayan et al. [51]. Here, the color map encodes the total intensity, and unlike in Figure 1, the linear polarization ticks do not scale with the polarized intensity.
EHT studies have identified the linear polarization fraction (on both resolved and unresolved scales) as well as the morphology of polarization ticks as important observables for theoretical interpretation. This “twistiness” can be quantified by the complex number , the rotationally symmetric component of a Fourier decomposition of the polarization pattern [55]. M87* and Sgr A* both exhibit percent level spatially-unresolved linear polarization fractions at 1.3 mm and ∼10–20% level resolved polarization fractions, e.g., [7,56], much lower than the ideal value of 70% for a uniform parcel of emitting plasma, e.g., [57,58,59], as do other AGN observed with cm-VLBI, e.g., [60,61]. This could be due to both Faraday depolarization and disordered magnetic field structures. For the EHT observations of M87*, Event Horizon Telescope Collaboration et al. [8] found that the low polarization fraction was attributable mainly to Faraday rotation in GRMHD models. Combining resolved linear polarization information with an upper limit on circular polarization, Event Horizon Telescope Collaboration et al. [8] found that MAD models were favored over their SANE counterparts for M87*, which could not be concluded based on total intensity alone. Fundamentally, this can be attributed to linear polarization’s sensitivity to the geometry of the magnetic field, as well as Faraday rotation’s sensitivity to cooler electrons that may otherwise be invisible. MAD models tend to have more ordered fields with stronger poloidal components, which produces twistier polarization patterns. Meanwhile, SANE models tend to require orders of magnitude larger mass density to compensate for their intrinsically weaker magnetic fields and lower temperatures, resulting in much greater Faraday depths. In retrograde systems, images can exhibit flips in the handedness of the polarization spiral with radius, quantified as a sign flip in the imaginary component of . This results from a flip in the angular velocity of inflowing streams due to frame dragging [62].
Sgr A* also exhibits interesting time variability in linear polarization, especially during flares, which are accompanied by large polarization fractions, swings in polarization angle, and “Q-U loops” on the timescale of hours [63,64,65,66,67]. These can be interpreted as the motion of hotspots or other structures as they light up different parts of the magnetic field structure during their orbit [52,68,69,70,71,72]. The hotspots themselves may originate from “flux eruption events” and magnetic reconnections that occur naturally in MAD accretion flows [73,74,75]. Thus, time variability of linear polarization offers unique insights into the magnetic field structure and direction of orbital motion that could potentially be linked to the inclination and spin of Sgr A*. The GRAVITY Collaboration has detected centroid motion coincident with a flare [66,76]. Spatially resolved movies created by the ngEHT would help test the hotspot interpretation, motivating high-cadence monitoring of this source.
4. Rotation Measure
In an ionic plasma, circularly polarized waves of opposite handedness propagate at different speeds, resulting in a circular birefringence effect known as Faraday rotation. The EVPA of propagating emission rotates an amount sensitive to the density, temperature, and line-of-sight magnetic field. As examined in several studies, internal Faraday rotation is important for depolarizing and scrambling images of GRMHD models of black hole accretion flows [8,42,43,44]. The magnitude of Faraday rotation has a wavelength-squared dependence, thus it is useful observationally to define the rotation measure , which offers insights into physical parameters of the Faraday rotating plasma. For a linearly polarized emitter entirely behind a uniform Faraday screen, the RM is related to the properties of the screen via
where is the electron number density, is the component of the magnetic field parallel to the photon wave-vector, and is a correction term suppressing Faraday rotation at relativistic temperatures [77]. For relativistic plasmas, , while asymptotes to 1 as . Here , is the Boltzmann constant, is the electron temperature, is the electron rest mass, and c is the speed of light [78]. In GRMHD models, the plasma responsible for synchrotron emission is sometimes completely separate from the plasma responsible for Faraday rotation. For example, some large SANE models exhibit a cold Faraday rotating midplane sandwiched between emission from their hot jet sheaths [44]. Moreover, while the EVPA probes the magnetic field as projected onto the sky, Faraday rotation is sensitive to the magnetic field along the line-of-sight. Hence, rotation measure and linear polarization can offer a view into electron populations that may otherwise be undetectable from total intensity alone.
At the time of writing, narrow observing bandwidths inhibit our ability to create spatially resolved rotation measure maps with currently published EHT data, but spatially unresolved RM measurements at millimeter wavelengths exist for Sgr A*, the core of M87*, and several other LLAGN, e.g., [79,80,81,82,83,84]. Note also that rotation measure from AGN generally increases with increasing frequency, e.g., [85] and can reach values of the order of [86] due to the opacity effect probing regions close to the central engine at the ngEHT frequencies. Without spatial resolution, unresolved rotation measure measurements are difficult to interpret because the assumptions underlying Equation (1) are not believed to generally hold. In GRMHD models, Faraday rotation occurs co-spatially with the plasma, can vary by orders of magnitude in different locations, and can also flip sign across the image due to turbulence [44]. As a result, unresolved EVPA measurements may exhibit significant temporal variation and not strictly follow a law. Figure 4 plots a rotation measure map of a MAD GRMHD model of M87*, with the spatially unresolved RM written at the bottom of each panel. This turbulence can explain the intra-week time variability of the RM observed for M87* [59]. On the other hand, Sgr A* has exhibited a constant sign of RM for decades, suggesting the existence of a more stable (but still variable) foreground Faraday screen [84]. Spatially resolved rotation measure maps could help disentangle the Faraday screen and give insights into both the turbulence of the accretion flow and the magnetic field structure of jets. This may be of increased importance, since EHT observations of Sgr A* indicate that GRMHD models are too variable [13].
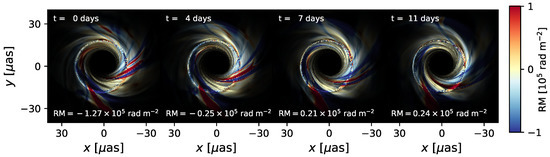
Figure 4.
Rotation measure map of a MAD simulation of M87* adapted from Figure 13 of Ricarte et al. [44]. Both positive and negative RM regions are simultaneously present, reflecting flips in the line-of-sight magnetic field direction due to turbulence in the accretion flow. The motion of these structures produces a time variable spatially unresolved RM, written at the bottom of each panel.
5. Circular Polarization
Circular polarization, Stokes V, can be generated both intrinsically through synchrotron emission or through Faraday conversion, which exchanges linear and circular polarization states, e.g., [35,78]. Circular polarization fractions are much lower than their linear counterparts for both Sgr A* () and M87* (), making it more challenging to study than linear polarization. In addition, the circular feed basis used for EHT sites makes it more challenging to construct circularly polarized images. However, Stokes V has the potential to encode not only the magnetic field direction and geometry, but also the plasma composition.
Unlike the near unity linear polarization fractions produced by a uniform parcel of plasma, intrinsically emitted Stokes V is typically produced at the ∼1% level for plasma parameters appropriate for M87* or Sgr A*. The sign of intrinsically emitted circular polarization generated encodes the sign of the magnetic field along the line of sight, following the right hand rule. Stokes V can also be generated via Faraday conversion, which exchanges linear and circular polarization states. The sign of circular polarization generated by conversion depends on the relative orientation of the EVPA with respect to the local magnetic field. Specifically, Stokes V generated by conversion inherits the sign of Stokes U, defined in the local plasma frame. Thus, Stokes V from Faraday conversion is sensitive to the line of sight “twist” in the magnetic field as well as any Faraday rotation affecting the EVPA of the linear polarization that gets converted. Interestingly, Faraday conversion has no effect in a unidirectional magnetic field lacking Faraday rotation.
Both intrinsic synchrotron emission and Faraday conversion are believed to be important for generating circular polarization on event horizon scales [36,37,38]. For Faraday conversion, both the line of sight twist in the magnetic field and Faraday rotation are important for determining the orientation of the linear polarization that is converted into circular. Small amounts of Faraday rotation can affect the relative alignment between linear polarization and the converting magnetic field. Large amounts of Faraday rotation can lead to depolarization by randomizing the sign of Stokes U that is converted into Stokes V.
Figure 5 depicts a cartoon of a typical helical field geometry as well as the circular polarization produced by a model that exhibits this structure reproduced from [37]. In the left panel, the background colors depict the line of sight direction of the magnetic field, viewed edge-on. In the time averaged image of viewed at 90, this structure produces a “four quadrants” pattern. Outside the immediate vicinity of the event horizon, Stokes V originates from intrinsic emission in this model, which reflects the line-of-sight direction of the magnetic field see also [38]. Another interesting feature that arises due to a generic helical field geometry is the successive sign flipping of sub-images in the photon ring also discussed in [36], which can be explained by Faraday conversion and parallel transport in a generic helical field geometry viewed face-on [37]. In this particular model, the spatially unresolved Stokes V is surprisingly dominated by this sign-flipped photon ring.
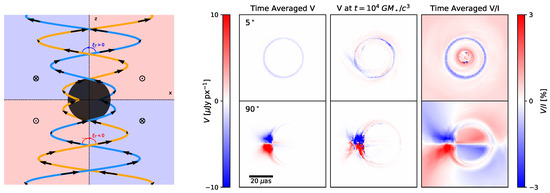
Figure 5.
Maps of circular polarization encode properties of the geometry of the magnetic field, both its line-of-sight direction and twist. A cartoon of a generic helical field geometry is depicted on the left. On the right, we plot the circular polarization of a MAD model of M87* at two inclinations. Both are reproduced from Ricarte et al. [37]. The top row depicts a 5 viewing angle, and the bottom row depicts a 90 viewing angle. The first column shows the time averaged circularly polarized image, the second column shows the same at a single snapshot, and the third column shows fractional circular polarization. For face-on viewing angles, the photon ring exhibits an interesting sign flip due to Faraday conversion and the sourcing of photons from the opposite side of the disk. For edge-on viewing angles, circular polarization exhibits a “four quadrants” pattern that reflects the line-of-sight magnetic field direction.
Finally, circular polarization is strongly affected by plasma composition, and can potentially be used to distinguish pair plasmas from ionic plasmas, e.g., [39]. Most models used to study EHT images have contained only ionic plasma. Electron-positron pairs can also be naturally produced on event horizon scales, but their abundance is highly theoretically uncertain. In a pair plasma, intrinsic circularly polarized emission and Faraday rotation both vanish, but Faraday conversion persists. Intuitively, a pair plasma with equal parts positively and negatively charged particles should not gyrate in a preferred direction. This can cause dramatic differences in images of circular polarization, and potentially also those of linear polarization [29,30].
6. Scattering
A major challenge for studies of Sgr A* with the EHT and ngEHT is interstellar scattering by dilute plasma in the ionized interstellar medium. This scattering arises from variations in the index of refraction of the plasma because of fluctuations in the electron number density see, e.g., [87]. In particular, the line of sight to Sgr A* is heavily scattered by plasma in the spiral arms of the Milky Way [88], resulting in angular broadening that is approximately three orders of magnitude larger than median values for lines of sight at higher galactic latitudes. The effects of scattering are two-fold: (1) small-scale modes in the scattering material result in diffractive “blurring,” described by a convolution with an anisotropic kernel, and (2) large-scale modes in the scattering material result in refractive “substructure,” described by additive image noise with a slowly falling power spectrum. For detailed discussion of the scattering of Sgr A*, see Psaltis et al. [89], Johnson et al. [90], Johnson et al. [91].
While the scattering severely affects images of Sgr A*, many polarimetric properties of the images are comparatively immune because the scattering is not significantly birefringent. For example, in the case of purely diffractive scattering, the image-integrated fractional polarization is independent of scattering. More generally, the interferometric fractional polarization is independent of diffractive scattering because convolution is multiplicative in the visibility domain and is identical for all Stokes parameters, thereby canceling in the quotient. Here, is the dimensionless baseline vector, projected orthogonal to the line of sight and measured in units of the observing wavelength, which corresponds to the sampled image wavevector in Fourier space; denotes the Fourier transform of some quantity F.
Figure 6 shows an example GRMHD snapshot before and after scattering, while the images look substantially different, key polarimetric observables such as the mode, which is highly constraining for GRMHD models [8] and carries information about black hole spin [55], are almost unaffected by scattering. Likewise, certain interferometric observables, such as the interferometric fractional polarization, are only mildly affected by scattering (see Figure 7). For additional discussion of how the deterministic frequency dependence of scattering can be used for scattering mitigation on images, see [56]; for discussion of how the lack of birefringence can be used to study the relative power spectra in different polarization modes, see Ni et al. (in prep).
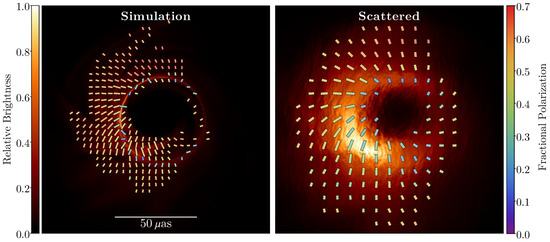
Figure 6.
GRMHD model of Sgr A* at 230 GHz before (left) and after (right) including the effects of interstellar scattering. This simulation is a MAD with , , and . The background image shows total intensity with respect to the image peak, while the ticks show the polarization magnitude and direction, colored by fractional polarization, while scattering severely affects the image, key polarimetric measures are nearly immune to scattering. For example, the unresolved fractional polarization is 10.5% before scattering and is 10.6% after scattering. Likewise, the mode in polarization [55] has and before scattering, and and after scattering.
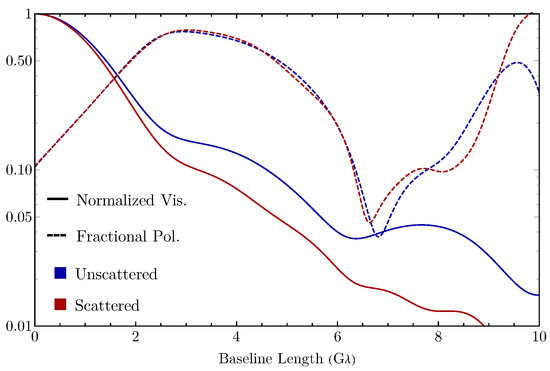
Figure 7.
Interferometric properties of the GRMHD model shown in Figure 6. Solid lines show the normalized intensity before (blue) and after (red) scattering, and the dashed lines show the interferometric fractional polarization magnitude . For these curves, baselines are oriented along the East–West direction: . Over the full range of baseline lengths accessible from the ground, the fractional polarization is largely immune to scattering, while diffractive scattering causes a substantial reduction in the flux on long baselines.
7. Studying Polarimetry with Interferometry
Thus, far, the discussion has focused on the polarimetric properties of simulated black hole images or images reconstructed from interferometric visibilities. In practice, since the measured visibilities are actually samples of the Fourier transform, image reconstruction can introduce significant systematic uncertainties. Reconstruction methods must find images consistent with incomplete and noisy information in Fourier space, to which there can be multiple families of solutions. Images cannot be constructed at all without sufficient coverage (or strict image priors). Thus, it can be useful to study signals in their native visibility space.
The visibility-domain response of polarimetric observables has some key differences from that of total intensity. For instance, the visibility amplitude for total intensity is guaranteed to be maximal for the zero baseline because the image is positive. However, because the Stokes parameters Q, U, and V are not constrained to be positive, their visibility functions may not be maximal on the zero baseline. This simple property can be used to make powerful inferences from sparse measurements (e.g., from the EHT or the space VLBI project RadioAstron). For instance, a single measurement of would demonstrate that the image does not have uniform sign of circular polarization. Likewise, if , where , then the linear polarization field must have variations in direction. This test can be performed with as few as two stations, but each must have dual polarization receivers. In addition, because polarization breaks the trivial baseline reflection degeneracy that is present in total intensity, the polarimetric structure can be compared on baselines and , effectively doubling the angular resolution relative to total intensity alone!
Another significant difference between the total intensity and polarization is that the linear polarization images can have changes in both amplitude and direction, allowing it to have significant image substructure relative to the intensity image. In the visibility domain, this substructure translates to a relative increase in the power on long baselines in polarization versus total intensity. In the limit of a heavily resolved source, the polarimetric signal may exceed that of the total intensity, even for a source with a low fractional polarization!
This can be quantified using the interferometric fractional polarization, . On a zero baseline, this complex quantity corresponds to the unresolved fractional polarization, , where the “tot” subscript denotes an image-integrated quantity. However, unlike the image fractional polarization, can exceed unity on long baselines. This was found out from ground-based observations of for Sgr A* [92] as well as within the RadioAstron Space VLBI survey of AGN [93]. These observations had one common feature: a very high angular resolution corresponding to several G spatial scales. In general, for a heavily resolved source with polarized substructure, we expect to generically grow with increasing baseline length.
From a calibration perspective, the interferometric fractional polarization has the benefit of properties analogous to VLBI closure quantities, since the source of rapidly varying gains at VLBI sites (e.g., changing atmospheric delay and reference frequency errors) are equivalent for both polarization feeds. In addition, the interferometric fractional polarization is resilient to the effects of interstellar scattering, which is likewise not significantly birefringent (see Figure 7). Finally, is a useful observable to measure the relative coherence of the polarization field. For a perfectly uniform polarization field, will be independent of baseline length. However, for a polarization field that varies on spatial scales much smaller than the the beam size of the interferometer, will grow roughly as , as the observations resolve the structure in total intensity without resolving the structure in polarization.
In Figure 8, we plot total intensity and linear polarization maps of two models of M87* with very different polarization characteristics. The top model is a MAD simulation with and , which exhibits an ordered polarization pattern due to ordered magnetic fields and little Faraday rotation. Meanwhile, the bottom model is a SANE simulation with and . As mentioned in Section 4, SANE simulations tend to have much larger Faraday depths than MADs, causing this model’s linear polarization to be much more disordered. The pixel-to-pixel intensity weighted Faraday depth is written at the bottom of each panel.
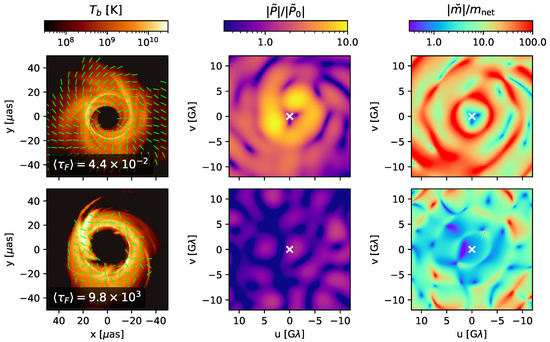
Figure 8.
Two GRMHD models imaged at 228 GHz and corresponding maps of linear polarization in visibility space. The top row corresponds to a MAD model of M87* with and , while the bottom row corresponds to a SANE model with and . Due to a much larger Faraday depth, written at the bottom of the images, the SANE model exhibits a much more disordered linear polarization pattern. In the ordered model, measures of the linear polarization rise dramatically with radius in the Fourier domain, while the disordered model is characterized by blobs with a coherence length corresponding to the size of the image.
These characteristics are reflected in their Fourier space maps of and , shown in the second and third columns, which can be directly sampled using an interferometer. Here, and , where ∼ denotes a Fourier transform. For the MAD model, and both rise dramatically with radius in Fourier space in the central region. rises because the linear polarization is higher on resolved scales than a spatially unresolved measurement would suggest. The rotational symmetry of the polarization pattern causes substantial cancellation of polarization without spatial resolution. also rises for this reason, and also because exhibits nulls in Fourier space that do not necessarily coincide with the nulls in . Meanwhile, the disordered SANE simulation exhibits a mottled pattern in with a characteristic length scale corresponding to the size of the image. These phenomena should not change much qualitatively as a function of wavelength in the sub-millimeter.
The previous discussion has focused on the relationship between expected image features and their appearance in the (Fourier-conjugate) interferometric visibility domain. However, a crucial consideration is how to study frequency-dependent effects, such as spectral index and rotation measure, using interferometry. Because the fringe spacing , interferometric measurements across multiple frequencies necessarily mix the effects of a changing dimensionless baseline with those of a changing image.
Specifically, the polarized visibility on a physical vector baseline at an observing frequency is
where denotes a partial derivative with respect to . The first term in the square brackets of Equation (2) accounts for the frequency dependence of the image, while the second accounts for the changing dimensionless baseline with frequency. For the first term, an image with spectral index has , so ; likewise, an image with finite rotation measure has , so . Roughly speaking, we expect that the relative dominance or subdominance of spectral index versus RM are independent of baseline length, so the relative effects on long baselines are likely similar to those for unresolved measurements of a source. For instance, the effects of rotation measure for observations of Sgr A* at millimeter wavelengths are likely to vastly dominate the effects of spectral index. Sgr A* has [94] but [59]. The second term gives a relative contribution that increases as the image is increasingly resolved. It becomes significant when the spanned frequencies change the baseline length by the inverse field-of-view, F.
8. Discussion and Conclusions
The EHT and upcoming ngEHT enable us to probe accreting supermassive black holes via a variety of multi-frequency polarimetric observables. In this contribution, we have discussed the many ways in which the physical properties of underlying accretion flow are mapped onto these observables. Total intensity and spectral index encode the density, temperature, and magnetic field strength of emitting plasma in different regions. Linear polarization encodes the geometry of the magnetic field, and its depolarization via Faraday rotation offers an observational probe into what may be otherwise invisible cool electrons, and a different component of the magnetic field vectors. Rotation measure maps probe this cooler Faraday rotating electron population directly, and can probe the magnetic field direction, which can reveal turbulent structures. Finally, circular polarization encodes both overall geometry and direction of the magnetic field via emission, Faraday rotation, and Faraday conversion. We have discussed that even if imaging proves prohibitively challenging for some datasets, constraining information exists already in visibility space. For some models, low polarization fractions in spatially unresolved measurements hide large polarization fractions in spatially resolved measurements. In the ngEHT era, we will have access to not only single snapshots, but also movies, with a much larger dynamic range in intensity than is presently possible with the EHT. Multiple snapshots will also enable cleaner theoretical connections via time averaging, e.g., [95,96]. This will enable an unprecedented deluge of data about the nearest SMBHs that will help us understand their accretion and feedback processes.
Author Contributions
Conceptualization, A.R., M.D.J., and Y.Y.K.; methodology, A.R., M.D.J., Y.Y.K., and D.C.M.P.; software, A.R., M.D.J., and D.C.M.P.; investigation, A.R., M.D.J., and D.C.M.P.; writing—original draft preparation, A.R., M.D.J., and Y.Y.K.; writing—review and editing, A.R., M.D.J., Y.Y.K., D.C.M.P., and R.E.; visualization, A.R., M.D.J., and D.C.M.P. All authors have read and agreed to the published version of the manuscript.
Funding
We thank the National Science Foundation (AST-1716536, AST-1935980, AST-2034306, AST-1816420, and OISE-1743747) for financial support of this work. YYK was supported by the Russian Science Foundation grant 21-12-00241. RE acknowledges the support from NASA via grant HST-GO-16173.001-A. This work was supported in part by the Black Hole Initiative, which is funded by grants from the John Templeton Foundation and the Gordon and Betty Moore Foundation to Harvard University. The opinions expressed in this publication are those of the author(s) and do not necessarily reflect the views of the Moore or Templeton Foundations.
Data Availability Statement
The data underlying the figures of this article can be provided upon reasonable request to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
Notes
| 1 | That is, the ion-to-electron temperature ratio asymptotes to a value of 40 in high- regions, which typically occur in the mid-plane. This is a typical value in EHT GRMHD studies, e.g., [5,8,13]. |
| 2 | is the temperature normalized by the electron rest mass energy, , where is the Boltzmann constant, T is the temperature in Kelvin, is the electron rest mass, and c is the speed of light. |
| 3 | These distributions are characterized by a thermal core with the addition of a high energy power-law tail, with slope . |
References
- Event Horizon Telescope Collaboration; Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.K.; Ball, D.; Baloković, M.; Barrett, J.; et al. First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole. ApJ 2019, 875, L1. [Google Scholar] [CrossRef]
- Event Horizon Telescope Collaboration; Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.K.; Ball, D.; Baloković, M.; Barrett, J.; et al. First M87 Event Horizon Telescope Results. II. Array and Instrumentation. ApJ 2019, 875, L2. [Google Scholar] [CrossRef]
- Event Horizon Telescope Collaboration; Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.K.; Ball, D.; Baloković, M.; Barrett, J.; et al. First M87 Event Horizon Telescope Results. III. Data Processing and Calibration. ApJ 2019, 875, L3. [Google Scholar] [CrossRef]
- Event Horizon Telescope Collaboration; Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.K.; Ball, D.; Baloković, M.; Barrett, J.; et al. First M87 Event Horizon Telescope Results. IV. Imaging the Central Supermassive Black Hole. ApJ 2019, 875, L4. [Google Scholar] [CrossRef]
- Event Horizon Telescope Collaboration; Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.K.; Ball, D.; Baloković, M.; Barrett, J.; et al. First M87 Event Horizon Telescope Results. V. Physical Origin of the Asymmetric Ring. ApJ 2019, 875, L5. [Google Scholar] [CrossRef]
- Event Horizon Telescope Collaboration; Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.K.; Ball, D.; Baloković, M.; Barrett, J.; et al. First M87 Event Horizon Telescope Results. VI. The Shadow and Mass of the Central Black Hole. ApJ 2019, 875, L6. [Google Scholar] [CrossRef]
- Event Horizon Telescope Collaboration; Akiyama, K.; Algaba, J.C.; Alberdi, A.; Alef, W.; Anantua, R.; Asada, K.; Azulay, R.; Baczko, A.K.; Ball, D.; et al. First M87 Event Horizon Telescope Results. VII. Polarization of the Ring. ApJ 2021, 910, L12. [Google Scholar] [CrossRef]
- Event Horizon Telescope Collaboration; Akiyama, K.; Algaba, J.C.; Alberdi, A.; Alef, W.; Anantua, R.; Asada, K.; Azulay, R.; Baczko, A.K.; Ball, D.; et al. First M87 Event Horizon Telescope Results. VIII. Magnetic Field Structure near The Event Horizon. ApJ 2021, 910, L13. [Google Scholar] [CrossRef]
- Akiyama, K.; Alberdi, A.; Alef, W.; Algaba, J.C.; Anantua, R.; Asada, K.; Azulay, R.; Bach, U.; Baczko, A.K.; Ball, D.; et al. First Sagittarius A* Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole in the Center of the Milky Way. ApJ 2022, 930, L12. [Google Scholar] [CrossRef]
- Akiyama, K.; Alberdi, A.; Alef, W.; Algaba, J.C.; Anantua, R.; Asada, K.; Azulay, R.; Bach, U.; Baczko, A.K.; Ball, D.; et al. First Sagittarius A* Event Horizon Telescope Results. II. EHT and Multiwavelength Observations, Data Processing, and Calibration. ApJ 2022, 930, L13. [Google Scholar] [CrossRef]
- Akiyama, K.; Alberdi, A.; Alef, W.; Algaba, J.C.; Anantua, R.; Asada, K.; Azulay, R.; Bach, U.; Baczko, A.K.; Ball, D.; et al. First Sagittarius A* Event Horizon Telescope Results. III. Imaging of the Galactic Center Supermassive Black Hole. ApJ 2022, 930, L14. [Google Scholar] [CrossRef]
- Akiyama, K.; Alberdi, A.; Alef, W.; Algaba, J.C.; Anantua, R.; Asada, K.; Azulay, R.; Bach, U.; Baczko, A.K.; Ball, D.; et al. First Sagittarius A* Event Horizon Telescope Results. IV. Variability, Morphology, and Black Hole Mass. ApJ 2022, 930, L15. [Google Scholar] [CrossRef]
- Akiyama, K.; Alberdi, A.; Alef, W.; Algaba, J.C.; Anantua, R.; Asada, K.; Azulay, R.; Bach, U.; Baczko, A.K.; Ball, D.; et al. First Sagittarius A* Event Horizon Telescope Results. V. Testing Astrophysical Models of the Galactic Center Black Hole. ApJ 2022, 930, L16. [Google Scholar] [CrossRef]
- Akiyama, K.; Alberdi, A.; Alef, W.; Algaba, J.C.; Anantua, R.; Asada, K.; Azulay, R.; Bach, U.; Baczko, A.K.; Ball, D.; et al. First Sagittarius A* Event Horizon Telescope Results. VI. Testing the Black Hole Metric. ApJ 2022, 930, L17. [Google Scholar] [CrossRef]
- Ricarte, A.; Tiede, P.; Emami, R.; Tamar, A.; Natarajan, P. The ngEHT’s Role in Measuring Supermassive Black Hole Spins. arXiv 2022, arXiv:2211.03910. [Google Scholar] [CrossRef]
- Bisnovatyi-Kogan, G.S.; Ruzmaikin, A.A. The Accretion of Matter by a Collapsing Star in the Presence of a Magnetic Field. Ap&SS 1974, 28, 45–59. [Google Scholar] [CrossRef]
- Igumenshchev, I.V.; Narayan, R.; Abramowicz, M.A. Three-dimensional Magnetohydrodynamic Simulations of Radiatively Inefficient Accretion Flows. ApJ 2003, 592, 1042–1059. [Google Scholar] [CrossRef]
- Narayan, R.; Igumenshchev, I.V.; Abramowicz, M.A. Magnetically Arrested Disk: An Energetically Efficient Accretion Flow. PASJ 2003, 55, L69–L72. [Google Scholar] [CrossRef]
- Narayan, R.; SÄ dowski, A.; Penna, R.F.; Kulkarni, A.K. GRMHD simulations of magnetized advection-dominated accretion on a non-spinning black hole: Role of outflows. MNRAS 2012, 426, 3241–3259. [Google Scholar] [CrossRef]
- Sądowski, A.; Narayan, R.; Penna, R.; Zhu, Y. Energy, momentum and mass outflows and feedback from thick accretion discs around rotating black holes. MNRAS 2013, 436, 3856–3874. [Google Scholar] [CrossRef]
- Shapiro, S.L.; Lightman, A.P.; Eardley, D.M. A two-temperature accretion disk model for Cygnus X-1: Structure and spectrum. ApJ 1976, 204, 187–199. [Google Scholar] [CrossRef]
- Rees, M.J.; Begelman, M.C.; Blandford, R.D.; Phinney, E.S. Ion-supported tori and the origin of radio jets. Nature 1982, 295, 17–21. [Google Scholar] [CrossRef]
- Narayan, R.; Yi, I.; Mahadevan, R. Explaining the spectrum of Sagittarius A* with a model of an accreting black hole. Nature 1995, 374, 623–625. [Google Scholar] [CrossRef]
- Mościbrodzka, M.; Falcke, H.; Shiokawa, H. General relativistic magnetohydrodynamical simulations of the jet in M 87. A&A 2016, 586, A38. [Google Scholar] [CrossRef]
- Özel, F.; Psaltis, D.; Narayan, R. Hybrid Thermal-Nonthermal Synchrotron Emission from Hot Accretion Flows. ApJ 2000, 541, 234–249. [Google Scholar] [CrossRef]
- Mao, S.A.; Dexter, J.; Quataert, E. The impact of non-thermal electrons on event horizon scale images and spectra of Sgr A*. MNRAS 2017, 466, 4307–4319. [Google Scholar] [CrossRef]
- Cruz-Osorio, A.; Fromm, C.M.; Mizuno, Y.; Nathanail, A.; Younsi, Z.; Porth, O.; Davelaar, J.; Falcke, H.; Kramer, M.; Rezzolla, L. State-of-the-art energetic and morphological modelling of the launching site of the M87 jet. Nat. Astron. 2022, 6, 103–108. [Google Scholar] [CrossRef]
- Fromm, C.M.; Cruz-Osorio, A.; Mizuno, Y.; Nathanail, A.; Younsi, Z.; Porth, O.; Olivares, H.; Davelaar, J.; Falcke, H.; Kramer, M.; et al. Impact of non-thermal particles on the spectral and structural properties of M87. A&A 2022, 660, A107. [Google Scholar] [CrossRef]
- Anantua, R.; Emami, R.; Loeb, A.; Chael, A. Determining the Composition of Relativistic Jets from Polarization Maps. ApJ 2020, 896, 30. [Google Scholar] [CrossRef]
- Emami, R.; Anantua, R.; Chael, A.A.; Loeb, A. Positron Effects on Polarized Images and Spectra from Jet and Accretion Flow Models of M87* and Sgr A*. ApJ 2021, 923, 272. [Google Scholar] [CrossRef]
- Wong, G.N.; Gammie, C.F. Effects of Hydrogen vs. Helium on Electromagnetic Black Hole Observables. arXiv 2022, arXiv:2207.13705. [Google Scholar]
- Fragile, P.C.; Blaes, O.M.; Anninos, P.; Salmonson, J.D. Global General Relativistic Magnetohydrodynamic Simulation of a Tilted Black Hole Accretion Disk. ApJ 2007, 668, 417–429. [Google Scholar] [CrossRef]
- Liska, M.; Hesp, C.; Tchekhovskoy, A.; Ingram, A.; van der Klis, M.; Markoff, S.B.; Van Moer, M. Disc tearing and Bardeen-Petterson alignment in GRMHD simulations of highly tilted thin accretion discs. MNRAS 2021, 507, 983–990. [Google Scholar] [CrossRef]
- Mościbrodzka, M.; Gammie, C.F. IPOLE—semi-analytic scheme for relativistic polarized radiative transport. MNRAS 2018, 475, 43–54. [Google Scholar] [CrossRef]
- Wardle, J.F.C.; Homan, D.C. Theoretical Models for Producing Circularly Polarized Radiation in Extragalactic Radio Sources. Ap&SS 2003, 288, 143–153. [Google Scholar] [CrossRef]
- Mościbrodzka, M.; Janiuk, A.; De Laurentis, M. Unraveling circular polarimetric images of magnetically arrested accretion flows near event horizon of a black hole. MNRAS 2021, 508, 4282–4296. [Google Scholar] [CrossRef]
- Ricarte, A.; Qiu, R.; Narayan, R. Black hole magnetic fields and their imprint on circular polarization images. MNRAS 2021, 505, 523–539. [Google Scholar] [CrossRef]
- Tsunetoe, Y.; Mineshige, S.; Ohsuga, K.; Kawashima, T.; Akiyama, K. Polarization images of accretion flow around supermassive black holes: Imprints of toroidal field structure. PASJ 2021, 73, 912–928. [Google Scholar] [CrossRef]
- Wardle, J.F.C.; Homan, D.C.; Ojha, R.; Roberts, D.H. Electron-positron jets associated with the quasar 3C279. Nature 1998, 395, 457–461. [Google Scholar] [CrossRef]
- Bower, G.C.; Dexter, J.; Asada, K.; Brinkerink, C.D.; Falcke, H.; Ho, P.; Inoue, M.; Markoff, S.; Marrone, D.P.; Matsushita, S.; et al. ALMA Observations of the Terahertz Spectrum of Sagittarius A*. ApJ 2019, 881, L2. [Google Scholar] [CrossRef]
- Ricarte, A.; Gammie, C.; Narayan, R.; Prather, B.S. Probing Plasma Physics with Spectral Index Maps of Accreting Black Holes on Event Horizon Scales. arXiv 2022, arXiv:2202.02408. [Google Scholar] [CrossRef]
- Mościbrodzka, M.; Dexter, J.; Davelaar, J.; Falcke, H. Faraday rotation in GRMHD simulations of the jet launching zone of M87. MNRAS 2017, 468, 2214–2221. [Google Scholar] [CrossRef]
- Jiménez-Rosales, A.; Dexter, J. The impact of Faraday effects on polarized black hole images of Sagittarius A*. MNRAS 2018, 478, 1875–1883. [Google Scholar] [CrossRef]
- Ricarte, A.; Prather, B.S.; Wong, G.N.; Narayan, R.; Gammie, C.; Johnson, M.D. Decomposing the internal faraday rotation of black hole accretion flows. MNRAS 2020, 498, 5468–5488. [Google Scholar] [CrossRef]
- Pandya, A.; Zhang, Z.; Chandra, M.; Gammie, C.F. Polarized Synchrotron Emissivities and Absorptivities for Relativistic Thermal, Power-law, and Kappa Distribution Functions. ApJ 2016, 822, 34. [Google Scholar] [CrossRef]
- Blandford, R.D.; Königl, A. Relativistic jets as compact radio sources. ApJ 1979, 232, 34–48. [Google Scholar] [CrossRef]
- Vasyliunas, V.M. A survey of low-energy electrons in the evening sector of the magnetosphere with OGO 1 and OGO 3. J. Geophys. Res. 1968, 73, 2839–2884. [Google Scholar] [CrossRef]
- Xiao, F. Modelling energetic particles by a relativistic kappa-loss-cone distribution function in plasmas. Plasma Phys. Control. Fusion 2006, 48, 203–213. [Google Scholar] [CrossRef]
- Rybicki, G.B.; Lightman, A.P. Radiative Processes in Astrophysics; John Wiley & Sons, Inc.: New York, NY, USA, 1986. [Google Scholar]
- Himwich, E.; Johnson, M.D.; Lupsasca, A.; Strominger, A. Universal polarimetric signatures of the black hole photon ring. Phys. Rev. D. 2020, 101, 084020. [Google Scholar] [CrossRef]
- Narayan, R.; Palumbo, D.C.M.; Johnson, M.D.; Gelles, Z.; Himwich, E.; Chang, D.O.; Ricarte, A.; Dexter, J.; Gammie, C.F.; Chael, A.A.; et al. The Polarized Image of a Synchrotron-emitting Ring of Gas Orbiting a Black Hole. ApJ 2021, 912, 35. [Google Scholar] [CrossRef]
- Gelles, Z.; Himwich, E.; Johnson, M.D.; Palumbo, D.C.M. Polarized image of equatorial emission in the Kerr geometry. Phys. Rev. D. 2021, 104, 044060. [Google Scholar] [CrossRef]
- Palumbo, D.C.M.; Wong, G.N. Photon Ring Symmetries in Simulated Linear Polarization Images of Messier 87*. ApJ 2022, 929, 49. [Google Scholar] [CrossRef]
- Walker, R.C.; Hardee, P.E.; Davies, F.B.; Ly, C.; Junor, W. The Structure and Dynamics of the Subparsec Jet in M87 Based on 50 VLBA Observations over 17 Years at 43 GHz. ApJ 2018, 855, 128. [Google Scholar] [CrossRef]
- Palumbo, D.C.M.; Wong, G.N.; Prather, B.S. Discriminating Accretion States via Rotational Symmetry in Simulated Polarimetric Images of M87. ApJ 2020, 894, 156. [Google Scholar] [CrossRef]
- Johnson, M.D. Stochastic Optics: A Scattering Mitigation Framework for Radio Interferometric Imaging. ApJ 2016, 833, 74. [Google Scholar] [CrossRef]
- Pacholczyk, A.G. Radio Astrophysics. Nonthermal Processes in Galactic and Extragalactic Sources; W. H. Freeman and Company: New York, NY, USA, 1970. [Google Scholar]
- Jones, T.W.; Hardee, P.E. Maxwellian synchrotron sources. ApJ 1979, 228, 268–278. [Google Scholar] [CrossRef]
- Goddi, C.; Martí-Vidal, I.; Messias, H.; Bower, G.C.; Broderick, A.E.; Dexter, J.; Marrone, D.P.; Moscibrodzka, M.; Nagai, H.; Algaba, J.C.; et al. Polarimetric Properties of Event Horizon Telescope Targets from ALMA. ApJ 2021, 910, L14. [Google Scholar] [CrossRef]
- Jorstad, S.G.; Marscher, A.P.; Lister, M.L.; Stirling, A.M.; Cawthorne, T.V.; Gear, W.K.; Gómez, J.L.; Stevens, J.A.; Smith, P.S.; Forster, J.R.; et al. Polarimetric Observations of 15 Active Galactic Nuclei at High Frequencies: Jet Kinematics from Bimonthly Monitoring with the Very Long Baseline Array. AJ 2005, 130, 1418–1465. [Google Scholar] [CrossRef]
- Lister, M.L.; Aller, M.F.; Aller, H.D.; Hodge, M.A.; Homan, D.C.; Kovalev, Y.Y.; Pushkarev, A.B.; Savolainen, T. MOJAVE. XV. VLBA 15 GHz Total Intensity and Polarization Maps of 437 Parsec-scale AGN Jets from 1996 to 2017. ApJS 2018, 234, 12. [Google Scholar] [CrossRef]
- Ricarte, A.; Palumbo, D.C.M.; Narayan, R.; Roelofs, F.; Emami, R. Observational Signatures of Frame Dragging in Strong Gravity. arXiv 2022, arXiv:2211.01810. [Google Scholar] [CrossRef]
- Marrone, D.P.; Moran, J.M.; Zhao, J.H.; Rao, R. The Submillimeter Polarization of Sgr A*. J. Phys. Conf. Ser. 2006, 54, 354–362. [Google Scholar] [CrossRef]
- Trippe, S.; Paumard, T.; Ott, T.; Gillessen, S.; Eisenhauer, F.; Martins, F.; Genzel, R. A polarized infrared flare from Sagittarius A* and the signatures of orbiting plasma hotspots. MNRAS 2007, 375, 764–772. [Google Scholar] [CrossRef]
- Zamaninasab, M.; Eckart, A.; Dovčiak, M.; Karas, V.; Schödel, R.; Witzel, G.; Sabha, N.; García-Marín, M.; Kunneriath, D.; Mužić, K.; et al. Near-infrared polarimetry as a tool for testing properties of accreting supermassive black holes. MNRAS 2011, 413, 322–332. [Google Scholar] [CrossRef]
- GRAVITY Collaboration; Abuter, R.; Amorim, A.; Bauböck, M.; Berger, J.P.; Bonnet, H.; Brandner, W.; Clénet, Y.; Coudé Du Foresto, V.; de Zeeuw, P.T.; et al. Detection of orbital motions near the last stable circular orbit of the massive black hole SgrA*. A&A 2018, 618, L10. [Google Scholar] [CrossRef]
- Wielgus, M.; Moscibrodzka, M.; Vos, J.; Gelles, Z.; Martí-Vidal, I.; Farah, J.; Marchili, N.; Goddi, C.; Messias, H. Orbital motion near Sagittarius A* . Constraints from polarimetric ALMA observations. A&A 2022, 665, L6. [Google Scholar] [CrossRef]
- Broderick, A.E.; Loeb, A. Imaging bright-spots in the accretion flow near the black hole horizon of Sgr A*. MNRAS 2005, 363, 353–362. [Google Scholar] [CrossRef]
- GRAVITY Collaboration; Jiménez-Rosales, A.; Dexter, J.; Widmann, F.; Bauböck, M.; Abuter, R.; Amorim, A.; Berger, J.P.; Bonnet, H.; Brandner, W.; et al. Dynamically important magnetic fields near the event horizon of Sgr A*. A&A 2020, 643, A56. [Google Scholar] [CrossRef]
- Vos, J.; Moscibrodzka, M.; Wielgus, M. Polarimetric signatures of hot spots in black hole accretion flows. arXiv 2022, arXiv:2209.09931. [Google Scholar] [CrossRef]
- Hu, Z.; Hou, Y.; Yan, H.; Guo, M.; Chen, B. Electromagnetic radiations and polarized images of synchrotron radiations in curved spacetime. arXiv 2022, arXiv:2203.02908. [Google Scholar]
- Lee, T.; Hu, Z.; Guo, M.; Chen, B. Circular orbits and polarized images of charged particles orbiting Kerr black hole with a weak magnetic field. arXiv 2022, arXiv:2211.04143. [Google Scholar]
- Ripperda, B.; Bacchini, F.; Philippov, A.A. Magnetic Reconnection and Hot Spot Formation in Black Hole Accretion Disks. ApJ 2020, 900, 100. [Google Scholar] [CrossRef]
- Dexter, J.; Tchekhovskoy, A.; Jiménez-Rosales, A.; Ressler, S.M.; Bauböck, M.; Dallilar, Y.; de Zeeuw, P.T.; Eisenhauer, F.; von Fellenberg, S.; Gao, F.; et al. Sgr A* near-infrared flares from reconnection events in a magnetically arrested disc. MNRAS 2020, 497, 4999–5007. [Google Scholar] [CrossRef]
- Chatterjee, K.; Narayan, R. Flux eruption events drive angular momentum transport in magnetically arrested accretion flows. arXiv 2022, arXiv:2210.08045. [Google Scholar] [CrossRef]
- GRAVITY Collaboration; Bauböck, M.; Dexter, J.; Abuter, R.; Amorim, A.; Berger, J.P.; Bonnet, H.; Brandner, W.; Clénet, Y.; Coudé Du Foresto, V.; et al. Modeling the orbital motion of Sgr A*’s near-infrared flares. A&A 2020, 635, A143. [Google Scholar] [CrossRef]
- Gardner, F.F.; Whiteoak, J.B. The Polarization of Cosmic Radio Waves. ARA&A 1966, 4, 245. [Google Scholar] [CrossRef]
- Jones, T.W.; Odell, S.L. Transfer of polarized radiation in self-absorbed synchrotron sources. I. Results for a homogeneous source. ApJ 1977, 214, 522–539. [Google Scholar] [CrossRef]
- Marrone, D.P.; Moran, J.M.; Zhao, J.H.; Rao, R. An Unambiguous Detection of Faraday Rotation in Sagittarius A*. ApJ 2007, 654, L57–L60. [Google Scholar] [CrossRef]
- Plambeck, R.L.; Bower, G.C.; Rao, R.; Marrone, D.P.; Jorstad, S.G.; Marscher, A.P.; Doeleman, S.S.; Fish, V.L.; Johnson, M.D. Probing the Parsec-scale Accretion Flow of 3C 84 with Millimeter Wavelength Polarimetry. ApJ 2014, 797, 66. [Google Scholar] [CrossRef]
- Kuo, C.Y.; Asada, K.; Rao, R.; Nakamura, M.; Algaba, J.C.; Liu, H.B.; Inoue, M.; Koch, P.M.; Ho, P.T.P.; Matsushita, S.; et al. Measuring Mass Accretion Rate onto the Supermassive Black Hole in M87 Using Faraday Rotation Measure with the Submillimeter Array. ApJ 2014, 783, L33. [Google Scholar] [CrossRef]
- Park, J.; Hada, K.; Kino, M.; Nakamura, M.; Ro, H.; Trippe, S. Faraday Rotation in the Jet of M87 inside the Bondi Radius: Indication of Winds from Hot Accretion Flows Confining the Relativistic Jet. ApJ 2019, 871, 257. [Google Scholar] [CrossRef]
- Marti-Vidal, I.; Muller, S. Submillimeter polarization and variability of quasar PKS 1830-211. A&A 2019, 621, A18. [Google Scholar] [CrossRef]
- Bower, G.C.; Broderick, A.; Dexter, J.; Doeleman, S.; Falcke, H.; Fish, V.; Johnson, M.D.; Marrone, D.P.; Moran, J.M.; Moscibrodzka, M.; et al. ALMA Polarimetry of Sgr A*: Probing the Accretion Flow from the Event Horizon to the Bondi Radius. ApJ 2018, 868, 101. [Google Scholar] [CrossRef]
- Kravchenko, E.V.; Kovalev, Y.Y.; Sokolovsky, K.V. Parsec-scale Faraday rotation and polarization of 20 active galactic nuclei jets. MNRAS 2017, 467, 83–101. [Google Scholar] [CrossRef][Green Version]
- Martí-Vidal, I.; Muller, S.; Vlemmings, W.; Horellou, C.; Aalto, S. A strong magnetic field in the jet base of a supermassive black hole. Science 2015, 348, 311–314. [Google Scholar] [CrossRef] [PubMed]
- Rickett, B.J. Radio propagation through the turbulent interstellar plasma. ARA&A 1990, 28, 561–605. [Google Scholar]
- Bower, G.C.; Deller, A.; Demorest, P.; Brunthaler, A.; Eatough, R.; Falcke, H.; Kramer, M.; Lee, K.J.; Spitler, L. The Angular Broadening of the Galactic Center Pulsar SGR J1745-29: A New Constraint on the Scattering Medium. ApJ 2014, 780, L2. [Google Scholar] [CrossRef]
- Psaltis, D.; Johnson, M.; Narayan, R.; Medeiros, L.; Blackburn, L.; Bower, G. A Model for Anisotropic Interstellar Scattering and its Application to Sgr A*. arXiv 2018, arXiv:1805.01242. [Google Scholar]
- Johnson, M.D.; Narayan, R.; Psaltis, D.; Blackburn, L.; Kovalev, Y.Y.; Gwinn, C.R.; Zhao, G.Y.; Bower, G.C.; Moran, J.M.; Kino, M.; et al. The Scattering and Intrinsic Structure of Sagittarius A* at Radio Wavelengths. ApJ 2018, 865, 104. [Google Scholar] [CrossRef]
- Johnson, M.D.; Kovalev, Y.Y.; Lisakov, M.M.; Voitsik, P.A.; Gwinn, C.R.; Bruni, G. First Space-VLBI Observations of Sagittarius A*. ApJ 2021, 922, L28. [Google Scholar] [CrossRef]
- Johnson, M.D.; Fish, V.L.; Doeleman, S.S.; Marrone, D.P.; Plambeck, R.L.; Wardle, J.F.C.; Akiyama, K.; Asada, K.; Beaudoin, C.; Blackburn, L.; et al. Resolved magnetic-field structure and variability near the event horizon of Sagittarius A*. Science 2015, 350, 1242–1245. [Google Scholar] [CrossRef]
- Kovalev, Y.Y.; Kardashev, N.S.; Sokolovsky, K.V.; Voitsik, P.A.; An, T.; Anderson, J.M.; Andrianov, A.S.; Avdeev, V.Y.; Bartel, N.; Bignall, H.E.; et al. Detection statistics of the RadioAstron AGN survey. Adv. Space Res. 2020, 65, 705–711. [Google Scholar] [CrossRef]
- Wielgus, M.; Marchili, N.; Martí-Vidal, I.; Keating, G.K.; Ramakrishnan, V.; Tiede, P.; Fomalont, E.; Issaoun, S.; Neilsen, J.; Nowak, M.A.; et al. Millimeter Light Curves of Sagittarius A* Observed during the 2017 Event Horizon Telescope Campaign. ApJ 2022, 930, L19. [Google Scholar] [CrossRef]
- Gold, R.; McKinney, J.C.; Johnson, M.D.; Doeleman, S.S. Probing the Magnetic Field Structure in Sgr A* on Black Hole Horizon Scales with Polarized Radiative Transfer Simulations. ApJ 2017, 837, 180. [Google Scholar] [CrossRef]
- Pushkarev, A.B.; Aller, M.F.; Aller, H.D.; Homan, D.C.; Kovalev, Y.Y.; Lister, M.L.; Pashchenko, I.N.; Savolainen, T.; Zobnina, D. MOJAVE. XXI. Persistent Linear Polarization Structure in Parsec-scale AGN Jets. arXiv 2022, arXiv:2209.04842. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).