Abstract
This work proposes a methodology for testing phenomenologically motivated emission processes that account for the flux and polarization distribution and global structure of the 230 GHz sources imaged by the Event Horizon Telescope (EHT): Messier (M)87* and Sagittarius (Sgr) A*. We introduce into general relativistic magnetohydrodynamic (GRMHD) simulations some novel models to bridge the largely uncertain mechanisms by which high-energy particles in jet/accretion flow/black hole (JAB) system plasmas attain billion-degree temperatures and emit synchrotron radiation. The “Observing” JAB Systems methodology then partitions the simulation to apply different parametric models to regions governed by different plasma physics—an advance over methods in which one parametrization is used over simulation regions spanning thousands of gravitational radii from the central supermassive black hole. We present several classes of viewing-angle-dependent morphologies and highlight signatures of piecewise modeling and positron effects, including a MAD/SANE dichotomy in which polarized maps appear dominated by intrinsic polarization in the MAD case and by Faraday effects in the SANE case. The library of images thus produced spans a wide range of morphologies awaiting discovery by the groundbreaking EHT instrument and its yet more sensitive, higher-resolution next-generation counterpart, ngEHT.
1. Introduction
With some of the highest-resolution images ever obtained in astronomy, the Event Horizon Telescope has probed the horizon scale of the supermassive black holes M87* [1] and Sagittarius A* [2]. Incidentally, both sources possess ringlike morphologies with diameters of 42 and as, respectively [1,2]. Based on a seminal 2017 data collection campaign, the ring imaged around M87* was seen in 2019 to possess brightness asymmetry dominated by a Doppler-boosted Southern bright spot, indicating a black hole spin direction pointing away from the Earth [3]. After the observations in 2017 and publication of the initial total intensity in 2019, the M87 image in linearly polarized light was published in 2021, revealing a dynamically important poloidal B-field threading a plasma with a polarization pattern that spiraled azimuthally into the hole and electrons with inferred synchrotron temperatures from 10 to 120 billion K [4]. Following this milestone, this year, the EHT published an image of the supermassive black hole at our Galactic Center, likewise observed in 2017, revealing a ring with a face-on inclination of and azimuthal hotspots in most reconstructions [5], affirming work done by the very large infrared telescopes of GRAVITY four years prior [6].
Vast simulation libraries have modeled tens of thousands of parameter combinations to infer properties of such accreting black hole systems, including black hole spin, surrounding magnetic flux, and emitting particles’ thermodynamics [3,7]. The M87 image libraries produced by the EHT Collaboration’s Theory and Simulations Team [3] strongly favored non-zero black hole spin values in order to exceed lower limits for the relativistic jet power in concordance with the Blandford–Znajek mechanism [8]. Some of the greatest uncertainties, however, lie in the interpretation of the heating mechanisms required to produce up-to-billion-degree bright features and the overall flux distribution of not only the emitting rings of M87 and Sgr A*, but of jet/accretion flow/black hole, or JAB, systems in general. To this end, we have developed “Observing” JAB Systems to bridge state-of-the-art simulations and cutting-edge observations.
2. Methodology
2.1. “Observing” JAB Systems
The “Observing” JAB Systems pipeline can be summarized as follows:
- Start with a general relativistic magnetohydrodynamic (GRMHD) simulation or semi-analytic model of a jet (or outflow)/accretion flow/black hole (JAB) system
- Convert GRMHD variables into radiation prescriptions for emission, absorption, polarization, particle acceleration, and/or dissipation to emulate sources, using piecewise models when appropriate to assign parametrizations to each distinct JAB system region
- Add a realistic, synthetic “observer” in postprocessing—which includes all radiating species that significantly contribute to radiative transfer—in order to view sources—specifically, images, spectra, light curves, and Stokes maps.
Repeated applications of “Observing” JAB Systems to broad classes of phenomenological processes can naturally lead to model feature libraries with significant clusters in parameter space, as shown in our application to Sgr A* [9]. Note the provisos in (2) and (3) are often overlooked without adherence to this methodology.1 We illustrate the importance of local piecewise modeling and the inclusion of significant radiating particle species, such as positrons, for our M87 application.
2.2. GRHMD
The first step in “Observing” JAB Systems makes use of the powerful simulated plasma physics laboratories produced by general relativistic magnetohydrodynamic (GRMHD) numerical methods. GRMHD methods are (typically) conservative in mass and stress–energy–momentum ;2 however, recent advances have enabled the inclusion of dissipative effects, such as viscous heating and heat conduction [11], as well as simulations of both thick torii and thin disks [12] and different implementations of the interaction between radiation and the background plasma fluid [13].
We use implementations of the HARM method [14,15] as a testbed for emission models. The simulations presented in this work were generated by using descendants of the harm code [14,15], a conservative second-order explicit shock-capturing finite-volume method for solving the equations of ideal GRMHD in arbitrary stationary spacetimes. On a coordinate basis, the governing equations are
along with the constraint
where the plasma is defined by its rest mass density and its four-velocity , and is the magnetic field four-vector. More details about the simulation process can be found in [16].
All simulations were initialized from a Fishbone–Moncrief (FM) torus [17] with a spin of (Sgr A*) or (M87) (the latter is loosely based on a well-performing model with respect to the M87 polarization constraints in [4]). The Sgr A* simulations were performed by using the iharm3d code [18]. The M87 simulations were produced by using iharm3d’s kokkos/GPU-based descendent, kharma.3 Other physically motivated flow geometries are possible. The Bondi spherical accretion flow solution [19] is analytically tractable, but requires an exquisite degree of symmetry and non-magnetized flows to be realistic. Magnetized Bondi flows in numerical calculations display similar properties to those of torus simulations in terms of horizon-scale emission [20,21]. Stellar winds from a small population of Wolf–Rayet stars were theorized, e.g., in [22,23,24,25] to source the disk and inflow of Sgr A* in a model that reasonably accounted for the diffuse X-ray emissions. However, the precise knowledge of the position and orbits of this population is currently only possible in our own Galactic Center, while the FM torus model can be generalized to other AGNs. This generalization includes the possibility that the FM torus can be tilted with respect to the black hole spin (a situation that could arise often in a low-luminosity AGN), but we neglect this possibility in our work, which is focused on emission physics.
The initial magnetic field geometry is computed as the curl of a prescribed axisymmetric electromagnetic vector potential , which is computed at simulation zone corners. In the SANE case, the vector potential is linear in the plasma density ; in the MAD case, . The field strength is normalized so that the ratio of the maximum gas pressure to the maximum magnetic pressure over the domain is 100. The simulations are performed in a cylindrified, modified spherical Kerr–Schild coordinate system that concentrates the resolution near the midplane and close to the event horizon. The domain extends to at least with a resolution of . More details about the simulation procedure and the initial conditions can be found in [16].
Magnetic flux is a key distinguishing factor among accreting plasmas. The time-averaged magnetic flux determines two distinct regimes. For , the disk is magnetically arrested (MAD) by its own magnetic pressure as it plunges into the hole. A much smaller governs standard and normal evolution (SANE). Analyses of EHT simulation libraries tend to prefer MAD models over SANE, e.g., with MAD earning the highest average image score for M87 with the parametric likelihood estimation procedure THEMIS [26].
2.3. Plasma-Heating-Based Emission Models
2.3.1. Model
In general, GRMHD simulations evolve only the bulk of a fluid, i.e., the dynamically important ions.4 Therefore, in radiative post-processing, we seek to bridge the ions to the radiating electrons by the ratio of their temperatures . In a hot, low-density, collision-less plasma, electrons can radiate and, therefore, cool efficiently, while the ion cooling through Coulomb collisions is suppressed. The heating processes believed to be in action, e.g., viscous, compressional, and turbulent heating, can have similarly asymmetric effects on the temperatures and are more poorly understood [27]. Based on the tendency of plasma turbulence to preferentially heat electrons at low gas-to-magnetic pressure ratios and ions at high [28,29], the model is well motivated (e.g., [10,30,31,32,33]):
The R- model is the primary model used by the EHT Collaboration [3,34]. The electron-to-ion temperature ratio asymptotically reaches in the low regime and in the high regime. In turn, this means that controls the electron temperature in the disk or torus, and governs in the jet or wind outflow. Often, is fixed to 1 and only is varied, since by normalizing the flux to fit observations, the jet appears comparatively brighter upon an increase in , i.e., upon a decrease in in the disk (see also Figure 3 in [10]). The model has been extensively compared to GRMHD simulations that readily employ heating models [35,36], concluding that on scales probed by the EHT, the model approximates the influences of electron heating physics reasonably well.
2.3.2. Critical Model
This alternative turbulent heating model has an exponential parameter that controls the transition between electron- and ion-dominated heating [9]
The exponential parametric control over the maximum contributing to the emitting region is the basis for distinctly different near-horizon electron heating behavior compared to the R- model.
We compare the R- and Critical Beta models in Figure 1. For the same range of electron-to-proton temperature ratios, the Critical Beta model can have a sharper or smoother decline in the emission contributions from the highest regions, smoothly transitioning from funnel/outflow- to near-horizon/inflow-dominant heating profiles as increases.
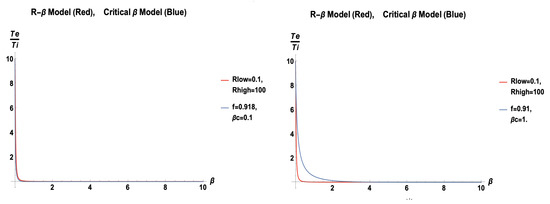
Figure 1.
Electron-to-proton temperature ratio variation between and ∼0 for the R-Beta and Critical Beta Models as a function of . The electron-to-ion temperature ratio varies as for the R- Model and for the Critical Beta Model. For the R-Beta parameters and Critical Beta parameters (Left), the models nearly coincide. For the R-beta parameters and Critical Beta parameters (Right), the Critical Beta model has a softer transition.
At low , the electron-to-ion temperature ratio approaches parametrically determined maximum values (f and ) for the Critical Beta and R-Beta models, respectively. However, at high , the electron temperature always asymptotes to 0 in the former model and is adjustable (through ) only for the latter model. The exponential rate of electron temperature fall-off in the Critical Beta parametrization should have testably different spectral properties, such as the lowering of the bremsstrahlung contribution to the spectral energy distribution.
2.4. Sub-Equipartition-Based Models
2.4.1. Constant
One of the simplest yet most powerful models for understanding jet emission in JAB systems is the Constant Electron Beta Model [37,38]:
This model exploits our analytic knowledge of relativistic jets as being commonly generated by the Blandford–Znajek mechanism [8], which converts energy from accreting magnetized plasmas and spinning black holes into Poynting flux relativistic electromagnetic outflows with a power of . We now assume that a fixed fraction of jet magnetic energy is available for the emission observed at radio VLBI frequencies, where is related to the efficiency of conversion.
2.4.2. Magnetic Bias
This class of model generalizes the Constant model by relating the pressure of relativistic emitters (electrons or positrons) to the conversion of magnetic energy into particle energy through the powers n of the magnetic pressure:
The constant ensures that the right-hand side has units of pressure, and it can be estimated from a simulation by taking the average value of (where ) over a simulation surface enclosing the flux threading the black hole. The Bias Model parameter n helps modulate jet collimation in circumstances in which azimuthal magnetic fields are expected to scale simply with the cylindrical radius [37,39], e.g., the Blandford–Königl [40] model, where for radio jets.
2.5. Hybrid Models
We recognize the broad diversity of plasma regimes represented in a typical GRMHD field of view. Disk plasmas at large radii (a few tens or hundreds of M) are often not in inflow/outflow equilibrium [9], and thus, many of the thermal emission modeling approaches fail. As a Keplerian or sub-Keplerian disk approaches the horizon, its behavior near the plunging region beyond the innermost stable circular orbit (ISCO) is heavily dependent on SANE and MAD. For the MAD case, the disk can barely trickle into the supermassive black hole. For SANE flows, plasma can continuously flow. In both cases, the black hole spin can interact magnetohydrodynamically with disk plasma to form stable relativistic jets in simulations [41]. These jets, which are of underdense material themselves, are subjected to instabilities that are often distinct from those found in the disk, such as pinch, kink, and magnetic Kelvin–Helmholtz instabilities.
The inflow/outflow division in JAB systems gives an impetus for generating piecewise models. Jet plasmas are characterized by their low density and high energy, making the magnetization
which is a natural demarcation for the transition from jet-dominated emission to accretion-flow-dominated emission. When jets are well collimated, we may also use parabolic or other geometric cuts to isolate the jet region [37,39,42,43].
2.6. Phenomenological Models
We postulate other mechanisms here (detailing their full functional form in the model compendium in Appendix A.1) by noting the synchrotron emissivity , where the pressure of relativistic emitters can be written as in terms of the dissipation rate per unit time W and the cooling time t. In the following, we proceed to specify more potential models in our arsenal, systematically carrying out the second step of “Observing” JAB Simulations by relating the pressure of relativistic emitters to energetic processes in an AGN.
The Current Density Model relates the dissipation of energy into emitting particles to the current density . This is seen to trace a co-axial current morphology with a central outgoing current and a return current, thus creating a boundary layer in jets [39].
The Jet Alpha Model parametrizes the efficiency of linear momentum transport in jets by , i.e., , in a manner analogous to that of the Shakura–Sunyaev model for angular momentum transport in accretion disks [44]. This dissipation rate is also linear in the shear stress, as seen in Appendix A.1, thus enabling the disk–jet interface to be visible [39].
Lastly, the Shear Model adopts a Newtonian framework for velocity shear , where is the dynamical viscosity and S is the shear stress ( in cylindrical coordinates). Then, . This quadratic dependence on shear stress gives us an edge-brightened model relative to the Jet Alpha Model.
These jet models may naturally be glued to disk and corona models (especially those based on turbulent heating), as they capture the behavior of the inflow/outflow interface. Together, these phenomenological emission prescriptions may form the building blocks for detailed hybrid models that account for different plasma flow physics throughout the JAB system.
2.7. Electron Distribution Functions
A fixed temperature for electron thermodynamics models is often an idealization when particles are found in nearly collisionless plasmas (such as in JAB systems with mean free paths of ). The influence of a non-thermal electron population on horizon- and jet-base-scale emission remains an important subject of investigation in the EHT Collaboration [3,7]. These non-thermal distributions need not be applied globally in the GRMHD domain. Rather, determining the proper region’s home for charged particle acceleration processes is an integral part of these studies. We explore some possibilities for particle acceleration and the concomitant energy distributions below.
2.7.1. Power Law
One of the simplest phenomenologically viable assumptions for the energy distribution of a population of emitting particles in an astrophysical plasma is a power-law energy decay:
The normalization factor K depends on the synchrotron pressure. Power-law particle distributions are naturally produced in shock waves through diffusive shock acceleration, whereby particles are energized by repeated interactions with magnetic inhomogeneities as they propagate alongside the shock. This is a first-order Fermi process, as the energy gain of the particles is linear in the shock velocity. Astrophysical shocks may occur at the interface of fluids with differing velocities, such as the interface of a jet with its ambient medium.
2.7.2. The Kappa Model
It is often preferable to be able to model the full SED with a single distribution function. This can be achieved with the kappa electron energy distribution function (e.g., [45,46]), which has its theoretical foundation in non-extensive Tsallis statistics [47,48]. Looking like a thermal distribution at low energies, it smoothly transitions into a non-thermal power-law tail with index s towards high energies, so that (see, e.g., Figure 4 in [10]). The thermal [49] and kappa [50] electron energy distribution functions read
where is the electron number density, is the gyrophase, is the electron Lorentz factor, is the electron pitch angle, and is the modified Bessel function of the second kind. From these distribution functions, emission and absorption coefficients are determined by using fit functions [51]. w is the “width” of the distribution and describes the energy in the system.
From particle-in-cell (PIC) simulations of magnetized current sheets, it is evident that the kappa index is not constant in all sub-regions of the system, requiring kappa to be variable and dependent on plasma quantities [52]. Further, since many GRMHD codes do not provide accurate values close to the jet spine due to boundary conditions, the inner spine is usually excluded from the emission by imposing a maximum in the magnetization (e.g., [10,31,32]).
Additionally, the distribution function can be modified to account for a thermal and a magnetic contribution to the total energy [10,31,32,53]. That way, it is possible to control the amount of magnetically accelerated electrons and the distance of their point of injection into the jet from the central engine.
It is important to distinguish the influences of the individual dials of this non-thermal model on the image morphology. This requires extensive parameter surveys, which would be too computationally expensive in a two-temperature GRMHD simulation. Therefore, an implementation in radiative post-processing is currently the only feasible option for these surveys [10]. Increasing or raises the SED at energies past the synchrotron turnover, with a growing influence towards the highest energies (e.g., Figure 12 in [10]).
2.8. Emission Modeling in Non-Kerr Spacetimes
For over a century, Einstein’s theory of general relativity has been thoroughly tested in many different ways (e.g., [54,55,56,57,58,59,60,61,62,63]). In the era of the EHT and ngEHT, a test of GR in an imaging-based approach is on the horizon for the first time. Specifically, the shape and size of the black hole shadow and photon ring are crucial characteristic properties of horizon-scale images. Photons rings in the Kerr metric are predicted to be nested in subrings with exponentially decreasing separation, the lowest orders of which may be observed with the aid of longer baselines in the ngEHT [64]. In addition to this observational test of the Kerr solution for the spacetime around astrophysical black holes, many studies on alternative theories to general relativity make use of semi-analytical models for both plasma accretion and emission processes to compare models to observations (e.g., [65,66,67]). Alternative spacetime geometries are rarely investigated in full GRMHD and GRRT, and if so, the emission physics are based on a constant proton-to-electron temperature ratio and purely thermal radiation [68,69]. Only recently have advances been made to study the influence of emission models more akin to reality in an alternative spacetime [33,53]. The fundamental difficulties in finding deviations from the Kerr metric arise from the presence of greater astrophysical uncertainties. For example, the magnetic field configuration in a GRMHD simulation appears to have a much larger influence on the source morphology on horizon scales than the background spacetime [33,53]. Moreover, the differences in image features, such as the shadow size or photon sub-ring spacing caused by a deviation from GR, are often small and subject to degeneracy with accretion and emission models. Still, past EHT observations of black hole shadows have helped constrain alternative theories to GR [65,70]. With the help of the ngEHT, we aim to resolve the degeneracy between the effects of plasma physics and GR and put even more robust constraints onto alternative spacetime geometries.
3. Commencing the Computing: Emission Models in Numerical Codes
The emission models discussed above have been implemented in a variety of numerical codes (e.g., [71,72,73,74,75,76,77]; for an extensive comparison, see [78]). Since GRMHD simulations are already computationally expensive, radiation is commonly modeled in post-processing. While there are a handful of radiative GRMHD (GRrMHD) codes (e.g., [36]), when evolving a two-temperature plasma while accounting for ions and electrons, the computational cost only increases. In the case of pure jet simulations, however, it is possible to bring the cost down by moving to special relativity (e.g., [79,80,81,82,83]).
On event horizon scales, i.e., in the strong-gravity regime, we are required to take the full effects of GR into account. Usually, radiative transfer codes first calculate light rays by integrating the geodesic equation and, subsequently, solve the radiative transfer equation along those rays. The use of post-processing enables us to freely investigate a variety of emission models, with many going beyond thermal synchrotron radiation. For example, Compton/inverse Compton scattering, bremsstrahlung, and non-thermal emission processes all have their own imprints on the SED and the image morphology in both total intensity and polarized light [43,76].
Positrons’ Effects on Radiative Transfer
Positrons in JAB systems can be produced through photon–photon (Breit–Wheeler) interactions in jet funnel walls [84] and spark gap processes near the magnetospheric poles of supermassive Kerr black holes [85]. Each of these processes may contribute electron–positron pair densities exceeding the Goldrich–Julien value [86], which is required in order to screen the large-scale electric fields responsible for high-energy lepton cascades. In sources such as M87 that have significant pair production through these channels, positron effects abound. These include the increase in linear and vanishing of circular polarization, as well as the higher energy fall-off of the circular polarization spectrum, all of which have been modeled as potential discriminators of JAB systems that are rich in ionic versus pair plasma [43,83].
4. Results: Adding an Observer
We present a suite of parametric emission models and illustrate them in GRMHD simulations that are scaled to the first horizons observed: M87* and Sgr A*. We start by painting a single semi-MAD Sgr A* simulation with several phenomenologically motivated prescriptions of electron thermodynamics. Thus, by using the second step of the “Observing” JAB Simulations pipeline, we illustrate the sensitivity of the interpretations of near-horizon structure in real-world observations to our models of plasma physics. We then use a SANE and MAD M87 simulation to reveal widely divergent—and observationally distinguishable—polarized emission signatures governed by Faraday and positron effects. The latter effects enable us to better constrain a fundamental, though largely uncertain, property of relativistic jets: ion- versus lepton-dominated composition. In what follows, we use perceptually uniform color maps to identify image morphology with the underlying emission mechanisms that energize relativistic particles to produce synchrotron radiation.
4.1. Sgr A*
4.1.1. Parametric Model Comparison
We explore the Critical Beta model parameter space from and , starting with an edge in view to highlight the lensing effects on image morphology in Figure 2. As the f parameter increases, the overall electron temperature increases, and changes in the image morphology at fixed flux are effected through the used in codes to scale the relative importance of inertial plasma properties, such as the density and mass accretion rate, relative to the plasma’s electromagnetic properties. As the critical beta parameter increases, the locus of the greatest electron contributions moves from the low outflow to higher regions that are lensed around a compact crescent near the horizon due to higher values of being found in the inflow around the black hole. Thus, serves as a dial in JAB emission modeling for compactifying emitting regions and asymmetrizing them from an edge-on orientation, as shown in Figure 2.
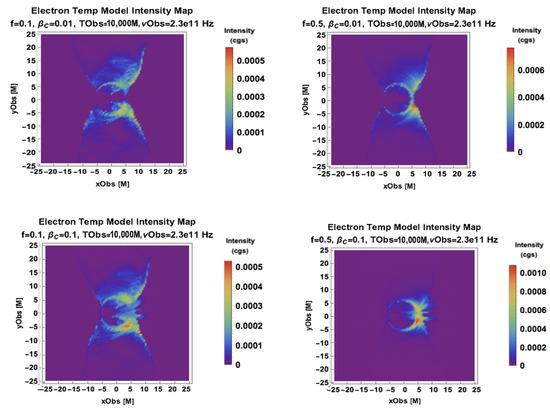
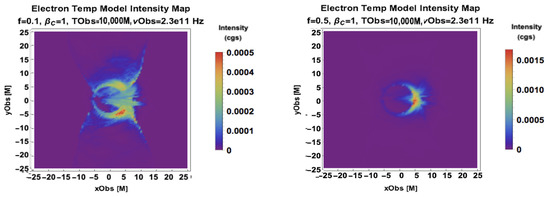
Figure 2.
A parameter scan of the Critical Beta Model with (Left) , (Right) , (Top), (Middle), and (Bottom) from an edge-on view. For Sgr A* models, the cgs conversion into Jy is found by multiplying each cgs-intensity-colored pixel value by 57.9 to get its flux density in Jy [9]. The scale is when used as a length and when used as time. The notation 1e2 is a compact form of the scientific notation .
In Figure 3, we see different morphologies associated with our equipartition-inspired Constant and Magnetic Bias models. The locus of emission for the Constant Electron Beta Model approaches the funnel for low and broadens into a thick, lensed torus for higher . When the bias parameter goes to 0, the pressure from relativistic electrons goes to a constant and does not sharply decline with the radius, leaving extended outflow signatures.
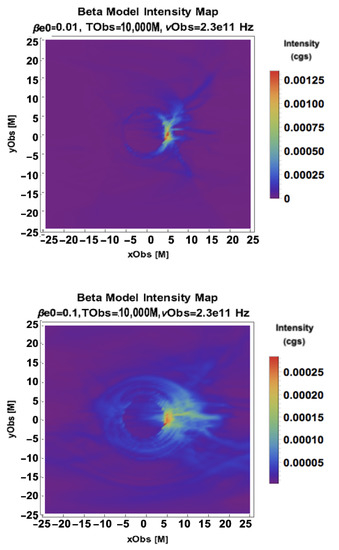
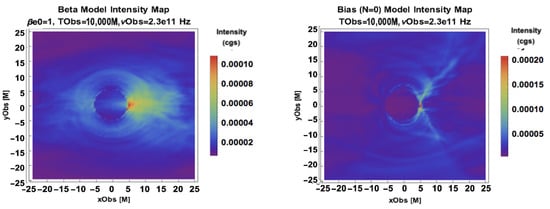
Figure 3.
A parameter scan of the Constant Electron Beta Model (Left) with , (Right) , (Top), (Middle), and (Bottom). Magnetic Bias Model with and (Bottom Right).
We now change the orientation and consider face-on models in Figure 4. An Sgr A* 20 spin axis orientation was observationally preferred by GRAVITY [6], and this was corroborated by the EHT, disfavoring inclination angles above 50. Here, tuning up the critical value of beta, , still leads to more compact images, but now they maintain a ring symmetry even near the gravitational lensing profile of a Kerr black hole.
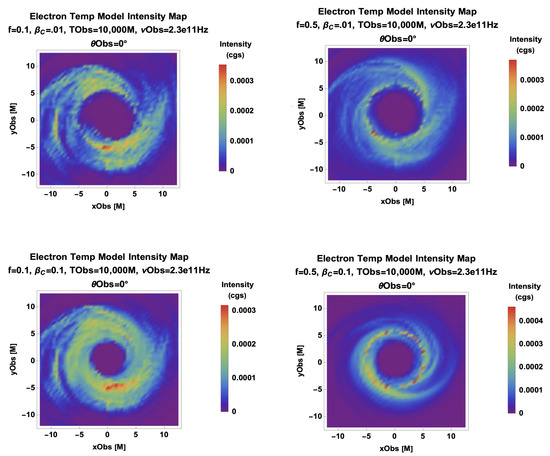
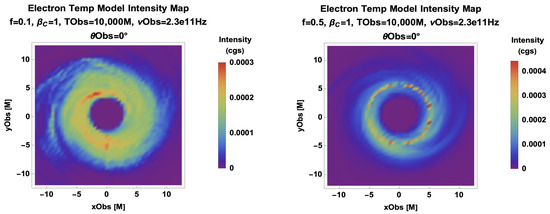
Figure 4.
A parameter scan of the face-on Critical Beta Model with (Left) , (Right) , (Top), (Middle), and (Bottom).
4.1.2. Morphological Classification
The ring morphology has dominated the focus of emission modeling since the advent of the first two ring-like images of the horizon scale were released by the EHT in 2019 and 2022. However, we showed examples of the strong inclination dependence of 230 GHz images above. It is worth taking stock of how fortuitous the near-face-on (∼20) spin axis viewing angles of Sgr A* and M87* are given that their main selection criterion is the exceptionally large angular width of their horizon gravitational radii as seen from Earth, which is independent of their spin inclination angle.
We preview the edge-on morphologies that the ngEHT will see based on morphological clusters in the parameter space of the Critical Beta, Constant Electron Beta, and Magnetic Bias Models in Figure 5. These types are:
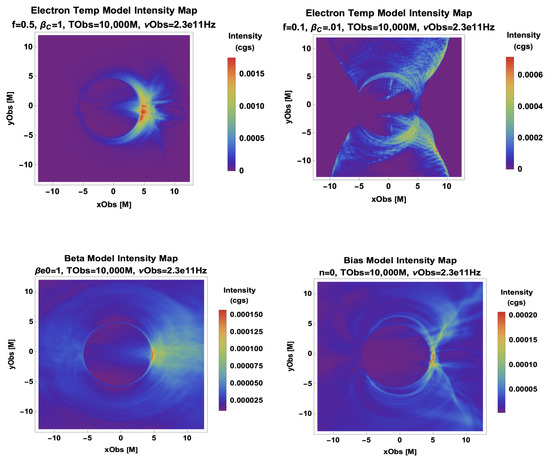
Figure 5.
Semi-MAD simulation [9] models that were ray traced at 230 GHz at T = 10,000 M: (Top Left) best-fit Critical Beta model (Top Right) R Beta with ; (Bottom Left) Constant Electron Beta model with ; (Bottom Right) Magnetic Bias with jet.
- 1
- A thin, compact asymmetric photon ring/crescent with the best fit or flat spectrum (with the spectral energy distribution shown in [9]);
- 2
- Inflow–outflow boundary + thin photon ring with a steep spectrum;
- 3
- Thick photon ring with spectral excesses at high and low frequencies;
- 4
- Extended outflow and a flat low frequency spectrum with excesses at high and low frequencies.
In Figure 6, we plot the morphological types on a common intensity scale to emulate observing with a single instrument. The EHT’s dynamical range of ∼2 orders of magnitude in intensity is used to set this scale. Morphological degeneracies, e.g., between Types I (large ) and III (large ) and between Types II (small ) and IV (small n), are more likely to emerge as more regions fall below the flux threshold of the observing instrument. The ngEHT’s dynamical range will span a few orders of magnitude. The ngEHT’s improved sensitivity down to ∼5 mJy and increased frequency range to ≳345 GHz [87] will enable us to resolve the currently excluded low-flux density regions in the field of view and at larger radii. This will lead to more accurate determination of the morphological type, thus breaking degeneracies. Thus, as the ngEHT increases the dynamic range of JAB system observations to lower fluxes, we are able to better classify images and pinpoint the underlying emission physics related to their morphologies.
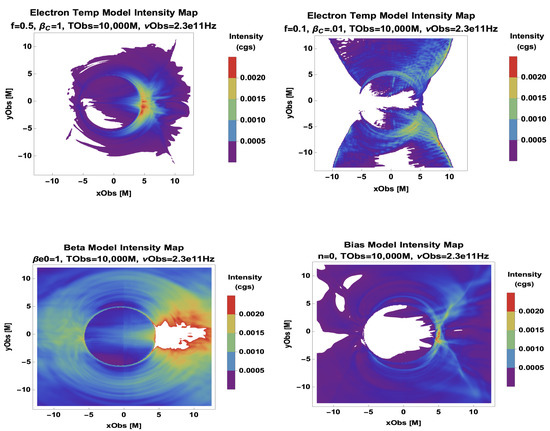
Figure 6.
Semi-MAD simulation [9] model classes that were ray traced at 230 GHz at T = 10,000 M, as shown in Figure 5, but with a common intensity scale.
4.2. M87
4.2.1. Parametric Model Comparison
We implement hybrid models that include turbulent heating and sub-equipartition emitting regions for M87. We make a natural choice to partition the simulation region according to the magnetization (i.e., the magnetic energy density to enthalpy density ratio ). The value that determines the jet regions is near the inflow/outflow interface and is less than the of 2 for these simulations.
A SANE/MAD dichotomy emerges in Figure 7 and Figure 8. The SANE intensity maps are more ring symmetric, whereas the MAD case has a prominent flux loop (lower left of all panels in Figure 8). The SANE circular polarization varies on smaller spatial scales than the MAD does. The sign of the circular polarization changes on sub-M scales for SANE. The SANE and MAD hybrid models that have added a Constant Electron Beta jet for have broader flux distributions over the field of view (all of the right panels in Figure 7 and Figure 8).
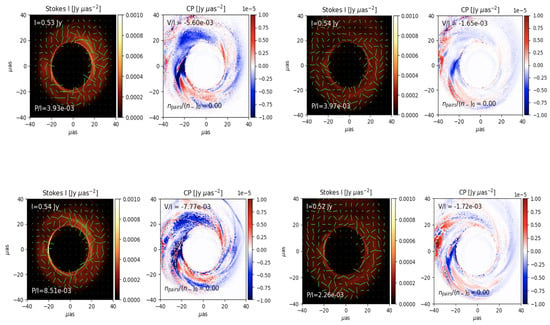
Figure 7.
Synthetic intensity with the electric vector polarization angle (EVPA) and circular polarization maps for models that include positron effects and piecewise modeling. For the SANE at 230 GHz and at T = 25,000 M: (Top Left) R-Beta with a jet model; (Top Right) R-Beta with a jet; (Bottom Left) Critical Beta Model; (Bottom Right) Critical Beta with a jet. For each case, the intensity is overplotted with the electric vector polarization angle on the left panel, and the circular polarization degree is mapped on the right panel.
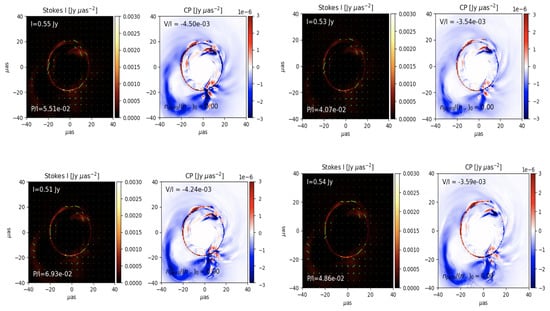
Figure 8.
For the MAD at 230 GHz and at T = 25,000 M: (Top Left) R-Beta Model; (Top Right) R-Beta with a jet; (Bottom Left) Critical Beta Model; (Bottom Right) Critical Beta with a jet. For each case, the intensity is overplotted with the electric vector polarization angle on the left panel, and the circular polarization degree is mapped on the right panel.
4.2.2. Positron Effects
We see the effect of the addition of positrons in Figure 9. There, we start with an ionic plasma with a number density of (see the top panels), and then add enough positron pairs so that the pair number density equals that of the original electrons (and the unit for M is adjusted to match the normalized flux (see the bottom panels)). In Figure 9, we see that in the MAD case (left), the degree of circular polarization is proportional to the unpaired emitter fraction (1/3 in the case of ) [43,88]. The SANE case (right), which has Faraday rotation depths that are thousands of times greater than the less dense, more highly magnetized MAD, does not have a simple linear relationship between the pair content and . In the linear polarization, we also see greater positron effects for SANE than for MAD, as the addition of positrons scrambles the EVPA pattern only in the SANE case.
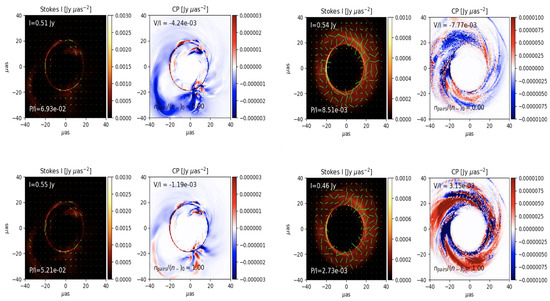
Figure 9.
For at 230 GHz and at T = 25,000 M: (Top) Critical Beta Model without positrons; (Bottom) Critical Beta with . We also compare MAD (Left) and SANE (Right).
5. Discussion and Conclusions
We have seen from a SANE and a MAD M87 simulation and one semi-MAD simulation for Sgr A* that the thermodynamic properties of emitting particle populations can be as important as those of the underlying plasma for predicting the properties of intensity and polarization maps near the horizon. Moreover, special relativistic effects, such as beaming and general relativistic lensing, can produce nonlinear modifications of the flux received by observers away from the JAB system. Understanding the relative contributions of these effects can be facilitated by idealized cases, such as in semi-analytic jet models, e.g., those in [42]. We considered the impacts of some of the competing effects listed here:
- The plasma controls the emitting region size in turbulent heating models, where parameter combinations with greater emission contributions from low tend to have more extended outflow/coronal regions, and those with contributions from high are more compact and dominated by near-horizon inflow, as shown in Figure 2, going from top to bottom.
- Inclination has a pronounced effect on the 230 GHz observer plane image morphology due to special relativistic beaming and the focusing properties of gravitational lensing. Thus, we predict a wide variety of image morphologies beyond ring structures that may be uncovered by the ngEHT, as shown in Figure 6.
- SANE and MAD simulations have widely divergent positron effects that are modulated by the larger Faraday depth of SANE plasmas, which are constrained to achieve the same image fluxes that MADs acquire through magnetic fields, with SANEs having EVPAs that are highly sensitive to positron content and MADs having a circular polarization degree that is greatly suppressed by positrons, as shown in Figure 9.
By using a variety of turbulent heating and magnetic-to-particle-energy-ratio-based emission models, we found a number of distinct image morphologies that we expect to encounter in future observational campaigns with the ngEHT. In particular, the ngEHT will have the resolution to probe images with areas a few times smaller than those probed with the EHT, allowing the imaging of more compact ringlike structures that are viewed face-on (corresponding to high values of Critical Beta, should this turbulent heating mechanism predominate). This will enable us to better determine which processes dominate the emissions. Furthermore, we showed the strong dependence on inclination of the relationship between electron thermodynamics and image morphology. We identified at least four distinct image signatures of turbulent heating and magnetic-to-particle energy ratios, mainly visible in the edge-on view. We also showed the EHT’s/ngEHT’s ability to discriminate between MAD and SANE accretion states based on ordered vs. scrambled polarization signatures. This dichotomy is accentuated by the presence of positrons, allowing us to probe the plasma composition of JAB systems, which remains a long-standing question.
5.1. Limits of Instrumentation
The 20 as angular resolution of the EHT (enough to resolve an atom at arm’s length or an apple on the Moon) is exquisite according to the VLBI observational standards. More remarkably still, the ngEHT may double this angular resolution. However, the angular gravitational radius of even the largest black hole shadow (as for Sgr A*) is still smaller than the size of the synthesized beam of the ngEHT (≲20 as). This leads to blurring in the image plane, washing out intricate features. Due to this instrumental limitation, numerical simulations are crucial for our understanding of the properties of accretion flows. Though simulations themselves produce grid-resolution-dependent models (cf. Appendix A.2), they remain our most reliable probe below the scale set by the gravitational radius, and will continue to motivate observing missions for the ngEHT and beyond to confirm their predictions.
5.2. Universality of Select Measures
The existence of flaring emissions in Sgr A* and extended synchrotron emissions in M87’s jet provide strong evidence for the presence of a high-energy tail to the lepton distribution, i.e., non-thermal lepton distribution functions. This is generally expected as a consequence of the microphysical processes responsible for the dissipation of turbulence and the attendant injection of energy explored above. However, the detailed shape and magnitude of this additional tail depend sensitively on the specific acceleration mechanism considered. Nevertheless, for the physical parameters that are relevant for Sgr A* and M87, below 690 GHz, the synchrotron coefficients are only weakly sensitive to the particular choice of the extension of the lepton distribution function [89].
The lepton distributions are expected to be rapidly isotropized on the cyclotron scale by plasma instabilities [14,15]. For such distributions, the synchrotron emission and absorption coefficients for all Stokes parameters may be expressed as convolutions with broad kernels in frequency space [90]. As a consequence, all of these transfer coefficients are well approximated by a universal expression that is dependent only on the local spectral index, which conceptually corresponds to a measure of the relative number of “hot” non-thermal and “cold” thermal leptons [89].
At a single observation frequency, this approximation is as good as to better than 2%. Thus, for images at 230 or 345 GHz, for example, the specific nature of the acceleration mechanism may be effectively and efficiently parameterized by a single lepton distribution model (e.g., thermal, , power law, etc.), thus eliminating a key systematic degeneracy between the location of and microphysical processes responsible for turbulence dissipation. Across large frequency ranges, e.g., from 230 to 345 GHz, the accuracy of this approximation falls to ∼10%, or from 230 to 480 GHz to ∼40%. Therefore, multi-frequency image reconstructions remain a powerful discriminant between different acceleration mechanisms.
Author Contributions
Conceptualization, R.A.; methodology, R.A.; software, A.R., R.E.; validation, J.D., L.O. and N.N. (Nathan Ngata); formal analysis, J.W.; investigation, R.A.; resources, A.R.; data curation, B.C. and S.R.; writing—original draft preparation, R.A., J.R., A.E.B. and G.N.W.; writing—review and editing, J.R., J.D., L.O. and N.N. (Nathan Ngata).; visualization, J.D., L.O., N.N. (Nathan Ngata), N.N. (Nitya Nigam) and E.D.; supervision, R.A.; project administration, R.A.; funding acquisition, R.E. All authors have read and agreed to the published version of the manuscript.
Funding
Jan Röder received financial support for this research from the International Max Planck Research School (IMPRS) for Astronomy and Astrophysics at the Universities of Bonn and Cologne. Razieh Emami acknowledges the support from the Institute for Theory and Computation at the Center for Astrophysics, as well as grant numbers 21-atp21-0077, NSF AST-1816420, and HST-GO-16173.001-A, for their very generous support.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| (ng)EHT | (Next-Generation) Event Horizon Telescope |
| GRMHD | General relativistic magnetohydrodynamics |
| GRRT | General relativistic radiative transfer |
| SED | Spectral energy distribution |
Appendix A
Appendix A.1. List of Emission Models
We summarize the emission models employed above (and more) in Table A1.

Table A1.
JAB Emission Model List. This is a compendium of the phonologically motivated emission models mentioned in this work. The shear stress and dimensional parameters and are set by the width of jet system.
Table A1.
JAB Emission Model List. This is a compendium of the phonologically motivated emission models mentioned in this work. The shear stress and dimensional parameters and are set by the width of jet system.
| Model Name | Parameters | Functional Form |
|---|---|---|
| R-Beta | ||
| Critical Beta | ||
| Const. Jet | ||
| Magnetic Bias Jet | ||
| R Beta w. Const. Jet | Const. in Jet, o.w. | |
| Critical Beta w. Const. Jet | Const. in Jet, Crit. o.w | |
| Current Density | ||
| Jet Alpha | , | |
| Shear | , , |
Appendix A.2. Resolution Dependence
In Figure A1, we briefly consider the robustness of image properties to resolution effects. Changing the resolution can shift the local and global maxima, as seen in these 50 M × 50 M fields of view, where going from 100 pixels per side to 500 pixels per side makes the maximum intensity (red) pixels more concentrated in a more compact equatorial region. Increasing the resolution also increases the overall maximum intensity, as one may expect due to the breaking up of the high-intensity regions into more pixels over which to perform the maximization. In both cases shown, as discussed in Section 5.1, the sub-gravitational-radius pixel spacing in the synthetic images exceeds current and planned observational resolution limits. However, for even the modestly sized supermassive black hole Sgr A*, cm, so the role of emission modeling to fill in the sizable gap left by subgrid physics will remain paramount for years to come.
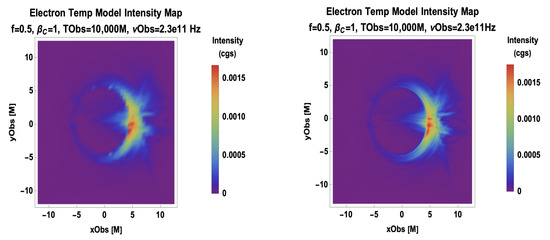
Figure A1.
Resolution dependence of the Critical Beta Model. Increasing from 2 pixels/M to 10 pixels/M alters the image morphology such that the overall image is sharper and the brightest features are more localized and extreme in intensity.
Notes
| 1 | There have been some notable recent attempts to bridge the gap through hybrid electron distribution functions (edfs), such as the -model smoothly joining thermal electrons to a high-energy power-law tail [10]. |
| 2 | Here, is the rest mass density, is the four-velocity, and is the stress–energy–momentum tensor. |
| 3 | This was written using Parthenon; see https://github.com/lanl/parthenon. |
| 4 | In this treatment, ions can be treated interchangeably with protons. |
References
- Event Horizon Telescope Collaboration; Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.K.; Ball, D.; Baloković, M.; Barrett, J.; et al. First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole. Astrophys. J. Lett. 2019, 875, L1. [Google Scholar] [CrossRef]
- Event Horizon Telescope Collaboration; Akiyama, K.; Alberdi, A.; Alef, W.; Algaba, J.C.; Anantua, R.; Asada, K.; Azulay, R.; Bach, U.; Baczko, A.K.; et al. First Sagittarius A* Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole in the Center of the Milky Way. Astrophys. J. Lett. 2022, 930, L12. [Google Scholar] [CrossRef]
- Event Horizon Telescope Collaboration; Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.K.; Ball, D.; Baloković, M.; Barrett, J.; et al. First M87 Event Horizon Telescope Results. V. Physical Origin of the Asymmetric Ring. Astrophys. J. Lett. 2019, 875, L5. [Google Scholar] [CrossRef]
- Event Horizon Telescope Collaboration; Akiyama, K.; Algaba, J.C.; Alberdi, A.; Alef, W.; Anantua, R.; Asada, K.; Azulay, R.; Baczko, A.K.; Ball, D.; et al. First M87 Event Horizon Telescope Results. VII. Polarization of the Ring. Astrophys. J. Lett. 2021, 910, L12. [Google Scholar] [CrossRef]
- Akiyama, K.; Alberdi, A.; Alef, W.; Algaba, J.C.; Anantua, R.; Asada, K.; Azulay, R.; Bach, U.; Baczko, A.-K.; Ball, D.; et al. First Sagittarius A* Event Horizon Telescope Results. III. Imaging of the Galactic Center Supermassive Black Hole. Astrophys. J. Lett. 2022, 930, L14. [Google Scholar]
- GRAVITY Collaboration; Abuter, R.; Amorim, A.; Anugu, N.; Bauböck, M.; Benisty, M.; Berger, J.P.; Blind, N.; Bonnet, H.; Brandner, W.; et al. Detection of the gravitational redshift in the orbit of the star S2 near the Galactic centre massive black hole. Astron. Astrophys. 2018, 615, L15. [Google Scholar] [CrossRef]
- Akiyama, K.; Alberdi, A.; Alef, W.; Algaba, J.C.; Anantua, R.; Asada, K.; Azulay, R.; Bach, U.; Baczko, A.K.; Ball, D.; et al. First Sagittarius A* Event Horizon Telescope Results. V. Testing Astrophysical Models of the Galactic Center Black Hole. Astrophys. J. Lett. 2022, 930, L16. [Google Scholar]
- Blandford, R.D.; Znajek, R.L. Electromagnetic extraction of energy from Kerr black holes. Mon. Not. R. Astron. Soc. 1977, 179, 433–456. [Google Scholar] [CrossRef]
- Anantua, R.; Ressler, S.; Quataert, E. On the comparison of AGN with GRMHD simulations: I. Sgr A*. Mon. Not. R. Astron. Soc. 2020, 493, 1404–1418. [Google Scholar] [CrossRef]
- Fromm, C.M.; Cruz-Osorio, A.; Mizuno, Y.; Nathanail, A.; Younsi, Z.; Porth, O.; Olivares, H.; Davelaar, J.; Falcke, H.; Kramer, M.; et al. Impact of non-thermal particles on the spectral and structural properties of M87. Astron. Astrophys. 2022, 660, A107. [Google Scholar] [CrossRef]
- Ressler, S.M.; Tchekhovskoy, A.; Quataert, E.; Chandra, M.; Gammie, C.F. Electron thermodynamics in GRMHD simulations of low-luminosity black hole accretion. Mon. Not. R. Astron. Soc. 2015, 454, 1848–1870. [Google Scholar] [CrossRef]
- Chatterjee, K.; Younsi, Z.; Liska, M.; Tchekhovskoy, A.; Markoff, S.B.; Yoon, D.; van Eijnatten, D.; Hesp, C.; Ingram, A.; van der Klis, M.B.M. Observational signatures of disc and jet misalignment in images of accreting black holes. Mon. Not. R. Astron. Soc. 2020, 499, 362–378. [Google Scholar] [CrossRef]
- Curd, B.; Emami, R.; Anantua, R.; Palumbo, D.; Doeleman, S.; Narayan, R. Jets from SANE Super-Eddington Accretion Disks: Morphology, Spectra, and Their Potential as Targets for ngEHT. arXiv 2022, arXiv:2206.06358. [Google Scholar] [CrossRef]
- Gammie, C.F.; McKinney, J.C.; Tóth, G. HARM: A Numerical Scheme for General Relativistic Magnetohydrodynamics. Astrophys. J. 2003, 589, 444–457. [Google Scholar] [CrossRef]
- Gammie, C.F.; McKinney, J.C.; Tóth, G. HARM: A Numerical Scheme for General Relativistic Magnetohydrodynamics. Astrophys. Source Code Libr. Available online: http://ascl.net/1209.005 (accessed on 10 November 2022).
- Wong, G.N.; Prather, B.S.; Dhruv, V.; Ryan, B.R.; Mościbrodzka, M.; Chan, C.k.; Joshi, A.V.; Yarza, R.; Ricarte, A.; Shiokawa, H.; et al. PATOKA: Simulating Electromagnetic Observables of Black Hole Accretion. Astrophys. J. Suppl. Ser. 2022, 259, 64. [Google Scholar] [CrossRef]
- Fishbone, L.G.; Moncrief, V. Relativistic fluid disks in orbit around Kerr black holes. Astrophys. J. 1976, 207, 962–976. [Google Scholar] [CrossRef]
- Prather, B.; Wong, G.; Dhruv, V.; Ryan, B.; Dolence, J.; Ressler, S.; Gammie, C. iharm3D: Vectorized General Relativistic Magnetohydrodynamics. J. Open Source Softw. 2021, 6, 3336. [Google Scholar] [CrossRef]
- Bondi, H. On spherically symmetrical accretion. Mon. Not. R. Astron. Soc. 1952, 112, 195. [Google Scholar] [CrossRef]
- Ressler, S.M.; Quataert, E.; White, C.J.; Blaes, O. Magnetically modified spherical accretion in GRMHD: Reconnection-driven convection and jet propagation. Mon. Not. R. Astron. Soc. 2021, 504, 6076–6095. [Google Scholar] [CrossRef]
- Jia, H.; White, C.J.; Quataert, E.; Ressler, S.M. Observational signatures of black hole accretion: Rotating versus spherical flows with tilted magnetic fields. Mon. Not. R. Astron. Soc. 2022, 515, 1392–1403. [Google Scholar] [CrossRef]
- Quataert, E. A Dynamical Model for Hot Gas in the Galactic Center. Astrophys. J. 2004, 613, 322–325. [Google Scholar] [CrossRef]
- Cuadra, J.; Nayakshin, S.; Martins, F. Variable accretion and emission from the stellar winds in the Galactic Centre. Mon. Not. R. Astron. Soc. 2008, 383, 458–466. [Google Scholar] [CrossRef][Green Version]
- Shcherbakov, R.V.; Baganoff, F.K. Inflow-Outflow Model with Conduction and Self-consistent Feeding for Sgr A*. Astrophys. J. 2010, 716, 504–509. [Google Scholar] [CrossRef]
- Ressler, S.M.; Quataert, E.; Stone, J.M. Hydrodynamic simulations of the inner accretion flow of Sagittarius A* fuelled by stellar winds. Mon. Not. R. Astron. Soc. 2018, 478, 3544–3563. [Google Scholar] [CrossRef]
- Broderick, A.E.; Gold, R.; Karami, M.; Preciado-López, J.A.; Tiede, P.; Pu, H.Y.; Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; et al. THEMIS: A Parameter Estimation Framework for the Event Horizon Telescope. Astrophys. J. 2020, 897, 139. [Google Scholar] [CrossRef]
- Yuan, F.; Narayan, R. Hot Accretion Flows Around Black Holes. Annu. Rev. Astron. Astrophys. 2014, 52, 529–588. [Google Scholar] [CrossRef]
- Quataert, E.; Gruzinov, A. Turbulence and Particle Heating in Advection-dominated Accretion Flows. Astrophys. J. 1999, 520, 248–255. [Google Scholar] [CrossRef]
- Howes, G.G. A prescription for the turbulent heating of astrophysical plasmas. Mon. Not. R. Astron. Soc. 2010, 409, L104–L108. [Google Scholar] [CrossRef]
- Mościbrodzka, M.; Falcke, H.; Shiokawa, H. General relativistic magnetohydrodynamical simulations of the jet in M 87. Astron. Astrophys. 2016, 586, A38. [Google Scholar] [CrossRef]
- Davelaar, J.; Olivares, H.; Porth, O.; Bronzwaer, T.; Janssen, M.; Roelofs, F.; Mizuno, Y.; Fromm, C.M.; Falcke, H.; Rezzolla, L. Modeling non-thermal emission from the jet-launching region of M 87 with adaptive mesh refinement. Astron. Astrophys. 2019, 632, A2. [Google Scholar] [CrossRef]
- Cruz-Osorio, A.; Fromm, C.M.; Mizuno, Y.; Nathanail, A.; Younsi, Z.; Porth, O.; Davelaar, J.; Falcke, H.; Kramer, M.; Rezzolla, L. State-of-the-art energetic and morphological modelling of the launching site of the M87 jet. Nat. Astron. 2022, 6, 103–108. [Google Scholar] [CrossRef]
- Röder, J.; Cruz-Osorio, A.; Fromm, C.M.; Mizuno, Y.; Younsi, Z.; Rezzolla, L. Comparison of Kerr and dilaton black hole shadows. In Proceedings of the European VLBI Network Mini-Symposium and Users’ Meeting 2021, Online, 12–14 July 2021; p. 24. [Google Scholar]
- Event Horizon Telescope Collaboration; Akiyama, K.; Algaba, J.C.; Alberdi, A.; Alef, W.; Anantua, R.; Asada, K.; Azulay, R.; Baczko, A.K.; Ball, D.; et al. First M87 Event Horizon Telescope Results. VIII. Magnetic Field Structure near The Event Horizon. Astrophys. J. Lett. 2021, 910, L13. [Google Scholar] [CrossRef]
- Mizuno, Y.; Fromm, C.M.; Younsi, Z.; Porth, O.; Olivares, H.; Rezzolla, L. Comparison of the ion-to-electron temperature ratio prescription: GRMHD simulations with electron thermodynamics. Mon. Not. R. Astron. Soc. 2021, 506, 741–758. [Google Scholar] [CrossRef]
- Chael, A.; Rowan, M.; Narayan, R.; Johnson, M.; Sironi, L. The role of electron heating physics in images and variability of the Galactic Centre black hole Sagittarius A*. Mon. Not. R. Astron. Soc. 2018, 478, 5209–5229. [Google Scholar] [CrossRef]
- Anantua, R.J. Towards Multi-Wavelength Observations of Relativistic Jets from General Relativistic Magnetohydrodynamic Simulations. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2016. [Google Scholar]
- Blandford, R.; Anantua, R. The Future of Black Hole Astrophysics in the LIGO-VIRGO-LPF Era. J. Phys. Conf. Ser. 2017, 840, 012023. [Google Scholar] [CrossRef]
- Anantua, R.; Blandford, R.; Tchekhovskoy, A. Multiwavelength Observations of Relativistic Jets from General Relativistic Magnetohydrodynamic Simulations. Galaxies 2018, 6, 31. [Google Scholar] [CrossRef]
- Blandford, R.D.; Königl, A. Relativistic jets as compact radio sources. Astrophys. J. 1979, 232, 34–48. [Google Scholar] [CrossRef]
- McKinney, J.C.; Blandford, R.D. Stability of relativistic jets from rotating, accreting black holes via fully three-dimensional magnetohydrodynamic simulations. Mon. Not. R. Astron. Soc. 2009, 394, L126–L130. [Google Scholar] [CrossRef]
- Anantua, R.; Emami, R.; Loeb, A.; Chael, A. Determining the Composition of Relativistic Jets from Polarization Maps. Astrophys. J. 2020, 896, 27. [Google Scholar] [CrossRef]
- Emami, R.; Anantua, R.; Chael, A.; Loeb, A. Positron Effects on Polarized Images and Spectra from Jet and Accretion Flow Models of M87* and Sgr A*. Astrophys. J. 2021, 923, 272. [Google Scholar] [CrossRef]
- Shakura, N.I.; Sunyaev, R.A. Black holes in binary systems. Observational appearance. Astron. Astrophys. 1973, 24, 337–355. [Google Scholar]
- Vasyliunas, V.M. Low-energy electrons on the day side of the magnetosphere. J. Geophys. Res. 1968, 73, 7519–7523. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J. Beyond kappa distributions: Exploiting Tsallis statistical mechanics in space plasmas. J. Geophys. Res. (Space Phys.) 2009, 114, A11105. [Google Scholar] [CrossRef]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Tsallis, C.; Mendes, R.; Plastino, A.R. The role of constraints within generalized nonextensive statistics. Phys. Stat. Mech. Its Appl. 1998, 261, 534–554. [Google Scholar] [CrossRef]
- Leung, P.K.; Gammie, C.F.; Noble, S.C. Numerical Calculation of Magnetobremsstrahlung Emission and Absorption Coefficients. Astrophys. J. 2011, 737, 21. [Google Scholar] [CrossRef]
- Xiao, F. Modelling energetic particles by a relativistic kappa-loss-cone distribution function in plasmas. Plasma Phys. Control. Fusion 2006, 48, 203–213. [Google Scholar] [CrossRef]
- Pandya, A.; Zhang, Z.; Chandra, M.; Gammie, C.F. Polarized Synchrotron Emissivities and Absorptivities for Relativistic Thermal, Power-law, and Kappa Distribution Functions. Astrophys. J. 2016, 822, 34. [Google Scholar] [CrossRef]
- Ball, D.; Sironi, L.; Özel, F. Electron and Proton Acceleration in Trans-relativistic Magnetic Reconnection: Dependence on Plasma Beta and Magnetization. Astrophys. J. 2018, 862, 80. [Google Scholar] [CrossRef]
- Röder, J.; Cruz-Osorio, A.; Fromm, C.M.; Mizuno, Y.; Younsi, Z.; Rezzolla, L. Probing spacetime and accretion model for the Galactic Center: Comparison of Kerr and dilaton black hole shadows. 2022; manuscript in preparation. [Google Scholar]
- Pound, R.V.; Rebka, G.A. Gravitational Red-Shift in Nuclear Resonance. Phys. Rev. Lett. 1959, 3, 439–441. [Google Scholar] [CrossRef]
- Pound, R.V.; Rebka, G.A. Apparent Weight of Photons. Phys. Rev. Lett. 1960, 4, 337–341. [Google Scholar] [CrossRef]
- Pound, R.V.; Snider, J.L. Effect of Gravity on Nuclear Resonance. Phys. Rev. Lett. 1964, 13, 539–540. [Google Scholar] [CrossRef]
- Weisberg, J.M.; Taylor, J.H.; Fowler, L.A. Gravitational waves from an orbiting pulsar. Sci. Am. 1981, 245, 74–82. [Google Scholar] [CrossRef]
- Hafele, J.C.; Keating, R.E. Around-the-World Atomic Clocks: Predicted Relativistic Time Gains. Science 1972, 177, 166–168. [Google Scholar] [CrossRef]
- Hafele, J.C.; Keating, R.E. Around-the-World Atomic Clocks: Observed Relativistic Time Gains. Science 1972, 177, 168–170. [Google Scholar] [CrossRef]
- Kramer, M.; Stairs, I.H.; Manchester, R.N.; McLaughlin, M.A.; Lyne, A.G.; Ferdman, R.D.; Burgay, M.; Lorimer, D.R.; Possenti, A.; D’Amico, N.; et al. Tests of General Relativity from Timing the Double Pulsar. Science 2006, 314, 97–102. [Google Scholar] [CrossRef]
- Stairs, I.H. Testing General Relativity with Pulsar Timing. Living Rev. Relativ. 2003, 6, 5. [Google Scholar] [CrossRef]
- Will, C.M. Testing the General Relativistic “No-Hair” Theorems Using the Galactic Center Black Hole Sagittarius A*. Astrophys. J. Lett. 2008, 674, L25. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef]
- Johnson, M.D.; Lupsasca, A.; Strominger, A.; Wong, G.N.; Hadar, S.; Kapec, D.; Narayan, R.; Chael, A.; Gammie, C.F.; Galison, P.; et al. Universal interferometric signatures of a black hole’s photon ring. Sci. Adv. 2020, 6, eaaz1310. [Google Scholar] [CrossRef]
- Kocherlakota, P.; Rezzolla, L. Distinguishing gravitational and emission physics in black hole imaging: Spherical symmetry. Mon. Not. R. Astron. Soc. 2022, 513, 1229–1243. [Google Scholar] [CrossRef]
- Younsi, Z.; Psaltis, D.; Özel, F. Black Hole Images as Tests of General Relativity: Effects of Spacetime Geometry. arXiv 2021, arXiv:2111.01752. [Google Scholar]
- Özel, F.; Psaltis, D.; Younsi, Z. Black Hole Images as Tests of General Relativity: Effects of Plasma Physics. arXiv 2021, arXiv:2111.01123. [Google Scholar] [CrossRef]
- Mizuno, Y.; Younsi, Z.; Fromm, C.M.; Porth, O.; De Laurentis, M.; Olivares, H.; Falcke, H.; Kramer, M.; Rezzolla, L. The current ability to test theories of gravity with black hole shadows. Nat. Astron. 2018, 2, 585–590. [Google Scholar] [CrossRef]
- Olivares, H.; Younsi, Z.; Fromm, C.M.; De Laurentis, M.; Porth, O.; Mizuno, Y.; Falcke, H.; Kramer, M.; Rezzolla, L. How to tell an accreting boson star from a black hole. Mon. Not. R. Astron. Soc. 2020, 497, 521–535. [Google Scholar] [CrossRef]
- Event Horizon Telescope Collaboration; Akiyama, K.; Alberdi, A.; Alef, W.; Algaba, J.C.; Anantua, R.; Asada, K.; Azulay, R.; Bach, U.; Baczko, A.K.; et al. First Sagittarius A* Event Horizon Telescope Results. VI. Testing the Black Hole Metric. Astrophys. J. Lett. 2022, 930, L17. [Google Scholar] [CrossRef]
- Younsi, Z.; Porth, O.; Mizuno, Y.; Fromm, C.M.; Olivares, H. Modelling the polarised emission from black holes on event horizon-scales. Proc. Int. Astron. Union 2020, 14, 9–12. [Google Scholar] [CrossRef]
- Pu, H.Y.; Yun, K.; Younsi, Z.; Yoon, S.J. Odyssey: A Public GPU-based Code for General Relativistic Radiative Transfer in Kerr Spacetime. Astrophys. J. 2016, 820, 105. [Google Scholar] [CrossRef]
- Dexter, J. A public code for general relativistic, polarised radiative transfer around spinning black holes. Mon. Not. R. Astron. Soc. 2016, 462, 115–136. [Google Scholar] [CrossRef]
- Mościbrodzka, M.; Gammie, C.F. IPOLE - semi-analytic scheme for relativistic polarized radiative transport. Mon. Not. R. Astron. Soc. 2018, 475, 43–54. [Google Scholar] [CrossRef]
- Chan, C.k.; Psaltis, D.; Özel, F. GRay: A Massively Parallel GPU-based Code for Ray Tracing in Relativistic Spacetimes. Astrophys. J. 2013, 777, 13. [Google Scholar] [CrossRef]
- Kawashima, T.; Ohsuga, K.; Takahashi, H.R. RAIKOU: A General Relativistic, Multi-wavelength Radiative Transfer Code. arXiv 2021, arXiv:2108.05131. [Google Scholar]
- Bronzwaer, T.; Davelaar, J.; Younsi, Z.; Mościbrodzka, M.; Falcke, H.; Kramer, M.; Rezzolla, L. RAPTOR. I. Time-dependent radiative transfer in arbitrary spacetimes. Astron. Astrophys. 2018, 613, A2. [Google Scholar] [CrossRef]
- Gold, R.; Broderick, A.E.; Younsi, Z.; Fromm, C.M.; Gammie, C.F.; Mościbrodzka, M.; Pu, H.Y.; Bronzwaer, T.; Davelaar, J.; Dexter, J.; et al. Verification of Radiative Transfer Schemes for the EHT. Astrophys. J. 2020, 897, 148. [Google Scholar] [CrossRef]
- Mignone, A.; Bodo, G.; Massaglia, S.; Matsakos, T.; Tesileanu, O.; Zanni, C.; Ferrari, A. PLUTO: A Numerical Code for Computational Astrophysics. Astrophys. J. Suppl. Ser. 2007, 170, 228–242. [Google Scholar] [CrossRef]
- Mignone, A.; Zanni, C.; Tzeferacos, P.; van Straalen, B.; Colella, P.; Bodo, G. The PLUTO Code for Adaptive Mesh Computations in Astrophysical Fluid Dynamics. Astrophys. J. Suppl. Ser. 2012, 198, 7. [Google Scholar] [CrossRef]
- Perucho, M.; Martí, J.M.; Cela, J.M.; Hanasz, M.; de La Cruz, R.; Rubio, F. Stability of three-dimensional relativistic jets: Implications for jet collimation. Astron. Astrophys. 2010, 519, A41. [Google Scholar] [CrossRef]
- Kramer, J.A.; MacDonald, N.R. Ray-tracing in relativistic jet simulations: A polarimetric study of magnetic field morphology and electron scaling relations. Astron. Astrophys. 2021, 656, A143. [Google Scholar] [CrossRef]
- MacDonald, N.R.; Nishikawa, K.I. From electrons to Janskys: Full stokes polarized radiative transfer in 3D relativistic particle-in-cell jet simulations. Astron. Astrophys. 2021, 653, A10. [Google Scholar] [CrossRef]
- Mościbrodzka, M.; Gammie, C.F.; Dolence, J.C.; Shiokawa, H. Pair Production in Low-luminosity Galactic Nuclei. Astrophys. J. 2011, 735, 9. [Google Scholar] [CrossRef]
- Broderick, A.E.; Tchekhovskoy, A. Horizon-Scale Lepton Acceleration in jets: Explaining the Compact Radio Emission in M87. Astrophys. J. 2015, 809, 97. [Google Scholar] [CrossRef]
- Goldreich, P.; Julian, W.H. Pulsar Electrodynamics. Astrophys. J. 1969, 157, 869. [Google Scholar] [CrossRef]
- Raymond, A.W.; Palumbo, D.; Paine, S.N.; Blackburn, L.; Córdova Rosado, R.; Doeleman, S.S.; Farah, J.R.; Johnson, M.D.; Roelofs, F.; Tilanus, R.P.J.; et al. Evaluation of New Submillimeter VLBI Sites for the Event Horizon Telescope. Astrophys. J. Suppl. Ser. 2021, 253, 5. [Google Scholar] [CrossRef]
- Emami, R.; Anantua, R.; Ricarte, A.; Doeleman, S.S.; Broderick, A.; Wong, G.; Blackburn, L.; Wielgus, M.; Narayan, R.; Tremblay, G.; et al. Probing plasma composition with the next generation Event Horizon Telescope (ngEHT). arXiv 2022, arXiv:2211.07306. [Google Scholar]
- Broderick, A.; Loeb, A. Local Universality of Nonthermal Synchrotron Emission from EHT Targets. 2022; manuscript in preparation. [Google Scholar]
- Rybicki, G.B.; Lightman, A.P. Radiative Processes in Astrophysics; Wiley-VCH: Weinheim, Germany, 1986. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).