The Closure Relations in High-Energy Gamma-ray Bursts Detected by Fermi-LAT
Abstract
1. Introduction
2. Methods
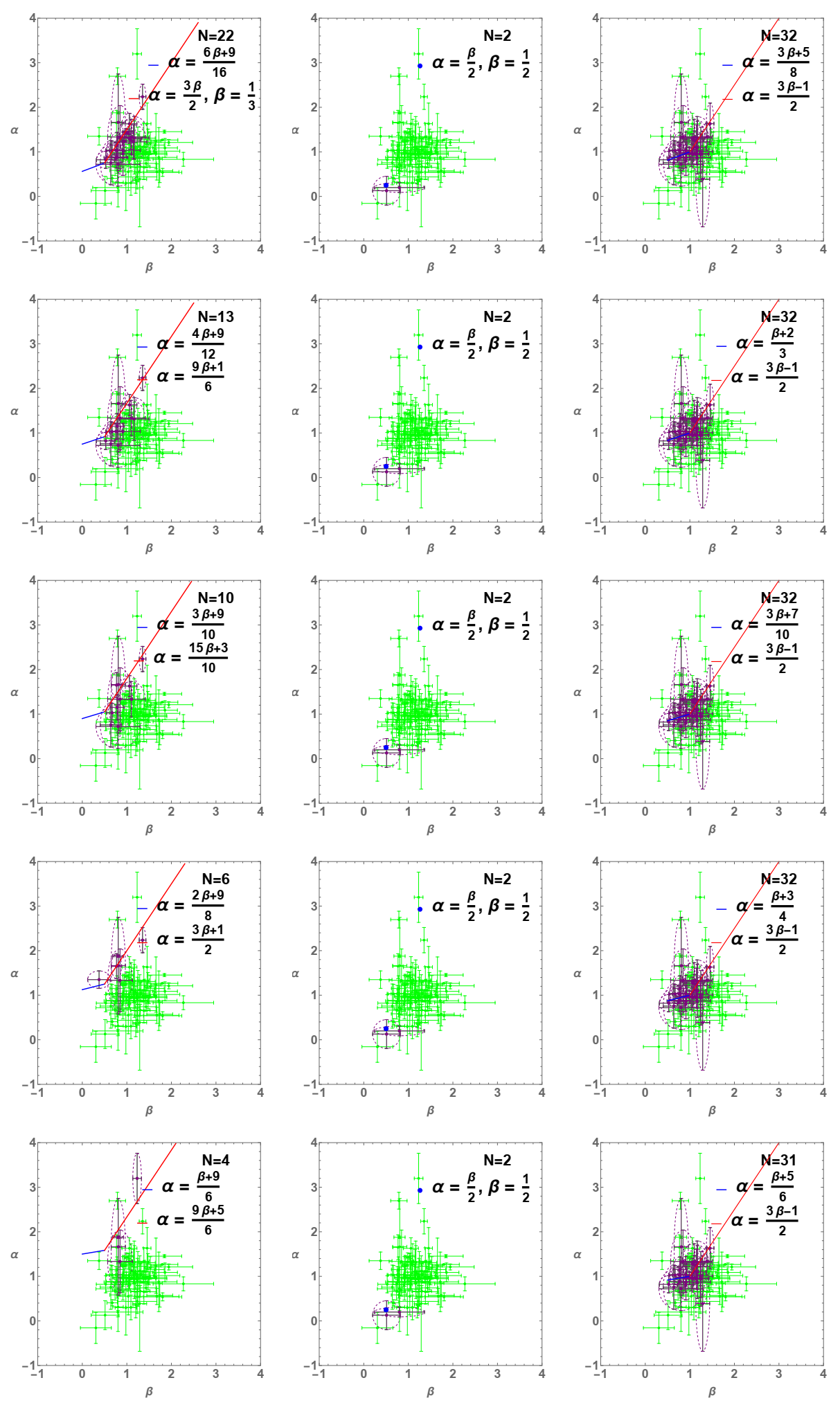
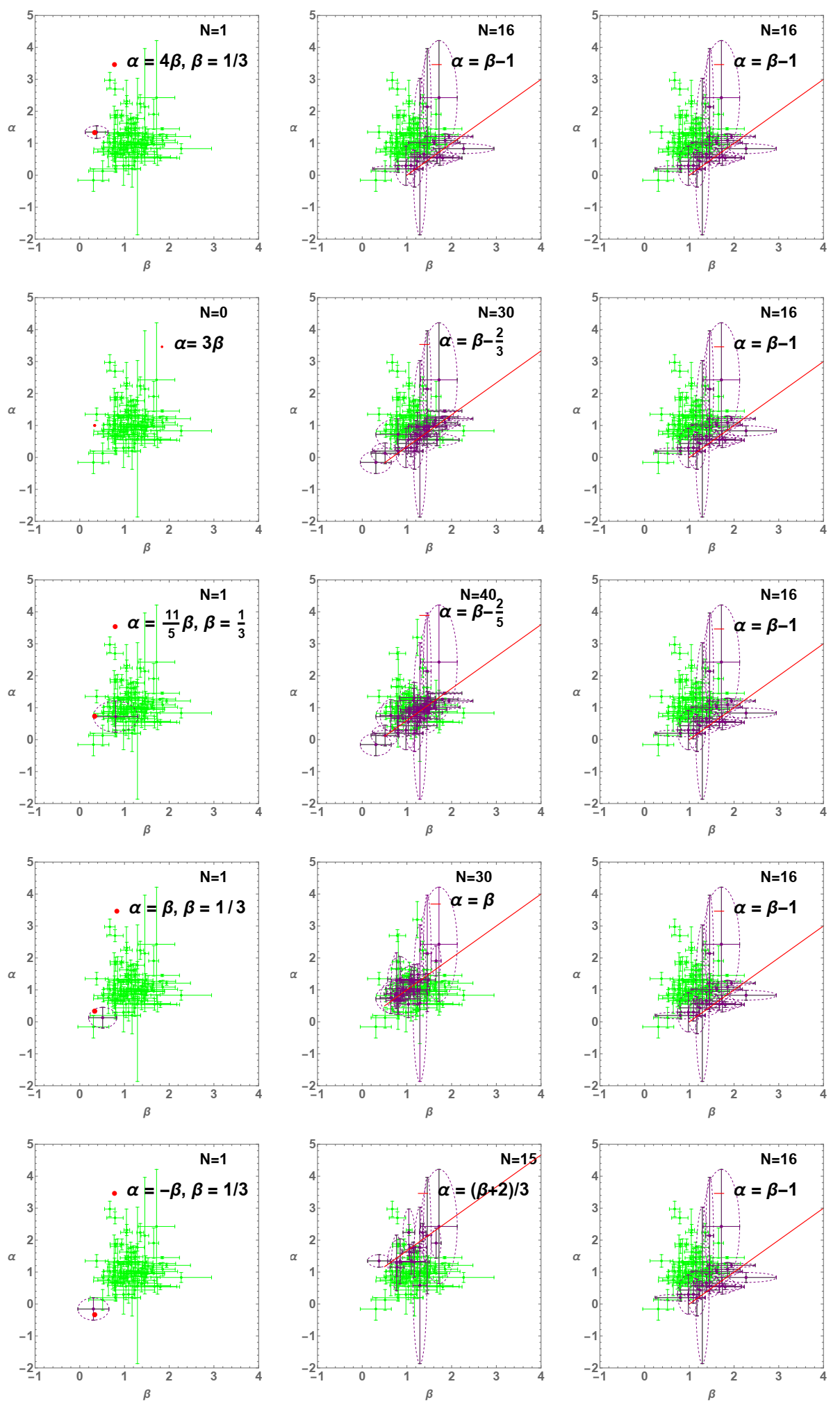
3. Testing the Closure Relations
4. Comparing to CRs in Other Bands
5. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | Where the cooling timescale for shocked electrons is comparable to, or longer than, the dynamic timescale of the GRB jet. |
| 2 | For a sample visualization of these fittings, see Figure 9 of Ajello et al. [8]. |
References
- Band, D.; Matteson, J.; Ford, L.; Schaefer, B.; Palmer, D.; Teegarden, B.; Cline, T.; Briggs, M.; Paciesas, W.; Pendleton, G.; et al. BATSE observations of gamma-ray burst spectra. I—Spectral diversity. Astrophys. J. 1993, 413, 281–292. [Google Scholar] [CrossRef]
- Ryde, F. Is Thermal Emission in Gamma-Ray Bursts Ubiquitous? Astrophys. J. Lett. 2005, 625, L95–L98. [Google Scholar] [CrossRef]
- Pe’er, A.; Barlow, H.; O’Mahony, S.; Margutti, R.; Ryde, F.; Larsson, J.; Lazzati, D.; Livio, M. Hydrodynamic Properties of Gamma-Ray Burst Outflows Deduced from the Thermal Component. Astrophys. J. 2015, 813, 127. [Google Scholar] [CrossRef]
- Kumar, P.; Zhang, B. The physics of gamma-ray bursts & relativistic jets. Phys. Rep. 2015, 561, 1–109. [Google Scholar]
- Ackermann, M.; Asano, K.; Atwood, W.B.; Axelsson, M.; Baldini, L.; Ballet, J.; Barbiellini, G.; Baring, M.G.; Bastieri, D.; Bechtol, K.; et al. Fermi Observations of GRB 090510: A Short-Hard Gamma-ray Burst with an Additional, Hard Power-law Component from 10 keV TO GeV Energies. Astrophys. J. 2010, 716, 1178–1190. [Google Scholar] [CrossRef]
- Atwood, W.B.; Abdo, A.A.; Ackermann, M.; Althouse, W.; Anderson, B.; Axelsson, M.; Baldini, L.; Ballet, J.; Band, D.L.; Barbiellini, G.; et al. The Large Area Telescope on the Fermi Gamma-Ray Space Telescope Mission. Astrophys. J. 2009, 697, 1071–1102. [Google Scholar] [CrossRef]
- Ackermann, M.; Ajello, M.; Asano, K.; Axelsson, M.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; Bechtol, K.; Bellazzini, R.; et al. The First Fermi-LAT Gamma-Ray Burst Catalog. Astrophys. J. Ser. 2013, 209, 11. [Google Scholar] [CrossRef]
- Ajello, M.; Arimoto, M.; Axelsson, M.; Baldini, L.; Barbiellini, G.; Bastieri, D.; Bellazzini, R.; Bhat, P.N.; Bissaldi, E.; Blandford, R.D.; et al. A Decade of Gamma-Ray Bursts Observed by Fermi-LAT: The Second GRB Catalog. Astrophys. J. 2019, 878, 52. [Google Scholar] [CrossRef]
- Ajello, M.; Arimoto, M.; Asano, K.; Axelsson, M.; Baldini, L.; Barbiellini, G.; Bastieri, D.; Bellazzini, R.; Berretta, A.; Bissaldi, E.; et al. Bright Gamma-Ray Flares Observed in GRB 131108A. Astrophys. J. Lett. 2019, 886, L33. [Google Scholar] [CrossRef]
- Laskar, T.; Alexander, K.D.; Berger, E.; Fong, W.f.; Margutti, R.; Shivvers, I.; Williams, P.K.G.; Kopač, D.; Kobayashi, S.; Mundell, C.; et al. A Reverse Shock in GRB 160509A. Astrophys. J. 2016, 833, 88. [Google Scholar] [CrossRef]
- Sharma, V.; Iyyani, S.; Bhattacharya, D.; Chattopadhyay, T.; Rao, A.R.; Aarthy, E.; Vadawale, S.V.; Mithun, N.P.S.; Bhalerao, V.B.; Ryde, F.; et al. Time-varying Polarized Gamma-Rays from GRB 160821A: Evidence for Ordered Magnetic Fields. Astrophys. J. Lett. 2019, 882, L10. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Omodei, N.; Srinivasaragavan, G.P.; Vianello, G.; Willingale, R.; O’Brien, P.; Nagataki, S.; Petrosian, V.; Nuygen, Z.; Hernandez, X.; et al. On the Existence of the Plateau Emission in High-energy Gamma-Ray Burst Light Curves Observed by Fermi-LAT. Astrophys. J. Ser. 2021, 255, 13. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Postnikov, S.; Hernandez, X.; Ostrowski, M. A Fundamental Plane for Long Gamma-Ray Bursts with X-Ray Plateaus. Astrophys. J. Lett. 2016, 825, L20. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Del Vecchio, R. Gamma Ray Burst afterglow and prompt-afterglow relations: An overview. New Astron. Rev. 2017, 77, 23–61. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Hernandez, X.; Postnikov, S.; Nagataki, S.; O’brien, P.; Willingale, R.; Striegel, S. A Study of the Gamma-Ray Burst Fundamental Plane. Astrophys. J. 2017, 848, 88. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Del Vecchio, R.; Tarnopolski, M. Gamma-Ray Burst Prompt Correlations. Adv. Astron. 2018, 2018, 4969503. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Livermore, S.; Kann, D.A.; Li, L.; Oates, S.; Yi, S.; Zhang, B.; Gendre, B.; Cenko, B.; Fraija, N. The Optical Luminosity-Time Correlation for More than 100 Gamma-Ray Burst Afterglows. Astrophys. J. Lett. 2020, 905, L26. [Google Scholar] [CrossRef]
- Sari, R.; Narayan, R.; Piran, T. Cooling Timescales and Temporal Structure of Gamma-Ray Bursts. Astrophys. J. 1996, 473, 204. [Google Scholar] [CrossRef]
- Sari, R.; Piran, T. Hydrodynamic Timescales and Temporal Structure of Gamma-Ray Bursts. Astrophys. J. Lett. 1995, 455, L143. [Google Scholar] [CrossRef]
- Sari, R.; Piran, T. The early afterglow. Astron. Astrophys. Suppl. Ser. 1999, 138, 537–538. [Google Scholar] [CrossRef]
- Kumar, P.; Piran, T. Some Observational Consequences of Gamma-Ray Burst Shock Models. Astrophys. J. 2000, 532, 286–293. [Google Scholar] [CrossRef]
- Granot, J.; Sari, R. The Shape of Spectral Breaks in Gamma-Ray Burst Afterglows. Astrophys. J. 2002, 568, 2. [Google Scholar] [CrossRef]
- Sari, R.; Piran, T.; Narayan, R. Spectra and Light Curves of Gamma-Ray Burst Afterglows. Astrophys. J. Lett. 1998, 497, L17. [Google Scholar] [CrossRef]
- Meszaros, P.; Rees, M.J. Delayed GEV Emission from Cosmological Gamma-Ray Bursts - Impact of a Relativistic Wind on External Matter. Mon. Not. R. Astron. Soc. 1994, 269, L41. [Google Scholar] [CrossRef]
- Daigne, F.; Mochkovitch, R. Gamma-ray bursts from internal shocks in a relativistic wind: Temporal and spectral properties. Mon. Not. R. Astron. Soc. 1998, 296, 275–286. [Google Scholar] [CrossRef]
- Chevalier, R.A.; Li, Z.Y. Wind Interaction Models for Gamma-Ray Burst Afterglows: The Case for Two Types of Progenitors. arXiv 2000, arXiv:astro-ph/9908272. [Google Scholar] [CrossRef]
- Panaitescu, A.; Kumar, P. Analytic Light Curves of Gamma-Ray Burst Afterglows: Homogeneous versus Wind External Media. Astrophys. J. 2000, 543, 66–76. [Google Scholar] [CrossRef]
- Schulze, S.; Klose, S.; Björnsson, G.; Jakobsson, P.; Kann, D.A.; Rossi, A.; Krühler, T.; Greiner, J.; Ferrero, P. The circumburst density profile around GRB progenitors: A statistical study. Astron. Astrophys. 2011, 526, A23. [Google Scholar] [CrossRef]
- De Colle, F.; Granot, J.; López-Cámara, D.; Ramirez-Ruiz, E. Gamma-Ray Burst Dynamics and Afterglow Radiation from Adaptive Mesh Refinement, Special Relativistic Hydrodynamic Simulations. Astrophys. J. 2012, 746, 122. [Google Scholar] [CrossRef]
- Yi, S.X.; Wu, X.F.; Dai, Z.G. Early Afterglows of Gamma-Ray Bursts in a Stratified Medium with a Power-law Density Distribution. Astrophys. J. 2013, 776, 120. [Google Scholar] [CrossRef]
- Yi, S.X.; Wu, X.F.; Zou, Y.C.; Dai, Z.G. The Bright Reverse Shock Emission in the Optical Afterglows of Gamma-Ray Bursts in a Stratified Medium. Astrophys. J. 2020, 895, 94. [Google Scholar] [CrossRef]
- Gompertz, B.P.; Fruchter, A.S.; Pe’er, A. The Environments of the Most Energetic Gamma-Ray Bursts. Astrophys. J. 2018, 866, 162. [Google Scholar] [CrossRef]
- Fraija, N.; De Colle, F.; Veres, P.; Dichiara, S.; Duran, R.B.; Pedreira, A.C.; Galvan-Gamez, A.; Betancourt Kamenetskaia, B. Description of Atypical Bursts Seen Slightly Off-axis. Astrophys. J. 2020, 896, 25. [Google Scholar] [CrossRef]
- Tagliaferri, G.; Goad, M.; Chincarini, G.; Moretti, A.; Campana, S.; Burrows, D.N.; Perri, M.; Barthelmy, S.D.; Gehrels, N.; Krimm, H.; et al. An unexpectedly rapid decline in the X-ray afterglow emission of long γ-ray bursts. Nature 2005, 436, 985–988. [Google Scholar] [CrossRef]
- Nousek, J.A.; Kouveliotou, C.; Grupe, D.; Page, K.L.; Granot, J.; Ramirez-Ruiz, E.; Patel, S.K.; Burrows, D.N.; Mangano, V.; Barthelmy, S.; et al. Evidence for a Canonical Gamma-Ray Burst Afterglow Light Curve in the Swift XRT Data. Astrophys. J. 2006, 642, 389–400. [Google Scholar] [CrossRef]
- O’Brien, P.T.; Willingale, R.; Osborne, J.; Goad, M.R.; Page, K.L.; Vaughan, S.; Rol, E.; Beardmore, A.; Godet, O.; Hurkett, C.P.; et al. The Early X-Ray Emission from GRBs. Astrophys. J. 2006, 647, 1213–1237. [Google Scholar] [CrossRef]
- Zhang, B.; Fan, Y.Z.; Dyks, J.; Kobayashi, S.; Mészáros, P.; Burrows, D.N.; Nousek, J.A.; Gehrels, N. Physical Processes Shaping Gamma-Ray Burst X-Ray Afterglow Light Curves: Theoretical Implications from the Swift X-Ray Telescope Observations. Astrophys. J. 2006, 642, 354–370. [Google Scholar] [CrossRef]
- Zhang, B.B.; Liang, E.W.; Zhang, B. A Comprehensive Analysis of Swift XRT Data. I. Apparent Spectral Evolution of Gamma-Ray Burst X-Ray Tails. Astrophys. J. 2007, 666, 1002–1011. [Google Scholar] [CrossRef]
- Zhang, B. Gamma-Ray Bursts in the Swift Era. Chin. J. Astron. Astrophys. 2007, 7, 1–50. [Google Scholar] [CrossRef]
- Zhang, B.; Zhang, B.B.; Liang, E.W.; Gehrels, N.; Burrows, D.N.; Mészáros, P. Making a Short Gamma-Ray Burst from a Long One: Implications for the Nature of GRB 060614. Astrophys. J. Lett. 2007, 655, L25–L28. [Google Scholar] [CrossRef]
- Zhang, B.; Liang, E.; Page, K.L.; Grupe, D.; Zhang, B.B.; Barthelmy, S.D.; Burrows, D.N.; Campana, S.; Chincarini, G.; Gehrels, N.; et al. GRB Radiative Efficiencies Derived from the Swift Data: GRBs versus XRFs, Long versus Short. Astrophys. J. 2007, 655, 989–1001. [Google Scholar] [CrossRef]
- Sakamoto, T.; Hill, J.E.; Yamazaki, R.; Angelini, L.; Krimm, H.A.; Sato, G.; Swindell, S.; Takami, K.; Osborne, J.P. Evidence of Exponential Decay Emission in the Swift Gamma-Ray Bursts. Astrophys. J. 2007, 669, 1115–1129. [Google Scholar] [CrossRef]
- Zhao, L.; Zhang, B.; Gao, H.; Lan, L.; Lü, H.; Zhang, B. The Shallow Decay Segment of GRB X-Ray Afterglow Revisited. Astrophys. J. 2019, 883, 97. [Google Scholar] [CrossRef]
- Fraija, N.; Dichiara, S.; Pedreira, A.C.C.d.E.S.; Galvan-Gamez, A.; Becerra, R.L.; Montalvo, A.; Montero, J.; Betancourt Kamenetskaia, B.; Zhang, B.B. Modeling the Observations of GRB 180720B: From Radio to Sub-TeV Gamma-Rays. Astrophys. J. 2019, 885, 29. [Google Scholar] [CrossRef]
- Evans, P.A.; Beardmore, A.P.; Page, K.L.; Osborne, J.P.; O’Brien, P.T.; Willingale, R.; Starling, R.L.C.; Burrows, D.N.; Godet, O.; Vetere, L.; et al. Methods and results of an automatic analysis of a complete sample of Swift-XRT observations of GRBs. Mon. Not. R. Astron. Soc. 2022, 397, 1177–1201. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Young, S.; Li, L.; Kalinowski, K.K.; Levine, D.; Kann, D.A.; Tran, B.; Zambrano-Tapia, L.; Zambrano-Tapia, A.; Cenko, B.; et al. The Optical Two and Three-Dimensional Fundamental Plane Correlations for Nearly 180 Gamma-Ray Burst Afterglows with Swift/UVOT, RATIR, and the SUBARU Telescope. arXiv 2022, arXiv:2203.12908. [Google Scholar] [CrossRef]
- Levine, D.; Dainotti, M.; Zvonarek, K.J.; Fraija, N.; Warren, D.C.; Chandra, P.; Lloyd-Ronning, N. Examining Two-dimensional Luminosity-Time Correlations for Gamma-Ray Burst Radio Afterglows with VLA and ALMA. Astrophys. J. 2022, 925, 15. [Google Scholar] [CrossRef]
- Kumar, P.; Barniol Duran, R. On the generation of high-energy photons detected by the Fermi Satellite from gamma-ray bursts. Mon. Not. R. Astron. Soc. 2009, 400, L75–L79. [Google Scholar] [CrossRef]
- Kumar, P.; Barniol Duran, R. External forward shock origin of high-energy emission for three gamma-ray bursts detected by Fermi. Mon. Not. R. Astron. Soc. 2010, 409, 226–236. [Google Scholar] [CrossRef]
- Tak, D.; Omodei, N.; Uhm, Z.L.; Racusin, J.; Asano, K.; McEnery, J. Closure Relations of Gamma-Ray Bursts in High Energy Emission. Astrophys. J. 2019, 883, 134. [Google Scholar] [CrossRef]
- Fraija, N.; Dainotti, M.G.; Ugale, S.; Jyoti, D.; Warren, D.C. Synchrotron Self-Compton Afterglow Closure Relations and Fermi-LAT-detected Gamma-Ray Bursts. Astrophys. J. 2022, 934, 188. [Google Scholar] [CrossRef]
- Warren, D.C.; Dainotti, M.; Barkov, M.V.; Ahlgren, B.; Ito, H.; Nagataki, S. A Semianalytic Afterglow with Thermal Electrons and Synchrotron Self-Compton Emission. Astrophys. J. 2022, 924, 40. [Google Scholar] [CrossRef]
- Veres, P.; Mészáros, P. Prospects for GeV-TeV Detection of Short Gamma-Ray Bursts with Extended Emission. Astrophys. J. 2014, 787, 168. [Google Scholar] [CrossRef]
- Racusin, J.L.; Liang, E.W.; Burrows, D.N.; Falcone, A.; Sakamoto, T.; Zhang, B.B.; Zhang, B.; Evans, P.; Osborne, J. Jet Breaks and Energetics of Swift Gamma-Ray Burst X-Ray Afterglows. Astrophys. J. 2009, 698, 43–74. [Google Scholar] [CrossRef]
- Srinivasaragavan, G.P.; Dainotti, M.G.; Fraija, N.; Hernandez, X.; Nagataki, S.; Lenart, A.; Bowden, L.; Wagner, R. On the Investigation of the Closure Relations for Gamma-Ray Bursts Observed by Swift in the Post-plateau Phase and the GRB Fundamental Plane. Astrophys. J. 2020, 903, 18. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Lenart, A.Ł.; Fraija, N.; Nagataki, S.; Warren, D.C.; De Simone, B.; Srinivasaragavan, G.; Mata, A. Closure relations during the plateau emission of Swift GRBs and the fundamental plane. Publ. Astron. Soc. Jpn. 2021, 73, 970–1000. [Google Scholar] [CrossRef]
- Ackermann, M.; Ajello, M.; Asano, K.; Baldini, L.; Barbiellini, G.; Baring, M.G.; Bastieri, D.; Bellazzini, R.; Blandford, R.D.; Bonamente, E.; et al. Multiwavelength Observations of GRB 110731A: GeV Emission from Onset to Afterglow. Astrophys. J. 2013, 763, 71. [Google Scholar] [CrossRef]
- Wang, X.G.; Zhang, B.; Liang, E.W.; Gao, H.; Li, L.; Deng, C.M.; Qin, S.M.; Tang, Q.W.; Kann, D.A.; Ryde, F.; et al. How Bad or Good Are the External Forward Shock Afterglow Models of Gamma-Ray Bursts? Astrophys. J. Ser. 2015, 219, 9. [Google Scholar] [CrossRef]
- Fukushima, T.; To, S.; Asano, K.; Fujita, Y. Temporal Evolution of the Gamma-ray Burst Afterglow Spectrum for an Observer: GeV-TeV Synchrotron Self-Compton Light Curve. Astrophys. J. 2017, 844, 92. [Google Scholar] [CrossRef]
- Kangas, T.; Fruchter, A.S. The Late-time Radio Behavior of Gamma-ray Burst Afterglows: Testing the Standard Model. Astrophys. J. 2021, 911, 14. [Google Scholar] [CrossRef]
- Misra, K.; Resmi, L.; Kann, D.A.; Marongiu, M.; Moin, A.; Klose, S.; Bernardi, G.; de Ugarte Postigo, A.; Jaiswal, V.K.; Schulze, S.; et al. Low frequency view of GRB 190114C reveals time varying shock micro-physics. Mon. Not. R. Astron. Soc. 2021, 504, 5685–5701. [Google Scholar] [CrossRef]
- Fraija, N.; Lee, W.; Veres, P. Modeling the Early Multiwavelength Emission in GRB130427A. Astrophys. J. 2016, 818, 190. [Google Scholar] [CrossRef]
- Fraija, N.; Laskar, T.; Dichiara, S.; Beniamini, P.; Duran, R.B.; Dainotti, M.G.; Becerra, R.L. GRB Fermi-LAT Afterglows: Explaining Flares, Breaks, and Energetic Photons. Astrophys. J. 2020, 905, 112. [Google Scholar] [CrossRef]
- Crowther, P.A. Physical Properties of Wolf-Rayet Stars. Annu. Rev. Astron. Astrophys. 2007, 45, 177–219. [Google Scholar] [CrossRef]
- De Colle, F.; Ramirez-Ruiz, E.; Granot, J.; Lopez-Camara, D. Simulations of Gamma-Ray Burst Jets in a Stratified External Medium: Dynamics, Afterglow Light Curves, Jet Breaks, and Radio Calorimetry. Astrophys. J. 2012, 751, 57. [Google Scholar] [CrossRef]
- Hotokezaka, K.; Kyutoku, K.; Tanaka, M.; Kiuchi, K.; Sekiguchi, Y.; Shibata, M.; Wanajo, S. Progenitor models of the electromagnetic transient associated with the short gamma ray burst 130603B. Astrophys. J. Lett. 2013, 778, L16. [Google Scholar] [CrossRef]
- Gao, H.; Lei, W.H.; Zou, Y.C.; Wu, X.F.; Zhang, B. A complete reference of the analytical synchrotron external shock models of gamma-ray bursts. New Astron. Rev. 2013, 57, 141–190. [Google Scholar] [CrossRef]
- Zhang, B.; Mészáros, P. Gamma-Ray Bursts: Progress, problems & prospects. Int. J. Mod. Phys. A 2004, 19, 2385–2472. [Google Scholar] [CrossRef]
- Dai, Z.G.; Cheng, K.S. Afterglow Emission from Highly Collimated Jets with Flat Electron Spectra: Application to the GRB 010222 Case? Astrophys. J. Lett. 2001, 558, L109–L112. [Google Scholar] [CrossRef]
- Panaitescu, A. Models for achromatic light-curve breaks in gamma-ray burst afterglows: Jets, structured outflows and energy injection. Mon. Not. R. Astron. Soc. 2005, 362, 921–930. [Google Scholar] [CrossRef]
- Panaitescu, A.; Mészáros, P.; Gehrels, N.; Burrows, D.; Nousek, J. Analysis of the X-ray emission of nine Swift afterglows. Mon. Not. R. Astron. Soc. 2006, 366, 1357–1366. [Google Scholar] [CrossRef]
- Dai, Z.G.; Lu, T. Gamma-ray burst afterglows: Effects of radiative corrections and non-uniformity of the surrounding medium. Mon. Not. R. Astron. Soc. 1998, 298, 87–92. [Google Scholar] [CrossRef]
- Zhang, B.; Mészáros, P. Gamma-Ray Burst Afterglow with Continuous Energy Injection: Signature of a Highly Magnetized Millisecond Pulsar. Astrophys. J. Lett. 2001, 552, L35–L38. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Levine, D.; Fraija, N.; Warren, D.; Sourav, S. The Closure Relations in Optical Afterglow of Gamma-Ray Bursts. Astrophys. J. 2022, 940, 169. [Google Scholar] [CrossRef]
- Levine, D.; Dainotti, M.; Fraija, N.; Warren, D.; Chandra, P.; Lloyd-Ronning, N. Interpretation of radio afterglows in the framework of the standard fireball and energy injection models. Mon. Not. R. Astron. Soc. 2022. [Google Scholar] [CrossRef]
- Fraija, N.; Veres, P.; Beniamini, P.; Galvan-Gamez, A.; Metzger, B.D.; Barniol Duran, R.; Becerra, R.L. On the origin of the multi-GeV photons from the closest burst with intermediate luminosity: GRB 190829A. arXiv 2020, arXiv:2003.11252. [Google Scholar] [CrossRef]
| GRB | ||
|---|---|---|
| GRB080825C | ||
| GRB081009A | ||
| GRB090626A | ||
| GRB091031A | ||
| GRB091120A | ||
| GRB100116A | ||
| GRB100423B | ||
| GRB100511A | ||
| GRB100728A | ||
| GRB101014A | ||
| GRB110120A | ||
| GRB110428A | ||
| GRB110518A | ||
| GRB110625A | ||
| GRB110721A | ||
| GRB111210B | ||
| GRB120226A | ||
| GRB120316A | ||
| GRB120526A | ||
| GRB120624B | ||
| GRB120709A | ||
| GRB120711A | ||
| GRB120911B | ||
| GRB130325A | ||
| GRB130502B | ||
| GRB130518A | ||
| GRB130606B | ||
| GRB130821A | ||
| GRB130828A | ||
| GRB131014A | ||
| GRB131029A | ||
| GRB131209A | ||
| GRB131231A | ||
| GRB140102A | ||
| GRB140104B | ||
| GRB140110A | ||
| GRB140206B | ||
| GRB140402A | ||
| GRB140523A | ||
| GRB140810A | ||
| GRB141028A | ||
| GRB141102A | ||
| GRB141207A | ||
| GRB141222A | ||
| GRB150314A | ||
| GRB150523A | ||
| GRB150702A | ||
| GRB150902A | ||
| GRB160325A | ||
| GRB160521B | ||
| GRB160623A | ||
| GRB160625B | ||
| GRB160821A | ||
| GRB160905A | ||
| GRB161109A | ||
| GRB170405A | ||
| GRB170409A | ||
| GRB170808B | ||
| GRB170906A | ||
| GRB171102A | ||
| GRB171124A | ||
| GRB171210A | ||
| GRB180210A | ||
| GRB180526A | ||
| GRB180703A |
| GRB | |||
|---|---|---|---|
| GRB080916C | |||
| GRB090323 | |||
| GRB090328 | |||
| GRB090510 | |||
| GRB090902B | |||
| GRB090926A | |||
| GRB091003 | |||
| GRB100414A | |||
| GRB110731A | |||
| GRB130327B | |||
| GRB130427A | |||
| GRB130504C | |||
| GRB131108A | |||
| GRB150627A | |||
| GRB160509A | |||
| GRB160816A | |||
| GRB170115B | |||
| GRB170214A | |||
| GRB171010A | |||
| GRB171120A | |||
| GRB180720B |
| No Energy Injection () | ||||||||
|---|---|---|---|---|---|---|---|---|
| Cooling | Range | CR: | CR: | GRBs | Occurrence Rate | Figure | ||
| Slow | 22 | 25.6% | (2a) | |||||
| Slow | 13 | 15.1% | (2d) | |||||
| Slow | 10 | 11.6% | (2g) | |||||
| Slow | 6 | 7.0% | (2j) | |||||
| Slow | 4 | 4.7% | (2m) | |||||
| Fast | 2 | 2.3% | (2b) | |||||
| Fast | 2 | 2.3% | (2e) | |||||
| Fast | 2 | 2.3% | (2h) | |||||
| Fast | 2 | 2.3% | (2k) | |||||
| Fast | 2 | 2.3% | (2n) | |||||
| Slow/Fast | max{} | 32 | 37.2% | (2c) | ||||
| Slow/Fast | max{} | 32 | 37.2% | (2f) | ||||
| Slow/Fast | max{} | 32 | 37.2% | (2i) | ||||
| Slow/Fast | max{} | 32 | 37.2% | (2l) | ||||
| Slow/Fast | max{} | 31 | 36% | (2o) | ||||
| Energy Injection () | ||||||||
| Cooling | Range | CR: | GRBs | Occurrence Rate | Figure | |||
| Slow | 16 | 18.6% | (3b) | |||||
| Slow | 30 | 34.9% | (3e) | |||||
| Slow | 40 | 46.5% | (3h) | |||||
| Slow | 30 | 34.9% | (3k) | |||||
| Slow | 15 | 17.4% | (3n) | |||||
| Fast | 0 | 0% | (-) | |||||
| Fast | 0 | 0% | (-) | |||||
| Fast | 0 | 0% | (-) | |||||
| Fast | 0 | 0% | (-) | |||||
| Fast | 0 | 0% | (-) | |||||
| Slow/Fast | max{} | 16 | 18.6% | (3c) | ||||
| Slow/Fast | max{} | 16 | 18.6% | (3f) | ||||
| Slow/Fast | max{} | 16 | 18.6% | (3i) | ||||
| Slow/Fast | max{} | 16 | 18.6% | (3l) | ||||
| Slow/Fast | max{} | 16 | 18.6% | (3o) | ||||
| GRB ID | ISM/Wind | k Values | Match | ||||||
|---|---|---|---|---|---|---|---|---|---|
| GRB090626A | ISM | No | |||||||
| GRB091031A | ISM | No | |||||||
| GRB100116A | None | None | None | None | Yes | ||||
| GRB100511A | None | None | None | None | Yes | ||||
| GRB110625A | None | None | None | None | Yes | ||||
| GRB120526A | None | None | None | None | Yes | ||||
| GRB120624B | None | None | None | None | Yes | ||||
| GRB120709A | None | None | None | None | Yes | ||||
| GRB120711A | ISM | Yes | |||||||
| GRB120911B | ISM/Wind | None | None | No | |||||
| GRB130325A | ISM/Wind | Yes | |||||||
| GRB130502B | ISM | Yes | |||||||
| GRB130518A | None | None | None | None | Yes | ||||
| GRB130606B | ISM | None | None | No | |||||
| GRB130821A | ISM/Wind | None | None | No | |||||
| GRB131014A | ISM/Wind | Yes | |||||||
| GRB131029A | ISM/Wind | None | None | No | |||||
| GRB131231A | ISM | ; | Yes | ||||||
| GRB140206B | None | None | None | None | Yes | ||||
| GRB140523A | ISM/Wind | Yes | |||||||
| GRB140810A | ISM | No | |||||||
| GRB141028A | ISM/Wind | None | None | No | |||||
| GRB141207A | Wind | No | |||||||
| GRB141222A | ISM/Wind | ; | Yes | ||||||
| GRB150523A | ISM | No | |||||||
| GRB150902A | ISM/Wind | None | None | No | |||||
| GRB160325A | None | None | None | None | Yes | ||||
| GRB160521B | Wind | Yes | |||||||
| GRB160623A | ISM | None | None | No | |||||
| GRB160625B | Wind | Yes | |||||||
| GRB160821A | ISM | None | None | No | |||||
| GRB160905A | ISM | ; | Yes | ||||||
| GRB170405A | ISM/Wind | None | None | No | |||||
| GRB170808B | ISM/Wind | Yes | |||||||
| GRB170906A | ISM/Wind | None | None | No | |||||
| GRB180210A | ISM | No | |||||||
| GRB180703A | ISM/Wind | None | None | No | |||||
| GRB180720B | ISM | No |
| ISM | Wind | ||||||
|---|---|---|---|---|---|---|---|
| GRB | Wavelength | max{} | max{} | ||||
| GRB090510 | , O, X | … | … | O | … | … | O |
| GRB100728A | , X | … | … | … | |||
| GRB110731A | , X | … | … | … | … | ||
| GRB120711A | , O | … | … | … | … | … | |
| GRB150314A | , X | … | … | … | … | … | … |
| GRB160509A | , R | … | … | … | … | ||
| GRB170405A | , X | … | … | … | … | … | … |
| GRB180720B | , X | … | … | … | … | … | … |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dainotti, M.; Levine, D.; Fraija, N.; Warren, D.; Veres, P.; Sourav, S. The Closure Relations in High-Energy Gamma-ray Bursts Detected by Fermi-LAT. Galaxies 2023, 11, 25. https://doi.org/10.3390/galaxies11010025
Dainotti M, Levine D, Fraija N, Warren D, Veres P, Sourav S. The Closure Relations in High-Energy Gamma-ray Bursts Detected by Fermi-LAT. Galaxies. 2023; 11(1):25. https://doi.org/10.3390/galaxies11010025
Chicago/Turabian StyleDainotti, Maria, Delina Levine, Nissim Fraija, Donald Warren, Peter Veres, and Shashwat Sourav. 2023. "The Closure Relations in High-Energy Gamma-ray Bursts Detected by Fermi-LAT" Galaxies 11, no. 1: 25. https://doi.org/10.3390/galaxies11010025
APA StyleDainotti, M., Levine, D., Fraija, N., Warren, D., Veres, P., & Sourav, S. (2023). The Closure Relations in High-Energy Gamma-ray Bursts Detected by Fermi-LAT. Galaxies, 11(1), 25. https://doi.org/10.3390/galaxies11010025







