Holographic Quantum-Foam Blurring Is Consistent with Observations of Gamma-Ray Burst GRB221009A
Abstract
1. Introduction
2. Method of Finding Quantum-Foam Blurring
2.1. Maximal Limit and Average Effect Redward of the Horizon-Crossing Wavelength
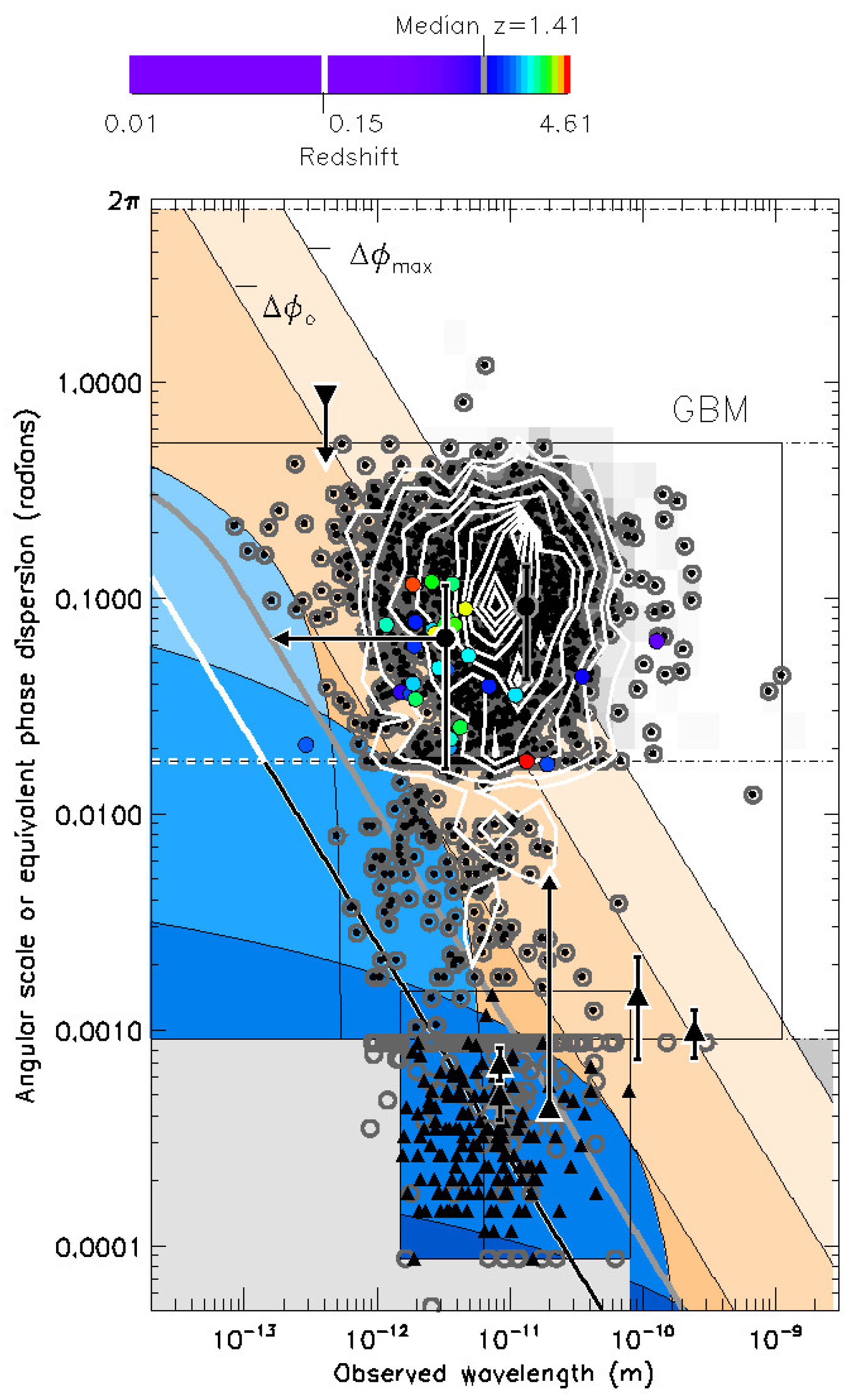
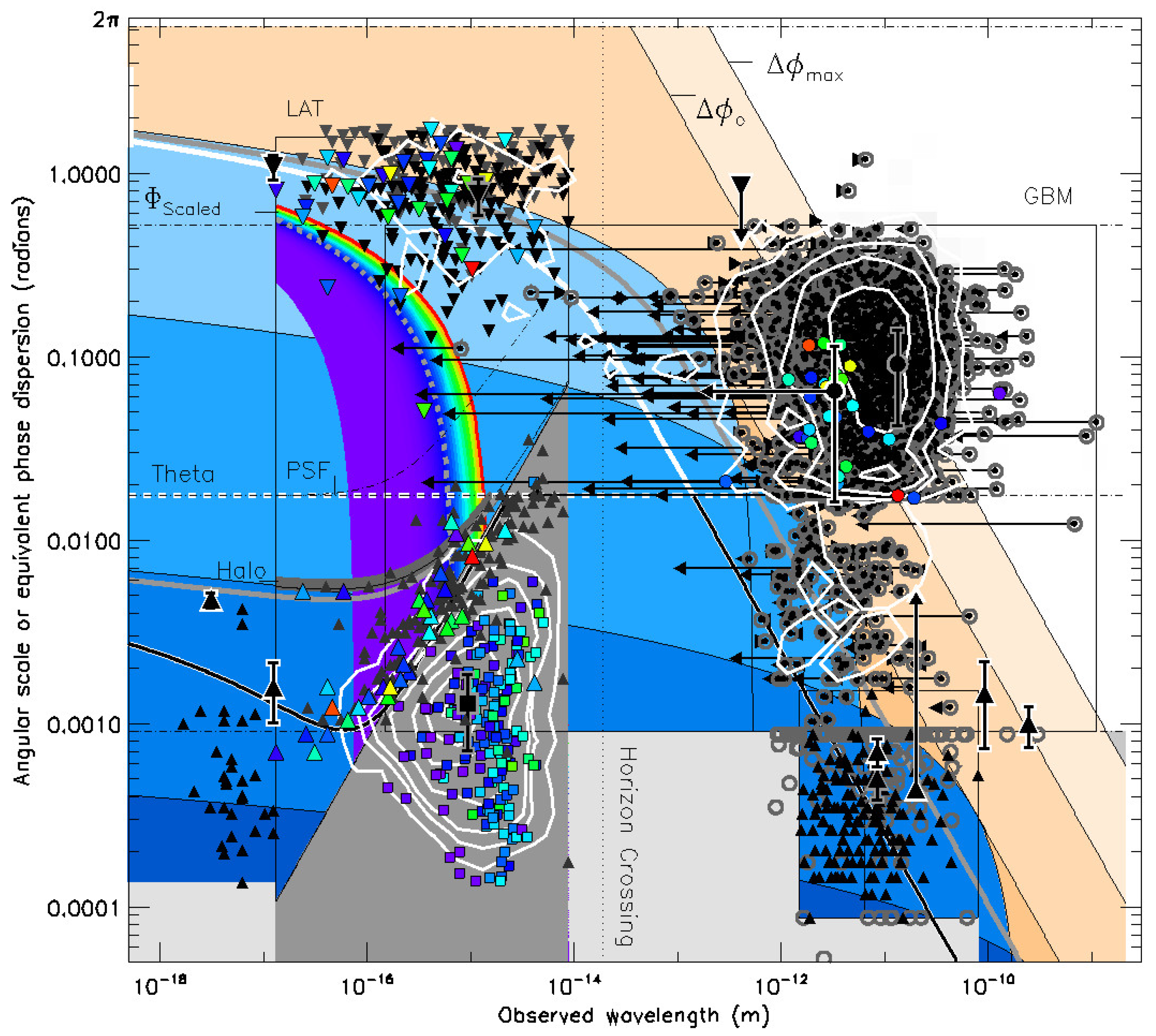
2.2. Combined Effect, Scaled between Telescope Field of View and Instrumental Angular Resolution
3. Analysis and Discussion
3.1. Alpha Lower Limit by Comparison with Peak-Energy X-rays
3.2. Alpha Upper Range by Fit to Mean-Energy Gamma-rays
4. Summary and Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. The In-Flight-Measured Fermi LAT Point-Spread Function
References
- Wheeler, J.A. On the Nature of Quantum Geometrodynamics. Ann. Phys. 1957, 2, 604–614. [Google Scholar] [CrossRef]
- Carlip, S. Spacetime foam: A review. Rep. Prog. Phys. 2023, 86, 066001. [Google Scholar] [CrossRef] [PubMed]
- Lieu, R.; Hillman, L.W. The Phase Coherence of Light from Extragalactic Sources—Direct Evidence Against First Order Planck Scale Fluctuations in Time and Space. Astrophys. J. 2003, 585, L77–L80. [Google Scholar] [CrossRef]
- Ng, Y.J.; Christiansen, W.A.; van Dam, H. Probing Planck-scale Physics with Extragalacic Sources? Astrophys. J. 2003, 591, L87–L90. [Google Scholar] [CrossRef]
- Ragazzoni, R.; Turatto, M.; Gaessler, W. The Lack of Observational Evidence for the Quantum Structure of Spacetime at Planck Scales. Astrophys. J. 2003, 587, L1–L4. [Google Scholar] [CrossRef]
- Steinbring, E. Are High-Redshift Quasars Blurry? Astrophys. J. 2007, 655, 714–717. [Google Scholar] [CrossRef][Green Version]
- Christiansen, W.A.; Ng, Y.J.; Floyd, D.J.E.; Perlman, E.S. Limits on spacetime foam. Phys. Rev. D 2011, 83, 84003. [Google Scholar] [CrossRef]
- Perlman, E.S.; Ng, Y.J.; Floyd, D.J.E.; Christiansen, W.A. Using Observations of Distant Quasars to Constrain Quantum Gravity. Astron. Astrophys. 2011, 535, L9. [Google Scholar] [CrossRef]
- Tamburini, F.; Cuofano, C.; Della Valle, M.; Gilmozzi, R. No quantum gravity signature from the farthest quasars. Astron. Astrophys. 2011, 533, A71–A75. [Google Scholar] [CrossRef]
- Cooke, R.; Welsh, L.; Fumagalli, M.; Pettini, M. A limit on Planck-scale froth with ESPRESSO. Mon. Not. R. Astron. Soc. 2020, 494, 4884–4890. [Google Scholar] [CrossRef]
- Amelino-Camelia, G.; Ellis, J.; Mavromatos, N.E.; Nanopoulos, D.V.; Sarkar, S. Tests of quantum gravity from observations of γ-ray bursts. Nature 1998, 393, 763–765. [Google Scholar] [CrossRef]
- Liu, Z.-K.; Zhang, B.-B.; Meng, Y.-Z. Spectral Lag Transition of 32 Fermi Gamma-Ray Bursts and Their Application on Constraining Lorentz Invariance Violation. Astrophys. J. 2022, 935, 79. [Google Scholar] [CrossRef]
- Perlman, E.S.; Rappaport, S.A.; Christiansen, W.A.; Ng, Y.J.; DeVore, J.; Pooley, D. New Constraints on Quantum Gravity from X-Ray and Gamma-Ray Observations. Astrophys. J. 2015, 805, 10–20. [Google Scholar] [CrossRef]
- Steinbring, E. Detectability of Planck-Scale-Induced Blurring with Gamma-Ray Bursts. Astrophys. J. 2015, 802, 38–43. [Google Scholar] [CrossRef]
- Ng, Y.J.; Perlman, E. Probing Spacetime Foam with Extragalactic Sources of High-Energy Photons. Universe 2022, 8, 382. [Google Scholar] [CrossRef]
- Steinbring, E. Limits to Seeing High-Redshift Galaxies Due to Planck-Scale-Induced Blurring. Int. Astron. Union Conf. Ser. 2016, 319, 54. [Google Scholar] [CrossRef]
- Chen, W.; Buckley, J.H.; Ferrer, F. Search for GeV γ-Ray Pair Halos Around Low Redshift Blazars. Phys. Rev. Lett. 2015, 115, 211103. [Google Scholar] [CrossRef]
- Veres, P.; Burns, E.; Bissaldi, E.; Lesage, S.; Roberts, O. GRB 221009A: Fermi GBM detection of an extraordinarily bright GRB. GRB Coord. Netw. Circ. Serv. 2022, 32636, 1. [Google Scholar]
- Bissaldi, E.; Omodei, N.; Kerr, M. GRB 221009A or Swift J1913.1+1946: Fermi-LAT detection. GRB Coord. Netw. Circ. Serv. 2022, 32637, 1. [Google Scholar]
- Ajello, M.; Atwood, W.B.; Axelsson, M.; Bagagli, R.; Bagni, M.; Baldini, L.; Bastieri, D.; Bellardi, F.; Bellazzini, R.; Bissaldi, E.; et al. Fermi Large Area Telescope Performance after 10 Years of Operation. Astrophys. J. Suppl. Ser. 2021, 256, 12. [Google Scholar] [CrossRef]
- Xia, Z.-Q.; Wang, Y.; Yuan, Q.; Fan, Y.-Z. GRB 221009A: A 397.7 GeV photon observed by Fermi-LAT at 0.4 day after the GBM trigger. GRB Coord. Netw. Circ. Serv. 2022, 32748, 1. [Google Scholar]
- Dzhappuev, D.D.; Afashokov, Y.Z.; Dzaparova, I.M.; Dzhatdoev, T.A.; Gorbacheva, A.; Karpikov, I.S.; Khadzhiev, M.M.; Klimenko, N.F.; Kudzhaev, A.U.; Kurenya, A.N.; et al. Swift J1913.1+1946/GRB 221009A: Detection of a 250-TeV photon-like air shower by Carpet-2. Astron. Telegr. 2023, 15669, 1. [Google Scholar]
- Dichiara, S.; Gropp, J.D.; Kennea, J.A.; Kuin, N.P.M.; Lien, A.Y.; Marshall, F.E.; Tohuvavohu, A.; Williams, M.A. Swift J1913.1+1946 a new bright hard X-ray and optical transient. Astron. Telegr. 2023, 15650, 1. [Google Scholar]
- Huang, Y.; Shicong, H.; Chen, S.; Zha, M.; Liu, C.; Yao, Z.; Cao, Z. LHAASO observed GRB 221009A with more than 5000 VHE photons up to around 18 TeV. GRB Coord. Netw. Circ. Serv. 2022, 32677, 1. [Google Scholar]
- Fredericks, D.; Svinkin, D.; Lysenko, A.L.; Molkov, S.; Tsvetkova, A.; Ulanov, M.; Ridnaia, A.; Lutovinov, A.A.; Lapshov, I.; Tkachenko, A.; et al. Properties of the Extremely Energetic GRB 221009A from Konus-WIND and SRG/ART-XC Observations. Astrophys. J. 2023, 949, L7. [Google Scholar] [CrossRef]
- Iwikiri, W.; Jaisawal, G.K.; Younes, G.; Wadiasingh, Z.; Guillot, S.; Gendreau, K.C.; Arzoumanian, Z.; Ferrara, E.C.; Mihara, T.; Pasham, D.; et al. GRB 221009A: NICER follow-up observations. Astron. Telegr. 2022, 15664, 1. [Google Scholar]
- Negoro, H.; Nakajima, M.; Kobayashi, K.; Tanaka, M.; Soejima, Y.; Mihara, T.; Kawamuro, T.; Yamada, S.; Tamagawa, T.; Matsuoka, M.; et al. MAXI/GSC detection of the new X-ray transient Swift J1913.1+1946. Astron. Telegr. 2022, 15651, 1. [Google Scholar]
- Negro, M.; Manfreda, A.; Omodei, N.; Muleriet, F. GRB 221009A: IXPE preliminary upper limits to X-ray polarization. Astron. Telegr. 2022, 15678, 1. [Google Scholar]
- Levan, A.J.; Barclay, T.; Bhirombhakdi, K.; Burns, E.; Cenko, S.B.; Chrimes, A.A.; D’Avanzo, P.; D’Elia, V.; Della Valle, M.; de Ugarte Postigo, A.; et al. GRB 221009A: Hubble Space Telescope observations. GRB Coord. Netw. Circ. Serv. 2022, 32921, 1. [Google Scholar]
- Levan, A.J.; Barclay, T.; Burns, B.; Cenko, S.B.; Chrimes, A.A.; D’Avanzo, P.; D’Elia, V.; Della Valle, M.; de Ugarte Postigo, A.; Fong, W.; et al. GRB 221009A: James Webb Space Telescope Observations. GRB Coord. Netw. Circ. Serv. 2022, 32821, 1. [Google Scholar]
- de Ugarte Postigo, A.; Izzo, L.; Pugliese, G.; Xu, D.; Schneider, B.; Fynbo, J.P.U.; Tanvir, N.R.; Malesani, D.B.; Saccardi, A.; Kann, D.A.; et al. GRB 221009A: Redshift from X-shooter/VLT. GRB Coord. Netw. Circ. Serv. 2023, 32648, 1. [Google Scholar]
- Ackermann, M.; Ajello, M.; Allafort, A.; Asano, K.; Atwood, W.B.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastier, D.; Bechtol, K.; et al. Determination of the Point-Spread Function for the Fermi Large Area Telescope From On-Orbit Data and Limits on Pair Halos of Active Galactic Nuclei. Astrophys. J. 2013, 765, 54. [Google Scholar] [CrossRef]
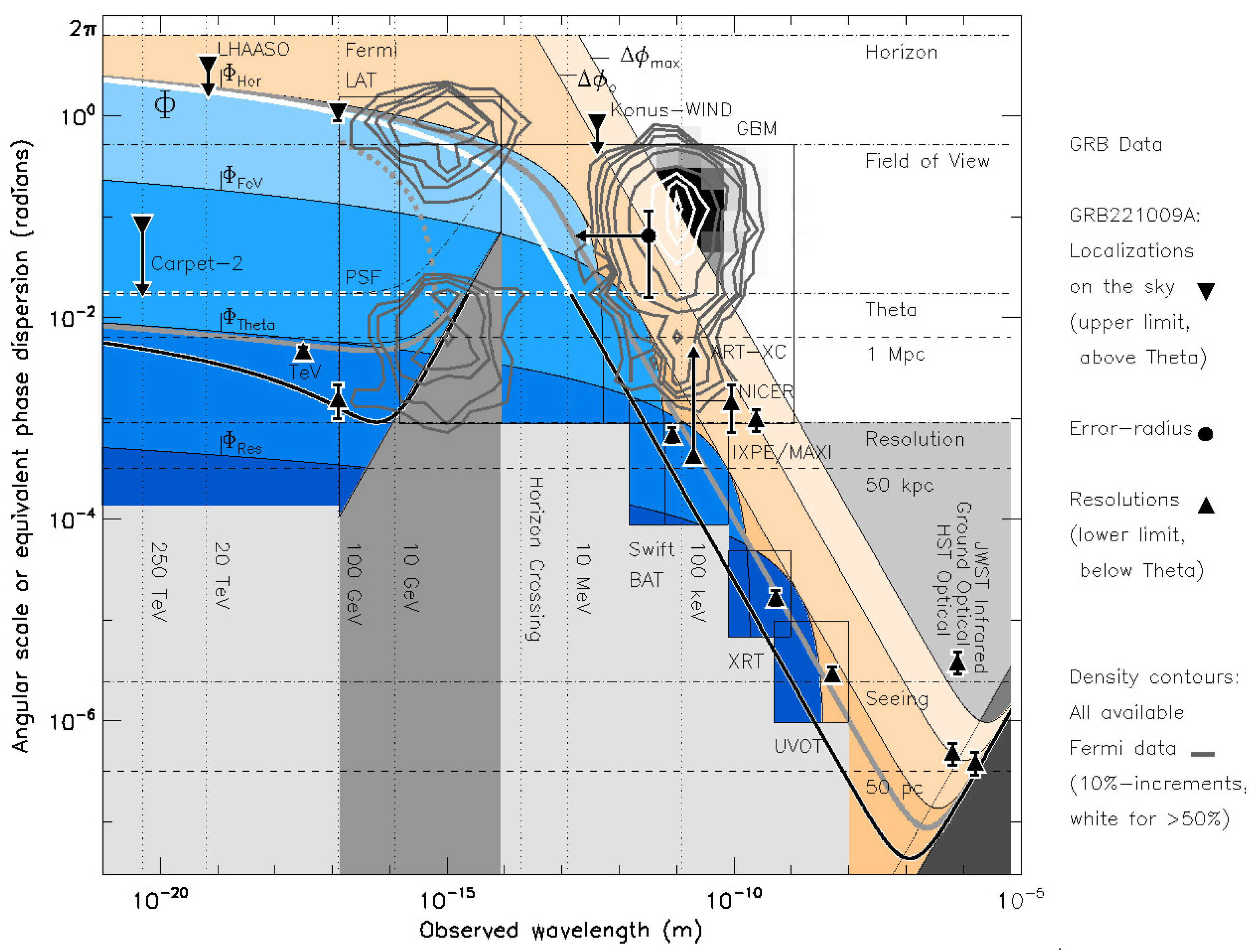
| Telescope or Instrument | Peak E or | Angle |
|---|---|---|
| Horizon | - | |
| Carpet-2 | 251 TeV | – |
| LHAASO VHE | 18 TeV | ≤ |
| Fermi LAT (roll angle) | 99.3 GeV | |
| Field of View | - | |
| Konus-WIND | 3.04 MeV | ≤ |
| Fermi GBM | 375 keV | |
| Theta | - | |
| Fermi LAT (extreme) | 397.7 GeV | |
| Fermi LAT (resolution) | 99.3 GeV | |
| Swift BAT | 146 keV | 2.4 |
| ART-XC | 4–120 keV | 36 |
| NICER/MAXI | 13.5 keV | 2.5–10 |
| IXPE | 5 keV | |
| Resolution | - | 1 |
| Swift XRT | 2.3 keV | 3.5 |
| Swift UVOT | 5.25 nm | 0.61 |
| Seeing | - | – |
| Ground-based optical | 800 nm | 0.80″ |
| HST | 650 nm | 0.10″ |
| JWST | 0.08″ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Steinbring, E. Holographic Quantum-Foam Blurring Is Consistent with Observations of Gamma-Ray Burst GRB221009A. Galaxies 2023, 11, 115. https://doi.org/10.3390/galaxies11060115
Steinbring E. Holographic Quantum-Foam Blurring Is Consistent with Observations of Gamma-Ray Burst GRB221009A. Galaxies. 2023; 11(6):115. https://doi.org/10.3390/galaxies11060115
Chicago/Turabian StyleSteinbring, Eric. 2023. "Holographic Quantum-Foam Blurring Is Consistent with Observations of Gamma-Ray Burst GRB221009A" Galaxies 11, no. 6: 115. https://doi.org/10.3390/galaxies11060115
APA StyleSteinbring, E. (2023). Holographic Quantum-Foam Blurring Is Consistent with Observations of Gamma-Ray Burst GRB221009A. Galaxies, 11(6), 115. https://doi.org/10.3390/galaxies11060115






