Fundamental Properties of Late-Type Stars in Eclipsing Binaries
Abstract
1. Introduction
2. Sample of Low-Mass Systems
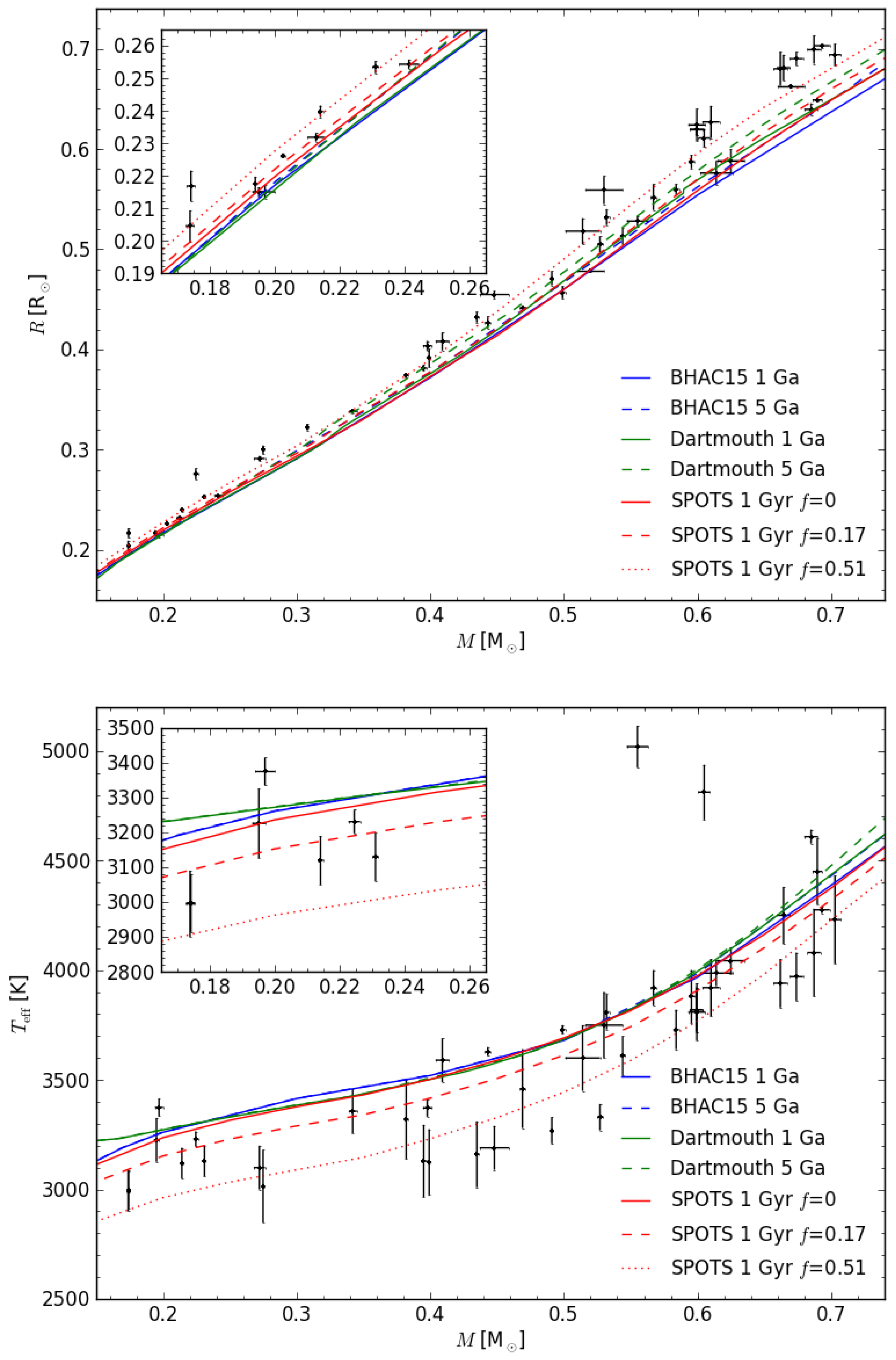
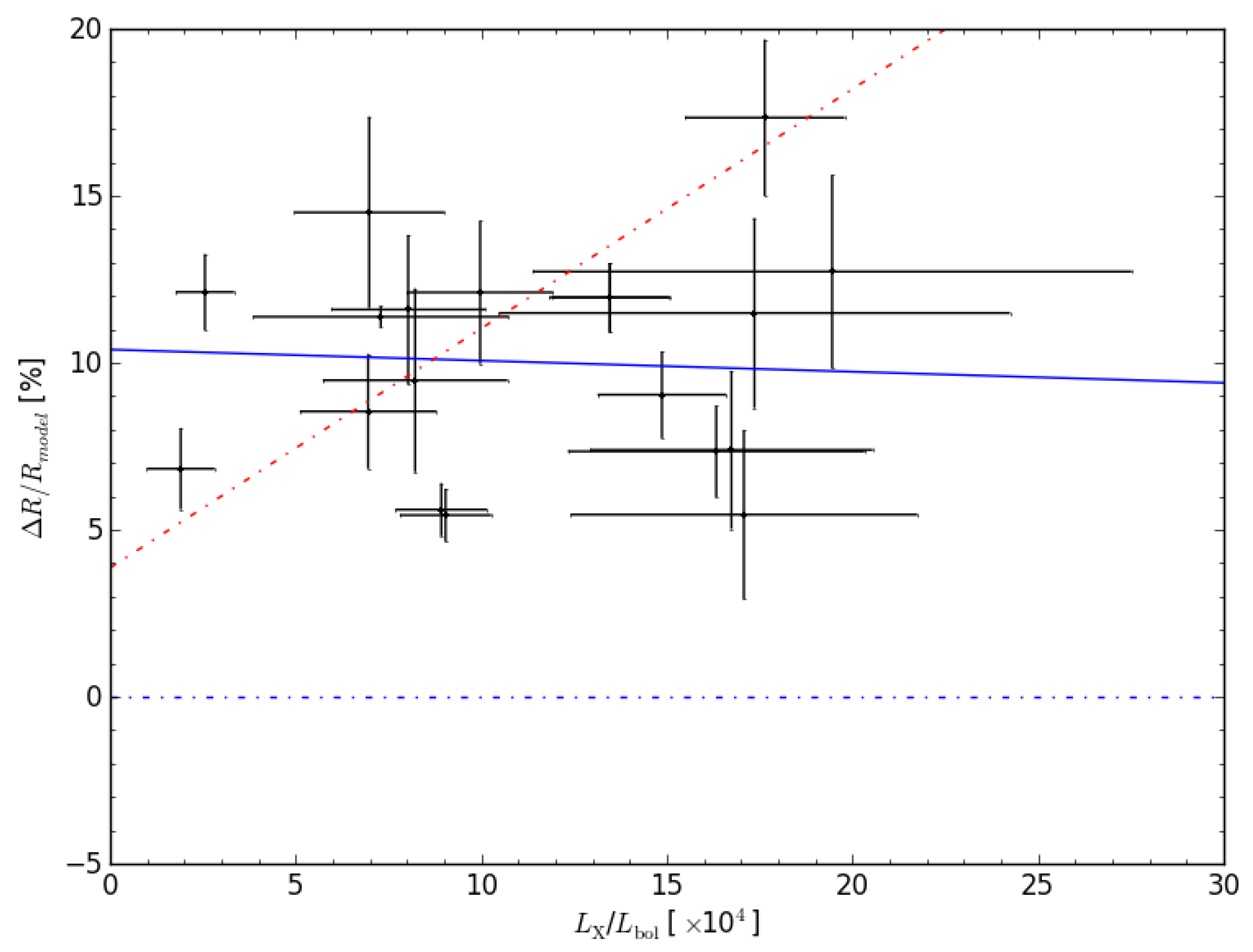
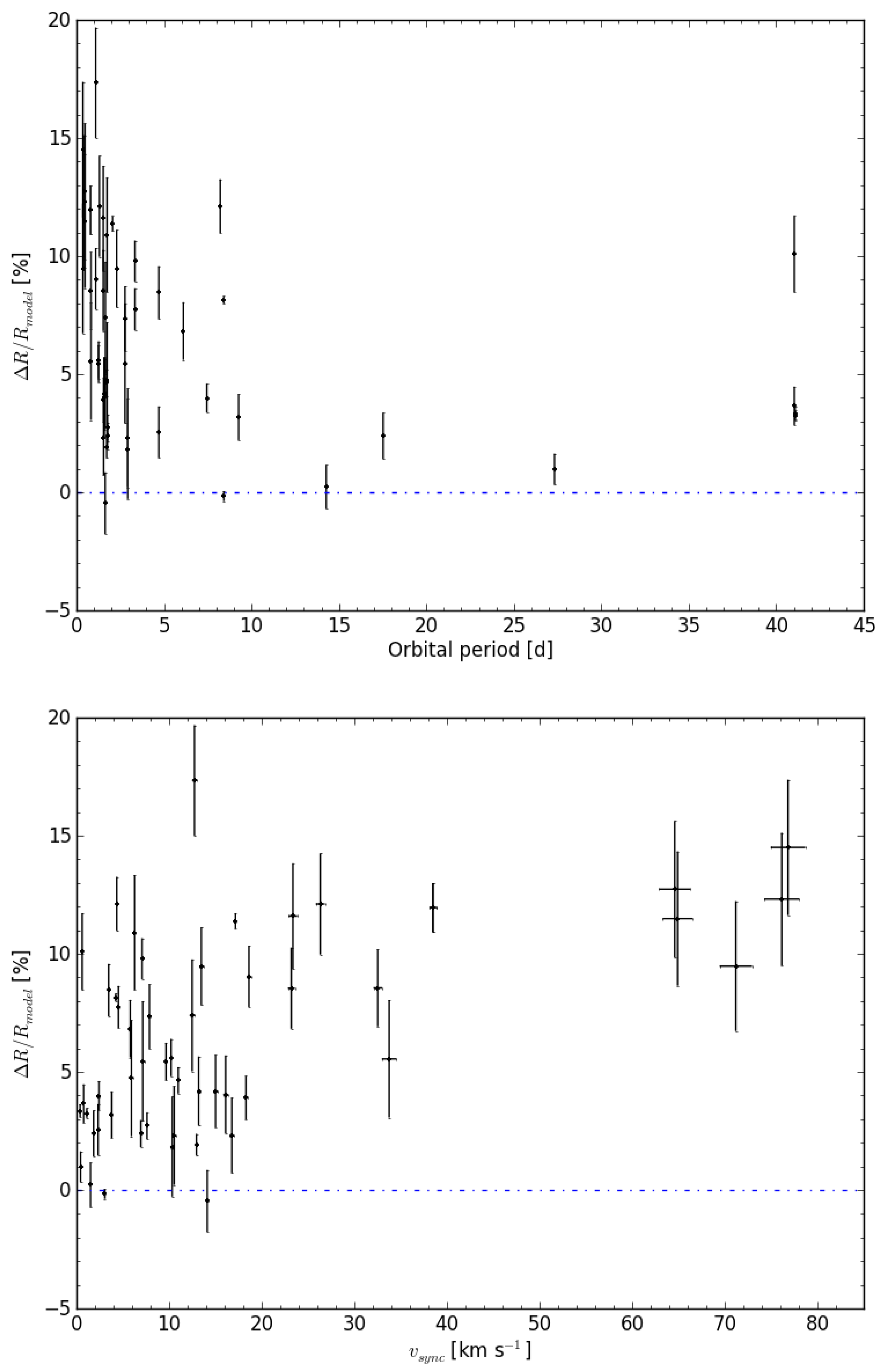
3. Models vs. Observations
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Marcy, G.W.; Butler, R.P.; Vogt, S.S.; Fischer, D.; Lissauer, J.J. A Planetary Companion to a Nearby M4 Dwarf, Gliese 876. Astrophys. J. 1998, 505, L147–L149. [Google Scholar] [CrossRef]
- Bonfils, X.; Lo Curto, G.; Correia, A.C.M.; Laskar, J.; Udry, S.; Delfosse, X.; Forveille, T.; Astudillo-Defru, N.; Benz, W.; Bouchy, F.; et al. The HARPS search for southern extra-solar planets. XXXIV. A planetary system around the nearby M dwarf GJ 163, with a super-Earth possibly in the habitable zone. Astron. Astrophys. 2013, 556, A110. [Google Scholar] [CrossRef]
- Quirrenbach, A.; Amado, P.J.; Ribas, I.; Reiners, A.; Caballero, J.A.; Seifert, W.; Aceituno, J.; Azzaro, M.; Baroch, D.; Barrado, D.; et al. CARMENES: High-resolution spectra and precise radial velocities in the red and infrared. In Proceedings of the Ground-based and Airborne Instrumentation for Astronomy VII, SPIE, Austin, TX, USA, 10–15 June 2018; Evans, C.J., Simard, L., Takami, H., Eds.; Volume 10702, p. 107020W. [Google Scholar] [CrossRef]
- Andersen, J. Accurate masses and radii of normal stars. Astron. Astrophys. Rev. 1991, 3, 91–126. [Google Scholar] [CrossRef]
- Torres, G.; Andersen, J.; Giménez, A. Accurate masses and radii of normal stars: Modern results and applications. Astron. Astrophys. Rev. 2010, 18, 67–126. [Google Scholar] [CrossRef]
- Serenelli, A.; Weiss, A.; Aerts, C.; Angelou, G.C.; Baroch, D.; Bastian, N.; Beck, P.G.; Bergemann, M.; Bestenlehner, J.M.; Czekala, I.; et al. Weighing stars from birth to death: Mass determination methods across the HRD. Astron. Astrophys. Rev. 2021, 29, 4. [Google Scholar] [CrossRef]
- Schweitzer, A.; Passegger, V.M.; Cifuentes, C.; Béjar, V.J.S.; Cortés-Contreras, M.; Caballero, J.A.; del Burgo, C.; Czesla, S.; Kürster, M.; Montes, D.; et al. The CARMENES search for exoplanets around M dwarfs. Different roads to radii and masses of the target stars. Astron. Astrophys. 2019, 625, A68. [Google Scholar] [CrossRef]
- Mann, A.W.; Dupuy, T.; Kraus, A.L.; Gaidos, E.; Ansdell, M.; Ireland, M.; Rizzuto, A.C.; Hung, C.L.; Dittmann, J.; Factor, S.; et al. How to Constrain Your M Dwarf. II. The Mass-Luminosity-Metallicity Relation from 0.075 to 0.70 Solar Masses. Astrophys. J. 2019, 871, 63. [Google Scholar] [CrossRef]
- Popper, D.M.; Lacy, C.H.; Frueh, M.L.; Turner, A.E. Properties of main-sequence eclipsing binaries: Into the G stars with HS Aurigae, FL Lyrae and EW Orionis. Astron. J. 1986, 91, 383–404. [Google Scholar] [CrossRef]
- Torres, G.; Ribas, I. Absolute Dimensions of the M-Type Eclipsing Binary YY Geminorum (Castor C): A Challenge to Evolutionary Models in the Lower Main Sequence. Astrophys. J. 2002, 567, 1140–1165. [Google Scholar] [CrossRef]
- Ribas, I. The 0.4-Msun eclipsing binary CU Cancri. Absolute dimensions, comparison with evolutionary models and possible evidence for a circumstellar dust disk. Astron. Astrophys. 2003, 398, 239–251. [Google Scholar] [CrossRef]
- Ribas, I. Masses and Radii of Low-Mass Stars: Theory Versus Observations. Astrophys. Space Sci. 2006, 304, 89–92. [Google Scholar] [CrossRef]
- López-Morales, M.; Ribas, I. GU Bootis: A New 0.6 Msolar Detached Eclipsing Binary. Astrophys. J. 2005, 631, 1120–1133. [Google Scholar] [CrossRef]
- López-Morales, M. On the Correlation between the Magnetic Activity Levels, Metallicities, and Radii of Low-Mass Stars. Astrophys. J. 2007, 660, 732–739. [Google Scholar] [CrossRef]
- Mazeh, T. Observational Evidence for Tidal Interaction in Close Binary Systems. EAS Publ. Ser. 2008, 29, 1–65. [Google Scholar] [CrossRef]
- Mullan, D.J.; MacDonald, J. Are Magnetically Active Low-Mass M Dwarfs Completely Convective? Astrophys. J. 2001, 559, 353–371. [Google Scholar] [CrossRef]
- Chabrier, G.; Gallardo, J.; Baraffe, I. Evolution of low-mass star and brown dwarf eclipsing binaries. Astron. Astrophys. 2007, 472, L17–L20. [Google Scholar] [CrossRef]
- Feiden, G.A.; Chaboyer, B. Reevaluating the Mass-Radius Relation for Low-mass, Main-sequence Stars. Astrophys. J. 2012, 757, 42. [Google Scholar] [CrossRef]
- Feiden, G.A.; Chaboyer, B. Magnetic Inhibition of Convection and the Fundamental Properties of Low-mass Stars. I. Stars with a Radiative Core. Astrophys. J. 2013, 779, 183. [Google Scholar] [CrossRef]
- Feiden, G.A.; Chaboyer, B. Magnetic Inhibition of Convection and the Fundamental Properties of Low-mass Stars. II. Fully Convective Main-sequence Stars. Astrophys. J. 2014, 789, 53. [Google Scholar] [CrossRef]
- Somers, G.; Cao, L.; Pinsonneault, M.H. The SPOTS Models: A Grid of Theoretical Stellar Evolution Tracks and Isochrones for Testing the Effects of Starspots on Structure and Colors. Astrophys. J. 2020, 891, 29. [Google Scholar] [CrossRef]
- Morales, J.C.; Gallardo, J.; Ribas, I.; Jordi, C.; Baraffe, I.; Chabrier, G. The Effect of Magnetic Activity on Low-Mass Stars in Eclipsing Binaries. Astrophys. J. 2010, 718, 502–512. [Google Scholar] [CrossRef]
- Windmiller, G.; Orosz, J.A.; Etzel, P.B. The Effect of Starspots on Accurate Radius Determination of the Low-Mass Double-Lined Eclipsing Binary Gu Boo. Astrophys. J. 2010, 712, 1003–1009. [Google Scholar] [CrossRef]
- Morales, J.C.; Ribas, I.; Jordi, C.; Torres, G.; Gallardo, J.; Guinan, E.F.; Charbonneau, D.; Wolf, M.; Latham, D.W.; Anglada-Escudé, G.; et al. Absolute Properties of the Low-Mass Eclipsing Binary CM Draconis. Astrophys. J. 2009, 691, 1400–1411. [Google Scholar] [CrossRef]
- Carter, J.A.; Fabrycky, D.C.; Ragozzine, D.; Holman, M.J.; Quinn, S.N.; Latham, D.W.; Buchhave, L.A.; Van Cleve, J.; Cochran, W.D.; Cote, M.T.; et al. KOI-126: A Triply Eclipsing Hierarchical Triple with Two Low-Mass Stars. Science 2011, 331, 562. [Google Scholar] [CrossRef]
- Doyle, L.R.; Carter, J.A.; Fabrycky, D.C.; Slawson, R.W.; Howell, S.B.; Winn, J.N.; Orosz, J.A.; Přsa, A.; Welsh, W.F.; Quinn, S.N.; et al. Kepler-16: A Transiting Circumbinary Planet. Science 2011, 333, 1602. [Google Scholar] [CrossRef]
- Welsh, W.F.; Orosz, J.A.; Short, D.R.; Cochran, W.D.; Endl, M.; Brugamyer, E.; Haghighipour, N.; Buchhave, L.A.; Doyle, L.R.; Fabrycky, D.C.; et al. Kepler 453 b—The 10th Kepler Transiting Circumbinary Planet. Astrophys. J. 2015, 809, 26. [Google Scholar] [CrossRef]
- Orosz, J.A.; Welsh, W.F.; Haghighipour, N.; Quarles, B.; Short, D.R.; Mills, S.M.; Satyal, S.; Torres, G.; Agol, E.; Fabrycky, D.C.; et al. Discovery of a Third Transiting Planet in the Kepler-47 Circumbinary System. Astron. J. 2019, 157, 174. [Google Scholar] [CrossRef]
- Claret, A.; Gimenez, A.; Cunha, N.C.S. Circularization and synchronization times in the main sequence of detached eclipsing binaries.I. Using the formalism by Tassoul. Astron. Astrophys. 1995, 299, 724. [Google Scholar]
- Claret, A.; Cunha, N.C.S. Circularization and synchronization times in Main-Sequence of detached eclipsing binaries II. Using the formalisms by Zahn. Astron. Astrophys. 1997, 318, 187–197. [Google Scholar]
- Barker, A.J. Tidal Dissipation Due to Inertial Waves Can Explain the Circularization Periods of Solar-type Binaries. Astrophys. J. 2022, 927, L36. [Google Scholar] [CrossRef]
- Maxted, P.F.L.; Miller, N.J.; Hoyer, S.; Adibekyan, V.; Sousa, S.G.; Billot, N.; Fortier, A.; Simon, A.E.; Collier Cameron, A.; Swayne, M.I.; et al. Fundamental effective temperature measurements for eclipsing binary stars—III. SPIRou near-infrared spectroscopy and CHEOPS photometry of the benchmark G0V star EBLM J0113+31. Mon. Not. R. Astron. Soc. 2022, 513, 6042–6057. [Google Scholar] [CrossRef]
- Hut, P.; Bahcall, J.N. Binary-single star scattering. I—Numerical experiments for equal masses. Astrophys. J. 1983, 268, 319–341. [Google Scholar] [CrossRef]
- Irwin, J.M.; Quinn, S.N.; Berta, Z.K.; Latham, D.W.; Torres, G.; Burke, C.J.; Charbonneau, D.; Dittmann, J.; Esquerdo, G.A.; Stefanik, R.P.; et al. LSPM J1112+7626: Detection of a 41 Day M-dwarf Eclipsing Binary from the MEarth Transit Survey. Astrophys. J. 2011, 742, 123. [Google Scholar] [CrossRef]
- Casewell, S.L.; Raynard, L.; Watson, C.A.; Gillen, E.; de Mooij, E.; Bayliss, D.; Bouchy, F.; Thompson, A.; Jackman, J.A.G.; Burleigh, M.R.; et al. A low-mass eclipsing binary within the fully convective zone from the Next Generation Transit Survey. Mon. Not. R. Astron. Soc. 2018, 481, 1897–1907. [Google Scholar] [CrossRef]
- Dittmann, J.A.; Irwin, J.M.; Charbonneau, D.; Berta-Thompson, Z.K.; Newton, E.R.; Latham, D.W.; Latham, C.A.; Esquerdo, G.; Berlind, P.; Calkins, M.L. Discovery and Precise Characterization by the MEarth Project of LP 661-13, an Eclipsing Binary Consisting of Two Fully Convective Low-mass Stars. Astrophys. J. 2017, 836, 124. [Google Scholar] [CrossRef]
- Smith, G.D.; Gillen, E.; Queloz, D.; Hillenbrand, L.A.; Acton, J.S.; Alves, D.R.; Anderson, D.R.; Bayliss, D.; Briegal, J.T.; Burleigh, M.R.; et al. NGTS clusters survey - III. A low-mass eclipsing binary in the Blanco 1 open cluster spanning the fully convective boundary. Mon. Not. R. Astron. Soc. 2021, 507, 5991–6011. [Google Scholar] [CrossRef]
- Hartman, J.D.; Quinn, S.N.; Bakos, G.Á.; Torres, G.; Kovács, G.; Latham, D.W.; Noyes, R.W.; Shporer, A.; Fulton, B.J.; Esquerdo, G.A.; et al. HAT-TR-318-007: A Double-lined M Dwarf Binary with Total Secondary Eclipses Discovered by HATNet and Observed by K2. Astron. J. 2018, 155, 114. [Google Scholar] [CrossRef]
- Kraus, A.L.; Tucker, R.A.; Thompson, M.I.; Craine, E.R.; Hillenbrand, L.A. The Mass-Radius(-Rotation?) Relation for Low-mass Stars. Astrophys. J. 2011, 728, 48. [Google Scholar] [CrossRef]
- López-Morales, M.; Shaw, J.S. Testing Low-Mass Stellar Models: Three New Detached Eclipsing Binaries below 0.75Msun. In Proceedings of the The Seventh Pacific Rim Conference on Stellar Astrophysics, Seoul, Korea, 1–5 November 2005; Astronomical Society of the Pacific Conference Series. Kang, Y.W., Lee, H.W., Leung, K.C., Cheng, K.S., Eds.; 2007; Voume 362, p. 26. [Google Scholar]
- Borkovits, T.; Sperauskas, J.; Tokovinin, A.; Latham, D.W.; Csányi, I.; Hajdu, T.; Molnár, L. The compact multiple system HIP 41431. Mon. Not. R. Astron. Soc. 2019, 487, 4631–4647. [Google Scholar] [CrossRef]
- Han, E.; Muirhead, P.S.; Swift, J.J. Magnetic Inflation and Stellar Mass. IV. Four Low-mass Kepler Eclipsing Binaries Consistent with Non-magnetic Stellar Evolutionary Models. Astron. J. 2019, 158, 111. [Google Scholar] [CrossRef]
- Hełminiak, K.G.; Konacki, M. Orbital and physical parameters of eclipsing binaries from the All-Sky Automated Survey catalogue. II. Two spotted M < 1 M_⊙ systems at different evolutionary stages. Astron. Astrophys. 2011, 526, A29. [Google Scholar] [CrossRef]
- Kaluzny, J.; Thompson, I.B.; Dotter, A.; Rozyczka, M.; Pych, W.; Rucinski, S.M.; Burley, G.S. The Clusters AgeS Experiment (CASE). VI. Analysis of Two Detached Eclipsing Binaries in the Globular Cluster M55. Acta Astron. 2014, 64, 11–26. [Google Scholar]
- Rozyczka, M.; Kaluzny, J.; Pietrukowicz, P.; Pych, W.; Mazur, B.; Catelan, M.; Thompson, I.B. A New Lower Main Sequence Eclipsing Binary with Detached Components. Acta Astron. 2009, 59, 385–401. [Google Scholar]
- Kaluzny, J.; Thompson, I.B.; Rozyczka, M.; Dotter, A.; Krzeminski, W.; Pych, W.; Rucinski, S.M.; Burley, G.S.; Shectman, S.A. The Cluster AgeS Experiment (CASE). V. Analysis of Three Eclipsing Binaries in the Globular Cluster M4. Astron. J 2013, 145, 43. [Google Scholar] [CrossRef][Green Version]
- Bass, G.; Orosz, J.A.; Welsh, W.F.; Windmiller, G.; Ames Gregg, T.; Fetherolf, T.; Wade, R.A.; Quinn, S.N. Kepler Studies of Low-mass Eclipsing Binaries. I. Parameters of the Long-period Binary KIC 6131659. Astrophys. J. 2012, 761, 157. [Google Scholar] [CrossRef]
- Hełminiak, K.G.; Moharana, A.; Pawar, T.; Ukita, N.; Sybilski, P.; Espinoza, N.; Kambe, E.; Ratajczak, M.; Jordán, A.; Maehara, H.; et al. Orbital and physical parameters of eclipsing binaries from the ASAS catalogue—XII. A sample of systems with K2 photometry. Mon. Not. R. Astron. Soc. 2021, 508, 5687–5708. [Google Scholar] [CrossRef]
- Hełminiak, K.G.; Tokovinin, A.; Niemczura, E.; Pawłaszek, R.; Yanagisawa, K.; Brahm, R.; Espinoza, N.; Ukita, N.; Kambe, E.; Ratajczak, M.; et al. Orbital and physical parameters of eclipsing binaries from the All-Sky Automated Survey catalogue. X. Three high-contrast systems with secondaries detected with IR spectroscopy. Astron. Astrophys. 2019, 622, A114. [Google Scholar] [CrossRef]
- Morales, J.C.; Torres, G.; Marschall, L.A.; Brehm, W. Absolute Dimensions of the G7+K7 Eclipsing Binary Star IM Virginis: Discrepancies with Stellar Evolution Models. Astrophys. J. 2009, 707, 671–685. [Google Scholar] [CrossRef]
- Torres, G.; Sandberg Lacy, C.H.; Pavlovski, K.; Feiden, G.A.; Sabby, J.A.; Bruntt, H.; Viggo Clausen, J. The G+M Eclipsing Binary V530 Orionis: A Stringent Test of Magnetic Stellar Evolution Models for Low-mass Stars. Astrophys. J. 2014, 797, 31. [Google Scholar] [CrossRef]
- MacDonald, J.; Mullan, D.J. Precision modelling of M dwarf stars: The magnetic components of CM Draconis. Mon. Not. R. Astron. Soc. 2012, 421, 3084–3101. [Google Scholar] [CrossRef]
- Baraffe, I.; Chabrier, G.; Allard, F.; Hauschildt, P.H. New Evolutionary Tracks for Very Low Mass Stars. Astrophys. J. Lett. 1995, 446, L35. [Google Scholar] [CrossRef]
- Somers, G.; Pinsonneault, M.H. Rotation, inflation, and lithium in the Pleiades. Mon. Not. R. Astron. Soc. 2015, 449, 4131–4146. [Google Scholar] [CrossRef]
- Berdyugina, S.V. Starspots: A Key to the Stellar Dynamo. Living Rev. Sol. Phys. 2005, 2, 8. [Google Scholar] [CrossRef]
- Baraffe, I.; Homeier, D.; Allard, F.; Chabrier, G. New evolutionary models for pre-main sequence and main sequence low-mass stars down to the hydrogen-burning limit. Astron. Astrophys. 2015, 577, A42. [Google Scholar] [CrossRef]
- Dotter, A.; Chaboyer, B.; Jevremović, D.; Kostov, V.; Baron, E.; Ferguson, J.W. The Dartmouth Stellar Evolution Database. Astrophys. J. 2008, 178, 89–101. [Google Scholar] [CrossRef]
- Torres, G.; Curtis, J.L.; Vanderburg, A.; Kraus, A.L.; Rizzuto, A. Eclipsing Binaries in the Open Cluster Ruprecht 147. I. EPIC 219394517. Astrophys. J. 2018, 866, 67. [Google Scholar] [CrossRef]
- Torres, G.; Vanderburg, A.; Curtis, J.L.; Ciardi, D.; Kraus, A.L.; Rizzuto, A.C.; Ireland, M.J.; Lund, M.B.; Christiansen, J.L.; Beichman, C.A. Eclipsing Binaries in the Open Cluster Ruprecht 147. II. Epic 219568666. Astrophys. J. 2019, 887, 109. [Google Scholar] [CrossRef]
- Torres, G.; Vanderburg, A.; Curtis, J.L.; Kraus, A.L.; Rizzuto, A.C.; Ireland, M.J. Eclipsing Binaries in the Open Cluster Ruprecht 147. III. The Triple System EPIC 219552514 at the Main-sequence Turnoff. Astrophys. J. 2020, 896, 162. [Google Scholar] [CrossRef]
- Torres, G.; Vanderburg, A.; Curtis, J.L.; Kraus, A.L.; Gaidos, E. Eclipsing Binaries in the Open Cluster Ruprecht 147. IV: The Active Triple System EPIC 219511354. Astrophys. J. 2021, 921, 133. [Google Scholar] [CrossRef]
- Torres, G.; Feiden, G.A.; Vanderburg, A.; Curtis, J.L. A Stringent Test of Magnetic Models of Stellar Evolution. Galaxies 2021, 10, 3. [Google Scholar] [CrossRef]
- Boller, T.; Freyberg, M.J.; Trümper, J.; Haberl, F.; Voges, W.; Nandra, K. Second ROSAT all-sky survey (2RXS) source catalogue. Astron. Astrophys. 2016, 588, A103. [Google Scholar] [CrossRef]
- Gaia Collaboration; Prusti, T.; de Bruijne, J.H.J.; Brown, A.G.A.; Vallenari, A.; Babusiaux, C.; Bailer-Jones, C.A.L.; Bastian, U.; Biermann, M.; Evans, D.W.; et al. The Gaia mission. Astron. Astrophys. 2016, 595, A1. [Google Scholar] [CrossRef]
- Babusiaux, C.; Fabricius, C.; Khanna, S.; Muraveva, T.; Reylé, C.; Spoto, F.; Vallenari, A.; Luri, X.; Arenou, F.; Alvarez, M.A.; et al. Gaia Data Release 3: Catalogue Validation. arXiv 2022, arXiv:2206.05989. [Google Scholar] [CrossRef]
- Schmitt, J.H.M.M.; Fleming, T.A.; Giampapa, M.S. The X-ray View of the Low-Mass Stars in the Solar Neighborhood. Astrophys. J. 1995, 450, 392. [Google Scholar] [CrossRef]
- Pizzolato, N.; Maggio, A.; Micela, G.; Sciortino, S.; Ventura, P. The stellar activity-rotation relationship revisited: Dependence of saturated and non-saturated X-ray emission regimes on stellar mass for late-type dwarfs. Astron. Astrophys. 2003, 397, 147–157. [Google Scholar] [CrossRef]
- Coughlin, J.L.; López-Morales, M.; Harrison, T.E.; Ule, N.; Hoffman, D.I. Low-mass Eclipsing Binaries in the Initial Kepler Data Release. Astron. J. 2011, 141, 78. [Google Scholar] [CrossRef]
- Gómez Maqueo Chew, Y.; Morales, J.C.; Faedi, F.; García-Melendo, E.; Hebb, L.; Rodler, F.; Deshpande, R.; Mahadevan, S.; McCormac, J.; Barnes, R.; et al. The EBLM project. II. A very hot, low-mass M dwarf in an eccentric and long-period, eclipsing binary system from the SuperWASP Survey. Astron. Astrophys. 2014, 572, A50. [Google Scholar] [CrossRef]
- Ricker, G.R.; Winn, J.N.; Vanderspek, R.; Latham, D.W.; Bakos, G.Á.; Bean, J.L.; Berta-Thompson, Z.K.; Brown, T.M.; Buchhave, L.; Butler, N.R.; et al. Transiting Exoplanet Survey Satellite (TESS). J. Astron. Telesc. Instrum. Syst. 2015, 1, 014003. [Google Scholar] [CrossRef]
- Benz, W.; Broeg, C.; Fortier, A.; Rando, N.; Beck, T.; Beck, M.; Queloz, D.; Ehrenreich, D.; Maxted, P.F.L.; Isaak, K.G.; et al. The CHEOPS mission. Exp. Astron. 2021, 51, 109–151. [Google Scholar] [CrossRef]
- Swayne, M.I.; Maxted, P.F.L.; Hodžić, V.K.; Triaud, A.H.M.J. The TESS light curve of the eccentric eclipsing binary 1SWASP J011351.29+314909.7—No evidence for a very hot M-dwarf companion. Mon. Not. R. Astron. Soc. 2020, 498, L15–L19. [Google Scholar] [CrossRef]
- Predehl, P.; Andritschke, R.; Arefiev, V.; Babyshkin, V.; Batanov, O.; Becker, W.; Böhringer, H.; Bogomolov, A.; Boller, T.; Borm, K.; et al. The eROSITA X-ray telescope on SRG. Astron. Astrophys. 2021, 647, A1. [Google Scholar] [CrossRef]
- Rauer, H.; Catala, C.; Aerts, C.; Appourchaux, T.; Benz, W.; Brandeker, A.; Christensen-Dalsgaard, J.; Deleuil, M.; Gizon, L.; Goupil, M.J.; et al. The PLATO 2.0 mission. Exp. Astron. 2014, 38, 249–330. [Google Scholar] [CrossRef]

| Name | Com. | P | M | R | [Fe/H] | Ref. | ||
|---|---|---|---|---|---|---|---|---|
| [d] | [M] | [R] | [K] | [km s] | [dex] | |||
| Eclipsing binary systems | ||||||||
| NGTS J052218.2-250710.4 | A | 1.7477 | 0.17391 ± 0.00126 | 0.2045 ± 0.0048 | 2995 ± 95 | 5.93 ± 0.13 | ⋯ | [35] |
| B | 0.17418 ± 0.00126 | 0.2168 ± 0.00475 | 2997 ± 84 | 6.29 ± 0.14 | ||||
| CM Dra | A | 1.2684 | 0.23102 ± 0.00089 | 0.2534 ± 0.0019 | 3130 ± 70 | 10.22 ± 0.08 | −0.3 | [5] |
| B | 0.2141 ± 0.0008 | 0.2398 ± 0.0018 | 3120 ± 70 | 9.67 ± 0.08 | ||||
| LP 661-13 | A | 4.7044 | 0.30795 ± 0.00084 | 0.3226 ± 0.0033 | ⋯ | 3.47 ± 0.04 | −0.07 ± 0.07 | [36] |
| B | 0.194 ± 0.00034 | 0.2174 ± 0.0023 | ⋯ | 2.338 ± 0.024 | ||||
| LSPMJ1112+7626 | A | 41.0324 | 0.3951 ± 0.0022 | 0.3815 ± 0.003 | 3130 ± 165 | 0.789 ± 0.006 | ⋯ | [34] |
| B | 0.2749 ± 0.0011 | 0.2999 ± 0.0044 | 3015 ± 166 | 0.620 ± 0.009 | ||||
| NGTS 0002-29 | A | 1.098 | 0.3978 ± 0.0033 | 0.4037 ± 0.0048 | 3372 ± 40 | 18.62 ± 0.22 | 0.04 ± 0.04 | [37] |
| B | 0.2245 ± 0.0018 | 0.2759 ± 0.0055 | 3231 ± 34 | 12.72 ± 0.24 | ||||
| CU Cnc | A | 2.7715 | 0.4349 ± 0.0012 | 0.4323 ± 0.0055 | 3160 ± 150 | 7.89 ± 0.10 | 0.0 | [5] |
| B | 0.3992 ± 0.0009 | 0.3916 ± 0.0094 | 3125 ± 150 | 7.15 ± 0.17 | ||||
| HAT-TR-318-007 | A | 3.344 | 0.448 ± 0.011 | 0.4548 ± 0.0036 | 3190 ± 100 | 7.07 ± 0.06 | 0.298 ± 0.08 | [38] |
| B | 0.2721 ± 0.0042 | 0.2913 ± 0.0024 | 3100 ± 100 | 4.53 ± 0.04 | ||||
| MG1-2056316 | A | 1.7228 | 0.469 ± 0.002 | 0.441 ± 0.002 | 3460 ± 180 | 12.95 ± 0.06 | ⋯ | [39] |
| B | 0.382 ± 0.001 | 0.374 ± 0.002 | 3320 ± 180 | 10.98 ± 0.06 | ||||
| MG1-646680 | A | 1.6375 | 0.499 ± 0.002 | 0.457 ± 0.006 | 3730 ± 20 | 14.12 ± 0.18 | ⋯ | [39] |
| B | 0.443 ± 0.002 | 0.427 ± 0.006 | 3630 ± 20 | 13.19 ± 0.18 | ||||
| MG1-78457 | A | 1.5862 | 0.527 ± 0.002 | 0.505 ± 0.008 | 3330 ± 60 | 16.11 ± 0.25 | −1.55 ± 0.05 | [39] |
| B | 0.491 ± 0.001 | 0.471 ± 0.007 | 3270 ± 60 | 15.02 ± 0.22 | ||||
| NSVS01031772 | A | 0.3681 | 0.53 ± 0.014 | 0.559 ± 0.014 | 3750 ± 150 | 76.8 ± 1.9 | ⋯ | [40] |
| B | 0.514 ± 0.013 | 0.518 ± 0.013 | 3600 ± 150 | 71.2 ± 1.8 | ||||
| MG1-116309 | A | 0.8271 | 0.567 ± 0.002 | 0.552 ± 0.013 | 3920 ± 80 | 33.76 ± 0.76 | −1.19 ± 0.04 | [39] |
| B | 0.532 ± 0.002 | 0.532 ± 0.008 | 3810 ± 80 | 32.54 ± 0.50 | ||||
| MG1-506664 | A | 1.5484 | 0.584 ± 0.002 | 0.56 ± 0.005 | 3730 ± 90 | 18.30 ± 0.16 | ⋯ | [39] |
| B | 0.544 ± 0.002 | 0.513 ± 0.008 | 3610 ± 90 | 16.76 ± 0.26 | ||||
| YY Gem | A&B | 0.8143 | 0.5992 ± 0.0047 | 0.6194 ± 0.0057 | 3820 ± 100 | 38.48 ± 0.36 | 0.0 | [5] |
| GU Boo | A | 0.4887 | 0.6101 ± 0.0064 | 0.627 ± 0.016 | 3920 ± 130 | 64.9 ± 1.7 | ⋯ | [5] |
| B | 0.5995 ± 0.0064 | 0.624 ± 0.016 | 3810 ± 130 | 64.6 ± 1.7 | ||||
| HIP 41431 | A | 2.9300 | 0.625 ± 0.010 | 0.588 ± 0.012 | 4043 ± 60 | 10.55 ± 0.22 | ⋯ | [41] |
| B | 0.614 ± 0.012 | 0.576 ± 0.012 | 3986 ± 60 | 10.33 ± 0.22 | ||||
| KIC 9821078 | A | 8.4294 | 0.67 ± 0.01 | 0.662 ± 0.001 | ⋯ | 4.233 ± 0.007 | ⋯ | [42] |
| B | 0.52 ± 0.01 | 0.478 ± 0.001 | ⋯ | 3.056 ± 0.007 | ||||
| BD-15 2429 | A | 1.5285 | 0.7029 ± 0.0045 | 0.694 ± 0.011 | 4230 ± 200 | 23.20 ± 0.35 | ⋯ | [43] |
| B | 0.6872 ± 0.0049 | 0.699 ± 0.014 | 4080 ± 200 | 23.37 ± 0.46 | ||||
| M55 V54 | A | 9.2692 | 0.726 ± 0.015 | 1.006 ± 0.009 | 6246 ± 71 | 7.24 ± 0.06 | −1.86 ± 0.15 | [44] |
| B | 0.555 ± 0.008 | 0.528 ± 0.005 | 5020 ± 95 | 3.80 ± 0.04 | ||||
| RXJ0239.1-1028 | A | 2.0719 | 0.73 ± 0.009 | 0.741 ± 0.004 | 4645 ± 20 | 18.09 ± 0.10 | ⋯ | [40] |
| B | 0.693 ± 0.006 | 0.703 ± 0.002 | 4275 ± 15 | 17.17 ± 0.05 | ||||
| NGC2204-S892 | A | 0.4518 | 0.733 ± 0.005 | 0.719 ± 0.014 | 4200 ± 100 | 80.5 ± 1.6 | ⋯ | [45] |
| B | 0.662 ± 0.005 | 0.68 ± 0.017 | 3940 ± 110 | 76.2 ± 1.9 | ||||
| UCAC3 127-192903 | A | 2.293 | 0.8035 ± 0.0086 | 1.147 ± 0.01 | 6088 ± 108 | 25.31 ± 0.22 | −1.18 ± 0.02 | [46] |
| B | 0.605 ± 0.0044 | 0.611 ± 0.0092 | 4812 ± 125 | 13.48 ± 0.21 | ||||
| KIC 6131659 | A | 17.5278 | 0.922 ± 0.007 | 0.88 ± 0.0028 | 5789 ± 50 | 2.540 ± 0.008 | −0.23 ± 0.2 | [47] |
| B | 0.685 ± 0.005 | 0.6395 ± 0.0061 | 4609 ± 32 | 1.846 ± 0.018 | ||||
| EPIC 247605441 | A | 1.6534 | 0.934 ± 0.017 | 1.058 ± 0.023 | 5668 ± 71 | 32.3 ± 0.7 | −0.26 ± 0.26 | [48] |
| B | 0.409 ± 0.005 | 0.408 ± 0.009 | 3590 ± 100 | 12.48 ± 0.28 | ||||
| ASAS J065134-2111.5 | A | 8.2196 | 0.956 ± 0.012 | 0.997 ± 0.004 | 5500 ± 100 | 6.277 ± 0.024 | 0.09 ± 0.13 | [49] |
| B | 0.674 ± 0.005 | 0.69 ± 0.007 | 3970 ± 110 | 4.34 ± 0.04 | ||||
| IM Vir | A | 1.3086 | 0.981 ± 0.012 | 1.061 ± 0.016 | 5570 ± 100 | 41.01962 ± 0.64 | −0.3 | [50] |
| B | 0.6644 ± 0.0048 | 0.681 ± 0.013 | 4250 ± 130 | 26.33 ± 0.51 | ||||
| V530 Ori | A | 6.1108 | 1.0038 ± 0.0066 | 0.98 ± 0.013 | 5890 ± 100 | 9.68 ± 0.13 | −0.12 ± 0.08 | [51] |
| B | 0.5955 ± 0.0022 | 0.5873 ± 0.0067 | 3880 ± 120 | 5.80 ± 0.06 | ||||
| EBLM J0113+31 | A | 14.2768 | 1.029 ± 0.025 | 1.417 ± 0.014 | 3.787 ± 0.003 | 10.00 ± 0.10 | −0.3 ± 0.1 | [32] |
| B | 0.197 ± 0.003 | 0.215 ± 0.002 | 3.528 ± 0.005 | 1.517 ± 0.014 | ||||
| Eclipsing triple systems | ||||||||
| KOI-126 | A | 33.9214 | 1.347 ± 0.032 | 2.20254 ± 0.0098 | 5875 ± 100 | ⋯ | 0.15 ± 0.08 | [25] |
| Ba | 1.7671 | 0.2413 ± 0.003 | 0.2543 ± 0.0014 | ⋯ | 7.62 ± 0.04 | |||
| Bb | 0.2127 ± 0.0026 | 0.2318 ± 0.0013 | ⋯ | 6.94 ± 0.04 | ||||
| Circumbinary planets | ||||||||
| Kepler 16 | A | 41.0792 | 0.6897 ± 0.0035 | 0.6489 ± 0.0013 | 4450 ± 150 | 1.1166 ± 0.0022 | −0.3 ± 0.2 | [26] |
| B | 0.20255 ± 0.00066 | 0.22623 ± 0.00059 | ⋯ | 0.3893 ± 0.0010 | ||||
| Kepler-453 | A | 27.322 | 0.944 ± 0.01 | 0.833 ± 0.011 | 5527 ± 100 | 1.715 ± 0.022 | 0.09 ± 0.1 | [27] |
| B | 0.1951 ± 0.002 | 0.215 ± 0.0014 | 3226 ± 100 | 0.4428 ± 0.0029 | ||||
| Kepler-47 | A | 7.4484 | 0.957 ± 0.014 | 0.936 ± 0.005 | 5636 ± 100 | 6.738 ± 0.037 | −0.25 ± 0.08 | [28] |
| B | 0.342 ± 0.003 | 0.338 ± 0.002 | 3357 ± 100 | 2.433 ± 0.015 |
| Name | X | HR | com. | ||
|---|---|---|---|---|---|
| [mas] | [ct s] | [×10] | |||
| CM Dra | 67.288 ± 0.034 | 0.210 ± 0.017 | −0.344 ± 0.061 | A | 8.9 ± 1.2 |
| B | 9.0 ± 1.2 | ||||
| NGTS 0002-29 | 3.80 ± 0.26 | ⋯ | ⋯ | A | 14.8 ± 1.6 |
| B | 17.6 ± 2.1 | ||||
| CU Cnc | 60.060 ± 0.036 | 0.732 ± 0.050 | −0.084 ± 0.054 | A | 16.3 ± 4.1 |
| B | 17.1 ± 4.6 | ||||
| NSVS01031772 | 16.572 ± 0.018 | 0.076 ± 0.013 | 0.016 ± 0.17 | A | 7.0 ± 2.2 |
| B | 8.2 ± 2.5 | ||||
| YY Gem | 66.310 ± 0.023 | 3.716 ± 0.091 | −0.152 ± 0.020 | A&B | 13.5 ± 1.7 |
| GU Boo | 6.187 ± 0.011 | 0.039 ± 0.012 | 0.16 ± 0.32 | A | 17.3 ± 7.0 |
| B | 19.4 ± 8.1 | ||||
| BD-15 2429 | 23.58 ± 0.14 | 0.495 ± 0.042 | −0.249 ± 0.068 | A | 7.0 ± 1.7 |
| B | 8.0 ± 2.3 | ||||
| RXJ0239.1-1028 | 8.144 ± 0.016 | 0.036 ± 0.014 | 1.00 ± 0.59 | A | 5.2 ± 2.4 |
| B | 7.3 ± 3.3 | ||||
| EPIC 247605441 | 9.99 ± 0.30 | 0.129 ± 0.019 | −0.06 ± 0.10 | A | 2.7 ± 0.5 |
| B | 16.7 ± 3.8 | ||||
| ASAS J065134-2111.5 | 10.819 ± 0.021 | 0.049 ± 0.012 | −0.35 ± 0.21 | A | 0.69 ± 0.22 |
| B | 2.56 ± 0.86 | ||||
| IM Vir | 11.136 ± 0.017 | 0.261 ± 0.031 | −0.232 ± 0.089 | A | 3.38 ± 0.56 |
| B | 10.0 ± 2.0 | ||||
| V530 Ori | 9.763 ± 0.018 | 0.0252 ± 0.0092 | −0.41 ± 0.26 | A | 0.36 ± 0.17 |
| B | 1.90 ± 0.94 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morales, J.C.; Ribas, I.; Giménez, Á.; Baroch, D. Fundamental Properties of Late-Type Stars in Eclipsing Binaries. Galaxies 2022, 10, 98. https://doi.org/10.3390/galaxies10050098
Morales JC, Ribas I, Giménez Á, Baroch D. Fundamental Properties of Late-Type Stars in Eclipsing Binaries. Galaxies. 2022; 10(5):98. https://doi.org/10.3390/galaxies10050098
Chicago/Turabian StyleMorales, Juan Carlos, Ignasi Ribas, Álvaro Giménez, and David Baroch. 2022. "Fundamental Properties of Late-Type Stars in Eclipsing Binaries" Galaxies 10, no. 5: 98. https://doi.org/10.3390/galaxies10050098
APA StyleMorales, J. C., Ribas, I., Giménez, Á., & Baroch, D. (2022). Fundamental Properties of Late-Type Stars in Eclipsing Binaries. Galaxies, 10(5), 98. https://doi.org/10.3390/galaxies10050098






