Ultra-High-Energy Particles at the Border of Kerr Black Holes Triggered by Magnetocentrifugal Winds

Abstract

The source, origin, and acceleration mechanisms of ultra-high-energy cosmic rays (UHECR) ($E>{10}^{20}$ eV, beyond the GZK limit) remain uncertain and unclear. The main explanations are associated with particular mechanisms, such as the Fermi mechanism, in which charged particles could be accelerated by clouds of magnetized gas moving within our Galaxy, or by the magnetic reconnection of field lines at, e.g., the core of high-energy astrophysical sources, where the topology of the magnetic field is rearranged and magnetic energy is converted into kinetic energy. However, the recent observation of extragalactic neutrinos may suggest that the source of UHECRs is likely an extragalactic supermassive black hole. In the present work, we propose that charged particles can be accelerated to ultrahigh energies in marginally bound orbits near extreme rotating black holes and could be triggered by collisions of magnetocentrifugal winds; the accretion disk surrounding the black hole would provide such winds. The ultra-high-energy process is governed by the frame-dragging effects of the black hole spacetime.

1. Introduction

It is mostly accepted that the great majority of galaxies contain a supermassive black hole (BH) at the center, and that some galaxies have active galactic nuclei (AGNs), which are luminous in all wavebands. The standard model for AGNs comprises an accretion disk around the black hole that furnishes mass and allows the BH to grow. Furthermore, it has been widely observed that magnetic fields are present in nearly all astrophysical objects [1]. For example, it is expected that the accretion disks surrounding supermassive BHs in the core of AGNs would contain highly conducting plasma, which can lead to the manifestation of regular electromagnetic fields in the vicinity of such central BHs.

In addition to the many energy features produced by accretion dynamics, such as the radiation pressure in accretion disks, there are the jets from compact stellar-mass objects (e.g., microquasars) or from the central BH of AGNs. The jets and the collimation of the jets are thought to arise from the combination of many factors, such as the presence of charged matter in the accretion disks, the gravitational field of the BH, and the presence of electromagnetic fields. On the other hand, the presence of plasma in such systems suggests the existence of local charges in small, confined regions of the accretion disk that are modulated by the presence of magnetic fields [2,3,4,5]. This implies that the role of magnetic fields in the vicinity of AGN BHs cannot be neglected.

There are plenty of possible high-energy astrophysical phenomena related to magnetic fields in the core of AGNs. The central black hole surrounded by an accretion disk plays a fundamental role in this picture. Although observations cannot discriminate the dominant physics of the wind launching in AGNs, radiatively driven winds and magnetocentrifugally driven winds provide increasingly robust depictions of the key physics inside AGNs. Models that explain the properties of magnetocentrifugal winds in AGNs and the general kinematics of these winds are fashioned both by radiative wind models investigations [6,7] and, to explain radio jets, by hydromagnetic models [8]; line-driven models are also employed in hydrodynamic simulations [9,10,11], which enlighten the density structure, geometry, and kinematics of the flow in two dimensions. A detailed picture of the radiative transfer within magnetocentrifugal winds were also investigated by [12,13,14,15].

In this respect, the novel and unparalleled observation of extragalactic high-energy neutrinos has permitted us to ascribe their source to blazars [16,17], which are supermassive BHs at a distance of ∼1.75 Gpc with relativistic jets directed toward us. It is mostly accepted that these neutrinos are tracers of ultra-high-energy cosmic rays (UHECRs), and it is now becoming clear that the central BHs of AGNs could indeed be sources of UHECRs. It is commonly accepted that UHECRs are produced either via the Fermi mechanism, i.e., where charged particles could be accelerated by clouds of magnetized gas moving within our Galaxy, or by magnetic reconnection, since it is particularly important in the magnetically dominated region of the black hole magnetosphere and relativistic jets [18]. Theoretically, it is indeed conceivable that UHECRs could be produced in the center of AGNs since it is possible that ultra-high center-of-mass energies ($E_{c.m.}$) can be produced by particles colliding in the vicinity of extremal rotating black holes ($a=1$) [19,20]. Ultra-high $E_{c.m.}$ particles were firstly proposed by Bañados, Silk, and West [19], who noticed that the collision of two neutral classical particles falling freely into extremal Kerr BHs ($a=1$) may have infinite values of $E_{c.m.}$ close to the event horizon if one of the particles is tracking marginally bound geodesics. In this respect, Refs. [20,21] concluded that, in fact, frame-dragging effects in Kerr BHs can accelerate particles to high energies, but astrophysical restrictions on the spin (i.e., apparently, real black holes never reach $a=1$) and restrictions on the maximum $E_{c.m.}$ caused by gravitational radiation and back-reaction would solely permit infinite $E_{c.m.}$ at an infinite time and on the horizon of the black hole. Regarding astrophysical limits on the BH spin, supermassive BHs in the center of AGNs would have prolonged disk accretion and mass evolution owing to galaxy merger events that, in both cases, yield black holes with a very high spin [22,23,24]. Nevertheless, the BH spin would be limited to $a\approx 0.998$ because the black hole would preferentially swallow negative angular momentum photons emitted by the accretion flow. This limit is also known as “the Thorne limit”. From now on, BHs with a spin in the Thorne limit regime will be called “near-extremal black holes”. Constituents of UHECRs were thought to be dominated by protons, as indicated by cosmic-ray fluorescence measurements [25,26], although recent observations are suggesting heavier constituents [27]. In this way, Refs. [28,29] proposed acceleration mechanisms where the Kerr central BHs in the presence of magnetic fields would accelerate charged particles to ultra-high-energies.

The aim of the present paper is to evaluate how the presence of magnetic fields could drive charged particles to be accelerated to infinity if they collided in the vicinity of Kerr BHs, as well as to see how magnetocentrifugal winds would contribute to such an endeavor. The structure of the paper is as follows: In Section 2, we describe Kerr black holes as particle accelerators. In particular, we detail the effect of the magnetic fields in driving charged particles. In Section 3, we discuss the accretion mechanism while considering the accretion fluid dynamics and the mass accretion rate in radiative phenomena. With our findings, in Section 4, we investigate the environment around Kerr BHs ISCOS. The results and a discussion of the models are summarized in Section 5. From here on, we will use the natural units $c=G=1$, and our spacetime has the $(-+++)$ signature.

2. Kerr Black Holes as Particle Accelerators?

The Kerr BH is described by two parameters: its mass M and its angular momentum J (here represented by $a=J/M$, i.e., the angular momentum per unit of mass). The Kerr line element describes a stationary spacetime with axial symmetry, and in Boyer–Lindquist coordinates, it is written as follows [30]:

$$d{s}^2=g_{tt}d{t}^2+2g_{t\varphi }dtd\varphi +g_{rr}d{r}^2+g_{\theta \theta }d{\theta }^2+g_{\varphi \varphi }d{\varphi }^2,$$

(1)

with

$$g_{tt}=-\left(1-\frac{2M}{\mathsf{\sum }}\right),$$

$$g_{t\varphi }=-\frac{2aMr{sin}^2\theta }{\mathsf{\sum }},$$

$$g_{rr}=\frac{\mathsf{\sum }}{\Delta },$$

$$g_{\theta \theta }=\mathsf{\sum },$$

$$g_{\varphi \varphi }=\frac{{(r^2+a^2)}^2-a^2\Delta {sin}^2\theta }{\mathsf{\sum }}{sin}^2\theta ,$$

where $\mathsf{\sum }=r^2+a^2{cos}^2\theta$ and $\Delta =r^2+a^2-2Mr$. The event horizon is located at $r_H=M+\sqrt{M^2-a^2}$. Since static holes have no rotation, then $a\to 0$ and the Kerr horizon coincides with the Schwarzschild one $r_H=r_S=2M$. The so-called ergoregion is described by $r_H<r<r_E\left(\theta \right)=M+\sqrt{M^2-a^2{cos}^2\theta }$. From here, we will consider that $M=1$. Note that in this situation, the horizons are $r_H=2$ for $a=0$ (static BH) and $r_H=1$ for $a=1$ (extremal BH).

When considering the motion of particles only under the action of gravity, the conserved quantities along geodesics play a fundamental role. The energy of the particle as well as its angular momentum relative to the axis of symmetry are conserved quantities as a consequence of Kerr metric symmetries and the Noether theorem. Considering the motion of neutral or charged particles near rotating BHs in a background described by (1), i.e., a vacuum rotating black hole, the conserved quantities are attached to Killing vectors ${\xi }_{\left(t\right)}={\xi }_{\left(t\right)}^{\mu }{\partial }_{\mu }=\frac{\partial }{\partial t}$ and ${\xi }_{\left(\varphi \right)}={\xi }_{\left(\varphi \right)}^{\mu }{\partial }_{\mu }=\frac{\partial }{\partial \varphi }$. Such vectors are attached to the concept that the Kerr metric depends neither on time t nor on the azimuthal angle $\varphi$, and these symmetries can be conveyed in a coordinate-independent way by these two Killing vectors. The first one is related to the free test particle energy conservation

$$\mathcal{E}=-g_{t\mu }{p}^{\mu },$$

(2)

and the other to the free test particle angular momentum conservation

$$\ell =-g_{\varphi \mu }{p}^{\mu }.$$

(3)

Here, the range of ℓ—the angular momentum per unit rest mass—for geodesics falling in is $-2(1+\sqrt{1+a})<\ell <2(1+\sqrt{1-a})$ (for details on such bounds and other issues on the treatment of geodesics in the Kerr background, see [31]).

Another important property related to Kerr black holes is the innermost circular stable (or marginally stable) orbit $r_{ms}$, which is the smallest marginally stable circular orbit where a test particle can stably orbit the BH. A Kerr metric is given by [32]

$$r_{ms}=\frac{R_S}{2}(3+Z_2\pm \sqrt{(3-Z_1)(3+Z_1+2Z_2)}),$$

(4)

where $Z_1=1+{(1-{\chi }^2)}^{1/3}[{(1+\chi )}^{1/3}+{(1-\chi )}^{1/3}]$, $Z_2={(3{\chi }^2+Z_1^2)}^{1/2}$, with $\chi =2a/R_S$. In (4), the plus sign indicates a retrograde orbit and the negative sign, a prograde BH orbit.

When two neutral or charged particles approach the horizon of a black hole, it is necessary to define the center-of-mass frame properly since the background is curved. The center-of-mass energy of the two-particle system (each with mass $m_0$) is given by [19]

$$E_{c.m.}=m_0\sqrt{2}\sqrt{1-g_{\mu \nu }{u}_{\left(1\right)}^{\mu }{u}_{\left(2\right)}^{\nu }},$$

(5)

where $u_{\left(1\right)}^{\mu }$ and $u_{\left(2\right)}^{\nu }$ are the 4-velocities of each particle, properly normalized by $g_{\mu \nu }{u}^{\mu }{u}^{\nu }=-1$. It is assumed that the main conditions for accelerating the particles can be derived from the BH spin, since spin influences the position of the innermost stable circular orbit (ISCO), the last stable circular orbit around the BH.

Magnetic fields could positively or negatively affect particle acceleration. For example, [28] showed that for a proper Lagrangian, the conserved quantities in the environment of rotating BHs with magnetic fields are

$$\mathcal{E}=-g_{t\mu }(m_0{u}^{\mu }+q{A}^{\mu }),$$

(6)

$$\ell =-g_{\varphi \mu }(m_0{u}^{\mu }+q{A}^{\mu }),$$

(7)

where $A_{\mu }$ is the electromagnetic 4-potential, q is the particle charge, $m_0$ is the particle mass, and satisfying the Lorentz gauge $A_{;\mu }^{\mu }=0$, the 4-potential can be

$$A_{\mu }=\left(\frac{2a{m}_{0}B}{q},0,0,\frac{m_{0}B}{q}\right),$$

(8)

where B represents the magnetic field in natural units (see [28,33]). Figure 1 shows one of the main results for some values of B, ${\ell }_1$, and ${\ell }_2$.

The following summary is presented textually in [28]: “Regarding the case of particles (charged or neutral) in the vicinity of non-near-extreme black holes, $a<0.998$, for any value of B, the particles cannot escape from the system. (…) for neutral-neutral colliding particles (…) the $E_{c.m.}$ energy of particles that collide in the vicinity of extreme black holes ($a\to 1$), particles can in fact be accelerated escaping from the system (as awaited, see [19]). Regarding the $E_{c.m.}$ energy of other type of particles that collide in the vicinity of extreme black holes ($a\to 1$), the results indicate that particles can in fact be accelerated escaping from the system (…). Regarding the $E_{c.m.}$ energy of neutral-charged particles that collide in the vicinity of near-extremal black holes ($a\approx 0.998$), the results indicate that particles can in fact be accelerated escaping from the system (…). Regarding the $E_{c.m.}$ energy of charged-charged particles that collide in the vicinity of near-extremal black holes, the results indicate that particles can in fact be accelerated escaping from the system. (…) only a certain range of magnetic fields actually cause the acceleration of the particle in positions increasingly farther from the horizon (…). Otherwise, magnetic fields of great magnitude can cause the ISCO particle to lose its stability and, after collision, it will fall onto the horizon”.

Such results motivate some pertinent questions, such as: why would the presence of magnetic fields drive charged particles (e.g., from an accretion disk plasma) to be accelerated to infinity? In the next sections, we will try to answer this using some simple aspects of the accretion mechanism in the presence of magnetic fields.

3. The Accretion Mechanism

3.1. Accretion Fluid Dynamics

The accretion mechanism present in astrophysical accretion disks generates a flow that carries out the transport of angular momentum. This is paramount as in many dissipative flows present in fluid mechanics, the energy can be converted into heat and then radiated away. Nevertheless, in many cases, the angular momentum is difficult to remove. Therefore, since most accretion flows in astrophysics rotate rapidly, one of the essential theoretical issues is understanding how to remove the angular momentum so that accretion can occur. The fluid in the accretion disk follows the main equations of fluid mechanics. For example, in the disk, the conservation of mass in one dimension is represented by

$$\frac{\partial \mathsf{\sum }}{\partial t}+\frac{1}{r}\frac{\partial }{\partial r}\left(r\mathsf{\sum }{u}_r\right)=0,$$

(9)

where $\mathsf{\sum }=\frac{1}{2\pi }{\int }_0^{2\pi }{\int }_{-\infty }^{\infty }\rho dzd\varphi$ is the surface density of the disk. Equation (9) is derived from the equation of mass conservation $\dot{\rho }+\nabla ·\left(\rho \mathbf{u}\right)=0$, where $\rho$ is the density and $\mathbf{u}$ is the velocity of the fluid, with $\dot{\rho }$ being the partial derivative with respect to time.

Now, assume that the azimuthal velocity in the disk is given by $u_{\varphi }=r\mathsf{\Omega }$, where $\mathsf{\Omega }\left(r\right)$ is the angular velocity of circular orbits in the axisymmetric potential $\mathsf{\Phi }(r,z)$. Then,

$$\rho u_r\frac{\mathrm{d}h}{\mathrm{d}r}=\frac{1}{r}\frac{\partial }{\partial r}\left(r^2{T}_{r\varphi }\right)+\frac{1}{r}\frac{\partial }{\partial \varphi }(-rp+r{T}_{\varphi \varphi })+\frac{\partial }{\partial z}\left(r{T}_{\varphi z}\right),$$

(10)

where $h=r^2\mathsf{\Omega }$ is the specific orbital angular momentum. This equation comes from the equation of the motion of the fluid, i.e.,

$$\rho (\dot{\mathbf{u}}+\mathbf{u}·\nabla \mathbf{u})=-\rho \nabla \mathsf{\Phi }-\nabla p+\nabla ·\mathbf{T},$$

(11)

where $\mathsf{\Phi }$ is the gravitational potential, p is the pressure, and $\mathbf{T}$ is the stress tensor. In Equation (10), the gravitational potential does not appear due to its axisymmetric nature. When considering only the radial shear $T_{r\varphi }$, multiplying it by r and integrating it with respect to $\varphi$ and z, one can obtain

$$\mathcal{F}\frac{\mathrm{d}h}{\mathrm{d}r}=-\frac{\partial \mathcal{G}}{\partial r}$$

(12)

where $\mathcal{F}={\int }_0^{2\pi }{\int }_{-\infty }^{\infty }r\rho u_{r}dzd\varphi$ is the radial mass flux, and $\mathcal{G}=-{\int }_0^{2\pi }{\int }_{-\infty }^{\infty }{r}^2{T}_{r\varphi }dzd\varphi$ is the viscous torque. In astrophysical disks, the molecular viscosity is too small and cannot explain the torque. However, it is usual to express the torque based on an effective viscosity. According to the Navier–Stokes equation, the viscous stress is the matrix

$$\mathbf{T}=\mu [\nabla \mathbf{u}+{(\nabla u)}^{\mathrm{T}}]+({\mu }_b-2/3\mu )(\nabla ·\mathbf{u})\mathbf{1},$$

(13)

where $\mu$ is the viscosity, ${\mu }_b$ is the bulk viscosity, and ${(\nabla u)}^{\mathrm{T}}$ is the transpose of the matrix $\nabla u$. In the case of a circular orbital motion, the only stress component is

$$T_{r\varphi }=T_{\varphi r}=\mu r\frac{\mathrm{d}\mathsf{\Omega }}{\mathrm{d}r},$$

(14)

that is, the viscosity multiplied by the shear rate. The (density-weighted) mean kinematic viscosity $\overline{\nu }(r,t)$ is defined according to the following equation:

$$\overline{\nu }\mathsf{\sum }=\frac{1}{2\pi }{\int }_0^{2\pi }{\int }_{-\infty }^{\infty }\mu dzd\varphi .$$

(15)

Using the information above along with Equations (9) and (12), one can find the diffusion equation for the surface density

$$\frac{\partial \mathsf{\sum }}{\partial t}+\frac{1}{r}\frac{\partial }{\partial r}\left[{\left(\frac{\mathrm{d}h}{\mathrm{d}r}\right)}^{-1}\frac{\partial }{\partial r}\left(\overline{\nu }\mathsf{\sum }{r}^3\frac{\mathrm{d}\mathsf{\Omega }}{\mathrm{d}r}\right)\right]=0,$$

(16)

which, combined with a point-mass potential for a Keplerian disk (where $\mathsf{\Omega }=\sqrt{(GM/r^3)}$ and $h=\sqrt{GMr}$), gives the following diffusion equation of the accretion disk:

$$\frac{\partial \mathsf{\sum }}{\partial t}=\frac{3}{r}\frac{\partial }{\partial r}\left[\sqrt{r}\frac{\partial }{\partial r}\left(\sqrt{r}\overline{\nu }\mathsf{\sum }\right)\right].$$

(17)

We can suppose that $\overline{\nu }(r,\mathsf{\sum })$ is a given function, such that if $\overline{\nu }=\overline{\nu }\left(r\right)$, we have a linear diffusion equation; if $\overline{\nu }=\overline{\nu }(r,\mathsf{\sum })$, we have a nonlinear diffusion equation. For simplicity, we assume that the inner boundary condition $\sqrt{r}\overline{\nu }\mathsf{\sum }\to 0$ is $r\to 0$. If the central object is a black hole, the disk does not extend to the event horizon. This is because of the existence of a marginally stable circular orbit at $r=r_{ms}$. For $r<r_{ms}$, circular orbits are unstable, and the gas spirals rapidly into the black hole without the need for a viscous torque. In order to conserve mass, the surface density $\mathsf{\sum }$ decreases very rapidly just inside $r_{ms}$ as the gas accelerates into the hole. The viscous stress is then essentially zero at $r_{ms}$.

3.2. Mass Accretion Rate and Radiative Phenomena

If the disk is in a steady state ($\partial /\partial t=0$), Equation (9) implies that

$$\frac{\partial \left(r\dot{r}\mathsf{\sum }\right)}{\partial r}=0.$$

(18)

Here, we substituted $u_r=\dot{r}$. It is possible to rewrite (18) as

$$\frac{\partial }{\partial t}{\int }_V\rho dV=const=-\dot{M},$$

(19)

where $\dot{M}$ is the mass accretion rate. The angular momentum from Equation (12) is integrated to give

$$-\dot{M}h+\mathcal{G}=const=-\dot{M}{h}_{in},$$

(20)

where $h_{in}=h\left(r_{in}\right)$ is the inner boundary condition for the angular momentum in the inner radius $r_{in}$, giving

$$\mathcal{G}=\dot{M}(h-h_{in}).$$

(21)

For a Keplerian disk,

$$\overline{\nu }\mathsf{\sum }=\frac{\dot{M}}{3\pi }\left[1-{\left(\frac{r_{in}}{r}\right)}^{1/2}\right].$$

(22)

In the disk, the rate of energy dissipation $ϵ$ per unit volume (from shear friction) is

$${ϵ}_V=T_{r\varphi }r\frac{\mathrm{d}\mathsf{\Omega }}{\mathrm{d}r}.$$

(23)

From Equation (14), we have

$${ϵ}_V=\mu {\left(r\frac{\mathrm{d}\mathsf{\Omega }}{\mathrm{d}r}\right)}^2.$$

(24)

Per unit area of the disk, and on each face of the disk, the energy emitted is

$${ϵ}_A=\frac{1}{2}\overline{\nu }\mathsf{\sum }{\left(r\frac{\mathrm{d}\mathsf{\Omega }}{\mathrm{d}r}\right)}^2.$$

(25)

If this is carried by black-body radiation, the surface temperature $T_{eff}(r,t)$ is given by

$${\sigma }_s{T}_{eff}^4=\frac{9}{8}\overline{\nu }\mathsf{\sum }{\mathsf{\Omega }}^2,$$

(26)

where ${\sigma }_s$ is the Stephan–Boltzmann constant. Using (22) for a Keplerian disk, we obtain

$${\sigma }_s{T}_{eff}^4=\frac{3GM\dot{M}}{8\pi r^3}\left[1-{\left(\frac{r_{in}}{r}\right)}^{1/2}\right].$$

(27)

Then, the total luminosity of a disk extending to infinity is

$$L={\int }_{r_{in}}^{\infty }\frac{3GM\dot{M}}{4\pi r^3}\left[1-{\left(\frac{r_{in}}{r}\right)}^{1/2}\right]2\pi rdr=\frac{1}{2}\frac{GM\dot{M}}{r_{in}}.$$

(28)

Assuming that the inner radius $r_{in}$ coincides with the innermost stable Kerr black hole orbit $r_{ms}$, we can use Equation (4) and rewrite (28) as

$$L_{\pm }=\frac{GM\dot{M}}{R_S(3+Z_2\pm \sqrt{(3-Z_1)(3+Z_1+2Z_2)})}.$$

(29)

where $L_{+}$ is the family of luminosities when the BH has retrograde rotation, and $L_{-}$ is the family of luminosities when the BH has prograde rotation. Figure 2 shows the profiles of luminosity (in terms of the Eddington luminosity $L_{Edd}$, defined through $\dot{M}$ [35]) for both retrograde BHs (dotted lines) and prograde BHs (full lines) as functions of the black hole spin a. A near-extremal BH ($a>0.9$) with a great mass accretion rate tend to be a super-Eddington (i.e., $L>L_{Edd}$).

The above approach can explain the radiative phenomena associated with Kerr astrophysical BHs, such as the X-ray and other spectra observed from AGN sources. In other words, Kerr BHs at a near-extremal regime can emit an energetic electromagnetic spectrum and tend to be a super-Eddington. In this aspect, when the accretion flows become a super-Eddington, accretion flows become slim disks (optically and geometrically thick). Nevertheless, could near-extremal Kerr BHs explain the emission of ultra-high-energy particles? In the next section, we will see how magnetic fields could increase (or not) the emission of charged particles from accretion disks that interact with near extremal Kerr BHs.

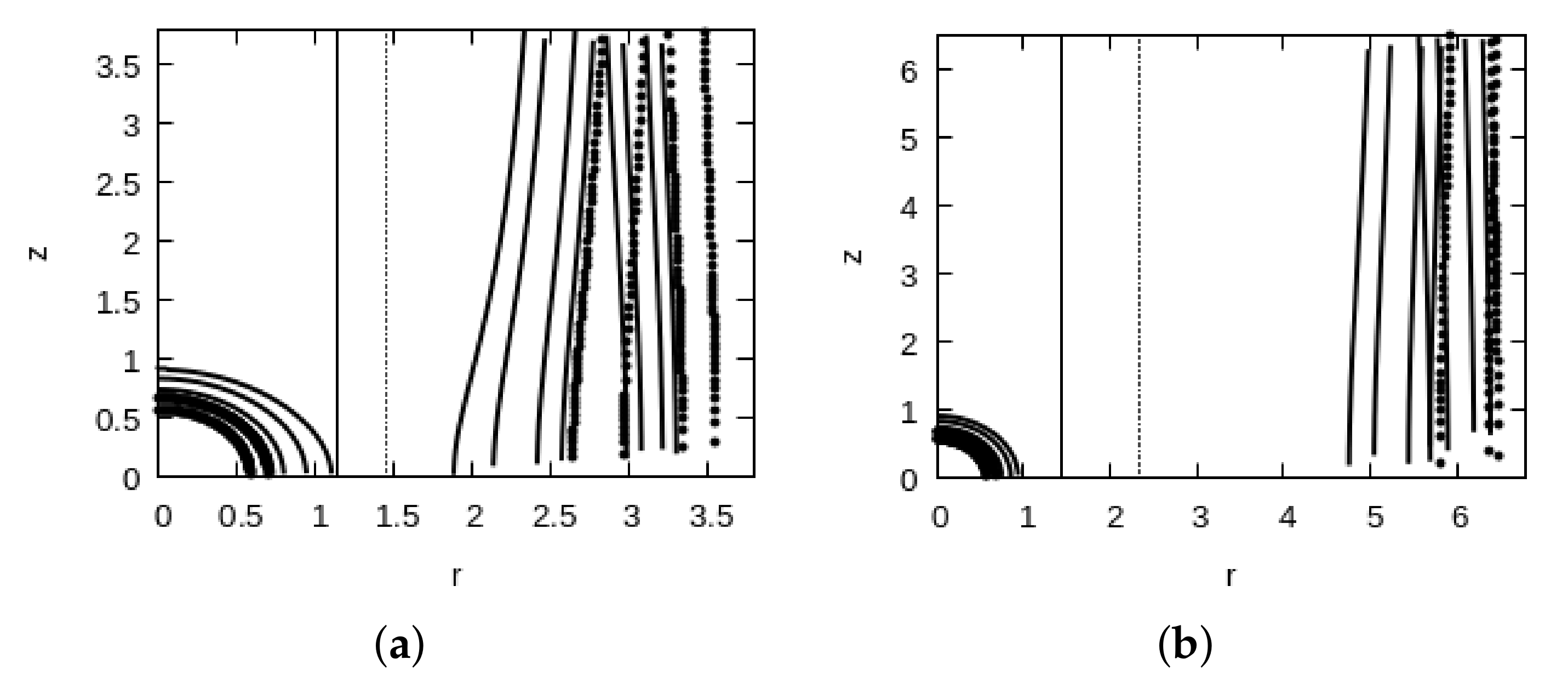
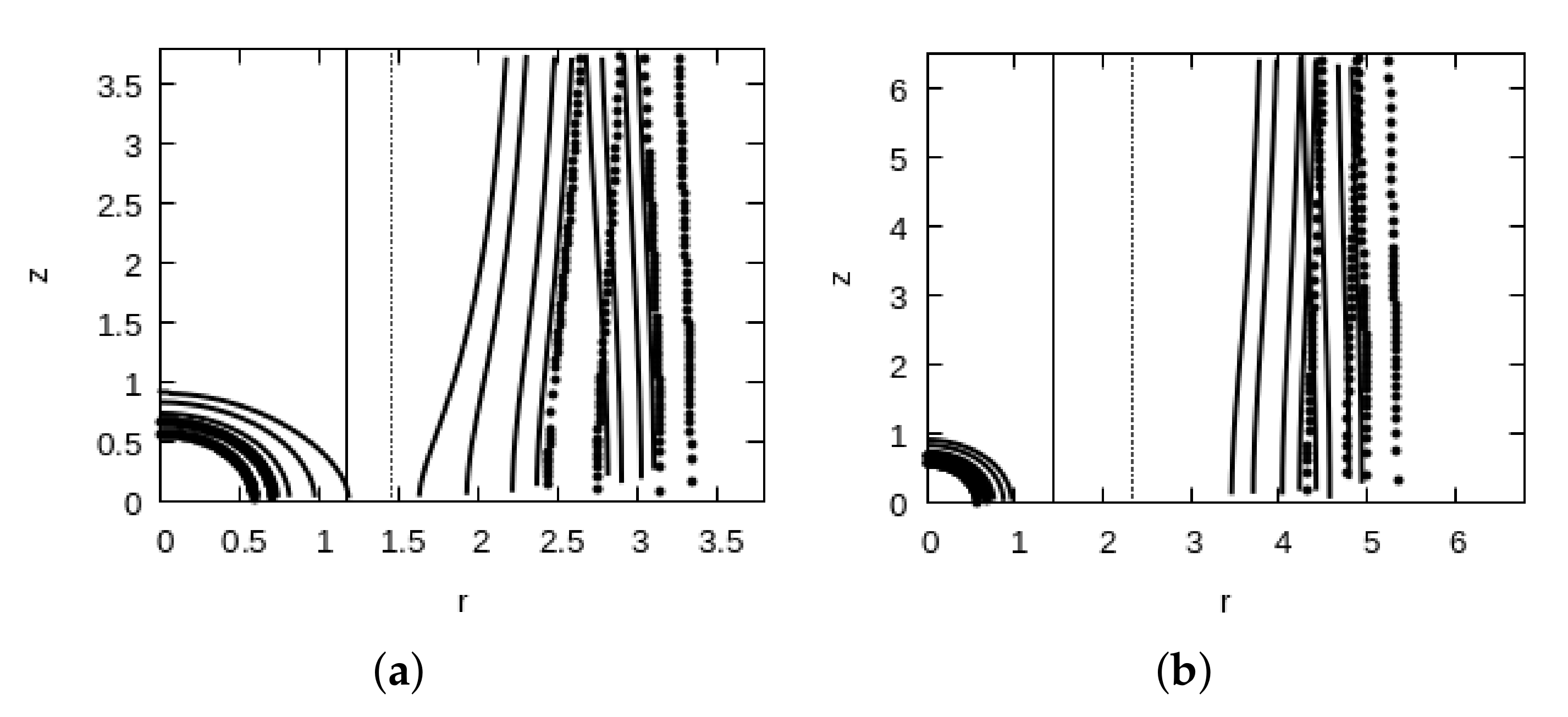
4. Magnetocentrifugal Winds

Accretion disks in AGNs are allegedly made of energetic plasma, i.e., an electrically conducting fluid moving at a certain velocity $\mathbf{u}$ and with a particular conductivity $\sigma$. In this case, Ohm’s Law is

$$\mathbf{J}=\sigma (\mathbf{E}+\mathbf{u}\times \mathbf{B}),$$

(30)

where $\mathbf{J}$, $\mathbf{E}$, and $\mathbf{B}$ are respectively the current density, the electric field, and the magnetic field. Using the Faraday and the Ampère–Maxwell equations (without the displacement current),

$$\nabla \times \mathbf{E}=-\frac{\partial \mathbf{B}}{\partial t},$$

$$\nabla \times \mathbf{B}={\mu }_0\mathbf{J},$$

where ${\mu }_0$ is the magnetic permeability, we obtain the induction equation

$$\frac{\partial \mathbf{B}}{\partial t}=\nabla \times \left(\mathbf{u}\times \mathbf{B}\right)-\nabla \times (\eta \nabla \times \mathbf{B})$$

(31)

where $\eta ={\left({\mu }_0\sigma \right)}^{-1}$ is the magnetic diffusivity. The induction equation is an evolutionary equation for the magnetic field $\mathbf{B}$. For a perfect electrical conductor, $\sigma \to \infty$, i.e., $\eta \to 0$. This limit defines the so-called ideal Magnetohydrodynamics (MHD), and the induction equation becomes

$$\frac{\partial \mathbf{B}}{\partial t}=\nabla \times \left(\mathbf{u}\times \mathbf{B}\right).$$

(32)

When the magnetic field is set on in the accretion disk system, a new equation for motion arises and Equation (11) is rewritten as

$$\rho (\dot{\mathbf{u}}+\mathbf{u}·\nabla \mathbf{u})=-\rho \nabla \mathsf{\Phi }-\nabla p+\nabla ·\mathbf{T}+\mathbf{J}\times \mathbf{B},$$

(33)

where the last term comes from the Lorentz force component per unit volume for a fluid carrying a current density $\mathbf{J}$. Supposing a shearless fluid, one can rewrite this expression by considering a kinetic energy equation formed from the inner product of $\mathbf{u}$ with Equation (33), which becomes

$$\rho \mathbf{u}·\nabla \left(u^2/2\right)=-\rho \mathbf{u}·\nabla \mathsf{\Phi }-\mathbf{u}·\nabla p+\mathbf{u}·(\mathbf{J}\times \mathbf{B}).$$

(34)

Since $\mathbf{u}·\nabla p=\rho \mathbf{u}·\nabla \omega$, where $\omega$ is the angular velocity of the magnetic field lines, the equation of motion is thus rearranged as

$$\rho \mathbf{u}·\nabla (u^2/2+\mathsf{\Phi }+\omega )=\mathbf{u}·(\mathbf{J}\times \mathbf{B}).$$

(35)

In the steady-state ideal MHD (i.e., $\nabla \times (\mathbf{u}\times \mathbf{B}=0)$), one can show that the term $\mathbf{u}·\left(\mathbf{J}\times \mathbf{B}\right)$ is related to the divergence of the Poynting flux as

$$\mathbf{u}·(\mathbf{J}\times \mathbf{B})=-\nabla ·\left(\frac{1}{{\mu }_0}\mathbf{E}\times \mathbf{B}\right)=\nabla ·\left[\frac{r\omega }{{\mu }_0}(B_{\varphi }\mathbf{B}-B^2{\mathbf{e}}_{\varphi })\right]=\mathbf{B}·\nabla \left(\frac{r\omega B_{\varphi }}{{\mu }_0}\right),$$

where $B_{\varphi }$ is the axial component of the magnetic field. Now, solving along the magnetic surfaces of the poloidal magnetic field (where the poloidal velocity is parallel to the poloidal magnetic field, i.e., $\rho {\mathbf{u}}_p=k{\mathbf{B}}_p$, with k being the ratio of the mass flux to the magnetic flux), the equation of motion (35) becomes

$$\rho {\mathbf{u}}_p·\nabla \left(\frac{1}{2}{u}^2+\mathsf{\Phi }+\omega -\frac{r\omega B_{\varphi }}{{\mu }_{0}k}\right)=0,$$

(36)

which means that $\epsilon =\frac{1}{2}{u}^2+\mathsf{\Phi }+\omega -\frac{r\omega B_{\varphi }}{{\mu }_{0}k}$ is an invariant under translations along the poloidal lines. Another invariant with this same aspect is

$${\epsilon }^{\prime }=\epsilon -\left(r{u}_{\varphi }-\frac{r{B}_{\varphi }}{{\mu }_{0}k}\right)=\frac{1}{2}{u}^2+\mathsf{\Phi }+\omega -r{u}_{\varphi }\omega ,$$

(37)

or

$${\epsilon }^{\prime }=\frac{1}{2}{u}_p^2+\frac{1}{2}{(u_{\varphi }-r\omega )}^2+{\mathsf{\Phi }}^{cg}+\omega ,$$

(38)

where

$${\mathsf{\Phi }}^{cg}=\mathsf{\Phi }-{\omega }^2{r}^2/2$$

(39)

is the centrifugal-gravitational potential associated with poloidal magnetic surfaces. In the case of the ideal MHD, the poloidal magnetic field lines are represented as being “frozen into” the fluid and can be identified with material lines. If the magnetic flow starts from rest, the angular velocity of the magnetic surface can be identified with the angular velocity of the disk at the foot point of the field line.

For a Keplerian disk, considering the foot point at $r=r_{in}$, the angular velocity of the field is

$$\omega ={\mathsf{\Omega }}_{in}=\left(\sqrt{\frac{M}{r_{in}^3}}\right).$$

(40)

Then, for a Keplerian disk with potential $\mathsf{\Phi }$, the centrifugal-gravitational potential is

$${\mathsf{\Phi }}_{Kepler}^{cg}=-\frac{M}{{(r^2+z^2)}^{1/2}}-\frac{1}{2}\frac{M}{r_{in}^3}{r}^2.$$

(41)

In this case, no stable circular motion is possible for $r<r_{ms}$, and we assume here that the inner radius of the accretion disk could at least be placed by $r_{ms}$ in Equation (4). Note that now, $r_{in}$ is a function of the black hole spin a (see Section 2), and therefore the profile of ${\mathsf{\Phi }}^{cg}$ now also depends on a. Figure 3 shows contours for ${\mathsf{\Phi }}^{cg}$, supposing a central near-extremal Kerr BH with $a\ge 0.9$, in units of M.

For a disk calculated from general relativity, considering the foot point at $r=r_{in}$, the angular velocity of the field is the frame-dragging angular velocity in the Kerr frame [35]:

$$\omega ={\mathsf{\Omega }}_{in}={\left.-\frac{g_{t\varphi }}{g_{\varphi \varphi }}\right|}_{r=r_{in}}=\frac{2aM{r}_{in}}{{(r_{in}^2+a^2)}^2}.$$

(42)

General relativistic (GR) potentials are very useful for understanding systems with strong fields. In this case, a simple example of a composite dust disk with a central black hole is, e.g., the Lemos–Letelier potential [36], where the centrifugal-gravitational potential (39) becomes

$${\mathsf{\Phi }}_{GR}^{cg}=-\frac{{\alpha }^{2}Mz}{{(r^2+z^2)}^{3/2}}+ln\left[\frac{-M-z+\sqrt{{(z+M)}^2+r^2}}{M-z+\sqrt{{(z-M)}^2+r^2}}\right]-\frac{2a^2{M}^2{r}_{in}^2}{{(r_{in}^2+a^2)}^4}{r}^2,$$

(43)

where $\alpha$ is an integration constant. In this case, no stable circular motion is possible for $r<r_{ms}$, and we assume here that the inner radius of the accretion disk could at least be placed by $r_{ms}$ in Equation (4). Note that now, $r_{in}$ is a function of the black hole spin a (see Section 2), and therefore the profile of ${\mathsf{\Phi }}^{cg}$ now also depends on a. Figure 4 shows contours for ${\mathsf{\Phi }}^{cg}$, supposing a central near-extremal Kerr BH with $a\ge 0.9$, in units of M. Logically, there are many other options for the relativistic disk potentials of thin or thick disks (for a review, see [37]), such as Novikov–Thorne GR disks [38], and our aim here is to present a general picture related to a simple GR potential that could describe magnetocentrifugal winds close to the black hole. Figure 5 shows a comparison between the Keplerian potential and the GR potential from Equations (41) and (43) at the disk equator.

5. Discussion and Concluding Remarks

Could magnetocentrifugal acceleration at the inner-disk border of Kerr BHs drive winds that trigger the acceleration of ultra-high-energy charged particles? Essentially, we saw in Section 3.2 (Figure 2) that accretion disks feeding a near-extremal BH ($a>0.9)$ can convert large amounts of gravitational energy into heat, and subsequently into high luminosities (by various processes we have not discussed here). The radiation then leaks through the disk, escapes from its surface, and, as in the case of stellar winds, if the gas is hot (in comparison with the escape temperature), an outflow can be driven by thermal pressure. This can dynamically produce matter outflows of charged particles since the plasma disk is made of charged particles. Whether the flow accelerates or not above the disk depends on the variation of the centrifugal-gravitational potential ${\mathsf{\Phi }}^{cg}$ along the field line. If the foot point lies at a saddle point of the centrifugal-gravitational potential, and if the inclination of the field line toward the vertical line on the surface of the disk exceeds ${30}^{\circ }$ [39], the flow is accelerated without thermal assistance. This is called magnetocentrifugal acceleration. Magnetocentrifugal acceleration depends on the proximity of the disk’s inner border with the BH horizon.

General relativistic disks could make the lines of the magnetocentrifugal winds that are approaching the inner orbits as compared to Keplerian disks (for the same values as that of the BH spin factor a). Stable orbits around Kerr black holes can function as a particle accelerator “ring”, where orbiting particles with a different angular momentum can collide head-on or not. The inner stable orbit (ISCO) is closer to the horizon as the value of the spin a approaches 1 (the extreme case). Nevertheless, black holes with $a\approx 0.998$ are of particular interest since they represent near-extremal BHs at the Thorne Limit, where the black hole would preferentially swallow negative angular momentum photons emitted by the accretion flow, hence limiting the angular momentum up to this mentioned superior limit [34]. Orbiting particles can thus extract more energy from the BH gravitational field and gain more kinetic energy. (In this case, for example, with $R_S$ being the Schwarzchild radius, static black holes have an ISCO located at 3$R_S$, while Kerr black holes have their ISCO located at ∼$R_S/2$. We found here that there is another component in the system that can inject particles into this natural “particle accelerator”: magnetocentrifugal winds. For $a>0.9$, these winds can work as a trigger mechanism. From Figure 3 and Figure 4, plasma matter could feed the BH in a magnetocentrifugal accretion, but it could also slingshot ISCO particles to infinity with ultra-high energies (the acceleration profile is presented in a previous work, [28]). See Figure 6 for a sketch of this trigger mechanism.

Could this be a plausible source of ultra-high-energy cosmic rays? From the present picture of the centrifugal-gravitational potential ${\mathsf{\Phi }}^{cg}$, it is possible to conceive the presence of a flow of particles at ISCO colliding with marginal orbiting particles to be accelerated to infinity. The results indicate that for $a=0.98$, the lines of the magnetocentrifugal winds are approaching the BH horizon and could be a source of particle flow that collides with other particles close to the BH. Nevertheless, when the black hole spin is $a\le 0.9$, the magnetocentrifugal winds are too distant of the horizon to form a flow of trigger particles.

As a future perspective, we intend to investigate slim and thick accretion disks, given that in the super-Eddington regime, this is the expected geometry for the disk [37] as well as the calculation of the local energy spectrum.