Dynamics and Kinematics of the EUV Wave Event on 6 May 2019
Abstract
1. Introduction
2. Observational Data Sets
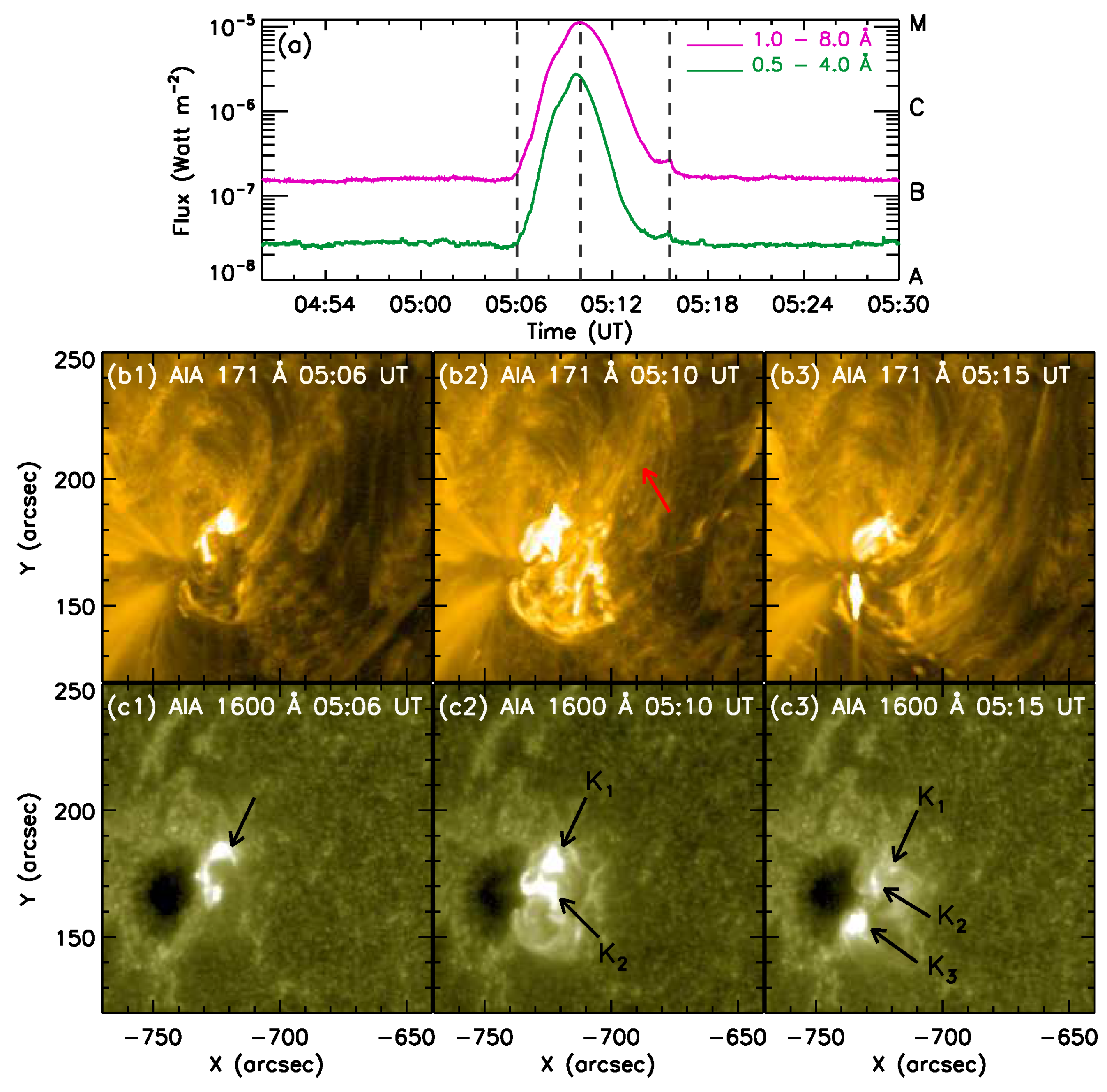
3. Flare Morphology
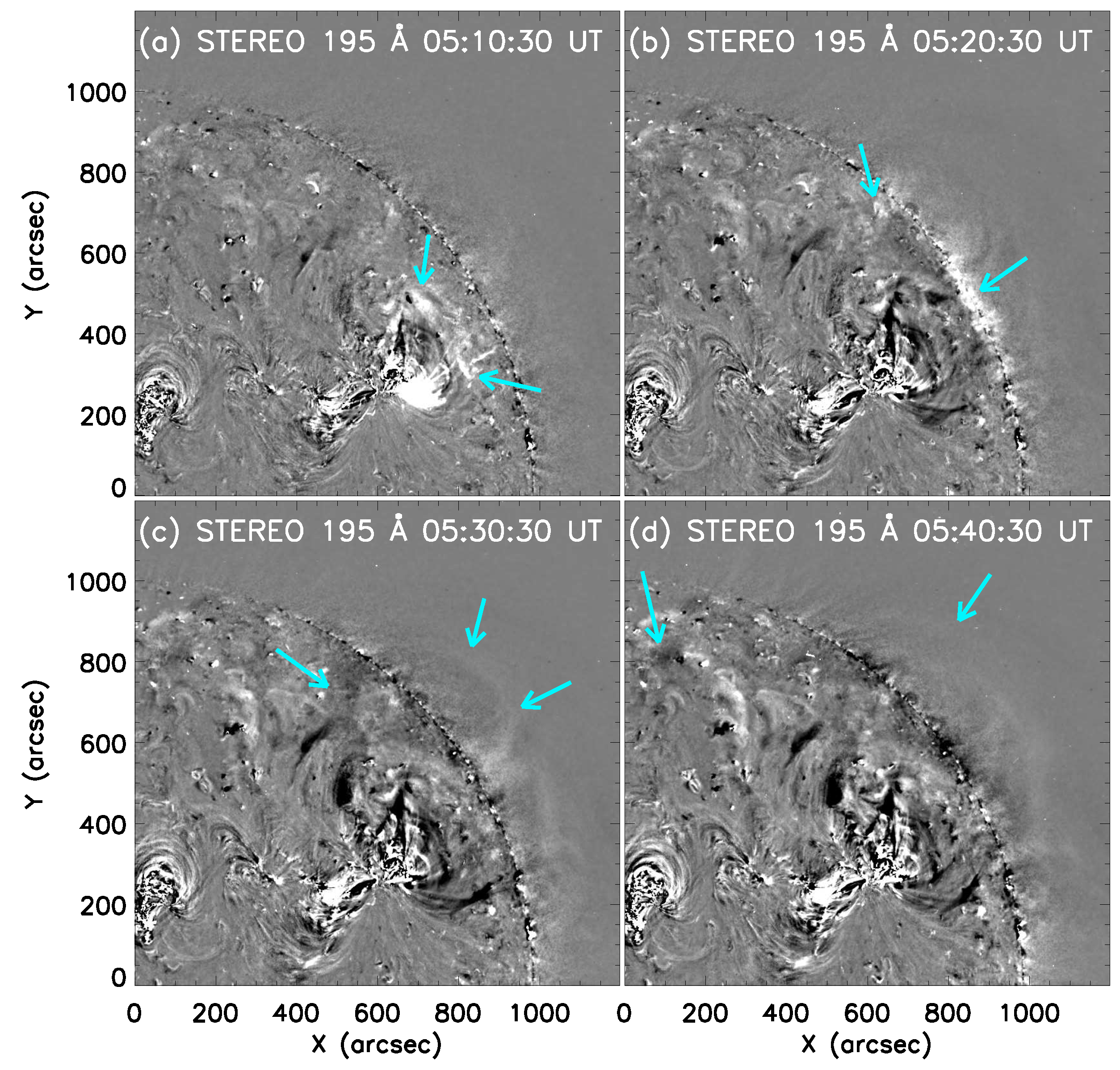
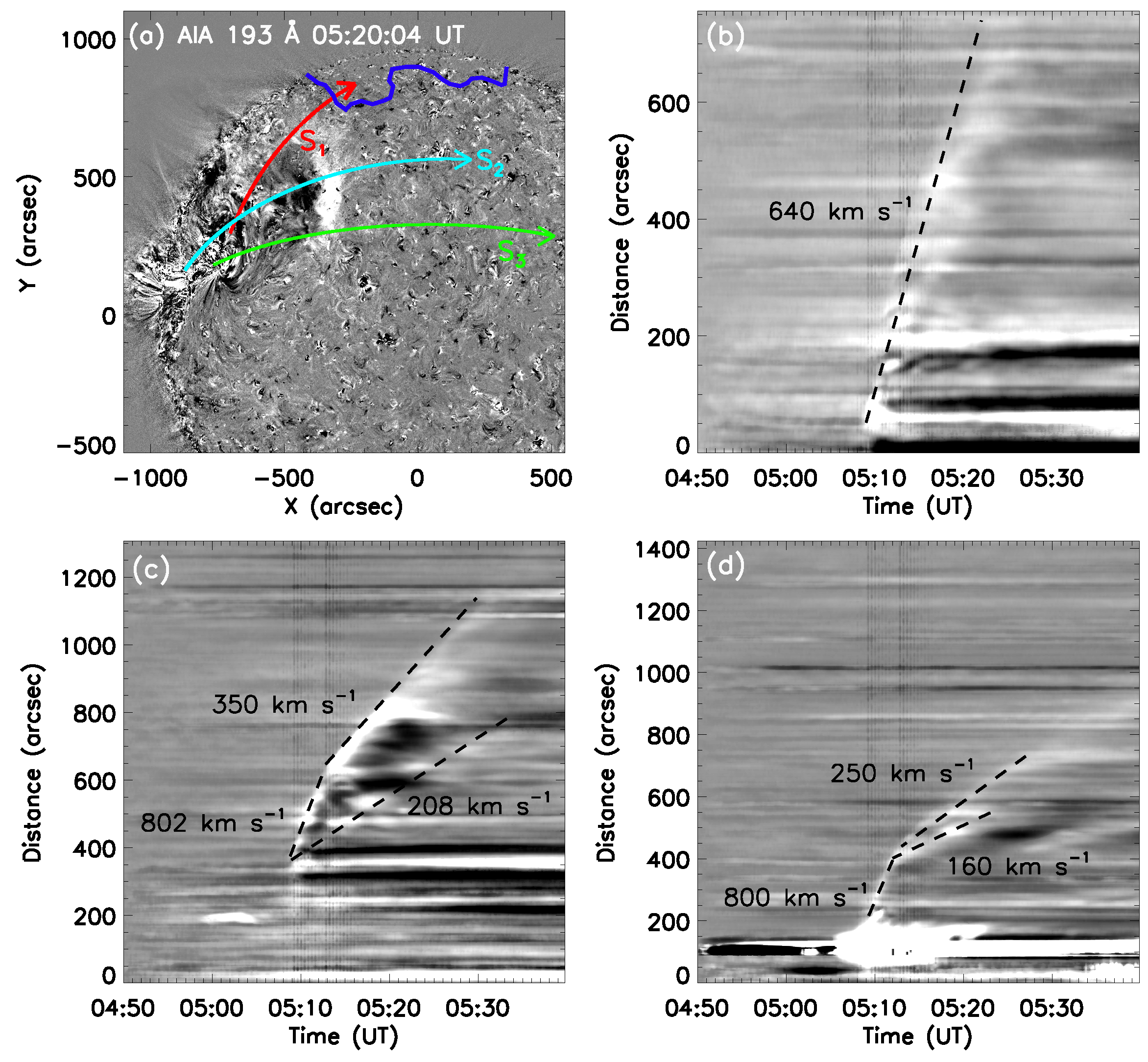
4. EUV Wave Kinematics
5. Summary and Discussions
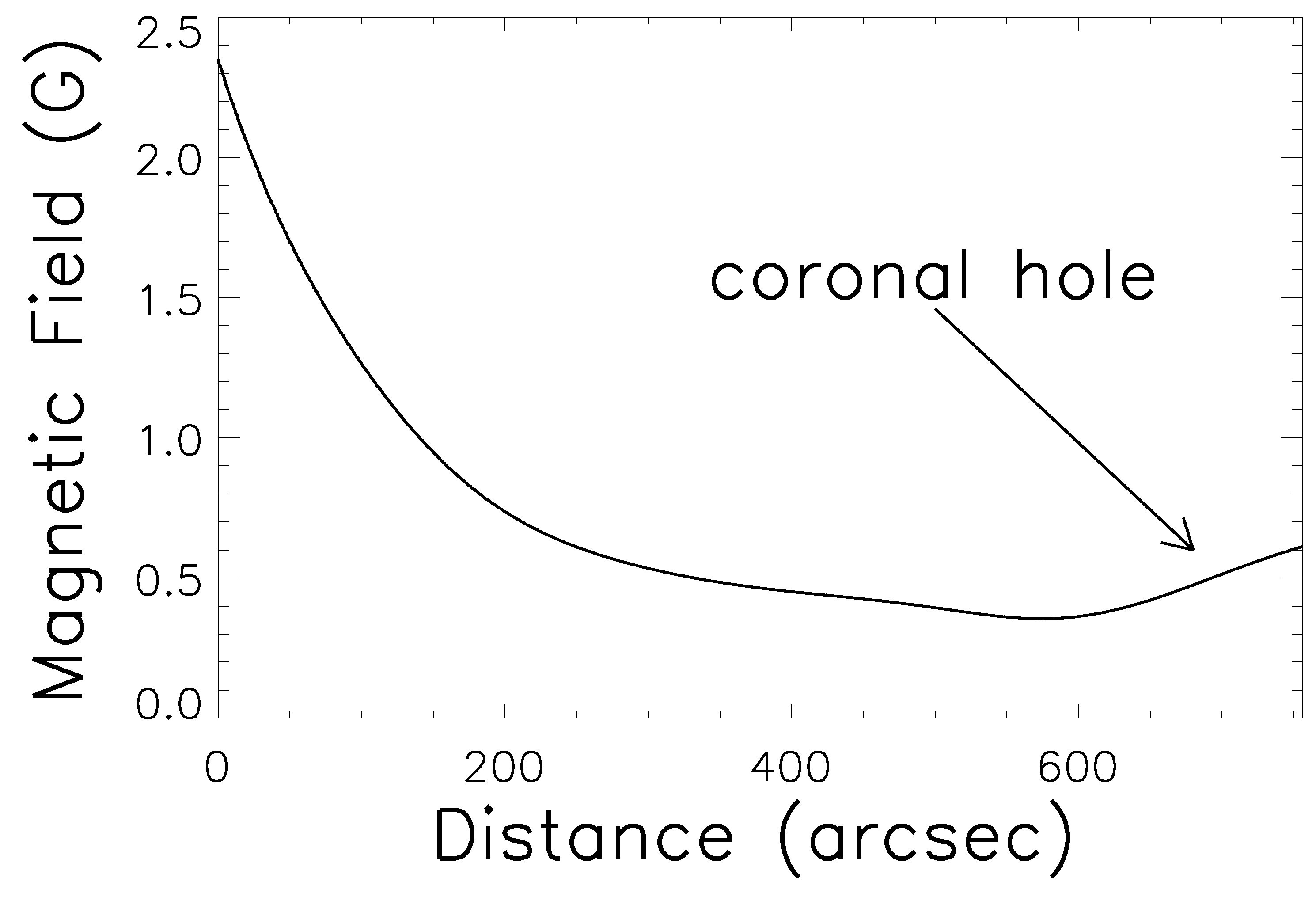
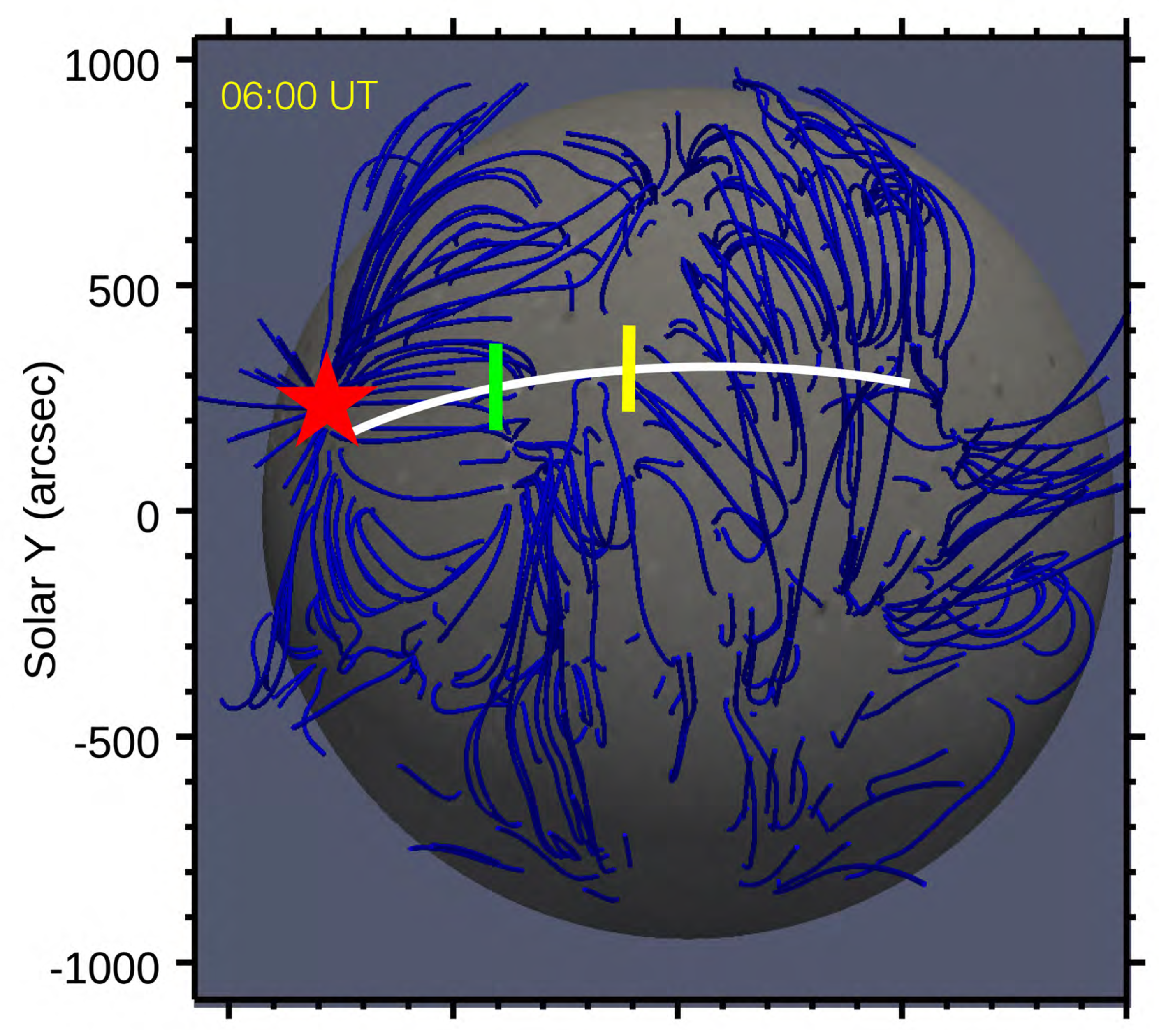
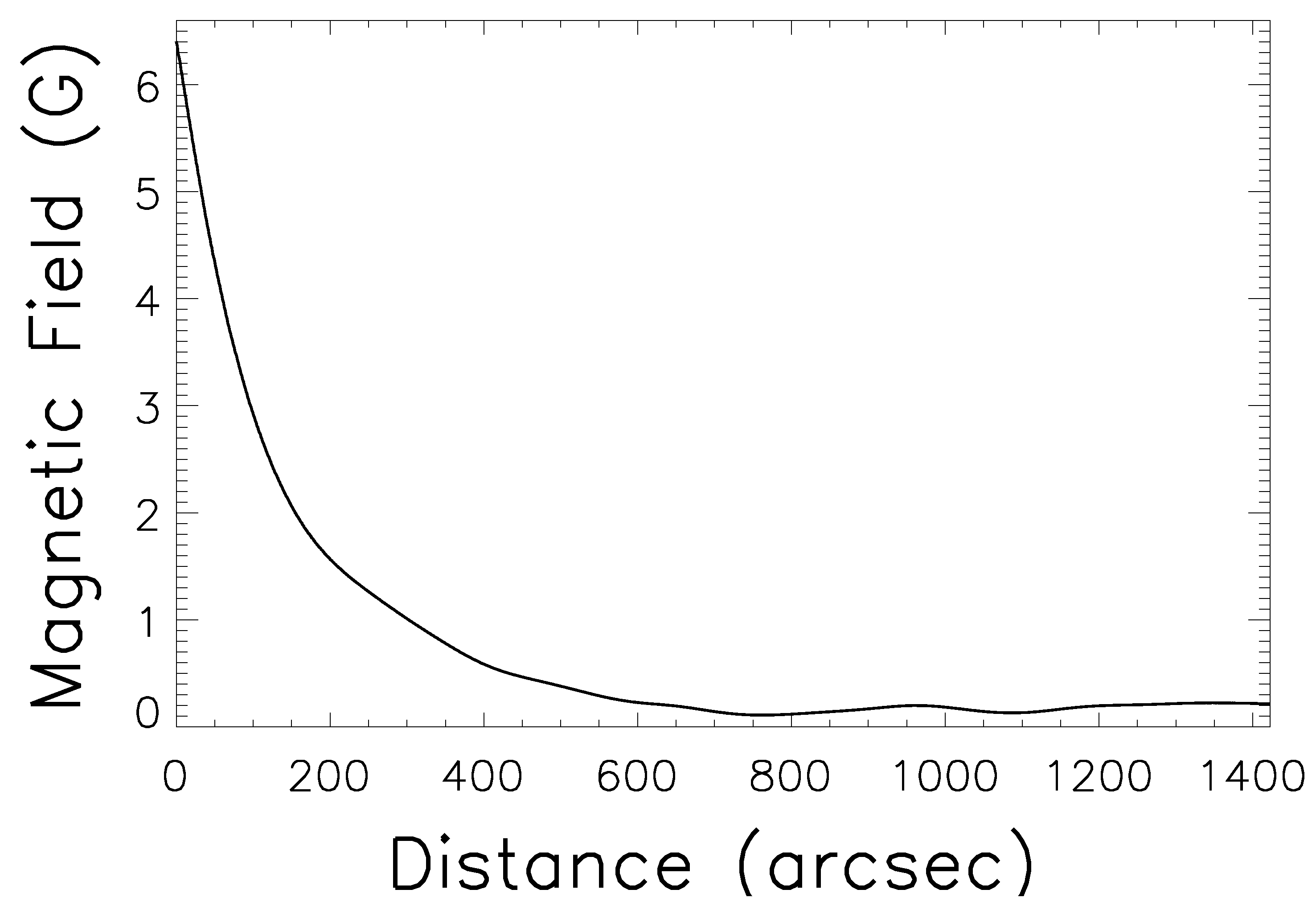
- The EUV wave event is strongly anisotropic. We selected three slices along different directions. It is seen that along the northwest direction S, only one wave was detected, and the propagation speed was km s. Along the west direction S, only one wave was detected initially, with a speed of km s. However, it split into two fronts with much smaller speeds, i.e., km s and km s, respectively. Along the direction S, which is between S and S, we detected two EUV waves, one is the fast-mode wave, and the other one is a pseudo-wave with patchy fronts.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Parker, E.N. The Solar-Flare Phenomenon and the Theory of Reconnection and Annihiliation of Magnetic Fields. Astrophys. J. Suppl. 1963, 8, 177. [Google Scholar] [CrossRef]
- Benz, A.O. Flare Observations. Living Rev. Sol. Phys. 2008, 5, 1. [Google Scholar] [CrossRef] [PubMed]
- Fletcher, L.; Dennis, B.R.; Hudson, H.S.; Krucker, S.; Phillips, K.; Veronig, A.; Battaglia, M.; Bone, L.; Caspi, A.; Chen, Q.; et al. An Observational Overview of Solar Flares. Space Sci. Rev. 2011, 159, 19–106. [Google Scholar] [CrossRef]
- Shibata, K.; Magara, T. Solar Flares: Magnetohydrodynamic Processes. Living Rev. Sol. Phys. 2011, 8, 6. [Google Scholar] [CrossRef]
- Svestka, Z. On the varieties of solar flares. In The Lower Atmosphere of Solar Flares, Proceedings of the Solar Maximum Mission Symposium, Sunspot, NM, USA, 20–24 August 1985; Neidig, D.F., Machado, M.E., Eds.; National Solar Observatory: Sunspot, NM, USA, 1986; pp. 332–355. Available online: https://ui.adsabs.harvard.edu/abs/1986lasf.conf..332S (accessed on 5 April 2022).
- Chen, P.F. Coronal Mass Ejections: Models and Their Observational Basis. Living Rev. Sol. Phys. 2011, 8, 1. [Google Scholar] [CrossRef]
- Uddin, W.; Jain, R.; Yoshimura, K.; Chandra, R.; Sakao, T.; Kosugi, T.; Joshi, A.; Despande, M.R. Multi-Wavelength Observations of an Unusual Impulsive Flare Associated with Cme. Sol. Phys. 2004, 225, 325–336. [Google Scholar] [CrossRef][Green Version]
- Chandra, R.; Jain, R.; Uddin, W.; Yoshimura, K.; Kosugi, T.; Sakao, T.; Joshi, A.; Deshpande, M.R. Energetics and Dynamics of an Impulsive Flare on 10 March 2001. Sol. Phys. 2006, 239, 239–256. [Google Scholar] [CrossRef]
- Warmuth, A. Large-scale Globally Propagating Coronal Waves. Living Rev. Sol. Phys. 2015, 12, 3. [Google Scholar] [CrossRef]
- Asai, A.; Ishii, T.T.; Isobe, H.; Kitai, R.; Ichimoto, K.; UeNo, S.; Nagata, S.; Morita, S.; Nishida, K.; Shiota, D.; et al. First Simultaneous Observation of an Hα Moreton Wave, EUV Wave, and Filament/Prominence Oscillations. Astrophys. J. Lett. 2012, 745, L18. [Google Scholar] [CrossRef]
- Kumar, P.; Cho, K.S. Simultaneous EUV and radio observations of bidirectional plasmoids ejection during magnetic reconnection. Astron. Astrophys. 2013, 557, A115. [Google Scholar] [CrossRef]
- Shen, Y.; Liu, Y.D.; Chen, P.F.; Ichimoto, K. Simultaneous Transverse Oscillations of a Prominence and a Filament and Longitudinal Oscillation of Another Filament Induced by a Single Shock Wave. Astrophys. J. 2014, 795, 130. [Google Scholar] [CrossRef]
- Guo, Y.; Ding, M.D.; Chen, P.F. Slow Patchy Extreme-ultraviolet Propagating Fronts Associated with Fast Coronal Magneto-acoustic Waves in Solar Eruptions. Astrophys. J. Suppl. 2015, 219, 36. [Google Scholar] [CrossRef]
- Srivastava, A.K.; Singh, T.; Ofman, L.; Dwivedi, B.N. Inference of magnetic field in the coronal streamer invoking kink wave motions generated by multiple EUV waves. Mon. Not. R. Astron. Soc. 2016, 463, 1409–1415. [Google Scholar] [CrossRef]
- Zhang, Q.M.; Ji, H.S. Vertical Oscillation of a Coronal Cavity Triggered by an EUV Wave. Astrophys. J. 2018, 860, 113. [Google Scholar] [CrossRef]
- Thompson, B.J.; Plunkett, S.P.; Gurman, J.B.; Newmark, J.S.; St. Cyr, O.C.; Michels, D.J. SOHO/EIT observations of an Earth-directed coronal mass ejection on 12 May 1997. Geophys. Res. Lett. 1998, 25, 2465–2468. [Google Scholar] [CrossRef]
- Hudson, H.S.; Karlický, M. Global Coronal Waves: Implications for HESSI. In High Energy Solar Physics Workshop—Anticipating HESSI; Ramaty, R., Mandzhavidze, N., Eds.; Astronomical Society of the Pacific Conference Series; Astronomical Society of the Pacific: San Francisco, CA, USA, 2000; Volume 206, p. 268. Available online: https://ui.adsabs.harvard.edu/abs/2000ASPC..206..268H (accessed on 5 April 2022).
- Nitta, N.V.; Schrijver, C.J.; Title, A.M.; Liu, W. Large-scale Coronal Propagating Fronts in Solar Eruptions as Observed by the Atmospheric Imaging Assembly on Board the Solar Dynamics Observatory—An Ensemble Study. Astrophys. J. 2013, 776, 58. [Google Scholar] [CrossRef]
- Chen, P.F. Global Coronal Waves. In Washington DC American Geophysical Union Geophysical Monograph Series; American Geophysical Union: Washington, DC, USA, 2016; Volume 216, pp. 381–394. [Google Scholar] [CrossRef]
- Delaboudinière, J.P.; Artzner, G.E.; Brunaud, J.; Gabriel, A.H.; Hochedez, J.F.; Millier, F.; Song, X.Y.; Au, B.; Dere, K.P.; Howard, R.A.; et al. EIT: Extreme-Ultraviolet Imaging Telescope for the SOHO Mission. Sol. Phys. 1995, 162, 291–312. [Google Scholar] [CrossRef]
- Moses, D.; Clette, F.; Delaboudinière, J.P.; Artzner, G.E.; Bougnet, M.; Brunaud, J.; Carabetian, C.; Gabriel, A.H.; Hochedez, J.F.; Millier, F.; et al. EIT Observations of the Extreme Ultraviolet Sun. Sol. Phys. 1997, 175, 571–599. [Google Scholar] [CrossRef]
- Cliver, E.W.; Laurenza, M.; Storini, M.; Thompson, B.J. On the Origins of Solar EIT Waves. Astrophys. J. 2005, 631, 604–611. [Google Scholar] [CrossRef][Green Version]
- Chen, P.F. The Relation between EIT Waves and Solar Flares. Astrophys. J. Lett. 2006, 641, L153–L156. [Google Scholar] [CrossRef]
- Patsourakos, S.; Vourlidas, A. On the Nature and Genesis of EUV Waves: A Synthesis of Observations from SOHO, STEREO, SDO, and Hinode (Invited Review). Sol. Phys. 2012, 281, 187–222. [Google Scholar] [CrossRef]
- White, S.M.; Thompson, B.J. High-Cadence Radio Observations of an EIT Wave. Astrophys. J. Lett. 2005, 620, L63–L66. [Google Scholar] [CrossRef][Green Version]
- Veronig, A.M.; Temmer, M.; Vršnak, B.; Thalmann, J.K. Interaction of a Moreton/EIT Wave and a Coronal Hole. Astrophys. J. 2006, 647, 1466–1471. [Google Scholar] [CrossRef]
- Long, D.M.; Gallagher, P.T.; McAteer, R.T.J.; Bloomfield, D.S. The Kinematics of a Globally Propagating Disturbance in the Solar Corona. Astrophys. J. Lett. 2008, 680, L81. [Google Scholar] [CrossRef]
- Warmuth, A.; Mann, G. Kinematical evidence for physically different classes of large-scale coronal EUV waves. Astron. Astrophys. 2011, 532, A151. [Google Scholar] [CrossRef]
- Chandra, R.; Chen, P.F.; Joshi, R.; Joshi, B.; Schmieder, B. Observations of Two Successive EUV Waves and Their Mode Conversion. Astrophys. J. 2018, 863, 101. [Google Scholar] [CrossRef]
- Chandra, R.; Chen, P.F.; Devi, P.; Joshi, R.; Schmieder, B.; Moon, Y.J.; Uddin, W. Fine Structures of an EUV Wave Event from Multi-viewpoint Observations. Astrophys. J. 2021, 919, 9. [Google Scholar] [CrossRef]
- Gopalswamy, N.; Yashiro, S.; Temmer, M.; Davila, J.; Thompson, W.T.; Jones, S.; McAteer, R.T.J.; Wuelser, J.P.; Freeland, S.; Howard, R.A. EUV Wave Reflection from a Coronal Hole. Astrophys. J. Lett. 2009, 691, L123–L127. [Google Scholar] [CrossRef]
- Zhukov, A.N.; Rodriguez, L.; de Patoul, J. STEREO/SECCHI Observations on 8 December 2007: Evidence Against the Wave Hypothesis of the EIT Wave Origin. Sol. Phys. 2009, 259, 73–85. [Google Scholar] [CrossRef]
- Delannée, C.; Aulanier, G. Cme Associated with Transequatorial Loops and a Bald Patch Flare. Sol. Phys. 1999, 190, 107–129. [Google Scholar] [CrossRef]
- Chen, P.F.; Wu, S.T.; Shibata, K.; Fang, C. Evidence of EIT and Moreton Waves in Numerical Simulations. Astrophys. J. Lett. 2002, 572, L99–L102. [Google Scholar] [CrossRef]
- Chen, P.F.; Fang, C.; Shibata, K. A Full View of EIT Waves. Astrophys. J. 2005, 622, 1202–1210. [Google Scholar] [CrossRef]
- Chandra, R.; Chen, P.F.; Fulara, A.; Srivastava, A.K.; Uddin, W. Peculiar Stationary EUV Wave Fronts in the Eruption on 2011 May 11. Astrophys. J. 2016, 822, 106. [Google Scholar] [CrossRef]
- Priest, E.R.; Démoulin, P. Three-dimensional magnetic reconnection without null points. 1. Basic theory of magnetic flipping. J. Geophys. Res. 1995, 100, 23443–23464. [Google Scholar] [CrossRef]
- Démoulin, P.; Priest, E.R.; Lonie, D.P. Three-dimensional magnetic reconnection without null points 2. Application to twisted flux tubes. J. Geophys. Res. 1996, 101, 7631–7646. [Google Scholar] [CrossRef]
- Zong, W.; Dai, Y. Mode Conversion of a Solar Extreme-ultraviolet Wave over a Coronal Cavity. Astrophys. J. Lett. 2017, 834, L15. [Google Scholar] [CrossRef]
- Chen, P.F.; Fang, C.; Chandra, R.; Srivastava, A.K. Can a Fast-Mode EUV Wave Generate a Stationary Front? Sol. Phys. 2016, 291, 3195–3206. [Google Scholar] [CrossRef]
- Lemen, J.R.; Title, A.M.; Akin, D.J.; Boerner, P.F.; Chou, C.; Drake, J.F.; Duncan, D.W.; Edwards, C.G.; Friedlaender, F.M.; Heyman, G.F.; et al. The Atmospheric Imaging Assembly (AIA) on the Solar Dynamics Observatory (SDO). Sol. Phys. 2012, 275, 17–40. [Google Scholar] [CrossRef]
- Pesnell, W.D.; Thompson, B.J.; Chamberlin, P.C. The Solar Dynamics Observatory (SDO). Sol. Phys. 2012, 275, 3–15. [Google Scholar] [CrossRef]
- Schou, J.; Scherrer, P.H.; Bush, R.I.; Wachter, R.; Couvidat, S.; Rabello-Soares, M.C.; Bogart, R.S.; Hoeksema, J.T.; Liu, Y.; Duvall, T.L.; et al. Design and Ground Calibration of the Helioseismic and Magnetic Imager (HMI) Instrument on the Solar Dynamics Observatory (SDO). Sol. Phys. 2012, 275, 229–259. [Google Scholar] [CrossRef]
- Gopalswamy, N.; Yashiro, S.; Michalek, G.; Stenborg, G.; Vourlidas, A.; Freeland, S.; Howard, R. The SOHO/LASCO CME Catalog. Earth Moon Planets 2009, 104, 295–313. [Google Scholar] [CrossRef]
- Moore, R.L.; Hagyard, M.J.; Davis, J.M.; Porter, J.G. The MSFC Vector Magnetograph, Eruptive Flares, and the SOLAR-A X-ray Images. In Flare Physics in Solar Activity Maximum 22; Uchida, Y., Canfield, R.C., Watanabe, T., Hiei, E., Eds.; Springer: Berlin/Heidelberg, Germany, 1991; Volume 387, p. 324. Available online: https://link.springer.com/chapter/10.1007/BFb0032658 (accessed on 5 April 2022). [CrossRef]
- Romano, P.; Zuccarello, F.P.; Guglielmino, S.L.; Zuccarello, F. Evolution of the Magnetic Helicity Flux during the Formation and Eruption of Flux Ropes. Astrophys. J. 2014, 794, 118. [Google Scholar] [CrossRef]
- Zuccarello, F.P.; Chandra, R.; Schmieder, B.; Aulanier, G.; Joshi, R. Transition from eruptive to confined flares in the same active region. Astron. Astrophys. 2017, 601, A26. [Google Scholar] [CrossRef]
- Veronig, A.M.; Temmer, M.; Vršnak, B. High-Cadence Observations of a Global Coronal Wave by STEREO EUVI. Astrophys. J. Lett. 2008, 681, L113. [Google Scholar] [CrossRef]
- Li, T.; Zhang, J.; Yang, S.; Liu, W. SDO/AIA Observations of Secondary Waves Generated by Interaction of the 2011 June 7 Global EUV Wave with Solar Coronal Structures. Astrophys. J. 2012, 746, 13. [Google Scholar] [CrossRef]
- Olmedo, O.; Vourlidas, A.; Zhang, J.; Cheng, X. Secondary Waves and/or the “Reflection” from and “Transmission” through a Coronal Hole of an Extreme Ultraviolet Wave Associated with the 2011 February 15 X2.2 Flare Observed with SDO/AIA and STEREO/EUVI. Astrophys. J. 2012, 756, 143. [Google Scholar] [CrossRef]
- Schmidt, J.M.; Ofman, L. Global Simulation of an Extreme Ultraviolet Imaging Telescope Wave. Astrophys. J. 2010, 713, 1008–1015. [Google Scholar] [CrossRef]
- Piantschitsch, I.; Vršnak, B.; Hanslmeier, A.; Lemmerer, B.; Veronig, A.; Hernandez-Perez, A.; Čalogović, J.; Žic, T. A Numerical Simulation of Coronal Waves Interacting with Coronal Holes. I. Basic Features. Astrophys. J. 2017, 850, 88. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chandra, R.; Chen, P.F.; Devi, P.; Joshi, R.; Ni, Y.W. Dynamics and Kinematics of the EUV Wave Event on 6 May 2019. Galaxies 2022, 10, 58. https://doi.org/10.3390/galaxies10020058
Chandra R, Chen PF, Devi P, Joshi R, Ni YW. Dynamics and Kinematics of the EUV Wave Event on 6 May 2019. Galaxies. 2022; 10(2):58. https://doi.org/10.3390/galaxies10020058
Chicago/Turabian StyleChandra, Ramesh, P. F. Chen, Pooja Devi, Reetika Joshi, and Y. W. Ni. 2022. "Dynamics and Kinematics of the EUV Wave Event on 6 May 2019" Galaxies 10, no. 2: 58. https://doi.org/10.3390/galaxies10020058
APA StyleChandra, R., Chen, P. F., Devi, P., Joshi, R., & Ni, Y. W. (2022). Dynamics and Kinematics of the EUV Wave Event on 6 May 2019. Galaxies, 10(2), 58. https://doi.org/10.3390/galaxies10020058






