Abstract
Injecting optical squeezed states of light, a technique known as squeezing, is now a tool for gravitational wave detection. Its ability to reduce quantum noise is helping to reveal more gravitational wave transients, expanding the catalog of observations in the last observing run. This review introduces squeezing and its history in the context of gravitational-wave detectors. It overviews the benefits, limitations and methods of incorporating squeezing into advanced interferometers, emphasizing the most relevant details for astrophysics instrumentation.
1. Introduction
The study of squeezed states, or squeezing, is a maturing field [1,2,3,4,5], finding applications in experiments limited by the quantum nature of light, including spectroscopy [6], quantum key distribution [7], and imaging [8]. Squeezing has expanded the reach of the LIGO and Virgo gravitational wave detectors in the most recent observing run [9,10] of these second generation detectors. Squeezing has a history in the first generation observatories of the GEO600 and LIGO Hanford detectors as a demonstration of principle [11,12] and reliable, sustained campaign of improving sensitivity of GEO600 through quantum optics [13]. At present, the combination of squeezing and diverse instrumentation improvements [14] has resulted in a nearly ten fold increase in gravitational wave detections in the most recent observing run, with 80 new events [15]. The goal of this review is to provide an overview of how squeezing can improve gravitational wave detectors, in a way that should be accessible to researchers in related fields looking for an introduction. We will introduce key considerations for squeezer performance, emphasizing those that are specific to gravitational wave detectors such as the stringent noise requirements and new techniques such as frequency dependent squeezing.
1.1. Introduction to Quantum Noise in Gravitational Wave Detectors
Gravitational wave detectors are Michelson interferometers that employ optical light to probe the spacetime along their arms. In the interferometer arms, passing gravitational waves shift or modulate the phase of the traversing optical field of carrier light, generating phase modulations at the observation frequency . Wave interference at the Michelson beamsplitter then causes the minuscule phase modulations to be observed as power fluctuations at the interferometer readout. The exquisite sensitivity of the detectors to gravitational waves is ultimately limited by the quantum nature of their probe light in detecting phase modulations.
Experimentally, the quantization of light causes “shot noise” from the independent arrival of photons on the readout detector from the interferometer. The average power on the detector and the observation time gives an expected total number of photons, while measurements of the number have a Poisson distribution. The distribution results in an uncertainty in the interferometer phase measurements, which limits the sensitivity of the current generation of gravitational wave detectors at frequencies above 50 Hz.
Amplitude uncertainty in the interferometer arms causes a fluctuating force on the suspended mirrors from the momentum fluctuations of the optical light. The acceleration from the force causes a displacement of the test mass which adds noise to the phase of the light. Thus, in gravitational wave detectors, quantum amplitude quadrature uncertainty creates phase quadrature uncertainty, with a stronger coupling at lower frequencies. This is quantum radiation pressure noise (QRPN), a manifestation of measurement back action whereby the precise measurements of the test mass positions impart uncertainty into their momentum via Heisenberg uncertainty. The momentum uncertainty causes position uncertainty during continuous observation. This is enforced physically because precise measurements of the test mass position require sufficient optical power that the momentum of the light significantly impacts the momentum of the test mass. This uncertainty results in a mechanical standard quantum limit for measurements of mechanical systems [16]. Increasing the optical power in the interferometer improves the phase sensitivity as well as increases the transfer of optical momentum and its uncertainty. The implication is shown by the dashed curve in Figure 1; as the power is increased the shot noise limited sensitivity improves while the radiation pressure noise increases.
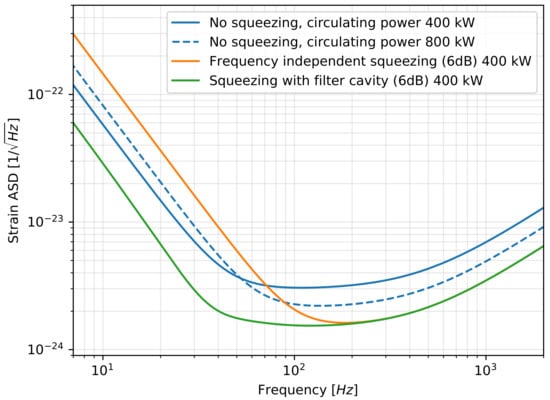
Figure 1.
Quantum noise, given in terms of equivalent gravitational-wave detector sensitivity, in the Advanced LIGO design configuration (other noises not shown), calculated using [17]. Gravitational-wave detectors are sensitive to strain, change in arm length over the total arm length. At frequencies above 200 Hz, shot noise is the dominant quantum noise while radiation pressure dominates below 50 Hz. The addition of frequency independent squeezing can reduce one type of quantum noise while increasing the other (see Section 2). Once other noise sources are reduced enough that radiation pressure dominates the low frequency sensitivity of an interferometer, injecting frequency independent squeezing will degrade the sensitivity at some frequencies. Reflecting the squeezed field off of a filter cavity can rotate and filter the squeezing in a frequency dependent way to achieve a broadband sensitivity improvement. The parameters of the injected squeezing, losses, and filter cavity are chosen here so that there is 6 dB of shot noise reduction, and 8 dB of increase in quantum radiation pressure without a filter cavity, and 6 dB improvement in quantum radiation pressure noise with a filter cavity.
1.2. Theoretical Description of Quantum Light, Squeezing
Light can be described by the two quadratures (sine and cosine) of an electric field, both of which have an associated quantum operator, and . Observations of either of these operators have a distribution or uncertainty that is imposed by the quantization of light. Figure 2 shows classic ball and stick style diagrams consisting of a field phasor, representing the quadratures of the classical mean field of the state of the carrier light, with a fuzzy ball showing the magnitude and orientation of the amplitude and phase uncertainties.
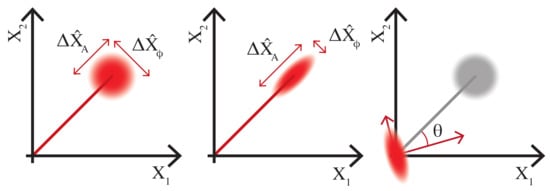
Figure 2.
Ball-and-stick diagrams for a coherent state of light (left), a squeezed state of light (center), and squeezed vacuum (right). The red line is a phasor: the amplitude of the state is represented by the length of the line, while the phase is represented by the angle of the line relative to the two quadrature axes—X and X. The uncertainty of the state is represented by a fuzzy ball at the end of the stick. The squeezed vacuum field is oriented with angle to the quadrature axes.
The first panel of Figure 2 represents a coherent state, the state of ideal laser light. These states have non-zero average field, the carrier amplitude, which provides an orientation of amplitude and phase in the phase space of the quadrature operators. Small modulations of amplitude and phase can be represented as linear combinations of the quadrature operators, and .1
The uncertainty in the two observable quadratures for vacuum and coherent states are symmetric, and equal, with . The scale N here represents the standard quantum limit (SQL) for the imprecision of optical measurements [16]. It can be in units of quanta, energy, or spectral density, depending on the experimental context and underlying normalization of the , operators. Here, such definitions are omitted, so N represents the scale of the “default” quantum noise from the vacuum state in an optical interferometer.
In the ball-and-stick picture, vacuum states (and squeezed vacuum states) are represented by an uncertainty ball (or ellipse) with no coherent amplitude. Squeezed states have reduced uncertainty in the observations of one quadrature operator compared to a vacuum or coherent state. The quadrature operators do not commute with one another, making them incompatible observables related through the uncertainty relation:
This relation indicates that the quantum phase space of any state has at least the uncertainty area, N, of the vacuum state. The squeezing level, in decibels of phase noise variance reduction with respect to the vacuum state, is given by
Due to the uncertainty relation, phase quadrature squeezing causes amplitude quadrature “anti-squeezing”, with corresponding increase in its noise variance.
Squeezed states in general are not required to independently affect only or . One can instead form a squeezed state using operators in a basis rotated by an angle with respect to and , known as the squeezing angle. More in-depth discussion of quantum optics can be found in [18,19].
To date, this theory describes squeezed states which promise to reduce with no apparent limit, arbitrarily improving the sensitivity of interferometers. Realistically, the observed noise reduction of squeezed states is limited through decoherence and degradations of purely-generated squeezed states into impure, mixed states. Those degradations and their implications are detailed in later sections.
1.3. Squeezing in Gravitational Wave Detectors
The “squeezed light upgrade” of gravitational wave detectors surprisingly does not require the main interferometer laser to be modified. Instead, squeezed states are separately produced and injected at the “output” port, see Figure 3. The interferometers are operated with nearly perfect destructive interference, in which case almost all of the input carrier light reflects back towards the laser. Caves realized that the quantum state entering the “output port” is similarly reflected, and thus, in conjunction with the input laser power and the mass of the test masses, establishes the quantum state of the light incident on the readout [20]. During its reflection, the state enters, and is modified by, the interferometer.
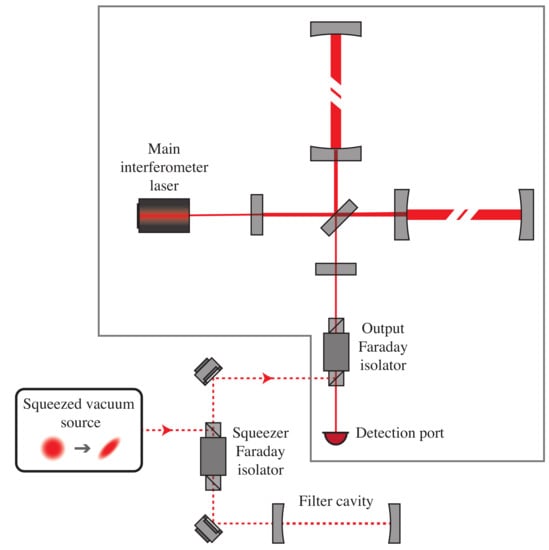
Figure 3.
Simplified optical layout of a dual-recycled Fabry–Perot Michelson interferometer (grey box), with frequency-dependent squeezing injected at the output port, as is planned the aLIGO and AdVirgo detectors in Observing Run 4. The squeezed vacuum source generates frequency-independent squeezed light. The squeezed beam (dashed red line) is reflected off the filter cavity, passes back through one or more squeezer Faraday isolators, and is injected into the main interferometer through the output Faraday isolator.
Another example of the phase quadrature displacement is the addition of the fringe light from a static offset in the arm lengths. This displacement adds a large coherent amplitude to the output state without changing the statistics of quadrature observations. By default, vacuum states are perpetually incident on the output port, and the output field consists of the vacuum states mixed with the interferometer field (see Figure 2), causing the readout to have shot noise with Poisson statistics. For squeezing, the vacuum is replaced by squeezed states [20] causing readout noise with sub-Poisson uncertainty for the correct squeezing orientation. This implies—remarkably—that the seemingly passive injection of a field at the output changes the manner by which the classical laser field in the interferometer is emitted and read as photon counts.
Figure 1 shows the impact of both squeezing and carrier power changes on the quantum noise of the Advanced LIGO design. Increasing the optical power in the interferometer improves the phase sensitivity but also directly increases the quantum radiation pressure noise due to backaction, as shown by the dashed curve in Figure 1. Injection of phase squeezing also improves the shot noise limited sensitivity, but increases the radiation pressure noise due to anti-squeezing of the amplitude quadrature.
2. Frequency Dependent Squeezing
The ball-and-stick description of squeezing introduced above shows the squeezing level at a single frequency. The squeezing ellipse can be oriented differently or more or less squeezed at different observation frequencies. Defining the quadrature operators independently for each observation frequency allows the classical description of the frequency response of optical cavities to describe transformations to squeezed states in the frequency domain. The formal description of the relevant frequency domain description of optical states, and its subtleties, is detailed in refs [21,22].
Because of quantum radiation pressure noise, reducing quantum noise throughout the gravitational wave frequency band requires amplitude squeezing at low frequencies and phase squeezing at high frequencies. This can be implemented by continuously rotating the squeezing angle as a function of the observation frequency. The appropriate rotation is achieved by reflecting the squeezed beam off of an optical cavity with its resonance detuned (shifted away) from the interferometer’s carrier frequency [23,24,25,26,27,28]. Quantum filter cavities and frequency dependent squeezing are planned to be used in both LIGO and Virgo in the next observing run. Some details of them and their history is included in Section 5.4.
3. Generating Squeezed States of Light
All gravitational-wave detectors currently implementing squeezing use a sub-threshold optical parametric oscillator (OPO), alternately called an optical parametric amplifier, to generate squeezed vacuum [9,10,29]. The squeezer system starts with a laser which is phase locked to have the exact frequency as the main interferometer laser. The squeezer laser pumps a second harmonic generator (SHG) which frequency doubles the 1064 nm light to 532 nm, as shown in Figure 4. The 532 nm light generated by the SHG is then used to pump the optical parametric oscillator.
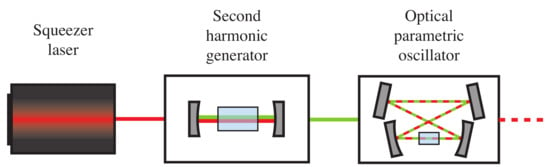
Figure 4.
Simplified schematic for squeezed light generation. Red lines indicate 1064 nm beams, green lines are 532 nm, dashed line is squeezed light. The squeezer laser pumps a second harmonic generator which creates the 532 nm light which in turn pumps an optical parametric oscillator.
Since the first experimental realization of squeezing in 1985 [30], several key advances have been made to generate squeezing suitable for use in gravitational wave observatories. The SHG and OPO both use three-wave mixing caused by a second order susceptibility in a crystal, where the induced polarization caused by an applied electric field has a quadratic term allowing exchange of energy between the field at 1064 nm and 532 nm [31]. In the SHG case, two photons of carrier light convert to frequency-doubled pump light. In OPOs for squeezing, pump photons are down converted into entangled pairs of photons. This process can occur spontaneously or be seeded by an injected field. In either case, the conservation of energy requires that a pump photon at twice the carrier frequency, , is down converted to a pair of photons at symmetric sideband frequencies , where is the audio band observation frequency. Vacuum fluctuations are incident on the OPO cavity; the correlated pairs of photons generated inside the OPO mean that the field reflected off the cavity can be highly squeezed. More detailed explanations of how an OPO generates squeezing can be found in several references, including [5,19,32,33].
All of the squeezers in use for gravitational wave detectors use a periodically-poled potassium titanyl phosphate (PPKTP) crystal to create their nonlinear interaction, chosen for low loss and high nonlinear coefficient, as discussed in [34]. This crystal is poled for quasi-phase matching [35], which requires that the crystal temperature be controlled to allow for efficient interactions between the two wavelengths. The weak nonlinearity additionally requires high intensity pump light via small beam sizes [36]. The interaction strength is further enhanced using multiple passes in an optical cavity, resonant for the interferometer carrier field. Some OPOs are also doubly resonant, meaning that both the interferometer wavelength and the second-harmonic pump resonate [34]. Doubly resonant cavities require the dispersion between the two wavelengths to be compensated to keep both wavelengths on resonance, while also maintaining the crystal temperature required for phase matching. Several key developments for generating squeezed vacuum states for use in gravitational wave detectors have been made over the last several decades [37,38], as reviewed in [39].
4. Results and History in GEO600, LIGO, Virgo
In the most recent gravitational wave observation run, known as O3, the LIGO, Virgo and GEO600 detectors used squeezing routinely to extend their astrophysical reach [9,10,29]. Figure 5 shows the sensitivity improvements in the LIGO and Virgo detectors, which were the results of decades of research and preparation.
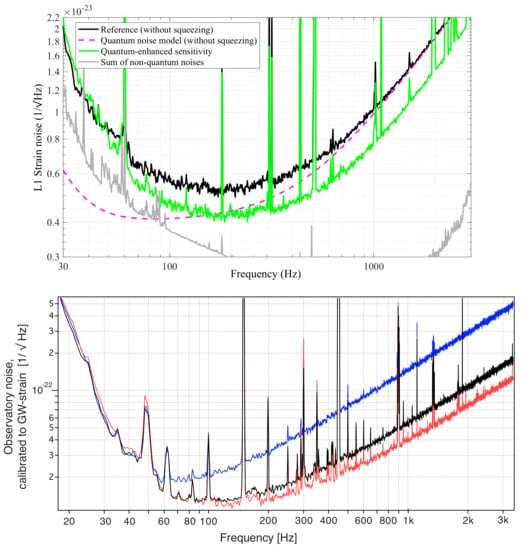
Figure 5.
(Top) Improved sensitivity of the LIGO Livingston detector in the 3rd observing run, reproduced from [9]. The black trace shows the sensitivity without squeezing injected, while the green trace shows the 2.7 ± 0.1 dB shot noise reduction with squeezing injected. The dashed magenta line shows a model of quantum noise in the detector without squeezing injected, while the gray trace is an estimate of the other noises. (Bottom) Improved sensitivity of the Virgo interferometer in the 3rd observing run, reproduced from [10]. The black trace shows the sensitivity without squeezing injected, the red trace shows the 3.2 ± 0.1 dB shot noise reduction with squeezing injected, and blue shows the 8.5 ± 0.1 dB increase in shot noise when the squeezing quadrature is rotated by 90 degrees.
The GEO600 gravitational wave observatory was the first kilometer scale gravitational wave detector to implement squeezing in 2010 [11]. The GEO squeezer uses a linear, hemilithic cavity with a PPKTP crystal resonant for 1064nm and pumped by a single pass 532 nm beam, on an in air optical bench [40]. Efforts at GEO have focused on long term stability [13,41], improvements to the coherent control technique (discussed in Section 5.3) [42], angular controls of squeezing [43], and loss reduction [44]. The GEO detector now routinely runs with 6 dB of shot noise reduction, after several improvements to reduce losses [29].
Virgo implemented squeezing in 2019 with a linear, doubly resonant OPO on an in air opticalTable [45]. The crystal used in this OPO has two regions with separate temperature controllers, most of the crystal is temperature controlled to maintain the phase matching condition, while a small region of the crystal is separately controlled to ensure that both wavelengths are resonant in the cavity. The integration of this squeezed light source with the Virgo controls and automation is described in [46]. The level of squeezing seen in Virgo is limited by optical losses, and shown in Figure 5.
A proof of principle experiment in the LIGO Hanford detector in 2012 demonstrated 2 dB of shot noise reduction [12]. An in air, doubly resonant, traveling wave OPO design with a wedged PPKTP crystal was used to produce squeezing [34]. The crystal temperature is controlled to maintain the phase matching condition in the nonlinear crystal, while a translation stage can adjust the path length in the wedged portion of the crystal to ensure that both wavelengths are resonant in the cavity at the required crystal temperature. This short term squeezing experiment was also used to study the backscatter noise introduced to the detector by squeezing from an in air squeezer [47] and the squeezing angle phase noise [48]. As discussed in Section 5.2, this experiment led LIGO and collaborators at ANU to develop an OPO that could be suspended inside the vacuum system to reduce noise [49,50,51,52].
In 2019, LIGO installed in vacuum, doubly resonant bow tie OPOs with wedged PPKTP crystals at both Hanford and Livingston observatories, which resulted in nearly 3 dB of shot noise reduction during the third observation run, as shown in Figure 5 [9]. The quantum radiation pressure noise limited the sensitivity of the Livingston detector, so that the degradation and improvement in quantum radiation pressure noise due to squeezing was observed when squeezing was injected with different squeezing angles [53]. When the maximum level of squeezing available was injected into the interferometer at Livingston, the increased radiation pressure noise degraded the overall sensitivity to astrophysical sources. For this reason the level of squeezing used for routine observations was less than the maximum available [9]. Frequency dependent losses limited the level of squeezing available in both LIGO detectors, as discussed in Section 5.5 and in [54].
5. Integration of Squeezing in Gravitational-Wave Detectors
Gravitational wave detectors are some of the most sensitive meteorology instruments in the world. They impose demanding requirements on optical field stability and physical motion in the audio signal band. High levels of squeezing and frequency dependent squeezing have been developed and demonstrated in lab scale experiments for decades, but require some adaptation to interoperate with gravitational wave interferometers. In this section, we will discuss some of the factors that limit squeezing, ways in which the squeezed light upgrade can add noise to these sensitive instruments, and approaches to improve performance.
5.1. Loss and Phase Noise
The level of squeezing measured in an interferometer or any other squeezing measurement is degraded in three main ways: optical losses, phase noise of the squeezing ellipse [55,56], and coherent light from the interferometer that can be modulated by the squeezer. The first and second degradations are discussed in this section, while the third is discussed in Section 5.2.
The first degradation, optical loss, mixes un-squeezed vacuum states into the squeezed states. This creates mixed states in which the squeezed quadrature is substantially less squeezed, while the anti-squeezed quadrature stays nearly the same. In short, optical losses representing the attenuation of power, , limit the level of observable noise reduction to be . Potential sources of losses are intracavity losses in the OPO, characterized by the escape efficiency, losses in relay optics including Faraday isolators [57,58,59], alignment fluctuations or misalignment of the squeezer beam [52], and mode mismatches between the squeezed beam and mode of the gravitational wave sidebands (or arm cavities)[54].
Fluctuations of the measurement quadrature relative to the squeezed quadrature, called phase noise, mix the increased noise of the anti-squeezed quadrature into the measurement. Phase noise at any frequency limits the useful squeezing level: fluctuations faster than the measurement frequency integrate to limit the measured squeezing while slow fluctuations limit the average interferometer sensitivity to gravitational waves. The phase noise requirements become increasingly stringent at high levels of squeezing [49]. Phase noise is introduced by a variety of mechanisms, including RF sidebands used for interferometer sensing, and sensing errors in the coherent control scheme discussed in Section 5.3. These errors are induced by OPO length noise, temperature fluctuations of the nonlinear crystal, and alignment fluctuations [48].
Levels of loss and phase noise in a squeezing measurement, either in a gravitational wave interferometer or on a balanced homodyne detector, can be characterized by making a series of measurements with different amounts of pump power in the OPO, as shown in Figure 6, and included in [44,48]. As the pump power is increased, the generated states are increasingly squeezed. The loss and phase noise are determined by mapping the dependence between the generated vs. observed noise levels in the squeezing and anti-squeezing quadratures.
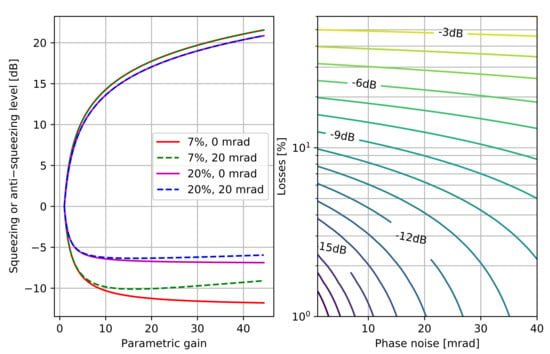
Figure 6.
(Left) Levels of loss and phase noise in a squeezing measurement can be characterized by measuring the level of squeezing as the parametric gain is varied by changing the OPO pump power. Expressions used to make this plot are explained in [55,56]. The 20% and 7% loss levels are expected requirements for reaching 6 dB and 10 dB of observed squeezing in current and future interferometers. (Right) Observable squeezing level with parametric gain optimized for high squeezing [48,52]. This figure shows that to improve from 3 dB to 6 dB of squeezing requires mostly loss reduction, but to reach the 10 dB level of squeezing will also require low phase noise.
Since the maximum level of squeezing is limited by both the losses and phase noise, measurements of the level of noise in the anti-squeezed quadrature are used to distinguish between the two effects. As the pump power and parametric gain increases, the level of anti-squeezing is increased, limited by losses with minimal impact from phase noise. Phase noise causes the squeezing level to decrease at high parametric gains by mixing in the increased noise from the anti-squeezed quadrature, so measurements of the squeezing level at high nonlinear gains provide information about the level of phase noise, as shown by the dashed curves in Figure 6. Because both loss and phase noise can be dependent on the observation frequency in a complex interferometer (see Section 5.5), these measurements may need to be analyzed at multiple frequencies, as in [54].
For any squeezing measurement there is a nonlinear gain setting that maximizes the level of squeezing given the level of RMS phase noise, and the amount of pump power can be adjusted to adjust the nonlinear gain. This maximum level of measured squeezing is plotted as a function of loss and phase noise in the right panel of Figure 6. While Figure 6 shows the maximum available shot noise reduction, a gravitational wave interferometer which is limited by quantum radiation pressure noise may need to use less than the maximum available to optimize sensitivity, as in [9].
5.2. Backscatter, Technical Noise Introduced by Squeezer
The extreme sensitivity of gravitational wave detectors means that care must be taken to ensure that the squeezer does not introduce noise that will mask gravitational wave signals. Light scattered out of the interferometer towards the squeezer adds coherent light that the squeezer or filter cavity can modulate and then return to the interferometer with the squeezed states, adding a potential noise source via spurious interference paths. This noise can arise both from path length fluctuations which modulate this coherent field in the phase quadrature as well as from noise added to the field within the OPO itself.
A proof of principle squeezing experiment in the LIGO Hanford detector studied noise introduced to the detector by scatter in the phase quadrature, which must be small compared to shot noise [60]. Scatter into the amplitude quadrature also introduces noise by driving differential radiation pressure within the interferometer.
The noise added by these spurious interference paths can be reduced by reducing the motion of the squeezer components and any intermediate path length fluctuations, by moving them into the vacuum system [50,52] and by suspending them [51]. Reducing the amplitude of scattered light can also reduce backscatter noise. Faraday isolators are a key means to reduce the amplitude of backscatter light, but they introduce loss that degrades the squeezing level.
A low loss Faraday isolator is needed to inject squeezing into the interferometer, and typically provides at least 30 dB of isolation between the interferometer and the squeezer components [57,58,59]. In the third observing run the LIGO, GEO, and Virgo interferometers, respectively, add one, two and three low loss Faraday isolators to further attenuate light reaching the OPO from the interferometer [9,10,29]. Linear OPO cavities reflect all of the scattered light incident on them back towards the interferometer, whereas traveling wave cavities, such as bow-tie cavities, provide nearly 50 dB of backscatter isolation limited by imperfections of the nonlinear crystal and mirrors used [47]. The use of high quality optics in the squeezer can prevent introducing additional sources of scattered light [61]. GEO has reported observing backscatter from the squeezer that is amplified or de-amplified by the nonlinear gain of the OPO [29]. This backscatter noise depends on the nonlinear gain of the OPO, scaling similarly to phase noise and limiting the maximum squeezing level.
5.3. Controls
One of the major challenges for building a squeezer suitable for use in gravitational wave detectors has been the control of the squeezing angle. Introducing a field with a coherent amplitude into the OPO creates several noise couplings that mask any squeezing in the audio frequency band (10 Hz–10 kHz) at which ground based gravitational wave detectors operate [37]. This presents a challenge for control of the squeezer, including the OPO cavity length, filter cavity length, and squeezing angle. To control the OPO cavity length, either a frequency shifted field in the orthogonal polarization [40] or the second harmonic field have been used [34]. In both cases, care has to be taken that the resonance of the field used for sensing is the same as the squeezed field.
Two techniques have been developed to control the squeezing angle without introducing a coherent amplitude at audio frequencies: coherent control [62] and noise locking [63]. The noise lock relies on a dither of the squeezing angle, and demodulation of a measurement of the noise power. This technique ensures that the squeezing angle is locked to a point which minimizes noise in the measurement, however it introduces phase noise which will limit the level of squeezing measured. While the coherent control technique is preferable, the experience at GEO600 has shown that a noise lock in addition to the coherent control can help improve the stability of the squeezing level [13,29].
5.4. Filter Cavity
A filter cavity is required to prepare the correct frequency dependent squeezing if an interferometer’s sensitivity is limited by radiation pressure noise, which the LIGO and Virgo detectors currently are [53]. The filter cavity is detuned, meaning that the resonance of the filter cavity is shifted away from the interferometer carrier frequency by a few 10 s of Hz. In reflecting off the detuned filter cavity, upper and lower optical sidebands experience different phase shifts, which rotates the squeezing ellipse [24]. The cavity linewidth must be <100 Hz to rotate the squeezing ellipse at the correct frequency, and can be adjusted for significant changes in interferometer circulating power by changing the filter cavity input coupler [64].
The earliest experiments in frequency dependent squeezing was a proof of the physical effect [25] followed by a demonstration in the audio band [26] using off-carrier control. Frequency dependent squeezing has been observed and characterized recently at the audio frequencies needed for gravitational wave detectors in a 300 m as well as a 16 m linear cavity [27,28]. Work is currently underway to install a 285 m long filter cavity at Virgo [65,66,67] and a 300 m long filter cavity at both LIGO observatories [68], KAGRA has similar plans for a future upgrade.
Adding a filter cavity to the squeezing path introduces frequency dependent losses from the resonantly-enhanced internal cavity loss and any beam mode mismatch (cf. Section 5.5). The losses reduce the level of squeezing at low frequencies [69]. The loss per length of a filter cavity is the figure to be minimized to preserve low frequency squeezing [70]; longer cavities have been shown to achieve lower loss per unit length [71,72]. Optical losses in the filter cavity not only mix squeezing with the vacuum, they also “de-phase” the squeezed state by de-correlating the upper and lower frequency components of the optical quantum state [54]. This creates a noise term that scales with the nonlinear gain.
The filter cavity rotates the squeezing angle only at observation frequencies inside its linewidth, and the rotation angle is determined by the offset (“detuning”) between the interferometer carrier frequency and the cavity resonance frequency. Length variations of the filter cavity shift that detuning, creating phase noise that only degrades squeezing in the mid or low frequency audio band [73]. The magnitude of the phase noise depends on the total RMS length noise, establishing requirements on the total environmental noise and the control system to suppress it.
Adding a linear filter cavity also adds an additional backscatter path and can require more Faraday isolators than just the squeezer OPO, especially compared to traveling-wave OPO cavities. Compared to the squeezer, filter cavities have a very high finesse and thus very strict length noise requirements to prevent backscatter noise [68]. The recent laboratory demonstrations of audio-band frequency dependent squeezing [27,28] observe this backscatter noise from the minuscule diffuse scatter from the local oscillator of their balanced homodyne readout. The backscatter power in gravitational-wave interferometers is expected to be substantially higher and drives many integration requirements unique to their implementation into observatories, such as multiple-stage suspensions, active seismic isolation, and new controls techniques [28,74].
5.5. Mode Matching and Frequency Dependence of Interferometer Response
In order to reduce the quantum noise of the interferometer, the transverse spatial field profile (“mode”) of the Gaussian beam emitted from the squeezed state source needs to match the optical mode of the interferometer’s resonating cavities. When there is a mode mismatch between the spatial profile of the squeezed beam and the interferometer, then the squeezed states do not have a full overlap with the interferometer states. The beam entering the interferometer mode in this case can be decomposed into a mixture of the squeezed field and unsqueezed vacuum in higher order transverse modes.
The mixed states formed from squeezed and vacuum states can behave like an optical loss (degrading squeezing) when observed, but unlike most losses, mode mismatch is a coherent process that depends on how optical cavities and optical telescopes transform the spatial modes. Additionally, optical cavity transmissions and reflections add frequency dependence to these transformations. In total, the optical loss and phase shifts of the squeezing ellipse can pick several frequency dependent changes which are relatively unique to their implementation in advanced gravitational wave interferometers. These effects were first observed, described, and analyzed in both LIGO Hanford and Livingston [54] during observing run three.
There are two key takeaways in the observation of frequency dependent losses. The first is that they indicate that squeezing in interferometers is uniquely more challenging to fully characterize than in broadband laboratory experiments. For interferometers which have both arm and signal extraction cavities, such as LIGO, losses typically increase at higher frequencies where the interferometer spectrum is predominantly quantum noise2. The increase in losses can bias estimates of the frequency-independent incoherent losses inferred using only high frequency measurements. More painstaking measurements at lower frequencies, where classical noises must be accounted and removed, are required to characterize the squeezing performance in the audio frequencies of the signal band. The second takeaway is that squeezing losses have a complicated relationship to independent measurements of mode matching between cavities: the impact of mode mismatch on squeezing cannot be simply estimated based on mode matching efficiencies. More fully understanding these relationships will be necessary to produce future specifications of telescope and optical design tolerances and to efficiently commission squeezing systems for interferometers.
Along with mode matching, the optomechanics of radiation pressure also cause frequency dependence in the interferometer response to squeezing. To increase the astrophysical range, this is addressed to first order using the frequency dependent squeezing from a filter cavity, as described above. To fully utilize and optimize filter cavities, we anticipate that yet more complex interactions between the squeezing systems, interferometer cavities, and their optomechanics will be observed. Gravitational wave interferometers are now contributing to squeezing research as well as benefiting from it.
6. Conclusions and Future Plans
6.1. Plans for Upgrading Existing Detectors
In 2023 LIGO, Virgo, and KAGRA plan to start the fourth observing run, with frequency-dependent squeezing implemented at the LIGO and Virgo observatories. The filter cavity is a major squeezer hardware upgrade. With broadband frequency-dependent squeezing, and active wavefront control elements which will reduce loss due to mode mismatch between the cavities of the squeezer and interferometer [75,76], the squeezing improvements to detector sensitivity are expected to be greater than in the third observing run.
Plans beyond the next observing run for the LIGO detectors include the remaining elements of the “A+” upgrade [77]. One of the upgrades for A+ is the detection scheme, which will change from the Michelson fringe to balanced homodyne detection, which will allow the quadrature measured at the detection port to be controlled.
6.2. Plans for Next Generation Detectors
Future ground-based gravitational-wave detectors all include the injection of frequency-dependent squeezed light in their design studies. Cosmic Explorer is a proposed future detector which uses a dual-recycled Fabry–Perot Michelson topology (like LIGO), with proposed arm lengths of 20 and 40 km. The Cosmic Explorer design includes a squeezed light source and 4 km long filter cavity to generate 10 dB of broadband squeezing improvement to the sensitivity [78]. To achieve this level of squeezing improvement, the design targets a total optical loss of ≲8% and phase noise of ≲10 mrad.
The Einstein telescope is another proposed future detector, using a triangular topology and collocated pairs of Michelson interferometers targeting different gravitational-wave frequencies. The Einstein Telescope (ET) also incorporates 10 dB of broadband frequency-dependent squeezing into its design [79]. For the high frequency detector and squeezed light source at 1064 nm and a 300 m filter cavity is proposed. The low frequency detector will operate in a detuned configuration, which means that two filter cavities will be required for frequency dependent squeezing [80]. The low frequency ET design also calls for a main laser wavelength of 1550 nm, which means that the squeezed light source will also need to operate at 1550 nm. The ET design is also investigating more elaborate quantum non-demolition schemes to further reduce the quantum noise.
The neutron star extreme matter observatory (NEMO) is another proposed future gravitational-wave detector targeting the high frequency audio band (2–4 kHz) [81]. In this detection band radiation pressure noise no longer limits the detector, and shot noise is the only relevant quantum noise term meaning that NEMO has no need for a filter cavity. The NEMO design thus injects frequency-independent squeezing, with design improvement at 7 dB.
6.3. Summary and Conclusions
Squeezing has become a tool for gravitational wave observatories, with demonstrated reliable performance at LIGO, Virgo and GEO600. The implementation of squeezing at these observatories has been accomplished without introducing noise that limits the sensitivity to gravitational waves, through successful mitigation of scattered light. While these implementations of squeezing have demonstrated improvements to the astrophysical reach of ground based interferometers, realizing the full potential of squeezing for this type of observatory remains a significant challenge.
Both Virgo and LIGO are currently building filter cavities to allow for improvements in quantum noise at frequencies limited by quantum radiation pressure noise as well as shot noise. These cavities need very low losses and creative and precise control schemes to achieve the desired sensitivity for observing runs planned in 2023.
The achievement of 6 dB of squeezing at GEO600 required years of careful effort in loss reduction and controls. LIGO and Virgo are both aiming to increase the level of squeezing in the next observing run. For LIGO, active mode matching will help reach the low levels of effective loss needed to reach 6 dB of squeezing, while challenging, increasing the level of squeezing to 6 dB in combination with filter cavities will provide significant improvements in the rate of gravitational wave observations.
Looking to the future, gravitational-wave observatories will aim to obtain the maximum possible benefit from squeezing, with plans for 10 dB of squeezing. The considerations covered in this review, including control of squeezing and filter cavities, optical losses, phase noise, mode matching and scattered light are going to continue to be crucial in squeezer designs. As ground based gravitational wave astronomy continues to grow as a field, the drive towards better sensitivity will require painstaking attention to each of the factors that can limit squeezing.
Funding
LIGO was constructed by the California Institute of Technology and Massachusetts Institute of Technology with funding from the National Science Foundation, and operates under Cooperative Agreement Grant No. PHY- 1764464. Advanced LIGO was built under Grant No. PHY- 0823459. A+ LIGO is being constructed under Grant PHY-1834382.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Notes
| 1 | Note, our definition of phase and amplitude quadrature operators is specifically by choosing a basis of the quadrature operators suitable to describe their respective first-order modulations of a reference classical field. This in contrast to conceptual operators defined to uniquely represent phase and amplitude measurements at all orders (e.g., the Susskind–Glogower or Pegg–Barnett phase operators). |
| 2 | In interferometers with either arm or signal extraction cavities, the effect is reversed. |
References
- Stoler, D. Equivalence Classes of Minimum Uncertainty Packets. Phys. Rev. D 1970, 1, 3217–3219. [Google Scholar] [CrossRef]
- Lu, E.Y.C. New Coherent States of the Electromagnetic Field. Lett. Nuovo C 1971, 2, 1241–1244. [Google Scholar] [CrossRef]
- Yuen, H.P. Two-Photon Coherent States of the Radiation Field. Phys. Rev. A 1976, 13, 2226–2243. [Google Scholar] [CrossRef] [Green Version]
- Walls, D.F. Squeezed States of Light. Nature 1983, 306, 141–146. [Google Scholar] [CrossRef]
- Collett, M.J.; Gardiner, C.W. Squeezing of Intracavity and Traveling-Wave Light Fields Produced in Parametric Amplification. Phys. Rev. A 1984, 30, 1386–1391. [Google Scholar] [CrossRef]
- Junker, J.; Wilken, D.; Huntington, E.; Heurs, M. High-precision cavity spectroscopy using high-frequency squeezed light. Opt. Express 2021, 29, 6053–6068. [Google Scholar] [CrossRef]
- Gehring, T.; Haendchen, V.; Duhme, J.; Furrer, F.; Franz, T.; Pacher, C.; Werner, R.F.W.; Schnabel, R. Implementation of continuous-variable quantum key distribution with composable and one-sided-device-independent security against coherent attacks. Nat. Commun. 2015, 6, 8795. [Google Scholar] [CrossRef] [Green Version]
- Lawrie, B.J.; Lett, P.D.; Marino, A.M.; Pooser, R.C. Quantum Sensing with Squeezed Light. ACS Photonics 2019, 6, 1307–1318. [Google Scholar] [CrossRef]
- Tse, M.; Yu, H.; Kijbunchoo, N.; Fernandez-Galiana, A.; Dupej, P.; Barsotti, L.; Blair, C.D.; Brown, D.D.; Dwyer, S.E.; Effler, A.; et al. Quantum-Enhanced Advanced LIGO Detectors in the Era of Gravitational-Wave Astronomy. Phys. Rev. Lett. 2019, 123, 231107. [Google Scholar] [CrossRef] [Green Version]
- Acernese, F.; Agathos, M.; Aiello, L.; Allocca, A.; Amato, A.; Ansoldi, S.; Antier, S.; Arène, M.; Arnaud, N.; Ascenzi, S.; et al. Increasing the Astrophysical Reach of the Advanced Virgo Detector via the Application of Squeezed Vacuum States of Light. Phys. Rev. Lett. 2019, 123, 231108. [Google Scholar] [CrossRef] [Green Version]
- LIGO Scientific Collaboration. A gravitational wave observatory operating beyond the quantum shot-noise limit. Nat. Phys. 2011, 7, 962–965. [Google Scholar] [CrossRef] [Green Version]
- LIGO Scientific Collaboration. Enhanced sensitivity of the LIGO gravitational wave detector by using squeezed states of light. Nat. Photon 2013, 7, 613–619. [Google Scholar] [CrossRef]
- Grote, H.; Danzmann, K.; Dooley, K.L.; Schnabel, R.; Slutsky, J.; Vahlbruch, H. First Long-Term Application of Squeezed States of Light in a Gravitational-Wave Observatory. Phys. Rev. Lett. 2013, 110, 181101. [Google Scholar] [CrossRef] [PubMed]
- Buikema, A.; Cahillane, C.; Mansell, G.L.; Blair, C.D.; Abbott, R.; Adams, C.; Adhikari, R.X.; Ananyeva, A.; Appert, S.; Arai, K.; et al. Sensitivity and Performance of the Advanced LIGO Detectors in the Third Observing Run. Phys. Rev. D 2020, 102, 062003. [Google Scholar] [CrossRef]
- LIGO Scientific Collaboration; Virgo Collaboration ; KAGRA Collaboration; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, N.; Adhikari, R.X. GWTC-3: Compact Binary Coalescences Observed by LIGO and Virgo During the Second Part of the Third Observing Run. arXiv 2021, arXiv:2111.03606. [Google Scholar]
- Braginsky, V.B.; Khalili, F.Y. Quantum nondemolition measurements: The route from toys to tools. Rev. Mod. Phys. 1996, 68, 1–11. [Google Scholar] [CrossRef]
- Pygwinc: Python Gravitational Wave Interferometer Noise Calculator. Available online: https://git.ligo.org/gwinc (accessed on 15 September 2021).
- Walls, D.F.; Milburn, G.J. Quantum Optics; Springer: New York, NY, USA, 1995. [Google Scholar]
- Gerry, C.; Knight, P. Introductory Quantum Optics; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar] [CrossRef]
- Caves, C.M. Quantum-mechanical noise in an interferometer. Phys. Rev. D 1981, 23, 1693–1708. [Google Scholar] [CrossRef]
- Caves, C.M.; Schumaker, B.L. New formalism for two-photon quantum optics. I. Quadrature phases and squeezed states. Phys. Rev. A 1985, 31, 3068–3092. [Google Scholar] [CrossRef]
- Schumaker, B.L.; Caves, C.M. New formalism for two-photon quantum optics. II. Mathematical foundation and compact notation. Phys. Rev. A 1985, 31, 3093–3111. [Google Scholar] [CrossRef]
- Unruh, W.G. Quantum Noise in the Interferometer Detector. In Quantum Optics, Experimental Gravity, and Measurement Theory; Meystre, P., Scully, M.O., Eds.; NATO Advanced Science Institutes Series; Springer: Boston, MA, USA, 1983; pp. 647–660. [Google Scholar] [CrossRef]
- Kimble, H.J.; Levin, Y.; Matsko, A.B.; Thorne, K.S.; Vyatchanin, S.P. Conversion of conventional gravitational-wave interferometers into quantum nondemolition interferometers by modifying their input and/or output optics. Phys. Rev. D 2001, 65, 022002. [Google Scholar] [CrossRef] [Green Version]
- Chelkowski, S.; Vahlbruch, H.; Hage, B.; Franzen, A.; Lastzka, N.; Danzmann, K.; Schnabel, R. Experimental Characterization of Frequency-Dependent Squeezed Light. Phys. Rev. A 2005, 71, 013806. [Google Scholar] [CrossRef] [Green Version]
- Oelker, E.; Isogai, T.; Miller, J.; Tse, M.; Barsotti, L.; Mavalvala, N.; Evans, M. Audio-Band Frequency-Dependent Squeezing for Gravitational-Wave Detectors. Phys. Rev. Lett. 2016, 116, 041102. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Aritomi, N.; Capocasa, E.; Leonardi, M.; Eisenmann, M.; Guo, Y.; Polini, E.; Tomura, A.; Arai, K.; Aso, Y.; et al. Frequency-Dependent Squeezed Vacuum Source for Broadband Quantum Noise Reduction in Advanced Gravitational-Wave Detectors. Phys. Rev. Lett. 2020, 124, 171101. [Google Scholar] [CrossRef] [PubMed]
- McCuller, L.; Whittle, C.; Ganapathy, D.; Komori, K.; Tse, M.; Fernandez-Galiana, A.; Barsotti, L.; Fritschel, P.; MacInnis, M.; Matichard, F.; et al. Frequency-Dependent Squeezing for Advanced LIGO. Phys. Rev. Lett. 2020, 124, 171102. [Google Scholar] [CrossRef] [PubMed]
- Lough, J.; Schreiber, E.; Bergamin, F.; Grote, H.; Mehmet, M.; Vahlbruch, H.; Affeldt, C.; Brinkmann, M.; Bisht, A.; Kringel, V.; et al. First Demonstration of 6 dB Quantum Noise Reduction in a Kilometer Scale Gravitational Wave Observatory. Phys. Rev. Lett. 2021, 126, 041102. [Google Scholar] [CrossRef] [PubMed]
- Slusher, R.E.; Hollberg, L.W.; Yurke, B.; Mertz, J.C.; Valley, J.F. Observation of Squeezed States Generated by Four-Wave Mixing in an Optical Cavity. Phys. Rev. Lett. 1985, 55, 2409–2412. [Google Scholar] [CrossRef]
- Boyd, R.W. Nonlinear Optics; Elsevier: Amsterdam, The Netherlands, 2008. [Google Scholar]
- Schnabel, R.; Mavalvala, N.; McClelland, D.E.; Lam, P.K. Quantum Metrology for Gravitational Wave Astronomy. Nat. Commun. 2010, 1, 121. [Google Scholar] [CrossRef] [Green Version]
- Schnabel, R. Squeezed States of Light and Their Applications in Laser Interferometers. Phys. Rep. 2017, 684, 1–51. [Google Scholar] [CrossRef] [Green Version]
- Stefszky, M.; Mow-Lowry, C.M.; McKenzie, K.; Chua, S.; Buchler, B.C.; Symul, T.; McClelland, D.E.; Lam, P.K. An Investigation of Doubly-Resonant Optical Parametric Oscillators and Nonlinear Crystals for Squeezing. J. Phys. B At. Mol. Opt. Phys. 2010, 44, 015502. [Google Scholar] [CrossRef]
- Fejer, M.M.; Magel, G.A.; Jundt, D.H.; Byer, R.L. Quasi-Phase-Matched Second Harmonic Generation: Tuning and Tolerances. IEEE J. Quantum Electron. 1992, 28, 2631–2654. [Google Scholar] [CrossRef] [Green Version]
- Boyd, G.D.; Kleinman, D.A. Parametric Interaction of Focused Gaussian Light Beams. J. Appl. Phys. 1968, 39, 3597–3639. [Google Scholar] [CrossRef]
- McKenzie, K.; Grosse, N.; Bowen, W.P.; Whitcomb, S.E.; Gray, M.B.; McClelland, D.E.; Lam, P.K. Squeezing in the Audio Gravitational-Wave Detection Band. Phys. Rev. Lett. 2004, 93, 161105. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vahlbruch, H.; Mehmet, M.; Chelkowski, S.; Hage, B.; Franzen, A.; Lastzka, N.; Goßler, S.; Danzmann, K.; Schnabel, R. Observation of Squeezed Light with 10-dB Quantum-Noise Reduction. Phys. Rev. Lett. 2008, 100, 033602. [Google Scholar] [CrossRef] [Green Version]
- Barsotti, L.; Harms, J.; Schnabel, R. Squeezed vacuum states of light for gravitational wave detectors. Rep. Prog. Phys. 2018, 82, 016905. [Google Scholar] [CrossRef]
- Vahlbruch, H.; Khalaidovski, A.; Lastzka, N.; Gräf, C.; Danzmann, K.; Schnabel, R. The GEO600 squeezed light source. Class. Quantum Gravity 2010, 27, 084027. [Google Scholar] [CrossRef] [Green Version]
- Khalaidovski, A.; Vahlbruch, H.; Lastzka, N.; Graf, C.; Danzmann, K.; Grote, H.; Schnabel, R. Long-term stable squeezed vacuum state of light for gravitational wave detectors. Class. Quantum Gravity 2012, 29, 075001. [Google Scholar] [CrossRef] [Green Version]
- Dooley, K.L.; Schreiber, E.; Vahlbruch, H.; Affeldt, C.; Leong, J.R.; Wittel, H.; Grote, H. Phase control of squeezed vacuum states of light in gravitational wave detectors. Opt. Express 2015, 23, 8235–8245. [Google Scholar] [CrossRef]
- Schreiber, E.; Dooley, K.L.; Vahlbruch, H.; Affeldt, C.; Bisht, A.; Leong, J.R.; Lough, J.; Prijatelj, M.; Slutsky, J.; Was, M.; et al. Alignment sensing and control for squeezed vacuum states of light. Opt. Express 2016, 24, 146–152. [Google Scholar] [CrossRef] [Green Version]
- Khalaidovski, A.; Vahlbruch, H.; Lastzka, N.; Gräf, C.; Lück, H.; Danzmann, K.; Grote, H.; Schnabel, R. Status of the GEO 600 squeezed-light laser. J. Phys. Conf. Ser. 2012, 363, 012013. [Google Scholar] [CrossRef] [Green Version]
- Mehmet, M.; Vahlbruch, H. The Squeezed Light Source for the Advanced Virgo Detector in the Observation Run O3. Galaxies 2020, 8, 79. [Google Scholar] [CrossRef]
- Nguyen, C.; Bawaj, M.; Sequino, V.; Barsuglia, M.; Bazzan, M.; Calloni, E.; Ciani, G.; Conti, L.; D’Angelo, B.; De Rosa, R.; et al. Automated source of squeezed vacuum states driven by finite state machine based software. Rev. Sci. Instrum. 2021, 92, 054504. [Google Scholar] [CrossRef] [PubMed]
- Chua, S.; Stefszky, M.; Mow-Lowry, C.; Buchler, B.; Dwyer, S.; Shaddock, D.; Lam, P.K.; McClelland, D. Backscatter tolerant squeezed light source for advanced gravitational-wave detectors. Opt. Lett. 2011, 36, 4680–4682. [Google Scholar] [CrossRef] [PubMed]
- Dwyer, S.; Barsotti, L.; Chua, S.S.Y.; Evans, M.; Factourovich, M.; Gustafson, D.; Isogai, T.; Kawabe, K.; Khalaidovski, A.; Lam, P.K.; et al. Squeezed quadrature fluctuations in a gravitational wave detector using squeezed light. Opt. Express 2013, 21, 19047–19060. [Google Scholar] [CrossRef] [PubMed]
- Oelker, E.; Mansell, G.; Tse, M.; Miller, J.; Matichard, F.; Barsotti, L.; Fritschel, P.; McClelland, D.E.; Evans, M.; Mavalvala, N. Ultra-low phase noise squeezed vacuum source for gravitational wave detectors. Optica 2016, 3, 682–685. [Google Scholar] [CrossRef]
- Wade, A.R.; Mansell, G.L.; Chua, S.S.; Ward, R.L.; Slagmolen, B.J.; Shaddock, D.A.; McClelland, D.E. A squeezed light source operated under high vacuum. Sci. Rep. 2015, 5, 18052. [Google Scholar] [CrossRef] [Green Version]
- Fernández-Galiana, Á.; McCuller, L.; Kissel, J.; Barsotti, L.; Miller, J.; Tse, M.; Evans, M.; Aston, S.M.; Abbott, R.; Shaffer, T.J.; et al. Advanced LIGO squeezer platform for backscattered light and optical loss reduction. Class. Quantum Gravity 2020, 37, 215015. [Google Scholar] [CrossRef]
- Oelker, E.; Barsotti, L.; Dwyer, S.; Sigg, D.; Mavalvala, N. Squeezed light for advanced gravitational wave detectors and beyond. Opt. Express 2014, 22, 21106–21121. [Google Scholar] [CrossRef] [Green Version]
- Yu, H.; McCuller, L.; Tse, M.; Kijbunchoo, N.; Barsotti, L.; Mavalvala, N. Quantum correlations between light and the kilogram-mass mirrors of LIGO. Nature 2020, 583, 43–47. [Google Scholar] [CrossRef]
- McCuller, L.; Dwyer, S.E.; Green, A.C.; Yu, H.; Kuns, K.; Barsotti, L.; Blair, C.D.; Brown, D.D.; Effler, A.; Evans, M.; et al. LIGO’s quantum response to squeezed states. Phys. Rev. D 2021, 104, 062006. [Google Scholar] [CrossRef]
- Aoki, T.; Takahashi, G.; Furasawa, A. Squeezing at 946 nm with periodically poled KTiOPO4. Opt. Express 2006, 14, 6930–6935. [Google Scholar] [CrossRef] [Green Version]
- Takeno, Y.; Yukawa, M.; Yonezawa, H.; Furusawa, A. Observation of -9 dB quadrature squeezing with improvement of phasestability in homodyne measurement. Opt. Express 2007, 15, 4321–4327. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Goetz, R.; Fulda, P.; Martin, R.; Tanner, D. Low Loss Faraday Isolators for Squeezed Vacuum Injection in Advanced LIGO. In APS April Meeting Abstracts; APS: College Park, MD, USA, 2016; p. 14. [Google Scholar]
- Martin, R.; Notte, J.; Reyes, J.; Fulda, P.; Goetz, R.; Tanner, D.B. The A+ Low-Loss Faraday Isolators. LIGO DCC G2101056, LIGO DCC. 2021. Available online: https://dcc.ligo.org/DocDB/0176/G2101056/001/G2101056_APlusLLFI_GWADW2021.pdf. (accessed on 15 December 2021).
- Genin, E.; Mantovani, M.; Pillant, G.; Rossi, C.D.; Pinard, L.; Michel, C.; Gosselin, M.; Casanueva, J. Vacuum-compatible low-loss Faraday isolator for efficient squeezed-light injection in laser-interferometer-based gravitational-wave detectors. Appl. Opt. 2018, 57, 9705–9713. [Google Scholar] [CrossRef] [PubMed]
- Chua, S.S.Y.; Dwyer, S.; Barsotti, L.; Sigg, D.; Schofield, R.M.S.; Frolov, V.V.; Kawabe, K.; Evans, M.; Meadors, G.D.; Factourovich, M.; et al. Impact of backscattered light in a squeezing-enhanced interferometric gravitational-wave detector. Class. Quantum Gravity 2014, 31, 035017. [Google Scholar] [CrossRef] [Green Version]
- Vahlbruch, H.; Chelkowski, S.; Danzmann, K.; Schnabel, R. Quantum Engineering of Squeezed States for Quantum Communication and Metrology. New J. Phys. 2007, 9, 371. [Google Scholar] [CrossRef]
- Chelkowski, S.; Vahlbruch, H.; Danzmann, K.; Schnabel, R. Coherent control of broadband vacuum squeezing. Phys. Rev. A 2007, 75, 043814. [Google Scholar] [CrossRef] [Green Version]
- McKenzie, K.; Mikhailov, E.E.; Goda, K.; Lam, P.K.; Grosse, N.; Gray, M.B.; Mavalvala, N.; McClelland, D.E. Quantum noise locking. J. Opt. B Quantum Semiclass. Opt. 2005, 7, S421. [Google Scholar] [CrossRef]
- Whittle, C.; Komori, K.; Ganapathy, D.; McCuller, L.; Barsotti, L.; Mavalvala, N.; Evans, M. Optimal Detuning for Quantum Filter Cavities. Phys. Rev. D 2020, 102, 102002. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adya, V.B.; Affeldt, C.; Agathos, M.; et al. Prospects for Observing and Localizing Gravitational-Wave Transients with Advanced LIGO, Advanced Virgo and KAGRA. Living Rev. Relativ. 2020, 23, 3. [Google Scholar] [CrossRef]
- Virgo Collaboration. Advanced Virgo Plus Phase I—Design Report. Technical Report VIR-0596A-19, Virgo TDS. 2019. Available online: https://tds.virgo-gw.eu/?content=3&r=15777. (accessed on 15 December 2021).
- Sequino, V. Quantum Noise Reduction in Advanced Virgo. Phys. Scr. 2021, 96, 104014. [Google Scholar] [CrossRef]
- McCuller, L.; Barsotti, L.; Design Requirements Document of the A+ Filter Cavity and Relay Optics for Squeezing Injection. Technical Report T1800447-v7, LIGO DCC. 2018. Available online: https://dcc.ligo.org/public/0156/T1800447/007/FC_DRD_T1800447-v7.pdf (accessed on 15 November 2021).
- Corbitt, T.; Mavalvala, N.; Whitcomb, S. Optical cavities as amplitude filters for squeezed fields. Phys. Rev. D 2004, 70, 022002. [Google Scholar] [CrossRef] [Green Version]
- Khalili, F.Y. Optimal configurations of filter cavity in future gravitational-wave detectors. Phys. Rev. D 2010, 81, 122002. [Google Scholar] [CrossRef] [Green Version]
- Evans, M.; Barsotti, L.; Kwee, P.; Harms, J.; Miao, H. Realistic filter cavities for advanced gravitational wave detectors. Phys. Rev. D 2013, 88, 022002. [Google Scholar] [CrossRef] [Green Version]
- Isogai, T.; Miller, J.; Kwee, P.; Barsotti, L.; Evans, M. Loss in long-storage-time optical cavities. Opt. Express 2013, 21, 30114–30125. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kwee, P.; Miller, J.; Isogai, T.; Barsotti, L.; Evans, M. Decoherence and degradation of squeezed states in quantum filter cavities. Phys. Rev. D 2014, 90, 062006. [Google Scholar] [CrossRef] [Green Version]
- Aritomi, N.; Leonardi, M.; Capocasa, E.; Zhao, Y.; Flaminio, R. Control of a Filter Cavity with Coherent Control Sidebands. Phys. Rev. D 2020, 102, 042003. [Google Scholar] [CrossRef]
- Srivastava, V.; Mansell, G.; Makarem, C.; Noh, M.; Abbott, R.; Ballmer, S.; Billingsley, G.; Brooks, A.; Cao, H.T.; Fritschel, P.; et al. Piezo-deformable Mirrors for Active Mode Matching in Advanced LIGO. arXiv 2021, arXiv:2110.00674. [Google Scholar]
- Cao, H.T.; Brooks, A.; Ng, S.W.S.; Ottaway, D.; Perreca, A.; Richardson, J.W.; Chaderjian, A.; Veitch, P.J. High dynamic range thermally actuated bimorph mirror for gravitational wave detectors. Appl. Opt. 2020, 59, 2784–2790. [Google Scholar] [CrossRef]
- LIGO Scientific Collaboration. Instrument Science White Paper LIGO-T2000407. Available online: dcc.ligo.org/LIGO-T2000407/public (accessed on 3 November 2021).
- Evans, M.; Adhikari, R.X.; Afle, C.; Ballmer, S.W.; Biscoveanu, S.; Borhanian, S.; Brown, D.A.; Chen, Y.; Eisenstein, R.; Gruson, A.; et al. A Horizon Study for Cosmic Explorer: Science, Observatories, and Community. arXiv 2021, arXiv:2109.09882. [Google Scholar]
- Einstein Telescope Steering Committee Einstein Telescope Design Report Update 2020. Available online: https://gwic.ligo.org/3Gsubcomm/docs/ET-0007B-20_ETDesignReportUpdate2020.pdf (accessed on 15 November 2021).
- Jones, P.; Zhang, T.; Miao, H.; Freise, A. Implications of the quantum noise target for the Einstein Telescope infrastructure design. Phys. Rev. D 2020, 101, 082002. [Google Scholar] [CrossRef]
- Ackley, K.; Adya, V.B.; Agrawal, P.; Altin, P.; Ashton, G.; Bailes, M.; Baltinas, E.; Barbuio, A.; Beniwal, D.; Blair, C.; et al. Neutron Star Extreme Matter Observatory: A kilohertz-band gravitational-wave detector in the global network. Publ. Astron. Soc. Aust. 2020, 37, e047. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).