Abstract
The aim of this manuscript is to explore singularity-free solution for a specific self-gravitating highly dense object known as gravastar suggested by Mazur and Mottola, in the context of gravity theory. Gravastars are regarded as a possible alternate to black hole. To derive modified field equations and law of conservation related to Gauss-Bonnet gravity, we assume cylindrically symmetric irrotational configuration. Particular equation of states are used for the illustration of three sectors of gravastar model. Furthermore, we are intended to obtain a regular solution for our model and graphs will be used to elaborate various substantial characteristics of it.
PACS:
04.70.Bw; 04.70.Dy; 11.25.-w
1. Introduction
The universe’s beginning has always been the topic of interest since the conception of life. The big bang explains the wide variety of phenomenon such as concentration of light elements and large scale structures, which were evolved originally from a high temperature and high-density state. With the lapse of time, the temperature of cosmos decreased to some extent that enabled the creation of atoms and subatomic particles. It is believed that at the earlier stage, the stars and galaxies were formed due to the existence of large clouds of hydrogen, lithium, and helium. Earlier astronomers were convinced with the view that our universe is static. Gold and Bondi proposed the “stationary model of the universe”, according to which the universe was not concerted at a point and the time had no specific origin. Later on, they suggested the constant cosmos density by claiming the continuous matter formation. Olber through the understanding of Kepler asked himself a question “Why the sky is dark at night”? Olber argued that the increasing size of the universe and uniform population of stars within it must increase the light received by the earth. The paradox was resolved by the concept of expansion of the universe.
The concept of expanding the universe is reasonable instead of the static one. Wirtz and Hubble suggested that galaxies are drifting away from our planet with velocities proportional to their distances from it. The expansion of the universe was proven theoretically by Friedmann by using Einstein field equations. According to the virial theorem, the gravitating potential energy should be doubled as compared to the internal thermal energy to preserve the stability of a star. In the case of a massive star, its matter will be attracted in the direction of its center of gravity and at the end of fuel, it diminishes due to its gravity. This phenomenon is known as gravitational collapse. Based on distinct masses of collapsing star white dwarf, neutron star, and black holes are devised as the outcome of gravitational collapse. The presence of numerous stellar-mass black holes is assumed in our galaxy. However, if we analyze the quantum gravitational effects then it may be possible that no event horizon is formed and in this scenario no black hole will be formed. By considering this fact many researchers proposed distinct compact objects as the alternate to a black hole and gravastar is one of these assumptions [1]. The solution related to distinct compact objects can also be seen in literature [2,3,4,5,6,7]. In the case of gravastar, a quantum vacuum phase transition is claimed which prevents the creation of event horizon. Mazur and Mottola (MM) [8] suggested the creation of a singularity-free object named gravastar as a result of the gravitational collapse of a massive star. For their proposal, they used the concept of Bose-Einstein condensation. The structure of gravastar is generally assumed to consist of three sectors named as an inner sector, shell, and outer sector. The thickness of the shell is taken as small within the limits , where is taken as the radius of the inner sector, whereas the radius of the outer sector is represented by while points out the width of the thin shell. These sectors are elaborated by the use of following Equation of states (EoS)
- Inner sector ,
- Intermediate thin shell ,
- Outer sector .
The inner region’s EoS indicates the dominance of dark energy in it. The repelling force generated by the dark energy evades the development of singularity in the inner sector. The absence of singularity and event horizon in gravastar play a vital role in differentiating it from a black hole [9]. After the inner region, we assume the presence of an intermediate thin layer shell consisting of ultra-relativistic matter that was firstly used by Zel’dovich [10] for the illustration of matter with high pressure. The equality between light speed and sound speed is assumed for such types of matter. The exterior of gravastar is a vacuum and we use Schwarzschild, Reissner-Nordström or Kerr-Newmann metric for its elaboration depending upon the assumed conditions.
A lot of theoretical and mathematical work related to gravastar exist in literature and is mostly done in general relativity (GR) [11,12,13,14,15,16,17,18,19,20]. Bhatti [21] constructed the gravastar model by assuming thin-shell representation and discussed its feasible characteristics with the help of cylindrically symmetric metric. Visser and Wiltshire [17] dynamically analyzed the gravastar model proposed by MM [8] and derived the EoS which was necessary for the dynamical consistency of the model. Cattoen et al. [22] deduced the result that the existence of anisotropic pressure is necessary in the case of no shell in gravastar. Bhatti et al. [23] evaluated the substantial attributes of gravastar in gravity. Specific junction conditions have been used to obtain even matching between two distinct zones. The consistency of gravastar was examined by Chirenti and Rezolla [9] and concluded that the difference in quasi-normal modes can be used in identifying a gravastar from a BH. The construction and evolution of string-like axially symmetric dense objects have been analyzed by Yousaf et al. [24] in gravity. Horvat et al. [25] investigated the radial stability of gravastar having sustained pressure. Sakai et al. [26] considered two distinct optical sources along with their detailed description to study the optical images of gravastar. The impact of the presence of charge on different physical features, i.e, energy, entropy, and length of the shell of a higher dimensional non- singular gravastar was analyzed by Rahaman et al. [27]. The junction conditions were used for the smooth matching between different spacetimes. The impact of presence or absence of event horizon on the production of gravitational waves from a celestial object was studied by Pani et al. [28]. They analyzed how a non-rotating gravastar can be distinguished from BH-based quasi-normal modes. Yousaf described the possible formation of compact structures in -dominated era [29] and [30] gravity.
Chirenti and Rezolla [31] examined the dependence of growth of a gravastar on its ergoregion instability. Based on their derived results, they concluded that rotating gravastar can also be stable. GR is widely accepted as an efficient theory for explaining a wide range of cosmological events [32,33,34]. However, the accelerated expansion of the universe can be elaborated more precisely after making some changing in the geometric part of the action in the result of which modified theories, i.e, and were introduced. One of the alternative theories is modified Gauss-Bonnet gravity [35], which involves an arbitrarily defined function f(G) in Einstein-Hilbert action in which G is Gauss-Bonnet invariant. Since G behaves as a topological constant in the case of four-dimensional manifold, it may give rise to some intriguing cosmological results that occur in the limited energy scale of string theory. Keeping this in mind, distinct gravity models are developed which have significant importance in explaining the prominent role of dark energy in the universe expansion [36]. Furthermore, these models may aid in the avoidance of finite time future singularities. A great deal of mathematical work in literature in the context of gravity theory is available [37,38]. Bhatti [39] analyzed the self-gravitating stars in the framework of theory of gravity. They considered spherically symmetric fluid having anisotropic pressure and energy density in this regard. The instability regions under Newtonian and post-Newtonian limits were also revealed with the help of the collapse equation. The late-time cosmic acceleration is studied by Easson [40] in the framework of Gauss-Bonnet theory of gravity. Neupane and Carter [41] assumed a feasible cosmological model in which the Gauss-Bonnet invariant was coupled with the effective action. This model provided the description of the heating process in the universe. Bhatti and Yousaf [42] briefly analyzed the important characteristic of inhomogeneous matter dispensation under the influence of electromagnetic field with the help of alternative gravity theory. Sharif and Fatima [43] extended the generalization of 2nd law of thermodynamics for FRW metric in the framework of gravity. They demonstrated with the help of graphs that this law can be used for the description of present and future eras. Cognola et al. [44] reformulated the scalar-Gauss-Bonnet and modified Gauss-Bonnet gravity theories by using the background of cosmos expansion. They observed that the existence of matter is sufficient condition for the conversion of decelerated acceleration. The 2nd law of thermodynamics was inspected in gravity by Sadjadi [45] and derived the necessary conditions for the law. Chatterjee and Parikh [46] inquired the role of Gauss-Bonnet term in the necessary entropy of a BH for the violation of 2nd law of thermodynamics. Bhatti and Yousaf [47] investigated the constraints of instability for astronomical objects in the framework of gravity. They concluded that the dynamical instability of fluid configuration can be elaborated by using adiabatic index whose systematic value depends upon energy density and anisotropic pressure.
The primary goal of our research is to study the development of gravastar for an isotropic cylindrical system in Gauss-Bonnet theory. In Section 2, the necessary mathematical formalism related to gravity is given. The revised field equations along with the conservation laws associated with the Gauss-Bonnet gravity are also calculated in this section. The construction of discussed in Section 3. Junction conditions are explored in Section 4, whereas some significant features of our model with their graphical demonstration are given in Section 5. In the end, important results are elaborated in Section 6.
2. Theory and Revised Field Equations
We shall study the elementary mathematical formulism of theory. The solution of revised field equations is also explored in this section. In the case of Gauss-Bonnet gravity, we consider an random function instead of Gauss-Bonnet invariant G which is written as
where and indicate the Riemann and Ricci tensors. The concept of is similar to that of gravity, having the action written as [48]
here, is a coupling constant. After the variation of action corresponding to , the following field equations are obtained
where is written for the differentiation corresponding to G. The non singular solution of gravastar model will be determined by using the following cylindrically static metric
where and . The metric given in above equation has following restraints on the coordinates , , , [49]. Furthermore, is a constant and the total gravitational mass is indicated by M. In order to investigate the gravastar’s stability in the domain of gravity theory, we consider the locally isotropic matter whose narration is given with the help of stress energy tensor whose mathematical form is written as
Here, is written for the four-velocity of matter and p specifies the pressure of fluid. The gravitating mass of the system can be derived with the help of scale factors which are related to the interior sector of our model. The role of solution of the modified field equations will be important in determining these values. The non-zero components of Einstein tensor related to the assumed model of gravastar will be
In above equations, prime specifies the differentiation related to r. The use of Equations (4)–(8) in (3), implies the revised field equations as
where , and represent the correction terms. The values of U and V (metric coefficients) will be derived with the help of following conservation equation
After assuming the energy density as constant and by using Equation (9), we can determine the value of as
Here, m and r point out the gravitating mass and the radius of inner sector, respectively.
3. Composition of Gravastar
Now, we shall study the distinct sectors of cylindrically symmetric gravastar model. Specific EoS related to different sectors will be used to obtain the required results. It is fascinating to consider that the inner zone of a gravastar structure is surrounded by a middle thin shell made up of stiff fluid dispersion, whereas the outside is completely vacuum. The analysis of this fluid will be used in order to attain even matching between internal and external zones of gravastar.
3.1. Zone (I)
In the primary model MM suggested that the interior sector of gravastar is not a vacuum. We assume that the construction of interior sector can be elaborated with the help of the EoS . This EoS reveals the appearance of dark energy in internal region of gravastar. The repellent effect of inner sector caused by dark energy prevents the development of singularity in gravastar. The absence of singularity is considered as one of the major differences between gravastar and the black hole. By using above mentioned EoS along with the law of conservation given in Equation (12), we can write
so that the value of pressure takes the form
The analytical solution can be calculated after considering the value of integration constant A equal to zero, so that
The dependence of metric potentials on each other can be determined by using Equations (9), (10), (14) and (15) and is written as
here, Y is a constant of integration and the mathematical expression for can be seen in Appendix A. The mathematical expression of total gravitating mass is calculated as
Equation (19) establishes the relation between r and M and it is regarded as the significant attribute of gravastar. The above integral will operate as an improper integral at .
3.2. Zone (II)
The presence of a thin shell consisting of ultrarelativistic matter is considered at the boundary of inner sector. In this subsection, we shall evaluate the construction of intermediate shell and the EoS used for the illustration of shell is taken as . This equation indicates the equality between pressure and density which reveals that the shell of gravastar is not a vacuum. Consequently, it implies that the shell is comprised of ultrarelativistic matter. The concept of this stiff fluid has been helpful in understanding many of the cosmological [50] and astrophysical [51,52] events. It is a challenging task to obtain the solution of field equations in the absence of pressure, therefore, we shall make some assumptions which will be helpful in determining the analytical solution. We consider that U and V are smaller than 1, which implies the value of V as . The use of Equations (9)–(11), in the scenario of above discussion, we can have
After integrating Equation (20), we can write
here D is an integration constant. The values and implies that the value of D will be smaller than 1. The use of Equations (20) and (21) yields
where P is written as integration constant and the values of and are given in Appendix A. The use of EoS in conservation law implies
The expression for can be seen in Appendix A and n is integration constant. From Equation (24), we can notice that the density of shell varies directly with the change in its radius. Therefore, the stiff fluid will be more denser at the external edge of shell as compared to the internal one. Moreover, Figure 1 indicates that the addition in density will result the increase in pressure of ultrarelativistic fluid and vice versa.
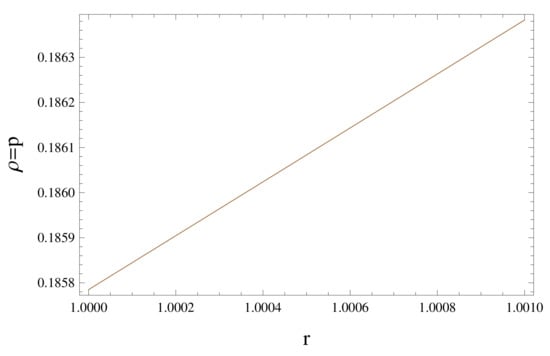
Figure 1.
Graphical demonstration of density (km) correspondence with r (km).
3.3. Zone (III)
The EoS can be used in order to explain the exterior of gravastar. This equation signifies that the exterior is totally a vacuum. We use the following cylindrically static metric for the description of exterior region as
4. Junction Conditions
We shall conceive specific junction conditions by connecting inner and outer sectors of gravastar. Different mathematical expressions will also be established that will enable the even matching between respective geometries. It is important to mention that gravastar is comprised of three sectors. In order to obtain even matching between internal and external geometries, we shall use matching conditions suggested by Darmois-Israel [53,54]. The persistence of metric coefficients at is of significant importance for the use of these conditions. Darmois-Israel formulation is also very useful in calculating the value of surface stress energy. Lanczos equation [55,56] leads to as
Here, shows the discontinuity related to extrinsic curvatures at the hyper surface. The “−” sign corresponds to the interior sector and “+” is written for the outer sector. The second fundamental form [57,58,59,60] connected to both the edges of shell is described as
here, specifies the intrinsic coordinates of shell and is written for the unit normal to the surface given as
and = 1. The stress energy tensor , is calculated by considering the Lanczos equation. The energy density of surface is represented by whereas indicates the amount of pressure of surface. The mathematical expressions for and are given in Equations (29) and (30), which turn out to be
The total mass of cylindrically symmetric gravastar can be derived by using surface energy density.
5. Significant Attributes of Gravastar
In this section, we intended to evaluate some important characteristics of cylindrically symmetric isotropic gravastar. The impact of theory on these features of model will also be analyzed. The length of shell as well as its energy and entropy will be studied in detail and graphs are used to represent their dependence on radial coordinate. In this way, cylindrically symmetric gravastar model will be analyzed in the context of theory of gravity.
5.1. Length of Shell
We suppose that and as the radii of internal and external zones of gravastar. We assumed the value of thickness as which implies the small change in the length of shell. By using Equation (22), length of shell is obtained as
This equation is not integrable, so we plot it to demonstrate its physical application on construction of gravastar. Figure 2 indicates the sudden change in the radial coordinate as expected for the gravastar formation. We also conclude from graph that the length of shell varies directly after the change in its thickness.
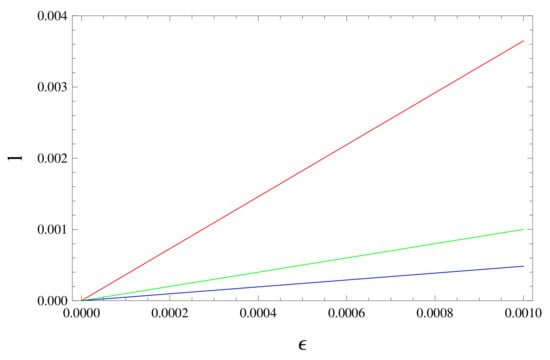
Figure 2.
Graphical illustration of correspondence between proper length ℓ (km) and the shell thickness (km).
5.1.1. Energy Content
The geometry of inner zone of gravastar is explained with the help of EoS . This EoS reveals the presence of negative pressure in the internal region. The repulsive effect generated by the dark energy will avoid the creation of singularity. Shell thickness plays a crucial part in calculating its energy. The shell energy is derived as
5.1.2. Entropy
The evaluation of disorderness of a compact object is called its entropy. The area of event horizon of a BH is used to determine its entropy. Since, in the case of gravastar, event horizon is not present so its entropy will be dependent on the thickness of shell [61]. According to the model proposed by MM, the entropy of interior sector of gravastar is zero and entropy within shell is determined as
The entropy density related to local temperature is written as
here, represents the specific temperature whereas is is written as a dimensionless constant. The values of Planckian constants are supposed to be 1. Consequently, entropy density can be written as
The entropy related to shell will be
The analytical solution of above equation is not possible so we consider numerical techniques to solve it. Moreover, the dependence of entropy of shell on its thickness is analyzed with the help of graph figure (Figure 3). It indicates that the entropy of shell will be zero corresponding to the zero thickness which is physically possible as suggested by [8].
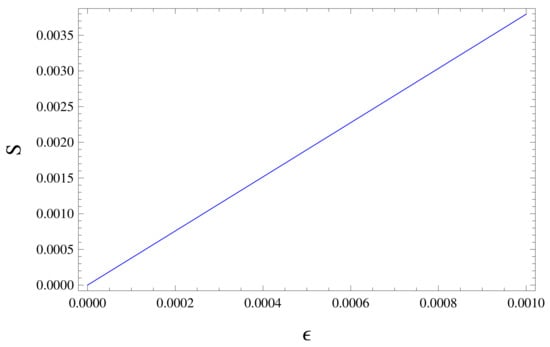
Figure 3.
Graphical representation of entropy S (km) relationship with shell thickness (km).
5.1.3. Equation of State
Several EoS have been used in research for the elaboration of distinct astrophysical events [62,63]. EoS relates the state variables that describe the states of matter within the specific physical conditions. It also plays a key role in evaluating the configuration of various fluids as well as the internal composition of compact stars. It is not possible to identify the features of all kinds of materials by using a unique EoS. The association of gas densities with their temperature is described by the EoS known as ideal gas law. Whereas, perfect fluid EoS is used in cosmology for understanding the internal configuration of distinct compact objects. Similarly, for the depiction of barotropic fluids we consider barotropic EoS. Equation (24) is barotropic EoS which elegantly connects surface pressure and the surface energy density which are the state variables of our model.
The appearance of positive terms in denominator and numerator of above equation is the significant condition for the viable solution. In order to make it possible, we ignore the higher order terms in binomial series.
Distinct values of have significant importance in the hypothetical study of our model because they describe the characteristics of matter of distinct regions of gravastar. The value suggests the influence of negative pressure and it is helpful in explaining the internal region of gravastar. Furthermore, is assumed for the illustration of ultra-relativistic fluid within the thin shell. Similarly, refers to the vacuum which is assumed for the elaboration of external region of gravastar.
6. Conclusions
The main objective of our research article is to analyze the formation and presence of gravastar. The basic formulation of gravity has been used in this regard. Moreover, we assumed the isotropic pressure with perfect fluid and irrotational cylindrical metric in order to derive the revised field equations and the law of conservation related to gravity. Gravastar is claimed to be a viable alternate to black hole structure. Black hole is a widely known compact object whose formation is assumed at the end of gravitational collapse. MM suggested in their primary model of gravastar that it is composed of three sectors. In order to elaborate these sectors, particular equation of states have been used. The EoS related to interior sector points out the appearance of dark energy in it. The formation of singularity in gravastar is prevented by the repulsive force generated force by dark energy. At the end of interior region there is an intermediate shell which is consisted of an ultrarelativistic fluid. The external sector of gravastar is completely a vacuum. Different physical features of our model have been discussed in detail and their dependence on the thickness of shell is signified by the use of graphs. Major findings of our analysis are the following.
- Characterization of density and pressure: (i) In the interior sector of gravastar, negative pressure will maintain its nature. Moreover, the values of pressure and energy density will be persistent. (ii) Figure 1 indicates the change in pressure of ultra relativistic fluid within the shell related to r which is the radial coordinate. Therefore, we can assume that the outer edge of shell will have more density than the inner one.
- Length of shell: We have examined the relation between of length of intermediate shell and shell thickness under the presence of constructive matter. Graph (Figure 2) between these two physical characteristics of model shows the continuous increase in length with the increase in its thickness.
- Entropy: (i) The area of event horizon of BH is used in order to determine its entropy. Because there is no event horizon in the case of gravastar, its entropy will be dependent on thickness of shell. (ii) Figure 3 specifies that by the increase (decrease) in shell thickness its entropy will also increase (decrease).
Author Contributions
Conceptualization, M.Z.B. and Z.Y.; methodology, M.Z.B. and Z.Y.; software, A.R.; investigation, A.R.; writing—original draft preparation, A.R.; writing—review and editing, M.Z.B. and Z.Y.; visualization, M.Z.B. and Z.Y.; supervision, M.Z.B. and Z.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
The extra curvature terms appearing in our analysis are given as
References
- Nakao, K.I.; Yoo, C.M.; Harada, T. Gravastar formation: What can be the evidence of a black hole? Phys. Rev. D 2019, 99, 044027. [Google Scholar] [CrossRef]
- Arbañil, J.D.; Panotopoulos, G. Tidal deformability and radial oscillations of anisotropic polytropic spheres. Phys. Rev. D 2022, 105, 024008. [Google Scholar] [CrossRef]
- Panotopoulos, G.; Rincón, Á.; Lopes, I. Slowly rotating dark energy stars. Phys. Dark Universe 2021, 34, 100885. [Google Scholar] [CrossRef]
- Panotopoulos, G.; Tangphati, T.; Banerjee, A.; Jasim, M. Anisotropic quark stars in R2 gravity. Phys. Lett. B 2021, 817, 136330. [Google Scholar] [CrossRef]
- Panotopoulos, G.; Rincón, Á.; Lopes, I. Interior solutions of relativistic stars with anisotropic matter in scale-dependent gravity. Eur. Phys. J. C 2021, 81, 63. [Google Scholar] [CrossRef]
- Tello-Ortiz, F.; Rincón, Á.; Bhar, P.; Gomez-Leyton, Y. Durgapal IV model considering the minimal geometric deformation approach. Chin. Phys. C 2020, 44, 105102. [Google Scholar] [CrossRef]
- Tello-Ortiz, F.; Malaver, M.; Rincón, Á.; Gomez-Leyton, Y. Relativistic anisotropic fluid spheres satisfying a non-linear equation of state. Eur. Phys. J. C 2020, 80, 371. [Google Scholar] [CrossRef]
- Mazur, P.O.; Mottola, E. Gravitational vacuum condensate stars. Proc. Natl. Acad. Sci. USA 2004, 101, 9545–9550. [Google Scholar] [CrossRef]
- Chirenti, C.B.; Rezzolla, L. How to tell a gravastar from a black hole. Class. Quantum Grav. 2007, 24, 4191. [Google Scholar] [CrossRef]
- Zeldovich, Y.B. A hypothesis, unifying the structure and the entropy of the Universe. Mon. Not. R. Astron. Soc. 1972, 160, 1P–3P. [Google Scholar] [CrossRef]
- Lobo, F.S.N.; Garattini, R. Linearized stability analysis of gravastars in noncommutative geometry. J. High Energy Phys. 2013, 2013, 65. [Google Scholar] [CrossRef]
- Nandi, K.K.; Zhang, Y.Z.; Cai, R.G.; Panchenko, A. Energetics in condensate star and wormholes. Phys. Rev. D 2009, 79, 024011. [Google Scholar] [CrossRef]
- Horvat, D.; Ilijić, S. Gravastar energy conditions revisited. Class. Quantum Grav. 2007, 24, 5637. [Google Scholar] [CrossRef]
- Furey, N.; DeBenedictis, A. Wormhole throats in Rm gravity. Class. Quantum Grav. 2004, 22, 313. [Google Scholar] [CrossRef]
- DeBenedictis, A.; Horvat, D.; Ilijić, S.; Kloster, S.; Viswanathan, K.S. Gravastar solutions with continuous pressures and equation of state. Class. Quantum Grav. 2006, 23, 2303. [Google Scholar] [CrossRef]
- Bilić, N.; Tupper, G.B.; Viollier, R.D. Born–Infeld phantom gravastars. J. Cosmol. Astropart. Phys. 2006, 2006, 013. [Google Scholar] [CrossRef]
- Visser, M.; Wiltshire, D.L. Stable gravastars an alternative to black holes? Class. Quantum Grav. 2004, 21, 1135. [Google Scholar] [CrossRef]
- Lobo, F.S.N.; Arellano, A.V.B. Gravastars supported by nonlinear electrodynamics. Class. Quantum Grav. 2007, 24, 1069. [Google Scholar] [CrossRef]
- Rocha, P.; Chan, R.; da Silva, M.; Wang, A. Stable and bounded excursion gravastars, and black holes in Einstein s theory of gravity. J. Cosmol. Astropart. Phys. 2008, 2008, 010. [Google Scholar] [CrossRef]
- Bhatti, M.Z.; Yousaf, Z.; Ajmal, M. Locally isotropic gravastars with cylindrical spacetime. Int. J. Mod. Phys. A 2019, 28, 1950123. [Google Scholar] [CrossRef]
- Bhatti, M.Z. Charged gravastars with cylindrical spacetime. Mod. Phys. Lett. A 2020, 35, 2050069. [Google Scholar] [CrossRef]
- Cattoen, C.; Faber, T.; Visser, M. Gravastars must have anisotropic pressures. Class. Quantum Grav. 2005, 22, 4189. [Google Scholar] [CrossRef]
- Bhatti, M.Z.; Yousaf, Z.; Rehman, A. Gravastars in f (R, G) gravity. Phys. Dark Universe 2020, 29, 100561. [Google Scholar] [CrossRef]
- Yousaf, Z.; Bhatti, M.Z.; Rehman, A. Electrically charged string-like axially symmetric object composition in f (R, G) gravity. Chin. J. Phys. 2021, 73, 493–502. [Google Scholar] [CrossRef]
- Horvat, D.; Ilijić, S.; Marunović, A. Radial stability analysis of the continuous pressure gravastar. Class. Quantum Grav 2011, 28, 195008. [Google Scholar] [CrossRef]
- Sakai, N.; Saida, H.; Tamaki, T. Gravastar shadows. Phys. Rev. D 2014, 90, 104013. [Google Scholar] [CrossRef]
- Rahaman, F.; Usmani, A.A.; Ray, S.; Islam, S. The (2+ 1)-dimensional charged gravastars. Phys. Lett. B 2012, 717, 1–5. [Google Scholar] [CrossRef]
- Pani, P.; Berti, E.; Cardoso, V.; Chen, Y.; Norte, R. Gravitational wave signatures of the absence of an event horizon: Nonradial oscillations of a thin-shell gravastar. Phys. Rev. D 2009, 80, 124047. [Google Scholar] [CrossRef]
- Yousaf, Z. Spatially Hyperbolic Gravitating Sources in Λ-Dominated Era. Universe 2022, 8, 131. [Google Scholar] [CrossRef]
- Yousaf, Z. Construction of charged cylindrical gravastar-like structures. Phys. Dark Universe 2020, 28, 100509. [Google Scholar] [CrossRef]
- Chirenti, C.B.; Rezzolla, L. Ergoregion instability in rotating gravastars. Phys. Rev. D 2008, 78, 084011. [Google Scholar] [CrossRef]
- Iorio, L. Editorial for the special issue 100 years of chronogeometrodynamics: The status of the Einstein s theory of gravitation in its centennial year. Universe 2015, 1, 38–81. [Google Scholar] [CrossRef]
- Debono, I.; Smoot, G.F. General relativity and cosmology: Unsolved questions and future directions. Universe 2016, 2, 23. [Google Scholar] [CrossRef]
- Vishwakarma, R.G. Einstein and beyond: A critical perspective on general relativity. Universe 2016, 2, 11. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Modified Gauss–Bonnet theory as gravitational alternative for dark energy. Phys. Lett. B 2005, 631, 1–6. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Future evolution and finite-time singularities in F (R) gravity unifying inflation and cosmic acceleration. Phys. Rev. D 2008, 78, 046006. [Google Scholar] [CrossRef]
- Lin, H.Y.; Deng, X.M. Rational orbits around 4D Einstein–Lovelock black holes. Phys. Dark Universe 2021, 31, 100745. [Google Scholar] [CrossRef]
- Deng, X.M.; Xie, Y. Study on an improved adaptive PSO algorithm for solving multi-objective gate assignment. Astrophys. Space Sci. 2017, 362, 1. [Google Scholar] [CrossRef]
- Bhatti, M.Z.; Yousaf, Z.; Khadim, A. Dynamical analysis of self-gravitating stars in modified Gauss-Bonnet gravity. Phys. Rev. D 2020, 101, 104029. [Google Scholar] [CrossRef]
- Easson, D.A. Modified gravitational theories and cosmic acceleration. Int. J. Mod. Phys. A 2004, 19, 5343–5350. [Google Scholar] [CrossRef]
- Neupane, I.P.; Carter, B.M. Towards inflation and dark energy cosmologies from modified Gauss–Bonnet theory. J. Cosmol. Astropart. Phys. 2006, 2006, 004. [Google Scholar] [CrossRef]
- Bhatti, M.Z.; Yousaf, Z. Dynamical variables and evolution of the universe. Int. J. Mod. Phys. D 2017, 26, 1750029. [Google Scholar] [CrossRef]
- Sharif, M.; Fatima, H.I. Thermodynamics with corrected entropies in f(G) gravity. Astrophys. Space Sci. 2014, 354, 507–515. [Google Scholar] [CrossRef]
- Cognola, G.; Elizalde, E.; Nojiri, S.I.; Odintsov, S.D.; Zerbini, S. String-inspired Gauss-Bonnet gravity reconstructed from the universe expansion history and yielding the transition from matter dominance to dark energy. Phys. Rev. D 2007, 75, 086002. [Google Scholar] [CrossRef]
- Sadjadi, H.M. On the second law of thermodynamics in modified Gauss–Bonnet gravity. Phys. Scr. 2011, 83, 055006. [Google Scholar] [CrossRef][Green Version]
- Chatterjee, S.; Parikh, M. The second law in four-dimensional Einstein–Gauss–Bonnet gravity. Class. Quantum Gravity 2014, 31, 155007. [Google Scholar] [CrossRef]
- Bhatti, M.Z.; Yousaf, Z. Dynamical instability of charged self-gravitating stars in modified gravity. Chin. J. Phys. 2021, 73, 115–135. [Google Scholar] [CrossRef]
- Li, B.; Barrow, J.D.; Mota, D.F. Cosmology of modified Gauss-Bonnet gravity. Phys. Rev. D 2007, 76, 044027. [Google Scholar] [CrossRef]
- Sharif, M.; Azam, M. Stability analysis of thin-shell wormholes from charged black string. J. Cosmol. Astropart. Phys. 2013, 2013, 023. [Google Scholar] [CrossRef]
- Madsen, M.S.; Mimoso, J.P. Evolution of the density parameter in inflationary cosmology reexamined. Phys. Rev. D 1992, 46, 1399. [Google Scholar] [CrossRef]
- Braje, T.M.; Romani, R.W. RX J1856–3754: Evidence for a stiff equation of state. Astrophys. J. 2002, 580, 1043. [Google Scholar] [CrossRef]
- Linares, L.P.; Malheiro, M.; Ray, S. The importance of the relativistic corrections in hyperon stars. Int. J. Mod. Phys. D 2004, 13, 1355. [Google Scholar] [CrossRef]
- Darmois, G. Les Equation de la Gravitation Einsteinnienne Memorial des Science Mathematiques Fasc; Gauthier-Villars: Paris, France, 1927; p. 25. [Google Scholar]
- Israel, W. Singular hypersurfaces and thin shells in general relativity. Il Nuovo Cimento B 1966, 44, 1. [Google Scholar] [CrossRef]
- Lanczos, K. Flächenhafte verteilung der materie in der einsteinschen gravitationstheorie. Ann. Phys. 1924, 379, 518–540. [Google Scholar] [CrossRef]
- Sen, N. Über die grenzbedingungen des schwerefeldes an unstetigkeitsflächen. Ann. Phys. 1924, 378, 365–396. [Google Scholar] [CrossRef]
- Rahaman, F.; Kalam, M.; Chakraborty, S. Thin shell wormholes in higher dimensional Einstein Maxwell theory. Gen. Relativ. Gravit. 2006, 38, 1687–1695. [Google Scholar] [CrossRef]
- Rahaman, F.; Rahman, K. Wormholes supported by polytropic phantom energy. Int. J. Theor. Phys 2010, 49, 2364. [Google Scholar] [CrossRef]
- Dias, G.A.S.; Lemos, J.P.S. Thin shell wormholes in d dimensional general relativity: Solutions, properties, and stability. Phys. Rev. D 2010, 82, 084023. [Google Scholar] [CrossRef]
- Rahaman, F.; Kuhfittig, P.K.F.; Kalam, M.; Usmani, A.A.; Ray, S. A comparison of Hořava–Lifshitz gravity and Einstein gravity through thin-shell wormhole construction. Class. Quantum Grav. 2011, 28, 155021. [Google Scholar] [CrossRef]
- Bhar, P. Higher dimensional charged gravastar admitting conformal motion. Astrophys. Space Sci. 2014, 354, 457–462. [Google Scholar] [CrossRef]
- Heiselberg, H.; Pandharipande, V. Recent progress in neutron star theory. Annu. Rev. Nucl. Part. Sci. 2000, 50, 481–524. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Prakash, M. The equation of state of hot, dense matter and neutron stars. Phys. Rep. 2016, 621, 127–164. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).