Plasma Diagnostics in the Era of Integral Field Spectroscopy

Abstract

To understand the physical conditions of various gaseous systems, plasma diagnostics must be performed properly. To that end, it is equally important to have extinction correction performed properly, even before performing plasma diagnostics. This means that the physical conditions of the target sources—the very quantities to be derived via plasma diagnostics—must be known even before performing extinction correction, because the degree of extinction is determined by comparing the observed spectra of the target sources with their theoretically predicted counterparts. One way to resolve this conundrum is to perform both extinction correction and plasma diagnostics together by iteratively seeking a converged solution. In fact, if these analyses are performed self-consistently, a converged solution can be found based solely on well-calibrated line intensities, given the adopted extinction law and the $R_V$ value. However, it is still rare to find these analyses performed numerically rigorously without unnecessary analytical approximations from start to finish. In this contribution for the APN 8e conference, we would like to review this convoluted problem and sort out critical issues based on the results of our recent experiments. It appears that the convoluted theoretical and observational progresses exacerbated by the highly numerical nature of these analyses necessitated a number of analytical simplifications to make the problem analytically tractable in the pre-computer era and that such analytical simplifications still remain rampant in the literature today, even after ample computational resources became readily available. Hence, the community is encouraged to do away with this old habit of sidestepping numerical calculations that was a necessary evil in the past. This is especially true in the context of spatially-resolved 2-D spectroscopy, which obviously conflicts with the uniformity assumption often blindly inherited from 1-D spectroscopy.

1. Introduction

To understand the physical conditions of various astrophysical gaseous systems, it is fundamental to perform plasma diagnostics [1,2]. The relative strengths of various diagnostic emission lines determine the excitation states of specific gaseous species, yielding their electron density ($n_{\mathrm{e}}$) and temperature ($T_{\mathrm{e}}$), and, subsequently, metal abundances [3,4]. Meanwhile, it is equally fundamental to perform extinction correction caused by both the interstellar and circumsource components, so that genuinely unattenuated intrinsic spectra are available for plasma diagnostics [5,6]. This is the quintessence of observational astronomy, in which all measurements made from a distance are affected by extinction.

However, the determination of extinction is not a trivial task. The extinction at $\lambda$, $c\left(\lambda \right)$, is the base-10 power-law index, which reduces the intrinsic flux, $I_0\left(\lambda \right)$, to the observed flux, $I\left(\lambda \right)$, as $I\left(\lambda \right)=I_0\left(\lambda \right)\times {10}^{-c\left(\lambda \right)}$. In plasma diagnostics, the amount of extinction is usually determined by comparing observed diagnostic H i recombination line ratios (e.g., $I\left(\mathrm{H}\alpha \right)/I\left(\mathrm{H}\beta \right)$ and $I\left(\mathrm{H}\beta \right)/I\left(\mathrm{H}\gamma \right)$) with the corresponding theoretical (i.e., unattenuated) counterparts [1,2]. Such theoretical/unattenuated line ratios depend simply on the specific $n_{\mathrm{e}}$ and $T_{\mathrm{e}}$ of line-emitting gas in the target sources and can be computed numerically given the desired complexity of the atomic physics [7,8]. Needless to say, $n_{\mathrm{e}}$ and $T_{\mathrm{e}}$ are the very quantities to be determined via plasma diagnostics with extinction-corrected line ratios.

In the meantime, in typical plasma diagnostics performed today, atoms are usually represented as n-level energy states. Thus, $n_{\mathrm{e}}$ and $T_{\mathrm{e}}$ are determined from a set of equilibrium equations for the adopted n-level system. In these equilibrium equations, the collisional excitation coefficient has the $n_{\mathrm{e}}\sqrt{T_{\mathrm{e}}}exp(-\Delta E/k{T}_{\mathrm{e}})$ dependence (where $\Delta E$ is the energy difference between any two levels) and the collisional de-excitation coefficient has the $n_{\mathrm{e}}\sqrt{T_{\mathrm{e}}}$ dependence, while the radiation de-excitation coefficient has no dependence on $n_{\mathrm{e}}$ and $T_{\mathrm{e}}$ to the first order [9]. Because these equations with exponential functions are transcendental, solutions are obtained only numerically.

Therefore, to overcome the conundrum pointed out above, both plasma diagnostics and extinction correction ought to be performed together as a streamlined iterative numerical process. This is, in fact, suggested even when the present procedure of plasma diagnostics was introduced to the community [1,2]. However, what has been traditionally exercised in the literature is to adopt a number of approximations to make the problem analytically tractable (which was performed originally for instructional purposes [1,2]). Moreover, ad hoc $n_{\mathrm{e}}$ and $T_{\mathrm{e}}$ are often adopted to force a value of $c\left(\mathrm{H}\beta \right)$ or an ad hoc $c\left(\mathrm{H}\beta \right)$ value may even be adopted to skip extinction correction altogether.

In recent years, spatially-resolved 2-D plasma diagnostics have been becoming very relevant in many branches of astronomy, especially with the increasing availability of integral field spectroscopy (IFS; e.g., [10]). For extended targets, $n_{\mathrm{e}}$ and $T_{\mathrm{e}}$ (and hence, $c\left(\mathrm{H}\beta \right)$) are of course expected to vary spatially. However, even for such spatially extended targets, the spatial variation of $n_{\mathrm{e}}$ and $T_{\mathrm{e}}$ (and $c\left(\mathrm{H}\beta \right)$) does not seem to have been considered carefully enough. Often, uniform $n_{\mathrm{e}}$ and $T_{\mathrm{e}}$ (or $c\left(\mathrm{H}\beta \right)$) are adopted across extended target sources, instead of performing calculations at each detector element (i.e., pixel or spaxel), defeating the purpose of spatially-resolved IFS observations. In such cases, self-consistency is regrettably nil.

The subtlety of self-consistency between extinction correction and plasma diagnostics seems to have been lost in translation, most likely because these analyses are often regarded as two separate problems. Hence, self-consistency between these two sets of $n_{\mathrm{e}}$ and $T_{\mathrm{e}}$ in extinction correction and plasma diagnostics is rarely scrutinized, let alone guaranteed. Consequently, such inconsistencies would usually invite uncertainties, albeit inadvertently.

2. Typical Procedure in the Literature

Because this problem turns out to be rather convoluted, let us first sort out critical points by closely examining the procedure of extinction correction and plasma diagnostics typically employed in the literature. Extinction correction begins with adopting an extinction law and the associated $R_V$ value to scale the extinction law. Then, the extinction c at a reference wavelength (customary at H$\beta$, i.e., $c\left(\beta \right)$) is determined by comparing observed diagnostic H i recombination line ratios (most commonly $I\left(\mathrm{H}\alpha \right)/I\left(\mathrm{H}\beta \right)$ and/or $I\left(\mathrm{H}\gamma \right)/I\left(\mathrm{H}\beta \right)$) with the theoretical predictions (i.e., unattenuated line ratios). Here, the theoretical H i recombination line ratios are nothing but functions of $n_{\mathrm{e}}$ and $T_{\mathrm{e}}$ [7,8]. Hence, to guarantee self-consistency between extinction correction and plasma diagnostics, the input $n_{\mathrm{e}}$ and $T_{\mathrm{e}}$ that define the unattenuated line ratios for comparison in extinction correction must be consistent with the resulting $n_{\mathrm{e}}$ and $T_{\mathrm{e}}$ to be derived via plasma diagnostics.

In the literature, there is often a reference to the “canonical” $I_0\left(\mathrm{H}\alpha \right)/I_0\left(\mathrm{H}\beta \right)$ ratio at this point in the process. The most often quoted ratio is probably 2.858, which is true only when $n_{\mathrm{e}}={10}^3$ cm${}^{-3}$ and $T_{\mathrm{e}}={10}^4$ K [7,8]. This is totally misleading for the uninitiated. The $I_0\left(\mathrm{H}\alpha \right)/I_0\left(\mathrm{H}\beta \right)$ ratio is simply a function of $n_{\mathrm{e}}$ and $T_{\mathrm{e}}$, and there is no such thing as the canonical ratio. Because no specific $(n_{\mathrm{e}},T_{\mathrm{e}})$ values would warrant any canonicality for the resulting $I_0\left(\mathrm{H}\alpha \right)/I_0\left(\mathrm{H}\beta \right)$ ratio, the ratio simply has to be computed based on the given $n_{\mathrm{e}}$ and $T_{\mathrm{e}}$. It appears that this unwarranted canonicality of the $I_0\left(\mathrm{H}\alpha \right)/I_0\left(\mathrm{H}\beta \right)$ ratio often referenced in the literature introduced an unfortunate disconnect between extinction correction and plasma diagnostics, because the inexperienced tend to blindly quote the “canonical” $I_0\left(\mathrm{H}\alpha \right)/I_0\left(\mathrm{H}\beta \right)$ ratio and be done with it rather than fully appreciating its $(n_{\mathrm{e}},T_{\mathrm{e}})$ dependence.

This is obviously a bad start for the subsequent plasma diagnostics, which require extinction-corrected line strengths as inputs. If $c\left(\mathrm{H}\beta \right)$ is not computed according to the correct $I_0\left(\mathrm{H}\alpha \right)/I_0\left(\mathrm{H}\beta \right)$ ratio via proper $n_{\mathrm{e}}$ and $T_{\mathrm{e}}$, the resulting extinction-corrected spectrum is already compromised. The uncertainty caused by this incorrect $c\left(\mathrm{H}\beta \right)$ would not just scale with it because $c\left(\lambda \right)$ varies with the wavelength. Moreover, the uncertainty in $c\left(\lambda \right)$ would amplify the uncertainty in the resulting line strengths by $ln\left(10\right)$. because $c\left(\lambda \right)$ is the base-10 power index. Hence, any line ratios measured from such an erroneously extinction-corrected spectrum are obviously faulty, and the results of plasma diagnostics undermined by such erroneous inputs would be clearly unreliable.

There are additional sources of inconsistency in plasma diagnostics. The high point of plasma diagnostics is determining $n_{\mathrm{e}}$ and $T_{\mathrm{e}}$ by pinpointing where two diagnostic curves of the measured line ratios intersect in the $n_{\mathrm{e}}$-$T_{\mathrm{e}}$ plane. In general, a line ratio can be computed as a function of $n_{\mathrm{e}}$-$T_{\mathrm{e}}$ based on the equilibrium equations of the adopted n-level system for the atomic species in question. As the equilibrium equations are transcendental in $n_{\mathrm{e}}$ and $T_{\mathrm{e}}$, the determination of the intersection between two diagnostic line ratio curves has to be performed numerically.

In practice, it is conventional to use the so-called $n_{\mathrm{e}}$- and $T_{\mathrm{e}}$-diagnostic line ratios as a pair. On the one hand, the $T_{\mathrm{e}}$-diagnostic line ratios are those having only weak $n_{\mathrm{e}}$ dependence. If one pushes the low-density limit (i.e., taking $n_{\mathrm{e}}\to 0$), the line ratio can be expressed analytically as a function of $T_{\mathrm{e}}$ only. On the other hand, the $n_{\mathrm{e}}$-diagnostic line ratios are those having only weak $T_{\mathrm{e}}$ dependence. The line ratio varies with $n_{\mathrm{e}}$ between two asymptotic values only within a specific range of $n_{\mathrm{e}}$. However, where this range of $n_{\mathrm{e}}$ falls is weakly dependent on $T_{\mathrm{e}}$. This step-function behavior of the ratio with $n_{\mathrm{e}}$ is often shown by a plot for a specific $T_{\mathrm{e}}$ case for instructional purposes (e.g., [1,2]). Then, such a plot, and especially an analytic translation of it, can become prevalent in the literature with the original $T_{\mathrm{e}}$ specificity forgotten. Hence, these weak $n_{\mathrm{e}}$- and $T_{\mathrm{e}}$-dependences in the corresponding $T_{\mathrm{e}}$- and $n_{\mathrm{e}}$-diagnostics wither away as the ease of use of such analytical expressions is favored over the cumbersomeness of rigorous numerical calculations.

In addition, the choice of $n_{\mathrm{e}}$- and $T_{\mathrm{e}}$-diagnostic line ratio pairs can be a source of inconsistency. Ideally, emission lines adopted as a diagnostic pair should originate from the same region of the target object along the line of sight so that plasma diagnostics actually probe $n_{\mathrm{e}}$ and $T_{\mathrm{e}}$ of this region. This practically means that these line emissions should be of roughly the same transition energies (e.g., [N ii], [S ii], and [O ii] lines for low-excitation regions, and [O iii], [Cl iii], and [Ar iv] lines for high-excitation regions; [1,2]). In the literature, however, diagnostic line pairs do not seem to be selected as deliberately as they ought to be. The resulting $n_{\mathrm{e}}$ and $T_{\mathrm{e}}$ values, therefore, often seem to be the mere average of as many permutations of diagnostic line pairs as possible. If lines associated with very different transition energy regimes are used together as a diagnostic line pair, the resulting $n_{\mathrm{e}}$ and $T_{\mathrm{e}}$ may not represent any part of the target along the line of sight.

3. PPAP: Proper Plasma Analysis Practice

On the whole, the discussion above can be distilled into the following four major points of consideration when extinction correction and plasma diagnostics are to be performed effectively as a single integrated procedure:

• Keep track of $n_{\mathrm{e}}$ and $T_{\mathrm{e}}$ from start to finish in order to not become distracted by secondary derivatives such as the diagnostic H i recombination line ratios that are simply functions of $n_{\mathrm{e}}$ and $T_{\mathrm{e}}$;
• Stick to rigorous numerical calculations without resorting to analytical approximations that may be true only for specific circumstances;
• Take into account the physical conditions of the regions of the target source to select appropriate diagnostic line pairs that actually represent the regions to be probed;
• Execute all calculations at each detector element to fully account for spatial variation when the target object is extended.

While performing an exhaustive investigation in the literature is practically not possible, it appears to be rare to find previous works of extinction correction and plasma diagnostics in which all four of the above are rigorously implemented. In the literature, it is often ambiguous as to how analyses were performed exactly, mainly because in works of plasma diagnostics, extinction correction is typically mentioned only in passing. To that end, we have recently carried out a small proof-of-concept experiment, in which all of the above are carefully carried out in performing extinction correction and plasma diagnostics (dubbed “proper plasma analysis practice” or PPAP [11]).

This experiment was conducted with a set of HST/WFC narrowband images of the NW quadrant of the PN NGC 6720, obtained from the data archive [12]. This experiment was performed as a demonstration follow-up of another work, in which a new algorithm was developed to isolate multiple emission line maps from a set of narrowband images whose filter profiles overlap with each other [13]. In particular, for the NGC 6720 data set, the H$\alpha$ 6563 Å and [N ii] 6548/83 Å maps were isolated from the F656N and F658N images, while the [S ii] 6717/31 Å maps were recovered from the F673N, FQ672N, and FQ674N images [11,13].

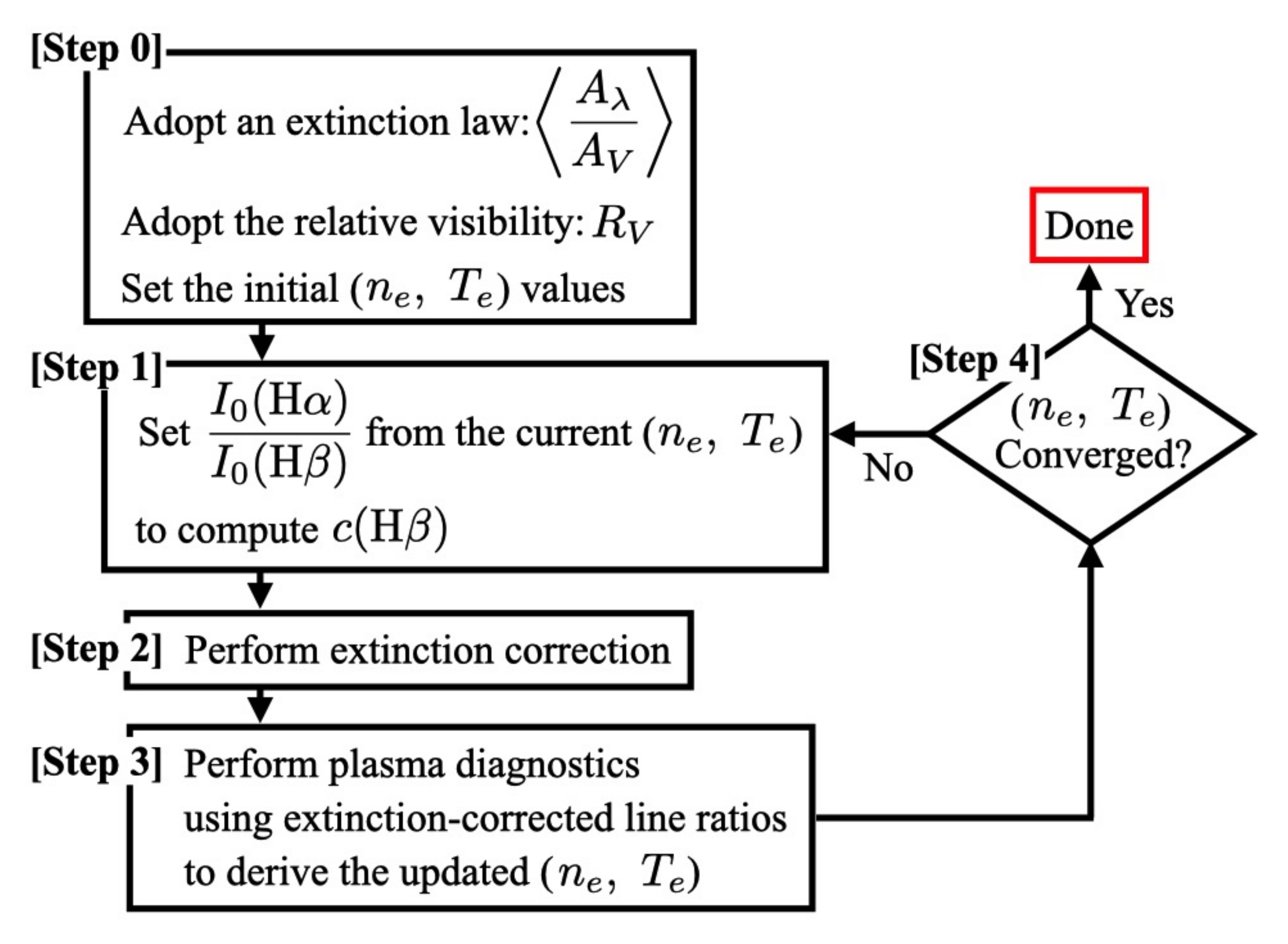
As presented in a flow chart (Figure 1), PPAP is an honest no-nonsense implementation of extinction correction and plasma diagnostics aiming at doing away with analytical approximations adopted previous to the modern computer era. After selecting an extinction law and the associated $R_V$ value toward the target object, the rest is essentially an autopilot of numerical evaluations that seeks a converged solution of $(n_{\mathrm{e}},T_{\mathrm{e}})$ between extinction correction (dictated by the present values of $n_{\mathrm{e}}$ and $T_{\mathrm{e}}$ in evaluating the theoretical predictions of the diagnostic H i recombination line ratios, e.g., [8]) and plasma diagnostics (based on the observed ratios of diagnostic lines whose transition energies are appropriate for the regions to be probed in the target objects). In addition, one can even automate the first step to set the initial $(n_{\mathrm{e}},T_{\mathrm{e}})$ values if they are estimated through plasma diagnostics using diagnostics lines whose wavelengths are close to each other, such as the [S ii] 6717/31 Å lines and [N ii] 6548+83/5755 Å lines (i.e., the results of diagnostics are less susceptible to extinction), as has been performed, for example, by Sánchez et al. [14].

An abridged list of important findings in this PPAP experiment includes:

• The $n_{\mathrm{e}}$ and $T_{\mathrm{e}}$ distributions are not at all uniform, and so are the derived diagnostic H i recombination line ratio (e.g., $I_0\left(\mathrm{H}\alpha \right)/I_0\left(\mathrm{H}\beta \right)$) and $c\left(\mathrm{H}\beta \right)$ distributions;
• If a constant $c\left(\mathrm{H}\beta \right)$, $I_0\left(\mathrm{H}\alpha \right)/I_0\left(\mathrm{H}\beta \right)$, or $(n_{\mathrm{e}},T_{\mathrm{e}})$ were assumed in extinction correction, spatially-varying over- and under-correction of extinction would have occurred as the degree of attenuation could have been off by several tens of % in the observed part of the nebula, compromising the resulting “extinction-corrected” emission line maps;
• The dust distributions ($=c\left(\mathrm{H}\beta \right)$ distributions) can be obtained solely from the optical spectral images (i.e., no need to obtain separate thermal dust emission maps in the infrared);
• The relative ionic abundance distributions of $n\left({\mathrm{N}}^{+}\right)/n\left({\mathrm{H}}^{+}\right)$ separately derived from each of the two diagnostic lines in the [N ii] 6583 Å and [N ii] 5755 Å turned out to be identical within uncertainties and so did the $n\left({\mathrm{S}}^{+}\right)/n\left({\mathrm{H}}^{+}\right)$ distributions derived from the [S ii] 6717 Å and [S ii] 6731 Å line maps;
• Simulated analyses tolerating the uniform $(n_{\mathrm{e}},T_{\mathrm{e}})$ (or $c\left(\mathrm{H}\beta \right)$) distribution in extinction correction would result in spatially varying uncertainties at several tens of % in the derived $(n_{\mathrm{e}},T_{\mathrm{e}})$ and relative ionic abundances distributions.

The significant takeaway from this experiment is that results of plasma diagnostics could be off by several tens of % if PPAP is not strictly followed. Again, PPAP is a straightforward implementation of extinction correction and plasma diagnostics with no frills as suggested from ages ago by many (e.g., [1,2,3,4]). As shown in the flow chart (Figure 1), it is as simple as performing both extinction correction and plasma diagnostics completely numerically as a streamlined iterative process to seek the converged solution of $(n_{\mathrm{e}},T_{\mathrm{e}})$ without resorting to any analytical approximations. There is neither a new theory nor new numerical procedure to adopt. The only thing necessary is an honest implementation of the existing analyses of extinction correction and plasma diagnostics at face value.

It is not too difficult to imagine that seeking $(n_{\mathrm{e}},T_{\mathrm{e}}$) completely numerically for convergence used to be too cumbersome to perform in the past, especially when computational resources were scarce. Hence, it is understandable that a number of analytical approximations had to be adopted as a necessary evil in the past to make the whole procedure analytically tractable. However, such temporary measures of the pre-computer era are still regularly practiced even today when sufficient computational resources are readily available. Therefore, there is only our negligence to blame. It is time to do away with this old habit of sidestepping numerical calculations, simply because we can now perform all these numerical calculations at ease.

4. Historical Perspective

Here, to mend our own negligence, let us briefly explore the historical developments around extinction correction and plasma diagnostics in the literature and gain more insights as to why

• extinction correction has not been incorporated as closely as it should have been with plasma diagnostics, and
• the community has not yet managed to have gone fully numerical,

which are the very questions that concern the main theme of PPAP.

According to Aller [15], Menzel and his collaborators performed the pioneering work to establish the process of plasma diagnostics based on spectral line intensities (which is presently known as the “Direct Method”) via a series of 18 papers from the 1930s to 1940s (e.g., [16,17,18]). It was still when observations were made by “eye estimates” from photographic plates and when the atomic parameters were largely unknown. Hence, Aller himself stated, even in 1951, that “Because of the uncertainties in the collisional cross-sections, we are unable to derive ionic abundances and electron temperatures from the nebular line intensities, nor does it seem worth while to calculate electron densities, since the nebular surface brightnesses and distances are so poorly known” [19]. It was only some 70 years ago.

Despite such adversities, Aller and collaborators pressed on in the 1950s and 1960s as modern techniques gradually improved observational uncertainties [20]. It was around that time when the need for extinction correction for spectral lines was pointed out [21]. Burgess and Seaton were the early adopters of extinction correction in the context of PN plasma diagnostics [22,23], following the ISM extinction work by Whitford [24]. Unfortunately, however, discrepancies between observations and theoretical predictions were larger than extinction alone could account for, because the recombination theory at the time did not take into account the collisional effects.

Then, it took two more decades through the 1970s and 1980s until the collisional effects in the recombination theory were fully taken into consideration, first implemented by Brocklehurst [25] for specific cases and later generalized by Hummer and Storey [7]. This theoretical development took nearly two decades not only because of the technical difficulty but also because observational uncertainties at the time were still often too large to corroborate theoretical predictions. Nevertheless, with both of the $n_{\mathrm{e}}$ and $T_{\mathrm{e}}$ dependences involved in plasma diagnostics established, it was the end of the 1980s when the de facto standard textbook for the subject matter was authored by Osterbrock [1], which many existing methods of plasma diagnostics, including PPAP, are based on.

Concerning PPAP, the works by Hummer and Storey [7] and Storey and Hummer [8], for example, essentially established a way to connect extinction correction and plasma diagnostics seamlessly via the Balmer line ratios, because these ratios turned out to be easier to establish observationally than the Balmer decrement and Paschen-to-Balmer ratios that were typically used before then [26]. However, as mentioned above, instead of thoroughly exploring the $n_{\mathrm{e}}$ and $T_{\mathrm{e}}$ dependences in extinction correction and plasma diagnostics numerically [7,8], the “canonical” Balmer line ratio was introduced to sidestep extinction correction even though there was nothing to vouch for the claimed canonicality. This happened most likely because the advantage of sidestepping the volume of numerical computation necessary in following the $n_{\mathrm{e}}$ and $T_{\mathrm{e}}$ dependences of extinction correction and plasma diagnostics rigorously outweighed the disadvantage of not doing so given the relative shallowness of the $n_{\mathrm{e}}$ and $T_{\mathrm{e}}$ dependences on the Balmer line ratio [7,8] and the computational resources typically available at the time. It is true that computational resources were still commodities in the 1980s and even in the 1990s.

While the consideration just above may answer the first of the two questions raised at the beginning of this section, the second question is very puzzling: why has the community not yet gone completely numerical on this matter two decades later? The PPAP experiment was performed using a laptop [11]. There exist many codes of plasma diagnostics both proprietary and in the public domain, including NEAT [27], which can even propagate uncertainties from line flux measurements to the derived abundances and PyNeb [28], a Python implementation of the latest nebular lineage of the IRAF fame [29], which popularized the diagnostics. Hence, the availability of computational resources cannot be an issue.

Looking back on the historical developments briefly summarized above, there seems to be a recurring pattern of competition between observational uncertainties and the cost of the adopted mode of analysis. At the very beginning, in the 1930s and 1940s, observational uncertainties at the time made it look as if plasma diagnostics was impossible. During the 1950s and 1960s, only the $T_{\mathrm{e}}$ dependence was considered because any consideration of the $n_{\mathrm{e}}$ dependence, even including extinction correction, was buried under observational uncertainties. Through the 1970s and 1980s, full consideration of the $n_{\mathrm{e}}$ and $T_{\mathrm{e}}$ dependence was yet again stagnated by observational uncertainties. This repeating pattern might have affected the collective psyche of the community to shy away from going fully numerical. In the following decades into the 21st century, the canonicality of the Balmer line ratio gained popularity because uncertainties caused by not following the $n_{\mathrm{e}}$ and $T_{\mathrm{e}}$ dependences thoroughly and self-consistently were deemed tolerable. For some unknown reason, the community seems to have always assumed that only negligible uncertainties would result by not going fully numerical. This may well be the collective psyche of the community influenced by the constant need to assess the balance between observational uncertainties and the cost of the adopted mode of analysis for the past 70 years or so.

5. Plasma Diagnostics in the Era of IFS

It is possible to keep speculating as to why a fully numerical approach such as PPAP has rarely been attempted to simultaneously seek a self-consistent converged solution for both extinction correction and plasma diagnostics iteratively. However, it does not seem to be figured out ever behind the rich but convoluted history of extinction correction and plasma diagnostics. Plus, there does not seem to be much point in doing so; we certainly did not review the history to point the finger at anyone. PPAP is simply one genuinely sensible adaptation of extinction correction and plasma diagnostics, aiming at performing these analyses with the least number of approximations and assumptions. As a result, what PPAP requires is just the input spectral imaging data set, plus a choice of the extinction law and the associated total-to-selective extinction, $R_V$, both of which can nowadays be set with a reasonable amount of confidence for any given target source.

Our predecessors simply had to be creative in dealing with these analyses that actually require fully numerical approaches when they did not possess appropriate computational resources. Now that each one in the community has a decent amount of computational resources, it is time to abolish all of such approximations and assumptions that may have been needed in the past but not any longer. This is simply because we can do so and because we can obtain less uncertain results by doing so. Hence, there really does not seem any reason not to do so. In fact, it must be undertaken if target sources exhibit spatial variations at 10% or less because the present “canonical” procedure ladened with approximations is prone to uncertainties at tens of %. Therefore, the community is encouraged to do away with this old habit that would do more harm than good and take up on PPAP or alike, especially in the context of extinction correction and plasma diagnostics by means of spatially-resolved 2-D integral field spectroscopy, with which we want to probe spatial variations at much less than 10%.