Explaining Holographic Dark Energy
Abstract
:1. Introduction
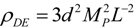
 , L is the event horizon of the universe. It has been shown that the HDE model can be in agreement with the latest observational data, including the sample of Type Ia supernovae (SNIa), the shift parameter of the cosmic microwave background (CMB), the baryon acoustic oscillation (BAO) measurement, and the Planck date etc. (see, e.g., [5,6]). Note that the conclusions of [5,6] depend on the set of data used to constrain the HDE model. Moreover, in some HDE models where L is not the event horizon of the universe (e.g., interacting HDE model [7]), the parameter d may slowly vary with expansion in general [8]. However, a plausible physical explanation of the HDE model is still lacking [9,10,11]. For example, a recent analysis shows that the well-accepted explanation of Equation (1), which is based on the UV/IR connection argument of Cohen et al. [1], has serious drawbacks when applying the model to different eras of the universe [10,11]. One conclusion of [11] is that “the basic framework underlying all HDE models seems too ad hoc to have any real explanatory value, which still keeps us in need of firmer theoretical background.” In this paper, we will mainly investigate the physical basis of the HDE model.
, L is the event horizon of the universe. It has been shown that the HDE model can be in agreement with the latest observational data, including the sample of Type Ia supernovae (SNIa), the shift parameter of the cosmic microwave background (CMB), the baryon acoustic oscillation (BAO) measurement, and the Planck date etc. (see, e.g., [5,6]). Note that the conclusions of [5,6] depend on the set of data used to constrain the HDE model. Moreover, in some HDE models where L is not the event horizon of the universe (e.g., interacting HDE model [7]), the parameter d may slowly vary with expansion in general [8]. However, a plausible physical explanation of the HDE model is still lacking [9,10,11]. For example, a recent analysis shows that the well-accepted explanation of Equation (1), which is based on the UV/IR connection argument of Cohen et al. [1], has serious drawbacks when applying the model to different eras of the universe [10,11]. One conclusion of [11] is that “the basic framework underlying all HDE models seems too ad hoc to have any real explanatory value, which still keeps us in need of firmer theoretical background.” In this paper, we will mainly investigate the physical basis of the HDE model.2. The UV/IR Connection Argument of Cohen et al.

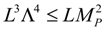
 . Cohen et al. suggested that an effective local QFT will be a good approximate description of physics when Equation (3) is satisfied, because those states that cannot be described by it has been excluded. In other words, when the UV cutoff and the IR cutoff are properly connected, an effective local QFT will be still viable.
. Cohen et al. suggested that an effective local QFT will be a good approximate description of physics when Equation (3) is satisfied, because those states that cannot be described by it has been excluded. In other words, when the UV cutoff and the IR cutoff are properly connected, an effective local QFT will be still viable. , and we can also obtain Equation (3). Note that this requirement automatically prevents the formations of black holes, as the Bekenstein bound does not involve the Newton gravitational constant. Thus, the above two derivations are equivalent.
, and we can also obtain Equation (3). Note that this requirement automatically prevents the formations of black holes, as the Bekenstein bound does not involve the Newton gravitational constant. Thus, the above two derivations are equivalent.3. Thomas’ Bulk Holography Argument
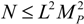 . Then the quantum contribution to the global vacuum energy density,
. Then the quantum contribution to the global vacuum energy density,  , is:
, is:
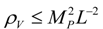
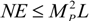 . Therefore, holography allows only finite quantum corrections, and it provides a natural solution to the cosmological constant problem. This follows first from the holographic reduction in the number of independent degrees of freedom, and second from the holographic energy per degree of freedom.
. Therefore, holography allows only finite quantum corrections, and it provides a natural solution to the cosmological constant problem. This follows first from the holographic reduction in the number of independent degrees of freedom, and second from the holographic energy per degree of freedom.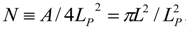 , where L is the horizon size of the universe, A is the area of horizon, and LP is the Planck length. For the convenience of later analysis, we write down all parameters and constants explicitly. According to Thomas’ argument, the Heisenberg quantum energy of each degree of freedom is
, where L is the horizon size of the universe, A is the area of horizon, and LP is the Planck length. For the convenience of later analysis, we write down all parameters and constants explicitly. According to Thomas’ argument, the Heisenberg quantum energy of each degree of freedom is 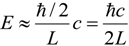 , where c is the speed of light. Then the quantum contribution to the global vacuum energy density is:
, where c is the speed of light. Then the quantum contribution to the global vacuum energy density is:
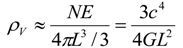
 . On the other hand, taking L as the particle horizon cannot account for the accelerated expansion of the current universe (see, e.g., [4]). The promising alternative is taking L as the event horizon of the universe. By using the definition of event horizon
. On the other hand, taking L as the particle horizon cannot account for the accelerated expansion of the current universe (see, e.g., [4]). The promising alternative is taking L as the event horizon of the universe. By using the definition of event horizon  , we can solve the Friedmann equation for a spatially flat universe. The evolution equation of ΩV is:
, we can solve the Friedmann equation for a spatially flat universe. The evolution equation of ΩV is:

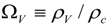 . Then the equation of state up to the first order is:
. Then the equation of state up to the first order is:

 . This result contradicts the latest observations of dark energy that requires w0 <−0.79 (see, e.g., [21,22]).
. This result contradicts the latest observations of dark energy that requires w0 <−0.79 (see, e.g., [21,22]).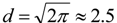 . This value is too large to be able to explain the observed dark energy. For example, the best-fit result of [5] is
. This value is too large to be able to explain the observed dark energy. For example, the best-fit result of [5] is  for 68.3% confidence level, and when combining with the Planck date, the best-fit result of d is smaller and around 0.5 [6]. When considering the Heisenberg uncertainty principle, one may reduce the Heisenberg quantum energy to
for 68.3% confidence level, and when combining with the Planck date, the best-fit result of d is smaller and around 0.5 [6]. When considering the Heisenberg uncertainty principle, one may reduce the Heisenberg quantum energy to  . Then the quantum contribution to the global vacuum energy density is:
. Then the quantum contribution to the global vacuum energy density is:
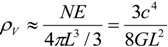
 , which is still more than the double of the current best-fit value. Therefore, the saturated form of Equation (4) cannot be consistent with the observational data of dark energy. Note that a holographic number of modes with the lowest frequency of quantum zero-point energy also gives more vacuum energy than the observed dark energy, as the quantum zero-point energy of the lowest frequency,
, which is still more than the double of the current best-fit value. Therefore, the saturated form of Equation (4) cannot be consistent with the observational data of dark energy. Note that a holographic number of modes with the lowest frequency of quantum zero-point energy also gives more vacuum energy than the observed dark energy, as the quantum zero-point energy of the lowest frequency,  , is still larger than the above Heisenberg quantum energy.
, is still larger than the above Heisenberg quantum energy.4. Ng’s Spacetime Foam Argument
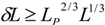 . Quantum mechanics requires
. Quantum mechanics requires  , and general relativity requires
, and general relativity requires 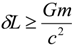 , where m is the mass of the clock used in the distance measurement. The product of these two inequalities then yields the above result. Similarly, the uncertainty δL in the measurement of a time interval T cannot be smaller than the cube root of
, where m is the mass of the clock used in the distance measurement. The product of these two inequalities then yields the above result. Similarly, the uncertainty δL in the measurement of a time interval T cannot be smaller than the cube root of  , namely
, namely  , where TP is the Planck time. These results were also obtained by Károlyházy et al. from somewhat different arguments [27,28].
, where TP is the Planck time. These results were also obtained by Károlyházy et al. from somewhat different arguments [27,28]. when the relation between the UV cutoff and distance uncertainty is
when the relation between the UV cutoff and distance uncertainty is 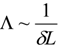 [14]. This relation seems reasonable because the UV cutoff usually determines the minimal detectable length. By assuming each minimum detectable space cube
[14]. This relation seems reasonable because the UV cutoff usually determines the minimal detectable length. By assuming each minimum detectable space cube  has typical Heisenberg energy of a delocalized state E~1/L, the energy density of the quantum fluctuations of spacetime is
has typical Heisenberg energy of a delocalized state E~1/L, the energy density of the quantum fluctuations of spacetime is 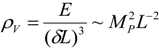 , and it assumes the same form as the HDE density denoted by Equation (1) [14]. A similar result is also obtained by Maziashvili in terms of time uncertainty [29], and it leads to the agegraphic dark energy model where the age of the universe determines L [30].
, and it assumes the same form as the HDE density denoted by Equation (1) [14]. A similar result is also obtained by Maziashvili in terms of time uncertainty [29], and it leads to the agegraphic dark energy model where the age of the universe determines L [30].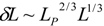 . Some authors have argued that the derivation of Ng is problematic, and distance can be measured much more accurately than Ng’s measuring method [31,32]. Moreover, different forms of spacetime fluctuations such as
. Some authors have argued that the derivation of Ng is problematic, and distance can be measured much more accurately than Ng’s measuring method [31,32]. Moreover, different forms of spacetime fluctuations such as 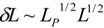 have also been suggested [33,34]. Next, even if Ng’s derivation of the minimum distance uncertainty in a Gedanken measurement is valid, it does not necessarily entail that spacetime itself does have the similar uncertainty or fluctuations. Maybe it is only that the physical principles lead to an intrinsic limitation to spacetime measurements. Thirdly, it is in want of a reasonable physical explanation why each minimum detectable space cube has typical Heisenberg energy of a delocalized state. Lastly, if the quantum fluctuations of spacetime indeed assume the very form suggested by Ng, then the holographic energy density will have the same form as Equation (8), namely
have also been suggested [33,34]. Next, even if Ng’s derivation of the minimum distance uncertainty in a Gedanken measurement is valid, it does not necessarily entail that spacetime itself does have the similar uncertainty or fluctuations. Maybe it is only that the physical principles lead to an intrinsic limitation to spacetime measurements. Thirdly, it is in want of a reasonable physical explanation why each minimum detectable space cube has typical Heisenberg energy of a delocalized state. Lastly, if the quantum fluctuations of spacetime indeed assume the very form suggested by Ng, then the holographic energy density will have the same form as Equation (8), namely 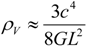 , as the calculation is the same as that in Thomas’ method (see also [14]). However, as we have shown in the last section, this energy density is about the quadruple of the observed dark energy density. Note that if one assumes the energy density is the same as the critical energy density [13], then the numerical factor in the formula of energy density will be nearer to the observed value. However, as we have argued in the last section, since the spatial scale for the critical energy density is the Hubble radius, not the event horizon, the predictions of such a model can hardly be consistent with the observational data.
, as the calculation is the same as that in Thomas’ method (see also [14]). However, as we have shown in the last section, this energy density is about the quadruple of the observed dark energy density. Note that if one assumes the energy density is the same as the critical energy density [13], then the numerical factor in the formula of energy density will be nearer to the observed value. However, as we have argued in the last section, since the spatial scale for the critical energy density is the Hubble radius, not the event horizon, the predictions of such a model can hardly be consistent with the observational data.5. A Conjecture on the Origin of Dark Energy
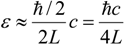 . Note that the size of space limited by the event horizon is 2L, not L. This is equivalent to introducing one numerical factor 1/2 into Equation (8) in Thomas’ model. Next, since such quantum fluctuations of spacetime of one degree of freedom corresponds to two Planck area units at the two ends of the event horizon, the total number of degrees of freedom for such quantum fluctuations is
. Note that the size of space limited by the event horizon is 2L, not L. This is equivalent to introducing one numerical factor 1/2 into Equation (8) in Thomas’ model. Next, since such quantum fluctuations of spacetime of one degree of freedom corresponds to two Planck area units at the two ends of the event horizon, the total number of degrees of freedom for such quantum fluctuations is  . Note that the holographic principle implies that the event horizon contains finite area units, whose number is
. Note that the holographic principle implies that the event horizon contains finite area units, whose number is  . This is equivalent to introducing another numerical factor 1/2 into Equation (8) in Thomas’ model. Therefore, the energy density of the quantum fluctuations of spacetime limited by the event horizon of the universe is:
. This is equivalent to introducing another numerical factor 1/2 into Equation (8) in Thomas’ model. Therefore, the energy density of the quantum fluctuations of spacetime limited by the event horizon of the universe is:

 . This value is basically consistent with the latest observations [5,6]. It is worth noting that since this new interpretation of the HDE model requires no particular connection between UV and IR cutoffs as in Equation (3), it has no problems related to the UV/IR connection in the model of Cohen et al., and may consistently describe all epochs of the universe, including the matter-dominated epoch and the radiation-dominated epoch.
. This value is basically consistent with the latest observations [5,6]. It is worth noting that since this new interpretation of the HDE model requires no particular connection between UV and IR cutoffs as in Equation (3), it has no problems related to the UV/IR connection in the model of Cohen et al., and may consistently describe all epochs of the universe, including the matter-dominated epoch and the radiation-dominated epoch. seems to have a firm basis, the concrete numerical factor in the relation is still unknown, which is expected to be determined by the application of a complete theory of quantum gravity to the universe. The numerical factor 1/2 in the formula
seems to have a firm basis, the concrete numerical factor in the relation is still unknown, which is expected to be determined by the application of a complete theory of quantum gravity to the universe. The numerical factor 1/2 in the formula 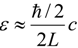 is only an assumption, which might be an interesting one when considering its consistency with the latest observations. Here we also stress that the use of Heisenberg’s uncertainty principle for spacetime fluctuations is still a tentative assumption, and it needs to be further justified. As we think, it might be reasonable to assume that any physical entity, no matter it is a matter field or a gravitational field, will have quantum fluctuations when limited in a finite space interval, and the fluctuation energy also satisfies Heisenberg’s uncertainty principle. This assumption is also used to derive the dark energy density in Thomas and Ng’s models [2,14,29]. In particular, Thomas implicitly used this assumption because the holographic vacuum energy in his argument may include the contributions from the quantum fluctuation of the gravitational field [2]. As a result, the energy is only related to the spatial scale, and especially, it is irrelevant to the nature of the field. For example, for a gravitational field the fluctuation energy of one degree of freedom does not contain the gravitational constant G [It is worth noting that the uncertainty relations for the length and time fluctuations of a spacetime region may directly contain the gravitational constant through the involved Planck scale (see, e.g., [12,33,34])]. However, the total fluctuation energy in a finite region contains G, as indicated by Equation (9), because the total number of degrees of freedom contains the gravitational constant G through the involved Planck scale. Certainly, whether this assumption is right or not can only be determined by experiments.
is only an assumption, which might be an interesting one when considering its consistency with the latest observations. Here we also stress that the use of Heisenberg’s uncertainty principle for spacetime fluctuations is still a tentative assumption, and it needs to be further justified. As we think, it might be reasonable to assume that any physical entity, no matter it is a matter field or a gravitational field, will have quantum fluctuations when limited in a finite space interval, and the fluctuation energy also satisfies Heisenberg’s uncertainty principle. This assumption is also used to derive the dark energy density in Thomas and Ng’s models [2,14,29]. In particular, Thomas implicitly used this assumption because the holographic vacuum energy in his argument may include the contributions from the quantum fluctuation of the gravitational field [2]. As a result, the energy is only related to the spatial scale, and especially, it is irrelevant to the nature of the field. For example, for a gravitational field the fluctuation energy of one degree of freedom does not contain the gravitational constant G [It is worth noting that the uncertainty relations for the length and time fluctuations of a spacetime region may directly contain the gravitational constant through the involved Planck scale (see, e.g., [12,33,34])]. However, the total fluctuation energy in a finite region contains G, as indicated by Equation (9), because the total number of degrees of freedom contains the gravitational constant G through the involved Planck scale. Certainly, whether this assumption is right or not can only be determined by experiments.6. Conclusions
 , is also consistent with the latest observations. Therefore, our proposal might provide a physically plausible interpretation of the HDE model. Besides, it also suggests that the dark energy may come from the quantum fluctuations of spacetime, not from the quantum fluctuations in spacetime such as quantum zero-point energy.
, is also consistent with the latest observations. Therefore, our proposal might provide a physically plausible interpretation of the HDE model. Besides, it also suggests that the dark energy may come from the quantum fluctuations of spacetime, not from the quantum fluctuations in spacetime such as quantum zero-point energy.Acknowledgments
Conflicts of Interest
References
- Cohen, A.G.; Kaplan, D.B.; Nelson, A.E. Effective field theory, black holes, and the cosmological constant. Phys. Rev. Lett. 1999, 82, 4971–4974. [Google Scholar] [CrossRef]
- Thomas, S. Holography stabilizes the vacuum energy. Phys. Rev. Lett. 2002, 89, 081301. [Google Scholar] [CrossRef]
- Hsu, S.D. Entropy bounds and dark energy. Phys. Lett. B 2004, 594, 13–16. [Google Scholar] [CrossRef]
- Li, M. A model of holographic dark energy. Phys. Lett. B 2004, 603, 1–5. [Google Scholar] [CrossRef]
- Li, M.; Li, X.D.; Wang, S.; Zhang, X. Holographic dark energy models: A comparison from the latest observational data. J. Cosmol. Astropart. Phys. 2009, 2009, 036. [Google Scholar] [CrossRef]
- Li, M.; Li, X.-D.; Ma, Y.-Z.; Zhang, X.; Zhang, Z. Planck constraints on holographic dark energy. ArXiv E-Prints 2013. arXiv:1305.5302. [Google Scholar]
- Pavón, D.; Zimdahl, W. Holographic dark energy and cosmic coincidence. Phys. Lett. B 2005, 628, 206–210. [Google Scholar] [CrossRef]
- Radicella, N.; Pavón, D. On the c2 term in the holographic formula for dark energy. J. Cosmol. Astropart. Phys. 2010, 2010, 005. [Google Scholar] [CrossRef]
- Medved, A.J. M. A comment or two on holographic dark energy. Gen. Relativ. Gravit. 2009, 41, 287–303. [Google Scholar] [CrossRef]
- Guberina, B.; Horvat, R.; Nikolić, H. Non-saturated holographic dark energy. J. Cosmol. Astropart. Phys. 2007, 2007, 012. [Google Scholar] [CrossRef]
- Horvat, R. On the internal consistency of holographic dark energy models. J. Cosmol. Astropart. Phys. 2008, 2008, 022. [Google Scholar] [CrossRef]
- Jack Ng, Y.; Van Dam, H. Limit to space-time measurement. Mod. Phys. Lett. A 1994, 9, 335–340. [Google Scholar] [CrossRef]
- Ng, Y.J. Holographic foam, dark energy and infinite statistics. Phys. Lett. B 2007, 657, 10–14. [Google Scholar] [CrossRef]
- Myung, Y.S.; Seo, M.G. Origin of holographic dark energy models. Phys. Lett. B 2009, 671, 435–439. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Universal upper bound on the entropy-to-energy ratio for bounded systems. Phys. Rev. D 1981, 23, 287–298. [Google Scholar] [CrossRef]
- ’t Hooft, G. Dimensional reduction in quantum gravity. ArXiv E-Prints 1993. arXiv:gr-qc/9310026. [Google Scholar]
- Susskind, L. The world as a hologram. J. Math. Phys. 1995, 36, 6377–6396. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Entropy bounds and black hole remnants. Phys. Rev. D 1994, 49, 1912–1921. [Google Scholar] [CrossRef]
- Schwinger, J. A Report on Quantum Electrodynamics. In The Physicist’s Conception of Nature; Mehra, J., Ed.; D. Reidel: Dordrecht, The Netherlands, 1973; pp. 413–429. [Google Scholar]
- Rugh, S.E.; Zinkernagel, H. The quantum vacuum and the cosmological constant problem. Studies Hist. Philos. Sci. Part B Studies Hist. Philos. Mod. Phys. 2002, 33, 663–705. [Google Scholar] [CrossRef]
- Riess, A.G.; Strolger, L.G.; Tonry, J.; Casertano, S.; Ferguson, H.C.; Mobasher, B.; Challis, P.; Filippenko, A.V.; Jha, S.; Li, W.; et al. Type Ia supernova discoveries at z > 1 from the Hubble space telescope: Evidence for past deceleration and constraints on dark energy evolution. Astrophys. J. 2004, 607, 665–687. [Google Scholar] [CrossRef]
- Tegmark, M.; Strauss, M.A.; Blanton, M.R.; Abazajian, K.; Dodelson, S.; Sandvik, H.; Wang, X.; Weinberg, D.H.; Zehavi, I.; Bahcall, N.A.; et al. Cosmological parameters from SDSS and WMAP. Phys. Rev. D 2004, 69, 103501. [Google Scholar] [CrossRef]
- Wheeler, J.A. Geometrodynamics; Academic Press: New York, NY, USA, 1962. [Google Scholar]
- Zizzi, P.A. Quantum computation toward quantum gravity. Gen. Relativ. Gravit. 2001, 33, 1305–1318. [Google Scholar] [CrossRef]
- Wigner, E.P. Relativistic invariance and quantum phenomena. Rev. Mod. Phys. 1957, 29, 255–268. [Google Scholar] [CrossRef]
- Salecker, H.; Wigner, E.P. Quantum limitations of the measurement of space-time distances. Phys. Rev. 1958, 109, 571–577. [Google Scholar] [CrossRef]
- Károlyházy, F. Gravitation and quantum mechanics of macroscopic objects. Il Nuovo Cimento A 1966, 42, 390–402. [Google Scholar] [CrossRef]
- Sasakura, N. An uncertainty relation of space-time. Prog. Theor. Phys. 1999, 102, 169–179. [Google Scholar] [CrossRef]
- Maziashvili, M. Cosmological implications of Karolyhazy uncertainty relation. Phys. Lett. B 2007, 652, 165–168. [Google Scholar] [CrossRef]
- Cai, R.G. A dark energy model characterized by the age of the universe. Phys. Lett. B 2007, 657, 228–231. [Google Scholar] [CrossRef]
- Adler, R.J.; Nemenman, I.M.; Overduin, J.M.; Santiago, D.I. On the detectability of quantum spacetime foam with gravitational-wave interferometers. Phys. Lett. B 2000, 477, 424–428. [Google Scholar] [CrossRef]
- Baez, J.C.; Olson, S.J. Uncertainty in measurements of distance. Class. Quantum Gravit. 2002, 19, L121–L126. [Google Scholar] [CrossRef]
- Amelino-Camelia, G. Limits on the measurability of space-time distances in (the semiclassical approximation of) quantum gravity. Mod. Phys. Lett. A 1994, 9, 3415–3422. [Google Scholar] [CrossRef]
- Adler, R.J.; Santiago, D.I. On gravity and the uncertainty principle. Mod. Phys. Lett. A 1999, 14, 1371–1381. [Google Scholar] [CrossRef]
- Gao, S. A conjecture on the origin of dark energy. Chin. Phys. Lett. 2005, 22, 783–784. [Google Scholar] [CrossRef]
- Gao, S. Quantum Motion: Unveiling the Mysterious Quantum World; Arima Publishing: Bury St Edmunds, UK, 2006; pp. 118–124. [Google Scholar]
- Kim, H.C.; Lee, J.W.; Lee, J. Causality problem in a holographic-dark-energy model. EPL 2013, 102, 29001. [Google Scholar] [CrossRef]
- Li, M.; Miao, R.X. A new model of holographic dark energy with action principle. ArXiv E-Prints 2012. arXiv:1210.0966. [Google Scholar]
- Li, M.; Li, X.D.; Meng, J.; Zhang, Z. Cosmological constraints on the new holographic dark energy model with action principle. Phys. Rev. D 2013, 88, 023503. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Gao, S. Explaining Holographic Dark Energy. Galaxies 2013, 1, 180-191. https://doi.org/10.3390/galaxies1030180
Gao S. Explaining Holographic Dark Energy. Galaxies. 2013; 1(3):180-191. https://doi.org/10.3390/galaxies1030180
Chicago/Turabian StyleGao, Shan. 2013. "Explaining Holographic Dark Energy" Galaxies 1, no. 3: 180-191. https://doi.org/10.3390/galaxies1030180
APA StyleGao, S. (2013). Explaining Holographic Dark Energy. Galaxies, 1(3), 180-191. https://doi.org/10.3390/galaxies1030180



