Evolving Black Hole Horizons in General Relativity and Alternative Gravity
Abstract
:1. Introduction

2. Various Notions of Horizon
2.1. Null Geodesic Congruences and Trapped Surfaces
- A normal surface corresponds to and (for example, a two-sphere in Minkowski space satisfies this property).
- A trapped surface [83] corresponds to and . The outgoing, in addition to the ingoing, future-directed null rays converge here instead of diverging, and outward-propagating light is dragged back by strong gravity.
- A marginally outer trapped (or marginal) surface (MOTS) corresponds to (where is the outgoing null normal to the surface) and .
- An untrapped surface is one with .
- An anti-trapped surface corresponds to and (both outgoing and ingoing future-directed null rays are diverging).
- A marginally outer trapped tube (MOTT) is a three-dimensional surface, which can be foliated entirely by marginally outer trapped (two-dimensional) surfaces.
2.2. Event Horizons
2.3. Killing Horizons
2.4. Apparent Horizons
2.5. Trapping Horizons
2.6. Isolated, Dynamical and Slowly Evolving Horizons
2.7. Kodama Vector
2.8. Surface Gravities
2.9. Spherical Symmetry
3. Evolving Horizons, Cosmological Black Holes and Naked Singularities in GR
3.1. The Schwarzschild-de Sitter-Kottler Spacetime
3.2. The McVittie Solution
- For , it is , and both and are complex. There are no apparent horizons.
- The critical time corresponds to . and coincide at a real value, and there is a single apparent horizon at .
- For , it is , and there are two apparent horizons of real positive radii, and .
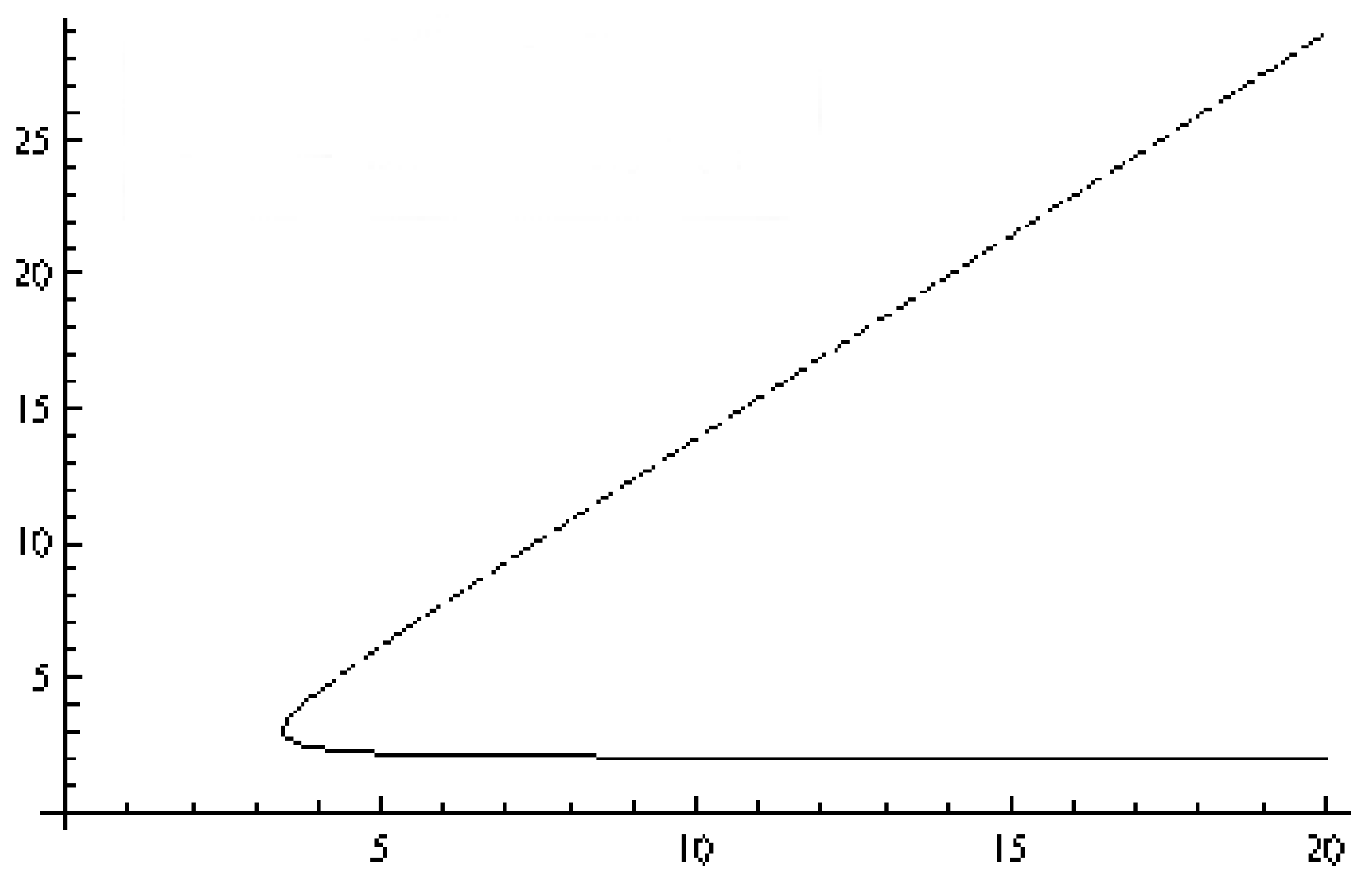
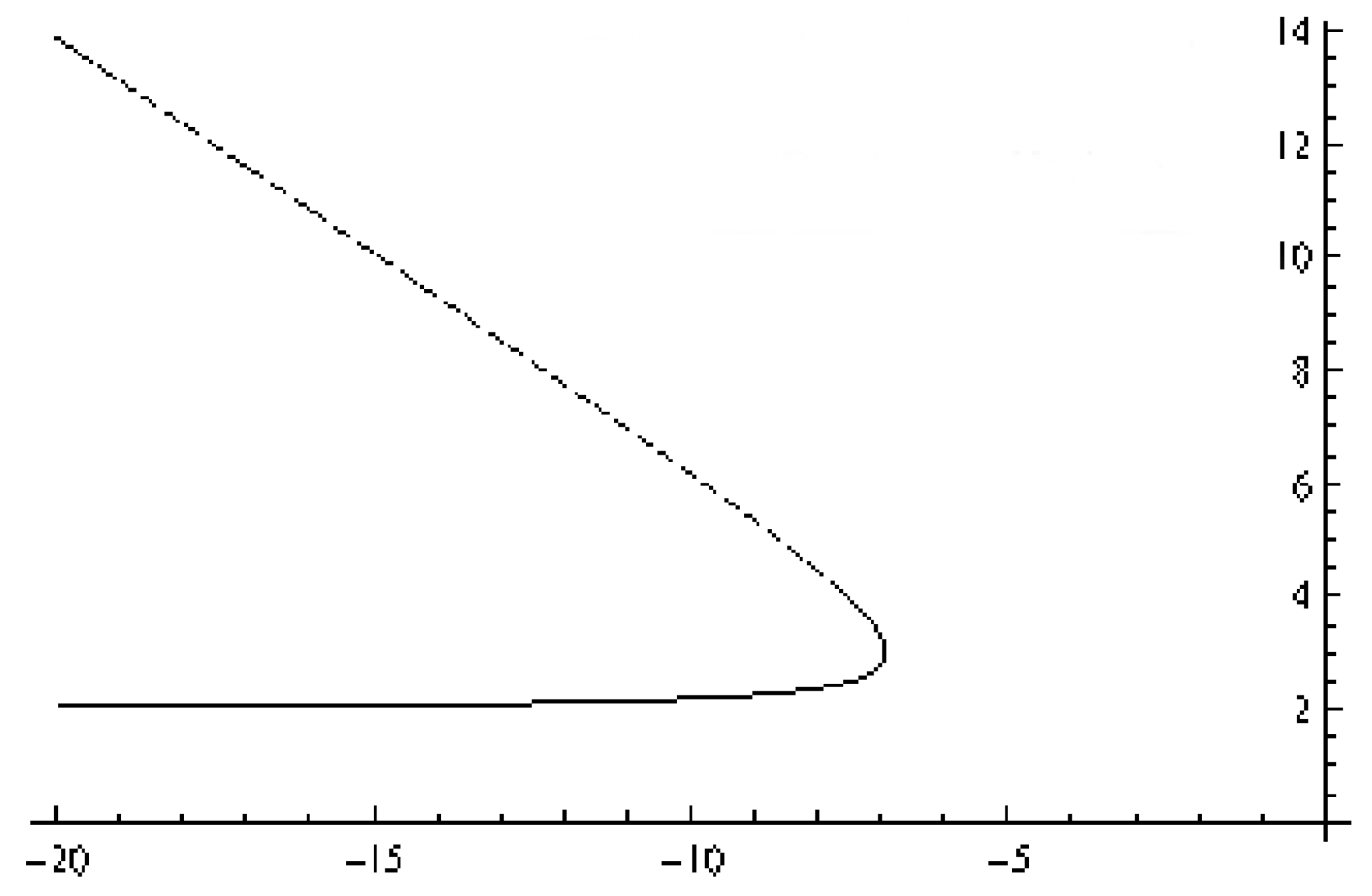
3.2.1. A Phantom Background
3.3. Area Quantization and McVittie Solutions as Toy Models
3.4. Generalized McVittie Solutions
3.4.1. Single Perfect Fluid
3.4.2. Imperfect Fluid and No Radial Mass Flow
3.4.3. Imperfect Fluid and Radial Mass Flow
3.4.4. The “Comoving Mass” Solution
3.4.5. The General Class of Solutions
3.4.6. Attractor Behaviour of the “Comoving Mass” Solution
3.5. The Sultana-Dyer Solution
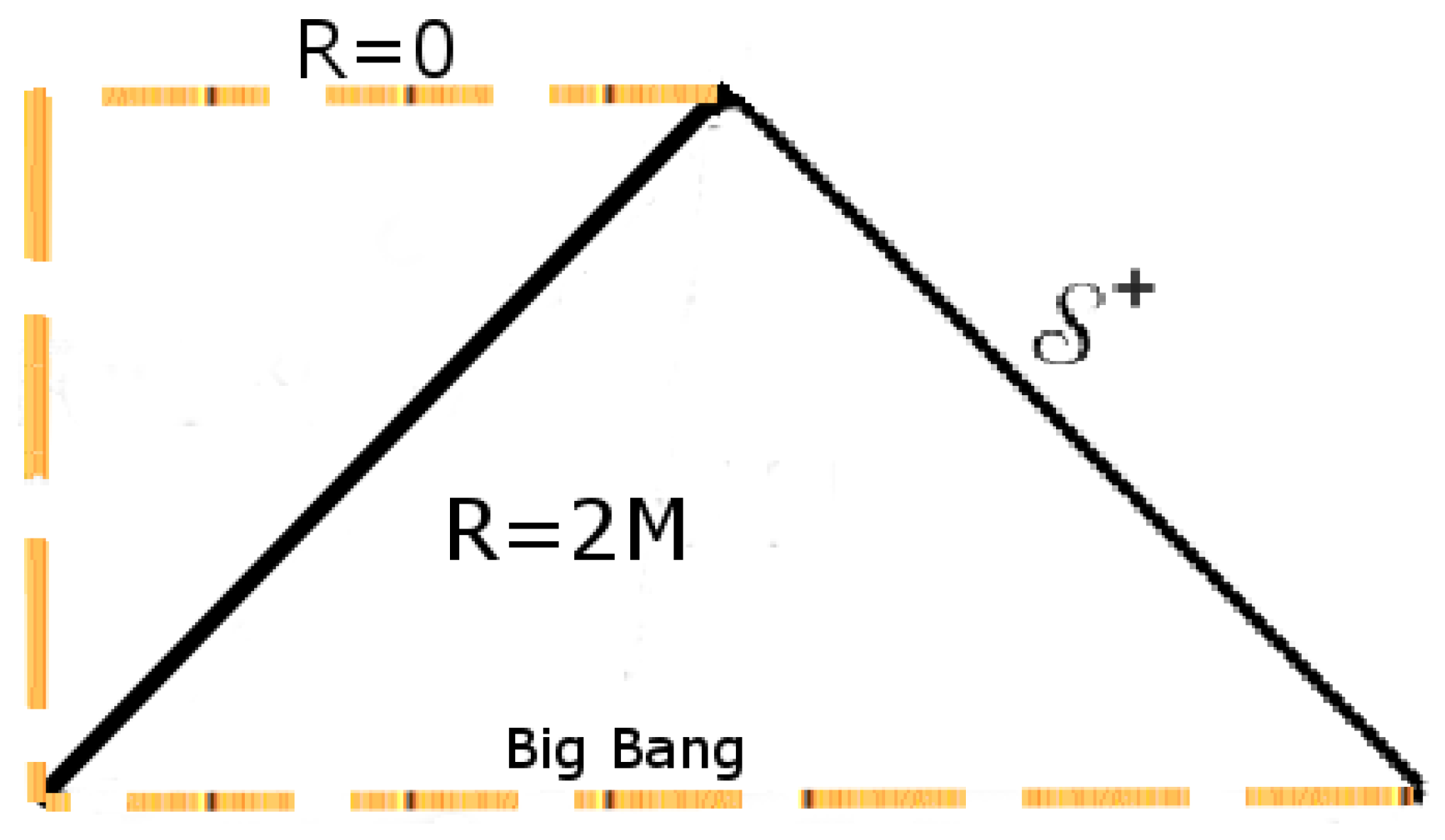
3.6. The Husain-Martinez-Nuñez Solution

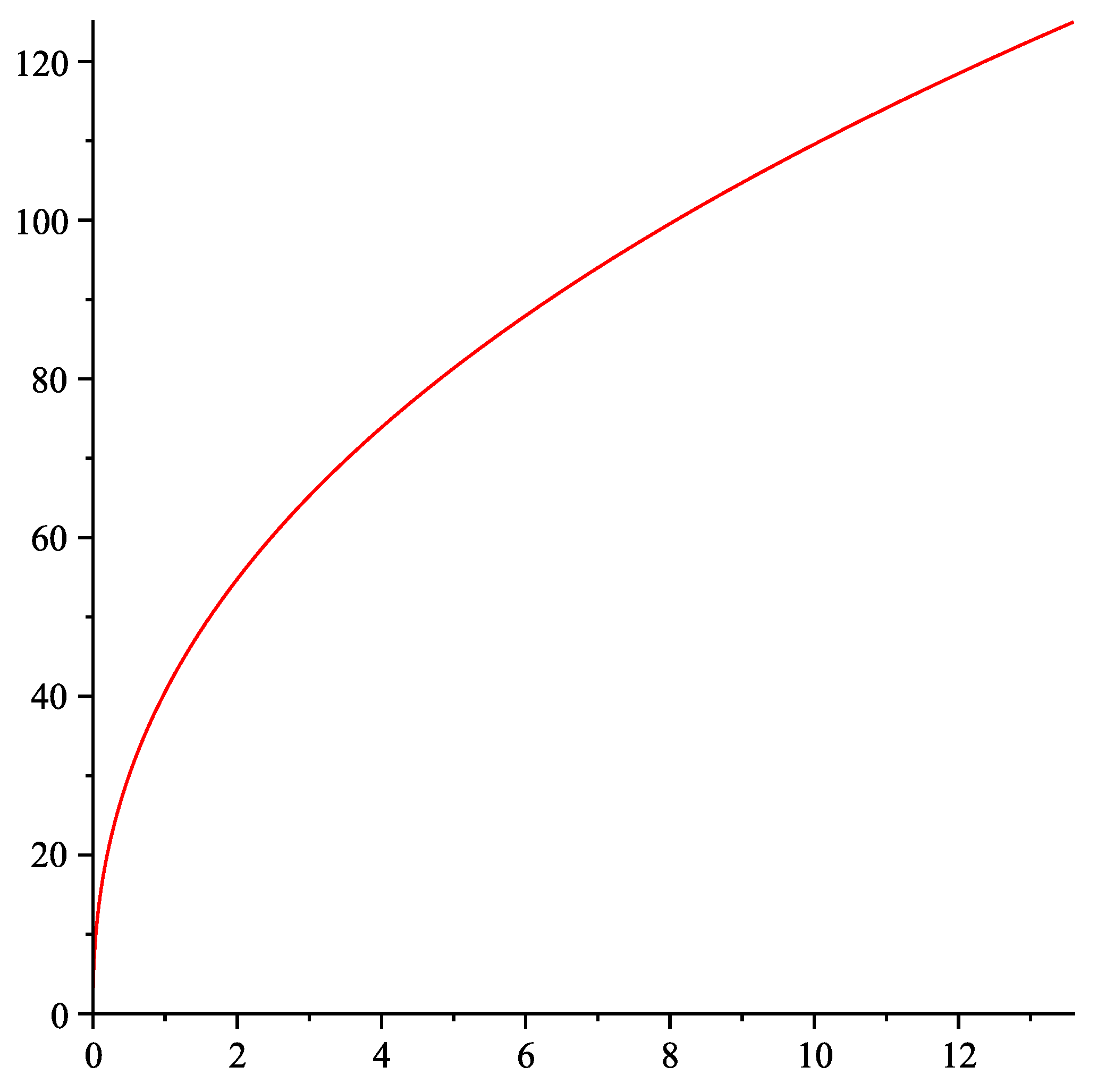
3.7. The Fonarev and Generalized Fonarev Solutions
3.7.1. A Generalized Fonarev Solution
3.8. The Swiss-Cheese Model
3.9. Other GR Solutions
4. Some Cosmological Black Holes and Naked Singularities in Alternative Gravity
4.1. The Conformal Cousin of the Husain-Martinez-Nuñez Solution
4.2. The Brans-Dicke Solutions of Clifton, Mota and Barrow
4.3. Clifton’s Solution of Gravity
4.4. Other Solutions
5. Conclusions
- Based on the type of matter filling the background FLRW universe (e.g., dust, general perfect fluid, imperfect fluid or scalar field);
- Based on the phenomenology of the apparent horizons.
Acknowledgments
Conflicts of Interest
References
- Poisson, E. A Relativist’s Toolkit: The Mathematics of Black-Hole Mechanics; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Frolov, V.P.; Novikov, I.D. Black Hole Physics, Basic Concepts and New Developments; Kluwer Academic Publishing: Dordrecht, The Netherlands, 1998. [Google Scholar]
- Wald, R.M. General Relativity; Chicago University Press: Chicago, IL, USA, 1984. [Google Scholar]
- Rindler, W. Visual horizons in world-models. Mon. Not. R. Astron. Soc. 1956, 116, 662–677, reprinted in Gen. Relativ. Gravit. 2002, 34, 133–153. [Google Scholar] [CrossRef]
- Booth, I. Black hole boundaries. Can. J. Phys. 2005, 83, 1073–1099. [Google Scholar] [CrossRef]
- Nielsen, A.B. Black holes and black hole thermodynamics without event horizons. Gen. Relativ. Gravit. 2009, 41, 1539–1584. [Google Scholar] [CrossRef]
- Ashtekar, A.; Krishnan, B. Isolated and dynamical horizons and their applications. Living Rev. Relativ. 2004, 7, 10. [Google Scholar] [CrossRef]
- Gourghoulhon, E.; Jaramillo, J.L. New theoretical approaches to black holes. New Astron. Rev. 2008, 51, 791–798. [Google Scholar] [CrossRef]
- Ben-Dov, I. Penrose inequality and apparent horizons. Phys. Rev. D 2005, 70, 124031. [Google Scholar] [CrossRef]
- Ashtekar, A.; Galloway, G.J. Some uniqueness results for dynamical horizons. Adv. Theor. Math. Phys. 2005, 9, 1–30. [Google Scholar] [CrossRef]
- Thornburg, J. Event and apparent horizon finders for 3 + 1 numerical relativity. Living Rev. Relativ. 2007, 10, 3. [Google Scholar] [CrossRef]
- Baumgarte, T.W.; Shapiro, S.L. Numerical relativity and compact binaries. Phys. Rep. 2003, 376, 41–131. [Google Scholar] [CrossRef]
- Chu, T.; Pfeiffer, H.P.; Cohen, M.I. Horizon dynamics of distorted rotating black holes. Phys. Rev. D 2011, 83, 104018. [Google Scholar] [CrossRef]
- Booth, I. Two physical characteristics of numerical apparent horizons. Can. J. Phys. 2008, 86, 669–673. [Google Scholar] [CrossRef]
- Kolb, E.W.; Turner, M.S. The Early Universe; Addison-Wesley: Reading, MA, USA, 1990. [Google Scholar]
- Liddle, A.R.; Lyth, D.H. Cosmological Inflation and Large Scale Structure; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Mukhanov, V. Physical Foundations of Cosmology; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Hawking, S.W. Black hole explosions. Nature 1970, 248, 30–31. [Google Scholar] [CrossRef]
- Hawking, S.W. Particle creation by black holes. Commun. Math. Phys. 1975, 43, 199–220, erratum in 1976, 46, 206. [Google Scholar] [CrossRef]
- Gibbons, W.; Hawking, S.W. Cosmological event horizon, thermodynamics, and particle creation. Phys. Rev. D 1977, 15, 2738–2751. [Google Scholar] [CrossRef]
- Collins, W. Mechanics of apparent horizons. Phys. Rev. D 1992, 45, 495–498. [Google Scholar] [CrossRef]
- Hayward, S.A. General laws of black hole dynamics. Phys. Rev. D 1994, 49, 6467–6474. [Google Scholar] [CrossRef]
- Faraoni, V. Black hole entropy in scalar-tensor and f(R) gravity: An overview. Entropy 2010, 12, 1246–1263. [Google Scholar] [CrossRef]
- Afshordi, N. Where will Einstein fail? Lessons for gravity and cosmology. ArXiv E-Prints 2012. arXiv:1203.3827. [Google Scholar]
- Sotiriou, T.P.; Faraoni, V. f(R) theories of gravity. Rev. Mod. Phys. 2010, 82, 451–497. [Google Scholar] [CrossRef]
- De Felice, A.; Tsujikawa, S. f(R) theories. Living Rev. Relativ. 2010, 13, 3. [Google Scholar] [CrossRef]
- Capozziello, S.; Faraoni, V. Beyond Einstein Gravity; Springer: New York, NY, USA, 2010. [Google Scholar]
- Amendola, L.; Tsujikawa, S. Dark Energy, Theory and Observations; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Wall, A.C. Testing the generalized second law in 1 + 1 dimensional conformal vacua: An argument for the causal horizon. Phys. Rev. D 2012, 85, 024015. [Google Scholar] [CrossRef]
- Brans, C.; Dicke, R.H. Mach’s principle and a relativistic theory of gravitation. Phys. Rev. 1961, 124, 925–935. [Google Scholar] [CrossRef]
- Bergmann, P.G. Comments on the scalar tensor theory. Int. J. Theor. Phys. 1968, 1, 25–36. [Google Scholar] [CrossRef]
- Wagoner, R.V. Scalar-tensor theory and gravitational waves. Phys. Rev. D 1970, 1, 3209–3216. [Google Scholar] [CrossRef]
- Nordtvedt, K. Post-Newtonian metric for a general class of scalar tensor gravitational theories and observational consequences. Astrophys. J. 1970, 161, 1059–1067. [Google Scholar] [CrossRef]
- McVittie, G.C. The mass-particle in an expanding universe. Mon. Not. R. Astron. Soc. 1933, 93, 325–339. [Google Scholar] [CrossRef]
- Carrera, M.; Giulini, D. Influence of global cosmological expansion on local dynamics and kinematics. Rev. Mod. Phys. 2010, 82, 169–208. [Google Scholar] [CrossRef]
- Kaloper, N.; Kleban, M.; Martin, D. McVitties legacy: Black holes in an expanding universe. Phys. Rev. D 2010, 81, 104044. [Google Scholar] [CrossRef]
- Lake, K.; Abdelqader, M. More on McVittie’s legacy: A Schwarzschild-de Sitter black and white hole embedded in an asymptotically ΛCDM cosmology. Phys. Rev. D 2011, 84, 044045. [Google Scholar] [CrossRef]
- Anderson, M. Horizons, singularities and causal structure of the generalized McVittie space-times. J. Phys. Conf. Ser. 2011, 283, 012001. [Google Scholar] [CrossRef]
- Nandra, R.; Lasenby, A.N.; Hobson, M.P. The effect of a massive object on an expanding universe. Mon. Not. R. Astron. Soc. 2012, 422, 2931–2944. [Google Scholar] [CrossRef]
- Nandra, R.; Lasenby, A.N.; Hobson, M.P. The effect of an expanding universe on massive objects. Mon. Not. R. Astron. Soc. 2012, 422, 2945–2959. [Google Scholar] [CrossRef]
- Faraoni, V.; Zambrano Moreno, A.F.; Nandra, R. Making sense of the bizarre behavior of horizons in the McVittie spacetime. Phys. Rev. D 2012, 85, 083526. [Google Scholar] [CrossRef]
- Da Silva, A.; Fontanini, M.; Guariento, D.C. How the expansion of the universe determines the causal structure of McVittie spacetimes. Phys. Rev. D 2013, 87, 064030. [Google Scholar] [CrossRef]
- Krasiński, A. Inhomogeneous Cosmological Models; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Buchert, T. On average properties of inhomogeneous fluids in general relativity. 1. Dust cosmologies. Gen. Relativ. Gravit. 2000, 32, 105–125. [Google Scholar] [CrossRef]
- Buchert, T.; Carfora, M. Regional averaging and scaling in relativistic cosmology. Class. Quantum Gravity 2002, 19, 6109–6105. [Google Scholar] [CrossRef]
- Kolb, E.W.; Matarrese, S.; Riotto, A. On cosmic acceleration without dark energy. New J. Phys. 2006, 8, 322–353. [Google Scholar] [CrossRef]
- Larena, J.; Buchert, T.; Alimi, J.-M. Correspondence between kinematical backreaction and scalar field cosmologies: The “Morphon field”. Class. Quantum Gravity 2006, 23, 6379–6408. [Google Scholar]
- Paranjape, A.; Singh, T.P. The spatial averaging limit of covariant macroscopic gravity: Scalar corrections to the cosmological equations. Phys. Rev. D 2007, 76, 044006. [Google Scholar] [CrossRef]
- Li, N.; Schwarz, D.J. Onset of cosmological backreaction. Phys. Rev. D 2007, 76, 083011. [Google Scholar] [CrossRef]
- Wiltshire, D.L. Cosmic clocks, cosmic variance and cosmic averages. New J. Phys. 2007, 9, 377–449. [Google Scholar] [CrossRef]
- Wiltshire, D.L. Exact solution to the averaging problem in cosmology. Phys. Rev. Lett. 2007, 99, 251101. [Google Scholar] [CrossRef] [PubMed]
- Buchert, T. Dark Energy from structure: A status report. Gen. Relativ. Gravit. 2008, 40, 467–527. [Google Scholar] [CrossRef]
- Li, N.; Schwartz, D.J. Scale dependence of cosmological backreaction. Phys. Rev. D 2008, 78, 083531. [Google Scholar] [CrossRef]
- Larena, J.; Alimi, J.-M.; Buchert, T.; Kunz, M.; Corasaniti, P. Testing backreaction effects with observations. Phys. Rev. D 2009, 79, 083011. [Google Scholar] [CrossRef]
- Tsagas, C.G.; Challinor, A.; Maartens, R. Relativistic cosmology and large-scale structure. Phys. Rep. 2008, 465, 61–147. [Google Scholar] [CrossRef]
- Vitagliano, V.; Liberati, S.; Faraoni, V. Averaging inhomogeneities in scalar-tensor cosmology. Class. Quantum Grav. 2009, 26, 215005. [Google Scholar] [CrossRef]
- Green, S.R.; Wald, R.M. A new framework for analyzing the effects of small scale inhomogeneities in cosmology. Phys. Rev. D 2011, 83, 084020. [Google Scholar] [CrossRef]
- Boleiko, K.; Célérier, M.-N.; Krasiński, A. Inhomogeneous cosmological models: Exact solutions and their applications. Class. Quantum Gravity 2011, 28, 164002. [Google Scholar] [CrossRef]
- Babichev, E.; Dokuchaev, V.; Eroshenko, Yu. Black hole mass decreasing due to phantom energy accretion. Phys. Rev. Lett. 2004, 93, 021102. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Jing, J. Quasinormal modes of a black hole surrounded by quintessence. Class. Quantum Gravity 2005, 22, 4651–4657. [Google Scholar] [CrossRef]
- Izquierdo, G.; Pavon, D. The generalized second law in phantom dominated universes in the presence of black holes. Phys. Lett. B 2006, 639, 1–4. [Google Scholar] [CrossRef]
- De Freitas Pacheco, J.A.; Horvath, J.E. Generalized second law and phantom cosmology: Accreting black holes. Class. Quantum Gravity 2007, 24, 5427–5434. [Google Scholar] [CrossRef]
- Maeda, H.; Harada, T.; Carr, B.J. Self-similar cosmological solutions with dark energy. II. Black holes, naked singularities and wormholes. Phys. Rev. D 2008, 77, 024023. [Google Scholar] [CrossRef]
- Gao, G.; Chen, X.; Faraoni, V.; Shen, Y.-G. Does the mass of a black hole decrease due to accretion of phantom energy? Phys. Rev. D 2008, 78, 024008. [Google Scholar] [CrossRef]
- Guariento, D.C.; Horvath, J.E.; Custodio, P.S.; de Freitas Pacheco, J.A. Evolution of primordial black holes in a radiation and phantom energy environment. Gen. Rel. Grav. 2008, 40, 1593–1602. [Google Scholar] [CrossRef]
- Lima, J.A.S.; Pereira, S.H.; Horvath, J.E.; Guariento, D.C. Phantom accretion by black holes and the generalized second law of thermodynamics. Astropart. Phys. 2010, 33, 292–295. [Google Scholar] [CrossRef]
- De Lima, J.A.S.; Guariento, D.C.; Horvath, J.E. ; Analytical solutions of accreting black holes immersed in a Lambda-CDM model. Phys. Lett. B 2010, 693, 218–220. [Google Scholar] [CrossRef]
- Guariento, D.C.; Horvath, J.E. Consistency of the mass variation formula for black holes accreting cosmological fluids. Gen. Relativ. Gravit. 2012, 44, 985–992. [Google Scholar] [CrossRef]
- Guariento, D.C.; Fontanini, M.; da Silva, A.M.; Abdalla, E. Realistic fluids as source for dynamically accreting black holes in a cosmological background. Phys. Rev. D 2012, 86, 124020. [Google Scholar] [CrossRef]
- Le Delliou, M.; Mimoso, J.P.; Mena, F.C.; Fontanini, M.; Guariento, D.C.; Abdalla, E. Separating expansion and collapse in general fluid models with heat flux. Phys. Rev. D 2013, 88, 027301. [Google Scholar] [CrossRef]
- Sun, C.-Y. Phantom energy accretion onto black holes in a cyclic universe. Phys. Rev. D 2008, 78, 064060. [Google Scholar] [CrossRef]
- Sun, C.-Y. Dark Energy accretion onto a black hole in an expanding universe. Commun. Theor. Phys. 2009, 52, 441–444. [Google Scholar]
- Gonzalez, J.A.; Guzman, F.S. Accretion of phantom scalar field into a black hole. Phys. Rev. D 2009, 79, 121501. [Google Scholar] [CrossRef]
- He, X.; Wang, B.; Wu, S.-F.; Lin, C.Y. Quasinormal modes of black holes absorbing dark energy. Phys. Lett. B 2009, 673, 156–160. [Google Scholar] [CrossRef]
- Babichev, E.O.; Dokuchaev, V.I.; Eroshenko, Yu.N. Perfect fluid and scalar field in the Reissner-Nordstrom metric. J. Exp. Theor. Phys. 2011, 112, 784–793. [Google Scholar] [CrossRef]
- Nouicer, K. Hawking radiation and thermodynamics of dynamical black holes in phantom dominated universe. Class. Quantum Gravity 2011, 28, 015005. [Google Scholar] [CrossRef]
- Chadburn, S.; Gregory, R. Time dependent black holes and scalar hair. ArXiv E-Prints 2013. arXiv:1304.6287. [Google Scholar] [CrossRef]
- Hawking, S.W.; Ellis, G.F.R. The Large Scale Structure of Space-Time; Cambridge University Press: Cambridge, UK, 1973. [Google Scholar]
- Nielsen, A.B.; Yoon, J.H. Dynamical surface gravity. Class. Quantum Gravity 2008, 25, 085010. [Google Scholar] [CrossRef]
- Pielahn, M.; Kunstatter, G.; Nielsen, A.B. Dynamical surface gravity in spherically symmetric black hole formation. Phys. Rev. D 2011, 84, 104008. [Google Scholar] [CrossRef]
- Booth, I.; Brits, L.; Gonzalez, J.A.; van den Broeck, V. Marginally trapped tubes and dynamical horizons. Class. Quantum Gravity 2006, 23, 413. [Google Scholar] [CrossRef]
- Ben-Dov, I. Outer trapped surfaces in Vaidya spacetimes. Phys. Rev. D 2007, 75, 064007. [Google Scholar] [CrossRef]
- Penrose, R. Gravitational collapse and spacetime singularities. Phys. Rev. Lett. 1965, 14, 57–59. [Google Scholar] [CrossRef]
- Eardley, D. Black hole boundary conditions and coordinate conditions. Phys. Rev. D 1998, 57, 2299–2304. [Google Scholar] [CrossRef]
- Andersson, L.; Mars, M.; Simon, W. Local existence of dynamical and trapping horizons. Phys. Rev. Lett. 2005, 95, 11102. [Google Scholar] [CrossRef]
- Hawking, S.W. Black holes in general relativity. Commun. Math. Phys. 1972, 25, 152–166. [Google Scholar] [CrossRef]
- Bengtsson, I.; Senovilla, J.M.M. Region with trapped surfaces in spherical symmetry, its core, and their boundaries. Phys. Rev. D 2011, 83, 044012. [Google Scholar] [CrossRef]
- Bengtsson, I. Some examples of trapped surfaces. ArXiv E-Prints 2011. arXiv:1112.5318. [Google Scholar]
- Chriusciel, P.T. Uniqueness of stationary, electro-vacuum black holes revisited. Helv. Phys. Acta 1996, 69, 529–552. [Google Scholar]
- Wald, R.M. The thermodynamics of black holes. Living Rev. Relativ. 2001, 4, 6. [Google Scholar] [CrossRef]
- Dyer, C.C.; Honig, E. Conformal Killing horizons. J. Math. Phys. 1979, 20, 409–412. [Google Scholar] [CrossRef]
- Sultana, J.; Dyer, C.C. Conformal Killing horizons. J. Math. Phys. 2004, 45, 4764–4776. [Google Scholar] [CrossRef]
- Sultana, J.; Dyer, C.C. Cosmological black holes: A black hole in the Einstein-de Sitter universe. Gen. Relativ. Gravit. 2005, 37, 1349–1370. [Google Scholar] [CrossRef]
- McClure, M.L.; Dyer, C.C. Asymptotically Einstein-de Sitter cosmological black holes and the problem of energy conditions. Class. Quantum Gravity 2006, 23, 1971–1987. [Google Scholar] [CrossRef]
- McClure, M.L.; Anderson, K.; Bardahl, K. Cosmological versions of Vaidya’s radiating stellar exterior, an accelerating reference frame, and Kinnersley’s photon rocket. ArXiv E-Prints 2008. arXiv:0709.3288. [Google Scholar]
- McClure, M.L.; Anderson, K.; Bardahl, K. Nonisolated dynamical black holes and white holes. Phys. Rev. D 2008, 77, 104008. [Google Scholar] [CrossRef]
- McClure, M.L. Cosmological Black Holes as Models of Cosmological Inhomogeneities. Ph.D. Thesis, University of Toronto, Toronto, Canada, 2005. [Google Scholar]
- Wald, R.M.; Iyer, V. Trapped surfaces in the Schwarzschild geometry and cosmic censorship. Phys. Rev. D 1991, 44, R3719–R3722. [Google Scholar] [CrossRef]
- Schnetter, E.; Krishnan, B. Non-symmetric trapped surfaces in the Schwarzschild and Vaidya spacetimes. Phys. Rev. D 2006, 73, 021502. [Google Scholar] [CrossRef]
- Figueras, P.; Hubeny, V.E.; Rangamani, M.; Ross, S.F. Dynamical black holes and expanding plasmas. J. High Energy Phys. 2009, 2009, 137. [Google Scholar] [CrossRef]
- Kavanagh, W.; Booth, I. Spacetimes containing slowly evolving horizons. Phys. Rev. D 2006, 74, 044027. [Google Scholar] [CrossRef]
- Visser, M. Gravitational vacuum polarization. I. Energy conditions in the Hartle-Hawking vacuum. Phys. Rev. D 1996, 54, 5103–5115. [Google Scholar] [CrossRef]
- Scheel, M.A.; Shapiro, S.L.; Teukolsky, S.A. Collapse to black holes in Brans-Dicke theory. 2. Comparison with general relativity. Phys. Rev. D 1995, 51, 4236–4249. [Google Scholar] [CrossRef]
- Hawking, S.W. Black holes in the Brans-Dicke theory of gravitation. Commun. Math. Phys. 1972, 25, 167–171. [Google Scholar] [CrossRef]
- Sotiriou, T.P.; Faraoni, V. Black holes in scalar-tensor gravity. Phys. Rev. Lett. 2012, 108, 081103. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, A.B.; Visser, M. Production and decay of evolving horizons. Class. Quantum Gravity 2006, 23, 4637. [Google Scholar] [CrossRef]
- Haijcek, P. On the origin of Hawking radiation. Phys. Rev. D 1987, 36, 1065–1107. [Google Scholar] [CrossRef]
- Hiscock, W.A. Gravitational entropy of nonstationary black holes and spherical shells. Phys. Rev. D 1989, 40, 1336–1339. [Google Scholar] [CrossRef]
- Sorkin, R.D. How wrinkled is the surface of a black hole? ArXiv E-Prints 1997. arXiv:gr-qc/9701056. [Google Scholar]
- Corichi, A.; Sudarsky, D. When is S = A/4? Mod. Phys. Lett. A 2002, 17, 1431–1444. [Google Scholar] [CrossRef]
- Nielsen, A.B.; Firouzjaee, J.T. Conformally rescaled spacetimes and hawking radiation. ArXiv E-Prints 2012. arXiv:1207.0064. [Google Scholar] [CrossRef]
- Parikh, M.K.; Wilczek, F. Hawking radiation as tunneling. Phys. Rev. Lett. 2000, 85, 5042. [Google Scholar] [CrossRef] [PubMed]
- Visser, M. Essential and inessential features of Hawking radiation. Int. J. Mod. Phys. D 2003, 12, 649–661. [Google Scholar] [CrossRef]
- Di Criscienzo, R.; Nadalini, M.; Vanzo, L.; Zerbini, S.; Zoccatelli, G. On the Hawking radiation as tunneling for a class of dynamical black holes. Phys. Lett. B 2007, 657, 107–111. [Google Scholar] [CrossRef]
- Clifton, T. Properties of black hole radiation from tunnelling. Class. Quantum Gravity 2008, 25, 175022. [Google Scholar] [CrossRef]
- Nielsen, A.B.; Yeom, D.-H. Spherically symmetric trapping horizons, the Misner-Sharp mass and black hole evaporation. Int. J. Mod. Phys. A 2009, 24, 5261–5285. [Google Scholar] [CrossRef]
- Jang, K.-X.; Feng, T.; Peng, D.-T. Hawking radiation of apparent horizon in a FRW universe as tunneling beyond semiclassical approximation. Int. J. Theor. Phys. 2009, 48, 2112–2121. [Google Scholar]
- Nielsen, A.B. Black holes without boundaries. Int. J. Mod. Phys. D 2009, 17, 2359–2366. [Google Scholar] [CrossRef]
- Angheben, M.; Nadalini, M.; Vanzo, L.; Zerbini, S. Hawking radiation as tunneling for extremal and rotating black holes. J. High Energy Phys. 2005, 2005, 014. [Google Scholar] [CrossRef]
- Hayward, S.A.; Di Criscienzo, R.; Nadalini, M.; Vanzo, L.; Zerbini, S. Local Hawking temperature for dynamical black holes. Class. Quantum Gravity 2009, 26, 062001. [Google Scholar] [CrossRef]
- Barcelo, C.; Liberati, S.; Sonego, S.; Visser, M. Hawking-like radiation does not require a trapped region. Phys. Rev. Lett. 2006, 97, 171301. [Google Scholar] [CrossRef] [PubMed]
- Roman, T.A.; Bergmann, P.G. Stellar collapse without singularities? Phys. Rev. D 1983, 28, 1265–1277. [Google Scholar] [CrossRef]
- Hayward, S.A. Formation and evaporation of nonsingular black holes. Phys. Rev. Lett. 2006, 96, 031103. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, A.B. The spatial relation between the event horizon and trapping horizon. Class. Quantum Gravity 2010, 27, 245016. [Google Scholar] [CrossRef]
- Ashtekar, A.; Beetle, C.; Fairhurst, S. Isolated horizons: A generalization of black hole mechanics. Class. Quantum Grav. 1999, 16, L1–L7. [Google Scholar] [CrossRef]
- Ashtekar, A.; Beetle, C.; Fairhurst, S. Mechanics of isolated horizons. Class. Quantum Gravity 2000, 17, 253–298. [Google Scholar] [CrossRef]
- Ashtekar, A.; Beetle, C.; Dreyer, O.; Fairhurst, S.; Krishnan, B.; Lewandowski, J.; Wiśnieski, J. Isolated horizons and their applications. Phys. Rev. Lett. 2000, 85, 3564–3567. [Google Scholar] [CrossRef] [PubMed]
- Ashtekar, A.; Corichi, A.; Krasnov, K. Isolated horizons: The classical phase space. Adv. Theor. Math. Phys. 2000, 3, 419–478. [Google Scholar]
- Ashtekar, A.; Corichi, A. Laws governing isolated horizons: Inclusion of dilaton couplings. Class. Quantum Gravity 2000, 17, 1317–1332. [Google Scholar] [CrossRef]
- Fairhurst, S.; Krishnan, B. Distorted black holes with charge. Int. J. Mod. Phys. D 2001, 10, 691–710. [Google Scholar] [CrossRef]
- Ashtekar, A.; Beetle, C.; Lewandowski, J. Geometry of generic isolated horizons. Class. Quantum Gravity 2002, 19, 1195–1225. [Google Scholar] [CrossRef]
- Ashtekar, A.; Beetle, C.; Lewandowski, J. Mechanics of rotating isolated horizons. Phys. Rev. D 2002, 64, 044016. [Google Scholar] [CrossRef]
- Booth, I.; Fairhurst, S. The first law for slowly evolving horizons. Phys. Rev. Lett. 2004, 92, 011102. [Google Scholar] [CrossRef] [PubMed]
- Booth, I.; Fairhurst, S. Isolated, slowly evolving, and dynamical trapping horizons: Geometry and mechanics from surface deformations. Phys. Rev. D 2007, 75, 084019. [Google Scholar] [CrossRef]
- Kodama, H. Conserved energy flux from the spherically symmetric system and the back reaction problem in the black hole evaporation. Prog. Theor. Phys. 1980, 63, 1217–1228. [Google Scholar] [CrossRef]
- Tung, R.-S. Stationary untrapped boundary conditions in general relativity. Class. Quantum Gravity 2008, 25, 085005. [Google Scholar] [CrossRef]
- Abreu, G.; Visser, M. Kodama time: Geometrically preferred foliations of spherically symmetric spacetimes. Phys. Rev. D 2010, 82, 044027. [Google Scholar] [CrossRef]
- Rácz, I. On the use of the Kodama vector field in spherically symmetric dynamical problems. Class. Quantum Gravity 2006, 23, 115. [Google Scholar] [CrossRef]
- Misner, C.W.; Sharp, D.H. Relativistic equations for adiabatic, spherically symmetric gravitational collapse. Phys. Rev. 1964, 136, B571–B576. [Google Scholar] [CrossRef]
- Hernandez, W.C.; Misner, C.W. Observer time as a coordinate in relativistic spherical hydrodynamics. Astrophys. J. 1966, 143, 452–464. [Google Scholar] [CrossRef]
- Hayward, S.A. Gravitational energy in spherical symmetry. Phys. Rev. D 1996, 53, 1938–1949. [Google Scholar] [CrossRef]
- Szabados, L. Quasi-local energy-momentum and angular momentum in GR: A review article. Living Rev. Relativ. 2004, 7, 4. [Google Scholar] [CrossRef]
- Hayward, S.A. Unified first law of black-hole dynamics and relativistic thermodynamics. Class. Quantum Gravity 1998, 15, 3147–3162. [Google Scholar] [CrossRef]
- Di Criscienzo, R.; Hayward, S.A.; Nadalini, M.; Vanzo, L.; Zerbini, S. Hamilton-Jacobi method for dynamical horizons in different coordinate gauges. Class. Quantum Gravity 2010, 27, 015006. [Google Scholar] [CrossRef]
- Vanzo, L.; Acquaviva, G.; Di Criscienzo, R. Tunnelling methods and Hawking’s radiation: Achievements and prospects. Class. Quantum Gravity 2011, 28, 183001. [Google Scholar] [CrossRef]
- Fodor, G.; Nakamura, K.; Oshiro, Y.; Tomimatsu, A. Surface gravity in dynamical spherically symmetric space-times. Phys. Rev. D 1996, 54, 3882–3891. [Google Scholar] [CrossRef]
- Ashtekar, A.; Fairhurst, S.; Krishnan, B. Isolated horizons: Hamiltonian evolution and the first law. Phys. Rev. D 2000, 62, 104025. [Google Scholar] [CrossRef]
- Mukohyama, S.; Hayward, S.A. Quasilocal first law of black hole dynamics. Class. Quantum Gravity 2000, 17, 2153–2157. [Google Scholar] [CrossRef]
- Hawking, S.W. Gravitational radiation in an expanding universe. J. Math. Phys. 1968, 9, 598–604. [Google Scholar] [CrossRef]
- Hayward, S.A. Quasilocal gravitational energy. Phys. Rev. D 1994, 49, 831–839. [Google Scholar] [CrossRef]
- Kottler, F. Über die physikalischen ndlagen der Einsteinschen gravitationstheorie [in German]. Annalen der Physik 1918, 361, 401–462. [Google Scholar] [CrossRef]
- Bousso, R. Adventures in de Sitter Space. ArXiv E-Prints 2002. arXiv:hep-th/0205177. [Google Scholar]
- Griffiths, J.B.; Podolsky, J. Exact Space-Times in Einstein’s General Relativity; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Hubeny, V. The fluid/gravity correspondence: A new perspective on the membrane paradigm. Class. Quantum Gravity 2011, 28, 114007. [Google Scholar] [CrossRef]
- Sussman, R. Conformal structure of a Schwarzschild black hole immersed in a Friedman universe. Gen. Relativ. Gravit. 1985, 17, 251–291. [Google Scholar] [CrossRef]
- Nolan, B.C. A point mass in an isotropic universe: Existence, uniqueness and basic properties. Phys. Rev. D 1998, 58, 064006. [Google Scholar] [CrossRef]
- Nolan, B.C. A point mass in an isotropic universe. 2. Global properties. Class. Quantum Gravity 1999, 16, 1227–1254. [Google Scholar] [CrossRef]
- Nolan, B.C. A point mass in an isotropic universe. 3. The region R ≤ 2m. Class. Quantum Gravity 1999, 16, 3183–3191. [Google Scholar] [CrossRef]
- Landry, P.; Abdelqader, M.; Lake, K. McVittie solution with a negative cosmological constant. Phys. Rev. D 2012, 86, 084002. [Google Scholar] [CrossRef]
- Gao, C.J.; Zhang, S.N. Reissner-Nordström metric in the Friedman-Robertson-Walker universe. Phys. Lett. B 2004, 595, 28–35. [Google Scholar] [CrossRef]
- Einstein, A.; Straus, E.G. The influence of the expansion of space on the gravitation fields surrounding the individual stars. Rev. Mod. Phys. 1945, 17, 120–124. [Google Scholar] [CrossRef]
- Einstein, A.; Straus, E.G. Corrections and additional remarks to our paper: The influence of the expansion of space on the gravitation fields surrounding the individual stars. Rev. Mod. Phys. 1946, 18, 148–149. [Google Scholar] [CrossRef]
- Ferraris, M.; Francaviglia, M.; Spallicci, A. Physical limitations of the McVittie metric. Nuovo Cimento 1996, 111B, 1031–1037. [Google Scholar] [CrossRef]
- McClure, M.L.; Dyer, C.C. Matching radiation-dominated and matter-dominated Einstein-de Sitter universes and an application for primordial black holes in evolving cosmological backgrounds. Gen. Relativ. Gravit. 2006, 38, 1347–1354. [Google Scholar] [CrossRef]
- Faraoni, V.; Jacques, A. Cosmological expansion and local physics. Phys. Rev. D 2007, 76, 063510. [Google Scholar] [CrossRef]
- Li, Z.-H.; Wang, A. Existence of black holes in Friedmann-Robertson-Walker universe dominated by dark energy. Mod. Phys. Lett. A 2007, 22, 1663–1676. [Google Scholar] [CrossRef]
- Barrow, J.D. Unusual features of varying speed of light cosmologies. Phys. Lett. B 2003, 564, 1–7. [Google Scholar] [CrossRef]
- Caldwell, R.R.; Kamionkowski, M.; Weinberg, N.N. Phantom energy and cosmic doomsday. Phys. Rev. Lett. 2003, 91, 071301. [Google Scholar] [CrossRef] [PubMed]
- Nolan, B.C. Sources for McVitties mass particle in an expanding universe. J. Math. Phys. 1993, 34, 178–185. [Google Scholar] [CrossRef]
- Larsen, F. String model of black hole microstates. Phys. Rev. D 1997, 56, 1005–1008. [Google Scholar] [CrossRef]
- Cvetic, M.; Larsen, F. General rotating black holes in string theory: Grey body factors and event horizons. Phys. Rev. D 1997, 56, 4994–5007. [Google Scholar] [CrossRef]
- Ansorg, M.; Hennig, J. The Inner Cauchy horizon of axisymmetric and stationary black holes with surrounding matter. Class. Quantum Gravity 2008, 25, 222001. [Google Scholar] [CrossRef]
- Ansorg, M.; Hennig, J. The Inner Cauchy horizon of axisymmetric and stationary black holes with surrounding matter in Einstein-Maxwell theory. Phys. Rev. Lett. 2009, 102, 221102. [Google Scholar] [CrossRef] [PubMed]
- Castro, A.; Rodriguez, M.J. Universal properties and the first law of black hole inner mechanics. Phys. Rev. D 2012, 86, 024008. [Google Scholar] [CrossRef]
- Castro, A.; Dehmami, N.; Giribet, G.; Kastor, D. On the universality of inner black hole mechanics and higher curvature gravity. ArXiv E-Prints 2013. arXiv:1304.1696. [Google Scholar] [CrossRef]
- Visser, M. Quantization of area for event and Cauchy horizons of the Kerr-Newman black hole. J. High Energy Phys. 2012, 1206, 023. [Google Scholar] [CrossRef]
- Visser, M. Area products for black hole horizons. Phys. Rev. D 2013, 88, 044014. [Google Scholar] [CrossRef]
- Faraoni, V.; Zambrano Moreno, A.F. Are quantization rules for horizon areas universal? Phys. Rev. D 2013, 88, 044011. [Google Scholar] [CrossRef]
- Carrera, M.; Giulini, D. Generalization of McVitties model for an inhomogeneity in a cosmological spacetime. Phys. Rev. D 2010, 81, 043521. [Google Scholar] [CrossRef]
- Faraoni, V.; Gao, C.; Chen, X.; Shen, Y.-G. What is the fate of a black hole embedded in an expanding universe? Phys. Lett. B 2009, 671, 7–9. [Google Scholar] [CrossRef]
- Saida, H.; Harada, T.; Maeda, H. Black hole evaporation in an expanding universe. Class. Quantum Gravity 2007, 24, 4711. [Google Scholar] [CrossRef]
- Faraoni, V. Hawking temperature of expanding cosmological black holes. Phys. Rev. D 2007, 76, 104042. [Google Scholar] [CrossRef]
- Husain, V.; Martinez, E.A.; Nuñez, D. Exact solution for scalar field collapse. Phys. Rev. D 1994, 50, 3783–3786. [Google Scholar] [CrossRef]
- Fisher, I.Z. Scalar mesostatic field with regard for gravitational effects. Zh. Eksp. Teor. Fiz. 1948, 18, 636–640, translated in arXiv:gr-qc/9911008. [Google Scholar]
- Bergman, O.; Leipnik, R. Space-time structure of a static spherically symmetric scalar field. Phys. Rev. 1957, 107, 1157–1161. [Google Scholar] [CrossRef]
- Janis, A.I.; Newman, E.T.; Winicour, J. Reality of the Schwarzschild singularity. Phys. Rev. Lett. 1968, 20, 878–880. [Google Scholar] [CrossRef]
- Buchdahl, H.A. Static solutions of the Brans-Dicke equations. Int. J. Theor. Phys. 1972, 6, 407–412. [Google Scholar] [CrossRef]
- Wyman, M. Static spherically symmetric scalar fields in general relativity. Phys. Rev. D 1981, 24, 839–841. [Google Scholar] [CrossRef]
- Agnese, A.G.; La Camera, M. Gravitation without black holes. Phys. Rev. D 1985, 31, 1280–1286. [Google Scholar] [CrossRef]
- Virbhadra, K.S. Janis-Newman-Winicour and Wyman solutions are the same. Int. J. Mod.Phys. A 1997, 12, 4831–4835. [Google Scholar] [CrossRef]
- Roberts, M.D. Massless scalar static spheres. Astrophys. Space Sci. 1993, 200, 331–335. [Google Scholar] [CrossRef]
- Abe, S. Stability of a collapsed scalar field and cosmic censorship. Phys. Rev. D 1988, 38, 1053–1055. [Google Scholar] [CrossRef]
- Fonarev, O.A. Exact Einstein scalar field solutions for formation of black holes in a cosmological setting. Class. Quantum Gravity 1995, 12, 1739–1752. [Google Scholar] [CrossRef]
- Maeda, H. Global structure and physical interpretation of the Fonarev solution for a scalar field with exponential potential. ArXiv E-Prints 2007. arXiv:0704.2731. [Google Scholar]
- Mars, M.; Mena, F.C.; Vera, R. Review on exact and perturbative deformations of the Einstein-Straus model: Uniqueness and rigidity results. ArXiv E-Prints 2013. arXiv:1307.4371. [Google Scholar] [CrossRef]
- Eisenstaedt, J. Density constraint on local inhomogeneities of a Robertson-Walker cosmological universe. Phys. Rev. D 1977, 16, 927–928. [Google Scholar] [CrossRef]
- Bonnor, W.B. Size of a hydrogen atom in the expanding universe. Class. Quantum Gravity 1999, 16, 1313–1321. [Google Scholar] [CrossRef]
- Senovilla, J.M.M.; Vera, R. Impossibility of the cylindrically symmetric Einstein-Straus model. Phys. Rev. Lett. 1997, 78, 2284–2287. [Google Scholar] [CrossRef]
- Mars, M. Axially symmetric Einstein-Straus models. Phys. Rev. D 1998, 57, 3389–3400. [Google Scholar] [CrossRef]
- Mena, F.C.; Tavakol, R.; Vera, R. Generalization of the Einstein-Straus model to anisotropic settings. Phys. Rev. D 2002, 66, 044004. [Google Scholar] [CrossRef]
- Balbinot, R.; Bergamini, R.; Comastri, A. Solution of the Einstein-Strauss problem with a Λ term. Phys. Rev. D 1988, 38, 2415–2418. [Google Scholar] [CrossRef]
- Bona, C.; Stela, J. “Swiss cheese” models with pressure. Phys. Rev. D 1987, 36, 2915–2918. [Google Scholar] [CrossRef]
- Bonnor, W.B. A generalization of the Einstein-Straus vacuole. Class. Quantum Gravity 2000, 17, 2739–2748. [Google Scholar] [CrossRef]
- Saida, H. Hawking radiation in the Swiss-cheese universe. Class. Quantum Gravity 2002, 19, 3179–3205. [Google Scholar] [CrossRef]
- Goncalves, S.M.C.V. Shell crossing in generalized Tolman-Bondi spacetimes. Phys. Rev. D 2001, 63, 124017. [Google Scholar] [CrossRef]
- Gao, C.; Chen, X.; Shen, Y.-G.; Faraoni, V. Black holes in the universe: Generalized Lemaitre-Tolman-Bondi solutions. Phys. Rev. D 2011, 84, 104047. [Google Scholar] [CrossRef]
- Firouzjaee, J.T.; Mansouri, R. Asymptotically FRW black holes. Gen. Relativ. Gravit. 2010, 42, 2431–2452. [Google Scholar] [CrossRef]
- Firouzjaee, J.T.; Parsi Mood, N. Do we know the mass of a black hole? Mass of some cosmological black hole models. Gen. Relativ. Gravit. 2012, 44, 639–656. [Google Scholar] [CrossRef]
- Firouzjaee, J.T. The spherical symmetry black hole collapse in expanding universe. Int. J. Mod. Phys. D 2012, 21, 1250039. [Google Scholar] [CrossRef]
- Firouzjaee, J.T.; Mansouri, M. Radiation from the LTB black hole. Europhys. Lett. 2012, 97, 29002. [Google Scholar] [CrossRef]
- Moradi, R.; Firouzjaee, J.T.; Mansouri, R. The spherical perfect fluid collapse in the cosmological background. ArXiv E-Prints 2013. arXiv:1301.1480. [Google Scholar]
- Krasiński, A.; Hellaby, C. Formation of a galaxy with a central black hole in the Lemaître-Tolman model. Phys. Rev. D 2004, 69, 043502. [Google Scholar] [CrossRef]
- Oppenheimer, J.R.; Snyder, H. On continued gravitational contraction. Phys. Rev. 1939, 56, 455–459. [Google Scholar] [CrossRef]
- Barnes, A. On shear free normal flows of a perfect fluid. Gen. Relativ. Gravit. 1973, 2, 105–129. [Google Scholar] [CrossRef]
- Roberts, M.D. Scalar field counterexamples to the Cosmic Censorship hypothesis. Gen. Relativ. Gravit. 1989, 21, 907–939. [Google Scholar] [CrossRef]
- Burko, L.M. Comment on the Roberts solution for the spherically-symmetric Einstein-scalar field equations. Gen. Relativ. Grav. 1997, 29, 259–262. [Google Scholar] [CrossRef]
- Patel, L.K.; Trivedi, H.B. Kerr-Newman metric in cosmological background. J. Astrophys. Astron. 1982, 3, 63–67. [Google Scholar] [CrossRef]
- Vaidya, P.C. The Kerr metric in cosmological background. Pramana 1977, 8, 512–517. [Google Scholar] [CrossRef]
- Balbinot, R. Hawking radiation and the back reaction—A first approach. Class. Quantum Gravity 1984, 1, 573–577. [Google Scholar] [CrossRef]
- Nayak, K.R.; MacCallum, M.A.H.; Vishveshwara, C.V. Black holes in nonflat backgrounds: The Schwarzschild black hole in the Einstein universe. Phys. Rev. D 2000, 63, 024020. [Google Scholar] [CrossRef]
- Cox, D.P.G. Vaidya’s “Kerr-Einstein” metric cannot be matched to the Kerr metric. Phys. Rev. D 2003, 68, 124008. [Google Scholar] [CrossRef]
- Lindesay, J. Coordinates with non-singular curvature for a time dependent black hole horizon. Found. Phys. 2007, 37, 1181–1196. [Google Scholar] [CrossRef]
- Brown, B.A.; Lindesay, J. Construction of a Penrose diagram for a spatially coherent evaporating black hole. Class. Quantum Gravity 2008, 25, 105026. [Google Scholar] [CrossRef]
- Brown, B.A.; Lindesay, J. Radial photon trajectories near an evaporating black hole. ArXiv E-Prints 2008. arXiv:0802.1660. [Google Scholar]
- Lindesay, J. Quantum behaviors on an excreting black hole. Class. Quantum Gravity 2009, 26, 125014. [Google Scholar] [CrossRef]
- Brown, B.A.; Lindesay, J. Construction of a Penrose diagram for an accreting black hole. Class. Quantum Gravity 2009, 26, 045010. [Google Scholar] [CrossRef]
- Lindesay, J.; Sheldon, P. Penrose diagram for a transient black hole. Class. Quantum Gravity 2010, 27, 215015. [Google Scholar] [CrossRef]
- Lindesay, J.; Finch, T. Global geometry of a transient black hole in a dynamic de Sitter cosmology. In Classical and Quantum Gravity: Theory and Applications; Frignanni, V.R., Ed.; Nova Science: New York, NY, USA, 2012; Chapter 16. [Google Scholar]
- Lindesay, J.; Finch, T. Global causal structure of a transient black object. ArXiv E-Prints 2011. arXiv:1110.6928. [Google Scholar]
- Adler, R.J.; Bjorken, J.D.; Chen, P.; Liu, J.S. Simple analytical models of gravitational collapse. Am. J. Phys. 2005, 73, 1148–1159. [Google Scholar] [CrossRef]
- Zilhão, M.; Cardoso, V.; Gualtieri, L.; Herdeiro, C.; Sperhake, U.; Witek, H. Dynamics of black holes in de Sitter spacetimes. Phys. Rev. D 2012, 85, 104039. [Google Scholar] [CrossRef]
- Kastor, D.; Traschen, J. Cosmological multi-black-hole solutions. Phys. Rev. D 1993, 47, 5370–5375. [Google Scholar] [CrossRef]
- Brill, D.R.; Horowitz, G.T.; Kastor, D.; Traschen, J. Testing cosmic censorship with black hole collisions. Phys. Rev. D 1994, 49, 840–852. [Google Scholar] [CrossRef]
- Koberlein, B.D.; Mallett, R.L. Charged, radiating black holes, inflation, and cosmic censorship. Phys. Rev. D 1994, 49, 5111–5114. [Google Scholar] [CrossRef]
- Husain, V. Exact solutions for null fluid collapse. Phys. Rev. D 1996, 53, R1759–R1762. [Google Scholar] [CrossRef]
- Dawood, A.K.; Ghosh, S.G. Generating dynamical black hole solutions. Phys. Rev. D 2004, 70, 104010. [Google Scholar] [CrossRef]
- Conboy, S.; Lake, K. Smooth transitions from the Schwarzschild vacuum to de Sitter space. Phys. Rev. D 2005, 71, 124017. [Google Scholar] [CrossRef]
- Kyo, M.; Harada, T.; Maeda, H. Asymptotically Friedmann self-similar scalar field solutions with potential. Phys. Rev. D 2008, 77, 124036. [Google Scholar] [CrossRef]
- Meissner, K.A. Horizons and the cosmological constant. ArXiv E-Prints 2009. arXiv:0901.0640. [Google Scholar]
- Gibbons, G.W.; Maeda, K. Black holes in an expanding universe. Phys. Rev. Lett. 2010, 104, 131101. [Google Scholar] [CrossRef] [PubMed]
- Maeda, H. Exact dynamical AdS black holes and wormholes with a Klein-Gordon field. Phys. Rev. D 2012, 86, 044016. [Google Scholar] [CrossRef]
- Culetu, H. Time-dependent embedding of a spherically symmetric Rindler-like spacetime. Class. Quantum Gravity 2012, 29, 235021. [Google Scholar] [CrossRef]
- Clifton, T.; Mota, D.F.; Barrow, J.D. Inhomogeneous gravity. Mon. Not. R. Astron. Soc. 2005, 358, 601–613. [Google Scholar] [CrossRef]
- Faraoni, V.; Zambrano Moreno, A.F. Interpreting the conformal cousin of the Husain-Martinez-Nuñez solution. Phys. Rev. D 2012, 86, 084044. [Google Scholar] [CrossRef]
- Faraoni, V.; Vitagliano, V.; Sotiriou, T.P.; Liberati, S. Dynamical apparent horizons in inhomogeneous Brans-Dicke universes. Phys. Rev. D 2012, 86, 064040. [Google Scholar] [CrossRef]
- Campanelli, M.; Lousto, C. Are black holes in Brans-Dicke theory precisely the same as in general relativity? Int. J. Mod. Phys. D 1993, 2, 451–462. [Google Scholar] [CrossRef]
- Lousto, C.; Campanelli, M. On Brans-Dicke Black Holes. In Proceedings of the Origin of Structure in the Universe, Pont d’Oye, Belgium, 27 April–2 May 1992; Gunzig, E., Nardone, P., Eds.; Kluwer Academic: Dordrecht, The Netherlands, 1993; pp. 123–130. [Google Scholar]
- Vanzo, L.; Zerbini, S.; Faraoni, V. Campanelli-Lousto and veiled spacetimes. Phys. Rev. D 2012, 86, 084031. [Google Scholar] [CrossRef]
- Clifton, T. Spherically symmetric solutions to fourth-order theories of gravity. Class. Quantum Gravity 2006, 23, 7445–7453. [Google Scholar] [CrossRef]
- Faraoni, V. Clifton’s spherical solution in f(R) vacuum harbours a naked singularity. Class. Quantum Gravity 2009, 26, 195013. [Google Scholar] [CrossRef]
- Faraoni, V. Jebsen-Birkhoff theorem in alternative gravity. Phys. Rev. D 2010, 81, 044002. [Google Scholar] [CrossRef]
- Clifton, T.; Barrow, J.D. The power of general relativity. Phys. Rev. D 2005, 72, 103005. [Google Scholar] [CrossRef]
- Clifton, T.; Barrow, J.D. Further exact cosmological solutions to higher-order gravity theories. Class. Quantum Grav. 2006, 23, 2951–2962. [Google Scholar] [CrossRef]
- Dolgov, A.D.; Kawasaki, M. Can modified gravity explain accelerated cosmic expansion? Phys. Lett. B 2003, 573, 1–4. [Google Scholar] [CrossRef]
- Faraoni, V. Matter instability in modified gravity. Phys. Rev. D 2006, 74, 104017. [Google Scholar] [CrossRef]
- Faraoni, V. De Sitter space and the equivalence between f(R) and scalar-tensor gravity. Phys. Rev. D 2007, 75, 067302. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Modified gravity with negative and positive powers of curvature: Unification of inflation and cosmic acceleration. Phys. Rev. D 2003, 68, 123512. [Google Scholar] [CrossRef]
- Sakai, N.; Barrow, J.D. Cosmological evolution of black holes in Brans-Dicke gravity. Class. Quantum Gravity 2001, 18, 4717–4724. [Google Scholar] [CrossRef]
- Sakai, N.; Barrow, J.D. Evolution of black holes in Brans-Dicke cosmology. ArXiv E-Prints 2000. arXiv:gr-qc/0012067. [Google Scholar]
- Nozawa, M.; Maeda, H. Dynamical black holes with symmetry in Einstein-Gauss-Bonnet gravity. Class. Quantum Gravity 2008, 25, 055009. [Google Scholar] [CrossRef]
- Charmousis, C. Higher order gravity theories and their black hole solutions. ArXiv E-Prints 2008. arXiv:0805.0568. [Google Scholar]
- Maeda, H.; Willison, S.; Ray, S. Lovelock black holes with maximally symmetric horizons. Class. Quantum Gravity 2011, 28, 165005. [Google Scholar] [CrossRef]
- Horowitz, G.T. Black Holes in Higher Dimensions; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Maeda, H.; Nozawa, M. Generalized Misner-Sharp quasilocal mass in Einstein-Gauss-Bonnet gravity. Phys. Rev. D 2008, 77, 064031. [Google Scholar] [CrossRef]
- Cai, R.-G.; Cao, L.-M.; Hu, Y.-P.; Ohta, N. Generalized Misner-Sharp energy in f(R) gravity. Phys. Rev. D 2009, 80, 104016. [Google Scholar] [CrossRef]
- Christodolou, D. Examples of naked singularity formation in the gravitational collapse of a scalar field. Ann. Math. 1994, 140, 607–653. [Google Scholar] [CrossRef]
- Christodolou, D. The instability of naked singularities in the gravitational collapse of a scalar field. Ann. Math. 1999, 149, 183–217. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Faraoni, V. Evolving Black Hole Horizons in General Relativity and Alternative Gravity. Galaxies 2013, 1, 114-179. https://doi.org/10.3390/galaxies1030114
Faraoni V. Evolving Black Hole Horizons in General Relativity and Alternative Gravity. Galaxies. 2013; 1(3):114-179. https://doi.org/10.3390/galaxies1030114
Chicago/Turabian StyleFaraoni, Valerio. 2013. "Evolving Black Hole Horizons in General Relativity and Alternative Gravity" Galaxies 1, no. 3: 114-179. https://doi.org/10.3390/galaxies1030114
APA StyleFaraoni, V. (2013). Evolving Black Hole Horizons in General Relativity and Alternative Gravity. Galaxies, 1(3), 114-179. https://doi.org/10.3390/galaxies1030114



