Quantitative Method for Monitoring Tumor Evolution During and After Therapy
Abstract
1. Introduction
2. Materials and Methods
Computational Setting
3. Results
3.1. Analysis of In Vivo Conventional Radiotherapy
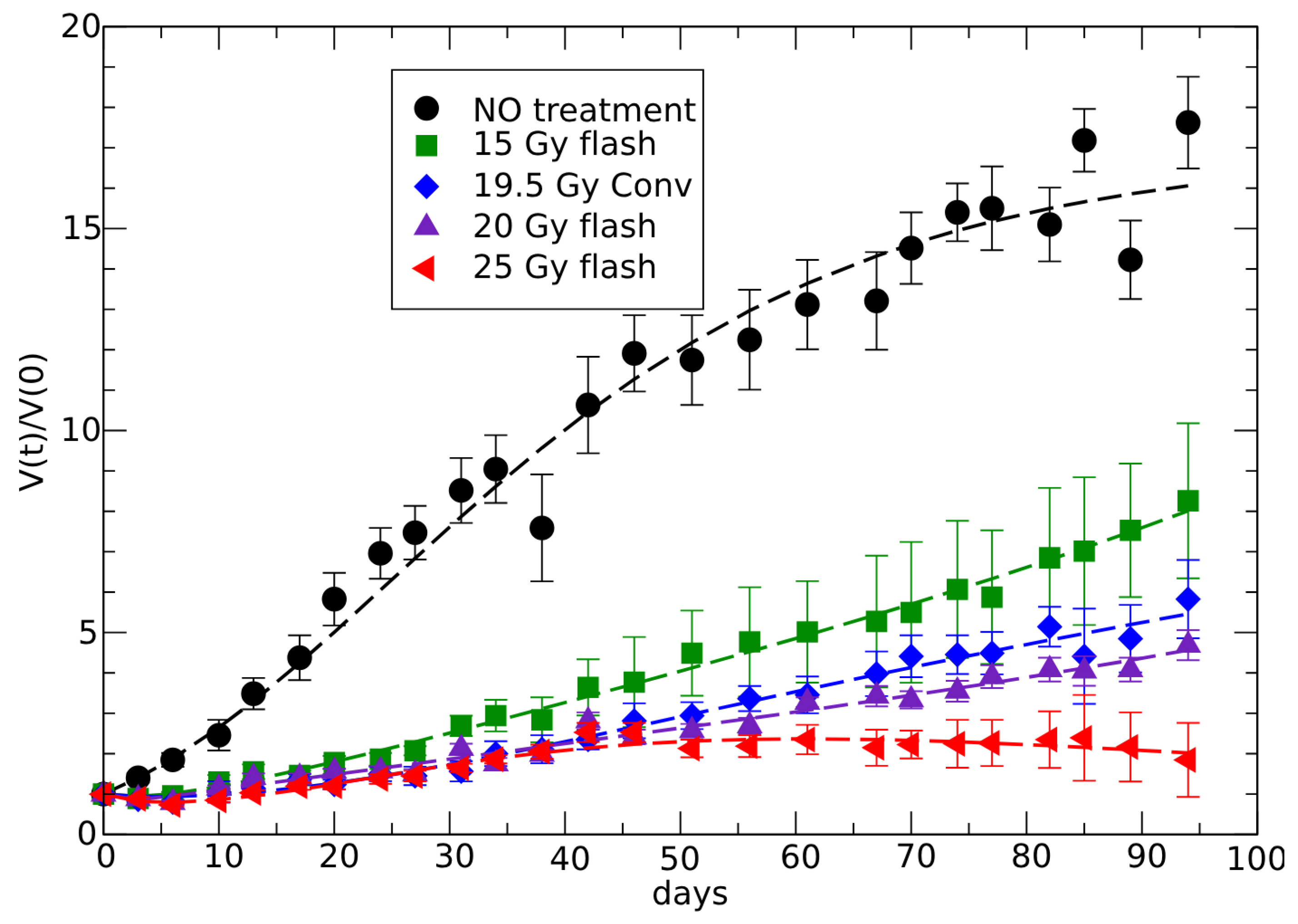
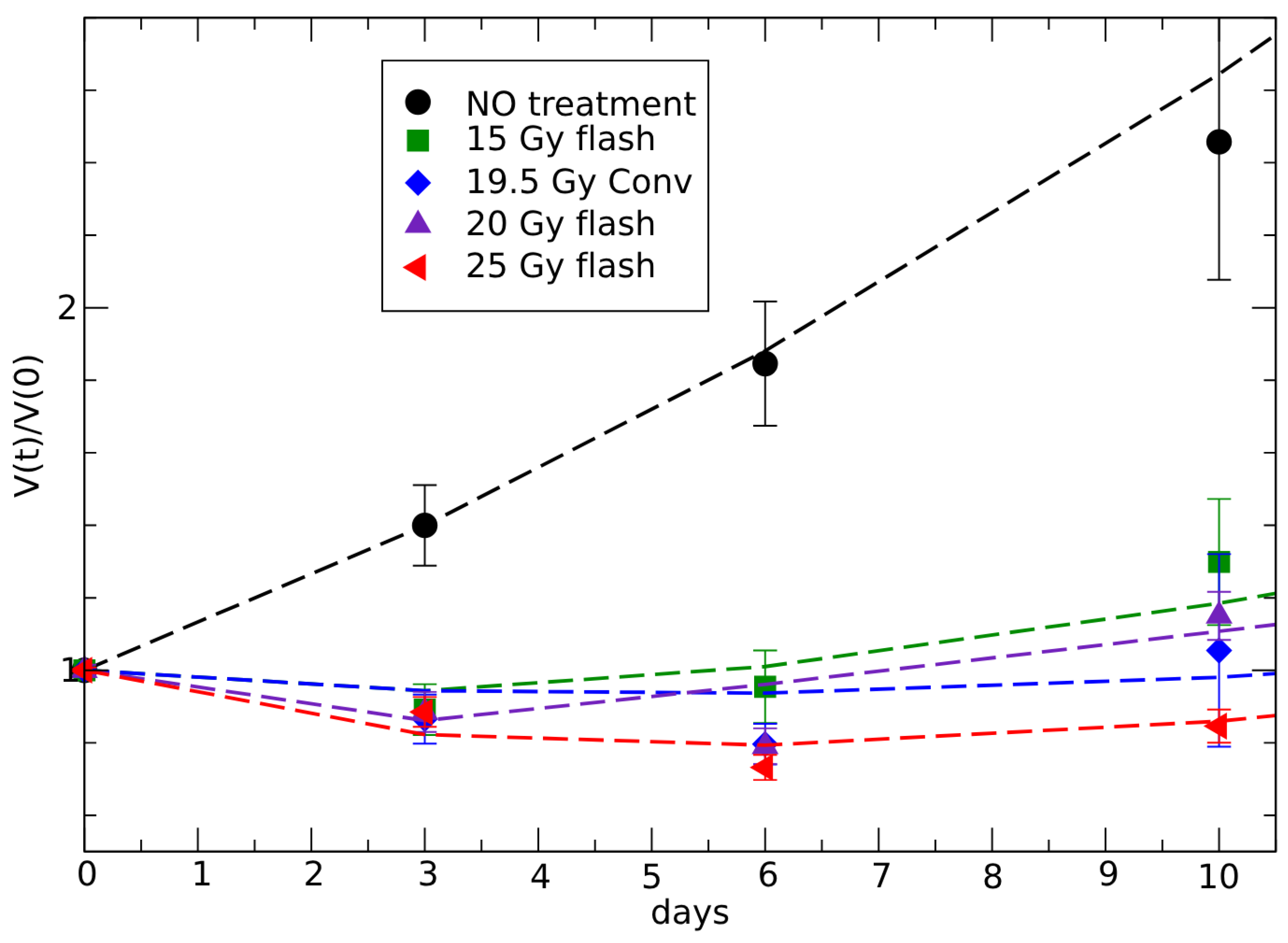
3.2. Analysis of In Vivo FLASH Radiotherapy
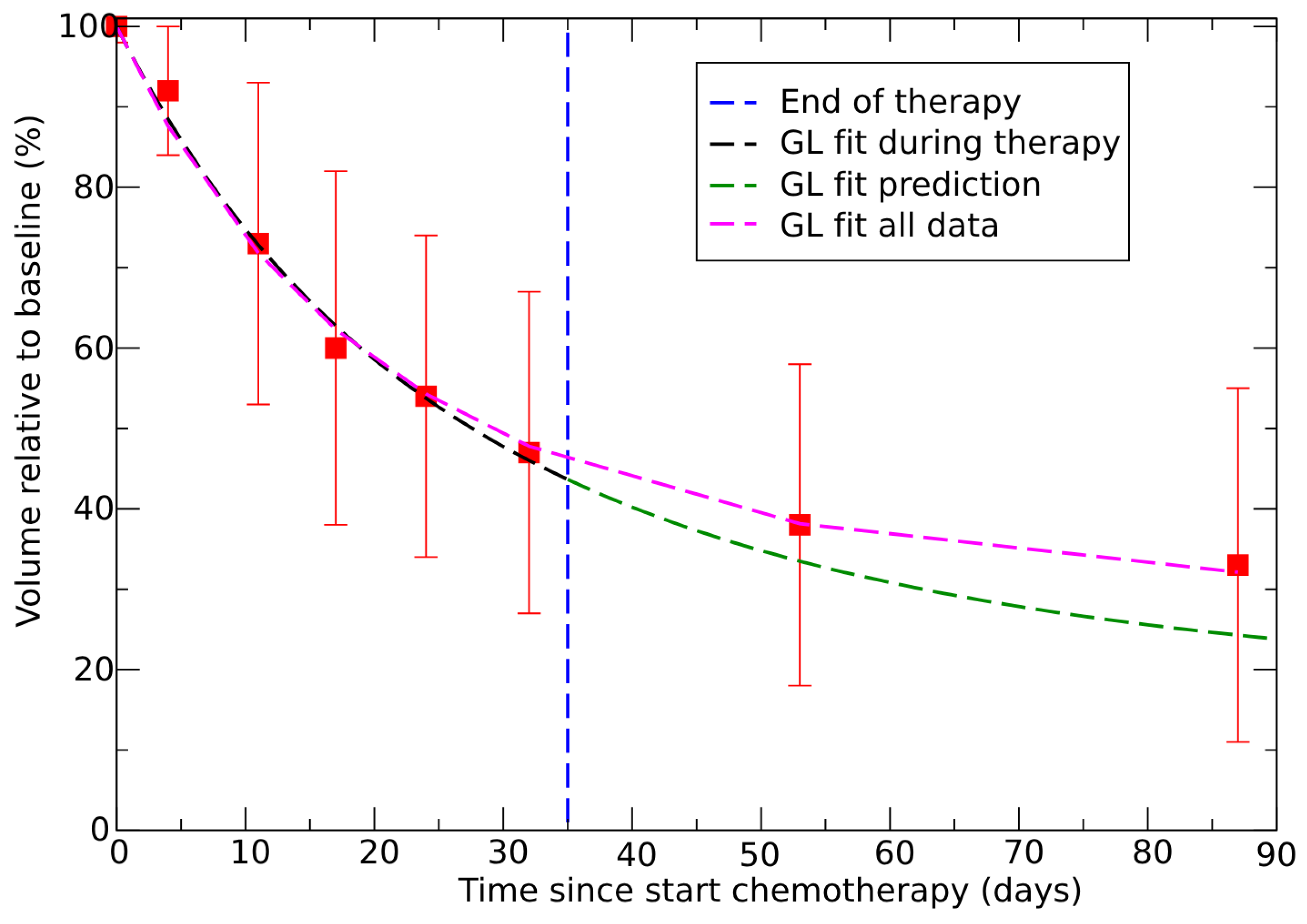
3.3. Neoadjuvant Therapy in Colorectal Cancer
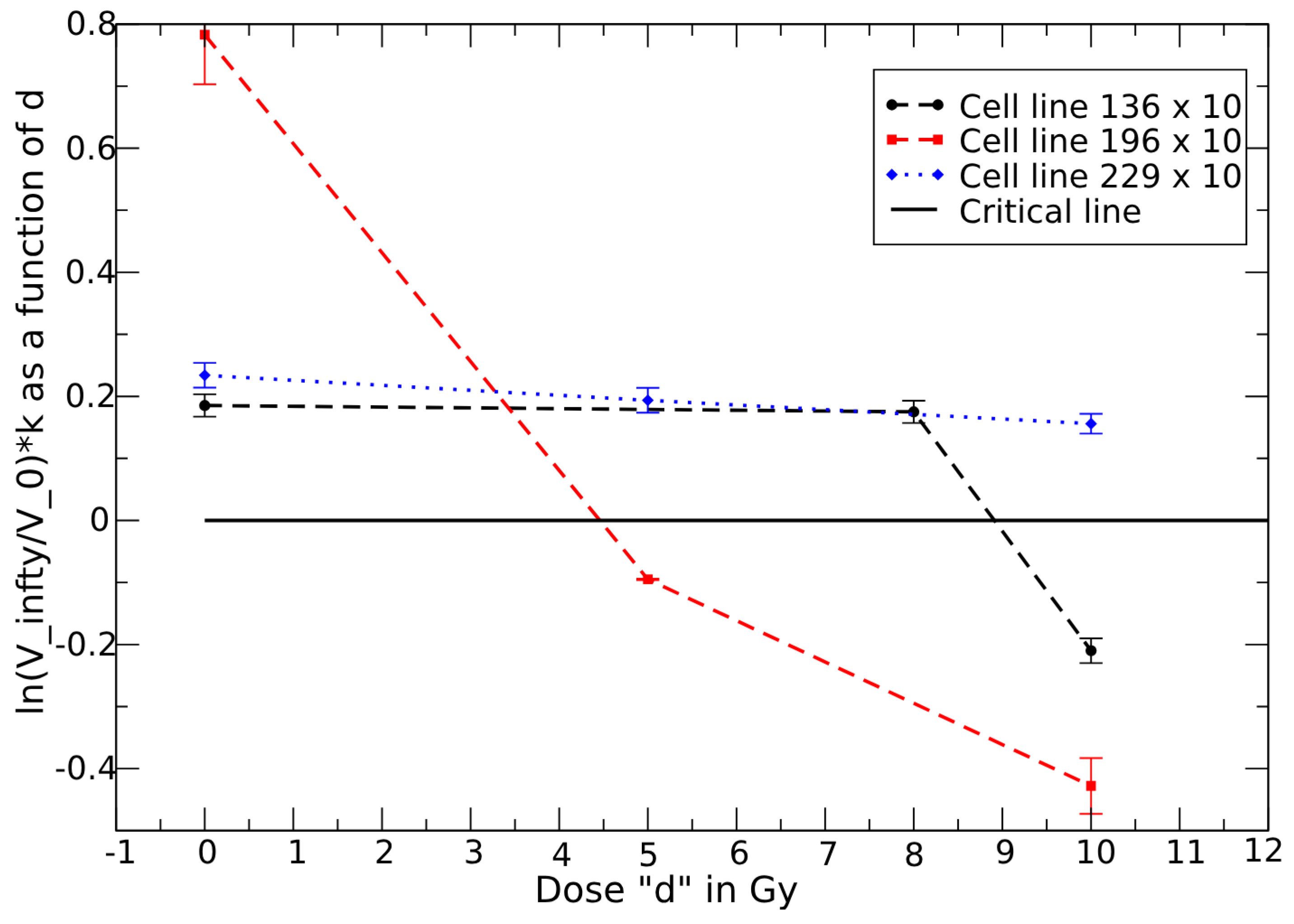
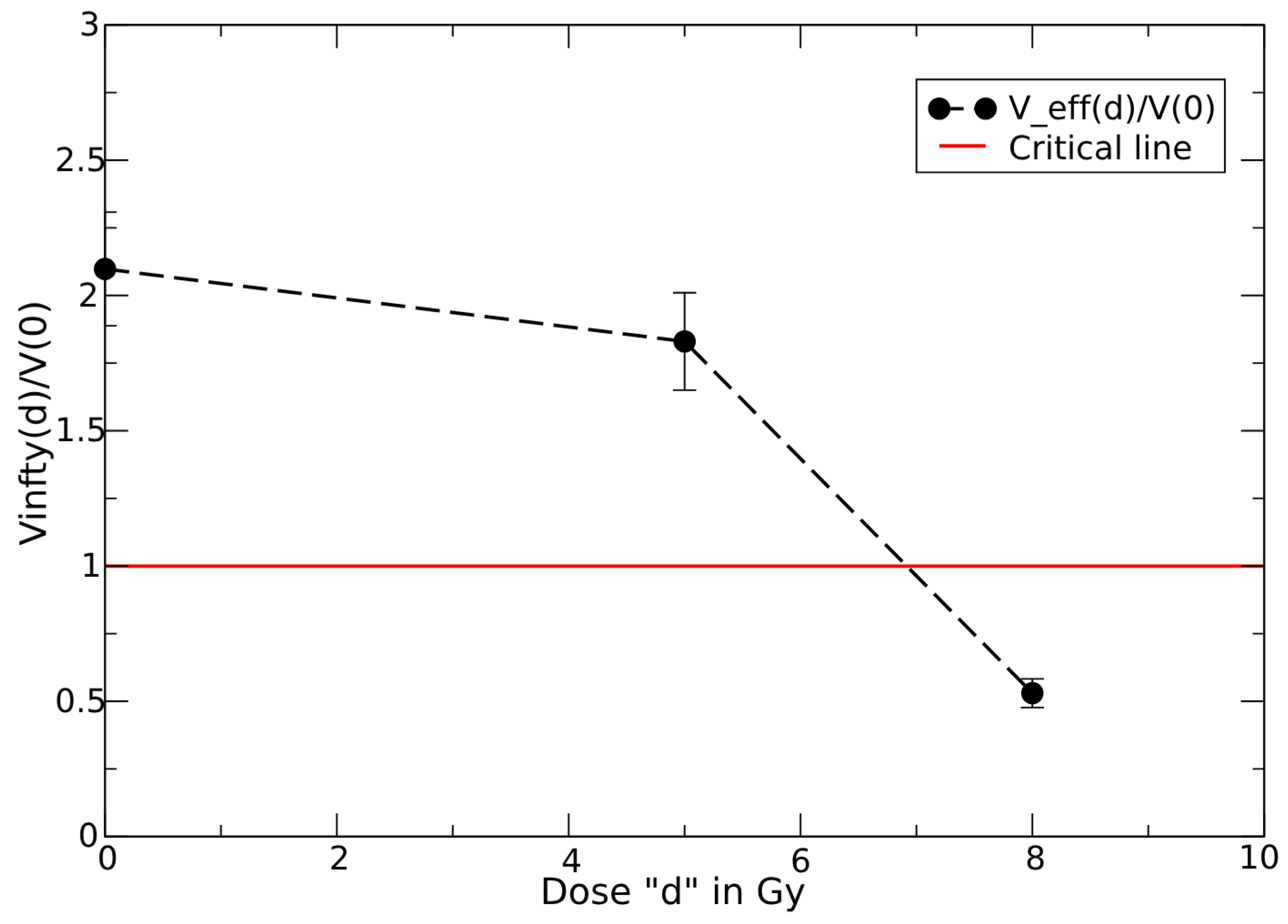
3.4. Dose–Response in Metastatic Renal Cell Carcinoma
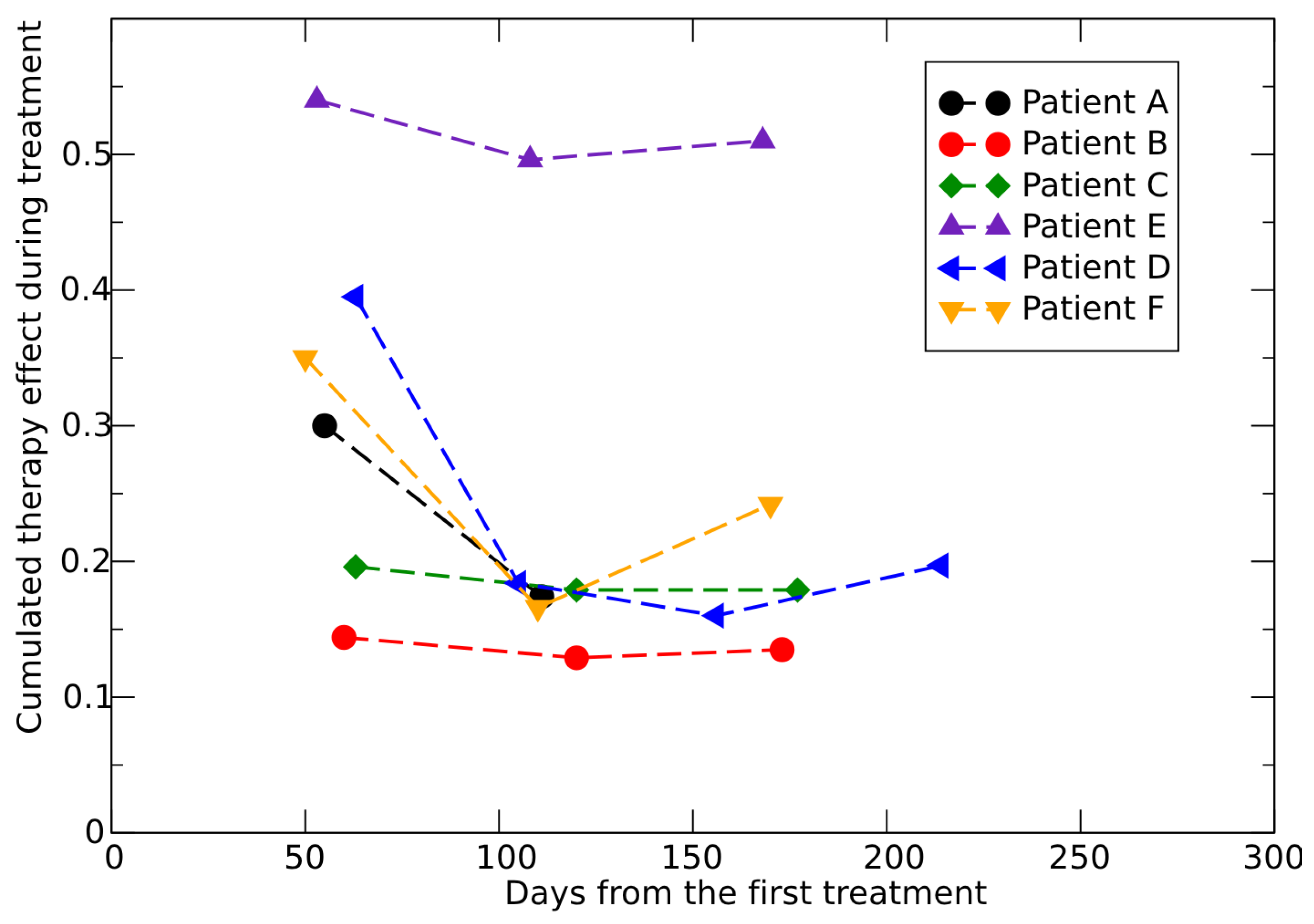
3.5. Above Critical Dose
- A very small CC compared to the final observed tumor volume, , indicates a complete response;
- A CC close to gives an almost equilibrium condition, with a slow evolution after the end of therapy, that is generally classified as PR;
- For a CC much larger than , the tumor can rapidly regrow.
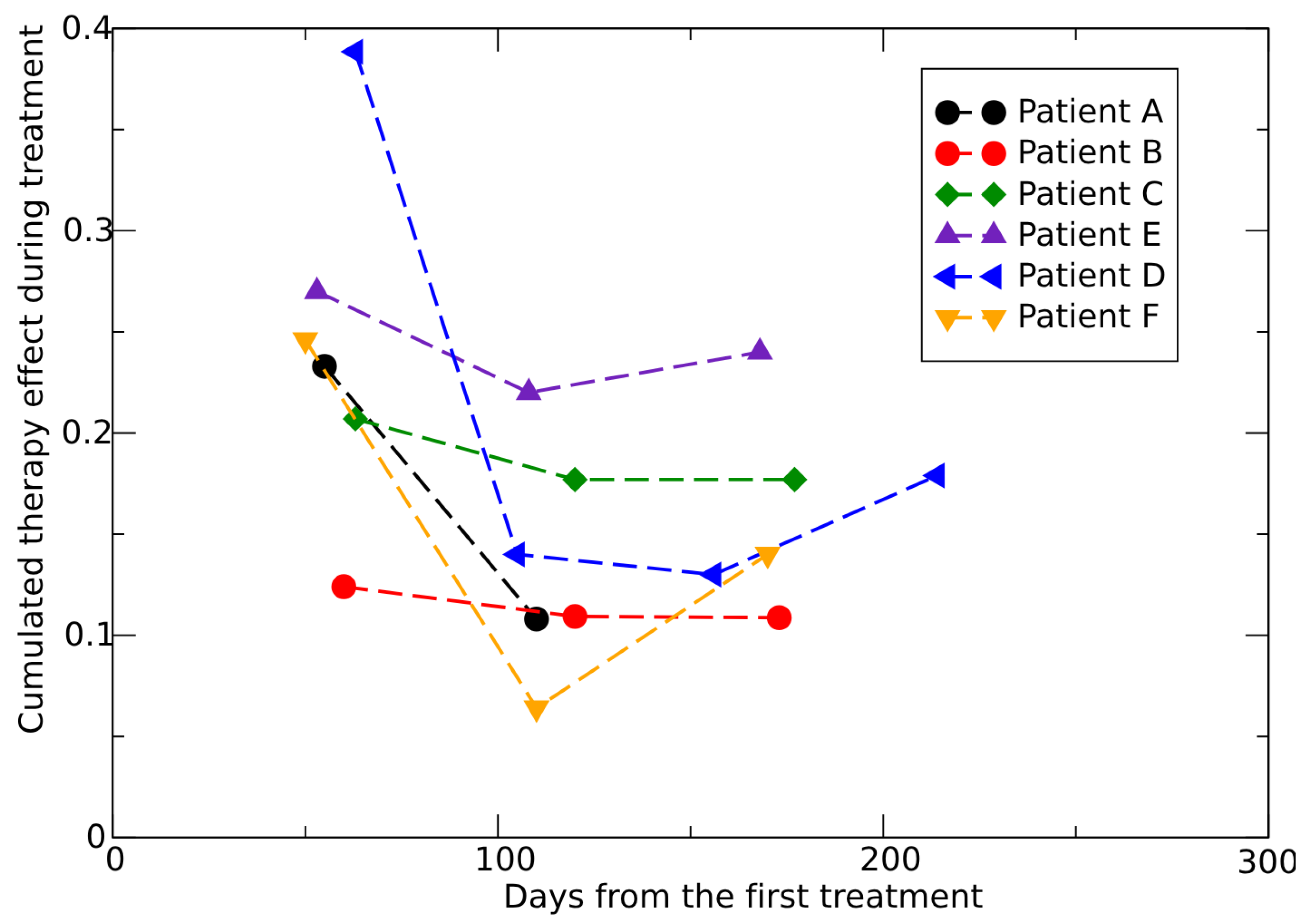
3.6. Below Critical Dose
4. Discussion
5. Conclusions
- (1)
- It is based on the patient-specific initial response to therapy;
- (2)
- Only two effective parameters are needed to characterize this response, depending on whether the dose is below the critical threshold (i.e., whether there is immediate tumor shrinkage);
- (3)
- It does not require specialized software, as any standard minimization routine can be used;
- (4)
- It is fully general and can be applied to any tumor phenotype.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- World Health Organization. Cancer. Available online: https://www.who.int/en/news-room/fact-sheets/detail/cancer (accessed on 3 June 2025).
- Filho, A.M.; Laversanne, M.; Ferlay, J.; Colombet, M.; Piñeros, M.; Znaor, A.; Parkin, D.M.; Soerjomataram, I.; Bray, F. The GLOBOCAN 2022 cancer estimates: Data sources, methods, and a snapshot of the cancer burden worldwide. Int. J. Cancer 2025, 156, 1336–1346. [Google Scholar] [CrossRef] [PubMed]
- Ghaffari Laleh, N.; Loeffler, C.M.L.; Grajek, J.; Staňková, K.; Pearson, A.T.; Muti, H.S.; Trautwein, C.; Enderling, H.; Poleszczuk, J.; Kather, J.N. Classical mathematical models for prediction of response to chemotherapy and immunotherapy. PLoS Comput. Biol. 2022, 18, e1009822. [Google Scholar] [CrossRef]
- Roudko, V.; Greenbaum, B.; Bhardwaj, N. Computational prediction and validation of tumor-associated neoantigens. Front. Immunol. 2020, 11, 27. [Google Scholar] [CrossRef]
- Bostel, T.; Dreher, C.; Wollschläger, D.; Mayer, A.; König, F.; Bickelhaupt, S.; Schlemmer, H.P.; Huber, P.E.; Sterzing, F.; Bäumer, P.; et al. Exploring MR regression patterns in rectal cancer during neoadjuvant radiochemotherapy with daily T2-and diffusion-weighted MRI. Radiat. Oncol. 2020, 15, 171. [Google Scholar] [CrossRef] [PubMed]
- Biros, G.; Mang, A.; Menze, B.H.; Schulte, M. Inverse Biophysical Modeling and Machine Learning in Personalized Oncology (Dagstuhl Seminar 23022). Dagstuhl Rep. 2023, 13, 36–67. [Google Scholar]
- Kutuva, A.R.; Caudell, J.J.; Yamoah, K.; Enderling, H.; Zahid, M.U. Mathematical modeling of radiotherapy: Impact of model selection on estimating minimum radiation dose for tumor control. Front. Oncol. 2023, 13, 1130966. [Google Scholar] [CrossRef]
- Van Houdt, P.J.; Yang, Y.; Van der Heide, U.A. Quantitative magnetic resonance imaging for biological image-guided adaptive radiotherapy. Front. Oncol. 2021, 10, 615643. [Google Scholar] [CrossRef]
- Metz, M.C.; Ezhov, I.; Peeken, J.C.; Buchner, J.A.; Lipkova, J.; Kofler, F.; Waldmannstetter, D.; Delbridge, C.; Diehl, C.; Bernhardt, D.; et al. Toward image-based personalization of glioblastoma therapy: A clinical and biological validation study of a novel, deep learning-driven tumor growth model. Neuro-Oncol. Adv. 2024, 6, vdad171. [Google Scholar] [CrossRef]
- Castorina, P.; Castiglione, F.; Ferini, G.; Forte, S.; Martorana, E. Computational Approach for Spatially Fractionated Radiation Therapy (SFRT) and Immunological Response in Precision Radiation Therapy. J. Pers. Med. 2024, 14, 436. [Google Scholar] [CrossRef]
- Cavalcante, B.R.R.; Freitas, R.D.; de Oliveira Siquara da Rocha, L.; de Souza Batista Dos Santos, R.; de Freitas Souza, B.S.; Ramos, P.I.P.; Rocha, G.V.; Rocha, C.A.G. In silico approaches for drug repurposing in oncology: A scoping review. Front. Pharmacol. 2024, 15, 1400029. [Google Scholar] [CrossRef]
- Martorana, E.; Castorina, P.; Ferini, G.; Forte, S.; Mare, M. Forecasting Individual Patients’ Best Time for Surgery in Colon-Rectal Cancer by Tumor Regression during and after Neoadjuvant Radiochemotherapy. J. Pers. Med. 2023, 13, 851. [Google Scholar] [CrossRef] [PubMed]
- Jung, S.H.; Heo, S.H.; Kim, J.W.; Jeong, Y.Y.; Shin, S.S.; Soung, M.G.; Kim, H.R.; Kang, H.K. Predicting response to neoadjuvant chemoradiation therapy in locally advanced rectal cancer: Diffusion-weighted 3 Tesla MR imaging. J. Magn. Reson. Imaging 2012, 35, 110–116. [Google Scholar] [CrossRef]
- Castorina, P.; Ferini, G.; Martorana, E.; Forte, S. Tumor volume regression during and after radiochemotherapy: A macroscopic description. J. Pers. Med. 2022, 12, 530. [Google Scholar] [CrossRef]
- Zahid, M.U.; Mohamed, A.S.; Caudell, J.J.; Harrison, L.B.; Fuller, C.D.; Moros, E.G.; Enderling, H. Dynamics-adapted radiotherapy dose (dard) for head and neck cancer radiotherapy dose personalization. J. Pers. Med. 2021, 11, 1124. [Google Scholar] [CrossRef]
- Delli Pizzi, A.; Cianci, R.; Genovesi, D.; Esposito, G.; Timpani, M.; Tavoletta, A.; Pulsone, P.; Basilico, R.; Gabrielli, D.; Rosa, C.; et al. Performance of diffusion-weighted magnetic resonance imaging at 3.0 T for early assessment of tumor response in locally advanced rectal cancer treated with preoperative chemoradiation therapy. Abdom. Radiol. 2018, 43, 2221–2230. [Google Scholar] [CrossRef] [PubMed]
- Wasserberg, N. Interval to surgery after neoadjuvant treatment for colorectal cancer. World J. Gastroenterol. WJG 2014, 20, 4256. [Google Scholar] [CrossRef] [PubMed]
- Park, S.; Lee, Y.; Kim, T.S.; Kim, S.K.; Han, J.Y. Response evaluation after immunotherapy in NSCLC: Early response assessment using FDG PET/CT. Medicine 2020, 99, e23815. [Google Scholar] [CrossRef]
- Nakata, J.; Isohashi, K.; Oka, Y.; Nakajima, H.; Morimoto, S.; Fujiki, F.; Oji, Y.; Tsuboi, A.; Kumanogoh, A.; Hashimoto, N.; et al. Imaging Assessment of Tumor Response in the Era of Immunotherapy. Diagnostics 2021, 11, 1041. [Google Scholar] [CrossRef]
- Jarrett, A.M.; Lima, E.A.; Hormuth, D.A.; McKenna, M.T.; Feng, X.; Ekrut, D.A.; Resende, A.C.M.; Brock, A.; Yankeelov, T.E. Mathematical models of tumor cell proliferation: A review of the literature. Expert Rev. Anticancer Ther. 2018, 18, 1271–1286. [Google Scholar] [CrossRef]
- Yin, A.; Moes, D.J.A.; van Hasselt, J.G.; Swen, J.J.; Guchelaar, H.J. A review of mathematical models for tumor dynamics and treatment resistance evolution of solid tumors. CPT Pharmacometrics Syst. Pharmacol. 2019, 8, 720–737. [Google Scholar] [CrossRef]
- Sfakianakis, N.; Chaplain, M.A. Mathematical modelling of cancer invasion: A review. In International Conference by Center for Mathematical Modeling and Data Science, Osaka University; Springer: Berlin/Heidelberg, Germany, 2020; pp. 153–172. [Google Scholar]
- Butner, J.D.; Dogra, P.; Chung, C.; Pasqualini, R.; Arap, W.; Lowengrub, J.; Cristini, V.; Wang, Z. Mathematical modeling of cancer immunotherapy for personalized clinical translation. Nat. Comput. Sci. 2022, 2, 785–796. [Google Scholar] [CrossRef] [PubMed]
- El-Sayed, S.M.; El-Gebaly, R.H.; Fathy, M.M.; Abdelaziz, D.M. Stereotactic body radiation therapy for prostate cancer: A dosimetric comparison of IMRT and VMAT using flattening filter and flattening filter-free beams. Radiat. Environ. Biophys. 2024, 63, 423–431. [Google Scholar] [CrossRef] [PubMed]
- Wei, Z.; Peng, X.; He, L.; Wang, J.; Liu, Z.; Xiao, J. Treatment plan comparison of volumetric-modulated arc therapy to intensity-modulated radiotherapy in lung stereotactic body radiotherapy using either 6- or 10-MV photon energies. J. Appl. Clin. Med. Phys. 2022, 23, e13714. [Google Scholar] [CrossRef]
- Faye, M.D.; Alfieri, J. Advances in Radiation Oncology for the Treatment of Cervical Cancer. Curr. Oncol. 2022, 29, 928–944. [Google Scholar] [CrossRef]
- Vadalà, R.E.; Santacaterina, A.; Sindoni, A.; Platania, A.; Arcudi, A.; Ferini, G.; Mazzei, M.M.; Marletta, D.; Rifatto, C.; Risoleti, E.V.I.; et al. Stereotactic body radiotherapy in non-operable lung cancer patients. Clin. Transl. Oncol. 2016, 18, 1158–1159. [Google Scholar] [CrossRef]
- Ferini, G.; Viola, A.; Valenti, V.; Tripoli, A.; Molino, L.; Marchese, A.V.; Illari, S.I.; Borzì, G.R.; Prestifilippo, A.; Umana, G.E.; et al. Whole Brain Irradiation or Stereotactic RadioSurgery for five or more brain metastases (WHOBI-STER): A prospective comparative study of neurocognitive outcomes, level of autonomy in daily activities and quality of life. Clin. Transl. Radiat. Oncol. 2021, 32, 52–58. [Google Scholar] [CrossRef]
- Onal, C.; Efe, E.; Bozca, R.; Yavas, C.; Yavas, G.; Arslan, G. The impact of margin reduction on radiation dose distribution of ultra-hypofractionated prostate radiotherapy utilizing a 1.5-T MR-Linac. J. Appl. Clin. Med. Phys. 2024, 25, e14179. [Google Scholar] [CrossRef]
- Ma, T.M.; Neylon, J.; Casado, M.; Sharma, S.; Sheng, K.; Low, D.; Yang, Y.; Steinberg, M.L.; Lamb, J.; Cao, M.; et al. Dosimetric impact of interfraction prostate and seminal vesicle volume changes and rotation: A post-hoc analysis of a phase III randomized trial of MRI-guided versus CT-guided stereotactic body radiotherapy. Radiother. Oncol. 2022, 167, 203–210. [Google Scholar] [CrossRef] [PubMed]
- Ferini, G.; Zagardo, V.; Valenti, V.; Aiello, D.; Federico, M.; Fazio, I.; Harikar, M.M.; Marchese, V.A.; Illari, S.I.; Viola, A.; et al. Towards Personalization of Planning Target Volume Margins Fitted to the Abdominal Adiposity in Localized Prostate Cancer Patients Receiving Definitive or Adjuvant/Salvage Radiotherapy: Suggestive Data from an ExacTrac vs. CBCT Comparison. Anticancer Res. 2023, 43, 4077–4088. [Google Scholar] [CrossRef]
- Royama, T. Analytical Population Dynamics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 10. [Google Scholar]
- Mir, Y.; Dubeau, F. Linear and logistic models with time dependent coefficients. Electron. J. Differ. Equ. 2016, 2016, 1–17. [Google Scholar]
- Foley, P. Predicting extinction times from environmental stochasticity and carrying capacity. Conserv. Biol. 1994, 8, 124–137. [Google Scholar] [CrossRef]
- Anderson, C.; Jovanoski, Z.; Towers, I.; Sidhu, H. A simple population model with a stochastic carrying capacity. In Proceedings of the 21st International Congress on Modelling and Simulation, Gold Coast, Australia, 29 November–4 December 2015; Volume 29. [Google Scholar]
- Lanteri, D.; Carco, D.; Castorina, P.; Ceccarelli, M.; Cacopardo, B. Containment effort reduction and regrowth patterns of the COVID-19 spreading. Infect. Dis. Model. 2021, 6, 632–642. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Deng, M. Permanence and extinction of a stochastic hybrid model for tumor growth. Appl. Math. Lett. 2019, 94, 66–72. [Google Scholar] [CrossRef]
- Enderling, H.; Chaplain, A.J. Mathematical modeling of tumor growth and treatment. Curr. Pharm. Des. 2013, 20, 4934–4940. [Google Scholar] [CrossRef] [PubMed]
- Puglisi, C.; Giuffrida, R.; Borzì, G.; Illari, S.; Caronia, F.; Di Mattia, P.; Colarossi, C.; Ferini, G.; Martorana, E.; Sette, G.; et al. Ex Vivo Irradiation of Lung Cancer Stem Cells Identifies the Lowest Therapeutic Dose Needed for Tumor Growth Arrest and Mass Reduction In Vivo. Front. Oncol. 2022, 12, 837400. [Google Scholar] [CrossRef]
- Gompertz, B. XXIV. On the nature of the function expressive of the law of human mortality, and on a new mode of determining the value of life contingencies. In a letter to Francis Baily, Esq. FRS &c. Philos. Trans. R. Soc. Lond. 1825, 115, 513–583. [Google Scholar]
- Norton, L. A Gompertzian model of human breast cancer growth. Cancer Res. 1988, 48, 7067–7071. [Google Scholar]
- Vaghi, C.; Rodallec, A.; Fanciullino, R.; Ciccolini, J.; Mochel, J.P.; Mastri, M.; Poignard, C.; Ebos, J.M.L.; Benzekry, S. Population modeling of tumor growth curves and the reduced Gompertz model improve prediction of the age of experimental tumors. PLoS Comput. Biol. 2020, 16, e1007178. [Google Scholar] [CrossRef]
- Castorina, P.; Carco’, D. Nutrient supply, cell spatial correlation and Gompertzian tumor growth. Theory Biosci. 2021, 140, 197–203. [Google Scholar] [CrossRef]
- Norton, L.; Simon, R. Tumor size, sensitivity to therapy and the design of treatment protocols. Cancer Treat. Rep. 1976, 61, 1307–1317. [Google Scholar]
- Wheldon, T.E. Mathematical Models in Cancer Research; Taylor & Francis: Oxfordshire, UK, 1988. [Google Scholar]
- Favaudon, V.; Caplier, L.; Monceau, V.; Pouzoulet, F.; Sayarath, M.; Fouillade, C.; Poupon, M.; Brito, I.; Hupé, P.; Bourhis, J.; et al. Ultrahigh dose-rate FLASH irradiation increases the differential response between normal and tumor tissue in mice. Sci. Transl. Med. 2014, 6, 245ra93. [Google Scholar] [CrossRef]
- Stein, A.; Wang, W.; Carter, A.A.; Chiparus, O.; Hollaender, N.; Kim, H.; Motzer, R.J.; Sarr, C. Dynamic tumor modeling of the dose–response relationship for everolimus in metastatic renal cell carcinoma using data from the phase 3 RECORD-1 trial. BMC Cancer 2012, 12, 311. [Google Scholar] [CrossRef] [PubMed]
- de Faria Bessa, J.; Marta, G.N. Triple-negative breast cancer and radiation therapy. Rep. Pract. Oncol. Radiother. 2022, 27, 545–551. [Google Scholar] [PubMed]
- Rahman, M.; Trigilio, A.; Franciosini, G.; Moeckli, R.; Zhang, R.; Böhlen, T.T. FLASH radiotherapy treatment planning and models for electron beams. Radiother. Oncol. 2022, 175, 210–221. [Google Scholar] [CrossRef] [PubMed]
- Lowe, D.; Roy, L.; Tabocchini, M.A.; Rühm, W.; Wakeford, R.; Woloschak, G.E.; Laurier, D. Radiation dose rate effects: What is new and what is needed? Radiat. Environ. Biophys. 2022, 61, 507–543. [Google Scholar] [CrossRef]
- Omyan, G.; Musa, A.E.; Shabeeb, D.; Akbardoost, N.; Gholami, S. Efficacy and toxicity of FLASH radiotherapy: A systematic review. J. Cancer Res. Ther. 2020, 16, 1203–1209. [Google Scholar]
- Bourhis, J.; Montay-Gruel, P.; Gonçalves Jorge, P.; Bailat, C.; Petit, B.; Ollivier, J.; Jeanneret-Sozzi, W.; Ozsahin, M.; Bochud, F.; Moeckli, R.; et al. Clinical translation of FLASH radiotherapy: Why and how? Radiother. Oncol. 2019, 139, 11–17. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, X.; Chen, D.; Yu, J. Radiotherapy combined with immunotherapy: The dawn of cancer treatment. Signal Transduct. Target. Ther. 2022, 7, 258. [Google Scholar] [CrossRef]
- Van den Begin, R.; Kleijnen, J.P.; Engels, B.; Philippens, M.; van Asselen, B.; Raaymakers, B.; Reerink, O.; Ridder, M.D.; Intven, M. Tumor volume regression during preoperative chemoradiotherapy for rectal cancer: A prospective observational study with weekly MRI. Acta Oncol. 2018, 57, 723–727. [Google Scholar] [CrossRef]
- Sarapata, E.A.; De Pillis, L. A comparison and catalog of intrinsic tumor growth models. Bull. Math. Biol. 2014, 76, 2010–2024. [Google Scholar] [CrossRef]
- Hu, A.; Zhou, W.; Qiu, R.; Li, J. Mathematical analysis of FLASH effect models based on theoretical hypotheses. Phys. Med. Biol. 2024, 69. [Google Scholar] [CrossRef] [PubMed]
- Zahid, M.U.; Mohsin, N.; Mohamed, A.S.R.; Caudell, J.J.; Harrison, L.B.; Fuller, C.D.; Moros, E.G.; Enderling, H. Forecasting Individual Patient Response to Radiation Therapy in Head and Neck Cancer With a Dynamic Carrying Capacity Model. Int. J. Radiat. Oncol. Biol. Phys. 2021, 111, 693–704. [Google Scholar] [CrossRef] [PubMed]
- Bourhis, J.; Sozzi, W.J.; Jorge, P.G.; Gaide, O.; Bailat, C.; Duclos, F.; Patin, D.; Ozsahin, M.; Bochud, F.; Germond, J.-F.; et al. Treatment of a first patient with FLASH-radiotherapy. Radiother. Oncol. 2019, 139, 18–22. [Google Scholar] [CrossRef] [PubMed]
- Mascia, A.E.; Daugherty, E.C.; Zhang, Y.; Lee, E.; Xiao, Z.; Sertorio, M.; Woo, J.; Backus, L.R.; McDonald, J.M.; McCann, C.; et al. Proton FLASH Radiotherapy for the Treatment of Symptomatic Bone Metastases: The FAST-01 Nonrandomized Trial. JAMA Oncol. 2023, 9, 62–69. [Google Scholar] [CrossRef]
- Liu, J.; Hormuth, D.A.; Davis, T. A time-resolved experimental–mathematical model for predicting the response of glioma cells to single-dose radiation therapy. Integr. Biol. 2021, 13, 167–183. [Google Scholar] [CrossRef]

| Cell Line | Parameter | d = 0 | d = 5 | d = 8 | d = 10 | c | ||
|---|---|---|---|---|---|---|---|---|
| 36 | 2.1 | 1.82 | 0.53 | n.a. | 0.00063 | 3.76 | 7.1 | |
| 136 | 0.01853 | n.a. | 0.0175 | −0.0206 | 3.85 × 10−17 | 15 | 9.5 | |
| 196 | 0.0783 | −0.0095 | n.a. | −0.043 | 0.038 | 0.5 | 4.2 | |
| 229 | 0.0234 | 0.019 | n.a. | 0.016 | - | - | - |
| Parameter | 15 Gy FLASH | 19.5 Gy Conv. | 20 Gy FLASH | 25 Gy FLASH |
|---|---|---|---|---|
| 0.067 ± 0.005 | 0.065 ± 0.004 | 0.0834 ± 0.004 | 0.056 ± 0.004 | |
| 0.127 ± 0.043 | 0.084 ± 0.017 | 0.304 ± 0.13 | 0.166 ± 0.018 | |
| 0.32 ± 0.1 | 0.073 ± 0.016 | 1.086 ± 0.26 | 0.159 ± 0.002 | |
| 0.00052 ± 0.0001 | 0.00029 ± 0.00009 | 0.00044 ± 0.00005 | −0.00043 ± 0.00013 |
| Patient | Parameters by All Data | Parameters by 4 Data | Parameters by 3 Data |
|---|---|---|---|
| G | 0.17 | 0.18 | 0.27 |
| H | 0.25 | 0.55 | 0.78 |
| I | 1.28 | 2.56 | 8.57 |
| J | 0.2 | 0.2 | 0.21 |
| K | 0.043 | 0.051 | 0.056 |
| Patient | Parameters by All Data | Parameters by 4 Data | Parameters by 3 Data |
|---|---|---|---|
| G | 0.31%—224 days | 0.42%—50 days | 1.02%—108 days |
| H | 0.66%—270 days | 2.67%—46 days | 3.35%—154 days |
| I | 3.5%—260 days | 7.4%—60 days | 13.8%—120 days |
| J | 1.45%—315 days | 1.55%—60 days | 1.6%—180 days |
| K | 0.22%—230 days | 0.62%—60 days | 0.74%—115 days |
| Patients | V2/V1 | V3/V2 | V4/V3 | V5/V4 |
|---|---|---|---|---|
| A | 0.86 | 0.98 | - | - |
| 1.16 | 1.16 | - | - | |
| 0.74 | 0.84 | - | - | |
| B | 0.97 | 0.98 | 0.97 | - |
| 1.12 | 1.12 | 1.11 | - | |
| 0.86 | 0.88 | 0.87 | - | |
| C | 0.98 | ≃1 | ≃1 | - |
| 1.2 | 1.2 | 1.2 | - | |
| 0.82 | 0.83 | 0.835 | - | |
| D | 0.82 | 0.99 | 1.03 | ≃1 |
| 1.22 | 1.19 | 1.21 | 1.22 | |
| 0.67 | 0.83 | 0.85 | 0.82 | |
| E | 0.94 | ≃1 | ≃1 | - |
| 1.63 | 1.64 | 1.66 | - | |
| 0.58 | 0.61 | 0.6 | - | |
| F | 0.85 | 1.039 | 0.96 | - |
| 1.2 | 1.22 | 1.23 | - | |
| 0.7 | 0.85 | 0.78 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Castorina, P.; Castiglione, F.; Ferini, G.; Forte, S.; Martorana, E. Quantitative Method for Monitoring Tumor Evolution During and After Therapy. J. Pers. Med. 2025, 15, 275. https://doi.org/10.3390/jpm15070275
Castorina P, Castiglione F, Ferini G, Forte S, Martorana E. Quantitative Method for Monitoring Tumor Evolution During and After Therapy. Journal of Personalized Medicine. 2025; 15(7):275. https://doi.org/10.3390/jpm15070275
Chicago/Turabian StyleCastorina, Paolo, Filippo Castiglione, Gianluca Ferini, Stefano Forte, and Emanuele Martorana. 2025. "Quantitative Method for Monitoring Tumor Evolution During and After Therapy" Journal of Personalized Medicine 15, no. 7: 275. https://doi.org/10.3390/jpm15070275
APA StyleCastorina, P., Castiglione, F., Ferini, G., Forte, S., & Martorana, E. (2025). Quantitative Method for Monitoring Tumor Evolution During and After Therapy. Journal of Personalized Medicine, 15(7), 275. https://doi.org/10.3390/jpm15070275








