Harnessing Code Interpreters for Enhanced Predictive Modeling: A Case Study on High-Density Lipoprotein Level Estimation in Romanian Diabetic Patients
Abstract
:1. Introduction
2. Materials and Methods
2.1. Diabetes Dataset
2.2. Data Correlations in Diabetes and Non-Diabetes Datasets
2.3. Data Analysis
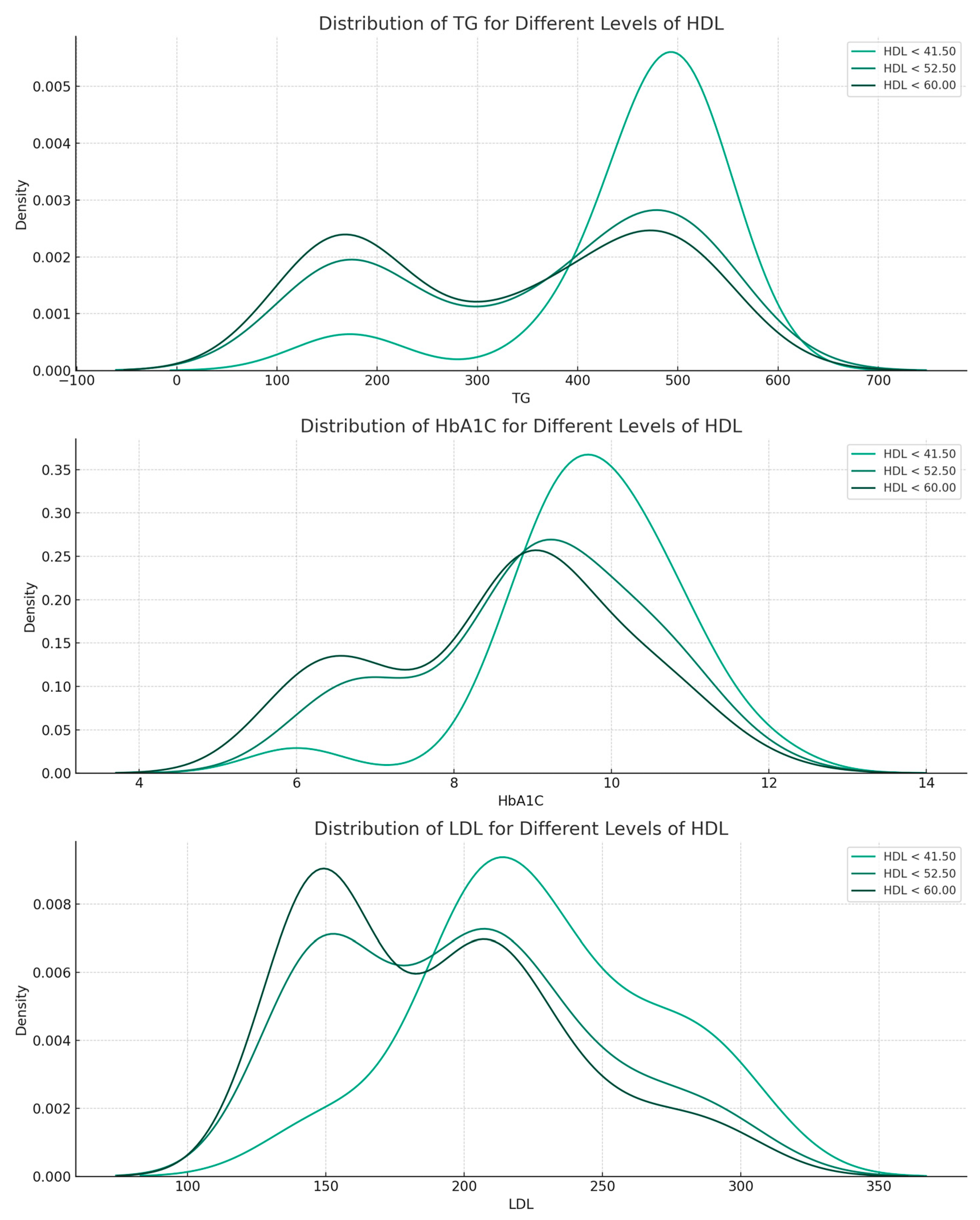
2.3.1. HDL Prediction Based on the Other Variables
Preliminary Checks and Preconditions
Model Selection and Comparison
2.3.2. Random Forest Models of All Variables
2.3.3. Modeling the Transition from Normal to Elevated HbA1c
2.3.4. Software and Tools
3. Results and Discussions
3.1. Correlation of Analyzed Parameters
3.2. Model Selection for Predicting HDL Levels
3.2.1. Assumptions and Preconditions Checking
3.2.2. Data Modeling and Optimal Model Selection
3.2.3. Data Relationships According to the Random Forest Model
3.3. Random Forest Models of All Variables
3.4. Modeling the Transition between Normal and High HbA1c Levels
3.5. Discussions and Perspectives
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kahn, S.E.; Cooper, M.E.; Del Prato, S. Pathophysiology and Treatment of Type 2 Diabetes: Perspectives on the Past, Present and Future. Lancet 2014, 383, 1068–1083. [Google Scholar] [CrossRef] [PubMed]
- Westman, E.C. Type 2 Diabetes Mellitus: A Pathophysiologic Perspective. Front. Nutr. 2021, 8, 707371. [Google Scholar] [CrossRef] [PubMed]
- Shetty, S.S.; Kumari, S. Fatty Acids and Their Role in Type-2 Diabetes (Review). Exp. Ther. Med. 2021, 22, 706. [Google Scholar] [CrossRef] [PubMed]
- Reed, J.; Bain, S.; Kanamarlapudi, V. A Review of Current Trends with Type 2 Diabetes Epidemiology, Aetiology, Pathogenesis, Treatments and Future Perspectives. Diabetes Metab. Syndr. Obes. 2021, 14, 3567–3602. [Google Scholar] [CrossRef]
- Al Quran, T.M.; Bataineh, Z.A.; Al-Mistarehi, A.-H.; Zein Alaabdin, A.M.; Allan, H.; Al Qura’an, A.; Weshah, S.M.; Alanazi, A.A.; Khader, Y.S. Prevalence and Pattern of Dyslipidemia and Its Associated Factors Among Patients with Type 2 Diabetes Mellitus in Jordan: A Cross-Sectional Study. Int. J. Gen. Med. 2022, 15, 7669–7683. [Google Scholar] [CrossRef]
- Li, J.; Nie, Z.; Ge, Z.; Shi, L.; Gao, B.; Yang, Y. Prevalence of Dyslipidemia, Treatment Rate and Its Control among Patients with Type 2 Diabetes Mellitus in Northwest China: A Cross-Sectional Study. Lipids Health Dis. 2022, 21, 77. [Google Scholar] [CrossRef]
- Mehta, R.K.; Koirala, P.; Mallick, R.L.; Parajuli, S.; Jha, R. Dyslipidemia in Patients with Type 2 Diabetes Mellitus in a Tertiary Care Centre: A Descriptive Cross-Sectional Study. J. Nepal Med. Assoc. 2021, 59, 305–309. [Google Scholar] [CrossRef]
- Wu, L.; Parhofer, K.G. Diabetic Dyslipidemia. Metab.-Clin. Exp. 2014, 63, 1469–1479. [Google Scholar] [CrossRef]
- Albajy, M.A.; Mihailescu, D.; Alexandra, M.; Maranda, I. Prevalence of Metabolic Syndrome in People with Type 2 Diabetes in Romania. J. Biosci. Med. 2023, 11, 247–268. [Google Scholar] [CrossRef]
- Fahed, G.; Aoun, L.; Bou Zerdan, M.; Allam, S.; Bou Zerdan, M.; Bouferraa, Y.; Assi, H.I. Metabolic Syndrome: Updates on Pathophysiology and Management in 2021. Int. J. Mol. Sci. 2022, 23, 786. [Google Scholar] [CrossRef]
- ChatGPT. Available online: https://chat.openai.com (accessed on 6 August 2023).
- ChatGPT Plugins. Available online: https://openai.com/blog/chatgpt-plugins#code-interpreter (accessed on 6 August 2023).
- Wang, L.; Ge, X.; Liu, L.; Hu, G. Code Interpreter for Bioinformatics: Are We There Yet? Ann. Biomed. Eng. 2023. [Google Scholar] [CrossRef] [PubMed]
- Jin, Q.; Lau, E.S.H.; Luk, A.O.; Tam, C.H.T.; Ozaki, R.; Lim, C.K.P.; Wu, H.; Chow, E.Y.K.; Kong, A.P.S.; Lee, H.M.; et al. High-Density Lipoprotein Subclasses and Cardiovascular Disease and Mortality in Type 2 Diabetes: Analysis from the Hong Kong Diabetes Biobank. Cardiovasc. Diabetol. 2022, 21, 293. [Google Scholar] [CrossRef]
- R: The R Project for Statistical Computing . Available online: https://www.r-project.org/ (accessed on 10 August 2023).
- Nguyen, M. Chapter 3 Descriptive Statistics. In A Guide on Data Analysis; Bookdown; Available online: https://bookdown.org/mike/data_analysis/ (accessed on 6 August 2023).
- Nelder, J.A.; Wedderburn, R.W.M. Generalized Linear Models. J. R. Stat. Soc. Ser. Gen. 1972, 135, 370–384. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression Shrinkage and Selection via the Lasso. J. R. Stat. Soc. Ser. B Methodol. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Zou, H.; Hastie, T. Regularization and Variable Selection via the Elastic Net. J. R. Stat. Soc. Ser. B Stat. Methodol. 2005, 67, 301–320. [Google Scholar] [CrossRef]
- Koenker, R.; Hallock, K.F. Quantile Regression. J. Econ. Perspect. 2001, 15, 143–156. [Google Scholar] [CrossRef]
- Ho, T.K. Random Decision Forests. In Proceedings of the 3rd International Conference on Document Analysis and Recognition, Montreal, QC, Canada, 14–16 August 1995; Volume 1, pp. 278–282. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Awad, M.; Khanna, R. Support Vector Regression. In Efficient Learning Machines: Theories, Concepts, and Applications for Engineers and System Designers; Awad, M., Khanna, R., Eds.; Apress: Berkeley, CA, USA, 2015; pp. 67–80. ISBN 978-1-4302-5990-9. [Google Scholar]
- Schmidhuber, J. Deep Learning in Neural Networks: An Overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef]
- Krämer, W. Durbin–Watson Test. In International Encyclopedia of Statistical Science; Lovric, M., Ed.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 408–409. ISBN 978-3-642-04898-2. [Google Scholar]
- Shapiro, S.S.; Wilk, M.B. An Analysis of Variance Test for Normality (Complete Samples). Biometrika 1965, 52, 591–611. [Google Scholar] [CrossRef]
- Wooldridge, J.M. Introductory Econometrics: A Modern Approach; Cengage Learning: Boston, MA, USA, 2015; ISBN 978-1-305-44638-0. [Google Scholar]
- Rich, J.T.; Neely, J.G.; Paniello, R.C.; Voelker, C.C.J.; Nussenbaum, B.; Wang, E.W. A Practical Guide to Understanding Kaplan-Meier Curves. Otolaryngol.—Head Neck Surg. 2010, 143, 331–336. [Google Scholar] [CrossRef] [PubMed]
- Python Software Foundation Python Language Reference, Version 3.11.4. Available online: https://www.python.org/ (accessed on 11 August 2023).
- McKinney, W. Data Structures for Statistical Computing in Python. In Proceedings of the 9th Python in Science Conference, Austin, TX, USA, 28 June–3 July 2010; pp. 56–61. [Google Scholar]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array Programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef] [PubMed]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed]
- Seabold, S.; Perktold, J. Statsmodels: Econometric and Statistical Modeling with Python. In Proceedings of the 9th Python in Science Conference, Austin, TX, USA, 28 June–3 July 2010; pp. 92–96. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-Learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Hunter, J.D. Matplotlib: A 2D Graphics Environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Waskom, M.; Botvinnik, O.; O’Kane, D.; Hobson, P.; Lukauskas, S.; Gemperline, D.C.; Augspurger, T.; Halchenko, Y.; Cole, J.B.; Warmenhoven, J.; et al. Mwaskom/Seaborn, V0.8.1 (September 2017); Zenodo: Geneva, Switzerland, 2017. [CrossRef]
- American Diabetes Association. Standards of Medical Care in Diabetes—2015 Abridged for Primary Care Providers. Clin. Diabetes Publ. 2015, 33, 97–111. [Google Scholar] [CrossRef]
- Baliga, R.R.; Yang, E.H.; Bossone, E. Linear Reverse Risk of HDL-C Levels for Predicting Cardiovascular Disease: It Is Not That Straightforward! Eur. J. Prev. Cardiol. 2022, 29, 2055–2057. [Google Scholar] [CrossRef]
- Libby, P. The Forgotten Majority: Unfinished Business in Cardiovascular Risk Reduction. J. Am. Coll. Cardiol. 2005, 46, 1225–1228. [Google Scholar] [CrossRef]
- Barter, P.; Gotto, A.M.; LaRosa, J.C.; Maroni, J.; Szarek, M.; Grundy, S.M.; Kastelein, J.J.P.; Bittner, V.; Fruchart, J.-C. Treating to New Targets Investigators HDL Cholesterol, Very Low Levels of LDL Cholesterol, and Cardiovascular Events. N. Engl. J. Med. 2007, 357, 1301–1310. [Google Scholar] [CrossRef]
- Ikura, K.; Hanai, K.; Shinjyo, T.; Uchigata, Y. HDL Cholesterol as a Predictor for the Incidence of Lower Extremity Amputation and Wound-Related Death in Patients with Diabetic Foot Ulcers. Atherosclerosis 2015, 239, 465–469. [Google Scholar] [CrossRef]
- Ishibashi, T.; Kaneko, H.; Matsuoka, S.; Suzuki, Y.; Ueno, K.; Ohno, R.; Okada, A.; Fujiu, K.; Michihata, N.; Jo, T.; et al. HDL Cholesterol and Clinical Outcomes in Diabetes Mellitus. Eur. J. Prev. Cardiol. 2023, 30, 646–653. [Google Scholar] [CrossRef] [PubMed]
- Brewer, H.B. Hypertriglyceridemia: Changes in the Plasma Lipoproteins Associated with an Increased Risk of Cardiovascular Disease. Am. J. Cardiol. 1999, 83, 3F–12F. [Google Scholar] [CrossRef] [PubMed]
- Huang, R.; Yan, L.; Lei, Y. The Relationship between High-Density Lipoprotein Cholesterol (HDL-C) and Glycosylated Hemoglobin in Diabetic Patients Aged 20 or above: A Cross-Sectional Study. BMC Endocr. Disord. 2021, 21, 198. [Google Scholar] [CrossRef] [PubMed]
- Marston, N.A.; Giugliano, R.P.; Im, K.; Silverman, M.G.; O’Donoghue, M.L.; Wiviott, S.D.; Ference, B.A.; Sabatine, M.S. Association Between Triglyceride Lowering and Reduction of Cardiovascular Risk Across Multiple Lipid-Lowering Therapeutic Classes. Circulation 2019, 140, 1308–1317. [Google Scholar] [CrossRef]






| Variable | Type | Description | Non-Null Count | Range |
|---|---|---|---|---|
| Disease | Integer (0 or 1) | 1 for Yes (the patient has diabetes) or 0 for No (the patient does not have diabetes), | 160 | NA |
| Sex | Object (Categorical—‘M’ or ‘F’) | Gender of the patient | 160 | NA |
| Age | Integer | Age of patient | 160 | 35–70 years |
| BMI | Float | Body Mass Index of patient | 160 | 3.0–40.0 |
| Blood Pressure—H | Integer | Systolic blood pressure measurement | 160 | 123–147 mmHg |
| Blood Pressure—L | Integer | Diastolic blood pressure measurement | 160 | 81–91 mmHg |
| TG | Integer | Triglyceride level of patient | 160 | 130–540 mg/dL |
| HDL | Integer | High-density lipoprotein level | 160 | 19–72 mg/dL |
| LDL | Integer | Low-density lipoprotein level | 160 | 60–300 mg/dL |
| Glucose | Integer | Blood glucose level | 160 | 70–295 mg/dL |
| HbA1C | Float | Hemoglobin A1c level, indicating average blood sugar over the past 2–3 months | 160 | 3.9–11.9% |
| Onset | Float | Time between the onset of diabetes and the moment of collecting data | 110 (50 missing values) | 1–13 years |
| Model | Preconditions |
|---|---|
| Generalized Linear Model (GLM) [17] | -linear variation of predictors and outcome -independence of errors -homoscedasticity of errors -normality of error distribution -no or little multicollinearity |
| Lasso [18] and Elastic Net [19] Regressions | -evaluation of multicollinearity |
| Quantile Regression [20] | -linear variation of predictors and outcome -independence of errors |
| Random Forest [21,22], GBM [23], SVR, [24] and Neural Network [25] | -no missing data -data normalization for Neural Networks |
| Variable | VIF—All Variables | VIF after Omitting ‘Glucose’ | VIF after Omitting ‘Glucose’ and ‘Age’ | VIF after Omitting ‘Glucose’, ‘Age’, and ‘Blood Pressure—H’ |
|---|---|---|---|---|
| Sex | 2.09 | 2.09 | 2.09 | 2.07 |
| Age | 117.24 | 115.19 | - | - |
| BMI | 43.82 | 43.60 | 43.58 | 22.70 |
| Blood Pressure—H | 189.24 | 155.07 | 122.14 | - |
| TG | 26.99 | 26.40 | 24.00 | 20.77 |
| LDL | 71.97 | 71.17 | 70.97 | 62.39 |
| Glucose | 509.68 | - | - | - |
| HbA1c | 825.05 | 79.00 | 73.82 | 46.19 |
| Onset | 8.05 | 7.92 | 6.78 | 6.76 |
| Model | Hyperparameter | Significance of Hyperparameter | Value | Best MSE |
|---|---|---|---|---|
| Random Forest | n_estimators | Number of trees in the forest | 100 | 55.48 |
| max_depth | Maximum depth of the tree | None | ||
| min_samples_split | Minimum samples required to split an internal node | 2 | ||
| Neural Network (MLPRegressor) | hidden_layer_sizes | Number of neurons in hidden layers | 100 | 74.46 |
| activation | Activation function for the hidden layer | tanh | ||
| alpha | L2 penalty (regularization term) parameter | 0.0001 | ||
| GBM | n_estimators | Number of boosting stages to run | 50 | 62.05 |
| learning_rate | Step size shrinkage used to prevent overfitting | 0.1 | ||
| max_depth | Maximum depth of the individual regression estimators | 3 |
| Dependent Variable | Mean Squared Error (MSE) |
|---|---|
| Blood Pressure—L | 0.0163 |
| HbA1c | 0.0753 |
| Blood Pressure—H | 0.1105 |
| Sex | 0.1498 |
| Onset | 12.7679 |
| Age | 12.9156 |
| BMI | 14.8431 |
| HDL | 53.59.98 |
| Glucose | 53.9048 |
| LDL | 421.2393 |
| TG | 745.7605 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Albajy, M.A.; Mernea, M.; Mihaila, A.; Pop, C.-E.; Mihăilescu, D.F. Harnessing Code Interpreters for Enhanced Predictive Modeling: A Case Study on High-Density Lipoprotein Level Estimation in Romanian Diabetic Patients. J. Pers. Med. 2023, 13, 1466. https://doi.org/10.3390/jpm13101466
Albajy MA, Mernea M, Mihaila A, Pop C-E, Mihăilescu DF. Harnessing Code Interpreters for Enhanced Predictive Modeling: A Case Study on High-Density Lipoprotein Level Estimation in Romanian Diabetic Patients. Journal of Personalized Medicine. 2023; 13(10):1466. https://doi.org/10.3390/jpm13101466
Chicago/Turabian StyleAlbajy, Maitham Abdallah, Maria Mernea, Alexandra Mihaila, Cristian-Emilian Pop, and Dan Florin Mihăilescu. 2023. "Harnessing Code Interpreters for Enhanced Predictive Modeling: A Case Study on High-Density Lipoprotein Level Estimation in Romanian Diabetic Patients" Journal of Personalized Medicine 13, no. 10: 1466. https://doi.org/10.3390/jpm13101466
APA StyleAlbajy, M. A., Mernea, M., Mihaila, A., Pop, C.-E., & Mihăilescu, D. F. (2023). Harnessing Code Interpreters for Enhanced Predictive Modeling: A Case Study on High-Density Lipoprotein Level Estimation in Romanian Diabetic Patients. Journal of Personalized Medicine, 13(10), 1466. https://doi.org/10.3390/jpm13101466








