Machine-Learning-Based Late Fusion on Multi-Omics and Multi-Scale Data for Non-Small-Cell Lung Cancer Diagnosis
Abstract
:1. Introduction
2. Related Work
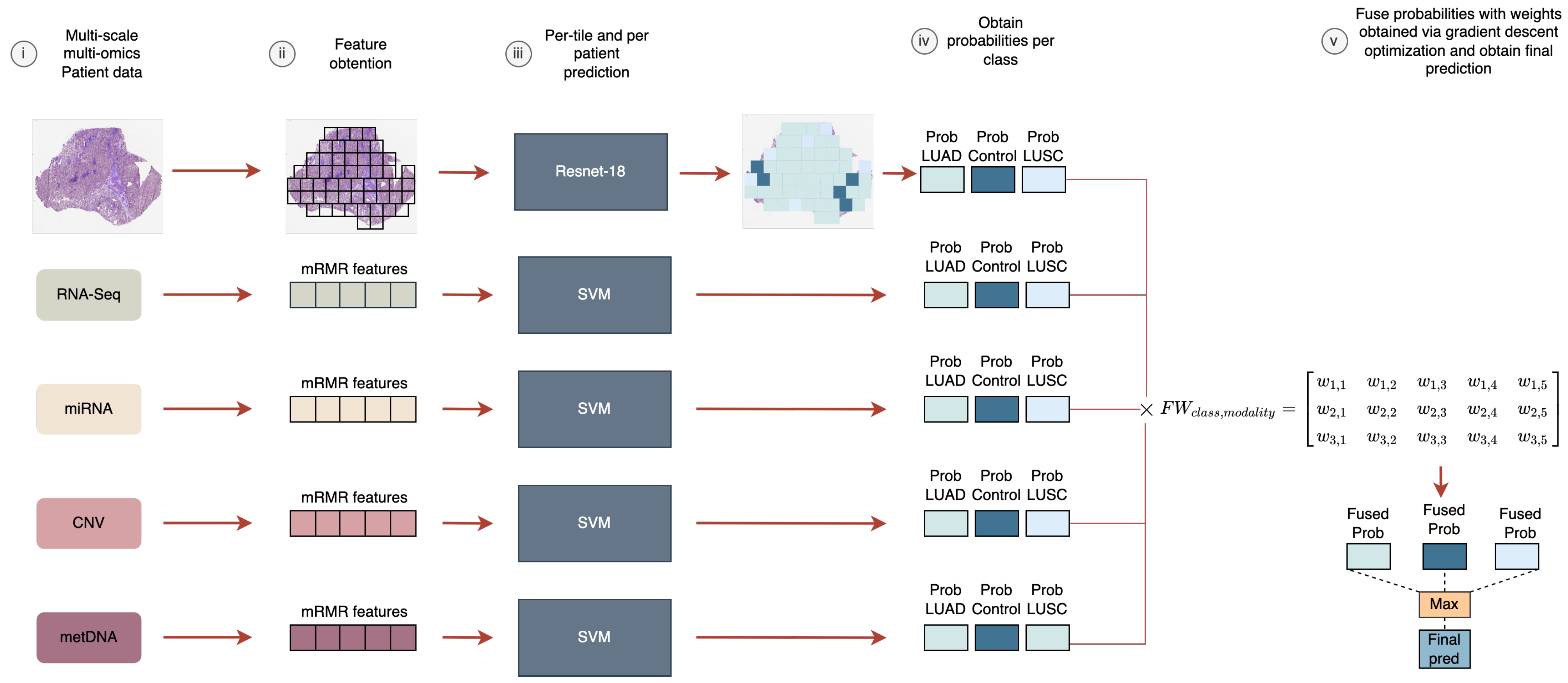
3. Materials and Methods
3.1. Data Acquisition and Pre-Processing
3.1.1. WSI Preprocessing
3.1.2. Omic Data Preprocessing
3.2. Model Selection and Training
3.3. Probability Fusion via Weight-Sum Optimization
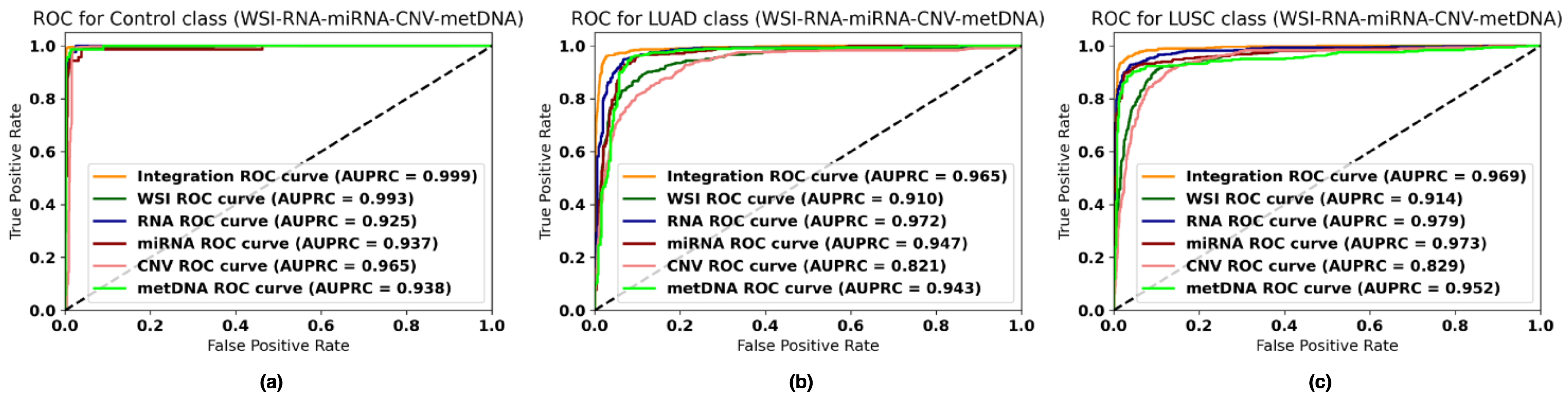
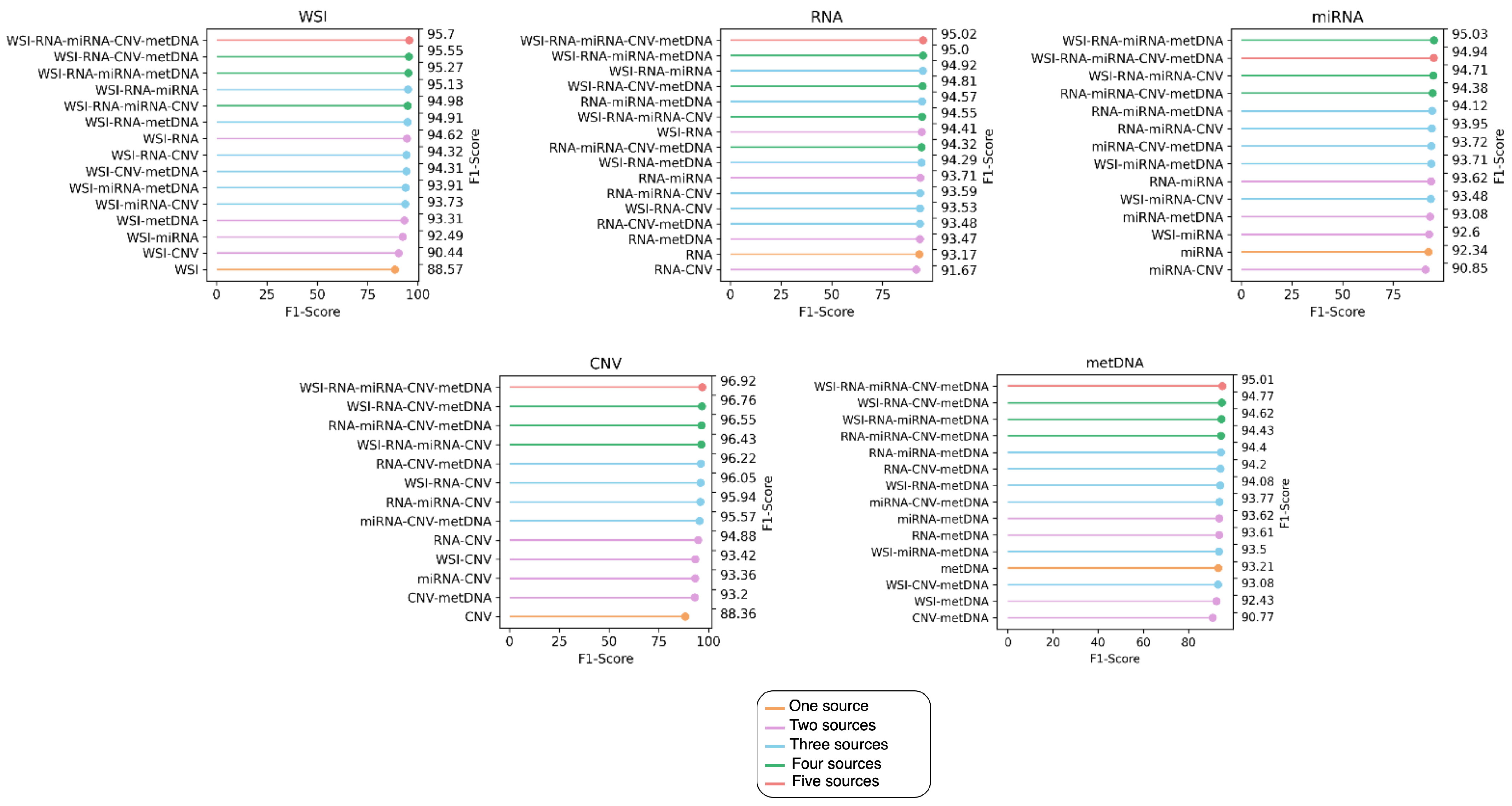
4. Results and Discussion
4.1. Performance of Each Data Modality
4.2. Performance of Late Fusion with Different Number of Sources
4.3. Performance of the Fusion Models with Missing Information
4.4. Comparison with Previous Work
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| LUAD | Lung adenocarcinoma |
| LUSC | Lung squamous cell carcinoma |
| NSCLC | Non-small-cell lung cancer |
| SVM | Support vector machines |
| CNN | Convolutional neural network |
| CNV | Copy number variation |
| metDNA | DNA methylation |
| WSI | Whole-slide imaging |
| CDSS | Clinical decision support system |
| RF | Random forest |
| mRMR | Minimum redundancy maximum relevance |
| AUC | Area under the curve |
| ANN | Artificial neural network |
References
- Sung, H.; Ferlay, J.; Siegel, R.L.; Laversanne, M.; Soerjomataram, I.; Jemal, A.; Bray, F. Global cancer statistics 2020: GLOBOCAN estimates of incidence and mortality worldwide for 36 cancers in 185 countries. CA Cancer J. Clin. 2021, 71, 209–249. [Google Scholar] [CrossRef] [PubMed]
- Cancer Research UK. Types of Lung Cancer. Available online: https://www.cancerresearchuk.org/about-cancer/lung-cancer/stages-types-grades/types (accessed on 5 April 2022).
- Subramanian, J.; Govindan, R. Lung cancer in never smokers: A review. J. Clin. Oncol. 2007, 25, 561–570. [Google Scholar] [CrossRef] [PubMed]
- Kenfield, S.A.; Wei, E.K.; Stampfer, M.J.; Rosner, B.A.; Colditz, G.A. Comparison of aspects of smoking among the four histological types of lung cancer. Tob. Control 2008, 17, 198–204. [Google Scholar] [CrossRef] [PubMed]
- Travis, W.D.; Travis, L.B.; Devesa, S.S. Lung cancer. Cancer 1995, 75, 191–202. [Google Scholar] [CrossRef]
- Hanna, N.; Johnson, D.; Temin, S.; Baker, S., Jr.; Brahmer, J.; Ellis, P.M.; Giaccone, G.; Hesketh, P.J.; Jaiyesimi, I.; Leighl, N.B.; et al. Systemic therapy for stage IV non-small-cell lung cancer: American Society of Clinical Oncology clinical practice guideline update. J. Clin. Oncol. 2017, 35, 3484–3515. [Google Scholar] [CrossRef]
- Coudray, N.; Ocampo, P.S.; Sakellaropoulos, T.; Narula, N.; Snuderl, M.; Fenyö, D.; Moreira, A.L.; Razavian, N.; Tsirigos, A. Classification and mutation prediction from non–small cell lung cancer histopathology images using deep learning. Nat. Med. 2018, 24, 1559–1567. [Google Scholar] [CrossRef]
- Castillo, D.; Galvez, J.M.; Herrera, L.J.; Rojas, F.; Valenzuela, O.; Caba, O.; Prados, J.; Rojas, I. Leukemia multiclass assessment and classification from Microarray and RNA-seq technologies integration at gene expression level. PLoS ONE 2019, 14, e0212127. [Google Scholar] [CrossRef]
- Qiu, Z.W.; Bi, J.H.; Gazdar, A.F.; Song, K. Genome-wide copy number variation pattern analysis and a classification signature for non-small cell lung cancer. Genes Chromosom. Cancer 2017, 56, 559–569. [Google Scholar] [CrossRef]
- Ye, Z.; Sun, B.; Xiao, Z. Machine learning identifies 10 feature miRNAs for lung squamous cell carcinoma. Gene 2020, 749, 144669. [Google Scholar] [CrossRef]
- Cai, Z.; Xu, D.; Zhang, Q.; Zhang, J.; Ngai, S.M.; Shao, J. Classification of lung cancer using ensemble-based feature selection and machine learning methods. Mol. Biosyst. 2015, 11, 791–800. [Google Scholar] [CrossRef]
- Wang, Y.y.; Ren, T.; Cai, Y.y.; He, X.y. MicroRNA let-7a inhibits the proliferation and invasion of nonsmall cell lung cancer cell line 95D by regulating K-Ras and HMGA2 gene expression. Cancer Biother. Radiopharm. 2013, 28, 131–137. [Google Scholar] [CrossRef]
- Zhang, J.g.; Wang, J.j.; Zhao, F.; Liu, Q.; Jiang, K.; Yang, G.h. MicroRNA-21 (miR-21) represses tumor suppressor PTEN and promotes growth and invasion in non-small cell lung cancer (NSCLC). Clin. Chim. Acta 2010, 411, 846–852. [Google Scholar] [CrossRef] [PubMed]
- Zheng, H.; Momeni, A.; Cedoz, P.L.; Vogel, H.; Gevaert, O. Whole slide images reflect DNA methylation patterns of human tumors. NPJ Genom. Med. 2020, 5, 11. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Daemen, A.; Gevaert, O.; Ojeda, F.; Debucquoy, A.; Suykens, J.A.; Sempoux, C.; Machiels, J.P.; Haustermans, K.; De Moor, B. A kernel-based integration of genome-wide data for clinical decision support. Genome Med. 2009, 1, 39. [Google Scholar] [CrossRef] [Green Version]
- Gevaert, O.; Smet, F.D.; Timmerman, D.; Moreau, Y.; Moor, B.D. Predicting the prognosis of breast cancer by integrating clinical and microarray data with Bayesian networks. Bioinformatics 2006, 22, e184–e190. [Google Scholar] [CrossRef] [Green Version]
- Cheerla, A.; Gevaert, O. Deep learning with multimodal representation for pancancer prognosis prediction. Bioinformatics 2019, 35, i446–i454. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Verma, G.K.; Tiwary, U.S. Multimodal fusion framework: A multiresolution approach for emotion classification and recognition from physiological signals. NeuroImage 2014, 102, 162–172. [Google Scholar] [CrossRef]
- Smolander, J.; Stupnikov, A.; Glazko, G.; Dehmer, M.; Emmert-Streib, F. Comparing biological information contained in mRNA and non-coding RNAs for classification of lung cancer patients. BMC Cancer 2019, 19, 1176. [Google Scholar] [CrossRef] [Green Version]
- Fan, Z.; Xue, W.; Li, L.; Zhang, C.; Lu, J.; Zhai, Y.; Suo, Z.; Zhao, J. Identification of an early diagnostic biomarker of lung adenocarcinoma based on co-expression similarity and construction of a diagnostic model. J. Transl. Med. 2018, 16, 205. [Google Scholar] [CrossRef]
- González, S.; Castillo, D.; Galvez, J.M.; Rojas, I.; Herrera, L.J. Feature Selection and Assessment of Lung Cancer Sub-types by Applying Predictive Models. In Proceedings of the International Work-Conference on Artificial Neural Networks, Gran Canaria, Spain, 12–14 June 2019; Springer: Berlin/Heidelberg, Germany, 2019; pp. 883–894. [Google Scholar]
- Castillo-Secilla, D.; Gálvez, J.M.; Carrillo-Perez, F.; Verona-Almeida, M.; Redondo-Sánchez, D.; Ortuno, F.M.; Herrera, L.J.; Rojas, I. KnowSeq R-Bioc package: The automatic smart gene expression tool for retrieving relevant biological knowledge. Comput. Biol. Med. 2021, 133, 104387. [Google Scholar] [CrossRef]
- Yang, Z.; Yin, H.; Shi, L.; Qian, X. A novel microRNA signature for pathological grading in lung adenocarcinoma based on TCGA and GEO data. Int. J. Mol. Med. 2020, 45, 1397–1408. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cheerla, N.; Gevaert, O. MicroRNA based pan-cancer diagnosis and treatment recommendation. BMC Bioinform. 2017, 18, 32. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shen, N.; Du, J.; Zhou, H.; Chen, N.; Pan, Y.; Hoheisel, J.D.; Jiang, Z.; Xiao, L.; Tao, Y.; Mo, X. A diagnostic panel of DNA methylation biomarkers for lung adenocarcinoma. Front. Oncol. 2019, 9, 1281. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gevaert, O.; Tibshirani, R.; Plevritis, S.K. Pancancer analysis of DNA methylation-driven genes using MethylMix. Genome Biol. 2015, 16, 17. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kanavati, F.; Toyokawa, G.; Momosaki, S.; Rambeau, M.; Kozuma, Y.; Shoji, F.; Yamazaki, K.; Takeo, S.; Iizuka, O.; Tsuneki, M. Weakly-supervised learning for lung carcinoma classification using deep learning. Sci. Rep. 2020, 10, 9297. [Google Scholar] [CrossRef] [PubMed]
- Graham, S.; Shaban, M.; Qaiser, T.; Koohbanani, N.A.; Khurram, S.A.; Rajpoot, N. Classification of lung cancer histology images using patch-level summary statistics. In Medical Imaging 2018: Digital Pathology. International Society for Optics and Photonics; SPIE: Bellingham, WA, USA, 2018; Volume 10581, p. 1058119. [Google Scholar]
- Lai, Y.H.; Chen, W.N.; Hsu, T.C.; Lin, C.; Tsao, Y.; Wu, S. Overall survival prediction of non-small cell lung cancer by integrating microarray and clinical data with deep learning. Sci. Rep. 2020, 10, 4679. [Google Scholar] [CrossRef]
- Lee, T.Y.; Huang, K.Y.; Chuang, C.H.; Lee, C.Y.; Chang, T.H. Incorporating deep learning and multi-omics autoencoding for analysis of lung adenocarcinoma prognostication. Comput. Biol. Chem. 2020, 87, 107277. [Google Scholar] [CrossRef]
- Dong, Y.; Yang, W.; Wang, J.; Zhao, J.; Qiang, Y.; Zhao, Z.; Kazihise, N.G.F.; Cui, Y.; Yang, X.; Liu, S. MLW-gcForest: A multi-weighted gcForest model towards the staging of lung adenocarcinoma based on multi-modal genetic data. BMC Bioinform. 2019, 20, 578. [Google Scholar] [CrossRef]
- Carrillo-Perez, F.; Morales, J.C.; Castillo-Secilla, D.; Molina-Castro, Y.; Guillén, A.; Rojas, I.; Herrera, L.J. Non-small-cell lung cancer classification via RNA-Seq and histology imaging probability fusion. BMC Bioinform. 2021, 22, 454. [Google Scholar] [CrossRef]
- Weinstein, J.N.; Collisson, E.A.; Mills, G.B.; Shaw, K.R.M.; Ozenberger, B.A.; Ellrott, K.; Shmulevich, I.; Sander, C.; Stuart, J.M.; Network, C.G.A.R.; et al. The cancer genome atlas pan-cancer analysis project. Nat. Genet. 2013, 45, 1113. [Google Scholar] [CrossRef]
- Grossman, R.L.; Heath, A.P.; Ferretti, V.; Varmus, H.E.; Lowy, D.R.; Kibbe, W.A.; Staudt, L.M. Toward a shared vision for cancer genomic data. N. Engl. J. Med. 2016, 375, 1109–1112. [Google Scholar] [CrossRef] [PubMed]
- Castillo, D.; Gálvez, J.M.; Herrera, L.J.; San Román, B.; Rojas, F.; Rojas, I. Integration of RNA-Seq data with heterogeneous microarray data for breast cancer profiling. BMC Bioinform. 2017, 18, 506. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Conesa, A.; Madrigal, P.; Tarazona, S.; Gomez-Cabrero, D.; Cervera, A.; McPherson, A.; Szcześniak, M.W.; Gaffney, D.J.; Elo, L.L.; Zhang, X.; et al. A survey of best practices for RNA-seq data analysis. Genome Biol. 2016, 17, 13. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [Green Version]
- Peng, H.; Long, F.; Ding, C. Feature selection based on mutual information criteria of max-dependency, max-relevance, and min-redundancy. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1226–1238. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M.; et al. Imagenet large scale visual recognition challenge. Int. J. Comput. Vis. 2015, 115, 211–252. [Google Scholar] [CrossRef] [Green Version]
- Gálvez, J.M.; Castillo-Secilla, D.; Herrera, L.J.; Valenzuela, O.; Caba, O.; Prados, J.C.; Ortuño, F.M.; Rojas, I. Towards improving skin cancer diagnosis by integrating microarray and RNA-seq datasets. IEEE J. Biomed. Health Inform. 2019, 24, 2119–2130. [Google Scholar] [CrossRef]
- Keerthi, S.S.; Lin, C.J. Asymptotic behaviors of support vector machines with Gaussian kernel. Neural Comput. 2003, 15, 1667–1689. [Google Scholar] [CrossRef]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Advances in Neural Information Processing Systems 32; Wallach, H., Larochelle, H., Beygelzimer, A., d’Alché-Buc, F., Fox, E., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2019; pp. 8024–8035. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Polikar, R.; Topalis, A.; Parikh, D.; Green, D.; Frymiare, J.; Kounios, J.; Clark, C.M. An ensemble based data fusion approach for early diagnosis of Alzheimer’s disease. Inf. Fusion 2008, 9, 83–95. [Google Scholar] [CrossRef]
- Depeursinge, A.; Racoceanu, D.; Iavindrasana, J.; Cohen, G.; Platon, A.; Poletti, P.A.; Müller, H. Fusing visual and clinical information for lung tissue classification in high-resolution computed tomography. Artif. Intell. Med. 2010, 50, 13–21. [Google Scholar] [CrossRef] [PubMed]
- Wu, T.F.; Lin, C.J.; Weng, R.C. Probability estimates for multi-class classification by pairwise coupling. J. Mach. Learn. Res. 2004, 5, 975–1005. [Google Scholar]
- Meng, T.; Lin, L.; Shyu, M.L.; Chen, S.C. Histology image classification using supervised classification and multimodal fusion. In Proceedings of the 2010 IEEE International Symposium on Multimedia, Taichung, Taiwan, 13–15 December 2010; pp. 145–152. [Google Scholar]
- Trong, V.H.; Gwang-Hyun, Y.; Vu, D.T.; Jin-Young, K. Late fusion of multimodal deep neural networks for weeds classification. Comput. Electron. Agric. 2020, 175, 105506. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Schmauch, B.; Romagnoni, A.; Pronier, E.; Saillard, C.; Maillé, P.; Calderaro, J.; Kamoun, A.; Sefta, M.; Toldo, S.; Zaslavskiy, M.; et al. A deep learning model to predict RNA-Seq expression of tumours from whole slide images. Nat. Commun. 2020, 11, 3877. [Google Scholar] [CrossRef]
| Modalities | Problem | Model | Metrics | Results | |
|---|---|---|---|---|---|
| Smolander et al. [19] | RNA-Seq | LUAD vs. control | DNN | Acc. | 95.97% |
| Fan et al. [20] | RNA-Seq | LUAD vs. control | SVM | Acc. | 91% |
| Gonzales et al. [21] | Microarray | SCLC vs. LUAD vs. LUSC vs. LCLC | k-NN | Acc. | 91% |
| Castillo-Secilla et al. [22] | RNA-Seq | LUAD vs. control vs. LUSC | RF | Acc. | 95.7% |
| Ye et al. [10] | miRNA-Seq | LUSC vs. control | SVM | F1 score | 99.4% |
| Qiu et al. [9] | CNV | LUAD vs. control vs. LUSC | EN-PLS-NB | Acc. | 84% |
| Shen et al. [25] | metDNA | LUAD vs. control | RF | Acc. | 95.57% |
| Cai et al. [11] | metDNA | LUAD vs. LUSC vs. SCLC | Ensemble | Acc. | 86.54% |
| Coudray et al. [7] | WSI | LUAD vs. control vs. LUSC | CNN | AUC | 0.978 |
| Kanavati et al. [27] | WSI | Lung carcinoma vs. control | CNN | AUC | 0.988 |
| Graham et al. [28] | WSI | LUAD vs. control vs. LUSC | CNN | Acc. | 81% |
| WSI | RNA-Seq | miRNA | CNV | metDNA | |
|---|---|---|---|---|---|
| LUAD | 495 | 457 | 413 | 465 | 431 |
| Control | 419 | 44 | 71 | 919 | 71 |
| LUSC | 506 | 479 | 420 | 472 | 381 |
| Total | 1420 | 980 | 904 | 1856 | 883 |
| # Tiles | |
|---|---|
| LUAD | 100,841 |
| Control | 62,715 |
| LUSC | 92,584 |
| Total | 256,140 |
| WSI | RNA-Seq | miRNA | CNV | metDNA | Acc. (Std) | F1 score (Std) | AUC (Std) | AUPRC (Std) |
|---|---|---|---|---|---|---|---|---|
| X | 88.56 (2.34) | 88.57 (2.36) | 0.965 (0.003) | 0.940 (0.014) | ||||
| X | 93.16 (1.87) | 93.17 (1.82) | 0.987 (0.007) | 0.973 (0.028) | ||||
| X | 92.31 (2.69) | 92.34 (2.65) | 0.976 (0.013) | 0.961 (0.023) | ||||
| X | 88.36 (1.34) | 88.36 (1.34) | 0.954 (0.009) | 0.879 (0.025) | ||||
| X | 93.21 (1.84) | 93.19 (1.87) | 0.972 (0.016) | 0.957 (0.030) | ||||
| X | X | 94.65 (1.80) | 94.69 (1.80) | 0.991 (0.004) | 0.979 (0.032) | |||
| X | X | 92.59 (2.57) | 92.60 (2.56) | 0.987 (0.006) | 0.982 (0.009) | |||
| X | X | 90.26 (1.98) | 90.20 (1.92) | 0.974 (0.010) | 0.962 (0.016) | |||
| X | X | 92.79 (1.77) | 92.80 (1.78) | 0.983 (0.009) | 0.979 (0.012) | |||
| X | X | 94.55 (1.83) | 94.74 (1.70) | 0.988 (0.007) | 0.980 (0.017) | |||
| X | X | 91.81 (2.34) | 92.12 (2.36) | 0.978 (0.006) | 0.953 (0.050) | |||
| X | X | 94.33 (1.81) | 94.33 (1.79) | 0.991 (0.007) | 0.989 (0.009) | |||
| X | X | 91.00 (1.97) | 91.36 (1.82) | 0.973 (0.009) | 0.944 (0.048) | |||
| X | X | 93.84 (2.88) | 93.85 (2.88) | 0.979 (0.015) | 0.980 (0.015) | |||
| X | X | 90.15 (3.09) | 90.28 (3.04) | 0.968 (0.010) | 0.947 (0.033) | |||
| X | X | X | 95.55 (1.78) | 95.69 (1.76) | 0.985 (0.008) | 0.990 (0.005) | ||
| X | X | X | 93.99 (1.47) | 94.00 (1.41) | 0.982 (0.022) | 0.974 (0.041) | ||
| X | X | X | 94.70 (2.11) | 94.73 (2.10) | 0.987 (0.010) | 0.990 (0.007) | ||
| X | X | X | 93.84 (2.05) | 93.97 (2.03) | 0.974 (0.030) | 0.977 (0.016) | ||
| X | X | X | 94.23 (2.55) | 94.23 (2.54) | 0.975 (0.022) | 0.986 (0.008) | ||
| X | X | X | 93.50 (2.98) | 93.52 (2.97) | 0.981 (0.009) | 0.978 (0.012) | ||
| X | X | X | 94.79 (1.76) | 95.10 (1.72) | 0.938 (0.059) | 0.963 (0.050) | ||
| X | X | X | 95.05 (2.05) | 95.10 (2.01) | 0.967 (0.027) | 0.989 (0.009) | ||
| X | X | X | 94.11 (1.76) | 94.20 (1.74) | 0.977 (0.012) | 0.981 (0.010) | ||
| X | X | X | 94.11 (2.92) | 94.36 (2.70) | 0.975 (0.005) | 0.966 (0.023) | ||
| X | X | X | X | 95.22 (2.13) | 95.47 (2.01) | - | 0.987 (0.007) | |
| X | X | X | X | 95.53 (2.09) | 95.62 (2.04) | - | 0.989 (0.007) | |
| X | X | X | X | 95.22 (2.10) | 95.30 (2.05) | - | 0.986 (0.009) | |
| X | X | X | X | 94.71 (2.29) | 94.9 (2.20) | - | 0.978 (0.013) | |
| X | X | X | X | 94.86 (2.19) | 95.14 (2.06) | - | 0.981 (0.010) | |
| X | X | X | X | X | 95.53 (2.20) | 95.82 (2.05) | - | 0.983 (0.012) |
| WSI | RNA | miRNA | CNV | metDNA | |
|---|---|---|---|---|---|
| Correct | 1232 | 913 | 834 | 1636 | 821 |
| Misclassified | 159 | 67 | 70 | 220 | 62 |
| Fusion | |||||
| Correct | 1328 | 929 | 857 | 1796 | 838 |
| Misclassified | 63 | 51 | 47 | 60 | 45 |
| Absolute difference in misclassified error rate (#samples (%)) | 96 (6.5%) | 16 (1.6%) | 23 (2.6%) | 160 (8.6%) | 17 (2%) |
| Modality | Metric | Score | |
|---|---|---|---|
| Qui et al. [9] | CNV | Acc. | 84% |
| Ours | CNV | Acc. | 96.93% |
| Cai et al. [11] | metDNA | Acc. | 86.54% |
| Ours | metDNA | Acc. | 95.01% |
| Cai et al. [11] | metDNA | F1 score | 74.55% |
| Ours | metDNA | F1 score | 95.01% |
| Castillo-Secilla et al. [22] | RNA-Seq | Acc. | 95.7% |
| Ours | RNA-Seq | Acc. | 95% |
| Castillo-Secilla et al. [22] | RNA-Seq | F1 score | 95.4% |
| Ours | RNA-Seq | F1 score | 95.02% |
| Coudray et al. [7] | WSI | AUC | 0.978 |
| Ours | WSI | AUC | 0.991 |
| Graham et al. [28] | WSI | Acc. | 81% |
| Ours | WSI | Acc. | 95.70% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carrillo-Perez, F.; Morales, J.C.; Castillo-Secilla, D.; Gevaert, O.; Rojas, I.; Herrera, L.J. Machine-Learning-Based Late Fusion on Multi-Omics and Multi-Scale Data for Non-Small-Cell Lung Cancer Diagnosis. J. Pers. Med. 2022, 12, 601. https://doi.org/10.3390/jpm12040601
Carrillo-Perez F, Morales JC, Castillo-Secilla D, Gevaert O, Rojas I, Herrera LJ. Machine-Learning-Based Late Fusion on Multi-Omics and Multi-Scale Data for Non-Small-Cell Lung Cancer Diagnosis. Journal of Personalized Medicine. 2022; 12(4):601. https://doi.org/10.3390/jpm12040601
Chicago/Turabian StyleCarrillo-Perez, Francisco, Juan Carlos Morales, Daniel Castillo-Secilla, Olivier Gevaert, Ignacio Rojas, and Luis Javier Herrera. 2022. "Machine-Learning-Based Late Fusion on Multi-Omics and Multi-Scale Data for Non-Small-Cell Lung Cancer Diagnosis" Journal of Personalized Medicine 12, no. 4: 601. https://doi.org/10.3390/jpm12040601
APA StyleCarrillo-Perez, F., Morales, J. C., Castillo-Secilla, D., Gevaert, O., Rojas, I., & Herrera, L. J. (2022). Machine-Learning-Based Late Fusion on Multi-Omics and Multi-Scale Data for Non-Small-Cell Lung Cancer Diagnosis. Journal of Personalized Medicine, 12(4), 601. https://doi.org/10.3390/jpm12040601







