1. Introduction
Acute myeloid leukemia (AML), characterized by the pathological accumulation of myeloblast cells in blood or bone marrow, is a heterogeneous and aggressive form of leukemia. About 30% of AML cases carry a mutation in the
FLT3 gene, which encodes a receptor critical for normal hematopoiesis [
1]. By far the most common mutation is an internal tandem duplication (
FLT3-ITD), which occurs in about 25% of all AML cases [
1], a mutation placing patients in a poor prognosis category [
2]. Highly specific
FLT3 inhibitors are therapeutically promising [
1,
2], though the disease often recurs.
Recent experimental results have suggested that while
FLT3-inhibition can kill
FLT3-ITD cells, some cells survive and become drug tolerant persisters (DTPs) [
3,
4]. Targeting the therapeutic vulnerabilities of drug-tolerant FLT3 mutant AML cells can enhance the anti-leukemic efficacy of FLT3 inhibitors to eliminate minimal residual disease, mutational drug resistance and relapse. The mechanisms underlying this phenotypic change are not fully understood. A recent study found that DTPs exhibit the upregulation of inflammation pathways, and combination treatment with quizartinib (a
FLT3 inhibitor) and dexamethasone (a glucocorticoid that reduces inflammation) was synergistic [
4]. This is an example of reprogramming therapy, in which the phenotypes or gene expression patterns induced by one drug are countered by another simultaneous intervention.
The idea of reprogramming cancer cells into drug-sensitive states [
5,
6,
7,
8,
9] or even non-malignant states [
10,
11] has become increasingly promising. Reprogramming drug-sensitivity follows from the hypothesis that drug treatment induces reversible, system-wide gene expression and epigenetic changes, causing cells to achieve a resistant or tolerant subtype [
12,
13]. Targeting these changes and reverting them may then reprogram the cells. With this view, we seek to gain a systems-level understanding of the gene expression and phenotypic changes of
FLT3-ITD AML cells in response to drug treatment with quizartinib and dexamethasone, and their evolution into DTPs.
To this end, we identified several modules of co-expressed genes that correspond to different treatment conditions with quizartinib, dexamethasone, or their combination. Based on genes within these modules, we built a network model of FLT3-ITD AML drug response. Using data-driven tools, we derived a probabilistic, dynamical gene regulatory model that recapitulates the expression changes of AML cells following these drug treatments and can be used to predict the effects of perturbations and interventions in the cells. We focused on identifying interventions that downregulate modules associated with drug resistance, and upregulate modules associated with cell death. The interventions we identified represent promising strategies to improve response to FLT3 inhibitors in FLT3-ITD AML.
2. Materials and Methods
2.1. Data Acquisition and Processing
RNAseq data of MV4-11 cells were collected by M. Gebru, as described in [
4], and previously made publicly available on GEO (GSE116432). Data consisted of triplicate measurements, each of (1) 10 nM quizartinib treatment for 48 h, (2) 10 nM quizartinib treatment for five days, (3) 100 nM dexamethasone treatment for 48 h, (4) combination 10 nM quizartinib + 100 nM dexamethasone for 48 h (we refer to this combination as Quiz + Dex), (5) Quiz + Dex for five days (quizartinib for five days and dexamethasone added on day 3 because the combination for 5 days would kill almost all cells), and (6) DMSO (GEO: GSE116432). Data were transformed as log(1 + FPKM). Only transcripts with a matched HGNC symbol were kept.
2.2. Weighted Gene Co-Expression Network Analysis
We used v1.69 of the WGCNA package in R v4.0.2. We used the pckSoftThresold function with a “signed” network type to identify power = 10 as the smallest power that achieved a scale-free R
2 value >= 0.9 (
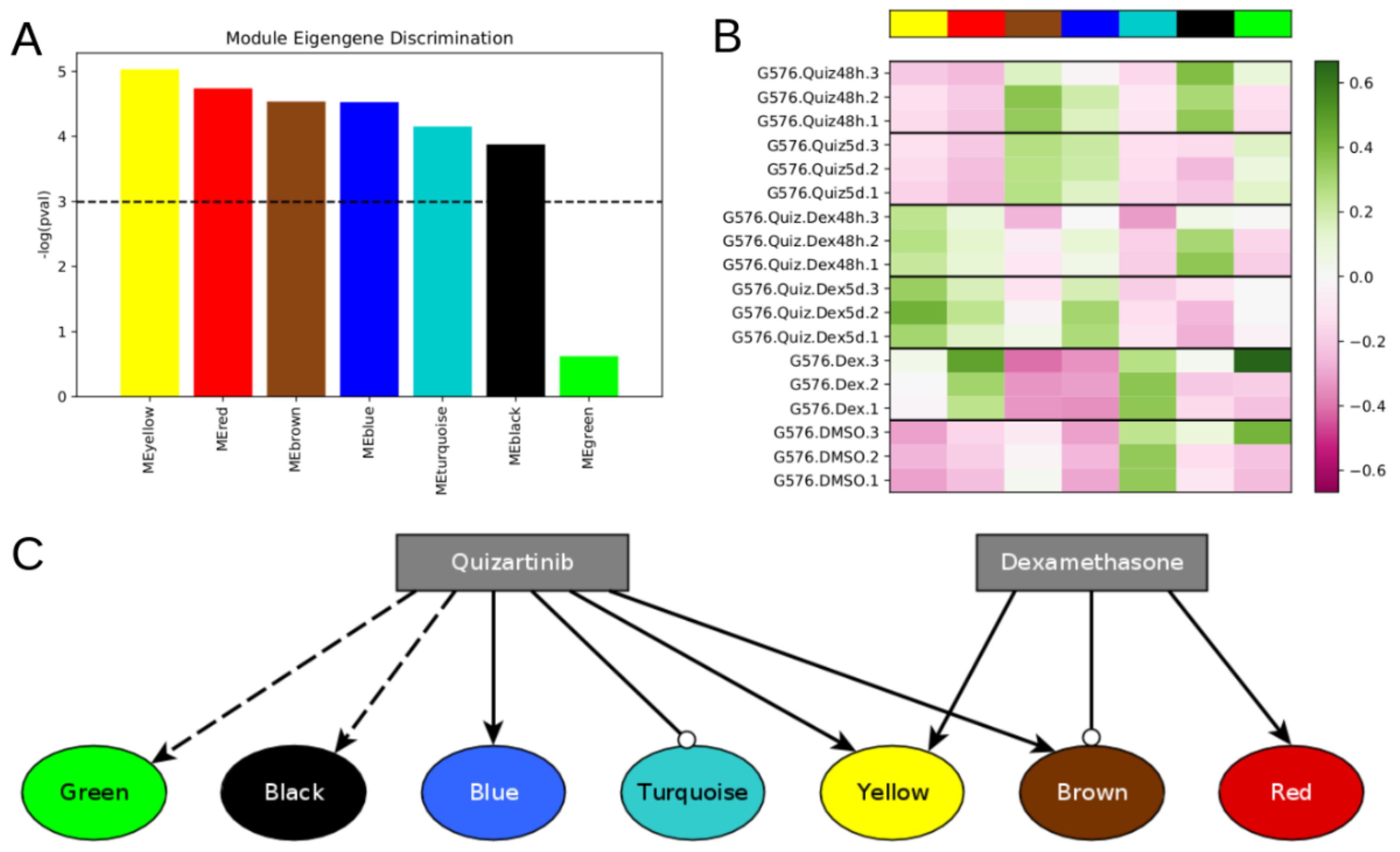
Figure S1). We built a topological overlap matrix using a signed adjacency matrix obtained from power = 10. Genes were hierarchically clustered using the “average” method, and genes were assigned to co-expression modules using WGCNA’s cutreeDynamic function with deepSplit = 2, pamRespectsDendro = FALSE, and minClusterSize = 100. This analysis resulted in seven modules of co-expressed genes (
Figure 1A and
Figure S1). Following WGCNA convention, the modules are denoted by color: turquoise (7219 genes), blue, yellow, brown, green, black (164 genes).
2.3. Molecular Biology of the Cell (MBCO) Ontology Analysis
2.4. Network Construction
To build the network, we integrated interactions from multiple databases that aggregated literature-based or predicted interactions, SIGNOR [
14], TRRUST [
15], and RegNetwork [
16], as well as published networks related to AML [
14,
17], NFKappaB signaling [
17], NOTCH signaling [
18], tumor promoting inflammation [
19,
20], and apoptosis [
20].
Many of these network resources have minor variations in gene names or use different aliases for different genes. We applied two methods to transform gene names from different sources into a common space so that all interactions with a given gene may be identified, even if the different sources use different names for that gene. First, we considered that many sources use different capitalization, or interchangeably use “.”, “-”, or “_” characters. To address this, we capitalized all characters in each gene name, and removed all “.”, “-”, and “_” characters. Second, to match gene aliases across different network sources, we used three separate gene name alias data sources, including Entrez Homo_sapiens gene info (
https://ftp.ncbi.nih.gov/gene/DATA/GENE_INFO/Mammalia/Homo_sapiens.gene_info.gz (accessed on 25 October 2020)), BioMart from Ensemble (
https://useast.ensembl.org/biomart (accessed on 25 October 2020)), and HGNC (
https://www.genenames.org/ (accessed on 25 October 2020)). Each source includes multiple aliases for each gene name. We constructed a gene name alias graph whose nodes represent gene names, and in which each edge represents that two nodes are aliases for the same gene from one of those resources. Within this alias graph, if there exists a path from one node to another, it indicates they refer to the same gene.
There were several properties we wanted the final AML network topology to have, and the strategy we used to build the network was refined until we reached a network that satisfied these properties. First, we wanted the network to be large enough to capture enough regulatory details (e.g., more than about four nodes per module, or about 30 nodes total), but not too large to be able to model or simulate well (e.g., fewer than about 200 nodes). Second, we wanted all seven gene co-expression modules to be similarly represented, even though some modules are much larger than others (turquoise and blue have thousands of genes each but green and black only have a few hundred genes each). Third, we wanted the in-degree of nodes to not be too large (e.g., more than about 7 incoming edges). This is because a Boolean regulatory function with N inputs has 2N possible input conditions for which an output value must be specified. When inferring Boolean functions of 7 or more variables using the BooleaBayes algorithm, the probability that any given sample constrains a given input condition becomes extremely small, and the resulting Boolean function becomes nearly completely stochastic.
The process we used to build the final network is shown in
Figure S9. First, we merged all the network sources (e.g., SIGNOR) into a single large network, wherein nodes that were aliases of one another from different sources were merged into a single node. This network contained 8614 nodes and 35,710 edges. Of the nodes, 2374 had non-zero out-degrees and represented a gene from the RNAseq dataset. We then extracted subgraphs consisting of only genes from the brown, red, green, yellow, and black modules. We focused on these first as they are smaller modules than blue and turquoise, and we wanted to include as many of these nodes as possible to ensure they are well represented in the final network. We merged these five subgraphs together, which resulted in a disconnected graph. This graph contained only two components with five or more nodes, one of which consisted of 18 green nodes, the other consisted of 53 brown nodes. We hypothesized that nodes from the red, yellow, or black modules may be connected into these components through paths (successions of edges) containing nodes not in the brown, red, green, yellow, or black modules. For example, no blue or turquoise nodes had been included at this point. We searched for paths of no more than four nodes that could connect nodes from the red, yellow, or black modules into the above-mentioned components (
Figure S9B). Anytime multiple paths were found, we only added the shortest path. If there were multiple equally short paths, all were added.
We removed all sink nodes because they do not feed back into the dynamics of the network, and thus cannot be drivers. The resulting graph contained 186 nodes and 888 edges. Of the nodes, 52 belonged to the brown module, 34 to turquoise, 23 blue, 21 yellow, 20 red, 15 green, and 9 black, while the others belonged to no module. This satisfied our goals of having approximately equal representation of the different modules, and not too few nor too many nodes. However, many nodes in the resulting graph had extremely high in-degree. For example, RELA had 43 in-edges, TP53 had 37, and FOXO3 had 36. The Boolean regulatory update function for RELA would then have 243 ~= 1012 conditions that must be specified, which would be impractical, and impossible given available data.
To avoid such excessively high in-degree nodes in the network, we calculated an edge score that we used to retain only the most confident edges. We set a threshold that must be exceeded to include an edge, and made this threshold increase as more in-edges are added to a node. This process preserves a node’s regulators if it has low in-degree, but provides an increasingly strict criterion for edges to be included as the in-degree becomes larger.
The edge score was based on the following factors: (1) whether or not the source node is a transcription factor (TF), (2) the number of references supporting the edge, (3) the number of different databases (e.g., SIGNOR) or literature-based networks that included the edge, and (4) the edge confidence given by the network resource, including “belief” (networks from Indra) or “score” (SIGNOR, TRUUST). Regarding point (1), if the source node is a TF, the edge score is multiplied by
. If not,
. Regarding point (4), for network resources that did not provide edge confidence, the confidence was assumed to be 0. With these metrics, the edge score was calculated as:
The minimum possible score was 2, as and were at least each 1 for every edge. For each node, all its incoming edges were scored and ordered from highest to lowest. The (up to) three edges with the three highest scores were always included. Following these, each subsequent edge was included if . For example, given five incoming edges with scores (5, 4.5, 4, 3, 2), the first three edges (scores 5, 4.5, and 3) are automatically included. The next edge has score = 3, which is greater than , so it is included. The next edge has score = 2, which is no longer greater than , so it, and any lower score edges, would not be included.
Finally, once again, all sink nodes, or nodes that do not belong to a component of at least size = 4, were removed. The final network had 106 nodes and 270 edges.
2.5. Regulatory Function Inference using the BooleaBayes Algorithm
Using the transcription data from the RNAseq dataset, the node activation data constructed as described in the next section, and the network topology, we inferred probabilistic Boolean regulatory functions using the BooleaBayes algorithm as described in [
6]. Briefly, BooleaBayes tries to find Boolean logic functions consistent with steady-state gene expression data and a network topology. As BooleaBayes needs normalized expression, RNAseq data for each gene were normalized between 0 and 1 by setting all values less than the 20th percentile to 0, all values above the 80% to 1, and all values in-between were linearly interpolated between 0 and 1.
BooleaBayes infers a probabilistic Boolean regulatory function for each node in the network. For each function, all input regulators are assigned a significance value by BooleaBayes, defined as the maximum possible (absolute value) difference in output value the regulator can make if it switches from OFF to ON. We set a minimum threshold of 0.1 for this value. With this threshold, each regulator must, in at least one condition, mean the difference between a 0.45 or less output, and a 0.55 or greater output.
When fitting the function for a node, if at least one regulator did not exceed this threshold, the regulator with the lowest significance was removed, and the function was inferred again using only the remaining regulators. This process was repeated until either all regulators exceeded the minimum significance threshold, or no regulators remained. In the latter case, the target node becomes a source node for later analyses.
2.6. Extension of BooleaBayes to Post-Translational Regulation
Unlike previous work with BooleaBayes, which focused purely on transcriptional regulation, the AML network includes post-translational modifications. However, the expression data only include transcription quantification. To apply the BooleaBayes algorithm, we must separate the probability of a node being transcribed from the probability of a node being active. For instance, if node A regulates node B, node A may be transcribed but not active, in which case the input value of node A into node B’s Boolean function should be OFF.
To this end, we first distinguished for each edge whether it represented transcriptional regulation or post-translational regulation. An edge whose source node is a transcription factor according to [
21] was considered to be a transcriptional edge. All other edges were considered as post-translational. Post-translational edges were assigned as positive (activating) or negative (de-activating) based on edge annotations from the source network. For example, SIGNOR and Indra edges indicate whether the regulator up-regulates or down-regulates the target. For edges with no consistent database annotation, edge weights were obtained from literature search when possible, or assumed to be positive if no specific supporting information could be found.
Any node that is only transcriptionally regulated is assumed to be active as long as it is transcribed. All nodes that are post-translationally regulated (such as a node named “X”) were split into transcript (X_T) and active protein (X_A) forms. Any outgoing edges (regulatory effects) from nodes that have _T and _A forms are assumed to come only from the _A form.
To fit BooleaBayes functions, the values from the RNAseq data are used directly for X_T. Values for X_A for each sample must be determined prior to applying BooleaBayes, so that the target nodes of X use X_A for their training data, instead of X_T. We assumed that protein post-translational activation follows an inhibitory dominant form. For example, if X_A is activated by nodes J and K, and deactivated by node M, we say
X_A = X_T and (J or K) and not M
(or J_A, K_A, or M_A, if any of those regulators require an activated form). As X_T, J, K, and M are not strictly Boolean variables, but rather probabilities, we transform this into a sloppy logic form by replacing “or” with “+”, “and” with “*”, and “not” with “1-”. Further, each term is strictly held within 0 and 1. Thus
X_A = X_T * min(J+K, 1) * max(1-M, 0)
More generally, as long as X has at least one activator we say
X_A = X_T * min(sum(ACTIVATORS_X), 1) * max(1-sum(INHIBITORS_X), 0)
while, if X has no activators, we say
X_A = X_T * max(1-sum(INHIBITORS_X), 0)
This distinction prevents nodes that have no activators from always being inactive—they are assumed to be active unless deactivated. We constructed such an equation for every node that must be activated. These equations formed a system of nonlinear algebraic equations which we solved numerically using the scipy.optimize.fsolve() function in Python v3.8, with an initial guess for each node of X_A = X_T. The resulting values of X_A were then added to the gene expression dataset to be used for inferring BooleaBayes functions for any node regulated by an _A form of a regulator.
2.7. Identification of Pseudo-Attractors
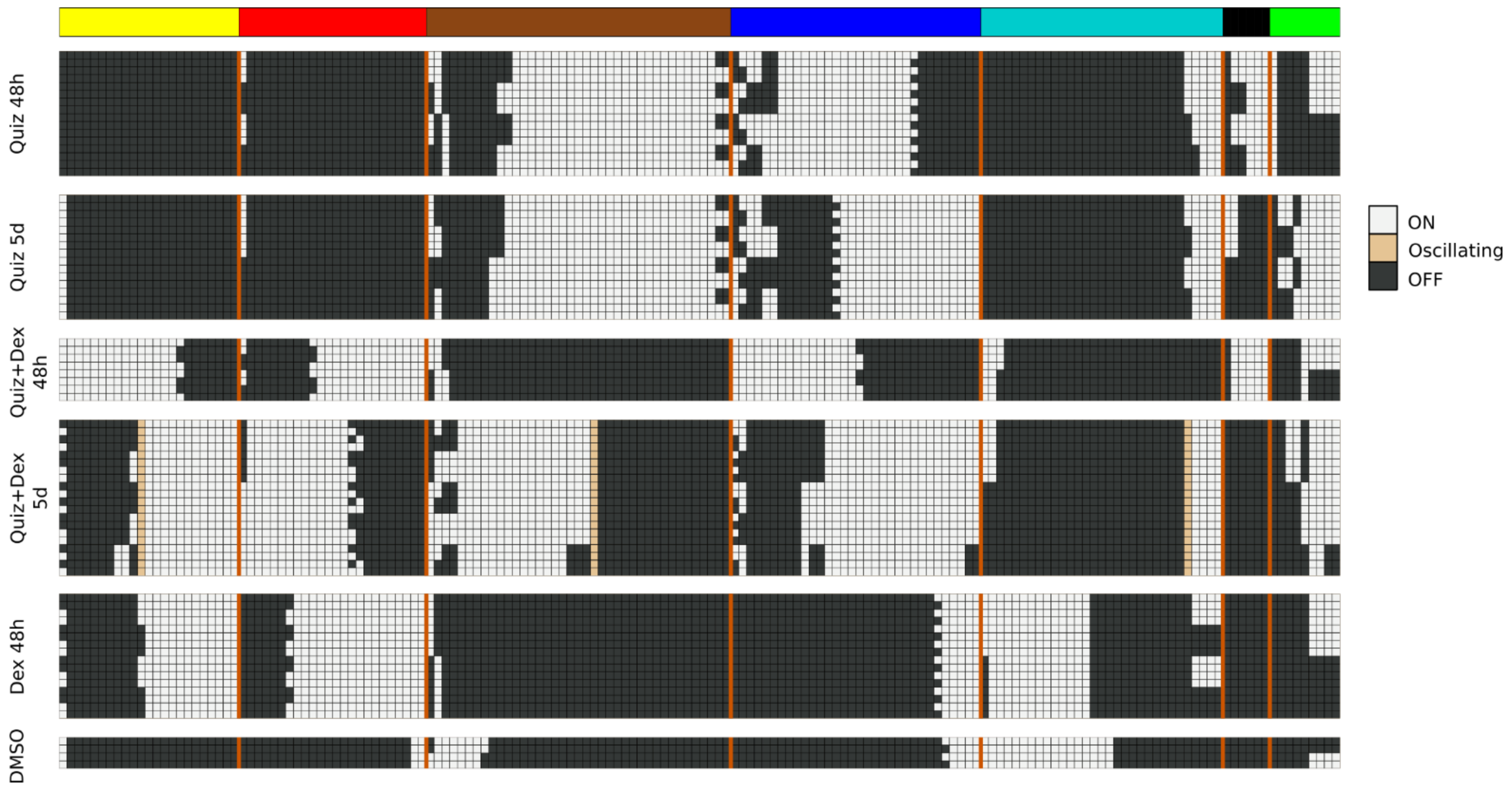
Pseudo-attractors of a probabilistic discrete system are states, or collections of states, that the system keeps revisiting. Expressed more technically, pseudo-attractors are collections of states for which transitions into them are more likely than transitions out, along every axis. The sum of forward and backward transition probabilities between two BooleaBayes states always adds up to 1. Therefore, if a transition is more likely into a state than out of a state, the out-transition will be less than 0.5. Thus, pseudo-attractors of a BooleaBayes-inferred system will correspond to the attracting strongly connected components of the state transition system, for which all transitions with probability less than 0.5 are removed. This corresponds exactly to the attractors of the closest approximating deterministic Boolean system, obtained by rounding all probabilities to the nearest 0 or 1—all transitions in the probabilistic system with probability less than 0.5 are absent.
Thus, to identify pseudo-attractors of the probabilistic AML drug network, we approximated each BooleaBayes-inferred update function to its closest deterministic function. We used the AttractorRepertoire module from the StableMotifs [
22] python package to find attractors of the deterministic system. The system has a very large number of source nodes (nodes with no regulators), which allows many attractors. To isolate the attractors most relevant to AML drug response, we determined the Boolean state of these source nodes for each of the six experimental conditions by averaging their probability to be ON or OFF from the data. For each node, if it was more likely to be ON across the three replicates, we plugged in the value ON to the deterministic system and propagated its value through the Boolean update functions, and likewise for OFF.
2.8. Node Interventions
We sought to understand how interventions that target specific nodes influence the stability of WGCNA gene modules. We considered two types of interventions: holding a node in the OFF (0) state, akin to knockout (KO) and holding a node in the ON (1) state, akin to constitutive activation (CA). We assumed that any intervention targeting a gene that was separated into transcribed and active protein forms applied to both forms. During simulations, the states of controlled nodes were held constant, and other nodes were updated as in the WT system.
2.9. Definition and Calculation of Influence Index
Systematic in silico intervention experiments require a significant number of computational resources, thus we wanted to prioritize the most likely candidates for up- or down-regulating a target module. To this end, we calculated an “influence index” for each node-intervention-module tuple, for example the tuple “GSK3B, KO, blue module”. The influence index is designed to estimate how likely it is that the influence of a node-intervention on the node’s direct targets aligns with the up- or down-regulation goal of a specified module.
The influence index is based on the concepts of necessary and sufficient regulation. If node A = ON is necessary for node B = ON, this means that A = OFF implies B = OFF. Conversely, if node A = ON is sufficient for node B = ON, this means that A = ON implies B = ON [
23]. For each edge we developed scores quantifying the likelihood that the edge represents necessary regulation or sufficient regulation. In total we calculated four scores for each edge: (1) the source is necessary for the target to be ON (called
), (2) the source is sufficient for the target to be ON (called
), (3) the source is necessary for the target to be OFF (called
), and (4) the source is sufficient for the target to be OFF (called
). These scores are based on the average value of the probabilistic function output when the node at the source of the edge is ON (
), or the source node is OFF (
). For example, consider a node C whose regulatory function is
. For the edge A→B,
while
.
Using this definition of and , , , , and were calculated as follows:
If an edge represents overall positive regulation (meaning that switching the source node from OFF to ON increases the likelihood that the target turns on)
Conversely, if an edge represents overall negative regulation (meaning that switching the source node from OFF to ON decreases the likelihood that the target turns on)
To illustrate these definitions, consider a node D with deterministic Boolean update function f(A,B,C) = A or (B and C). This function means that node D will turn on if A is ON or if B and C are simultaneously ON. For the edge A → D, we can calculate
A is a positive regulator of D, so , , and . This means that in 75% of input conditions A would be necessary to turn D ON (only when B=C=1 does D turn ON without A). Conversely, A is sufficient to turn D ON in all input conditions. Finally, A is never sufficient nor necessary to turn D OFF, as A is a positive regulator of D.
With this, we define the influence index of each node-intervention-module tuple using one of the following formulas:
Source node intervention: KO; Target module goal: DOWN
Source node intervention: KO; Target module goal: UP
Source node intervention: CA; Target module goal: DOWN
Source node intervention: CA; Target module goal: UP
where in each case the sum is over all target nodes of the perturbed node that are in the target gene module. The higher weight on necessary edges in KO interventions reflects the fact that turning OFF a necessary regulator is sufficient to control its output. The higher weight on sufficient edges in CA interventions reflects the fact that turning ON a sufficient regulator is sufficient to control its output.
2.10. Analyzing the Effect of Node Interventions
In contrast to attractors of deterministic systems, our stochastic model can evolve away from pseudo-attractors (i.e., pseudo-attractors are not trap spaces). We start simulations from a system state that corresponds to the average state of all pseudo-attractors associated to a given experimental condition, and examine how many steps are required for a given module’s overall expression to increase or decrease relative to its start state.
To accomplish this, we quantify a module’s “activation” as the fraction of nodes in the module that are ON. For the purpose of this calculation, we exclude all source nodes, as those nodes cannot be activated or silenced based on interventions of other nodes, and are, therefore, insensitive to any perturbation. During simulations we very rarely observed a module achieve more than 3/4 of non-source nodes becoming ON. We thus considered switches between states that have low module activation (fewer than 1/4 non-source nodes are ON) and intermediate module activation (between 1/4 and 3/4 non-source nodes are ON).
We simulated the dynamics of the WT system by starting from a pseudo-attractor and updating a single, randomly selected node at each time step [
6]. For modules that start in the low activation state, we counted how many steps were required for the module to switch to the intermediate state for the first time. For modules that start in the intermediate state, we instead counted how many steps were required to switch to the low activation state for the first time. We repeated these simulations, restarting from the start state, 100 times. For each simulation, we updated the system 5000 times. If a module did not switch within that time, we assigned a value 5001. For subsequent statistical analyses, we used a non-parametric ordinal test, so in most cases it does not practically matter how much above 5001 it really would have been.
We then chose a set of interventions to test, based on analysis of the network and influence index of various nodes. We considered single node KO or CA, or combinations of multiple nodes individually controlled. As in the WT system, we performed 100 iterations of 5000 steps, counting how many steps were required for a module to switch for the first time. We used a two-sided Mann–Whitney U test to test whether the average number of steps from the intervention simulations was statistically different from the WT. All p-values were FDR-corrected using the Benjamini–Hochberg (BH) method, and the threshold for significance was defined as BH-adjusted p < 0.05.
Following intervention, if a module requires more steps before it switches from low to intermediate activation, or vice versa, compared to WT, then the module’s original state was stabilized by the intervention. If the module began in the low state, we then classified the intervention as down-regulating. If the module began in the high state, we classified the intervention as up-regulating. Conversely, if an intervention makes a module require fewer steps to switch, then the module’s original state was destabilized by the intervention. If the module began in the intermediate state, we classified the intervention as down-regulating. If the module began in the low state, we classified the intervention as upregulating.
4. Discussion
Here we constructed a dynamic model of a gene regulatory network relevant to FLT3-mutant acute myeloid leukemia. The model integrates multiple types of information: RNAseq data consisting of MV4-11 cells exposed to drug treatment and several databases of signal transduction and gene regulation. Model development included multiple state of the art analysis methodologies: weighted gene co-expression analysis, ontology analysis, inference of regulatory relationships using BooleaBayes, attractor analysis, and control theory. We also developed new capabilities for BooleaBayes, and new confidence scores to prioritize interactions to be included in the network and new influence scores to prioritize interventions. Overall, this work illustrates the challenges and capabilities of computational systems biology analysis in cancer research and the potential for this type of analysis to advance personalized medicine.
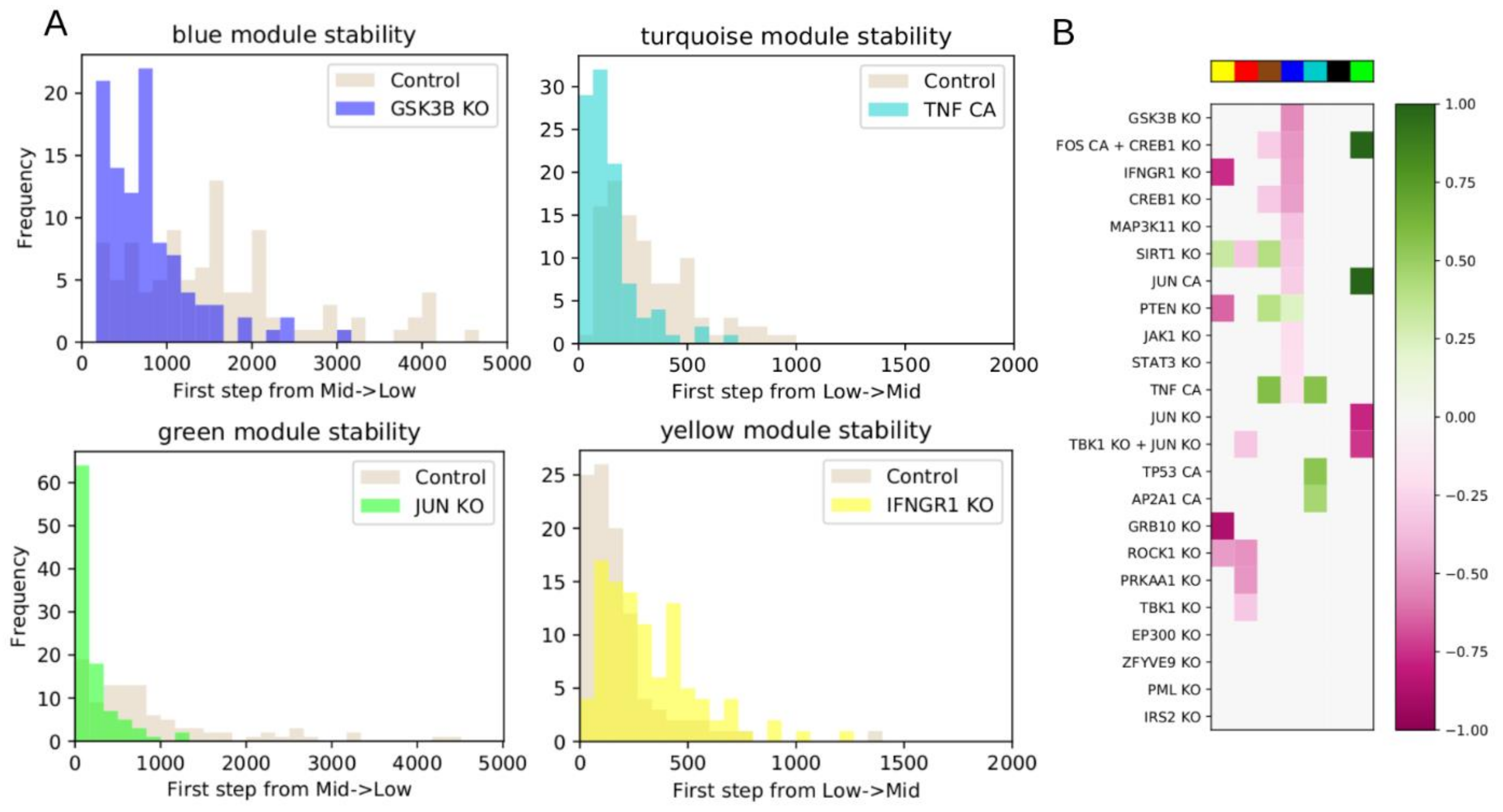
The model attractors recapitulate the activation of the modules (compare
Figure 4 to
Figure 1B), and the most significant predicted model interventions match well with literature reports on drivers of proliferation, survival, and drug resistance (
Figure 5). Collectively, these results strongly support the model’s validity. Nevertheless, there are several possible avenues for further model improvement. This model was derived from data in MV4-11 cells treated with quizartinib and dexamethasone. We previously showed that the gene expression profile of MV4-11 cells was predictive of sensitivity of multiple
FLT3-ITD cell lines and patient cells to treatment with quizartinib and dexamethasone [
4]. Nevertheless, including data collected from other cell lines, or cells treated with other drugs, such as other
FLT3 inhibitors or glucocorticoids may reveal alternative pathways and processes involved in mediating drug resistance. Finding common resistance mechanisms, as well as system-specific resistance mechanisms, may lead to a more generalizable model. Furthermore, during network construction we removed sink nodes to focus on nodes that contribute feedback into the network dynamics. Nevertheless, those sink nodes may be valuable phenotypic markers, or could be regulators of other nodes we may include in the future. Additionally, the large number of source nodes (65) should eventually be decreased. Many of these became source nodes because BooleaBayes was not able to determine a significant role for their regulators, and so those edges were removed. Additional expression datasets, or literature knowledge, may elucidate functional forms of those interactions. Additionally, more nodes may be added by including more AML-specific literature knowledge (e.g., MCL as downstream target of GSK3B, downstream targets of JUN to further elucidate the dual effect of its inhibition on apoptosis and inflammation).
In
Figure 5 we showed four interventions that had high influence indices, but this did not translate into significant up- or down-regulation of any modules. In at least two cases, we determined that these interventions led to sink nodes, or nodes with weak influence, explaining why the influence index was not predictive of overall impact. To address this, the influence index of a node may be extended to consider the influence index of its downstream targets. Further, nodes can have conflicting downstream effects, and resolving these may improve the predictive value of influence index.
The dynamic model may eventually be used to answer other fundamental questions, such as how does drug treatments lead to the resistant state. To this end, the network could be extended by integrating known drug targets, though in practice drugs often have multiple off-target effects. One possible way to overcome this would be to prioritize adding drug targets that can induce the changes between the status of the source nodes in the untreated and drug-treated conditions. Future work is focused on expanding and improving the network model by incorporating information about drug targets, additional cell lines, and additional drug perturbation datasets. We are also working to validate the model’s novel predictions, such as combining Quiz+Dex treatment with KO of IFNG1 or MAP3K11, or CA of AP2A1.
Finally, we anticipate that data-driven predictive modeling, as demonstrated in this work, may eventually help accelerate patient-specific precision treatments. The dynamics of the AML model emerged from the expression data we used to train it, thus incorporating patient-specific data may help reveal patient-specific drug resistance pathways or targets.